Statistical Power to Detect the Correct Number of Classes in Latent Profile Analysis

Abstract

Little research has examined factors influencing statistical power to detect the correct number of latent classes using latent profile analysis (LPA). This simulation study examined power related to inter-class distance between latent classes given true number of classes, sample size, and number of indicators. Seven model selection methods were evaluated. None had adequate power to select the correct number of classes with a small (Cohen’s d = .2) or medium (d = .5) degree of separation. With a very large degree of separation (d = 1.5), the Lo-Mendell-Rubin test (LMR), adjusted LMR, bootstrap likelihood-ratio test, BIC, and sample-size adjusted BIC were good at selecting the correct number of classes. However, with a large degree of separation (d = .8), power depended on number of indicators and sample size. The AIC and entropy poorly selected the correct number of classes, regardless of degree of separation, number of indicators, or sample size.

Latent class models (Vermunt & Magidson, 2002; Muthén & Muthén, 1998–2010), often referred to as mixture models, are statistical tools for building typologies based on observed variables. The technique is helpful for researchers who seek to identify subgroups (i.e., latent classes) within large, heterogeneous populations. Latent class models were originally designed to be used with dichotomous observed variables or indicators (Lazarsfeld, 1950; Lazarsfeld & Henry, 1968), but were later extended to models with continuous (Gibson, 1959; Lazarsfeld & Henry, 1968), polytomous (Goodman, 1974a, 1974b; Haberman, 1979), and ordinal, rank, count and mixed scale (Muthén & Muthén, 1998–2010; Vermunt & Magidson, 2000) variables. Latent class models involving continuous indicators are also termed latent profile models (Gibson, 1959; Lazarsfeld and Henry, 1968) which will be the focus of this study.

Latent profile analyses (LPA) have been increasingly utilized in many different fields in recent years (e.g., criminology, education, marketing, psychology, psychiatry, sociology). However, statistical power and sample size requirements are under-studied in LPA. A better understanding of sample characteristics and requirements in studies that employ LPA is critical in order to design studies with sufficient power to detect the underlying latent classes. In addition, it is important to be able to demonstrate sufficient statistical power to detect latent classes for secondary data analysis of previously collected data. If a study is under-powered, the selection of too few or too many latent classes is likely. The purpose of this article is to examine how the distance between latent classes, as well as various sample characteristics, affect statistical power to detect the correct number of latent classes. The ultimate goal is to offer guidelines for researchers to determine the sample characteristics necessary to conduct LPA.

Latent profile analysis is a probabilistic or model-based technique that is a variant of the traditional cluster analysis. Simulation studies have shown that probability-based mixture modeling is superior to traditional cluster analyses in detecting latent taxonomy (Cleland, Rothschild, & Haslam, 2000; McLachlan & Peel, 2000). In model-based clustering, a statistical model is assumed for the population from which the sample under study is drawn (Vermunt & Magidson, 2002). Specifically, the observed sample is a mixture of individuals from different latent classes; individuals belonging to the same class are similar to one another such that their observed scores on a set of indicators are assumed to come from the same probability distributions (Vermunt & Magidson, 2002). Assuming that the continuous indicators are normally distributed within each latent class, the latent profile model represents the distributions of the observed scores on a set of indicators, x_i (i = 1, …, n), as a function of the probability of being a member of latent class k (π_k; k = 1, 2, …, k) and the class-specific normal density f_k(x_i|θ_k) as follows:

$$f(x_i\mid \theta )=\sum _1^k{\pi }_k{f}_k(x_i\mid {\theta }_k)$$ (1)

Note that π_k is the probability of belonging to latent class k (where the values of π_k sum to 1 across the k classes) and f_k is a class-specific normal density function (with class specific mean vector and covariance matrix θ_k = (μ_k, Σ_k). A mean and a set of variances/covariances are estimated for each latent class.

In practice, LPA is used to identify a set of discrete, exhaustive, and non-overlapping latent classes of individuals based on individual responses to a set of indicators. Latent class analysis generally makes the assumption of “local independence” or “conditional independence”. That is, after accounting for the latent class membership, the values of the indicators within each latent class are independent. This assumption is similar to the “uncorrelated uniqueness” assumption made in factor analysis. As in factor analysis, conditional independence for LPA can be relaxed when some indicators within a class remain correlated even after accounting for class membership. The constraint of local independence is useful for statistical reasons because it minimizes the number of parameters to be estimated (Vermunt & Magidson, 2002). In general, as the number of indicators and/or the number of latent classes increase, the number of parameters to be estimated increases rapidly; in particular, the number of free parameters associated with variances and covariances increases. To obtain more parsimonious and stable models, researchers often assume that Σ_k (the class-specific covariance matrix) is a diagonal matrix (i.e., all within-cluster covariances are equal to zero) and also impose a constraint of homogeneity of variances across latent classes (i.e., Σ_k = Σ). The result of these constraints is that all of the latent classes have the same form of distribution, differing only in their means. In this study, we used only models in which the local independence and homogeneity of variance assumptions hold.

The large amount of research devoted to analytical techniques and software design (e.g., Latent Gold – Vermunt & Magidson, 2005; Mplus – Muthén & Muthén, 1998–2010) has led to applications of latent class modeling in many disciplines. One of the most important tasks in using latent class modeling is correctly identifying the number of underlying latent classes and correctly placing individuals into their respective classes with a high degree of confidence. Properly selecting the correct number of latent classes is critical because the number of classes selected can have a strong impact on substantive interpretations of the modeling results. However, statistical power in latent class analyses is understudied; only a handful of studies have examined power or the effect of sample size on selecting the correct number of latent classes (see Nylund et al., 2007; Tofighi & Enders, 2006; Yang, 2006).

In studies of statistical power for LPA models, the effect of degree of separation (distance) between classes on power is generally ignored. Class separation, analogous to a measure of the effect size in multivariate analyses, is a crucial element in determining power. Indicators should have a certain degree of distance between latent classes. Meehl and Yonce (1996) refer to an indicator with good separation as a variable with good “taxon validity”. We have found only a handful of studies that examined the effect of class separation on latent class analyses. Lubke and colleagues (Lubke & Muthén, 2007; Lubke & Neale, 2006) investigated the relation between class separation and model performance. They used a factor mixture model framework (i.e., whether a common factor model holds within each latent class) to assess model selection. Their focus was primarily on correct model choice with respect to the correct latent class structure and within-class factor structure, but not on statistical power to detect the correct number of classes per se. Meehl and Yonce (1996) examined the effects of separation on detecting latent classes. However, their work focused only on very large class separation (e.g., 1.5 or 2 SD separation between latent classes for each indicator) using only four observed variables. All of these studies emphasize the importance of class separation in selecting the correct model, but none of them assess the extent to which separation can affect the statistical power to detect the correct number of classes.

In this study we conducted a simulation study to examine how class separation in conjunction with sample size, number of classes, and number of indicators relates to statistical power. In the next section, we review the seven selection methods used to determine the number of classes, define the meaning of statistical power for selecting the models under these different selection techniques, and define the distance between latent classes.

Model Selection

Statistical power to detect the correct number of latent classes in a latent class or latent profile model depends heavily on the selection method or criterion used to determine the number of classes. Selecting the number of classes typically involves estimating models with incremental numbers of latent classes (e.g., 2, 3 and 4 latent classes) and choosing the number of classes based upon which model provides the best fit to the observed data. Despite informed suggestions and simulation studies (e.g., Jedidi, Jagpal, & DeSarbo,1997; Nylund et al., 2007; Tofighi & Enders, 2006; Yang, 2006), there is no common standard for the best fit criteria and researchers typically use a combination of fit criteria in determining the number of latent classes. Most of the common methods for deciding on the number of classes fall into three categories: information-theoretic methods, likelihood ratio statistical test methods, and entropy-based criterion.

Akaike’s Information Criterion (AIC; Akaike, 1973, 1987) and Bayesian Information Criterion (BIC; Schwarz, 1978) are the two original and most commonly used information-theoretic methods for model selections. The AIC and BIC are based on the maximum likelihood estimates of the model parameters for selecting the most parsimonious and correct model. The AIC is calculated as

$$-2\text{LL}+2m$$ (2)

and the BIC is calculated as

$$-2\text{LL}+m\ast ln(n)$$ (3)

where −2LL is −2 times the log-likelihood of the estimated model, m is the number of estimated parameters and n is the number of observations. The last term in each expression is referred to as a “penalty” component. The penalty component serves to discourage overfitting of a model (i.e., increasing the number of estimated parameters solely to improve model fit). Many other information criteria have been derived from these two ICs by adjusting the penalty term. For example, the sample-size adjusted BIC (SABIC, Sclove, 1987) replaces sample size (n) in Equation 2 with n* ((n +2)/24). The information-theoretic methods generally favor models that produce a high log-likelihood value using relatively few parameters and are scaled such that a lower value represents a better fit.

The second category of methods for evaluating model fit in latent class models involves likelihood ratio (LR) statistic tests. These tests compare the relative fit of two models that differ by a set of parameter restrictions. This means, for example, comparing a nested 2-class solution to a 3-class solution. However, comparisons of latent class models do not meet certain regularity assumptions for a traditional LR difference test with a chi-squared distribution (Aitkin & Rubin, 1985). The Lo-Mendell-Rubin likelihood ratio test (LMR; also known as Vong-Lo-Mendell-Rubin test) and the ad hoc adjusted LMR (Lo, Mendell, & Rubin, 2001) were derived to use the adjusted asymptotic distribution of the likelihood ratio statistics to compare a K₀-class normal mixture distribution model against an alternative K ₋₁-class normal mixture distribution model (where K ₋₁ < K₀). Another test in this category is the bootstrap likelihood ratio test (BLRT) derived by McCutcheon (1987) and McLachlan and Peel (2000). The BLRT uses a bootstrap resampling method to approximate the p-value of the generalized likelihood ratio test comparing the K₀-class mixture model with the K ₋₁-class mixture model. For LMR, adjusted LMR, and BLRT, a small probability value (e.g., p < .05) indicates that the K₀-class model provides significantly better fit to the observed data than the K ₋₁-class model.

The final category of the fit tests used to assess latent class models is the measure of entropy. The entropy index is based on the uncertainty of classification (see Celeux & Soromenho, 1996). Essentially classification uncertainty is assessed at the individual level by the posterior probability; entropy then is a measure of aggregated classification uncertainty. The uncertainty of classification is high when the posterior probabilities are very similar across classes. The normalized version of entropy, which scales to the interval [0, 1], is commonly used as a model selection criteria indicating the level of separation between classes. A higher value of normalized entropy represents a better fit; values > 0.80 indicate that the latent classes are highly discriminating (Muthén & Muthén, 2007).

There are other selection methods beyond those mentioned above, but these methods are the most commonly used fit indices for determining model fit and selecting the number of classes in latent class models. In addition, these methods are readily available in software programs, including the Mplus software used in this study. We used these methods as criteria for selecting the best fitting models.

Statistical Power to Detect the Correct Model

For a true K₀-class model, the model selection criteria may wrongfully direct the choice to a model with one less class (K ₋₁-class model) or a model with one more class (K₊₁-class model). In general, statistical power for a method is defined as the probability that the method will reject a false null hypothesis. However, the null model is not clearly defined for these methods. For example, in comparing the 2, 3, and 4 class solutions when the true solution is 3 classes, two LMR tests are conducted. One LMR test compares the 3-class solution to the 2-class solution and one compares the 4-class solution to the 3-class solution. In the former case, the K ₋₁-class model is the null model and the correct solution is to reject the null model. In the latter, the K₀-class model is the null model and the correct solution is to not reject the null model. Therefore, in this study, we define power for the likelihood ratio tests (LMR, adjusted LMR, and BLRT) as the probability of selecting the true model from which the sample is drawn. Specifically, since a significant test result (e.g., p ≤ .05) indicates that the model with more classes is the preferred solution, we select the K₊₁-class model if both “K₀ test”(i.e., the K₀-class model provides a better solution than the K ₋₁-class model) and “K₊₁ test” (i.e., the K₊₁-class model provides a better solution than the K₀-class model) are significant, we select the K₀-class model if the “K₀ test” is significant and the “K₊₁ test” is non-significant. Likewise, we select the K ₋₁-class model if both “K₀ test” and “K₊₁ test” are non-significant. The proportion of replications in which the K₀-class solution is chosen is defined as the power for these techniques. For the information criteria (AIC, BIC, SABIC) and the entropy measures, we fit the K ₋₁-class solution, the K₀-class solution, and the K₊₁-class solution and compare the estimated information criterion (IC) and the entropy values. The solution with the lowest IC or highest entropy value is the selected solution. As with the likelihood ratio statistic tests, statistical power for the IC and the entropy measure is the proportion of replications in which the K₀-class model is selected. We recognize that with each of the selection techniques, there is a possibility that the best fitting model is beyond the K ₋₁-class solution or the K₊₁-class solution, but it should not affect the probability of selecting the K₀-class solution as the best fitting model. Conditions in which the K₀-class solution was selected in at least 80% of the replications were considered to have adequate statistical power.

Measure of Distance between Classes

Mahalanobis distance (D) is commonly used to define the distance between latent classes. Mahalanobis D measures the dissimilarity between two random vectors, X (x₁, x₂, …x_j) and Y (y₁, y₂, …y_j), that have the same distribution and covariance matrix S. Mahalanobis D between two vectors is defined as

$$D(x,y)=\sqrt{\sum _1^j{(x_j-y_j)}^{\prime }{S}^{-1}(x_j-y_j)}$$ (4)

where j is the number of elements or variables. To simplify the conditions in this study, in addition to local independence and homogeneity of variance across latent classes, we assumed that the covariance matrix is the identity matrix (i.e., x_j and y_j have variances of 1). Under unit variance, the Maholonobis D simplifies to the Euclidean distance:

$$E(x,y)=\sqrt{\sum _1^j{(x_j-y_j)}^2}$$ (5)

Cohen’s d (Cohen, 1988) is a commonly used effect size measure of the univariate mean difference between two groups, reflecting the difference between the means divided by the averaged population standard deviations of the two groups. Mahalanobis D can be viewed as the multivariate expansion of Cohen’s d and as a multivariate effect size (McLachlan, 1999).

In our study, all indicators within the same class have the same population mean with variance equal to one. The magnitude of distance between latent classes in the population is guided by the conventions of Cohen’s d, such that the difference in the means of the indicators across adjacent classes is defined by Cohen’s d. We examined distances of .2, .5, and .8, defined by Cohen (1988) as small, medium, and large effects, on each indicator across adjacent latent classes. In addition, we included a Cohen’s d of 1.5 for a very large effect. In their work applying the MAXCOV procedure (a taxometric analysis procedure) to detect latent classes, Meehl and Yonce (1996) advocated that good separation occurs when Cohen’s d is at least 1.25.

The equations for Mahalanobis D and Euclidean distance show that class separation is affected not only by the distance between the indicators but also by the number of indicators. For example, keeping (x_j – y_j)constant, the Euclidian distance in Eq. 5 is a function of $\sqrt{j}$. We included models with 6, 10, or 15 indicators to examine the interplay of distance between classes and number of indicators in determining statistical power. In our study, the population Mahalanobis Ds for each adjacent pair of latent classes ranged from .49 to 3.67 for the 6-indicator model, .63 to 4.74 for the 10-item model, and .77 to 5.81 for the 15-item model.

In summary, we expect that larger class separation and more indicators will result in better statistical power to detect the correct number of classes. However, it is not clear how large the distance between classes has to be in order to detect the correct number of classes under conditions with different sample sizes, different numbers of true classes, and different numbers of indicators. This power analysis simulation study explores these issues.

Literature Review

Given the popularity of latent class analyses in recent years, we conducted a literature review of studies that utilized latent profile analysis to get a sense of the range of distances between latent classes as well as their sample characteristics. Sample size, number of latent classes, and type of method for selecting the number of latent classes for these studies were also reviewed. The review provided an indication of how latent profile analyses were utilized empirically. A search of the PsychINFO database between January 2007 and March 2010 using the keywords “latent profile analysis” was conducted. A total of 32 peer-reviewed articles and 6 dissertations were identified, spanning the areas of education, psychology, law, and social work. Among the 38 articles, the median total sample size was 377 (Range = 79 – 5183), the median number of latent classes was 3 (Range = 2 – 6), the median number of observations in each latent class was 88 (Range = 7 – 3044), and the median number of observed variables was 9 (Range = 3 –30). Most of the studies used multiple fit indices to evaluate model fit and model selection, including BIC (35 [studies]), Entropy (20), AIC (15), LMR (15), SABIC (11), adjusted LMR (11), χ² statistics (10), and BLRT (6). Almost all of the studies included BIC as a criterion for model selection. Entropy was the second most frequently used selection method.

Of the 38 studies, 16 (42%) reported either the estimated means and variances/covariances of the indicators for each latent class or the posterior MANOVA estimated means and variances/covariances of the indicators after assigning participants to one particular latent class. We used these values to calculate the pairwise Cohen’s d for each indicator and the estimated Mahalanobis D across latent classes using Equation 4. Ten of the sixteen studies (62.5%) had Cohen’s d in the .8 to 1.25 range, corresponding to Mahalanobis D between 2.69 to 4.34. None of the studies had Cohen’s d below .8, while three studies had Cohen’s d larger than 1.5.

Method

We used a Monte Carlo simulation to evaluate statistical power to detect the correct number of latent classes. We included the following factors that can affect the ability to detect the correct number of classes: 1) true number of classes, 2) sample size, 3) total number of indicators for class membership, and 4) distance or separation between classes. All data were generated in SAS 9.2 and analyzed in Mplus 5 (Muthén & Muthén, 1998–2010). The true number of classes in the population was either three or five. We evaluated sample sizes of 250, 500, and 1000. Class membership was identified by 6, 10, or 15 indicators. As previously described, the separation or distance between classes was calculated as the standardized distance between the mean values of the indicators (i.e., Cohen’s d). The distance between indicators across the adjacent classes was .2, .5, .8, or 1.5, representing small, medium, large, and very large distances corresponding to effect sizes (Cohen, 1988). In the rest of the article, we refer to the distance as inter-class distance or Cohen’s d. The four manipulated factors were varied in a fully factorial design, resulting in 3 × 2 × 3 × 4 = 72 conditions. For each condition, 500 replications were conducted.

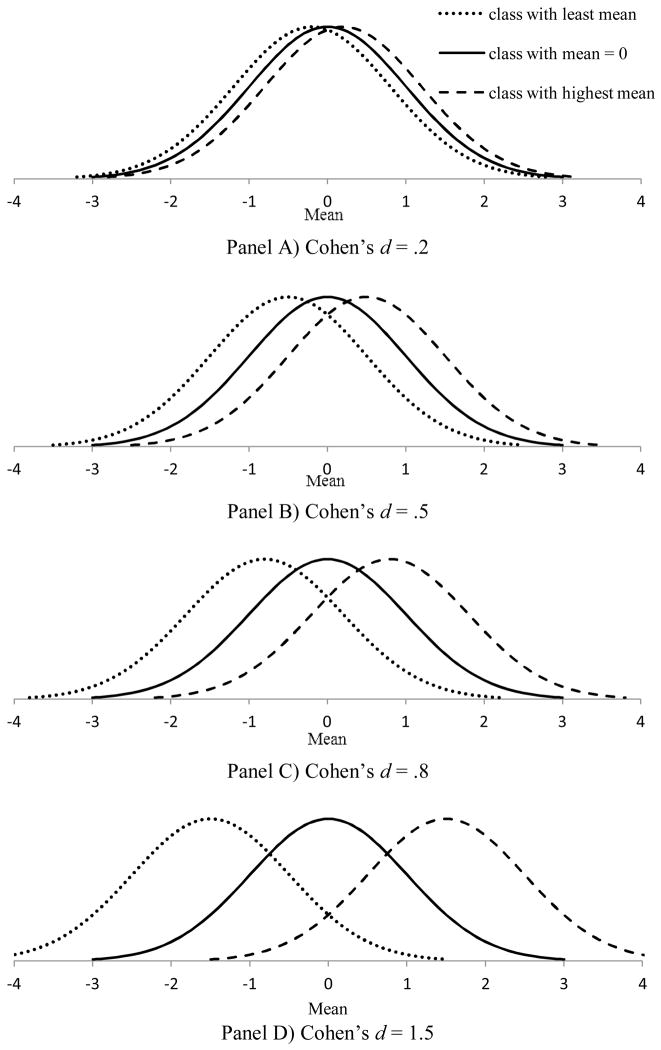
For each replication, individual cases were assigned to classes in roughly equal numbers. For example, for a sample size of 1,000 and 3 classes, 333, 333, and 334 cases were assigned to Classes 1, 2, and 3 respectively. Observed values for each of the 6, 10, or 15 indicators were generated based on the latent class membership, inter-class distance between classes, and random normal error. All indicator variables were equally good indicators of class membership. The indicators for all classes were simulated as normal distributions with a variance of 1, with the mean of the distributions determined by the class membership and the specified inter-class distance between the classes. For example, for a 3-class model with 6 indicators and an inter-class distance between classes of .5, the individual cases have values on all 6 indicators that are drawn from a standard normal distribution with a mean of −.5 in Class 1, with a mean of 0 in Class 2, and with a mean of .5 in Class 3. Each indicator was generated separately. Figure 1 illustrates the normal distributions for the 3-class models with the four values of inter-class distance.

Figure 1.

Normal Distributions for the 3-class Models with the Four Values of Inter-class Distance

All data were analyzed in Mplus 5 using the Monte Carlo feature to allow us to easily save the fit indices of each replication from each selection method. Latent class analyses under mixture modeling were used. For each dataset, we conducted the analyses with the specified number of latent classes in the mixture models being either the correct number of classes from the population (i.e., K₀ = 3 or 5), one class less than in the population (i.e., K ₋₁ = 2 or 4), or one class more than in the population (i.e., K₊₁ = 4 or 6). To avoid local maximum solutions, all models used 100 sets of random starting values and 10 final stage optimizations. For the likelihood-ratio bootstrap tests, which were time-intensive procedures, we used 100 bootstrap samples, each with two sets of random starting values and one final stage optimization for the null model (model with one less class) as well as 50 sets of random starting values and 15 final stage optimizations for the alternative model (see Muthén & Muthén, 1998–2010). Seven model selection techniques were used to evaluate statistical power to detect the correct model and number of classes: AIC, BIC, sample-size adjusted BIC (SABIC), entropy, LMR, adjusted LMR, and bootstrap LRT (BLRT).

Results

Defining model convergence as a model that has no error messages and no negative variances or standard errors, almost all of the replications converged. Only two datasets did not converge and both were from the condition with a small inter-class distance (Cohen’s d = 0.2) which were from a true 5-class model in the population. The results for the three types of selection methods are presented separately in the following. The results under the true 3-class model and the true 5-class model were in general consistent. In this paper, we present the results of both the true 3-class and the true 5-class model, but the complete findings in table format are shown only for the true 5-class model. Please refer to the first author’s website (http://prc.asu.edu/Tein_Power_LPA) for the complete findings.

Information-theoretic Methods

Table 1 shows the probabilities of selecting the K ₋₁-class, the K₀-class, and the K₊₁-class solutions, respectively, for the three information criterion measures (AIC, BIC, and SABIC) under the true 5-class model. Recall that we defined statistical power as the proportion of replications in which the K₀-class solution had the lowest information criteria (IC), comparing to the K ₋₁-class and K₊₁-class solutions. Statistical power for the AIC was extremely low, ranging from .2 to .5, regardless of the number of true latent classes, sample size, inter-class distance, or number of indicators. In fact, having a bigger sample size, larger number of indicators, or larger inter-class distance did not result in better power. The AIC showed a preference toward selecting the K ₋₁-class solution for the conditions with small inter-class distances and fewer indicators, but a preference toward selecting the K₊₁-class solution for the conditions with large inter-class distances and more indicators.

Table 1.

K ₋₁-class, K₀-class, and K₊₁-class solutions under true 5-class model for information-theoretic methods

Solution		(K −1-class) 4-class Solution									(K0-class) 5-class Solution									(K +1-class) 6-class Solution
Items		6-Item			10-Item			15-Item			6-Item			10-Item			15-Item			6-Item			10-Item			15-Item
d	n	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000
.2	AIC	.59	.70	.68	.65	.63	.70	.65	.66	.63	.21	.14	.16	.19	.19	.15	.19	.21	.21	.19	.15	.15	.15	.17	.14	.15	.12	.15
	BIC	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	SA BIC	.89	.99	.99	.93	1	1	.96	1	1	.06	.01	.01	.06	0	0	.04	0	0	.05	0	0	.01	0	0	.01	0	0
.5	AIC	.59	.62	.59	.48	.44	.30	.36	.21	.16	.21	.21	.22	.26	.25	.34	.31	.33	.38	.19	.16	.18	.25	.30	.35	.32	.44	.45
	BIC	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	SA BIC	.84	.98	1	.87	.99	.99	.83	.99	1	.10	.01	0	.10	.02	.02	.13	.01	0	.05	.01	0	.03	0	0	.04	0	0
.8	AIC	.36	.33	.29	.14	.03	.00	0	0	0	.31	.31	.30	.28	.26	.23	.31	.27	.25	.31	.35	.39	.57	.70	.76	.68	.72	.74
	BIC	1	1	1	1	1	.91	.99	.40	0	0	0	0	0	0	.09	.01	.60	1	0	0	0	0	0	0	0	0	0
	SA BIC	.67	.91	.96	.42	.54	.13	.03	0	0	.25	.08	.04	.38	.43	.86	.71	.99	1	.08	.00	0	.19	.02	0	.25	.01	0
1.5	AIC	0	0	0	0	0	0	0	0	0	.30	.34	.28	.29	.27	.22	.30	.29	.23	.69	.65	.72	.70	.72	.78	.69	.70	.76
	BIC	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0
	SA BIC	0	0	0	0	0	0	0	0	0	.59	.91	.98	.70	.96	.99	.78	.99	1	.41	.08	.02	.30	.04	.00	.22	.00	0

Note: The values were truncated to two decimal points.

Statistical power for BIC and SABIC were consistent with a few exceptions. Statistical power for the BIC was ≥ .80 for conditions with Cohen’s d = 1.5 and some conditions with Cohen’s d = .8, particularly with 10 or more indicators and sample sizes of 500 or more for the true 3-class model and with 15 indicators and sample sizes of 1,000 for the true 5-class model. Power was essentially zero when Cohen’s d = .2 or .5. When the correct K₀-class solution was not selected, the BIC would always select the K ₋₁-class solution, regardless of the number of true latent classes, sample size, inter-class distance, or number of indicators. Statistical power for the SABIC was also ≥ .80 for nearly all conditions with Cohen’s d = 1.5 unless the sample size was 250. Compared to BIC, SABIC had power ≥ .80 for a few more conditions with Cohen’s d = .8. Unlike the BIC, the SABIC would select both the K ₋₁-class and the K₊₁-class solutions when the correct K₀-class solution was not selected, especially when sample size = 250. Power for the BIC as well as SABIC increased with the number of indicators, sample size, and effect size for conditions with Cohen’s d ≥ .8 but not Cohen’s d = .2 or .5.

Likelihood Ratio (LR) Statistical Tests

Table 2 shows the probabilities of selecting the K ₋₁-class, the K₀-class, and the K₊₁-class solutions, respectively, for the three likelihood ratio statistical tests (LMR, adjust LMR, and BLRT) under the true 5-class model. The statistical power rates were almost identical across the LMR test and the adjusted LMR test. As with the BIC and SABIC measures, the two LMR tests showed higher statistical power for larger sample size and more indicators for conditions with Cohen’s d ≥ .8 but not Cohen’s d = .2 or .5. The statistical power was ≥ .8 for the conditions with Cohen’s d = 1.5 and some of the conditions with Cohen’s d = .8, especially with larger sample sizes and more indicators. In conditions in which the incorrect model was selected, LMR and adjusted LMR tests almost always resulted in the K ₋₁-class solution with the following exception; when Cohen’s d = 1.5, the two LMR tests selected the K₊₁-class solution when the K₀-class solution was not selected.

Table 2.

K ₋₁-class, K₀-class, and K₊₁-class solutions under true 5-class model for likelihood ratio statistical test methods

Solution		(K −1-class) 4-class Solution									(K0-class) 5-class Solution									(K +1-class) 6-class Solution
Items		6-Item			10-Item			15-Item			6-Item			10-Item			15-Item			6-Item			10-Item			15-Item
d	n	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000
.2	LMR	.93	.93	.93	.96	.96	.95	.97	.98	.97	.02	.03	.03	.02	.02	.02	.00	.00	.01	.04	.03	.02	.01	.01	.02	.01	.00	.01
	Adjust LMR	.93	.93	.94	.96	.96	.95	.97	.98	.97	.02	.03	.03	.02	.02	.02	.00	.00	.01	.04	.03	.02	.01	.01	.02	.01	.00	.01
	BLRT	1	1	1	1	.99	1	1	.99	1	0	0	0	0	0	0	0	.00	0	0	0	0	0	.00	0	0	0	0
.5	LMR	.93	.91	.93	.96	.96	.96	.98	.98	.99	.03	.05	.02	.01	.02	.02	.01	.01	.00	.02	.03	.04	.02	.01	.01	.00	.00	.00
	Adjust LMR	.94	.91	.93	.96	.96	.96	.98	.98	.99	.02	.05	.02	.01	.02	.02	.01	.01	.00	.02	.03	.04	.02	.01	.01	.00	.00	.00
	BLRT	1	.99	.99	.98	.99	.97	.98	.97	.92	0	.00	.00	.01	.00	.02	.01	.02	.08	0	.00	.00	0	0	.00	0	.00	0
.8	LMR	.89	.08	.87	.96	.84	.25	.87	.09	.00	.06	.08	.07	.02	.13	.71	.11	.90	.99	.03	.06	.04	.01	.02	.03	.01	.00	.00
	Adjust LMR	.90	.85	.88	.96	.85	.25	.87	.09	.00	.06	.08	.06	.02	.12	.71	.11	.90	.99	.03	.06	.04	.01	.02	.03	.01	.00	.00
	BLRT	.95	.94	.91	.79	.48	.03	.09	.00	.00	.03	.04	.08	.19	.48	.91	.86	.93	.96	.01	.00	.00	.01	.02	.05	.04	.06	.03
1.5	LMR	.00	.00	.00	.00	.00	.00	.01	.00	.00	.85	.86	.86	.92	.92	.94	.94	.95	.98	.14	.14	.13	.07	.07	.05	.04	.04	.01
	Adjust LMR	.00	.00	.00	.00	.00	.00	.01	.00	.00	.86	.87	.86	.92	.92	.94	.94	.95	.98	.12	.12	.13	.07	.07	.05	.04	.04	.01
	BLRT	.00	.00	.00	.00	.00	.00	.00	.00	.00	.92	.94	.92	.94	.94	.94	.92	.93	.94	.07	.05	.07	.05	.05	.05	.07	.06	.05

Note: The values were truncated to two decimal points.

The bootstrap LR test showed higher statistical power rates than the two LMR tests when Cohen’s d ≥ .8. The BLRT had adequate power in several conditions for which the LMR and adjusted LMR did not under Cohen’s d = .8. The patterns of power for the BLRT and SABIC were more similar to one another than to their respective group, except that the BLRT had better power than SABIC on the conditions with sample size = 250 and Cohen’s d = 1.5.

Entropy

The probabilities of selecting the K ₋₁-class, K₀-class, or K₊₁-class solutions for the entropy measure under the true 5-class model are presented in Table 3. Power was consistent between the true 3-class model and the true 5-class model. However, examination of the entropy values revealed that the solutions for the true 5-class model produced larger entropies than those for the true 3-class model in nearly every condition, regardless of the number of classes in the tested model (i.e., K ₋₁-class, K₀-class, or K₊₁-class). The patterns of findings for entropy were rather mixed. The power for the entropy measure to select the K₀-class solution was only adequate (i.e., ≥ .8) or marginal (i.e., ≥ .7) for the conditions where Cohen’s d = 1.5 and the number of indicators ≥ 10. For the conditions with Cohen’s d = .8, entropy had a high probability of selecting the K ₋₁-class solution over the K₀-class or the K₊₁-class solution. Entropy showed a preference toward the K₊₁-class solution for low inter-class distances.

Table 3.

K ₋₁-class, K₀-class, and K₊₁-class solutions under true 5-class model for entropy-based criterion

Solution		(K −1-class) 4-class Solution									(K0-class) 5-class Solution									(K +1-class) 6-class Solution
Items		6-Item			10-Item			15-Item			6-Item			10-Item			15-Item			6-Item			10-Item			15-Item
d	n	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000	250	500	1000
.2	En.	.15	.23	.25	.16	.23	.26	.17	.25	.24	.23	.26	.29	.25	.25	.29	.22	.27	.31	.61	.49	.45	.58	.50	.44	.60	.46	.38
.5	En.	.18	.30	.34	.31	.32	.32	.28	.18	.24	.27	.26	.30	.24	.27	.28	.23	.31	.30	.54	.42	.35	.44	.40	.39	.47	.50	.44
.8	En.	.24	.35	.47	.59	.90	.99	.94	.99	.99	.28	.32	.28	.24	.07	.00	.01	0	0	.47	.32	.24	.16	.02	0	.04	.00	.00
1.5	En.	.44	.25	.11	.01	0	0	.00	0	0	.27	.44	.56	.73	.75	.76	.83	.87	.90	.28	.30	.32	.25	.24	.23	.15	.12	.09

Note: ‘En.’ for entropy. The values were truncated to two decimal points.

Note that statistical power values were based on choosing the model with the largest entropy among the K ₋₁-class, K₀-class, and K₊₁-class solutions. This did not take into account the actual value of entropy, such as whether the entropy value was in the acceptable range (i.e., > .80). Table 4 shows the average entropy across sample size, inter-class distance, number of indicators for the true 5-class model. Four distinct features emerged. First, the entropy values increased as the inter-class distance widened. However, only when Cohen’s d = 1.5 and some Cohen’s d = .8 were acceptable entropy values observed. Second, the entropy values were very similar among the K ₋₁-class, K₀-class, and K₊₁-class solutions under each condition. Almost all of the differences were at or beyond the second decimal point. Third, with few exceptions (e.g., under the true 3-class model and Cohen’s d =.2), entropy values increased as the number of indicators increased. Finally, contrary to convention, when keeping the other conditions constant, entropy was negatively related to sample size; the average entropy for the sample with n = 250 was larger than the average entropy for the sample with n = 1,000 for any of the K ₋₁-class, K₀-class, and K₊₁-class solutions.

Table 4.

Average Entropy for conditions across sample size, number of items, Cohen’s d, and number of true classes under true 5-class model

		Entropy under True 5-class Model
Items		6-Item			10-Item			15-Item
n		250	500	1000	250	500	1000	250	500	1000
d	Solutions
0.2	4 (K −1-class)	0.63	0.56	0.51	0.66	0.60	0.57	0.70	0.65	0.62
	5 (K0-class)	0.65	0.58	0.52	0.68	0.61	0.57	0.72	0.66	0.62
	6 (K+1-class)	0.67	0.59	0.53	0.70	0.62	0.58	0.74	0.67	0.62
0.5	4 (K −1-class)	0.70	0.66	0.63	0.77	0.73	0.68	0.81	0.76	0.73
	5 (K0-class)	0.71	0.66	0.63	0.77	0.73	0.68	0.81	0.76	0.73
	6 (K+1-class)	0.72	0.66	0.63	0.78	0.72	0.68	0.82	0.77	0.73
0.8	4 (K −1-class)	0.77	0.74	0.72	0.84	0.83	0.82	0.90	0.89	0.88
	5 (K0-class)	0.77	0.74	0.71	0.83	0.79	0.76	0.87	0.86	0.85
	6 (K+1-class)	0.78	0.73	0.71	0.83	0.79	0.77	0.88	0.86	0.85
1.5	4 (K −1-class)	0.92	0.91	0.91	0.96	0.95	0.95	0.98	0.98	0.97
	5 (K0-class)	0.92	0.91	0.91	0.97	0.97	0.97	0.99	0.99	0.99
	6 (K+1-class)	0.91	0.90	0.90	0.96	0.96	0.96	0.98	0.98	0.97

Conclusion and Discussion

This simulation study examined statistical power for latent profile analysis, specifically how statistical power relates to the inter-class distance between latent classes given the sample characteristics of true number of latent classes, sample size, and number of indicators. The statistical power of seven popular selection methods (AIC, BIC, sample-size adjusted BIC, entropy, LMR, adjusted LMR, and bootstrap LRT) were assessed. The results consistently showed that distance between latent classes played a major role in determining power, much more than other sample characteristics. We will discuss in a general fashion how inter-class distances affect statistical power in the context of the number of true classes, sample size, and number of indicators. We also briefly offer general guidelines regarding inter-class distance, sample size, and number of indicators for conducting latent profile analysis.

Number of True Classes

We simulated data under the true 3-class model and the true 5-class model. The AIC showed higher statistical power for the true 3-class model than the true 5-class model for 29 out of 36 conditions; however, in no condition did the power exceed .5. The patterns of findings and the statistical power for LMR, adjusted LMR, BLRT, BIC and SABIC were consistent between the true 3-class model and the true 5-class model with some exceptions under Cohen’s d = .8. Note that in this study, we set the total sample size to be equal across latent classes. This resulted in the 5-class model having smaller cell sizes than the 3-class model; for example, for a sample size of 1000, each class in the 3-class model had 333 or 334 members, while each class in the 5-class model had 200 members. In addition, more parameters are estimated in the 5-class model. Despite the 5-class model having a smaller within-class sample size and estimating more parameters, the results seem to indicate that as long as the inter-class distance is above a certain threshold (e.g., Cohen’s d = 1.5) or under a certain threshold (e.g., Cohen’s d = .5), power was little affected by the number of true classes. Between these thresholds (e.g., when Cohen’s d = .8), the true 3-class model had higher statistical power than the true 5-class model, especially with few indicators or small sample size. Note that the smallest cell size for this study was 50 (i.e., sample size = 250 and number of classes = 5). It is possible that any differences between the true 3-class model solution and the true 5-class model solution might be more noticeable with smaller cell sizes.

Sample Size

The three sample sizes used in this study spanned common sample sizes used in the substantive literature. Surprisingly, the effect of sample size on power was minimal compared to the effect of the other manipulated factors. For LMR, adjusted LMR, BLRT, and BIC, larger sample sizes in general did not result in higher statistical power except when Cohen’s d = .8. Power was consistently close to zero for Cohen’s d ≤ .5 and consistently close to 1 for Cohen’s d =1.5, regardless of sample size. The effect of sample size on the SABIC was similar to the LMR, adjusted LMR, BLRT, BIC except that the SABIC had much lower and sometimes inadequate power for sample size = 250 and Cohen’s d = 1.5. Sample size did not seem to relate to power for AIC and entropy. For the AIC and entropy, conditions with a sample size of 1,000 did not show higher statistical power than the conditions with sample size of 250 or 500, regardless of inter-class distance and number of indicators.

Number of Indicators

As discussed earlier and shown in Equations 4 (Mahalonobis distance) and 5 (Euclidean distance), class separation is affected not only by the distance between the indicators but also by the number of the indicators. Therefore, we expected that more indicators would result in higher statistical power. This expectation was supported by LMR, adjusted LMR, BLRT, BIC and SABIC, in which we observed higher statistical power with more indicators when Cohen’s d ≥ .8. Entropy had increased power with more indicators only for Cohen’s d =1.5. Entropy produced an unusual effect when Cohen’s d =.8; more indicators was associated with decreased statistical power especially for the true 5-class model. The AIC did not show any relationship between number of indicators and statistical power, regardless of sample size and inter-class distance.

Recommendations

Our literature review of 38 recent articles that applied latent profile analyses showed that the BIC was the most commonly used selection method, followed by entropy, AIC, LMR, SABIC, adjusted LMR, and BLRT, in descending order. In previous simulation studies involving mixture models, the SABIC was considered the most accurate information criterion test (Yang, 2006). Tofighi and Enders (2006) also noted the consistency of SABIC as well as LMR and adjusted LMR in model selection. In one of the very few studies that evaluated BLRT, Nylund, Asparouhov, and Muthén (2007) concluded that BLRT outperformed other information-theoretic and likelihood-ratio statistical test methods.

Consistent with previous studies of mixture models, our simulation study showed that the AIC and entropy were not reliable methods for selecting the number of classes. The LMR, adjusted LMR, BLRT, BIC, and SABIC showed varying degrees of accuracy in selecting the model with the correct number of classes. The LMR, adjusted LMR, and BIC produced similar statistical power rates. Consistent with the findings of Nylund et al. (2007), our study showed that the BLRT often outperformed the LMR, adjusted LMR, and BIC, especially for conditions in which Cohen’s d = .8. Except for the smallest sample size (n = 250), the SABIC provided comparable power to BLRT for most conditions., The SABIC had lower power and underperformed compared even to the BIC, LMR, adjusted LMR under the condition of sample size = 250 and Cohen’s d = 1.5. Among these measures, there was no single method that always produced the largest statistical power. The performance of each of these methods also depended on number of indicators and sample size, even with a large or very large inter-class distance.

Our simulations show that there is little power to detect the correct number of classes for small (d = .2) or even medium (d = .5) inter-class distances, under any conditions or with any selection methods. BIC, LMR, adjusted LMR, and BLRT were more inclined to select a model with fewer classes than were actually present. As discussed earlier, for our simulated data, the best fitting model might be beyond the K ₋₁-class solution or K₊₁-class solution. This was indeed the situation for the LMR and adjusted LMR measures. The probability of the LMR and adjusted LMR tests selecting the K ₋₁-class solution over the K ₋₂-class solution ranged from .002 to .058 for the true 3-class model and .004 to .598 for the true 5-class model. That is, in the majority of cases, the LMR and adjusted LMR tests preferred a model with 2 fewer classes than were actually present. This conclusion might also apply to BIC, SABIC, and BLRT, however, it is beyond the scope of this simulation.

Meehl and Yonce (1996) suggested that valid indicators for taxometric analyses should have a mean separation of Cohen’s d of 1.25 and above. Our study shows that LPA can be done for Cohen’s d of .8, provided the sample size is at least 500 and there are at least 10 indicators of class membership. For the 16 studies in our literature review in which we were able to obtain Cohen’s d, the average Cohen’s d was greater than .8, with the majority in the .8 to 1.25 range. Our review uncovered no studies in which Cohen’s d < .8. It may be the case that studies with smaller Cohen’s d were never completed and published due to poor results in latent classification. In most LPA studies, the researchers would not know the inter-class distances before the analysis and would be forced to calculate inter-class distances in a post-hoc fashion. If most of the indicators have inter-class distance of Cohen’s d <.8, it would be difficult to detect the correct number of classes and a researcher should not be confident that the number of classes extracted in their LPA reflects the true number of classes in the population.

Limitations

More indicators resulted in better statistical power for conditions in which Cohen’s d =1.5 or Cohen’s d =.8, using LMR, adjusted LMR, BLRT, BIC, and SABIC. However, as the number of indicators increases, the number of parameters to be estimated also increases. Measures of model fit in the latent variable modeling framework, number of free parameters in the model, and sample size are closely linked factors (MacCallum, Browne, & Sugawara, 1996). It is likely that there is a balance between sample size, number of indicators, number of free parameters, and interclass distance. Though we show fairly consistent monotonic effects of the number of indicator variables on power, it is unknown whether there is a point at which this monotonic effect starts breaking down.

In this study, we generated the indicators such that all indicators in the same class have the same mean and variance; that is, the inter-class distance was the same for each indicator between latent classes. What this means is that all indicators distinguish between classes equally well. In real world situations, the indicators are not likely to be so uniform in nature. Some indicators will be very good at distinguishing between classes and others will not - the means, variances, and inter-class distances will vary for different indicators. Under the multivariate normality and local independence assumptions of LPA, the heterogeneity of the means and variances on indicators does not necessarily have meaningful effects on extracting the correct number of classes. However, this study cannot inform on the extent to which statistical power is affected by the indicators having a mixture of variables with small, medium, and large inter-class distances. We advise researchers to conduct LPA iteratively and consider discarding indicators that have small inter-class distances. Given that the measures we investigated tended to select models with fewer classes when the inter-class distance was small, these items are more likely to bias the solution toward a model with fewer classes than are truly present.

Related to the limitation above, it should be noted that we simulated the data under the assumptions of local independence and homogeneity of variance across latent classes. Although these assumptions are common for latent class analyses, these specifications might be too restrictive and limit the generalizibility of the findings. How potential correlations between the observed variables within latent classes and different variance-covariance matrices across latent classes affect class solutions and power remain to be seen especially for models with smaller sample sizes.