Analysis of Local and Global Topographic Order in Mouse Retinocollicular Maps

Abstract

We introduce the Lattice Method for the quantitative assessment of the topographic order within the pattern of connections between two structures. We apply this method to published visuocollicular mapping data obtained by Fourier-based intrinsic imaging of mouse colliculus. We find that, in maps from wild types and β2 knock-outs, at least 150 points on the colliculus are represented in the visual field in the correct relative order. In maps from animals with knock-out of the three ephrinA ligands (TKO), thought to specify the rostrocaudal axis of the map, the projection on the colliculus of each small circular area of visual field is elongated approximately rostrocaudally. Of these projections, 9% are made up of two distinct regions lying along the direction of ingrowth of retinal fibers. These are similar to the ectopic projections found in other ephrinA knock-out data. Coexisting with the ectopic projections, each TKO map contains a submap where neighbor–neighbor relations are preserved, which is ordered along both rostrocaudal and mediolateral axes, in the orientation found in wild-type maps. The submaps vary in size with order well above chance level, which can approach the order in wild-type maps. Knock-out of both β2 and two of the three ephrinAs yields maps with some order. The ordered TKO maps cannot be produced by correlated neural activity acting alone, as this mechanism is unable to specify map orientation. These results invite reassessment of the role of molecular signaling, particularly that of ephrinAs, in the formation of ordered nerve connections.

Introduction

Retinal ganglion cell axons project directly onto the contralateral superior colliculus (mammals) or optic tectum (nonmammalian vertebrates) to form a 2D retinotopic map in a consistent orientation (Gaze, 1958; Sperry, 1963; Dräger and Hubel, 1976). This is a paradigm system for investigating the development of neural connectivity. Possible mechanisms for the formation of topographic maps are as follows: time of arrival, fiber-following, molecular guidance, and electrical activity, a combination of the latter two being most likely (Sperry, 1943, 1963; Gaze, 1970; Prestige and Willshaw, 1975; Simon and O'Leary, 1992; McLaughlin and O'Leary, 2005; Pfeiffenberger et al., 2006).

Selective deletion of a candidate mechanism through genetic manipulations (Frisén et al., 1998; Feldheim et al., 2000; Cang et al., 2008) causes map order to degrade. To assess the importance of the deleted mechanism signaled by this degradation requires quantitative approaches. The existing method for the datasets that we analyze involves computation of how smoothly the visual field positions identified with specific collicular locations vary over each dimension of the map (Cang et al., 2005). More general methods calculate a cost function over each pair of points in one space and their respective image in the other space (Goodhill and Sejnowski, 1997; Vidaurre and Muruzábal, 2007). Both approaches yield either one or two numbers per map, which is not sufficient to reflect the complexity of many types of map.

We introduce the Lattice Method for measuring order in a one-to-one map and apply it to previously published data from visuocollicular Fourier-based intrinsic imaging of mice (Cang et al., 2008). To establish a benchmark, we analyzed ordered wild-type (WT) maps. We then examined maps from animals in which the β2 component of the acetylcholine receptor had been knocked out. By affecting the patterns of correlated activity across the retina, this is thought to disrupt neighbor–neighbor signaling that refines the crude map set up through Eph/ephrin interactions (McLaughlin et al., 2003; Mrsic-Flogel et al., 2005). We then looked at the effects of knock-out of the ligands ephrinA2, ephrinA3, and ephrinA5, distributed in graded fashion along the rostrocaudal axis of the colliculus, which could specify map order along this axis (Feldheim et al., 1998, 2000; Frisén et al., 1998; Pfeiffenberger et al., 2006). Although these triple ephrinA knock-out (TKO) maps seem disordered (Cang et al., 2008), each contains a large submap with order along both rostrocaudal and mediolateral dimensions, in the correct orientation. Order in these maps is indistinguishable from that in maps from animals with knock-out of β2 and two of the three ephrinAs (β2DKO).

In TKO maps, some of the projections from small circular areas of visual field are elongated along the direction of innervation of the colliculus and each contains two foci, reminiscent of ectopic projections in other ephrinA knock-outs (Feldheim et al., 1998, 2000; Frisén et al., 1998; Pfeiffenberger et al., 2006).

These results question the commonly held view of the role of ephrinAs in establishing the topographic map and suggest new experiments using mutants to understand the interplay of electrical and molecular signaling.

Materials and Methods

Data preparation: one-to-one maps.

A one-to-one map of visual field onto superior colliculus is defined in terms of how a number of distinct locations in the visual field project to the same number of locations in the colliculus. Each location represents a small circumscribed area of visual field or colliculus, both projected onto the 2D plane. In an ordered one-to-one map, the relative positions of the locations in visual field are reproduced in the arrangement of the corresponding locations on the colliculus (F → C map). The map of colliculus onto visual field can be defined in a similar way (C → F map).

The Fourier-based imaging method.

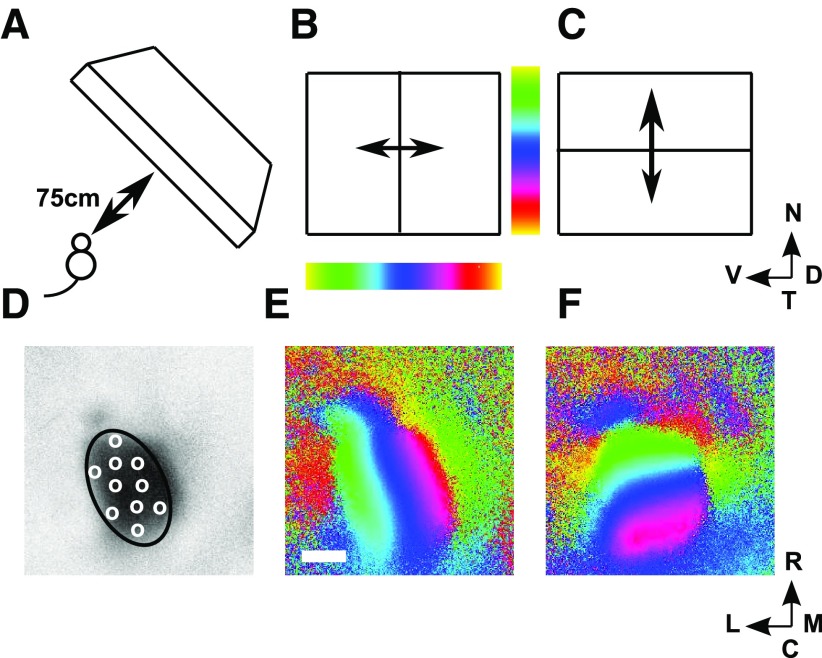
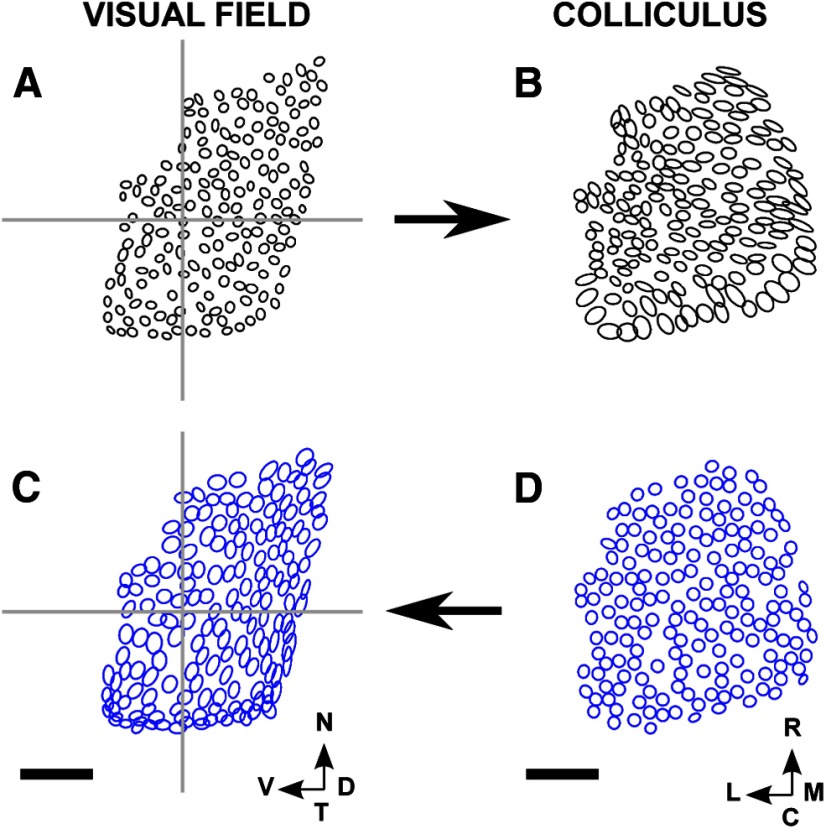
This method, as applied to mouse superior colliculus (Kalatsky and Stryker, 2003), supplies the visual field position identified with each 8.9 μm × 8.9 μm square in a 250 × 250 grid laid over the colliculus, covering a 2 mm × 2 mm region. The visual field positions (and hence positions on the retina) identified with each individual point on the colliculus are obtained through carrying out two experiments (Fig. 1) (Kalatsky and Stryker, 2003). First, a long straight horizontal bar is moved slowly, continuously, and at a constant rate backwards and forwards over the visual field, along the dorsoventral axis (elevational scan; Fig. 1B). The accumulated spatiotemporal hemodynamic response is recorded at each of the pixels. From the signal component extracted at the scanning frequency, the field position along the dorsoventral axis producing maximum response at each pixel is calculated from the phase of this component (Fig. 1E). Repeating this procedure by scanning continuously with a long, straight vertical bar along the nasotemporal axis (azimuthal scan; Fig. 1C) gives for each pixel the field position along this axis that produces maximal response (Fig. 1F). Taking these two sets of readings together identifies the position in 2D visual space that evokes maximal response at each of the 62,500 pixels over the part of the brain assessed.

Figure 1.

The Fourier-based intrinsic imaging method. A, The positioning of the scanning monitor, which covers nasal field. B, C, The elevational (B) and azimuthal (C) scans. D, The region defining the extent of the colliculus (ROI) drawn on a plot of the activity profile for the elevational scan, with illustrative pseudo-randomly positioned nodes shown as white circles. E, WT map. Each of the 62,500 pixels making up the brain area scanned is colored to indicate the position along the dorsoventral axis that yields maximal excitation in the elevational scan (B). Scale bar, 500 μm; color bar shown in B. F, The same pixels are colored according to the position along the nasotemporal axis that yields maximal excitation in the azimuthal scan (D), with the color bar shown in C. Visual field: N, nasal; T, temporal; D, dorsal; V, ventral. Directions on the colliculus: R, rostral; C, caudal; M, medial; L, lateral. B–F are oriented as in Cang et al. (2008) (their Fig. 1) from which this figure is redrawn.

The Lattice Method requires two sets of coordinate positions specifying the matched locations in visual field and superior colliculus in a one-to-one map. This involves several steps of preprocessing the imaging data: (1) identifying the superior colliculus in the region of the brain scanned; (2) smoothing the data; (3) filtering out ambiguities inherent in the Fourier scanning method; (4) choosing the locations defining the one-to-one C → F and the F → C maps; and (5) identifying those locations in the visual field that have a multiple representation on the colliculus: ectopic projections.

Identifying the superior colliculus.

The strength of the total optical signal over the region scanned was used to identify the colliculus (Kalatsky and Stryker, 2003). For wild types (WTs), both elevational and azimuthal scans give similar activity profiles. In the mutant maps, elevational scans are known to give reliably higher levels of activity in the ROI than azimuthal scans (Cang et al., 2008), and so we used the activity pattern produced in the elevational scan to identify the ROI (Fig. 1D) as the colliculus. We then designated as eligible the most active pixels within the ROI, defined here as the pixels with total signal strength >90% of the mean within the ROI. These were taken to be the only pixels that could give reliable information about their matching positions in the visual field. Comparing to a mean level was thought to be more reliable than comparing to a maximum value, the method used by Kalatsky and Stryker (2003) and Cang et al. (2008). Eligible field positions are the positions in the visual field that correspond to eligible pixels on the colliculus. Table 1 shows the level of activity within the ROI compared with that outside, for both elevational and azimuthal scans.

Table 1.

General properties of the data^a

Animal and map type	Elevational scan: activity ratio (%)	Azimuthal scan: activity ratio (%)	Number of pixels discarded by initial filtering (%)	Number of nodes
WT	2.27 ± 0.23	2.23 ± 0.29	0.4 ± 0.6	151 ± 13
β2	2.36 ± 0.35	1.60 ± 0.28	3.4 ± 3.9	109 ± 21
HetTKO	2.35 ± 0.41	1.86 ± 0.56	14.0 ± 8.2	127 ± 48
HomTKO	2.44 ± 0.33	1.40 ± 0.35	22.3 ± 7.7	129 ± 25
β2DKO	1.53 ± 0.24	0.85 ± 0.15	37.9 ± 13.7	114 ± 30

^aThe description of the main animal types is given at the beginning of Results. Activity ratio is the ratio of the mean activity within the ROI on the brain surface scanned to the activity outside, expressed as a percentage. All figures, except for the numbers of nodes, are means and SDs calculated over the datasets in the given group. The numbers of nodes are calculated from the means obtained from the 20 runs performed for each dataset.

Smoothing the data.

To construct a one-to-one map requires a one-to-one correspondence between locations in the colliculus and locations in the visual field. At the single pixel level, there is such a correspondence as the Fourier-based method ensures that each pixel is identified with a unique field position. However, neighboring pixels project onto the visual field with a degree of scatter (Cang et al., 2008). To calculate the visual field location to be identified with a given pixel on the colliculus, this scatter was smoothed out by averaging over the field locations associated with all the eligible pixels within a certain distance of the given pixel. We set this distance at 3 pixels (∼27 μm), corresponding to the extent over which the visual field responses were summed in calculating phase scatter as the index of map quality (Cang et al., 2005). If the visual field positions over which the average was taken are also grouped in a circumscribed region, then the average in the visual field is truly representative of the average on the colliculus. Similarly, to construct a F → C map, we averaged over the pixel positions in the colliculus associated with the field positions within a certain distance of the given field position. This distance was chosen to be 1.7° as it corresponds to the distance of 27 μm used for the colliculus assuming an inverse magnification factor of 70° per mm, characteristic of the WT maps analyzed here (Table 2) (Dräger and Hubel, 1976).

Table 2.

Properties of the maps^a

Animal and map type	Area of colliculus covered (mm2)	Inverse magnification factor (°/mm)	Number of edges in the largest ordered submap (%)	Orientation of the largest ordered submap (°)	Mediolateral polarity (%)	Rostrocaudal polarity (%)
F → C
WT	0.50 ± 0.06	73.4 ± 7.0	99.9 ± 0.1	−20.6 ± 6.4	87.8 ± 2.8	89.0 ± 4.1
β2	0.31 ± 0.05	68.5 ± 8.3	98.3 ± 1.0	−14.0 ± 8.1	92.4 ± 3.4	88.3 ± 3.3
HetTKO	0.36 ± 0.17	76.1 ± 22.7	87.2 ± 11.8	−18.7 ± 8.0	86.6 ± 2.8	79.3 ± 7.7
HomTKO	0.38 ± 0.11	85.6 ± 11.3	65.2 ± 13.0	−16.3 ± 12.3	85.1 ± 4.9	63.5 ± 8.8
β2DKO	0.25 ± 0.11	116.7 ± 29.3	36.0 ± 21.2	−14.4 ± 12.8	83.1 ± 5.1	53.9 ± 4.7
RCrand	0.50 ± 0.06	73.4 ± 7.0	11.2 ± 1.6	−27.6 ± 9.8	87.5 ± 2.7	50.2 ± 0.9
C → F
WT	0.55 ± 0.06	68.5 ± 7.1	98.8 ± 1.4	+20.3 ± 6.2
β2	0.36 ± 0.07	61.1 ± 8.9	96.3 ± 2.9	+13.8 ± 8.2
HetTKO	0.46 ± 0.18	63.6 ± 16.3	76.2 ± 10.7	+20.3 ± 7.8
HomTKO	0.49 ± 0.08	67.1 ± 8.6	62.3 ± 12.2	+20.4 ± 15.1
β2DKO	0.46 ± 0.13	59.2 ± 6.6	33.9 ± 19.1	+24.6 ± 20.1

^aInverse magnification factor is the square root of the ratio of the area of visual field covered to the area of colliculus covered. The number of edges is the ratio of the number of edges in the largest submap to the number in the full map, expressed as a percentage. The RCrand (rostrocaudally randomized) WT map was constructed as described in Materials and Methods. In calculating statistics from F → C submaps, data from nodes yielding ectopic projections have been included. Means and SDs are calculated from the means over 20 runs.

We call the distribution of pixels on the colliculus associated with the eligible points within each small circular area of visual field of radius 1.7° the “projection field”. There are a variety of projection fields, depending on the genotype. In some cases, the pixels are clustered tightly. In other cases, there is a single elongated region or there are two or more distinct regions. Similar distributions in the visual field can be defined for the C → F map. The simplest way of referring to these distributions (although slightly unconventional) is to call them “receptive fields”.

To understand why elevational scans can produce higher activity than azimuthal scans (Table 1), we performed a computer simulation of the scanning experiment. We looked at the activity profiles for different patterns of connectivity between visual field and colliculus. Simulated azimuthal scans gave weaker activity profiles than elevational scans only when each small circular area of colliculus was connected to an area of visual field that is elongated along the nasotemporal axis. This is because, in the elevational scan, the elongated projections in the visual field are orientated in the same direction as the bar used in the scan and therefore induce more activity in the colliculus than in an azimuthal scan. In the experiments where azimuthal scans gave weaker activity profiles, the visual field projections were elongated in this way (Cang et al., 2008) (see Fig. 3G,K,O).

Figure 3.

Examples of visual and projection fields, after initial filtering. Data from the four primary groups of data are illustrated, the groups being defined at the beginning of Results. A, WT dataset. Two examples, distinguished by color, of individual projection fields. B, Superposition of all the projection fields from all the nodes in the visual field for that dataset. C, Similar to B but showing the superposition of all the receptive fields from the nodes defined on the colliculus, individual examples being shown in D. D, Similar to A but showing two examples of receptive fields. E–H, Similar distributions taken from a β2 knock-out dataset. I–L, Similar distributions taken from a HetTKO dataset. M–P, Similar distributions taken from a HomTKO dataset. Scale bar, 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

Filtering out ambiguities inherent in the scanning method.

For the C → F maps, in the WT, the receptive fields are also circular, whereas in the knock-out maps in some cases the receptive field is in the form of a long straight line directed nasotemporally.

We interpret these straight-line configurations as representing cases where a small area of colliculus is identified with two areas in the visual field (or more than two areas that are collinear). Such areas cannot be disambiguated by the Fourier method. For example, when there are two areas, the position in the visual field along one axis, as calculated by the Fourier scanning method (which involves summing two sinusoids of the same frequency but different phases), lies between the positions, V₁ and V₂, of the individual areas. The precise position as calculated depends on the relative strengths of the projections from the two areas. Each of the pixels in the small area of colliculus being considered will be represented in the visual field at slightly different positions between V₁ and V₂, and so the representation of all the pixels will be arranged along a straight line. This introduces an uncertainty into the underlying connectivity pattern for this small area of the colliculus. We therefore removed data points with a large associated spread from the analysis using the following filtering procedure.

For each eligible pixel, P, on the colliculus, we found its receptive field. We then used a k-means algorithm to separate out the receptive field into one cluster and also into two clusters if possible. Each cluster had to contain at least 5 pixels, ∼20% of the maximum number of eligible pixels within the circle, which is 28 for a radius of 3 pixel-widths (27 μm). We then represented each cluster as an ellipse where the length of each subaxis is equal to the SD along that subaxis, being calculated from the covariance matrix of the point locations. Point P was then marked as ineligible if (1) either of the two SDs measured for the single cluster exceeded 10° and (2) in the case when the distribution was resolved into two clusters, they could not be separated clearly (i.e., when the distance between cluster centers was less than the mean of the two SDs along the major axis). By this means, between 0% and 38% (average 15% over all datasets) of the pixels previously marked as eligible were removed (Fig. 2; Table 1). Figure 3 shows examples of projection fields and receptive fields after filtering (F → C: Fig. 3A,E,I,M; C → F: Fig. 3D,H,L,P). Instead of removing ambiguous pixels, a possible alternative approach would be to examine the time-varying signals underlying the Fourier method using such techniques as reverse correlation (Gabbiani et al., 1996; Ringach and Shapley, 2004).

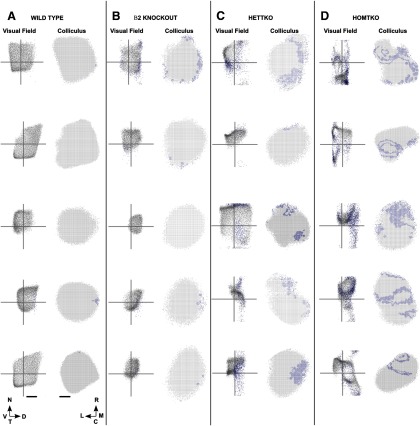
Figure 2.

The distributions of eligible pixels on the superior colliculus and the corresponding eligible points in the visual field before and after filtering, for the 20 primary datasets examined. The original eligible pixels and corresponding points in the visual field are colored gray, and those removed by filtering are colored blue. These datasets fall in five groups of four, as defined in Results. Each column contains the five maps in each group. A, WT data. B, β2 knock-out data. C, HetTKO data. D, HomTKO data. Scale bar: 250 μm (colliculus). Calibration: 20° (visual field). The gray cross in a visual field plot marks the center of the visual field. N, nasal; T, temporal; D, dorsal; V, ventral; R, rostral; C, caudal; M, medial; L, lateral.

Choosing the locations defining the one-to-one C → F and F → C maps.

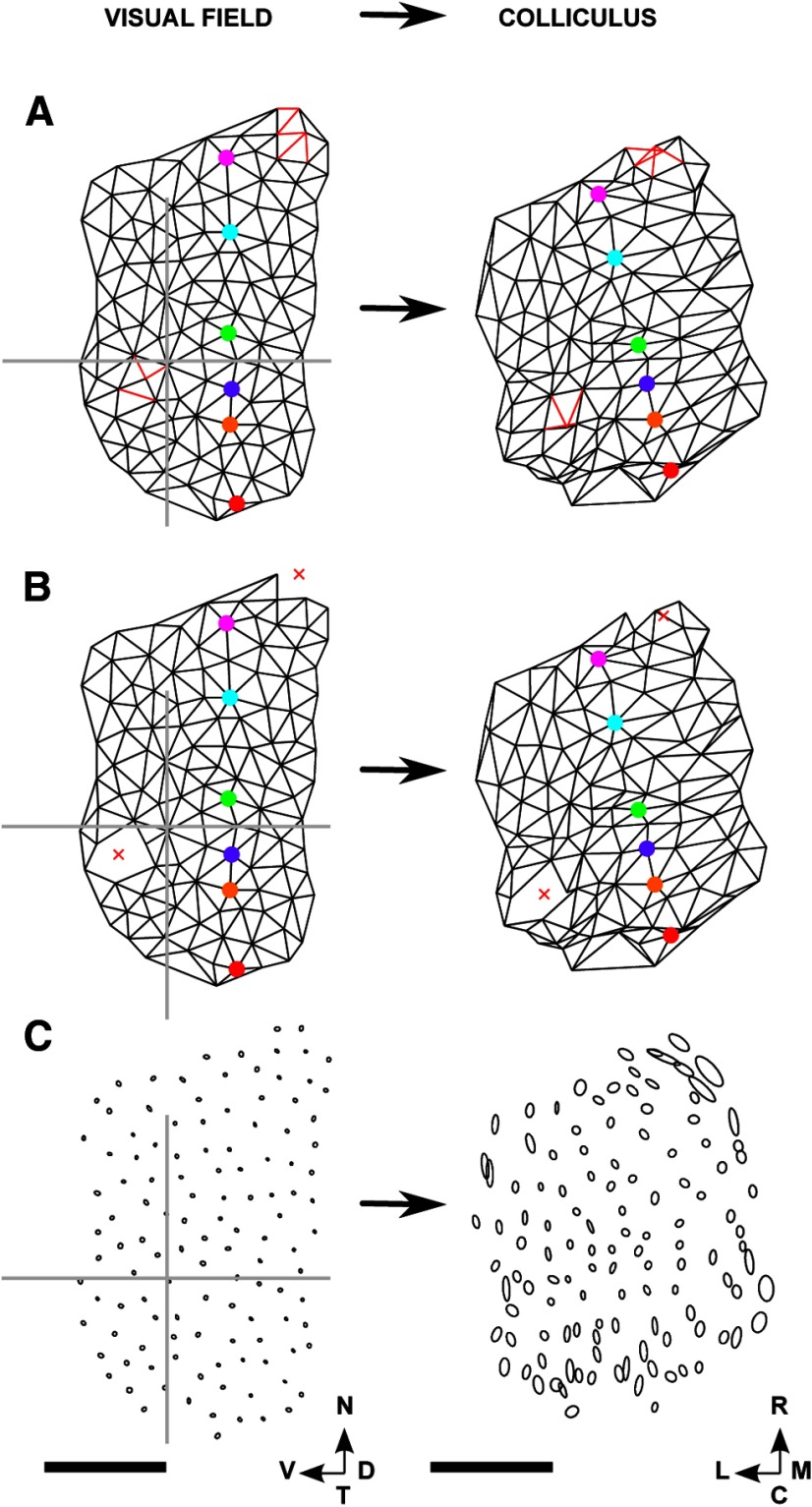
First, the representative locations on the colliculus were chosen. The aim was to find a set of locations for which the mean distance between nearest neighbors was 6.0 ± 0.1 pixel-widths (1 pixel-width 8.9 μm; 6 pixel-widths ∼ 54 μm). Preliminary simulations had shown that this spacing gave very good WT maps (e.g., see Fig. 6), which established a baseline. Using this spacing also allowed the individual areas of the colliculus over which smoothing took place to cover the entire area of colliculus with minimal overlap (e.g., see Fig. 5).

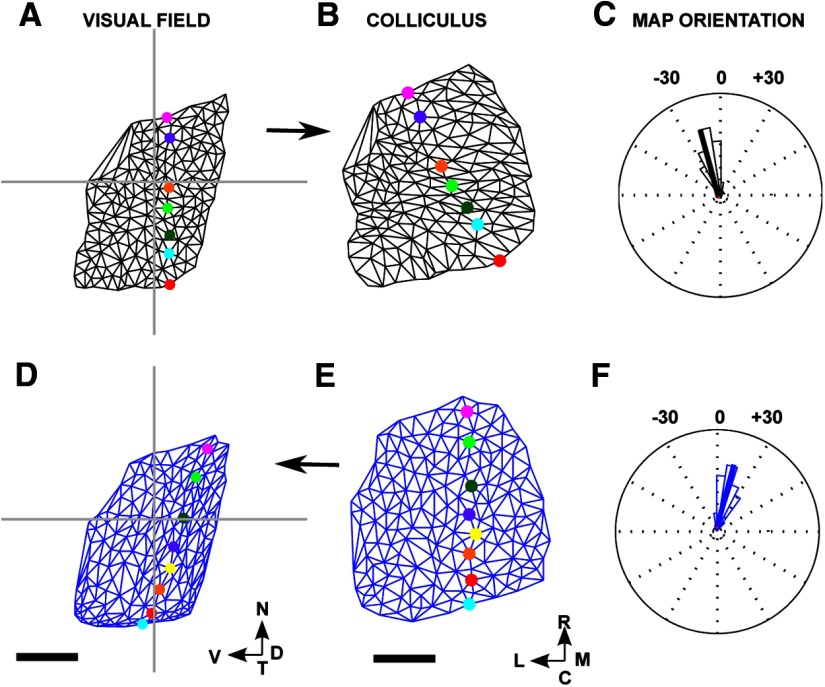
Figure 6.

F → C and C → F maps for the WT dataset used for Figure 5. Lattices and networks were constructed as illustrated in Figure 4. A, Lattice of the selected nodes constructed in the visual field, with the nasotemporal direction indicated by a set of colored nodes. B, The map constructed on the colliculus. C, The circular histogram of the orientation of each edge in the map, with the mean orientation indicated by a black line. Units are degrees. This distribution of orientations was found by comparing the relative orientation of each edge in the lattice in A with that of the corresponding edge in B. The mean orientation of −15° corresponds approximately to the difference in orientation between the two lines of colored nodes in A and B. D, E, The map in the visual field (D) as projected from the lattice constructed in the colliculus (E). F, Circular histogram of the map defined in D and E. In neither the F → C map (A, B) nor the C → F map (D, E), do any edges cross over. Number of nodes: 175. Scale bar, 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

Figure 5.

Projections of small circular areas of visual field on the colliculus, and vice versa, for a WT dataset. A, B, Map of visual field onto colliculus (F → C map). A, Ellipses fitted to the eligible points within the circles of radius 1.7°, each drawn around a node. B, Ellipses fitted to the projection fields. C, D, Similar plots for the map of colliculus into visual field (C → F map). D, Ellipses fitted to the eligible pixels within the circles of radius ∼27 μm, each drawn around a node on the colliculus. C, Ellipses fitted to the receptive fields. In all four plots, the lengths of the major and minor subaxes of the ellipses are equal to the SDs of the appropriate distributions as measured along these axes. Number of nodes: 175. Scale bar, 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

A preliminary value for the number of nodes in the lattice was then estimated so as to give the required lattice spacing and an initial minimum distance between nodes was set. Pixels were then selected one by one and at random from the population of eligible pixels. Each selected pixel was retained if (1) it was at least this minimum distance away from all previously selected pixels and (2) there were at least 10 eligible pixels within 3 pixel-widths (∼27 μm) of it, which is the extent over which smoothing took place. A systematic study in WTs of how the mean position in the visual field varied with the number of pixels over which this was computed had established that for sample sizes >10, the change in visual field position calculated when adding one more pixel became <0.1° (results not shown).

If it was not possible to find such a set of locations after 10,000 attempts to select a pixel, the value of the desired minimum spacing was reduced and the procedure repeated. Different numbers of locations were tried until a number, N, was found that satisfied constraints (1) and (2). The corresponding N positions in the visual field were then found, for each collicular location, by averaging over the field positions from the eligible pixels within 27 μm of this location. As a result, two sets of N matching locations were obtained: one from the colliculus and one from the visual field. By this means, the C → F map was defined.

For the F → C map, the procedure for constructing the lattice in the visual field was analogous, except that we did not have to try different numbers of nodes as the number was set to that for the collicular lattice. In this case, the circle used in satisfying condition (2) above had radius 1.7°. The N matching locations in the colliculus were then found by the same smoothing technique used for the C → F maps, averaging over the projections from eligible visual field positions within a circle of this radius.

Multiple representations of visual field on the colliculus: calculating ectopic projections.

Some of the projection fields from the chosen locations in the visual field are made up of two distinct clusters, which we call ectopic projections (Fig. 3I, red; M, red).

To investigate systematically the existence of two clusters of eligible points in these projection fields, we again used the k-means algorithm to separate out each distribution into two clusters, each modeled as an ellipse. As described earlier, clusters with <10 eligible points were ignored. Two putative clusters were confirmed as being present when the distance between the two cluster centers was greater than the average of the SDs of the two clusters, each measured along the major axis of the ellipse. The cluster containing the larger number of points is called the major projection and the other cluster the minor, or ectopic, projection.

A view of the superposed pattern of projection fields in a given dataset can be gained by superposing on the same plot the individual projection fields from all the chosen locations after transforming them to a common origin and then modeling the superposed distribution as a 2D Gaussian. The ellipse with subaxes of lengths equal to the SDs in the directions of these axes encloses 68.5% of all the points in the superposed distribution. Figure 3B, F, J, N shows examples of superposed distributions on the colliculus for the four datasets examined and the corresponding field plots are shown in Figure 3C, G, K, O.

The Lattice Method for one-to-one maps.

The Lattice Method is a graphical method and was developed from an earlier method based on quantifying receptive field size and overlap (Willshaw, 2006). It is applicable to any one-to-one projection between two spaces. It can be used to investigate at a more detailed level than other methods how local order is preserved in a map as well as to discover the orientation of the map. In this application to visuocollicular mappings, we focus on maps of visual field onto superior colliculus (rather than of colliculus to visual field) as these are readily comparable with other experimental data.

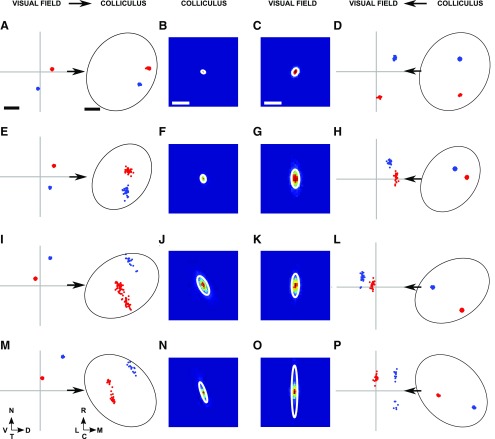
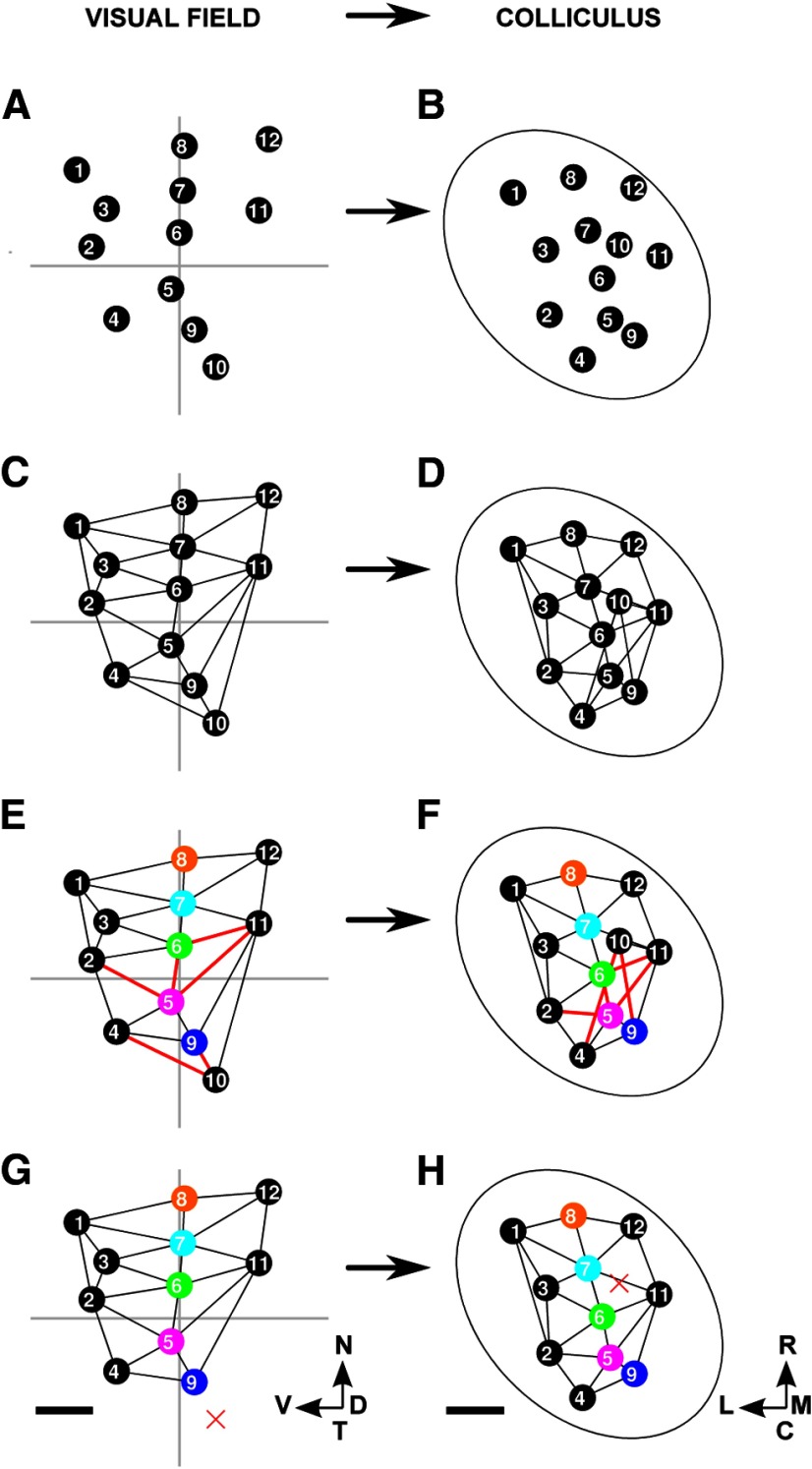
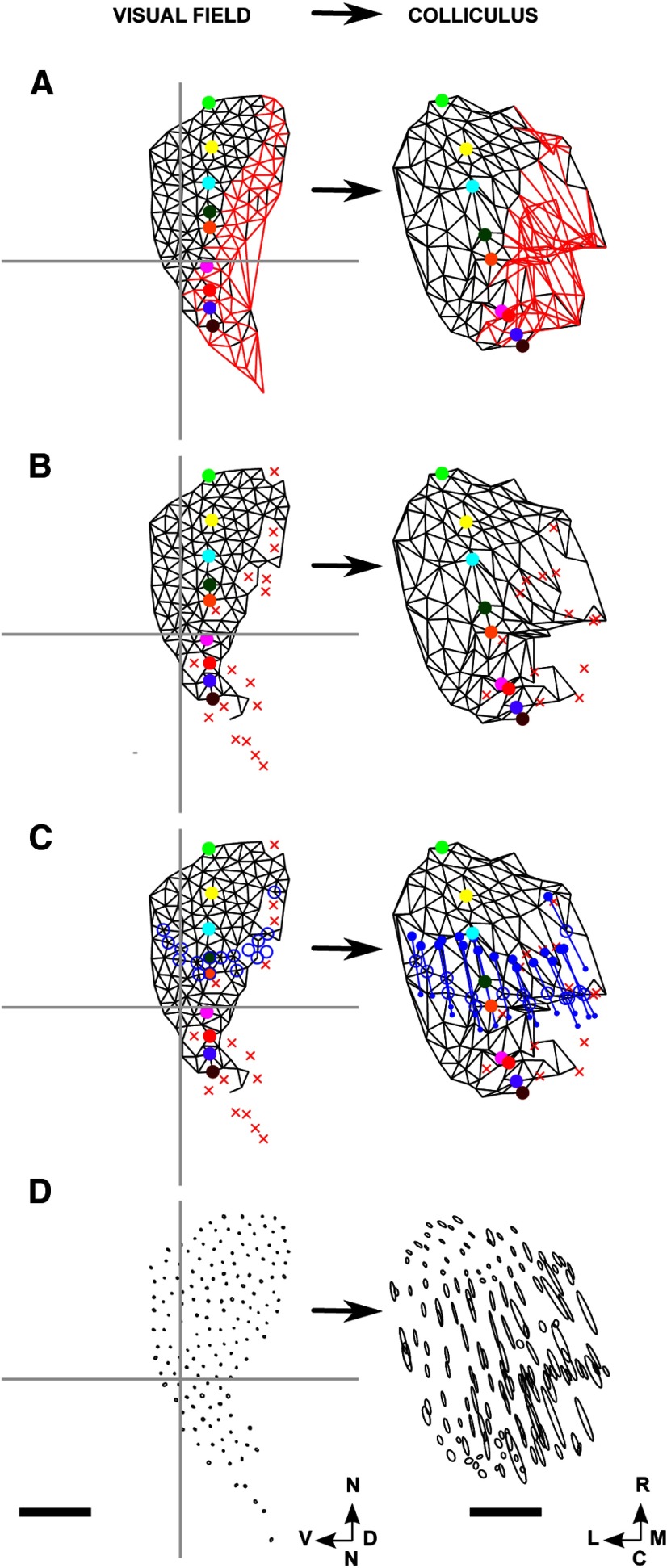
We now introduce the Lattice Method and illustrate its use on a simple example of a F → C map (Fig. 4). Each location in the visual field or on the colliculus that is used as a point in the map is called a “node.” Figure 4A shows 12 nodes that were distributed at random over the entire visual field while maximizing the mean distance between nearest neighbors. Figure 4B displays the matching set of nodes in the colliculus, numbers being used to show the one-to-one correspondence between nodes in the visual field and on the colliculus. Nodes in the visual field that are neighbors, defined using Delaunay triangulation, were interconnected to form a 2D structure in which no edges intersect, which we call a “lattice” (Fig. 4C). As shown in Figure 4D, the pairs of nodes on the colliculus for which the corresponding nodes in the field are neighbors were then interconnected. If all neighborhood relationships between the nodes in the field are preserved on the colliculus, then the network so formed will itself be a lattice. However, in general, this will not be so and some of the edges in the network will cross over (Fig. 4D). In Figure 4F, these five edges were colored red and the corresponding links in the reference lattice were also colored red (Fig. 4E). To indicate the orientation of the map, in Figure 4E, F, specific node pairs are highlighted using different colors. In this example, the nasotemporally directed line of highlighted nodes in the visual field is directed approximately rostrocaudally on the colliculus.

Figure 4.

The construction of a map from visual field to colliculus using the Lattice Method. A, Twelve nodes were chosen within the area of field that is projected to by eligible pixels in the colliculus. This small number of nodes was chosen for illustrative purposes. The nodes were positioned at random, subject to the mean distance between neighbors being maximized as described in Materials and Methods. B, The positions of the corresponding 12 nodes on the colliculus. Each node was placed at the mean position of all pixels on the colliculus that project to within 1.7° of the corresponding node in the visual field. C, The lattice formed by joining up nearest neighbors in A as defined by the Delaunay triangulation method. D, The network formed by joining up each pair of nodes in B for which the corresponding nodes in C are neighbors. E, Edges of the lattice that correspond to the edges in D that cross are colored red. Certain nodes are distinguished by color to indicate the nasotemporal direction. F, Edges in the network that intersect are red. The nodes that correspond to the nodes in E that are colored uniquely are each given the matching color. G, The lattice constructed on the largest subset of nodes that when projected onto the colliculus yields a network with no crossovers. Nodes that have been removed are shown by a red X. By removing the pair of nodes labeled “10” along with the three associated edges, a completely ordered submap results. H, The network corresponding to G which has no crossovers. A and B together define the entire map; G and H together define the largest ordered submap. The data shown here was adapted from one of the datasets. Scale bar, 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

Comparisons of the properties of the network constructed on the colliculus with those of the lattice on the field are used to provide measures of map quality.

Local order.

The percentage number of nodes with no edges that cross is one measure of internal order in the overall map: the larger this number, the greater the order. However, this measure can hide the order existing in part of the map, which is revealed by finding the largest connected subset of the original nodes that yields a map with no crossovers. Figure 4G, H shows the largest ordered submap for this simple example. By removing the node pair labeled 10, the remaining map has become a lattice, being completely ordered with no crossovers. In our heuristic method, node pairs were removed one by one. At each step, for each node in the map on the target structure, the ratio of (1) the number of nodes that would become disconnected were the node to be removed to (2) the number of crossing edges removed if all these potentially disconnected nodes had then been removed was calculated. The node with the smallest ratio was then removed (together with its partner) and the procedure repeated until no crossing edges remained. The number of nodes removed by our approximate method was on average only 8% more than the exact solution we found by linear programming, which allowed the final submap to be made of disconnected regions. As a measure of how well nearest-neighbor relations are preserved in this submap, we used the percentage number of edges that remain from the original map (Table 2).

Global order–orientation of the map.

The orientation of the overall map is found by comparing the orientation of each of the three sides of each triangle in the network drawn on the colliculus with the orientation of the corresponding side in the lattice drawn in the visual field. Overall orientation is best measured for the largest ordered submap; in maps containing crossovers, some of the triangles will have an orientation inverted in one axis and so their orientations have to be measured separately. Figure 6C, F shows the distribution of orientation differences for one of the WT maps.

Measures for use with ephrinA knock-out maps.

To establish a baseline when examining the order of a F → C map along its rostrocaudal dimension, which is particularly relevant to the ephrinA knock-out maps, an additional map was generated from WT data. This map (rostrocaudally randomized [RCrand]) was formed by permuting at random the rostrocaudal coordinates of the nodes in a WT map. To assess the orientation of ephrinA knock-out maps and these disordered maps, our existing method of finding the overall mean and SD of map orientation is unsuitable as it is insensitive to the axis along which the disorder occurs. We developed a new method, which measures the ordering of the mapping along the rostrocaudal axis and the mediolateral axis of the colliculus separately. To calculate the rostrocaudal “polarity”, for each pair of neighboring nodes in the lattice constructed in the visual field, we find whether the corresponding nodes in the map on the colliculus have the correct rostrocaudal order, given the map orientation found in WTs. The measure used is the percentage of nodes in the correct relative order. Mediolateral polarity is measured in a similar fashion.

Treatment of inhomogeneous datasets.

In several of the datasets from mutants, the maps formed from the individual examples were quite different from one another. To ensure that these were not artifacts of the particular choice of nodes in a map, in each case 20 runs were performed using different choices of locations in the visual field or the colliculus. As described later, the variation in the key parameter values of the maps varied little between runs.

Conventions and abbreviations.

Angles in the visual field are measured with reference to the nasotemporal axis (oriented vertically in the figures, following Cang et al. (2008)), which is directed along the zero degree line. Angles in the colliculus are measured with respect to the rostrocaudal axis (also oriented vertically in the figures), which is directed along the zero degree line. In both coordinate systems, a clockwise rotation indicates a positive angle. If the straight line joining two nodes in the field has orientation X° and the straight line joining the corresponding nodes on the colliculus has an orientation Y°, then the relative orientation in the map from field to colliculus is (X-Y)° and from colliculus to field is (Y-X)°. For example, in a map where the nasotemporal and rostrocaudal axes are aligned, the relative orientation of the map is 0°.

All calculations and simulations for this paper were performed using MATLAB version 7.11.1 (MathWorks). The code for generating the maps is available at github.com/davidwillshaw/map-analysis.

Results

Our dataset comprised 24 maps obtained using Fourier-based intrinsic imaging (Cang et al., 2008) from adult mice of either sex aged between 2 and 6 months. These formed into five groups, with four groups of five making up our primary data and one additional group of four: (1) WT; (2) β2 (homozygous knock-out of the β2 subunit of the acetylcholine receptor); (3) HetTKO (homozygous knock-out of ephrinA2 combined with either (i) homozygous knock-out of ephrinA3 and heterozygous knock-out of ephrinA5 or (ii) heterozygous knock-out of ephrinA3 and homozygous knock-out of ephrinA5; (4) HomTKO (homozygous knock-out of ephrinA2, ephrinA3, and ephrinA5); and (5) β2DKO (β2 knock-out combined with homozygous knock-out of ephrinA2 and ephrinA5). These were used to test the effect of knock-out of both activity-based and molecular-based signaling cues. These data are of poor quality as signaled by the lower ratio of the mean strength of the signal recorded within the ROI to that recorded outside the ROI, for both azimuthal and elevational scans. In addition, a large number of pixels had to be rejected in the filtering performed before the maps were constructed (Table 1). On average, 38% of eligible pixels were rejected, compared with 10% from the other datasets.

The general characteristics of the data are given in Table 1. The main body of results is classified under five headings: (1) local and global order in the WT and β2 knock-out maps; (2) local and global order in the HetTKO and HomTKO maps; (3) local and global order in the β2DKO combination maps; (4) ordering of maps along the rostrocaudal axis; and (5) elongated and ectopic projections.

Local and global order in the WT and the β2 knock-out maps

Figure 5 shows the projection fields in a typical WT F → C projection (Fig. 5A,B) and the receptive fields for the corresponding C → F projection (Fig. 5C,D). These distributions are each represented as an ellipse in which the lengths of the major and minor subaxes are equal to the SDs along these two axes. Small areas in one structure map to small areas in the other structure with very little overlap between neighboring areas. Figure 6 illustrates the ordered F → C and C → F maps produced by the Lattice Method, both of which have very few crossovers. In this animal, the F → C map is oriented so that the nasotemporal axis projects at an angle of −15 ± 12° to the rostrocaudal axis (Fig. 6C). This matches closely the angle of +15 ± 13° relative to the nasotemporal axis at which the rostrocaudal axis of the colliculus projects into the field (Fig. 6F).

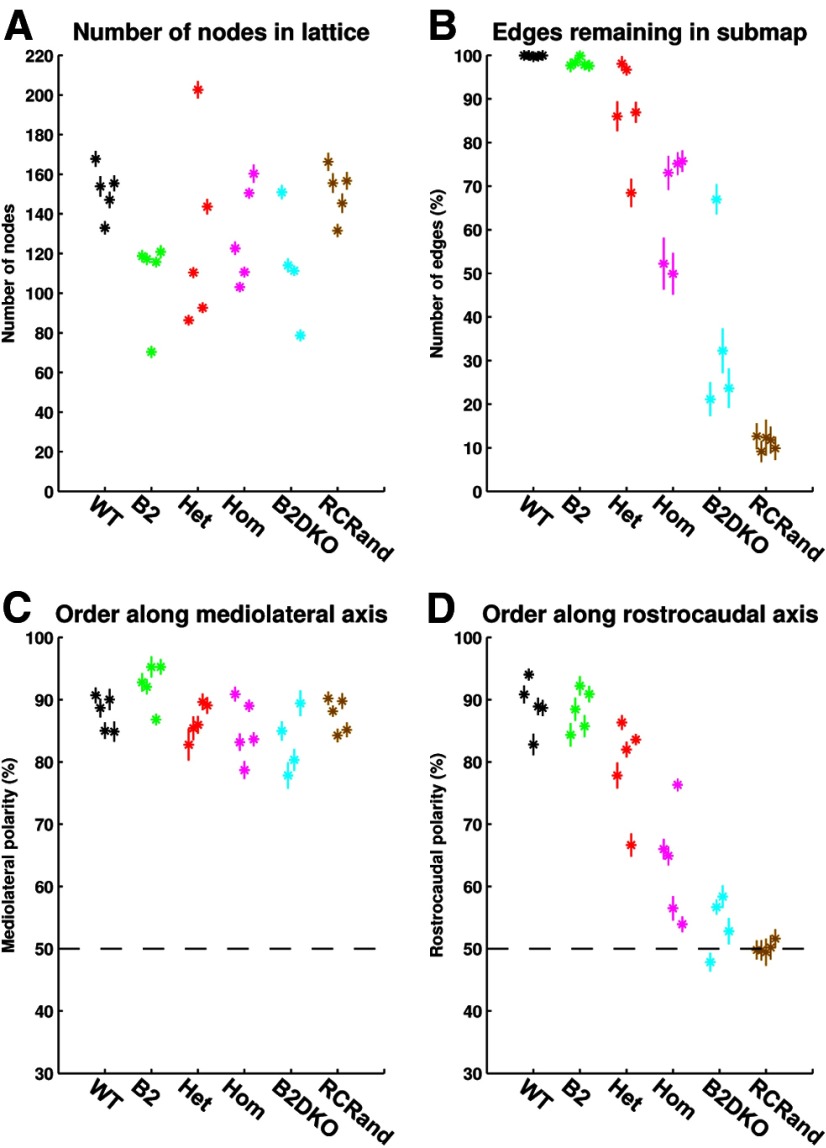
All maps in this group have almost perfect order. There are very few crossings, with many of the maps having no crossings (e.g., Fig. 6), and the maps are in a consistent orientation (Table 2). The largest ordered submaps span almost all the nodes; the sizes of these submaps, measured in terms of the percentage number of edges in the full map that remain in the largest ordered submap, are also summarized in Table 2.

In the F → C maps, the SDs of the ellipses fitted to the superposed projection fields, measured along the two principal axes, are 38 ± 9 μm and 30 ± 6 μm. (Table 3); the SDs expected were every visual field location to be mapped in perfect order is 22 μm.

Table 3.

SDs of the superposed receptive fields and projection fields^a

Animal and map type	SD along the minor axis	SD along the major axis	Orientation of the major axis of the superposed distribution
F → C
WT	30.0 ± 6.4 μm	38.4 ± 9.4 μm	−18.4 ± 60.9°
β2	40.0 ± 7.5 μm	60.6 ± 17.3 μm	−11.3 ± 27.4°
HetTKO	48.7 ± 15.1 μm	115.4 ± 37.0 μm	−17.5 ± 13.1°
HomTKO	45.3 ± 17.9 μm	139.0 ± 50.0 μm	−20.3 ± 12.6°
β2DKO	67.9 ± 24.5 μm	239.0 ± 55.5 μm	−21.9 ± 4.7°
C → F
WT	1.89 ± 0.36°	2.62 ± 0.26°	12.9 ± 9.80°
β2	2.13 ± 0.32°	4.04 ± 0.90°	−0.10 ± 1.53°
HetTKO	2.41 ± 0.37°	9.06 ± 6.29°	1.11 ± 2.16°
HomTKO	1.95 ± 0.50°	15.30 ± 2.32°	0.01 ± 0.19°
β2DKO	3.64 ± 0.99°	38.11 ± 16.47°	−0.08 ± 0.05°

^aEach distribution was formed by superposing all the individual receptive fields (C → F) or projection fields (F → C) from the same dataset onto a common origin. SDs were measured along the major and minor axes of the ellipse fitted to the distribution. Mean orientation of the major axis of the ellipse is also given. The zero degree line is along the rostrocaudal axis. Clockwise rotations in relation to the colliculus as oriented in the figures are positive.

β2 knock-out maps

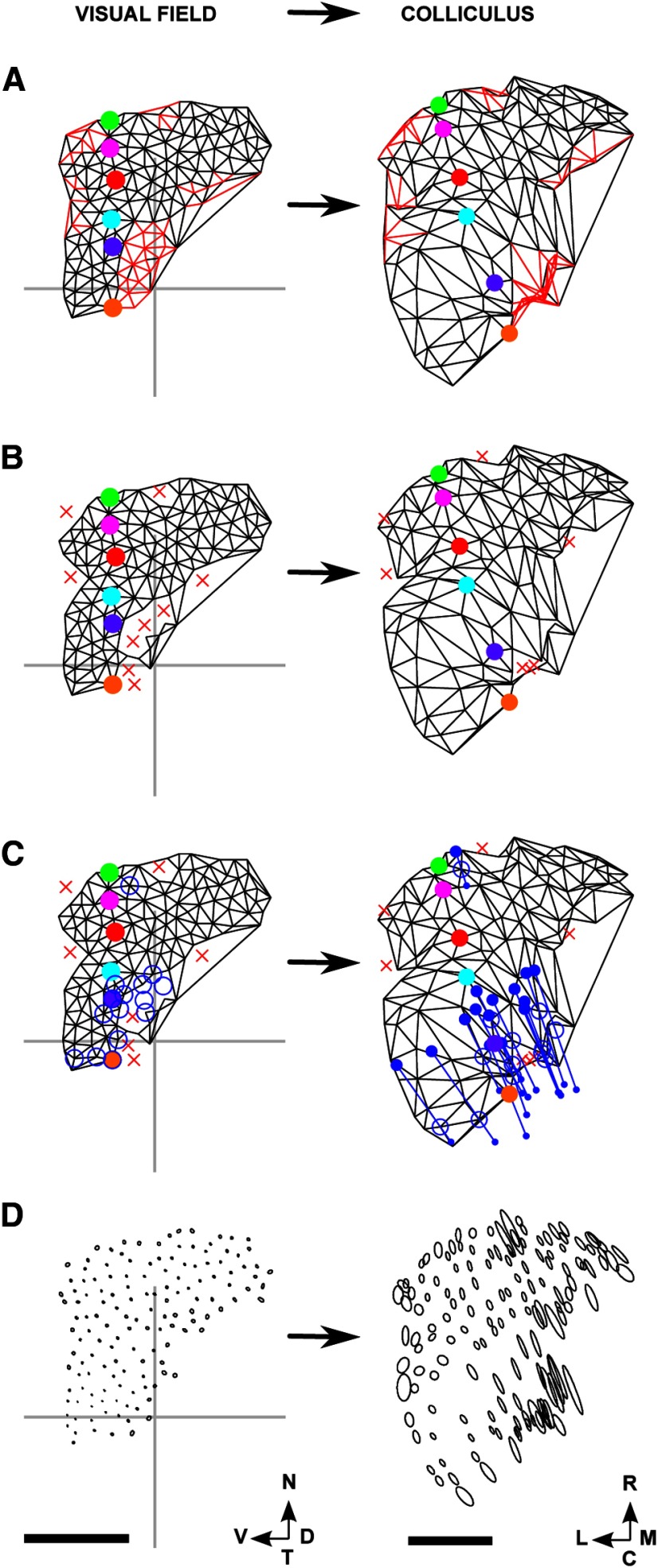
The area of colliculus covered by these maps is only ∼60% of that covered by the WT maps. As summarized in Table 2, the mean number of edges in the largest ordered F → C submap is almost identical to that for WTs, 98.3% compared with 99.9%. The orientation of the largest ordered submap is −14 ± 8° compared with −21 ± 6° for WTs. Figure 7 shows for one of the β2s the entire F → C map (Fig. 7A) and the corresponding largest ordered submap (Fig. 7B).

Figure 7.

F → C maps for a β2 knock-out dataset. A, Lattice constructed in the visual field (left) and the map on the colliculus (right). The two small regions of edges that cross over on the colliculus (in red) are located rostromedially and caudolaterally. B, Lattice drawn on the nodes involved in the largest ordered submap, together with the submap constructed on the colliculus, with nodes not involved indicated by a red X. C, Projections of small areas of visual field on the colliculus. Each area is represented as an ellipse with the lengths of the major and minor subaxes being equal to the SEM of the distribution as measured along these axes. Number of nodes: 130. Scale bar: 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

The measure that defines how well the projections from neighboring nodes are distinguished from one another is the SEM of the appropriate projection fields. In well-ordered maps, the SEM should be less than half the minimum spacing between adjacent projection locations, which is 27 μm (3 pixels) for F → C maps.

In the F → C β2 maps, the representations on the colliculus of the superposed projection fields are more elongated than in the WTs, with the mean length of the major subaxis (set at the SD along that axis) increasing from 38 μm (WT) to 61 μm (β2) in the F → C projection and from 2.6° to 4.0° in the C → F projection (Table 3). The SEMs of the individual F → C projection fields are 12 μm (major axis) and 8 μm (minor axis), well below half the minimal distance of 27 μm between neighboring nodes. To illustrate that in a β2 map neighboring points are distinguishable from one another, plots of the individual projection fields with axis lengths given by individual SEMs are shown in Figure 7C. These results are in qualitative agreement with those from Mrsic-Flogel et al. (2005), who used standard intrinsic imaging at a lower resolution. In their results, the area of colliculus covered by the β2 map was also smaller than in the WTs.

Local and global order in the HetTKO and the HomTKO maps

HetTKO maps

For the F → C projections, the number of nodes with edges that cross is now substantially greater than in WT or β2 knock-out maps. However, the mean number of edges in the largest ordered submap is still high, at 87% (Table 2). Figure 8A, B shows the full map and the largest ordered submap for one HetTKO, where the nodes in the visual field yielding ectopic projections have been included. To show how well the projections on the colliculus from individual areas of visual field are distinguishable, Figure 8D shows for this HetTKO the individual projection fields where the lengths of the subaxes of the ellipses are the SEs in the means. Comparison of Figure 8D with Figure 8A illustrates that high SEs occur in caudomedial colliculus, where edges cross. Figure 9A, B, D–F gives the largest ordered submaps for all five HetTKO cases, showing heterogeneity between the five datasets in this group. The degree of coverage varies widely from submap to submap, and in most cases a substantial portion of temporadorsal field is not represented on the colliculus. Figure 9A, B shows the best ordered maps, with order very close to that of the WT (Fig. 9C). These are from the two animals with heterozygous knock-out of ephrinA5; the maps shown in Figure 9D–F were from animals where the heterozygous knock-out was of ephrinA3. In all 5 cases, the orientation of the normal map is very well maintained.

Figure 8.

F → C maps for a heterozygous ephrinA knock-out (HetTKO) dataset. A, Lattice constructed on the nodes in the field (left) and the corresponding map on the colliculus (right). B, Lattice drawn on the nodes involved in the largest ordered submap together with the map on the colliculus, with nodes not involved indicated by a red cross. C, A copy of B to which information about ectopic projections was added. In the visual field plot, the nodes involved in ectopic projections are indicated by blue unfilled circles and are located in central field. In the colliculus plot, the positions of the major and minor projections, mainly located caudomedially, are shown as large and small filled blue circles, and the average positions by unfilled blue circles. Corresponding major and minor projections are connected by a straight line. D, Projections of small areas of visual field on the colliculus. Each area is represented as an ellipse with the lengths of the major and minor subaxes being the SEM of the appropriate projection field as measured along these axes. Number of nodes: 175. Scale bar: 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

Figure 9.

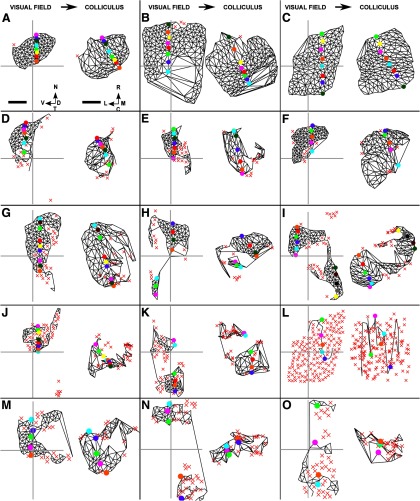
The largest ordered submaps of the visual field on the superior colliculus for the five HetTKOs, the five HomTKO datasets, and three of the four β2DKO datasets. A, B, HetTKOs where homozygous knock-out of ephrinA2 and ephrinA3 was combined with heterozygous knock-out of ephrinA5. The local and global order in these maps approach that seen in WT maps. C, WT map. D–F, HetTKOs where homozygous knock-out of ephrinA2 and ephrinA5 was combined with heterozygous knock-out of ephrinA3. G–K, HomTKOs involving homozygous knock-out of ephrinA2, ephrinA3, and ephrinA5. I, The nasoventral portion of the visual field projects in the correct orientation, whereas the temporodorsal portion does not. L, The largest ordered submap formed after taking the WT map shown in C and then permuting randomly the set of rostrocaudal coordinate positions assigned to the nodes in the visual field. M–O, Three of the four β2DKO datasets where β2 knock-out was combined with homozygous knock-out of ephrinA2 and ephrinA5. Scale bar: 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

In the HetTKO F → C data, the mean SDs measured along the two principal axes of the ellipse fitted to the projection fields are 115 and 49 μm (SEMs of individual projection fields: 23 and 10 μm) compared with 38 and 30 μm for WTs (Table 3). The major axis of the ellipse fitted to the superposed distribution is orientated at a mean angle of −18 ± 13° to the rostrocaudal axis (Table 3).

HomTKO maps

In the F → C maps, the percentage of nodes with edges that cross is increased further (Fig. 10A), but the size of the largest ordered submap is still large, on average 65% (Table 2).

Figure 10.

F → C maps for a homozygous ephrinA knock-out (HomTKO) dataset. A, Lattice constructed on the nodes in the visual field (left) and the map on the colliculus (right). B, Lattice involving the nodes in the largest ordered submap together with the map on the colliculus, with nodes not involved in the submap indicated by a red X. C, A copy of B to which information about ectopic projections was added, with the ectopics indicated as in Figure 8. Here the ectopics are located in a mediolaterally running band across the colliculus. D, Projections of small areas of visual field on the colliculus. Each area is represented as an ellipse, with subaxis lengths representing the SEMs. Number of nodes: 165. Scale bar, 250 μm (colliculus). Calibration: 20° (visual field). Other conventions as in Figure 2.

Figure 10A shows the most ordered F → C map, and Figure 10B shows the corresponding largest ordered submap, with the corresponding plots of the ellipses fitted to the projection fields given in Figure 10D. There is substantial disorder in medial and caudomedial colliculus, but the largest ordered submap still contains considerable order along both rostrocaudal and mediolateral axes (Fig. 10B) and the normal orientation is maintained.

Figure 9G–K shows the largest ordered submap for each of the five HomTKOs. Although the maps are different from each other, they are significantly more ordered than the random control RCrand, defined in Materials and Methods. These maps display patches of order on the colliculus, which can be quite extensive. Patch size on the colliculus varies between ∼300 μm² and 600 μm². With one exception (the caudally located patch of the two shown in Fig. 9I), the patches have normal orientation, suggesting that in this class of maps rostrocaudal order is maintained. The mean SDs measured along the two principal axes of the ellipses of the superposed projections are now 139 and 45 μm (SEMs: 28 and 9 μm) (Table 3). The major axis of the superposed projection fields is oriented at −21 ± 13° to the rostrocaudal axis. The orientation of the largest ordered submap is −16 ± 12° compared with −21 ± 6° for WT maps (Table 2).

Local and global order in the β2DKO knock-out maps

In these animals, there had been knock-out of the β2 component of the acetylcholine receptor and of ephrinA2 and ephrinA5, two of the three ephrinAs present in the colliculus. This was intended to represent, as far as possible, complete abolition of rostrocaudal guidance cues (Cang et al., 2008). It is not possible to knock out the third ephrinA, ephrinA3, as well for the technical reason that the β2 and ephrinA3 genes are located on the same chromosome. The lower quality of these maps is indicated by the poorer signal recorded in the scan and the large percentage number of pixels filtered out (Table 1). As summarized in Table 3, the superposed projections are more elongated than in the four other groups and with similar orientations to the HetTKOs and the HomTKOs. The mean SDs along the two principal axes of the ellipses of the superposed projection fields are 239 and 68 μm (SEMs of individual distributions: 49 and 15 μm) and the major axis is at 22 ± 5° to the rostrocaudal axis (Table 3). As shown in Figure 9M, one of the four maps has local order that approaches that in the HomTKO maps. Two of the other three maps are shown in Figure 11N, O.

Figure 11.

Variation in the key properties of the map over 20 different placements of the nodes forming the map, for each of the 29 different sets of analysis. A, Number of nodes in the lattice. B, Local order: percentage number of edges in the full map that are retained in the largest ordered submap. C, Global order: polarity measured along the mediolateral axis. The dotted line indicates the 50% level, corresponding to no order. D, Global order: polarity measured along the rostrocaudal axis. The dotted line indicates the 50% level, corresponding to no order. In all figures, data for each of the 29 cases are plotted separately. Means and SDs are shown. Black represents WT; green, β2; red, HetTKO; magenta, HomTKO; cyan, β2DKO; brown, RCrand.

Ordering of TKO maps along the rostrocaudal axis

If ephrinA guides axons to their correct position along the rostrocaudal axis, then knock-out of ephrinA might be expected to remove map order along this axis. As described above, we found that knock-out of ephrinAs has a variable effect. Qualitatively, the largest ordered submaps are different from WT maps (Fig. 9C), although the best maps of the HetTKOs, where the heterozygous knock-out was of ephrinA5 (Fig. 9A,B), do not differ greatly from WT maps. HomTKO submaps have differing degrees of order, the best of which (Fig. 9G,H) are not clearly distinguishable from the HetTKO submaps. The difference in genetic makeup between a HetTKO and a HomTKO is slight, one half of either ephrinA3 or ephrinA5 remaining in a HetTKO. In all TKO maps except one (the rostral portion of Fig. 9I), the orientation of the WT map is maintained (i.e., the ordering along the rostrocaudal axis of the map been retained).

To examine the possibility that the degree of ordering observed along this axis could have occurred by chance, we show in Figure 9L the RCrand version of the WT F → C map shown in Figure 9C. Here, the rostrocaudal coordinates assigned to the nodes of the WT map had been permuted randomly, to simulate the removal of rostrocaudal guidance cues from a normal animal. This map is grossly disordered and quite different from both HetTKO and HomTKO maps.

To estimate the order in maps having axial disorder, we use the procedure described in the Materials and Methods whereby order, called here polarity, is calculated along each axis separately. The polarity is the percentage number of edges in the visual field lattice for which the two nodes making up each edge project onto the colliculus in the correct relative order along the axis in question. A value of 100% indicates perfect order along the specified axis, 50% indicates randomness, and 0% indicates perfect but reversed order. Over all the data examined, the mean mediolateral polarity varied between 85% and 93%. Rostrocaudal polarity ranged from 89% (WT; e.g., Fig. 9C), 64% (HomTKO, Fig. 9G–K) to 50% (RCrand; e.g., Fig. 9L).

Using data from the repeated runs, we tested for significance in the amount of map order between the different groups examined. Figure 11 shows the means and SDs, calculated over 20 replications, for the number of nodes (Fig. 11A), the local order in the map expressed in terms of the percentage number of edges from the entire map that remain in the largest ordered submap (Fig. 11B) and the mediolateral and rostrocaudal polarities (Fig. 11C,D). Data for the 29 individual cases are shown separately. Whereas there are some marked intragroup differences, the SDs are relatively small, confirming that it is indeed valid to quote mean values as representative of an individual dataset. The largest SDs are found in the poorer quality β2DKO group.

We used the Kruskal–Wallis rank sum test to establish that at the 5% level there are significant differences between the means of the six groups for local order (p = 7 × 10⁻⁵; Fig. 11B) and rostrocaudal polarity (p = 2 × 10⁻⁴; Fig. 11D). For mediolateral polarity, there was no significant difference between the groups (Fig. 11C).

We then used the Wilcoxon rank sum test to look at differences between specific groups with respect to local order and rostrocaudal polarity. There is a significant difference between WTs and HomTKOs in local order (p = 8 × 10⁻³) and rostrocaudal polarity (p = 8 × 10⁻³) and between HomTKOs and the RCrands (local order: p = 8 × 10⁻³; rostrocaudal polarity: p = 8 × 10⁻³). This establishes that, as suggested by Figure 11D, although order in the HomTKOs has been degraded from that in WTs, there is still significant rostrocaudal order remaining.

The next question is whether the β2/ephrinA combination knock-outs, the β2DKOs, provide evidence that the rostrocaudal order seen in the EphrinA knock-outs is removed by the disruption of neural activity caused by β2 knock-outs. Map order in pure β2 knock-outs is distinguishable from WTs with respect to local order (p = 0.016) but indistinguishable as regards rostrocaudal polarity. In β2DKO maps, both local order (p = 0.016) and rostrocaudal polarity (p = 0.016) are significantly different from the order in HetTKOs, but there is no significant difference compared with HomTKOs. There is a difference in local order only between β2DKOs and RCrands (local: p = 0.016). These results indicate that (1) the effect of β2 knock-out either on its own or in combination with ephrinA knock-out is to degrade local order; and (2) β2DKO maps contain residual order and are not clearly distinguishable from TKO maps. Table 4 summarizes the results of these statistical tests.

Table 4.

Summary of significance tests for order in F → C maps^a

Animal type	WT	β2	HetTKO	HomTKO	β2DKO	RCrand
Local order
WT	—	0.016	0.008	0.008	0.016	0.008
β2DKO	0.016	0.016	0.016	0.111*	—	0.016
RCrand	0.008	0.008	0.008	0.008	0.016	—
Rostrocaudal polarity
WT	—	1.000*	0.031	0.008	0.016	0.008
β2DKO	0.016	0.016	0.016	0.286*	—	0.905*
RCrand	0.008	0.008	0.008	0.008	0.905*	—

^aThe hypothesis being tested is that there is no difference in local order or in rostrocaudal polarity between certain groups. Probabilities are calculated using the Wilcoxon rank order test.

*No significant difference between the two groups in question at the 5% level.

Elongated and ectopic projections

So far, the one-to-one projections of visual field onto colliculus have been examined assuming that each node in the map represents a small circumscribed area of field or colliculus. However, as demonstrated in Figure 3, in some cases the projection of a small circumscribed area is extremely elongated, and within the elongated projection field there may be two or more foci (Fig. 3I,M). Table 3 shows that, in the F → C plots, the mean length of the major subaxis of the superposed projection field varies from 38 μm (WTs) to 239 μm (β2DKOs). In the C → F plots, the corresponding length of the superposed receptive field varies from 2.6° (WTs) to 38° (β2DKOs). The length of the minor subaxis is much less variable, between 30 and 68 μm and between 1.9° and 3.6°, respectively. As summarized in Table 3 and illustrated in Figure 3 for the primary datasets, examining the superposed receptive fields in the order WT, β2, HetTKO, HomTKO, and β2DKO reveals a progressive tendency for the C → F projection fields to become elongated along the nasotemporal axis (Fig. 3C,G,K,O). In the F → C plots, there is a corresponding progressive tendency for the superposed projection fields to become elongated along a direction at ∼−20° to the rostrocaudal axis (Figs. 3B,F,J,N). The relevant data are given in Table 3.

We asked whether these elongated distributions are an artifact of the method of measurement. In an elevational scan (which is used to determine the dorsoventral coordinate of visual field position), the total activity recorded at a single pixel on the colliculus is high, whereas in an azimuthal scan (determining the nasotemporal component of visual field position) this activity is lower (Cang et al., 2008). If the reliability of determining visual field position is greater when the activity is greater, visual field position along the dorsoventral axis would be determined more precisely than along the nasotemporal axis. As a result, the individual points making up a receptive field would be scattered more widely along the nasotemporal axis.

To test this possibility, we took WT data and for each eligible pixel we plotted visual field position against activity, for the elevational and the azimuthal scans separately The scatter in position seen for the elevational scan was found to be comparable with that for the azimuthal scan, where the activity levels were significantly lower (data not shown). Therefore, the elongated distributions do not seem to be caused by differences in signal strength.

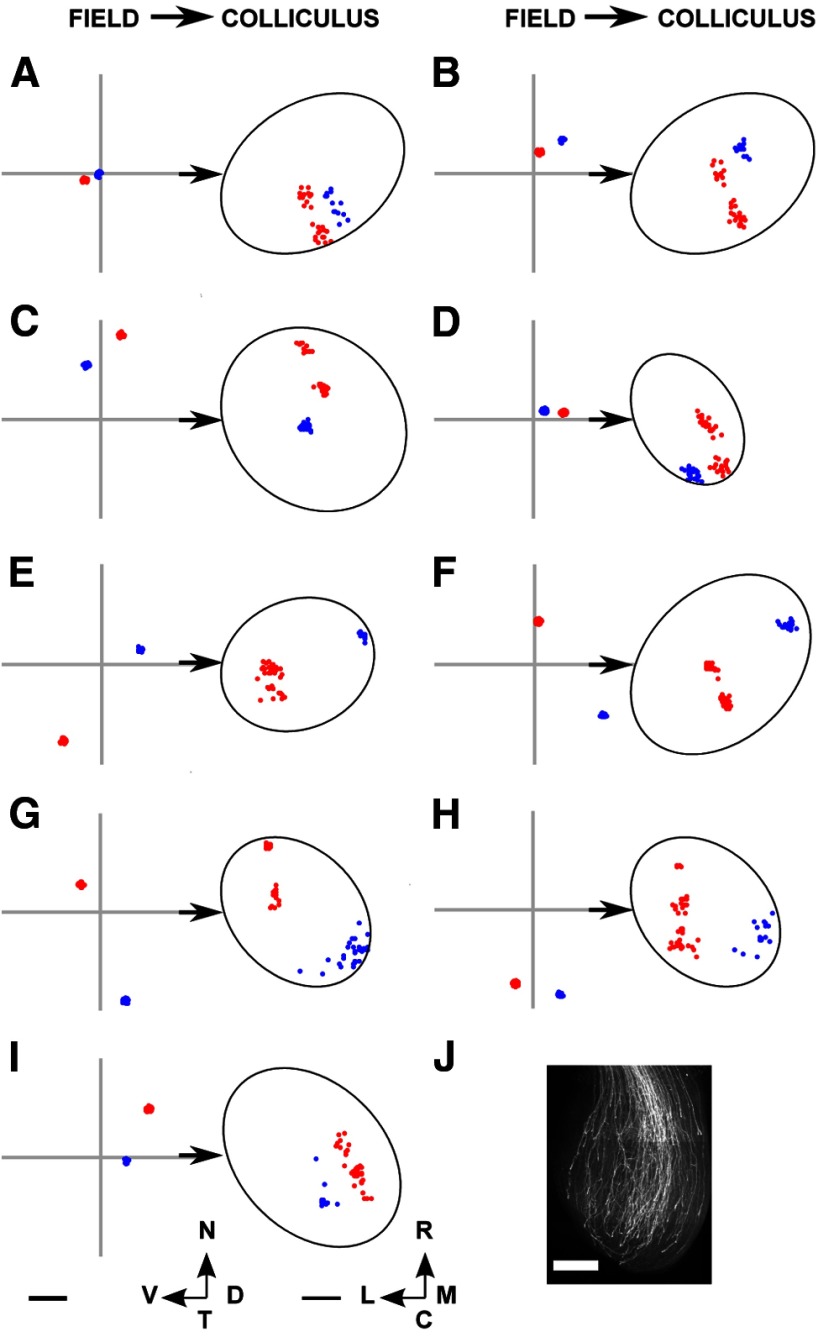
We looked for double projections within the collicular projection fields (Fig. 3I,M) by using the clustering algorithm described in Materials and Methods. Isolated occurrences of double projections were found among the WT and the β2 data, but they were more prevalent within the TKOs and the β2DKOs. Figure 12 gives examples of F → C projection fields for four different datasets from the HomTKO series. A range of projection fields was seen. Blue projection fields are those classified as single, and red ones were classified as double.

Figure 12.

The projection fields from selected nodes in the visual field from seven of the TKO datasets examined. A–D, HetTKOs. E–I, HomTKOs. In each subfigure, two examples are shown, distinguished by color. A red distribution was classified by the clustering algorithm described in Materials and Methods as representing a double projection (ectopic), and a blue distributions as a single projection. A, B, Corresponding largest ordered submap shown in Figure 9F. C, Corresponding submap shown in Figure 9B. D, Corresponding submap shown in Figure 9E. E, Corresponding submap shown in Figure 9I. F, Corresponding submap shown in Figure 9H. G, H, Corresponding submap shown in Figure 9K. I, Corresponding submap shown in Figure 9G. J, DiI staining of axon distribution over the colliculus at P1, courtesy of Robert Hindges. Scale bars: A–I, 250 μm (colliculus); J, 1 mm. Calibration: 20° (visual field). Other conventions as in Figure 2.

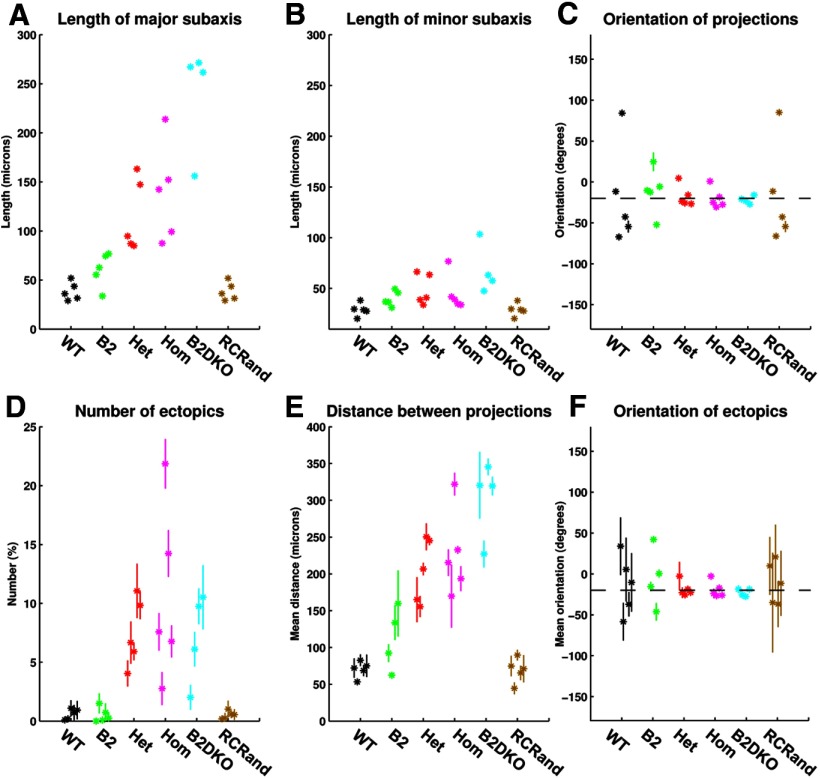
In Figure 13, we tabulate six measures relating to the projections from single areas of visual field to the colliculus, data for each of the 29 cases examined being shown separately. Figure 13A–C shows the properties of the ellipses fitted to the superposed projection fields from small circular areas of visual field where the lengths of the major and minor subaxes represent the corresponding SDs along the corresponding axes. Examining the groups in the order WT, β2, HetTKO, HomTKO, and β2DKO, the SD along the major axis of the ellipse increases (Fig. 13A), whereas that along the minor subaxis remains relatively unchanged (Fig. 13B). The orientation of the ellipse remains at −20° to the rostrocaudal axis (Fig. 13C). In these three figures, SDs calculated over the 20 replications are again very small. In contrast, Figure 13D–F shows the measures characterizing the ectopic projections, which show a wide variation of values over the 20 replications. There are very few ectopics in WT and β2 maps, with larger numbers in the other groups: 8% in HetTKOs, 11% in HomTKOs, and 7% in β2DKOs (Fig. 13D; Table 5). The distance between the two projection sites also varies widely over replications on the same data (Fig. 13E), with mean distances in the range of 70–300 μm. In all cases, the orientation of the line joining the two projections clusters at −20° to the rostrocaudal axis (Fig. 13F). The large SDs seen in Figure 13E, F are mainly seen in the groups where there are very few examples of ectopics. See Table 5 for the numerical data.

Figure 13.

Variation in the properties of the projection from small areas of visual field onto colliculus taken over 20 different placements of the nodes forming the map, for each of the 29 different sets of analysis. A, Length of the major subaxis of the ellipse characterizing the superposed projection fields (from small circular areas of field onto the colliculus). B, Length of the minor subaxis of the ellipse characterizing the superposed projection fields. C, Orientation of the major axis of the ellipse with reference to the rostrocaudal axis. The dotted line indicates an orientation of −20°, running from rostrolateral to caudomedial. D, Number of ectopic projections. E, Distance between the two termination sites involved in the ectopic projection. F, Orientation of the line joining the two termination sites forming the ectopic projection. The dotted line indicates an orientation of −20°. In all figures, data for each of the 29 cases are plotted separately. Means and SDs calculated over the 20 runs are shown. Most large SDs derive from data with very small numbers of ectopics. Color key as in Figure 11.

Table 5.

Characterization of the ectopic projections in F → C maps^a

Animal type	Number of nodes in the map	Percentage number of nodes projecting to ectopic sites	Distance between major and minor (ectopic) sites (μm)	Orientation of the line joining the major and minor (ectopic) sites (°)
WT	151 ± 13	0.60 ± 0.44b	70 ± 11	−13.3 ± 36.0
β2	109 ± 21	0.51 ± 0.62b	112 ± 43	−4.8 ± 36.8
HetTKO	127 ± 48	7.5 ± 2.9	205 ± 44	−18.5 ± 9.2
HomTKO	130 ± 25	10.6 ± 7.5	227 ± 58	−19.3 ± 9.9
β2DKO	114 ± 30	7.1 ± 3.9	303 ± 52	−22.6 ± 4.6

^aThe numbers of ectopics are expressed as percentages of the total number of nodes in the entire map. Means and standard deviations are based on the mean figures calculated from the 20 replications.

^bIn these groups the number of ectopics is of the order of 1 or 2 per map.

As illustrated in Figures 8C (HetTKO) and 10C (HomTKO), the nodes in the visual field, which give rise to ectopic projections tend to be clustered together, with the sites of termination in the colliculus also clustered. In most cases, the ectopic (minor) site was situated more caudally than the major site. Jianhua Cang also gave us a Fourier-based imaging dataset of one example of the double map found in animals where 50% of the retinal ganglion cells had acquired the EphA3 receptor (Brown et al., 2000). We found a very similar pattern of ectopics with 11% of the nodes in the F → C projection forming ectopic projections. At present, the Lattice Method cannot be used for analysis of the topography of such one-to-many mappings without an independent method of deciding which projection area belongs to which map.

Discussion

To examine detailed hypotheses about mechanisms for the formation of ordered nerve connections requires a quantitative approach. Our Lattice Method enables a quantitative assessment of the topographic ordering in the one-to-one map between two structures. By plotting how small areas in one structure are represented in the other structure, the ordered one-to-one portion of the map can be found, even in an apparently disordered projection. The measures developed are invariant to the absolute size of the map and do not involve assumptions about the precise positions to which individual locations project. This method provides a more detailed assessment of topography than previous general methods (Goodhill and Sejnowski, 1997; Vidaurre and Muruzábal, 2007). We have applied the Lattice Method to Fourier-based intrinsic imaging data from the mouse retinocollicular system (Cang et al., 2008), developing techniques to overcome the intrinsic limitations of the Fourier techniques. We examined in detail the projections made in each part of the map. This enabled us to estimate the degree of local order and the orientation of both WT and knock-out maps. Furthermore, we established that triple knock-out ephrinA maps are inhomogeneous and contain a high degree of residual order along the rostrocaudal axis. We verified that the large variability between individual maps found in some of the mutant series is a true variation and not an artifact of the method. The phase scatter measure used in previous analysis (Cang et al., 2005, 2008) provides only two numbers per map and does not capture the inhomogeneities within mutant maps.

Precision and order in the WT and β2 knock-out maps

In WT maps, on average 150 distinct collicular locations, at a spacing of ∼54 μm and representing a small circular area of radius ∼27 μm, are represented in the visual field in the correct relative order. Receptive field size is close to that expected if the individual 9 μm × 9 μm pixels in the image were projected in the correct topographic order. This is an ordering of higher precision than found previously. Dräger and Hubel (1976) found topographic ordering using electrodes placed 200 μm apart; the spacing between neighboring points in the ordered maps obtained by standard intrinsic imaging (Mrsic-Flogel et al., 2005) was ∼120 μm. The ordered WT map has a consistent orientation, with the rostrocaudal axis projected at 21° to the nasotemporal axis, in agreement with Dräger and Hubel (1976). The same orientation was found in the projection from visual field onto colliculus. Characterizing WT maps provides a firm basis for assessing experimental maps.

The β2 knock-out maps cover substantially less of the visual field and colliculus than WT maps but are almost as ordered. The visual fields are elongated along the nasotemporal axis, in agreement with other studies (Chandrasekaran et al., 2005). The projection fields on the colliculus are also elongated, being largest in areas where nearest-neighbor order is lost. This local disorder may be the result of the elongation of the axonal arbors (compare Fig. 7A with Fig. 7C, Fig. 8A with Fig. 8D, and Fig. 10A with Fig. 10D). Elongated projection fields in the colliculus occur in both developing (Chandrasekaran et al., 2005) and adult β2 knock-out maps (Pfeiffenberger et al., 2006).

The determinants of order along the rostrocaudal axis

Eph–ephrin interactions are thought to specify the approximate positions of retinal axons on the colliculus (Feldheim et al., 1998; McLaughlin and O'Leary, 2005), the map then being refined by neighbor–neighbor interactions mediated by electrical activity (e.g., see Pfeiffenberger et al., 2006). We examined data from animals in which ephrinA2, ephrinA3, and ephrinA5 had been knocked out. Normally, these ligands are distributed in graded form across the rostrocaudal dimension of the colliculus (McLaughlin and O'Leary, 2005), and so their knock-out might be expected to remove rostrocaudal order. We confirmed that there is apparent disorder, but this masks an underlying order, which we uncovered by finding the largest ordered one-to-one submap. In the 10 TKO maps examined, there was nonuniform coverage of both visual field and superior colliculus, resulting in a variety of maps (Fig. 9), some of which approached the order in WT maps. In the two HetTKOs where the ephrinA5 gradient is retained at half its normal strength, the maps are of higher quality (Fig. 9A,B) than in the three HetTKOs, which retain a half-strength ephrinA3 gradient (Fig. 9D–F). These results suggest that this might be because the ephrinA5 gradient across the colliculus is pronounced, whereas the ephrinA3 gradient is weak or absent (Pfeiffenberger et al., 2006).

To investigate the relative roles played by molecular and electrical signaling in the formation of an ordered map, we compared data from four different types of knock-out: β2, HetTKO, HomTKO, and β2DKO. In all cases, order along the mediolateral axis was indistinguishable from that in the WT (Fig. 11C). In pure ephrinA knock-outs (HetTKO and HomTKO), the rostrocaudal order found in wild types is degraded but not destroyed (Fig. 11D). This order is significantly greater than the order in wild types in which the rostrocaudal order had been abolished (RCrand; Fig. 11D; Table 4). This establishes that ephrinAs are not the sole determinants of rostrocaudal order.

Electrical signaling is usually thought to affect neighbor–neighbor interactions (i.e., local order). This agrees with our finding that the difference in order between β2 knock-outs and WTs is in the degree of local order (Fig. 11B; Table 4). If map orientation is controlled by neural activity, this cannot be through nearest-neighbor interactions, as these can only determine local relative order (Willshaw and von der Malsburg, 1976). A possibility could be a molecular-based mechanism not involving EphA/ephrinA interactions, which is gated by neural activity.

One way of testing the role of electrical signaling is to look at mutants with knock-out of the β2 receptor as well as of the three ephrinAs. We found that, in the double ephrinA/β2 knock-out maps (β2DKO), the order is significantly different from that found in random controls (RCrand). However, clear conclusions about how far activity-mediated neighbor–neighbor interactions contribute to the residual rostrocaudal order cannot be drawn. This is because the order in β2DKOs is not clearly distinguishable from that in the TKOs, each type of mutant contains different configurations of ephrinAs, and the β2DKO data are poor, as assessed by the low total level of signal within the collicular region (Table 1).

Ectopic projections

The receptive fields are elongated strictly along the nasotemporal axis. We examined the similarly elongated projection fields for signs of two distinct projection sites, which we treated as evidence for ectopic projections. In the five β2 knock-out maps, an occasional ectopic projection was found. In contrast, ectopic projections have been found in young β2 knock-out mice by both physiological (Chandrasekaran et al., 2005; Xu et al., 2011) and anatomical (Dhande et al., 2011) means. This difference may be due to age as the data that we analyzed came from mice aged between 2 and 6 months.

In the TKO data, ∼9% of the nodes in the visual field have ectopic projections. The straight line joining the two projection sites tends to lie in the direction along which the nasotemporal axis projects (Figs. 8C and 10C). In many cases, the averaged position of the two termination regions forming an ectopic projection is in the appropriate position to be part of an ordered map (compare Fig. 8B with Fig. 8C, and Fig. 10B with Fig. 10C).

Ectopic projections have been identified in ephrinA knock-outs (Feldheim et al., 1998, 2000; Frisén et al., 1998; Pfeiffenberger et al., 2006). Our analysis is the first to characterize quantitatively the ectopics within a single map. Rather than being associated with a disordered map, in TKO maps ectopic projections coexist with a topographically ordered projection and are associated with low or zero levels of ephrinAs. It is noteworthy that the relative positioning of the two sites of projection is along the direction in which the nasotemporal axis of visual field is projected onto the colliculus as this direction corresponds approximately to the direction of ingrowth of retinal axons, which initially extend rostrocaudally to form a diffuse projection before becoming localized (Simon and O'Leary, 1992; McLaughlin et al., 2003) (Fig. 12J).

Our results suggest further investigations, including the following: (1) application of the Lattice Method to further examples of the TKO and β2DKO types to completely characterize these inhomogeneous classes of maps found, such as those from the two types of HetTKOs; (2) application of the Lattice Method to ephrinA2 and ephrinA5 double knock-out maps to provide a better comparison with the effects of β2 knock-out on ephrinA knock-outs; (3) characterization anatomically of ectopic projections in both young and adult TKOs, particularly how the relative orientation of the two termination sites relates to the direction of fiber ingrowth; and (4) investigation of the nature of the maps and projections from small areas of visual field or retina in ephrinB knock-out animals. As well as establishing how far ephrinBs determine mediolateral order in a topographic map, this approach could be used together with the suggested anatomical investigation to test hypotheses about the role of fiber ingrowth in map formation.