Hierarchical clustering of high-throughput expression data based on general dependencies

Abstract

High-throughput expression technologies, including gene expression array and liquid chromatography – mass spectrometry (LC-MS) etc., measure thousands of features, i.e. genes or metabolites, on a continuous scale. In such data, both linear and nonlinear relations exist between features. Nonlinear relations can reflect critical regulation patterns in the biological system. However they are not identified and utilized by traditional clustering methods based on linear associations. Clustering based on general dependencies, i.e. both linear and nonlinear relations, is hampered by the high dimensionality and high noise level of the data. We developed a sensitive nonparametric measure of general dependency between (groups of) random variables in high-dimensions. Based on this dependency measure, we developed a hierarchical clustering method. In simulation studies, the method outperformed correlation- and mutual information (MI) – based hierarchical clustering methods in clustering features with nonlinear dependencies. We applied the method to a microarray dataset measuring the gene expression in cell-cycle time series to show it generates biologically relevant results. The R code is available at http://userwww.service.emory.edu/~tyu8/GDHC.

1 INTRODUCTION

High-throughput expression data, such as microarray gene expression data, liquid chromatography – tandem mass spectrometry (LC/MS/MS) proteomics data, and liquid chromatography – mass spectrometry (LC/MS) metabolomics data [1–3], contain measurements on thousands of features (genes, proteins or metabolites) on a continuous scale. In the context of unsupervised learning, several types of approaches can be used to simplify the data and provide indications on the relationships between features [4]. Among them the most prominent ones include dimension reduction to reduce the data to lower dimensional subspace [4–6], clustering to group features with similar or related expression profiles [7, 8], and profile-based approaches aiming at finding features that show specific behaviors [9, 10] including very flexible patterns [11].

Clustering can reveal global patterns and reduce the number of features for the purpose of data interpretation. Various similarity measures and models were proposed, most of which are based on linear association or geometric proximity between data points [7]. Hierarchical clustering is a popular approach in the study of high-throughput data. It is computationally feasible when tens of thousands of features are to be clustered, and the results are easy to interpret [12].

Nonlinear and complex dependencies have been known to exist between biological units. Examples include clear non-linear associations between genes in high-dimensional gene expression data [13], and gene pairs that change correlation patterns conditioned on the level of other genes or experimental conditions [14, 15]. General dependency measures such as mutual information (MI) have been used successfully in the inference of gene regulatory networks [16–18]. In a previous work, we developed a distance between features based on general dependency, which showed improved performance in microarray missing value imputation compared to its linear counterpart [19].

Here we consider the problem of clustering features based on general dependency that includes both linear and nonlinear relationship. The difficulty in developing such a method is four fold. First, features having nonlinear relations may not be close to each other in the high-dimensional space. Second, with nonlinear relations between features in a cluster, it is difficult to define a cluster profile. Here we use “profile” to refer to a set of values that can summarize a cluster. For example, in clustering based on geometric proximity such as K-means clustering, the mean vector is used to describe the cluster. In model based clustering, the summary of a cluster may be more complex, including both the mean vector and the variance-covariance matrix [7]. Third, nonlinear relations are more easily concealed by random additive noise compared to linear relations, and high-throughput data often contain high levels of noise caused by biological variations and measurement errors. Fourth, the large number of features in the data prohibits the use of methods that accurately model nonlinear relationships, but at a high computational cost. An example is the class of methods named principal curves, which estimate a smooth curve that passes through the middle of a cloud of data points, i.e. a nonlinear generalization of the first principal component [20, 21]. Such methods are too computationally costly to be used on datasets with thousands of features.

To address these issues, we developed a clustering method based on a general dependency distance, a new definition of cluster profile, combined with an agglomerative clustering scheme. Statistical properties of the distance were developed to guide results interpretation. In the following discussions, we refer to our method as GDHC (General Dependency Hierarchical Clustering). For statistical inference, we consider the measurement values of the features, i.e. the data points, as realizations of random variables.

2 METHODS

2.1 A general dependency distance between two variables

We first defined the Distance based on Conditional Ordered List (DCOL) between a pair of random variables in [19]. Here we consider two random variables X and Y. Briefly, we sort the data {(x_i, y_i)} by the x values:

$$\left\{\right(x_i^{*},y_i^{*}\left)\right\}:x_1^{*}\le x_2^{*}\le \dots \le x_n^{*}.$$ (1)

Then we take the sum of absolute differences between the adjacent y values in the ordered list,

$$d_{col}(Y|X)=\frac{1}{n-1}\sum _{i=2}^n|y_i^{*}-y_{i-1}^{*}|.$$ (2)

When the spread of Y|X is small, the distance is small.

2.2 Limiting distribution of DCOL when X and Y are independent

We develop the distribution of d_col (Y | X) under the null hypothesis that there is no dependency between the two random variables. Under the null hypothesis, sorting the data pairs {(x_i, y_i)} based on the x values is equivalent to a random re-ordering of the y values, and adjacent y values in the re-ordered list are simply i.i.d. samples from the underlying distribution of Y. Let z_i = |y_i+1 − y_i|. The sequence of z_i is 1-dependent. In two scenarios, we can show that the distribution of $d_{col}(Y|X)=\frac{1}{n-1}{\sum }_{i=1}^{n-1}{z}_i$ is asymptotically normal following Billingsley (theorem 27.4) [22]. The first scenario is Y follows a normal distribution. The second scenario is Y follows an arbitrary bounded domain distribution, i.e. a distribution supported on a bounded interval [a, b], where a and b are two finite real numbers. The cumulative density function F() follows

$$F(a-)=0,0<F(y)<1\mathit{\text{for}}a<y<b,\mathit{\text{and}}F(b+)=1$$ (3)

For details please refer to Supporting File 1. We note that the bounded domain distribution scenario covers high-throughput expression data, because in every sample analyzed, each gene/protein/metabolite can exist only in a finite amount. Thus under the null hypothesis of independence, d_col(Y|X) always converges to normal when n is large.

When Y is drawn from a normal distribution, we can derive theoretical mean and variance of d_col(Y|X) under the null. If we normalize Y to be standard normal, we can show that the expectation of d_col(Y|X) is $\mu =\frac{2}{\sqrt{\pi }}$, and the variance

$${\sigma }^2={\text{lim}}_{n\to \infty }E({(Z-\mu )}^2)=4(2\pi +3\sqrt{3}-9)/3\pi .$$ (4)

For details please refer to Supporting File 1.

When normality of Y cannot be assumed, we can resort to permutation to obtain the mean and variance. Under the null hypothesis, sorting the data pairs {(x_i, y_i)} based on X is equivalent to a random re-ordering of Y. We repeatedly re-order the y vector in random to generate permuted vectors ${\{{\mathit{y}}^{*(j)}\}}_{j=1}^m$, and compute the DCOL distances from the permuted vectors,

$$Z^{(j)}=\frac{1}{n-1}{\sum }_{i=1}^{n-1}|y_{i+1}^{*(j)}-y_i^{*(j)}|,j=1,\dots ,m.$$ (5)

We then take the sample mean and sample variance of ${\{Z^{(j)}\}}_{j=1}^m$ as the estimates of μ and σ² of the DCOL under the null hypothesis that X and Y are independent, and calculate the p-value based on $\frac{d_{col}(Y|X)-\mathrm{\mu ̂}}{\mathrm{\sigma ̂}}$ and the standard normal distribution. The null distribution only depends on the Y values, but not on the X values.

2.3 Clustering strategy 1: agglomerative hierarchical clustering based on DCOL

In the following sections we consider a data matrix G_p×n with p features measured at n conditions. Let g_i represent the vector of expression levels of the i^th feature. Our interest is to cluster the p features based on the general dependency between them.

First, we randomly permute the columns of the data matrix and compute the DCOL for each feature (row) m times to estimate the feature-specific null distribution parameters μ_i and ${\sigma }_i^2$, i = 1, …, p. Note the null distribution is with regard to any other gene, and this procedure bears no meaning with regard to the biological conditions.

In this study we used m = 500. Based on our discussion in the previous section (above eq. 5), the null DCOL distribution of gene i only depends on its own expression values, not on the values of other genes. That is why we can generate μ_i and ${\sigma }_i^2$ just once, and use them to judge the relations between gene i with any other gene.

Second, we find the DCOL distance matrix D_p×p, in which

$$d_{i,j}=d_{col}(g_i|g_j),$$ (6)

following the procedure described in section 2.1, eq. 1 and 2.

Third, we find the significance level of each d_i,j by comparing it with the feature-specific null distribution and obtaining the one-sided p-value on the left tail of the distribution. Then we take the log p-values as the similarity measure. After this step, we have a similarity matrix, S_p×p, with elements

$$s_{i,j}=\mathit{\text{log}}\left(\mathrm{\Phi }\right(\frac{d_{col}(g_i|g_j)-{\mathrm{\mu ̂}}_i}{{\mathrm{\sigma ̂}}_i}\left)\right),$$ (7)

where Φ() is the CDF of the standard normal distribution, and μ̂_i and σ̂_i are the feature-specific parameter estimates of gene i found by permutation. The reason for not using DCOL distance directly is because the same DCOL can mean different significance levels for different features depending on the feature-specific distributions.

Once we have the S matrix, we can use two alternative approaches for clustering. The first is relatively simple - using the agglomerative procedure of hierarchical clustering. We obtain the symmetrized matrix S* by taking

$$s_{i,j}^{*}=s_{j,i}^{*}=\mathit{\text{min}}(s_{i,j},s_{j,i}),i=1,\dots ,p,j=1,\dots ,p.$$ (8)

The reason for symmetrizing the matrix by taking minimum is that either a significant d_col(g_i|g_j) or a significant d_col(g_j|g_i) signify dependency between the two genes g_i and g_j. In some situations of non-linear relationship, only one of the DCOL value is small. An example is plotted in the Figure 1 of [19]. Elements of the S* matrix are all negative, with lower values signifying stronger association. We add a constant to make all the non-diagonal values positive. The choice of the constant doesn’t impact the clustering outcome. Then we apply the standard agglomerative hierarchical clustering approach using the S* matrix as the distance matrix [7].

Figure 1.

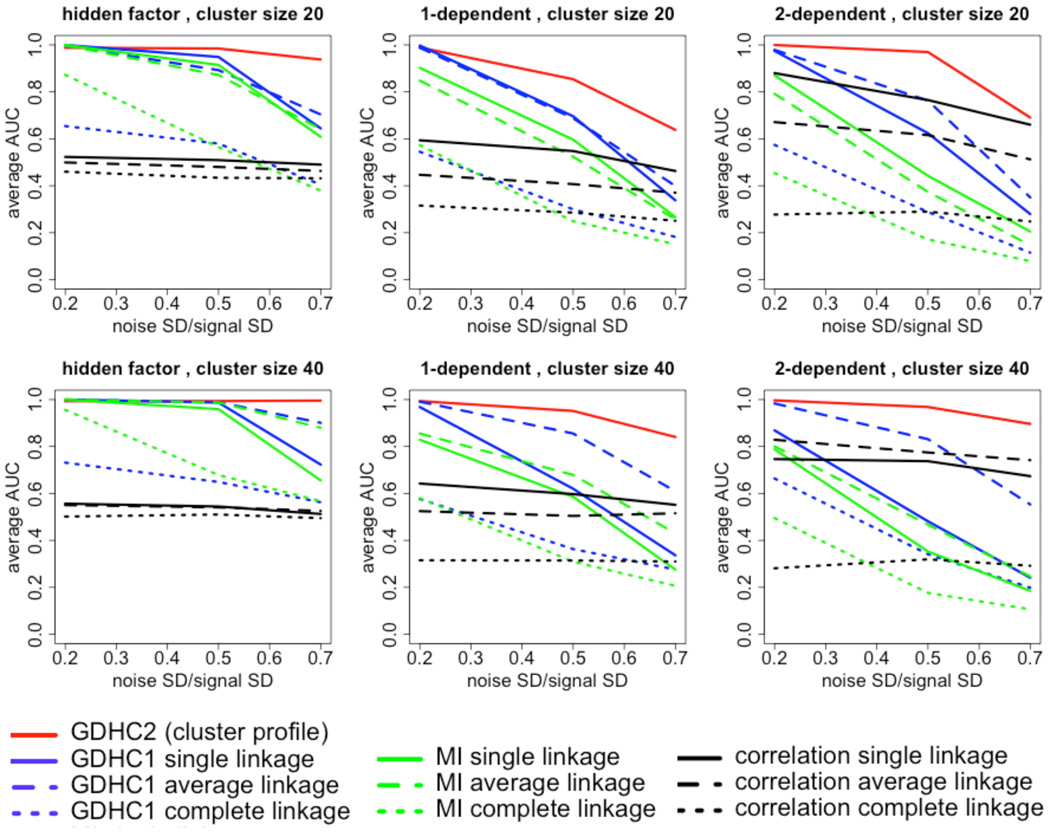
Simulation results. The average AUC of the sensitivity-FDR curve is plotted against the noise level. Higher AUC values indicate better performance. Every column represents a situation. Column 1: all features in a true cluster are linearly/nonlinearly linked to a latent factor. Column 2: features in each cluster are constructed using the 1-dependent procedure. Column 3: features in each cluster are constructed using the 2-dependent procedure. Upper row: true cluster size 20; lower row: true cluster size 40.

In the second approach (next two sections), instead of using only the pairwise similarities between features, we seek to find a profile to represent each cluster, and define similarities between clusters using it. In section 2.4, we extend DCOL-based similarity from between random variables to between random vectors. Then we develop the clustering scheme in section 2.5.

2.4 Extending DCOL-based similarity to higher dimensions

Consider two random vectors, U = (X₁, X₂, …, X_K) and V= (Y₁, Y₂, …, Y_L), each representing the set of features in a cluster, measured in an n-dimensional space. To define a similarity between the random vectors, we use the simple consideration – for U and V to be linearly or nonlinearly associated in the form of V = f(U) + ε, where f() is an unknown continuous mapping f: R^K → R^L, and ε is additive noise of dimension L with mean zero, when two u values are close, the corresponding v values also tend to be close. Yet in the nonlinear case, when two u values are far apart, the corresponding v values need not necessarily be far apart. This is the same consideration that the original DCOL is based on [19]. Here we define the cluster profile using the shortest Hamiltonian path, which is the shortest traversal through the n points, visiting each point exactly once. This profile definition uses a set, but not all, of between-point distances that are small.

First, we find the shortest Hamiltonian path through the n points in the K-dimensional space of U. Solving for the shortest Hamiltonian path is intrinsically related to the traveling salesman problem, and a mature literature and a number of existing methods can be used [23]. In this study we use one of the leading methods for solving the traveling salesman problem, the Lin-Kerninghan algorithm [24].

Second, we re-order the n points {Y₁, Y₂,…, Y_L} using their order in the traversal found in the previous step, ${\mathit{\upsilon }}_{\mathbf{1}}^{*}\to {\mathbf{\upsilon }}_{\mathbf{2}}^{*}\to \cdots \to {\mathbf{\upsilon }}_{\mathit{n}}^{*}$. We find the DCOL distance of each Y_l variable given the order by U,

$$d_{col}({\mathit{Y}}_{\mathit{l}}|\mathit{U})={\sum }_{i=2}^n|y_{l,i}^{*}-y_{l,i-1}^{*}|.$$ (9)

Third, let μ̂_l and σ̂_l be the parameter estimates of the null distribution of the Y_l variable found by permutation. We then find the statistic for each variable Y_l,

$$b_l=\frac{d_{col}({\mathit{Y}}_{\mathit{l}}|\mathit{U})-{\mathrm{\mu ̂}}_l}{{\mathrm{\sigma ̂}}_l},l=1,\dots ,L.$$ (10)

We take the mean value of the b_l statistics, and compare it to the standard normal distribution to find the significance level of the association:

$$s_{V,U}=\mathit{\text{log}}\left(\mathrm{\Phi }\right(\frac{1}{L}{\sum }_{l=1}^L{b}_l\left)\right),$$ (11)

Here we define the significance of the association between two random vectors (groups of variables), without explicitly defining their DCOL distance. This is because each individual variable may have substantially different null distributions, in which case directly adding their DCOL distance is not sensible. The heuristic procedure in equation 11 is inspired by the extensive use of average test statistics in the field of gene set analysis [25].

Similar to the single variable case, the between-group similarity s_V,U and s_U,V are not symmetric. We take the smaller value, min(s_V,U, s_U,V), as the similarity score between the two random vectors (clusters). Notice when each random vector contains only one random variable, this definition of similarity naturally reduces to that between a pair of variables as defined in section 2.2.

2.5. Clustering strategy 2: agglomerative hierarchical clustering between-random vector similarities

This procedure is similar to the agglomerative hierarchical clustering in section 2.3. The difference is that the distance between two clusters are found using the method described in the previous section, rather than the regular single/average/complete linkage methods. Starting from the two features with the lowest log p-value, we iteratively merge items. In every step, the between-cluster distance is calculated as described in section 2.4, eq. 9~11. After all features are merged into a single cluster, the tree cutting can be performed either based on a p-value cutoff, or using the topology-based dynamic tree-cutting procedure [26].

2.6 Simulation study

Each simulated dataset contained 1000 features (rows) and 80 observations (columns). Among the 1000 features there were 20 clusters. Two cluster size values were used: 20 and 40. Within each cluster, the features were linearly or nonlinearly related. We used four link functions – (1) linear, X_j = X_i + ε; (2) sine curve, X_j = sin(2X_i − 2μ_Xi) + ε; (3) square function, X_j = (X_i − μ_Xi)² + ε; and (4) absolute value, X_j = |X_i − μ_Xi| + ε.

In each simulated dataset, clusters were generated separately. After the matrices corresponding to different clusters were generated, they were row-combined to generate the simulated data matrix. If the total number of features was less than 1000, additional pure noise features were generated to make the total number of features (rows of the matrix) 1000. The true cluster membership of each simulated feature was known. We then analyzed the data matrix with the proposed and other methods to find if a method would recover the known hidden cluster membership faithfully.

The clusters were constructed in three different ways. The first was the latent variable approach. To construct a cluster,

1. A latent factor z was generated from the standard normal distribution.

2. The features in the cluster were generated one-by-one. Each feature in the cluster was dependent on the latent factor: x^(new) = f(z) + ε. The link between the feature and the latent factor f() was randomly drawn from the four possible link functions described above. Various levels of noise were added (noise S.D./signal S.D.=0.2, 0.5, 0.7). The noise S.D. refers to the S.D. of ε, and the signal S.D. refers to the S.D. of x^(new) before adding noise.

3. We iterated step (2) until the desired cluster size was reached.

The second approach of data generation was the 1-dependent approach. To construct a cluster,

1. We generated the first feature from the standard normal distribution.

2. The other features in the cluster were generated one-by-one. For every newly generated feature, we randomly selected one existing feature in the cluster, and made the new feature dependent on the selected existing feature: x^(new) = f(x^(selected)) + ε. Again the link function f() was randomly drawn from the four possible link functions. Various levels of noise were added (noise S.D./signal S.D.=0.2, 0.5, 0.7). The noise S.D. refers to the S.D. of ε, and the signal S.D. refers to the S.D. of x^(new) before adding noise.

3. We iterated step (2) until the desired cluster size was reached.

The third approach of generating the clusters was 2-dependent. It was similar to the 1-dependent approach, except each newly generated feature was dependent on two randomly selected existing features: x^(new) = β₁f(x^(selected_1)) + β₂g(x^(selected_2)) + ε, where the two link functions f() and g() were independently drawn from the four possible link functions, and the β′s were independently drawn from the uniform(−1, 1) distribution.

At each parameter setting, 50 datasets were simulated and analyzed separately. The average results were used to gauge the performance of clustering methods. Our methods were compared with two other hierarchical clustering methods – (1) Regular hierarchical clustering (single/average/complete linkage) using the matrix of one minus correlation coefficient between variable pairs as distance matrix. (2) Regular hierarchical clustering (single/average/complete linkage) using the matrix of mutual information (MI) – based distance between variable pairs. The observations of each feature were first discretized using equal frequency bins, i.e. each bin contains the same number of observations. Then the empirical mutual information was calculated between every pair of features [17]. The MI values were transformed into a distance measure using the method by Joe [27], $D(X_i,X_j)=1-\sqrt{1-e^{-2MI(X_i,X_j)}}$. Three bin numbers (3, 4, and 5) were used in each simulation setting, and the results from best-performing bin number value was reported.

To judge the performance of a method, we cut the hierarchical clustering tree at all clustering heights, i.e. the p-1 values associated with the merges, from the bottom to the top of the tree. With every tree cut, some features are clustered. We translate this result into pairwise co-clustering between features. We find the sensitivity (percentage of feature pairs truly belonging to the same cluster being clustered together) and the false discovery rate (FDR, number of feature pairs not belonging to the same true cluster being clustered together, divided by all pairs of features clustered together). This approach is inspired by the widely used Rand Index to judge the agreement between clustering results [28], which uses the information of pairwise co-clustering between features. However in this study, a large number of simulated features do not belong to any cluster and the Rand Index cannot be applied. Thus we use the sensitivity-FDR approach to compare clustering results to the truth [29, 30], which is a variant of the receiver operating characteristic (ROC) curve. The traditional ROC curve is not suitable here because the true negative (TN) count is magnitudes higher than the true positive (TP) count. We calculate the area under curve (AUC) of each sensitivity-FDR curve. The AUC values are compared between the methods. Higher AUC value means the method recovers the true clusters with higher fidelity.

3 RESULTS

3.1. Simulation results

We compared the two variants of GDHC with two other hierarchical clustering methods in terms of AUC under the sensitivity-FDR curve (Fig. 1). Higher values in the plot indicating higher AUC, hence higher fidelity in true cluster recovery. We will refer to the GDHC using traditional agglomerative approach as GDHC1, and the GDHC using cluster profiles as GDHC2. We tried three linkage methods for GDHC1, MI and linear hierarchical clustering – the single linkage, average linkage and complete linkage methods.

Under the hidden factor data generation mechanism, i.e. every variable in a cluster is related to the same hidden factor with a linear/nonlinear link, GDHC2 clearly outperformed other non-linear methods when the noise was medium or high (Fig. 1, left column). In addition, clustering based on linear relations (black curves) trailed most nonlinear methods.

In the 1-dependent data generation scenario (Fig. 1, middle column), GDHC2 achieved the best AUC in all noise settings. Similar to the hidden factor scenarios, GDHC1 with average linkage clustering approached GDHC2’s performance when the noise was low to medium. Although GDHC1 and MI methods used the same agglomerative scheme, their performance is very different, indicating an advantage of the DCOL distance measure over MI, at least in the simulation settings. The performance of GDHC1 dropped much faster than GDHC2 with the increase of noise. One plausible explanation is that GDHC2 was more noise-resistant because it re-estimates the cluster profile in every iteration, thus reducing the impact of noise by pooling information from multiple features in the cluster.

With the 2-dependent data generation mechanism, partial linear relations become more pervasive between the features within a true cluster. Thus the linear method sees an improved performance compared to the other two scenarios (Fig. 1, right column). However GDHC2 still led the performance at all noise levels. GDHC1 with average linkage performed the second at low to medium noise settings, yet it was surpassed by linear method at high noise level. This is because linear relation is much less sensitive to additive noise compared to nonlinear relations. Overall, GDHC2 achieved better performance than the other methods in the simulations, and GDHC1 with average linkage closely followed.

3.2. Real data analysis – the yeast cell cycle microarray data

The Spellman yeast cell cycle data consists of four time-series synchronized by different reagents, each covering roughly two cell cycles [31]. One of the time series, the cdc15 data, contains a strong oscillating signal that is not cell-cycle related [15]. We removed the cdc15 dataset and used the three remaining time series. The data consists of 49 conditions and 6178 genes. A number of cell cycle – related genes exhibited strong periodicity in expression [15, 31, 32].

We applied the GDHC methods to the cell cycle data, together with MI and linear hierarchical clustering. We used average linkage for all the methods as it is the most used linkage function in hierarchical clustering of genes. In order to compare the methods, we applied the dynamic tree cutting method [26] to cut each tree with a limit of minimum cluster size of 50. We then judged the performance of the methods using functional annotations – finding the proportion of gene pairs in the same cluster that are functionally related based on Gene Ontology (GO) [33].

We used two sets of GO terms. The first is a set of broader terms – the GO Slim terms downloaded from the Saccharomyces Genome Database (SGD) [34]. Because some of the GO Slim terms are too broad, we limited our analysis to terms with 2000 annotated genes or less. The second set of GO terms are more specific. We selected biological processes using an organism-specific procedure modified from a method we described before [35–37]. Briefly, the procedure examined the number of yeast genes assigned to each GO term and its direct descendants. It ignored all terms with less than 5 assigned genes. Starting from the term “biological_process”, it examined if 40% of the term’s genes (70% if the term contains less than 500 genes) were assigned to its children terms. If the answer was yes, the term was abandoned for being too broad, and its children terms were examined one-by-one using the same criterion; if the answer was no, the term was kept in the final collection. The procedure continued until all biological process terms were exhausted. Due to the structure of the GO system, a small fraction of the terms in the collection had ancestor-descendant relations, in which case the descendant terms were eliminated. The final selection contained 430 GO biological process terms.

Table 1 shows the comparison of the functional relations between co-clustered genes. We see that the four methods clustered similar number of genes into similar number of clusters. GDHC1 with average linkage achieved the best result in terms of genes sharing functional annotations, both using the GO Slim terms and using the more specific terms selected by our method. The linear method was slightly better than GDHC2 and MI, which performed similarly. In simulations, GDHC2 led the performance, and GDHC1 with average linkage achieved the second best performance. The difference between real data analysis and the simulations indicate some different characteristics in the data. One of the main reasons may be the more prevalent linear associations in the real data.

Table 1.

Comparing the clustering methods using functional annotations.

Method	Boxplots of cluster sizes	# Clusters	# Genes clustered	% Clustered genes belonging to same GO slim#	% Clustered genes belonging to same selected GO terms$
Linear average linkage		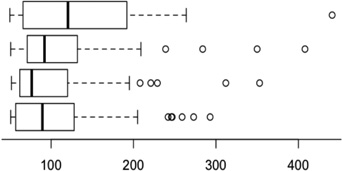50	4502	26.5%	14.4%
MI average linkage		54	4565	25.6%	13.9%
GDHC2 (cluster profile)		48	4585	25.7%	13.8%
GDHC1 average linkage		42	4659	28.5%	15.9%

^#Limited to GO slim terms with 2000 or less yeast genes assigned. Percentage between random gene pairs: 22.6%.

^$Percentage between random gene pairs: 11.0%

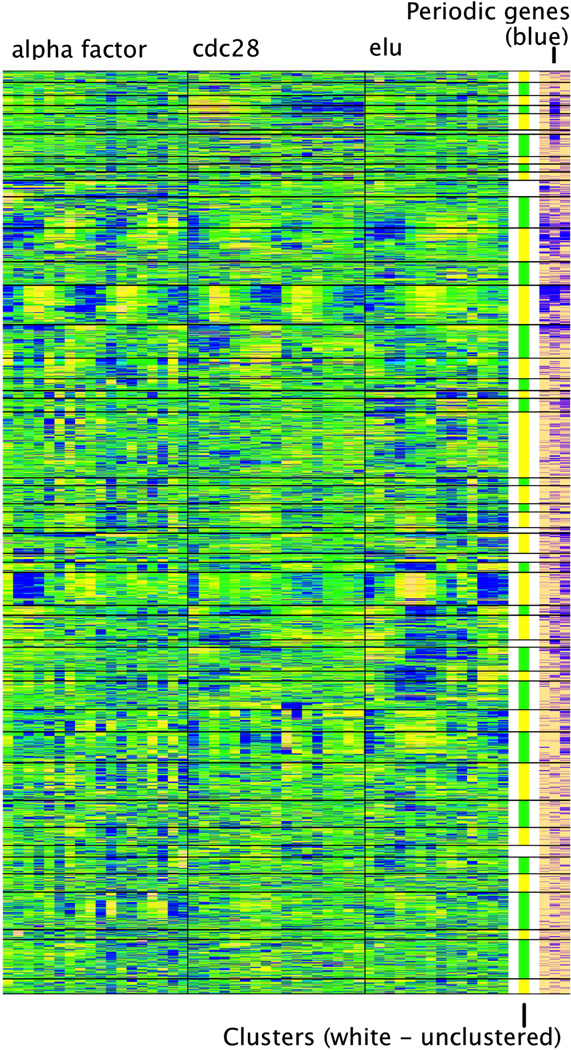
Figure 2 shows the clustering results by GDHC1 with average linkage. Denoted by horizontal lines, each block is a cluster of genes found by dynamic tree cutting. The three right columns of Figure 2 indicate genes with periodic behavior found by the Fisher’s exact g test for periodicity [38]. The three indicator columns represent the three time series experiments respectively. We can clearly see a few clusters are dominated by genes with periodic behavior. To analyze functional relevance of the clusters, we resorted to gene set enrichment analysis using the GOstats [39]. We used the 430 selected gene ontology biological processes [33]. We applied the hypergeometric test to find if genes in the clusters were associated with the GO terms. At the p-value cutoff of 0.01, three clusters showed strong enrichment of cell-cycle related GO terms. Among the GO terms associated with them, cell cycle terms represent 26/32 (81%), 11/19 (58%), and 3/9 (33%) respectively, while cell-cycle related terms represent 15% of the 430 selected terms. Three clusters showed strong enrichment of translation-related terms. Among the GO terms associated with them, translation related terms represent 7/11 (64%), 7/8 (88%), and 5/8 (63%) respectively, while translation related terms represent 3.5% of the 430 selected terms. Five clusters showed strong enrichment of RNA metabolism terms. Among the GO terms associated with them, RNA metabolism terms represent 3/7 (43%), 8/11 (73%), 3/8 (38%), 6/7 (86%), and 5/8 (63%) respectively, while RNA metabolism terms represent 12% of the 430 selected terms.

Figure 2.

Plot of clustering results using GDHC with average linkage. The tree was cut using dynamic tree cutting with a limit of minimum cluster size of 50. Indicator of periodic genes (right): blue indicate the gene was identified as periodic gene using Fisher’s exact g test for periodicity [38]. The three columns represent the three cell cycle datasets.

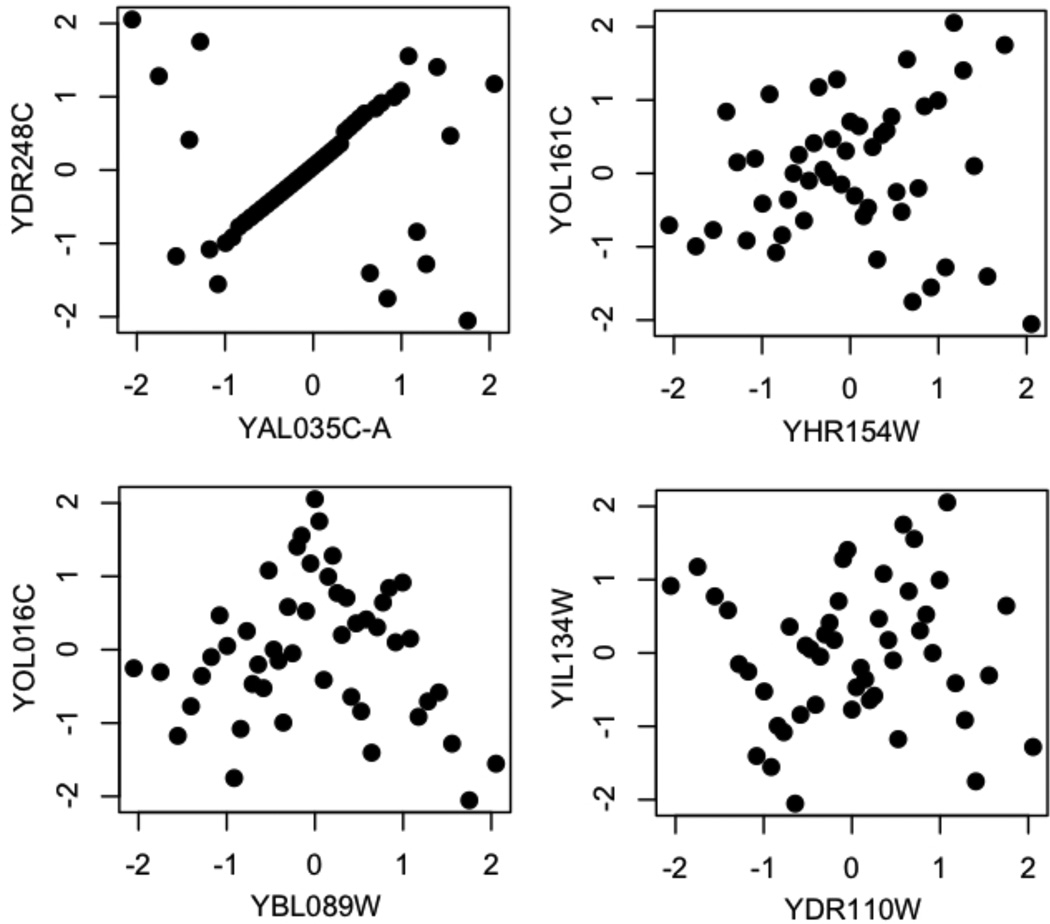
Figure 3 shows some example variable pairs being co-clustered while having correlation coefficients close to zero. The nonlinear relations are evident by visual inspection. An interesting scenario is the upper-left panel of Figure 3, where the two genes clearly have linear relation in the middle range, yet when the genes take large/small values, the response between the two genes become dichotomized. Hence the correlation coefficient between the two genes is close to zero. The upper-right panel and the lower-left panel show a “V” shaped relation between the genes. The correlation between the two genes changes sign when the expression level of one gene changes from low to high. The lower-right panel shows a more complex relationship, when gene 1 (x-axis) is lowly expressed, the two genes are negatively correlated. The correlation becomes positive when the expression of gene 1 is in the middle range, and it changes to negative again when gene 1 is highly expressed (Fig. 3). These scenarios correspond well to those we used in the simulations. The upper-right and lower-left panels of Figure 3 correspond to the quadratic and absolute functions we used in the simulations (link functions 3 and 4). The lower-right panel of Figure 3 corresponds to the sine-curve type of relation in our simulations (link function 2). The only other type of relation in our simulations, the linear function (link function 1), is clearly abundant in the real data and an example needs not to be plotted. We cannot ascertain if the relations shown in Fig. 3 are biologically true or simply an experimental artifact. Nonetheless, the GDHC procedure can pick up such relation from the data and allow the user to judge if it is biologically meaningful.

Figure 3.

Some examples of non-linearly related genes co-clustered by GDHC.

In the development of GDHC2, we defined a cluster profile that allows us to judge the level of general dependency between two random variables, a random variable and a random vector, and two random vectors. It could be used in clustering schemes such as K-means clustering for general dependencies. In this study, the general dependency distance is based on absolute differences between adjacent points in the list. Other distance metrics, such as squared distance, could also be potentially used.

Overall, we described a new method for hierarchical clustering based on general dependency between features. The method is advantageous over the regular hierarchical clustering schemes using linear association or mutual information (MI) – based distances. Applying GDHC finds both linear and nonlinear relations. The method can be used on clustering high-throughput data to reveal nonlinear relations that are biologically relevant.