Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jan 29;4:3918. doi: 10.1038/srep03918

Ultrasonically encoded wavefront shaping for focusing into random media

Jian Wei Tay 1,2, Puxiang Lai 1,2, Yuta Suzuki 1, Lihong V Wang 1,a
PMCID: PMC3905274  PMID: 24472822

Abstract

Phase distortions due to scattering in random media restrict optical focusing beyond one transport mean free path. However, scattering can be compensated for by applying a correction to the illumination wavefront using spatial light modulators. One method of obtaining the wavefront correction is by iterative determination using an optimization algorithm. In the past, obtaining a feedback signal required either direct optical access to the target region, or invasive embedding of molecular probes within the random media. Here, we propose using ultrasonically encoded light as feedback to guide the optimization dynamically and non-invasively. In our proof-of-principle demonstration, diffuse light was refocused to the ultrasound focal zone, with a focus-to-background ratio of more than one order of magnitude after 600 iterations. With further improvements, especially in optimization speed, the proposed method should find broad applications in deep tissue optical imaging and therapy.

One of the greatest challenges in biomedical optics is focusing light to a target region in biological tissue, which is mostly random or scattering media. Delivering focused light is important in nearly all disciplines of biomedical optics. In optical therapy1,2,3, manipulation4, and stimulation5, having a sufficient photon density in a targeted region determines both efficacy and specificity, while for imaging, the optical spot size determines the resolution. However, focusing with conventional lenses is restricted to a depth of one transport mean free path6 in scattering media, as the wavefront becomes distorted from wavelength scale refractive index changes. This distortion causes the optical field to no longer add up in phase at the focal point7, giving rise to a speckle field, and limiting both optical penetration depth and resolution. Recent advances have shown that focusing beyond one transport mean free path is possible by using optical phase conjugation (OPC)7,8,9,10,11,12,13 or iterative wavefront shaping techniques14,15,16,17,18. In both OPC and wavefront shaping, the phase of the distorted beam is spatially tailored to compensate for the effects of scattering. The compensated optical field at the target position then adds up in phase once more, generating a focus.

While related, OPC and wavefront shaping have different principles of operation. In OPC, a phase hologram of the distorted light exiting the scattering medium is recorded. Reading out the hologram generates a backwards-propagating beam, whose phase is the conjugate of the recorded light, thereby reversing the distortion from multiple scattering events. To form a focal spot within a turbid medium, a guide star is defined, for example by using focused ultrasound encoding (TRUE7,11,12,13 and TROVE10), fluorescence8, or second harmonic radiation9 from embedded molecules. OPC has been demonstrated both by using analogue photorefractive media7,12 and digitally, by using a camera and a spatial light modulator (SLM) for reproduction8,10,11,19. The quality of reproduction depends on the number of controls: an SLM typically has a pixel count of several million, while photorefractive media can support over 1011 effective pixels12. However, when intense light is delivered into the medium, digital reconstruction is preferred since the photorefractive hologram is erased upon readout, thereby limiting the total energy delivered. On the other hand, stricter alignment is required for digital OPC, as separate devices are used for hologram recording and readout (typically a camera and an SLM, respectively), which need to be perfectly pixel-matched to each other10,13,19.

In comparison, focusing by wavefront shaping techniques does not involve the use of holograms. Instead, the phase of the illuminating beam is shaped using an SLM. The optimum phase pattern is determined using an iterative algorithm to optimize a feedback signal20,21,22, typically chosen to be the intensity of a single speckle. By avoiding holograms, the experimental setup is much simpler, with more robust optical alignment than OPC. In addition, high-speed single element photodetectors can be used in place of cameras, which tend to be much slower due to data transfer limitations. Photodetectors also allow analogue post-processing, such as filtering and amplification.

To obtain the feedback signal in wavefront shaping techniques, physical access to the target position is generally required, whether directly by using a photodiode or camera to detect in situ speckles17,20,21,22, or indirectly by using fluorescent molecules14,15,16. In practical applications, however, it is generally unfeasible to position a physical detector at the target position within the medium. Using probe molecules in biological applications requires undesirable invasive procedures, as well as being potentially toxic. Furthermore, in both these cases, light delivery is restricted to fixed positions. To overcome these issues, we propose using ultrasonically encoded (UE) light as feedback for iterative wavefront shaping, with the target region defined by the focus of the ultrasound field.

Light travelling through the ultrasonic focal zone is frequency-shifted (encoded) by acoustically induced refractive index variations and optical scatterer displacements23,24 within the medium. The UE light is subsequently detected using a photorefractive interferometer, and used as feedback to an iterative optimization algorithm in order to determine the phase map which best focuses light to the target region. Using UE light as feedback has several advantages: It is non-invasive, non-harmful, and allows dynamic focusing by translation of the ultrasonic focus. Furthermore, in biological tissue, ultrasound has orders of magnitude weaker scattering than light25,26, enabling ultrasonically limited resolution at greater depths. We envision that our method could be used with ultrasound imaging or ultrasound-modulated optical tomography27,28 (UOT) to first locate a point of interest, and then to optimize light delivery to that region, thereby boosting the signal-to-noise ratio of existing optical imaging or to implement photodynamic therapy.

Results

Implementation

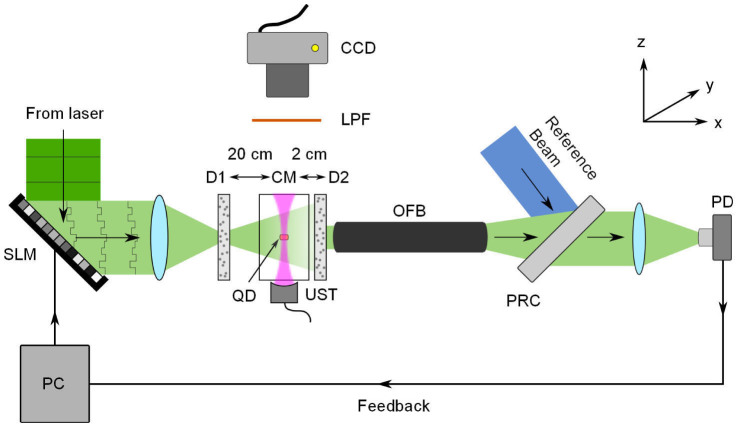
Our experimental setup is shown schematically in Fig. 1. We used a computer-controlled SLM, divided into 20 × 20 independently controlled segments, to shape the incident wavefront. The SLM response was calibrated29 to provide a linear phase shift of 2π over 191 grayscale values for each segment.

Figure 1. Experimental setup.

Figure 1

Open in a new tab

The incident beam on the first diffuser (D1), initially planar, is spatially tailored using a phase-only spatial light modulator (SLM). Five cycles from a focused 6 MHz ultrasonic transducer (UST) are sent through a clear gelatin medium (CM), modulating light within the acoustic focus. After the second diffuser (D2), the modulated beam is collected using an optical fiber bundle (OFB). The signal is measured using a photorefractive detection (PRC) system and a photodiode (PD), and its amplitude is subsequently used as feedback to optimize the pattern on the SLM. To visualize the focal spot, a bar of fluorescent quantum dots (QD) is embedded along the y-axis of the acoustic focal zone. The resulting fluorescence intensity is longpass filtered (LPF) and measured using a CCD camera.

As a proof-of-principle demonstration, we used two ground glass diffusers to scatter light. Viewed head on, the diffusers appeared opaque, and an optical focus was unable to be formed beyond the first diffuser. To visualize the optimized focal spot, we embedded a bar (1 mm in both x and z dimensions) containing fluorescent quantum dots along the y-axis within a gelatin layer. The gelatin layer was inserted between the two diffusers, and the ultrasonic transducer was positioned so the bar was within its focal zone in both x and z directions. A focused 6 MHz ultrasonic transducer, with a 400 μm transverse focal width, was used to modulate the scattered light. After the second diffuser, light was collected and sent to a photorefractive crystal (PRC)-based interferometer27,28 (details in the Methods), whose output was proportional to the UE light. We averaged each measurement over 75 acquisitions.

Optimization

We used a genetic algorithm21 to optimize the phase pattern on the SLM by maximizing the UE light signal from the interferometer (details in the Supplementary Information). By maximizing the UE signal, the light intensity within the ultrasonic focal region was also maximized, thereby forming an optical focal spot in the turbid medium. The results from the optimization procedure are shown in Fig. 2. For every iteration, the highest UE signal value was recorded (Fig. 2a), and we found that after 600 iterations, the UE signal was increased by 11 times over the initial randomized value (Fig. 2b), indicating a corresponding increase of the in situ light intensity within the ultrasound focus.

Figure 2.

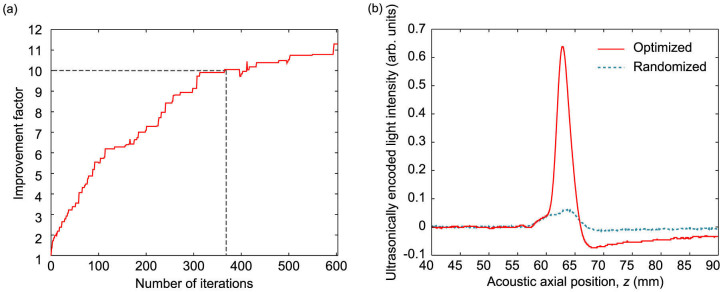
Figure 2

Open in a new tab

(a) Improvement over the initial signal amplitude as the algorithm progresses. An improvement of 11 times in signal amplitude was obtained, which corresponds to a similar increase in light intensity within the acoustic focal zone. An order of magnitude improvement was achieved at 370 iterations, as indicated by the dotted line. (b) Measured ultrasonically encoded signal amplitude with the optimized pattern (red, solid line), and with an initial, randomized pattern (blue, dashed line) displayed on the SLM. The traces were averaged over 75 acquisitions.

Visualization of optical focusing

A CCD camera was used to image the fluorescent bar embedded between the two diffusers when a uniform (black), randomized, and optimized phase map (Fig. 3a–c) were displayed on the SLM. The resulting fluorescence images are shown in Fig. 3d–f. As can be seen, the fluorescence emissions were relatively evenly distributed along the bar when the uniform and randomized phase maps were displayed, indicating diffuse light. However, when the optimized phase pattern was displayed, a bright focal spot emerged at the ultrasound focal position. Note that the focal spot (Fig. 3f) appears to be larger than the 400 μm transverse width of the acoustic beam, which could be due to the acoustic sidebands (see Supplementary Fig. S2). Also note that in comparison to Ref. 8, fluorescence from the embedded molecules was not used as feedback to the iterative algorithm, but to visualize the procedure.

Figure 3.

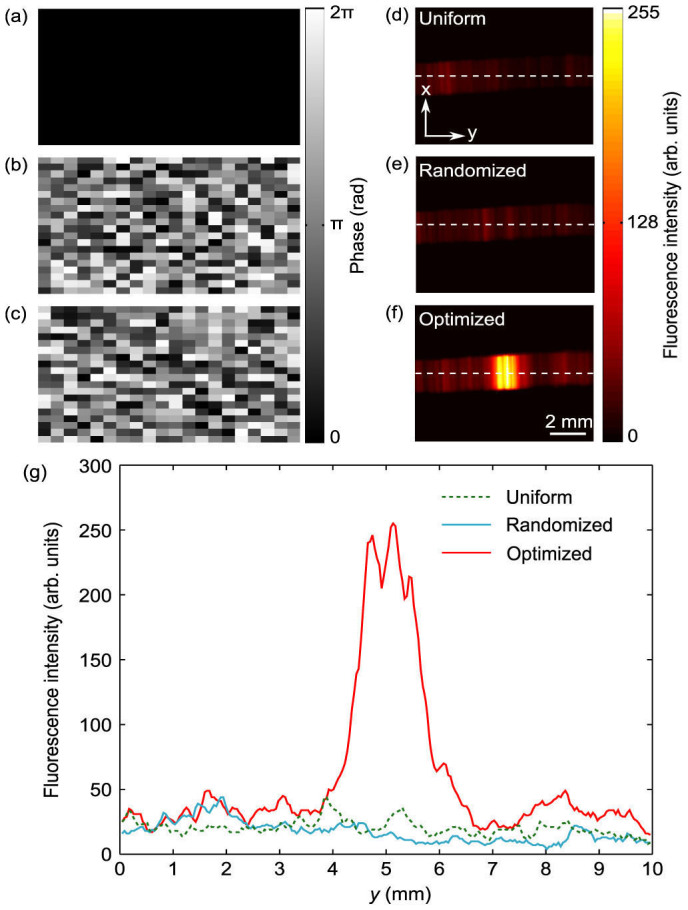
Figure 3

Open in a new tab

Visualization of the optimized focal spot when uniform, randomized, and optimized phase patterns (a–c) were displayed.The captured CCD images of the fluorescent bar are given in (d–f). The color bars indicate the phase for (a–c) and the CCD intensity for (d–f). (g) The cross sectional intensity, as indicated by the white dotted lines in (d–f). An increase of an order of magnitude is seen using the optimized pattern, compared to both uniform and randomized patterns.

Similar to the increase in UE signal, when displaying the optimized pattern, the focus-to-background ratio (defined as the ratio of the peak to the averaged background) of the cross-sectional fluorescence intensity was also an order of magnitude greater than when displaying a randomized pattern (Fig. 3g). We also found that the fluorescence intensity from the randomized pattern was similar to the intensity from a uniform phase pattern, indicating that the wavefront was completely scrambled by the first diffuser. The Supplementary Materials provide a video of the evolution of the optimization procedure, showing step-by-step how the focus is formed.

Theoretical estimation

It was previously shown14 that the expected increase in light intensity η within the ultrasound focus is proportional to the ratio of the number of independent SLM segments N to the number of speckle grains in the ultrasound focus M,

graphic file with name srep03918-m1.jpg

Based on an illumination diameter of 1 mm on the first diffuser, and a distance of 20 cm from the first diffuser to the acoustic focus, we estimated speckle grains of 130 μm at the acoustic focal plane (see Supplementary Materials). To modulate the light, we used an ultrasound pulse of five cycles at 6 MHz, equivalent to a length of 1.25 mm. This pulse length, along with the acoustic transverse width, yielded a calculated 29 ultrasonically encoded speckles within the cross-sectional area of the acoustic focus. Hence, using equation (1), we expected η = 12, which is close to the experimentally measured value. The difference could be due to a variety of factors, including system noise contributing to errors in the optimized phase pattern, as well as typical variability in the final value from the genetic algorithm21. Moreover, the illumination spot size of 1 mm on the first diffuser was determined using a uniform phase pattern on the SLM. The illumination spot after optimization could be slightly larger, due to diffraction caused by the 20 × 20-block pattern, which would result in smaller speckles in the acoustic focus, and hence a lower enhancement.

Discussion

Several factors directly impact the performance of this technique. In particular, the choice of optimization algorithm, the achievable focusing resolution, the number of SLM segments, and the optimization speed, warrant discussion.

In this experiment, we chose to use a genetic optimization algorithm that was previously shown to outperform other algorithms in noisy environments21. The algorithm (further described in the Supplementary Materials) generates possible solutions from a population of phase patterns, which initially is randomly seeded. To generate subsequent patterns, two patterns are chosen based on the weights of their UE signals, then combined and mutated randomly. The advantage of this method is that the signal-to-noise ratio of measurements is higher, as the entire phase pattern contributes to the measured signal. The algorithm also provides a faster initial increase, yielding near optimization — such as 90% of the maximum — sooner, although the final convergence is slow.

The optimized focusing resolution was determined by the transducer's acoustic focal zone. Along the transverse direction, the focal zone is determined by the numerical aperture (NA) of the transducer's acoustic lens, which is inversely proportional to the transducer diameter and frequency. Hence, it can be improved by using large diameter transducers, as well as higher acoustic frequencies. Along the axial direction, the acoustic focal zone is determined by the length of the ultrasonic pulse train, provided the length of the pulse train is shorter than the FWHM of the transducer's depth of focus (measured to be 2.8 mm). Here, we used 5 cycles of 6 MHz ultrasound, which, given the speed of sound in water and gelatin of ~1.5 mm/μs, provided a resolvable axial length of 1.25 mm. The axial resolution could be improved by using a lower number of ultrasound cycles. Apart from affecting the resolution, the dimensions of the transducer's focal zone also impact the expected enhancement: The smaller the focal zone, the fewer the speckles modulated and the greater the potential enhancement. However, this enhancement must be balanced by a reduction of the UE light intensity resulting from fewer photons being modulated.

The number of SLM segments was chosen based on the algorithm termination time. From equation (1), we see that the expected enhancement in the target region can be increased by segmenting the SLM into a greater number of blocks. However, through numerical simulation, we found that the number of iterations required to optimize the phase pattern also scaled linearly with the number of controlled blocks (for details see the Supplementary Materials). Hence, for a given number of iterations, the intensity increase is the same. This result agrees with previously published results by Conkey et al21. Therefore, in the current study we chose to use 20 × 20 SLM segments for practical reasons. By speeding up the acquisition, the number of segments could also be increased, allowing more light to be focused at the target position, while maintaining a reasonable optimization time.

As with any iterative optimization procedure, the time it takes for the algorithm to terminate must be comparable to the sample's persistence or correlation time τp, which can be determined by measuring the correlation of the speckle pattern over time. In general, the optimization time needs to be less than τp, otherwise changes in the sample's transmission would invalidate the stored information about previous phase maps. Optimization currently takes several hours, due mainly to the slow PRC detection time (~1.8 s per measurement), as well as the time needed for data acquisition and processing (~1.5 s), which was limited by the data transfer rate between the oscilloscope and computer. Therefore, we were restricted to mechanically stable diffusers for this proof-of-principle demonstration. We note that the algorithm could have been stopped at about 370 iterations, just over half the total iterations as shown in Fig. 2a, due to the slow final convergence.

In this work, we used UE light as feedback. A related technique using photoacoustic signals as feedback was demonstrated by Kong et al30. There, a laser pulse incident on an obscured absorber produced an ultrasound pulse, which was then detected by a transducer. However, our proposed method is complementary to that technique: Photoacoustic generation requires an absorber, while this method can be used in non-absorbing optical media. Moreover, by optimizing the residual modulation envelope, it may be possible to focus to an absorber that is smaller than the ultrasonic focal zone.

In summary, we proposed and demonstrated the use of ultrasonically encoded light as feedback in iterative wavefront shaping. While the optimization time is currently too long for in vivo biological applications, this technique could potentially be applied to other fields such as probing inorganic structures14,15,16. The optimization speed could be improved by using faster acousto-optic detection methods, such as spectral hole burning31,32,33 or confocal Fabry-Perot interferometry34, as well as by using faster data acquisition devices. Furthermore, the use of faster SLMs, such as digital mirror devices (DMD), coupled with parallel wavefront measurement techniques could further speed up the optimization22,35. Such refinements should allow this method to be used in a variety of applications, such as in phototherapy, photoactivation of medicine, and optogenetics, as well as improving existing imaging techniques such as optical13, photoacoustic36, and acousto-optic37,38 microscopy.

Methods

Experimental setup

A detailed schematic of our system is shown in Supplementary Fig. S1. We used a 2 W laser at 532 nm (Verdi V-5, Coherent, USA). A liquid-crystal-on-silicon (LCoS) based phase-only SLM (PLUTO, Holoeye Photonics, Germany) shaped the incident wavefront. The SLM had a resolution of 1920 × 1080 pixels, which were then divided evenly into 20 × 20 blocks of 96 × 54 pixels each. The laser beam was expanded to completely fill the SLM surface. After the SLM, a 40 mm lens focused the light onto the diffuser surface. Approximately 1.47 W of laser power illuminated the diffuser.

To modulate the light, a focused ultrasonic transducer (H148, Sonic Concepts, USA), with a transverse focal width (FWHM of the transducer response in the focal plane) of 400 μm was used. The transverse profile at the focal plane was measured by a hydrophone, and is shown in Supplementary Fig. S2. To drive the transducer, five cycles of a sinusoidal wave at 6 MHz were used, with 150 mVpp amplitude before a 50 dB amplifier, and a repetition rate of 1 kHz. The repetition rate was chosen both to reduce the transducer duty cycle and to maximize acquisition speed, while ensuring that consecutive pulse trains did not overlap within a single acquisition, in order to limit the axial ultrasound focal length. We assumed that less than 1% of the total light was modulated39. After the second diffuser D2, approximately 0.4 mW of light was collected using an optical fiber bundle (NT 39-370, Edmund Optics, USA), and directed at the photorefractive interferometer.

The optimization procedure was controlled by a computer. We used MATLAB (R2012b, MathWorks, USA) and a USB-VISA interface to connect the oscilloscope with the computer. The phase maps were displayed on the SLM using a video card (GeForce GT520, NVidia, USA). Although the information was uploaded to the SLM at 60 Hz, we found that it took about half a second to obtain a steady pattern due to the operation of the device driver, which we could not control.

Detection of ultrasonically encoded light by photorefractive interferometry

To detect the UE light, a photorefractive interferometer28,39,40 employing a Bi12SiO20 (BSO) crystal (20 × 10 × 20 mm3 along x, y, and z, respectively; Elan, Russia) was used. A 28.7 mW/cm2 planar reference beam, together with the signal beam collected by the fiber bundle, was directed to the BSO crystal, at about ±10 degrees to the crystal normal. The reference beam had the same frequency as the unmodulated signal beam. A refractive index hologram was formed within the crystal, which recorded the complex amplitude of the interference field. The crystal then behaved like an adaptive beam-splitter, and a part of the reference beam was diffracted into the same mode and direction as the signal beam. Thus, at the output of the interferometer, the transmitted signal beam and the diffracted reference beam added coherently, giving a signal that was proportional to the intensity of the scattered signal beam.

The photorefractive hologram is able to adapt only to fluctuations that are slower than the photorefractive response time of the crystal (measured to be about 100 ms). Since the time-of-flight of the ultrasound pulse (1.9 μs) was much shorter than the photorefractive response time, the photorefractive grating did not adapt to the modulated light, so the signal and diffracted reference beams were no longer in phase. The result was a reduction of the detected signal beam intensity after the crystal that was proportional to the intensity of UE light27.

To measure the signal beam, we used a photodiode (PDA36A, Thorlabs, USA) with a 40 dB gain after the PRC interferometer. Using a preamplifier, the signal was high-pass filtered at 30 kHz to remove the large DC background, then amplified 500 times. The signal was then digitized by an oscilloscope (TDS 5034, Tektronix, USA), and inverted to get a positive value. The UE signal, defined as the peak of the signal minus the mean of the background, was used as the weight of the displayed phase pattern in the genetic algorithm.

Diffuse sample preparation

For this proof-of-principle demonstration, we used ground glass diffusers (DG10-120, Thorlabs, USA) to scatter light. No optical focus was discernible after a single diffuser, indicating that the wavefront was sufficiently scrambled. Furthermore, neighboring pixels in the optimized phase map appeared randomized, which indicated that the light was fully scrambled by the diffusers17.

An optical path to visualize the optical focus from above (shown in Fig. 1) was created by inserting a clear gelatin layer between the two diffusers. The layer was made using 10% by weight of porcine skin gelatin (G2500, Sigma-Aldrich, USA) and 90% distilled water. A gelatin bar containing fluorescent quantum dots (QSA-600-2, Ocean Nanotech, USA; conc. 0.26 μM) was embedded within the clear layer. The transducer was then positioned so that its focus overlapped the bar in both the x and z directions.

Author Contributions

J.W.T. and P.L. designed and ran the experiment. J.W.T. wrote code for the experiment and simulations. P.L. implemented the PR detection system. J.W.T., P.L. and Y.S. prepared the manuscript. L.V.W. provided overall supervision. All authors were involved in analysis of the results and manuscript revision.

Supplementary Material

Supplementary Information

Supplementary Information

srep03918-s1.pdf (482.8KB, pdf)
Supplementary Information

Evolution of the genetic algorithm.

Download video file (298.5KB, avi)

Acknowledgments

This work was sponsored in part by the National Academies Keck Futures Initiative grant IS 13 and National Institute of Health grant DP1 EB016986 (NIH Director's Pioneer Award).

References

  1. Dolmans D. E., Fukumara D. & Jain R. K. Photodynamic therapy for cancer. Nat. Rev. Cancer 3, 380–387 (2003). [DOI] [PubMed] [Google Scholar]
  2. Birchler M., Viti F., Zardi L., Spiess B. & Neri D. Selective targeting and photocoagulation of ocular angiogenesis mediated by a phage-derived human antibody fragment. Nat. Biotechnol 17(10), 984–8 (1999). [DOI] [PubMed] [Google Scholar]
  3. Zhuo S. et al. Label-free multiphoton imaging and photoablation of preinvasive cancer cells. Appl. Phys. Lett. 100(2), 023703 (2012). [Google Scholar]
  4. Cižmár T. & Dholakia K. Shaping the light transmission through a multimode optical fibre: complex transformation analysis and applications in biophotonics. Opt. Express 19(20), 18871–84 (2011). [DOI] [PubMed] [Google Scholar]
  5. Williams J. C. & Denison T. From optogenetic technologies to neuromodulation therapies. Sci. Transl. Med. 5(177), 177ps6 (2013). [DOI] [PubMed] [Google Scholar]
  6. Wang L. V. Biomedical Optics: Principles and Imaging (Wiley-Interscience, New Jersey, 2007). [Google Scholar]
  7. Xu X., Liu H. & Wang L. V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nat. Photon. 5(March), 154–157 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Vellekoop I. M., Cui M. & Yang C. Digital optical phase conjugation of fluorescence in turbid tissue. Appl. Phys. Lett. 101(8), 81108 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hsieh C.-l., Pu Y., Grange R. & Psaltis D. Digital phase conjugation of second harmonic radiation emitted by nanoparticles in turbid media. Opt. Express 18(12), 533–537 (2010). [DOI] [PubMed] [Google Scholar]
  10. Judkewitz B., Wang Y. M., Horstmeyer R., Mathy A. & Yang C. Speckle-scale focusing in the diffusive regime with time reversal of variance-encoded light (TROVE). Nat. Photon. (March), 1–6 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Wang Y. M., Judkewitz B., Dimarzio C. A. & Yang C. Deep-tissue focal fluorescence imaging with digitally time-reversed ultrasound-encoded light. Nat. Commun. 3(M), 928 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lai P., Suzuki Y., Xu X. & Wang L. V. Focused fluorescence excitation with time-reversed ultrasonically encoded light and imaging in thick scattering media. Laser Phys. Lett. 10(7), 075604 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Si K., Fiolka R. & Cui M. Fluorescence imaging beyond the ballistic regime by ultrasound-pulse-guided digital phase conjugation. Nat. Photon. 6, 657–661 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Vellekoop I. M., van Putten E. G., Lagendijk A. & Mosk A. P. Demixing light paths inside disordered metamaterials. Opt. Express 16(1), 67–80 (2008). [DOI] [PubMed] [Google Scholar]
  15. Aulbach J., Gjonaj B., Johnson P. & Lagendijk A. Spatiotemporal focusing in opaque scattering media by wave front shaping with nonlinear feedback. Opt. Express 20(28), 29237–29251 (2012). [DOI] [PubMed] [Google Scholar]
  16. van Putten E. G., Lagendijk A. & Mosk A. P. Optimal concentration of light in turbid materials. JOSA B 28(5), 1200–1203 (2011). [Google Scholar]
  17. Vellekoop I. M. & Mosk A. P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 32, 2309–2311 (2007). [DOI] [PubMed] [Google Scholar]
  18. Vellekoop I. & Mosk A. P. Universal Optimal Transmission of Light Through Disordered Materials. Phys. Rev. Lett. 101(12), 1–4 (2008). [DOI] [PubMed] [Google Scholar]
  19. Cui M. & Yang C. Implementation of a digital optical phase conjugation system and its application to study the robustness of turbidity surpression by phase conjugation. Opt. Express 18, 3444–3455 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Vellekoop I. M. & Mosk A. P. Phase control algorithms for focusing light through turbid media. Opt. Commun. 11, 3071–3080 (2008). [Google Scholar]
  21. Conkey D. B., Brown A. N., Caravaca-Aguirre A. M. & Piestun R. Genetic algorithm optimization for focusing through turbid media in noisy environments. Opt. Express 20(5), 4840–9 (2012). [DOI] [PubMed] [Google Scholar]
  22. Cui M. Parallel wavefront optimization method for focusing light through random scattering media. Opt. Lett. 36, 870–872 (2011). [DOI] [PubMed] [Google Scholar]
  23. Leutz W. & Maret G. Ultrasonic modulation of multiply scattered light. Physica B 204(1–4), 14–19 (1995). [Google Scholar]
  24. Wang L. Mechanisms of Ultrasonic Modulation of Multiply Scattered Coherent Light: An Analytic Model. Physical Review Letters 87(4), 1–4 (2001). [DOI] [PubMed] [Google Scholar]
  25. Yao G. & Wang L. V. Theoretical and experimental studies of ultrasound-modulated optical tomography in biological tissue. Appl. Opt. 39(4), 659–64 (2000). [DOI] [PubMed] [Google Scholar]
  26. Prince J. L. & Links J. M. Medical Imaging: Systems and Signals (Pearson Prentice Hall, New Jersey, 2006). [Google Scholar]
  27. Lai P., Xu X. & Wang L. V. Ultrasound-modulated optical tomography at new depth. J. Biomed. Opt. 17(6), 066006 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Murray T. W. et al. Detection of ultrasound-modulation photons in diffuse media using the photorefractive effect. Opt. Lett. 29, 2509–2511 (2004). [DOI] [PubMed] [Google Scholar]
  29. Tay J. W., Taylor M. A. & Bowen W. P. Sagnac-interferometer-based characterization of spatial light modulators. Appl. Opt. 48(12), 2236–2242 (2009). [DOI] [PubMed] [Google Scholar]
  30. Kong F. et al. Photoacoustic-guided convergence of light through optically diffusive media. Opt. Lett. 36, 2053–2055 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Tay J. W., Ledingham P. M. & Longdell J. J. Coherent optical ultrasound detection with rare-earth ion dopants. Appl. Opt. 49(23), 4331–4334 (2010). [DOI] [PubMed] [Google Scholar]
  32. Li Y. et al. Pulsed ultrasound-modulated optical tomography using spectral-hole burning as a narrowband spectral filter. Appl. Phys. Lett. 93(1), 11111 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Zhang H. et al. Slow light for deep tissue imaging with ultrasound modulation. Appl. Phys. Lett. 100(13), 131102 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Rousseau G., Blouin A. & Monchalin J.-P. Ultrasound-modulated optical imaging using a high-power pulsed laser and a double-pass confocal Fabry-Perot interferometer. Opt, Lett. 34(21), 3445–7 (2009). [DOI] [PubMed] [Google Scholar]
  35. Popoff S. M. et al. Measuring the Transmission Matrix in Optics: An Approach to the Study and Control of Light Propagation in Disordered Media. Phys. Rev. Lett. 104, 100601 (2010). [DOI] [PubMed] [Google Scholar]
  36. Wang L. & Hu S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science 335(6075), 1458–1462 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Kothapalli S.-R. & Wang L. V. Ultrasound-modulated optical microscopy. J. Biomed. Opt. 13(5), 054046 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Sakadzić S. & Wang L. V. High-resolution ultrasound-modulated optical tomography in biological tissues. Opt. Lett. 29(23), 2770–2 (2004). [DOI] [PubMed] [Google Scholar]
  39. Gross M. et al. Theoretical description of the photorefractive detection of the ultrasound modulated photons in scattering media. Opt. Express 13, 7097–7112 (2005). [DOI] [PubMed] [Google Scholar]
  40. Ing R. K. & Monchalin J.-P. Broadband optical detection of ultrasound by two-wave mixing in a photorefractive crystal. Appl. Phys. Lett. 59, 3233 (1991). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep03918-s1.pdf (482.8KB, pdf)
Supplementary Information

Evolution of the genetic algorithm.

Download video file (298.5KB, avi)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES