Changes in Running Speeds in a 100 KM Ultra-Marathon Race

Abstract

The purpose of this study was to determine if runners who completed a 100 km ultramarathon race in the fastest times changed their running speeds differently compared to those runners who ran an overall slower race. Times were taken from the race results of the 1995 100 km IAU World Challenge in Winschoten, Netherlands. Race times and 10 km split times were analyzed. Runners (n = 67) were divided into groups of ten with the last group consisting of seven runners. The mean running speed for each 10 km segment was calculated using each runner’s 10 km split times. Mean running speed was calculated using each runner’s race time. The first 10 km split time was normalized to 100, with all subsequent times adjusted accordingly. The mean running speed for each group at each 10 km split was then calculated. The faster runners started at a faster running speed, finished the race within 15 % of their starting speed, and maintained their starting speed for longer (approximately 50 km) before slowing. The slower runners showed a greater percentage decrease in their mean running speed, and were unable to maintain their initial pace for as long. It is concluded that the faster runners: 1) ran with fewer changes in speed, 2) started the race at a faster running speed than the slower runners, and 3) were able to maintain their initial speed for a longer distance before slowing.

Key Points.

Faster runners in the 100 km race;

• ran with fewer changes in running speed compared to the slower runners;

• started the race at a faster running speed than the slower runners;

• were able to maintain their initial running speed for longer distances than slower runners.

Introduction

In an attempt to improve running performance, the physiological characteristics of elite performers and the energy demands of the athletic events in which they participate have been studied (Robinson et al., 1991; Sparling et al., 1993; Brandon, 1995). However, changes in running speed, either preplanned or as a consequence of fatigue during competition may also have an effect on the outcome of a race. Pacing can be defined as the subjective competitive strategy in which an individual manipulates speed to achieve his/her performance goal. From a physiological perspective pacing may be influenced by a “central programmer” which integrates afferent signals arising from the muscle and peripheral organs and regulates power output to optimize performance (Ulmer, 1996; Lambert et al., 2004). The presence of this “central programmer” has been supported in various research models (Kay et al., 2001; St Clair Gibson et al., 2001; Kay and Marino, 2003; Marino et al., 2004).

Previous studies examining pacing have focused mainly on short duration events lasting less than five minutes (Foster et al., 1994; van Ingen Schenau et al., 1994) and have generally concluded that optimal pacing is often the result of a learning process and that it may be in the best interest of the athlete to practise such pacing in preparation for an event (Foster et al., 1994). Few studies have addressed the pacing of athletes during longer endurance events (Townsend et al., 1982). This could be due to the fact that several different mechanisms have been identified as contributors to fatigue during prolonged exercise (Gibson and Edwards 1985; Noakes, 2000), making a systematic experimental approach difficult. Studies that have attempted to analyze the pacing of long duration events have incorporated mathematical models into their research design. Townsend et al. (1982) used a mathematical model to assign values to runners’ capabilities to complete specific distances over different terrain. Through a series of calculations, the pace at which a runner should complete each respective segment of the race can be determined. However, this technique is complex and thus has limited practical applications.

An alternative approach to determine the pacing of athletes during long endurance events is to study the pacing of elite performers, assuming that these athletes have practised such pacing in preparation for the event (Foster et al., 1994) and that their pacing is optimal for these events and results in the fastest race times. Accordingly, the running speeds of the competitors of the 1995 100 km IAU World Challenge were analyzed. The aim of the study was to determine if the runners who completed the race with the fastest race times changed their running speeds differently compared to those runners who ran slower overall race times. It was assumed that all the runners had similar racing experience, were highly trained and were all equally motivated for the event and were performing to the best of their abilities.

Methods

Racing data

The 10 km split times of the 107 male runners who competed in the 1995 100 km IAU World Challenge in Winschoten, Netherlands, were obtained from the race statistician and analyzed for the study. The race was run over a flat course consisting of a 10 km loop and times were recorded manually. The data of forty runners were excluded from the analysis based on two exclusion criteria: 1) not finishing the race, (n = 24), and 2) missing split times, (n = 16). Runners were then divided into seven groups (A-G) by grouping the remaining runners by time as follows: first 10 runners (A), the next 10 runners (B), and so on. The final group (G) included only seven runners.

Analysis of running speed

Mean running speed (m·s^-1) for each 10 km segment was calculated using each runner’s 10 km split times. The mean running speed (m·s^-1) for the race was calculated using each runner’s race time. ‘Normalized’ running speed for each runner’s 10 km segment was calculated by assigning the first 10 km running speed to 100%. All the subsequent splits were adjusted accordingly.

The mean running speed for each 10 km split was calculated for each group (A-G). Best-fit non-linear and linear regressions of distance vs. mean running speed were calculated for each group (A-G). Similarly, the mean normalized speed was calculated for each group at each 10 km split, and the line of best fit of distance vs. normalized speed was determined for each group.

A similar analysis was done using the 10 km split-time data of the same race in 1997. The top 10 finishers (1997) were compared with group A (1995). The 10 finishers (1997) whose mean time was similar to that of group F (1995) were also used for comparison. Coefficient of variation and the relationship between mean running speed and distance were calculated. The 1997 data were analyzed using the same methods as were used for the 1995 data.

The 5 km splits for the 42.2 km world record established in Berlin, Germany, in September, 2003, and the 10 km splits of the 100 km world record (Lake Saroma, Japan, June 1998) were analyzed in a similar way as the times from the IAU 1995 and 1997 races. Coefficient of variation and mean running speed were calculated for the marathon and 100 km race and the mean change in speed and mean running speed for each split were also calculated for the 100 km race (Table 1).

Table 1.

Characteristics used to describe the running speeds of runners in groups A-G (n= 10 in groups A- F; n = 7 in group G). All values are means (± SD).

Groups		Mean Race time (hh: min. s)	Mean speed (m·s−1)	Mean CV for mean speed	Mean Δ speed (m·s−1)	R2 (curvilinear)	Normalized Slope
A	6:36.50 (0:11.39)b,C,D,E,F,G		4.2 (.1) b,C,D,E,F,G	5.4 (2.0)F,G	.5 (.2)G	.96 (.05)	-.16 (.06)E,F,G
B	7:03.44 (0:06.34)c,D,E,F,G		3.9 (.1) c,D,E,F,G	8.2 (3.1)G	.6 (.4)G	.77 (.32)	-.17 (.08) E,F,G
C	7:26.26 (0:05.41)E,F,G		3.7 (.1) E,F,G	11.5 (3.1)	1.0 (.4)	.95 (.05)	-.30 (.08) E,F,G
D	7:47.18 (0:05.26)F,G		3.6 (.1) F,G	10.8 (3.0)	.8 (.3)	.90 (.11)	-.27 (.06) E,F,G
E	8:03.07 (0:05.47)F,G		3.5 (.1) F,G	12.2 (5.2)	.9 (.5)	.88 (.13)	-2.90 (1.30)
F	8:43.34 (0:19.09)G		3.2 (.1) G	15.6 (6.9)	1.0 (.4)	.90 (.10)	-3.80 (1.50)
G	10:02.25 (0:34.40)		2.8 (.1)	19.6 (6.9)	1.4 (.8)	.97 (.03)	-4.60 (1.50)
P <	.05-.01		.05-.01	.01	.05		.01

Only significant differences are listed. Small and capital superscript letters denote p < .05 and .01 respectively. CV = coefficient of variation.

Statistical Analysis

All results are expressed as mean ± standard deviation (X ± SD). An analysis of variance (ANOVA) was used to identify differences between groups. A Scheffe’s post-hoc test was used to identify the differences when the overall F-value of the model was significant. Statistical significance was accepted when p < 0.05. The relationship between running speed and distance was examined using the coefficient of determination (R²) for linear and curvilinear regression.

Results

The mean race time of all the 1995 groups was 7:52.05 ± 1:00.58 (h:mm.ss). The fastest time recorded was 6:18.09 and the slowest time was 11:12.36 (h:mm.ss). The mean race time for each group (A to G) is shown in Table 1. Group A (1995) had a mean race time of 6:36.58 ± 0:11.39 compared to group A (1997) of 6:40.12 ± 0:08.23 (h:mm.ss) (Table 2). Similarly, group F (1995) had an mean race time of 8:43.25 ± 0:19.09 (h:mm.ss) compared to group F (1997) (8:44.34 ± 0:16.52) (h:mm.ss) (Table 2). The mean race times of groups A-G ranged from 6:36.58 ± 0:11.39 to 10:02.04 ± 0:34.40 (h:mm.ss) (Table 1).

Table 2.

Characteristics used to describe the running speeds of runners in groups A and F (1995 and 1997) (n=10 in all groups) and the marathon and 100 km world records (WR). All values are means (± SD).

Group	Mean Race Time (hh:mm.s)	Mean speed (m·s–1)	Mean CV for mean speed	Mean Δ Speed (m·s–1)
A ‘95	6:36.58 (0:11.39)	4.2 (.1)	5.4 (2.0)	.5 (.2)
A ‘97	6:40.12 (0:08.00)	4.2 (.1)	4.2 (1.2)	.4 (.2)
F ‘95	8:43.25 (0:19.09)	3.2 (.1)	15.6 (6.9)	1.0 (.4)
F ‘97	8:44.34 (0:16.52)	3.2 (.1)	13.3 (4.4)	.9 (.2)
42.2km WR	2:04.55	5.6	1.2	-------
100 km WR	6:13.33	4.5	3.2	0.03

CV = coefficient of variation.

The mean running speed of each runner in the seven groups is shown in Figure 1a with the line of best fit for each group shown in bold. Groups A-C started at a faster and very similar running speed (4.3 ± 0.2 m·s^-1) compared to groups D-F (4.0 ± 0.3 m·s^-1, Figure 1a). Runners who finished in group A completed the entire race at running speeds within 15% of their initial starting speed (Figure 1b). Slower runners showed the greatest change in mean speed from 0-10 km vs. 90-100 km (group G; 1.4 ± 0.7 m·s^-1) in contrast to group A (0.5 ± 0.2 m·s^-1) (Table 1). Figure 1a shows that runners in group A ran at relatively constant speeds during the first half of the race. This was also true for the second half of the race, although their pace was slower during this period.

Figure 1.

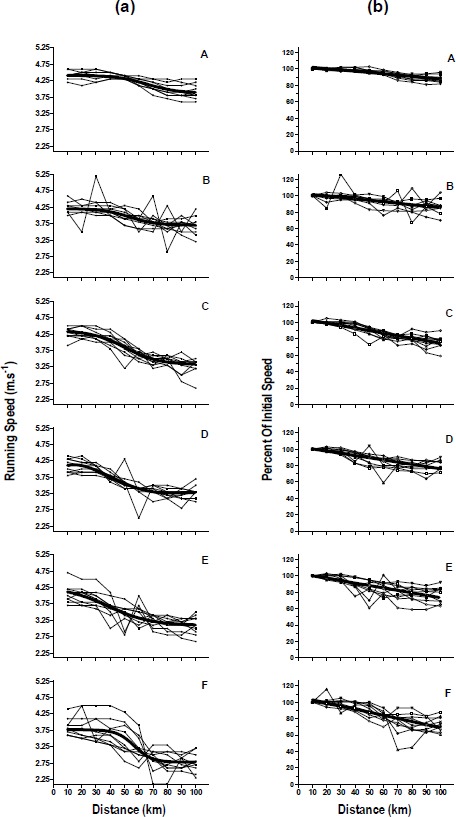
(a) Mean running speed of runners from the 1995 IAU World Challenge (Groups A-F; n = 10 in each group). The line of best fit for each group mean is shown in bold. (b) Normalized running speed of runners from the 1995 IAU World Challenge (Groups A-F; n = 10 in each group). The line of best fit for each group mean is shown in bold.

The mean linear and curvilinear lines of best fit for each group are shown in Figure 2a. For the graph of mean running speed vs. distance, both linear and curvilinear lines were calculated for each group’s mean values. However, the curvilinear calculations produced better fit lines (R² = 0.61 vs. R² = 0.90, mean linear vs. mean curvilinear regressions, respectively; Table 1). Therefore, curvilinear lines are shown in figure 1a and figure 2a.

Figure 2.

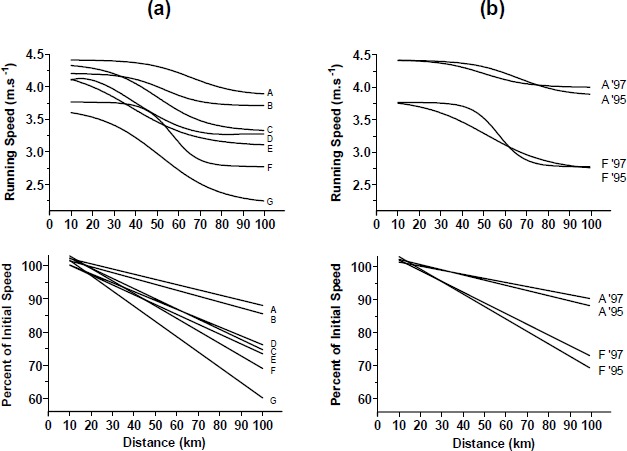
(a) Top: Lines of best fit for each group (1995) of running speed vs. distance. Bottom: Lines of best fit for each group (1995) of normalized running speed vs. distance. n = 10, groups A-F; n = 7, group G. (b) Top: Lines of best fit of running speed vs. distance for groups A and F (1995) and groups A and F (1997). Bottom: Lines of best fit of normalized running speed vs. distance for groups A and F (1995) and groups A and F (1997). n = 10 in all groups.

The slopes of the normalized running speeds ranged from -0.16 ± 0.06 to -4.60 ± 1.50 (groups A to G) (Table 1). The slopes of groups A, B, C and D were significantly less than the slopes of groups E, F and G (P < 0.01), suggesting that groups A-D ran at a more even speed compared to groups E-G (Table 1).

Figure 2b shows the combined graphs of groups A and F for 1995 and 1997. Group A (1995) had an mean speed of 4.2 ± 0.1 m·s⁻¹ compared to Group A (1997) (4.2 ± 0.1 m·s⁻¹) (Table 2). Group F (1995) had an mean speed of 3.2 ± 0.1 m·s⁻¹ compared to group F (1997) (3.2 ± 0.1 m.s⁻¹) (Table 2). It is clear from Figure 2b that specific trends regarding distance vs. speed exist between the two data sets.

The time for the marathon world record (2003) was 2:04.55 (h:mm.ss) (Table 2). The mean running speed was 5.6 m·s^-1, and the CV was 1.2% (Table 2). The time for the 100 km world record is 6:13.33 (h:mm.ss) (Table 2). The mean running speed is 4.5 m·s^-1, and the CV is 3.2% (Table 2).

Discussion

The aim of this study was to describe the changes in running speed of national class runners in a 100 km ultra-marathon race to determine if the faster runners showed different changes in their running speeds compared to the slower runners. Runners in group A completed the race at running speeds within 15% of their starting speed (0-10 km) (Figure 1b). Runners from other groups had a greater difference between starting and finishing speeds than the top runners (Table 1, Figure 1b). For example, group G had the greatest difference between starting (0-10 km) and finishing (90-100 km) speeds (1.4 ± 0.8 m·s^-1) vs. group A (0.5 ± 0.2 m·s^-1) (Table 1). The slower runners had greater variation in running speed compared to faster runners. This is shown by the greater mean change in running speed and the greater CV for mean running speed in slower runners (Table 1, Figure 1a and 1b).

The faster runners maintained their initial running speed up to a distance of approximately 50 km before they decreased their running speed (Figure 1a). Their reduction in running speed thereafter was relatively small as the race progressed. In contrast, runners with slower race times were unable to maintain their initial speed as long as the faster runners, and decreased their speed more rapidly. The design of this study does not allow us to explain the mechanisms causing the differences in the rate at which running speed changed, particularly as the perception of effort may be dissociated from running speed (Hampson et al., 2004). However, we can speculate that the inability to maintain running speed may be attributed to physiological mechanisms (Milvy et al. 1977). It is suggested that although runners utilize about 65% VO₂ max during a 100 km race (Davies and Thompson, 1979), there is a large variation in resistance to fatigue and running economy– which would account for different levels of performance (Sjodin and Svedenhag, 1985). Fatigue after prolonged exercise is associated with glycogen depletion (Bosch et al., 1993), which would occur after 40 – 50 km running at about 65% VO₂ max (Karlsson and Saltin, 1971). An alternative explanation for the decreased running speed after about 50 km is that there are neuromuscular changes caused by repetitive eccentric muscle actions, resulting in fatigue and impaired muscle function (Nicol et al., 1991).

Training habits (Lambert and Keytel, 2000) and genotype (Bouchard et al., 1992) of the runners are additional explanations for the varying reductions in running speed after about 50 km. Also, in accordance with the findings of Foster et al., (1994), the slower runners may not have sufficiently practised their pacing strategies over the longer distance. This observation is interesting and needs further investigation, particularly if it is related to training habits.

It is clear that the runners who had faster race times regulated their speed more accurately than the slower runners, and had fewer changes in running speed than the slower runners. This seems to be a consistent finding as groups A and F in 1995 and 1997 had similar patterns of changes in running speed. In accordance with these findings, the current marathon world record of 2:04.55 held by Paul Tergat (Berlin, Germany, September 2003) and the 100 km world record of 6:13.33 held by Takahiro Sunada (Lake Saroma, Japan, June 1998) are additional examples of races run at an almost even pace (CV = 1.2 and 3.2 %, marathon and 100 km world records respectively, Table 2). These examples show that elite world record performances are run with very few changes in running speed.

Due to the nature of this study and the information available, certain assumptions had to be made. We assumed that all runners produced similar effort and were equally tired at the end of the race; and that all runners had similar racing experience. In addition, in the analysis we also assumed that the runners were highly motivated and trained because they were representing their countries at an international event. A limitation to this study was that training histories and biographical information were not available. These data would have added more interpretive value to this study, and should be included in future studies of this nature.

Conclusions

These results indicate that the faster runners in the 1995 IAU 100 km World Challenge: 1) ran with fewer changes in running speed compared to the slower runners; 2) started the race at a faster running speed than the slower runners; and 3) were able to maintain their initial running speed for longer distances than slower runners. Future studies need to determine whether running performance in ultra-endurance events is enhanced by adopting a more even running speed as a pacing strategy, or whether the ability to run at even running speeds is dependent on a combination of the physiological, psychological, and training habits of the runner.

Biographies

Mike I. LAMBERT

Employment

Associate Professor, University of Cape Town

Degrees

PhD

Research interests

Adaptations to exercise training and their relationship to performance

E-mail: mlambert@sports.uct.ac.za

Jonathan P. DUGAS

Employment

Postgraduate student, University of Cape Town

Degrees

BSc(Med)(Hon) Exercise Science

Research interests

Fluid ingestion and prolonged exercise

E-mail: jdugas@sports.uct.ac.za

Mark C. KIRKMAN

Employment

Postgraduate student, University of Cape Town

Degrees

BSc(Med)(Hon) Exercise Science

Research interests

Training adaptations after high intensity running training

E-mail: mkirkman@sports.uct.ac.za

Gaonyadiwe G. MOKONE

Employment

Postgraduate student, University of Cape Town

Degrees

BSc(Med)Hons

Research interests

Genetic basis of tendon injuries

E-mail: gmokone@sports.uct.ac.za

Miriam R. WALDECK

Employment

Postgraduate student, University of Cape Town

Degrees

B.Curr (Ed et Admin)

Research interests

Heart rate and monitoring performance

E-mail: mwaldeck@sports.uct.ac.za