Auditory Discrimination of Frequency Ratios: The Octave Singularity

Abstract

Sensitivity to frequency ratios is essential for the perceptual processing of complex sounds and the appreciation of music. This study assessed the effect of ratio simplicity on ratio discrimination for pure tones presented either simultaneously or sequentially. Each stimulus consisted of four 100-ms pure tones, equally spaced in terms of frequency ratio and presented at a low intensity to limit interactions in the auditory periphery. Listeners had to discriminate between a reference frequency ratio of 0.97 octave (about 1.96:1) and target frequency ratios, which were larger than the reference. In the simultaneous condition, the obtained psychometric functions were nonmonotonic: as the target frequency ratio increased from 0.98 octave to 1.04 octaves, discrimination performance initially increased, then decreased, and then increased again; performance was better when the target was exactly one octave (2:1) than when the target was slightly larger. In the sequential condition, by contrast, the psychometric functions were monotonic and there was no effect of frequency ratio simplicity. A control experiment verified that the nonmonotonicity observed in the simultaneous condition did not originate from peripheral interactions between the tones. Our results indicate that simultaneous octaves are recognized as “special” frequency intervals by a mechanism that is insensitive to the sign (positive or negative) of deviations from the octave, whereas this is apparently not the case for sequential octaves.

Human listeners are, to some extent, sensitive to the frequency ratios formed by pure tones. For pure tones presented sequentially, this is shown by the fact that a melody retains its perceptual identity when it is transposed in the frequency domain, that is, when the frequencies of the tones are multiplied by a common factor (Attneave & Olson, 1971). Moreover, a familiar melody is easier to recognize when it is presented with the correct frequency ratios than when the ratios are substantially distorted, even if, in the latter case, the global melodic contour is preserved (Dowling & Fujitani, 1971). For pure tones presented simultaneously, a well-known perceptual effect which seems to indicate that listeners are also sensitive to frequency ratios is the phenomenon of “harmonic fusion.” A sum of simultaneous pure tones with frequencies forming a harmonic series (f, 2f, 3f, 4f, etc.) is perceived as a single sound, with a pitch corresponding to f, rather than as a mixture of tones with different pitches. If one component of a harmonic series is mistuned by a few percent from the “correct” frequency, then this component pops out perceptually, while the other components remain fused (Moore, Peters, & Glasberg, 1986; Hartmann, Mc-Adams & Smith, 1990; Lin & Hartmann, 1998; Roberts & Brunstrom, 1998). Because the components of a harmonic series are related by simple frequency ratios (i.e., ratios of small whole numbers), the phenomenon of harmonic fusion reveals a sensitivity to the simplicity of frequency ratios of simultaneous tones. However, in the case of sequentially presented tones, there is also evidence that people are, to some extent, sensitive to frequency-ratio simplicity. In particular, several studies have suggested that successive pure tones that are one octave apart and thus form a frequency ratio of 2:1 are perceptually similar (see, e.g., Deutsch, 1973; Idson & Massaro, 1978; Demany & Armand, 1984).

The present study is an investigation of human listeners’ ability to detect slight differences between the frequency ratios formed by pure tones presented either simultaneously or sequentially. We wished to clarify the mechanisms underlying ratio discrimination in both cases. More specifically, we were especially interested in the influence of ratio simplicity on ratio discrimination. With regard to this influence, three hypotheses are a priori possible; they are hereafter referred to as H0, H1, and H2. According to H0, even though listeners are sensitive to frequency-ratio simplicity, as indicated by the evidence mentioned above, the discriminability of frequency ratios does not depend on their simplicity. Under this hypothesis, the discriminability of two ratios is expected to be a monotonic function of their difference or their ratio (Levelt, van de Geer & Plomp, 1966; Plomp, Wagenaar & Mimpen, 1973). Contrary to H0, H1 posits that frequency-ratio discriminability is influenced by ratio simplicity. As a result, discrimination thresholds may vary nonmonotically as a function of ratio magnitude. However, both H0 and H1 posit that ratio discrimination takes place along a single, unidimensional perceptual continuum on which ratio magnitude is represented in an orderly fashion, with “small” ratios (i.e., ratios close to 1) at one end and large ratios at the other end. This means that for any set of three ratios, r1, r2, and r3, such that r1 < r2 < r3, it will always be easier to discriminate r1 from r3 than to discriminate r1 from r2 or r2 from r3. According to H2, on the other hand, ratio simplicity has a deeper impact on ratio discrimination because differences in ratio simplicity can be by themselves effective discrimination cues, independently of—and in addition to— differences in ratio magnitude. Thus, H2 posits that ratio discrimination takes place along two distinct perceptual continua representing simplicity and magnitude, rather than along a single continuum representing magnitude. As explained below, if this hypothesis is correct, then one might find that for three ratios, r1, r2, and r3, such that r1 < r2 < r3, discriminating r1 from r3 is more difficult than discriminating r1 from r2. In other words, H2 implies that comparative judgments of frequency ratios may not always obey the transitivity principle.

The effect of ratio simplicity on ratio discrimination for simultaneously presented pure tones has been investigated in a few previous studies (Viemeister & Fantini, 1987; Demany & Semal, 1988, 1992; Schellenberg & Trehub, 1996b; Schellenberg, 2002; Trainor, 1997; Stoelinga & Lutfi, 2010). All of these studies indicate that, for simultaneous tones, discriminating two frequency ratios is often much easier when the standard ratio is simple (so that the stimulus is harmonic) than when this is not the case. The results are therefore globally inconsistent with hypothesis H0; they are consistent with both H1 and H2. However, the simplicity effects observed in most of these studies can in fact be interpreted in a rather trivial way. Because of the limited frequency resolution of the cochlea (see, e.g., Moore, 2003, chap. 3), two simultaneous pure tones that are presented to the same ear and that are not both soft and well-separated in frequency will interact in the cochlea. As a result, some auditory-nerve fibers will respond to both tones and will encode properties of the global waveform. If the frequency ratio of the two tones is simple, for example, 2:1 or 3:2, then the global waveform has a short periodicity, in the pitch range. If, on the other hand, the frequency ratio deviates slightly from a simple value such as 2:1 or 3:2, then the global waveform has a much longer periodicity, which may be audible as a periodic beat (Plomp, 1967, 1976; Viemeister, Rickert & Stellmack, 2001).¹ This provides a cue for the discrimination between simple ratios and ratios close to a simple value.

The cue in question was probably available in most of the studies quoted above. However, Demany and Semal (1988, 1992) endeavored to eliminate it by presenting the two components of each stimulus dichotically and at a low SPL, namely 45 dB. The present research was again specifically concerned with the auditory processing of frequency relations across peripheral frequency channels, rather than with the temporal analysis of information available within peripheral frequency channels. Therefore, care was taken to minimize peripheral interactions between the tones and the audibility of beats resulting from such interactions. In addition, a control experiment was performed to check that beats of that kind were not audible.

For pure tones presented sequentially, previous studies have yielded conflicting results concerning the effect of frequency-ratio simplicity on ratio discrimination. Houtsma (1968) measured discrimination thresholds for ratios in the vicinity of one octave. One of the three listeners whom he tested had extensive musical training and all listeners received extensive training in the discrimination task before data collection. The results of Houtsma’s study showed no significant variation in thresholds (expressed on a logarithmic scale, i.e., in octaves or in semitones; 1 octave = 12 semitones) across ratios ranging from 1.9 (about 11 semitones) to 2.1 (about 13 semitones). Burns and Ward (1978) performed similar experiments, but they used a different range of frequency ratios (2.5–5.5 semitones) and they compared the thresholds of musicians and nonmusicians. In the nonmusical group, they obtained results akin to those of Houtsma, in that thresholds were approximately independent of the standard ratio; ratio simplicity had no effect. In the musical group, on the other hand, performance was markedly better than for nonmusicians overall and it was systematically worse for ratios very close to simple values (4:3, 5:4, or 6:5) than for ratios roughly halfway between these simple values. The latter finding was interpreted as evidence for categorical perception of musical intervals based on musical acculturation and practice. The authors concluded that “there is no evidence for the existence of natural perceptual boundaries for melodic musical intervals” (Burns & Ward, 1978, p. 466). In the same vein and in a broader perspective, McDermott, Keebler, Micheyl, and Oxenham (2010) have claimed that, contrary to a common belief, melodic intervals are not perceived more precisely than, and differently from, relations between successive sounds differing in loudness or brightness of timbre. However, the findings of Burns and Ward (1978) and Houtsma (1968) are at odds with results reported more recently by Schellenberg and Trehub (1994, 1996a, 1996b) and Schellenberg (2002). In these four studies, it was found that discriminating a melodic interval corresponding to a simple frequency ratio (3:2 or 4:3) from a somewhat smaller or larger interval (corresponding to a complex ratio) is easier when the simple ratio is presented before the complex ratio than when the two ratios are presented in the reverse order. This asymmetry was observed not only in musically educated adults (Schellenberg, 2002) but also in 6-year-old children (Schellenberg & Trehub, 1996a) and 6-month-old infants (Schellenberg & Trehub, 1996b). Even younger infants appear to perceive two melodies as similar when they differ from each other by octave transpositions of some of their components (Demany & Armand, 1984). The results of Schellenberg and Trehub (1996b) and Demany and Armand (1984) clearly suggest that some melodic intervals are more “natural” than others, contrary to the conclusion drawn by Burns and Ward (1978).

In sum, none of the three hypotheses labeled above as H0, H1, and H2 seems to be definitely ruled out by the current experimental evidence relating to the discrimination of melodic intervals. Nevertheless, the idea that, in the melodic domain, frequency-ratio discriminability could depend on ratio simplicity per se is challenged by the fact that the simplest frequency ratio formed by nonidentical successive tones, that is, 2:1, can be perceived as mistuned: when listeners are required to adjust two successive pure tones one octave apart, the obtained frequency ratio is often slightly but significantly larger than 2:1, especially for high-frequency tones (Ward, 1954; Walliser, 1969: Sundberg & Lindqvist, 1973; Demany & Semal, 1990; Hartmann, 1993). The neural basis of this “octave enlargement” effect is unclear, although tentative explanations have been proposed (Terhardt, 1974; Ohgushi, 1983; Hartmann, 1993; McKinney & Delgutte, 1999).

The current study stemmed from introspective observations that we made about the perception of stimuli consisting of four synchronous pure tones presented at a low SPL and regularly spaced on a logarithmic frequency scale. Each stimulus was defined by two parameters: Fmin, the frequency of the lowest tone, and Oct, the frequency spacing of the tones expressed in octaves. In our stimulus set, Oct varied in the range 0.9–1.1. We focused our attention on the perceptual correlate of changes in Oct while Fmin was varied concomitantly and randomly, in a wide range. Because of the randomness of the variations in Fmin, there was essentially no correlation between Oct and the global pitch of the stimuli or the frequency of individual tones. We first observed that the stimuli obtained for two values of Oct equidistant from 1, and not too close from each other (e.g., 0.9 and 1.1), were discriminable on the basis of a spectral “compactness” cue. This perceptual variable was a monotonic function of Oct: a stimulus with a relatively small value of Oct, for example, 0.9, sounded more compact than a stimulus with a relatively large value of Oct, for example, 1.1. It was also apparent, however, that a different perceptual variable, namely spectral fusion, was more efficient for the detection of changes from Oct = 1 to Oct ≠ 1. For Oct = 1, the four tones were perceptually fused into a single sound; this fusion decreased as Oct deviated from 1. Because fusion decreased for both positive and negative deviations from 1, this cue was not a monotonic function of Oct, in contrast to the compactness cue. Overall, therefore, our informal observations suggested that within a small range of Oct values centered on 1, changes in Oct were detectable on the basis of two different perceptual variables, each of them being more efficient than the other in certain conditions. This fitted with the hypothesis identified above as H2.

We reasoned that the just-described stimuli could be used to test objectively H2 as follows. Let Oct_reference be an Oct value slightly smaller than 1 and moderately discriminable from 1. Suppose that, as suggested by our introspective observations, (1) the discrimination between Oct_reference and 1 essentially rests on the fusion cue, and (2) fusion decreases as soon as Oct exceeds 1. It can then be expected that Oct_reference will be easier to discriminate from 1 than from Oct values slightly larger than 1. However, even larger Oct values will be discriminable from Oct_reference on the basis of the compactness cue. So, the psychometric function obtained for the discrimination between Oct_reference and progressively larger values of Oct might show an initial rise followed by a fall and then a second rise. Such a nonmonotonic psychometric function would provide strong evidence for H2.

This was the rationale underlying the first half of Experiment 1, our main experiment. The second half of this experiment was identical to the first, except that the pure tones forming the stimuli were now presented successively rather than simultaneously. This allowed us to compare the mechanisms subtending frequency-ratio discrimination for simultaneous versus successive tones. Experiment 2 was a control experiment intended to check, as mentioned above, that all the data collected in the main experiment reflected frequency comparisons across peripheral frequency channels.

Experiment 1

Method

Participants

The tested listeners were six students in their twenties (three male, three female). They all had normal hearing. Some of them were amateur musicians, but none had received a thorough musical education. All listeners were paid for their participation, except listener L5, who was the first author.

Stimuli, conditions, and task

Each stimulus consisted of four diotically presented pure tones. In the “simultaneous” condition, these four tones were synchronous. In the “sequential” condition, they were presented consecutively, in ascending frequency order, with 100-ms silent interstimulus intervals (ISIs) between them. In both conditions, each tone had a total duration of 100 ms and was gated on and off with 20-ms raised cosine functions. The tones had a nominal SPL of 31 dB for listeners L1 and L2, and 46 dB for the four remaining listeners.² The four components of each stimulus were equally spaced on a logarithmic frequency scale. Their spacing, Oct, was expressed in octaves. On each stimulus presentation, the frequency of the lowest tone (Fmin) was selected randomly between 125 and 250 Hz; the corresponding probability distribution was rectangular, frequency being scaled logarithmically. The starting phases of the tones were random variables and did not depend on frequency.

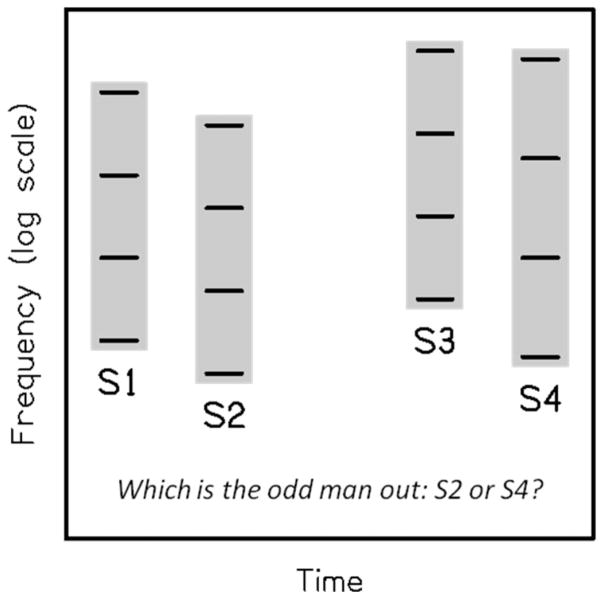
On every trial, four successive stimuli were presented, as illustrated in Figure 1 for the “simultaneous” condition. There was a silent ISI of 300 ms between the first two stimuli (S1 and S2) and between the last two stimuli (S3 and S4). A longer ISI— 600 ms—separated S3 from S2, thus segmenting the whole sequence into two pairs of stimuli. In three of the four stimuli, Oct had a fixed reference value (Oct_reference) of 0.97. In the remaining stimulus, which was either S2 or S4, at random, Oct was larger; this target value of Oct (Oct_target) could be equal to 0.98, 0.99, 1.00, 1.01, 1.02, 1.03, or 1.04. The listener’s task was to indicate whether the odd man out was S2 or S4, by making a mouse click on one of two virtual buttons on a computer screen. Immediately after this response, the button was colored in white if the response was correct, or in black otherwise. Response time was not limited. Within each block of trials, a response triggered the next trial after a delay of about 1 s.

Figure 1.

Schematic representation of listeners’ task in the “simultaneous” condition of Experiment 1. On each trial, four stimuli (S1, S2, S3, S4) were successively presented (their relative timing is not faithfully depicted in this Figure). Each stimulus consisted of four synchronous pure tones, equally spaced on a logarithmic frequency scale. The spacing of the tones was the same (namely, 0.97 octave) for three stimuli, and was larger for the remaining stimulus, which was either S2 or S4. Listeners had to identify the odd man out as S2 or S4. The frequency of the lowest component of each stimulus was randomly chosen between 125 and 250 Hz. The “sequential” condition of Experiment 1 was similar, except that in this case the four components of each stimulus were presented consecutively.

The stimuli were generated at a 44.1-kHz sampling rate, using 24-bit digital-to-analog converters (RME). They were presented via headphones (Sennheiser HD 650). Harmonic distortion at the output of the headphones was assessed using an artificial ear (Bruel & Kjaer 4153 equipped with a flat-plate coupler; microphone model: 4134) and a spectrum analyzer (Stanford Research, SR 780). For nominally pure tones ranging in frequency from 125 to 1000 Hz and produced at 80–90 dB SPL, it was found that each component of the harmonic distortion was at least 50 dB below the fundamental.

Procedure

Listeners were tested individually in a triple-walled sound-attenuating booth (Gisol, Bordeaux). Trials were run in blocks of 50, during which Oct_target had a fixed value, known by the listener. Each experimental session consisted of seven blocks of trials, one block for each of the seven possible values of Oct_target. These seven blocks were randomly ordered.

For each listener, the experiment proper was preceded by at least six practice sessions in the “simultaneous” condition. Then, 10 formal sessions were run in that condition. They were followed by one or two practice sessions in the “sequential” condition, and then 10 formal sessions in that condition. Overall, therefore, the formal data resulted from 500 trials per listener for each combination of condition and Oct_target value.

Results

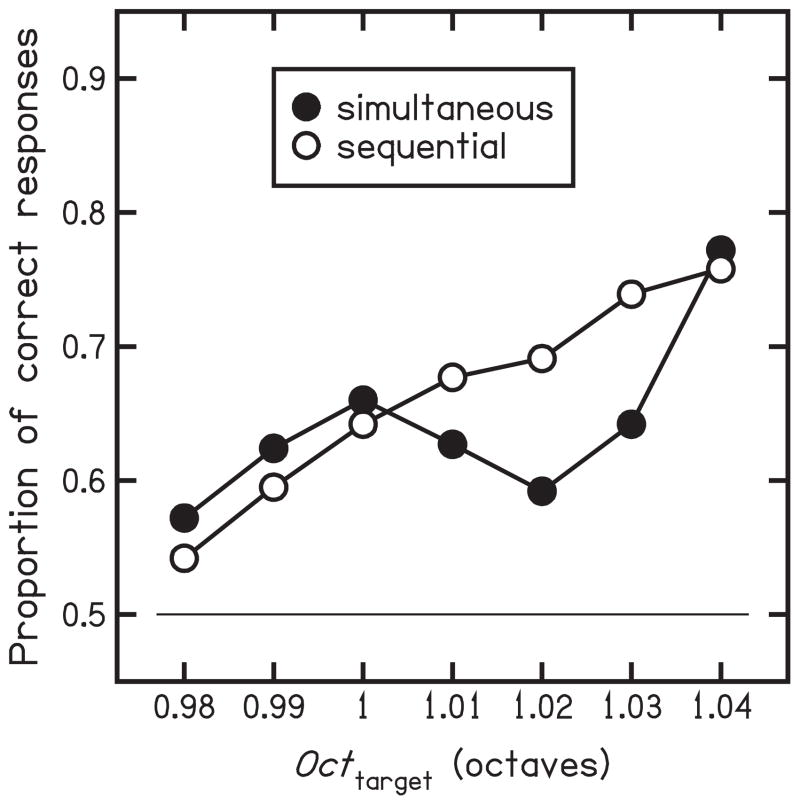
Before considering the results obtained in each individual listener, we shall focus on the mean data. Figure 2 shows the overall proportion of correct responses obtained in each condition (“simultaneous”: black disks; “sequential”: white disks) for each Oct_target value. Performance was not markedly better in one condition than the other, but the effect of Oct_target on performance clearly differed across the two conditions. In the “sequential” condition, the mean psychometric function obtained was approximately a straight line, consistent with the hypothesis identified above as H0 (no effect of frequency-ratio simplicity on ratio discrimination). In the “simultaneous” condition, by contrast, the mean psychometric function obtained was clearly nonmonotonic; it showed a peak for Oct_target = 1, followed by a dip for Oct_target = 1.02; this outcome is consistent with hypothesis H2.

Figure 2.

Results obtained in the “simultaneous” and “sequential” conditions of Experiment 1. Each data point represents the mean performance of six listeners. The thin horizontal line indicates the chance level of performance (50% of correct responses).

The data were submitted to a repeated-measures ANOVA, Listener × Condition × Oct_target, which revealed a significant main effect of Oct_target, F(6, 30) = 14.80, p < .001, and a significant interaction between Condition and Oct_target, F(6, 30) = 4.81, p = .0015. There was no significant main effect of Condition, F(1, 5) = 0.03, p = .88. Given the existence of a reliable interaction between Condition and Oct_target, we then submitted the data obtained in each condition to a separate repeated-measures ANOVA, Listener × Oct_target. In each case, not surprisingly, the effect of Oct_target appeared to be significant, F(6, 30) ≥ 8.45, p < .001. Our main goal was to determine whether there were significant cubic trends in the effect of Oct_target, as predicted by H2. There was indeed a significant trend of this type for the “simultaneous” condition, t(30) = 5.11, p < .001, but not for the “sequential” condition, t(30) = 0.27, p = .79.

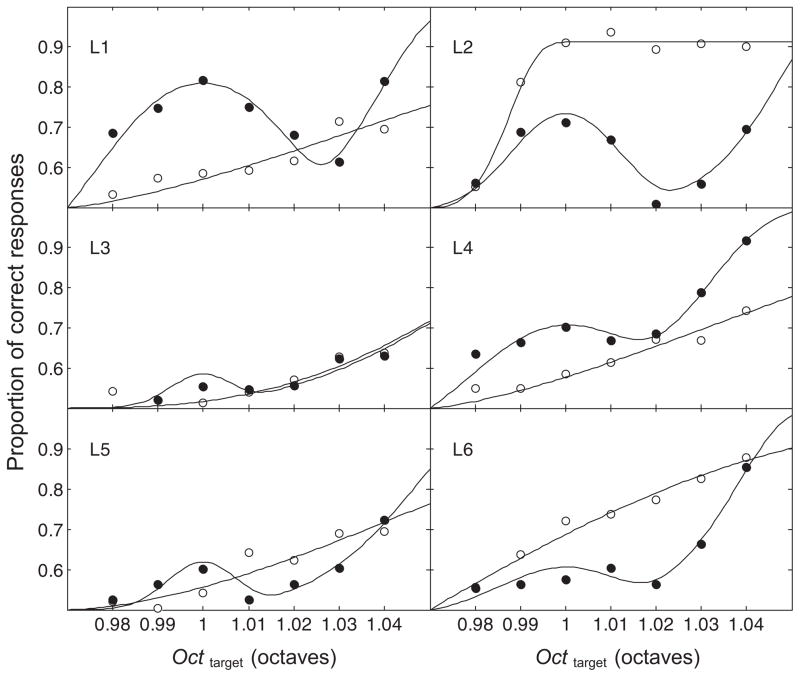
The data provided by each listener are plotted in Figure 3, where the curves represent best-fitting psychometric functions obtained from two quantitative models of perceptual processing, one model for each condition. These models are described in detail in the Appendix to this manuscript. It is especially noticeable in Figure 3 that there was essentially no correlation, across listeners, between the overall level of performance in the two conditions. For instance, while listener L1 performed markedly better in the “simultaneous” condition than in the “sequential” condition, the reverse was found in listener L2.

Figure 3.

Each panel represents the results obtained from a given listener in Experiment 1. As in Fig. 2, black disks represent the “simultaneous” condition and white disks represent the “sequential” condition. Each data point is the outcome of 500 trials. The curves represent best-fitting psychometric functions derived from two models described in the Appendix. The model used for the “sequential” condition assumes that listeners used a single perceptual cue, which was a monotonic function of Oct_target. The model used for the “simultaneous” condition assumes that, in addition to a cue that was a monotonic function of Oct_target, listeners used a cue determined by the absolute value of the distance of Oct_target (and Oct_reference) from 1.

Discussion

Can we be sure that performance in this experiment always reflected listeners’ ability to discriminate between frequency ratios, rather than between frequencies? To minimize the latter possibility, we had randomized the frequency of the lowest component of each stimulus, as pointed out above and illustrated in Figure 1. However, was the randomization range (1 octave) large enough? To answer that question, we determined by means of Monte Carlo simulations the performance expected from a virtual listener insensitive to changes in frequency ratio but producing optimal responses on the basis of frequency comparisons between stimuli. This virtual listener votes for stimulus S2 if the frequency of the highest component of S2 is higher than the frequency of the highest component of S4, and votes for S4 otherwise. We found that the proportion of correct responses provided by the virtual listener is approximately a linear function of Oct_target − Oct_reference. This proportion is 0.664 for Oct_target = 1.03 and 0.688 for Oct_target = 1.04. In the “sequential” condition, for these two values of Oct_target, five of the six listeners tested in the experiment (all participants except L3) performed better than the virtual listener; therefore, those five listeners must have based their judgments on comparisons between frequency ratios, as intended, rather than on comparisons between frequencies; listener L3, on the other hand, may have been unable to perform the task as intended. In the “simultaneous” condition, for all listeners except again L3, the nonmonotonic effect of Oct_target on performance is of course at odds with the idea that performance was merely determined by frequency comparisons.

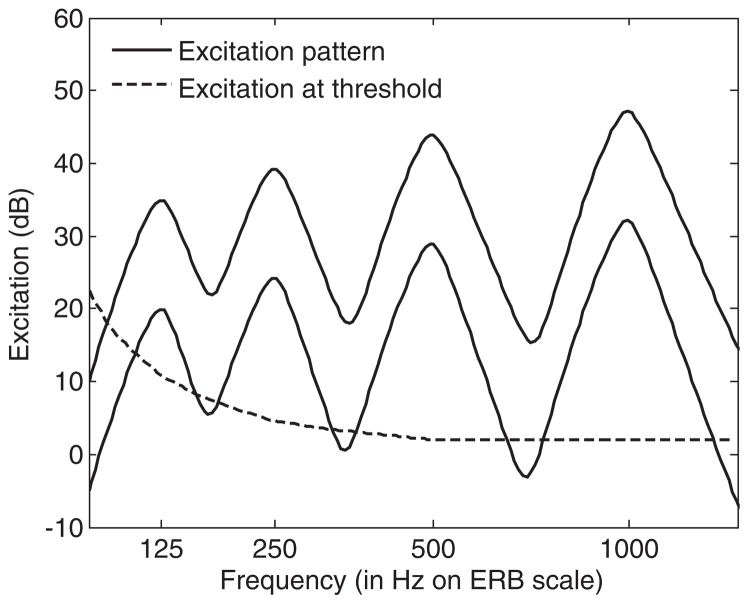
Our main finding is that frequency–ratio discrimination was generally a nonmonotonic function of Oct_target in the “simultaneous” condition but not in the “sequential” condition. One conceivable explanation of this difference is that in the “simultaneous” condition, the pure tones forming the stimuli interacted in the cochlea, whereas this was precluded in the “sequential” condition. As pointed out above, cochlear interactions of simultaneous tones would have allowed listeners to discriminate between frequency ratios on the basis of beat cues. Beats were liable to be elicited by all of the stimuli used in the “simultaneous” condition, except those composed of tones exactly one octave apart. This can potentially account for the fact that, in the “simultaneous” condition, a local peak in discriminability was observed for Oct_target = 1. To limit cochlear interactions, we presented the tones at a low SPL, namely 46 dB for four listeners and 31 dB for the remaining two listeners. To further investigate the extent of interactions between the tones, we computed “excitation patterns” for the stimuli of the “simultaneous” condition, using the model of Moore, Glasberg and Baer (1997) revised by Glasberg and Moore (2006). Figure 4 shows the simulated excitation pattern obtained for the harmonic stimulus formed of tones at 125, 250, 500, and 1000 Hz when the SPL per tone was 46 dB (upper solid curve) and 31 dB (lower solid curve). Note that 125 Hz was the lowest possible tone frequency in the experiment, and that in this case cochlear interactions between tones were maximized (because the relative bandwidth of the peripheral auditory filters tends to increase at low frequencies). The dashed curve in Figure 4 shows the excitation corresponding to the absolute threshold of hearing (in normal young listeners). This curve thus represents a detection floor for the excitation patterns: portions of the patterns that fall below it are, in principle, undetectable by a normal-hearing listener. It can be seen that in the case of the lower-level excitation pattern, any detectable excitation originates from a single tone. At the higher level, however, listeners could in theory detect excitation produced by two simultaneous tones.

Figure 4.

The two solid curves represent the cochlear excitation pattern produced by a sum of four pure tones at 125, 250, 500, and 1000 Hz when the SPL of each tone is 46 dB (upper curve) and 31 dB (lower curve). The dashed curve represents the amount of excitation produced by a just-detectable pure tone, as a function of its frequency. Frequency, on the abscissa, is scaled in accordance with the frequency dependence of the auditory filters’ equivalent rectangular bandwidth (ERB; cf. Moore, 2003, chap. 3). The three curves were calculated on the basis of the model proposed by Moore, Glasberg, and Baer (1997) and revised by Glasberg and Moore (2006).

As a matter of fact, investigations on the audibility of beats of mistuned consonances in monaural dyads of pure tones have suggested that such beats are not audible when each of the tones is below 50 dB SPL (Plomp, 1967, 1976; Viemeister et al., 2001). Nevertheless, it was important to check that beats resulting from cochlear interactions were indeed never detectable in Experiment 1. This was the main purpose of Experiment 2.

Experiment 2

Rationale

In a previous study by Demany, Semal, and Carlyon (1991), listeners’ ability to detect deviations from the octave interval was investigated using dyads of simultaneous pure tones. On each trial, listeners were presented with two successive dyads, one composed of tones exactly one octave apart and one in which the interval formed by the tones was either slightly larger (positive mistuning) or slightly smaller (negative mistuning); the task was to indicate which of the two dyads was a mistuned octave. The two components of each dyad were presented at a low sensation level in a pink-noise background, so that they were unlikely to interact in the cochlea. Unexpectedly, the experimental results showed that negative mistunings were easier to detect than positive mistunings of the same size in terms of relative frequency deviation.³ Although the origin of this perceptual asymmetry was not elucidated, one could infer from it that the listeners did not detect mistuning by detecting beats resulting from cochlear interactions: Had this been the case, no significant effect of the sign of mistuning was expected because the waveform obtained by adding two tones with frequencies f and (2f + ε) Hz is essentially a mere temporal inversion of the waveform obtained when 2f + ε is replaced by 2f − ε. We thought that if the same perceptual asymmetry was observable for stimuli similar to those used in Experiment 1, this would provide evidence that, in the latter experiment as well as in the previous study, mistuned octaves did not elicit significant cochlear beats. That was the rationale underlying Experiment 2.

Method

As in the “simultaneous” condition of Experiment 1, the stimuli consisted of four synchronous pure tones equally spaced on a logarithmic frequency scale, gated on and off with 20-ms raised cosine functions, and presented diotically at the same nominal SPL. Once more, the frequency of the lowest component of each stimulus was selected randomly between 125 and 250 Hz, and each component had a random initial phase. However, the stimuli now had a total duration of 500 ms instead of 100 ms; this increase in duration facilitated beat detection (Hartmann, 1988). As in Experiment 1, four successive stimuli (S1, S2, S3, S4) were presented on each trial and listeners were requested to identify the odd man out, which was equiprobably either S2 or S4. Again, the odd man out differed from the other three stimuli with respect to the frequency ratio of neighboring tones (Oct). The silent ISIs separating the four stimuli were the same as in Experiment 1, and correct-answer feedback was again provided visually following each response.

The main novelty of Experiment 2 was that Oct now had a reference value (Oct_reference) of exactly 1 octave. On each trial, therefore, the odd man out was the only stimulus for which Oct differed from 1 octave. In one condition, named the “stretching” condition, the value of Oct in the odd man out (Oct_target) was always larger than 1 octave. In another condition, named the “compression” condition, Oct_target was always smaller than 1 octave. In both conditions, Oct_target was varied adaptively within blocks of trials, in order to measure a perceptual threshold corresponding to the mistuning value, Δ_oct = |Oct_target − Oct_reference|, for which the probability of a correct response was 0.75. This was done using the “weighted up-down” paradigm described by Kaernbach (1991). At the onset of each block of trials, Δ_oct was large, well above the expected threshold. Then, Δ_oct was decreased after each correct response and increased after each incorrect response. A block ended after the 14th reversal in the variation of Δ_oct. Until the 4th reversal, Δ_oct was multiplied by 2.25 when it was increased, and divided by the cube root of the same factor when it was decreased. After the 4th reversal, Δ_oct was either multiplied by 1.5 or divided by the cube root of this factor. The threshold measure obtained in a block of trials was computed as the geometric mean of all the Δ_oct values used from the 5th reversal on. Within each experimental session, thresholds were measured alternately in the “stretching” condition and the “compression” condition; the switch occurred after each threshold measurement.

The component tones of the stimuli were varied in SPL from 46 dB (the highest SPL of the tones in Experiment 1) to 76 dB, or vice versa, in 10-dB steps. The SPL was fixed within sessions. At each SPL and for each listener, 10 threshold measurements were made in the “stretching” condition and in the “compression” condition.

The apparatus used in this experiment was the same as in Experiment 1. Seven listeners (four male, three female) were tested. Three of them were listeners L4, L5, and L6 in Experiment 1. The four additional listeners (L7–L10) included three students in their twenties and author LD (aged 58 and designated as L7); these four listeners had normal hearing, at least for the frequency range covered by the stimuli; none of them had received a thorough musical education, but two (L7 and L10) had substantial previous experience with psychoacoustics. For each of the seven listeners, the experiment proper was preceded by a single practice session.

Results and Discussion

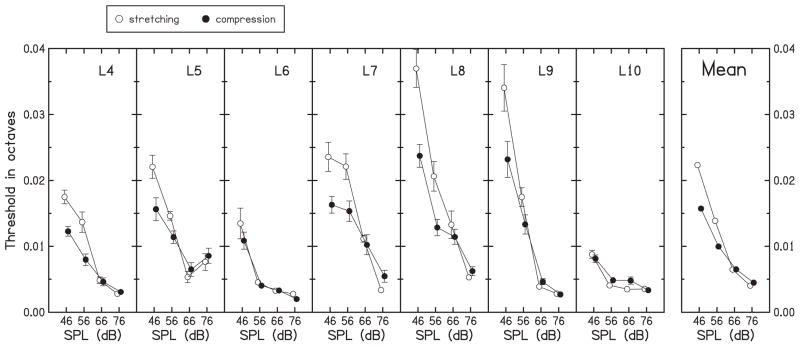
Figure 5 displays the results. Seven panels show, as a function of SPL, the mean threshold measured in each listener for the two conditions (“stretching” vs. “compression”). The individual results are averaged in the rightmost panel. Note first that SPL had a strong effect on thresholds: as the stimuli increased in SPL, thresholds systematically decreased (except in the case of L5 for the highest SPL). This trend was predictable because an increase in SPL increased the potential influence of beat cues originating from cochlear interactions between the tones. In line with the hypothesis that the task was performed using beat cues when the SPL was high, there was no significant difference between the thresholds obtained in the “stretching” and “compression” conditions at 66 dB, t(6) < 1, as well as at 76 dB, t(6) = 1.25, p = .26. By contrast, there was a marginally significant effect of condition at 56 dB, t(6) = 2.02, p = .06, and the effect of condition was definitely significant at 46 dB, t(6) = 3.97, p = .007. At these two lower SPLs, thresholds were better in the “compression” condition than in the “stretching” condition, as expected from the study by Demany et al. (1991).

Figure 5.

Results of Experiment 2: mistuning thresholds measured in the “stretching” condition and the “compression” condition as a function of the SPL of the tones. The data obtained from each of the seven listeners (L4, L5, … L10) are displayed in a separate panel. In these seven panels, each data point is the mean of 10 threshold measurements and the error bars represent ± 1 standard error of the mean. In the rightmost panel, the results of the seven listeners are averaged. In each panel, for clarity, the data points corresponding to the two mistuning conditions are slightly shifted horizontally (to the left for the “stretching” condition and to the right for the “compression” condition).

For 46-dB tones, we obtained a mean threshold of 0.0223 octave in the “stretching” condition and 0.0157 octave in the “compression” condition. It must be underlined that, in comparison with the reference value of Oct (1 octave), these thresholds represent quite small frequency deviations, although listeners’ performance was even better at higher SPLs. If the thresholds obtained at 46 dB had been markedly higher, then their dependence on the sign of mistuning might have been accounted for under the hypothesis that, even for this low SPL, mistuning detection rested on beat detection. It would have been so because a compressive mistuning, by decreasing the frequency distance between the tones, increased the possibility of cochlear interactions, whereas the opposite occurred in the case of stretching. To quantify the corresponding contrast for 46-dB tones and mistunings such as the thresholds mentioned above, we used again the excitation-pattern model of Moore et al. (1997). We assumed that the magnitude of a cochlear interaction between two tones was directly reflected by the height of the excitation-pattern trough between their frequencies. The height of the troughs increased as Oct decreased. According to the model, this effect was strongest for the third trough, representing a potential interaction of the upper two tones; on average, the third trough was about 1.7-dB higher for the Oct value corresponding to a just-detectable compression than for the Oct value corresponding to a just-detectable stretching. Such a small difference does not seem able to account for the very substantial dependence of thresholds on the sign of mistuning. Moreover, if a 1.7-dB difference in excitation level were responsible for this dependence, then increasing the SPL of the tones by 10 dB should have improved thresholds considerably, whatever the sign of mistuning. According to the model of Moore et al. (1997), the third trough in the excitation pattern was about 12 dB higher for 56-dB tones than for 46-dB tones. In spite of this, the thresholds measured in the “stretching” condition with 56-dB tones did not differ significantly from those measured in the “compression” condition for 46-dB tones, t(6) = 1,14, p = .30. Clearly, therefore, the perceptual asymmetry observed in the present experiment for 46-dB tones does not seem consistent with the hypothesis that, at this level, deviations from one octave were detected by means of beat cues originating from cochlear interactions. Consequently, this hypothesis also appears inadequate to account for the nonmonotonic psychometric functions found in Experiment 1.

It has been reported that, for some listeners, a mistuned octave composed of simultaneous pure tones can elicit the perception of faint beats when the two tones are presented to opposite ears (Thurlow & Bernstein, 1957; Thurlow & Elfner, 1959; Tobias, 1964; Feeney, 1997); according to Thurlow (Thurlow & Bernstein, 1957; Thurlow & Elfner, 1959), this is possible even for tones at a sensation level as low as 30 dB. The corresponding “dichotic beats of mistuned consonances (DBMCs)” have been interpreted as a between-channel phase effect originating from neural processes involved in sound localization by the binaural system (Feeney, 1997). Because in our two experiments the stimuli were presented diotically, it is conceivable that beat detection was facilitated by the binaural mechanism responsible for the audibility of DBMCs. However, the perceptual asymmetry disclosed by Experiment 2 does not seem easier to fit in with this “central beats” hypothesis than with the “peripheral beats” hypothesis considered above.

We still have no explanation for the perceptual asymmetry. As discussed later in this article, it might be expected, in theory, that simultaneous and soft pure tones approximately one octave apart fuse maximally when the octave is slightly stretched rather than perfectly tuned from the physical point of view. This bias could give rise to a perceptual advantage of negative mistunings (compressions) in mistuning detection. However, the results of Experiment 1 fail to provide evidence for the bias in question. Of course, negative mistunings could still be better detected than positive mistunings if maximum fusion was systematically obtained for the physically perfect octave: it may simply be, for some reason, that fusion decreases more rapidly for negative deviations from the perfect octave than for positive deviations.

General Discussion

The underpinnings of auditory sensitivity to frequency relations, and more specifically to the simplicity of frequency ratios, remain a matter of controversy. Although it is now understood why two simultaneous complex tones (for instance two vowels or violin sounds) are perceived as more consonant when their fundamental frequencies are in a simple frequency ratio than when this is not the case (Plomp, 1976; McDermott, Lehr, & Oxenham, 2010), the roots of harmonic fusion for simultaneous pure tones are still unclear. Moreover, the reason why an affinity is perceived between sequentially presented pure tones one octave apart is also unknown. As discussed below, both of these phenomena might originate from a learning mechanism, or they might stem from innate properties of the auditory system. In the present study, we sought to clarify the processes underlying the perception of frequency-ratio simplicity for pure tones. In particular, we sought to test the idea that the same processes are at work for simultaneous tones and for consecutive tones. We assessed the effect of ratio simplicity on ratio discrimination, for simultaneous and sequentially presented tones. Markedly different results were obtained in these two situations (Experiment 1), in spite of the absence of significant cochlear interactions between the tones when they were simultaneous (Experiment 2). For simultaneous tones, frequency-ratio discrimination appeared to be affected by ratio simplicity. Moreover, we found that ratio simplicity— or, more precisely, distance to the simple ratio 2:1—was in itself the physical correlate of one discrimination cue. This result fitted with a hypothesis called “H2” in the introduction of our article; according to H2, frequency-ratio discrimination takes place along two distinct perceptual continua, representing ratio simplicity and ratio magnitude. For sequentially presented tones, on the other hand, ratio simplicity had no effect.

Can the latter finding, concerning sequential tones, be ascribed to peculiarities of our stimuli? The tones that we presented either simultaneously or sequentially were the same in these two conditions; this was of course mandatory for a fair comparison between the two conditions. One might think, however, that the melodic sequences produced in the “sequential” condition were such that the frequency ratios of the tones could not be perceived optimally. Against this concern, it may be noted first that the speed of the sequences (five tones per second) was far from amusical: this speed is that of a series of eighth notes in “allegro” tempo; such series are very common in music. More crucially, it must be emphasized that, overall, listeners did not perform more poorly in the “sequential” condition than in the “simultaneous” condition, as shown by Figure 2; this is clearly at odds with the idea that frequency-ratio perception was disadvantaged in the “sequential” condition.

The fact that ratio simplicity had no effect in the “sequential” condition is not particularly surprising in the light of previous research. Although, for consecutive tones, Schellenberg and Trehub (1994, 1996a, 1996b) found an advantage of ratio simplicity in ratio discrimination, Houtsma (1968) reported that ratio discrimination thresholds do not vary significantly when the standard ratio varies from 1.9 to 2.1. Moreover, Dobbins and Cuddy (1982), who used stimuli similar to those used by Houtsma (1968), concluded from their frequency-ratio categorization experiment that the function relating physical frequency ratios to their perceptual representations is simply logarithmic (for musicians as well as nonmusicians). It may be that, for consecutive tones, ratio simplicity affects ratio discrimination only if special stimuli and/or experimental procedures are used, while simplicity effects are easier to demonstrate with simultaneous tones. We must also point out that although the results obtained in our “sequential” condition are inconsistent with the hypothesis referred to above as H2, they are not clearly inconsistent with H1. H2 posits that frequency-ratio discrimination takes place along two distinct perceptual continua representing simplicity and magnitude. According to H1, by contrast, magnitude is the only discrimination cue; simplicity is not in itself a discrimination cue; however, discriminability is better near simple ratios than near complex ratios. Our measurement of psychometric functions with a reference ratio of 0.97 octave was not well suited for a confrontation of H1 with H0 (according to which ratio simplicity has no influence at all on ratio discrimination).

Given that we obtained no effect of ratio simplicity with sequentially presented tones, and that a simultaneous presentation of the same tones did not produce extra cues resulting from cochlear interactions, it is remarkable that in the latter condition we did obtain an effect of ratio simplicity. This contrast reflects the fact that ratio simplicity produces quite different perceptual effects in the melodic and harmonic domains. Two successive pure tones forming a melodic octave are perceived as having related pitches, but, at least for normal adult listeners, they are easily distinguishable from each other. Indeed, with respect to pitch, their difference is not less obvious than their affinity. By contrast, two simultaneous pure tones forming an octave interval are perceptually fused into a single entity. In the auditory system, this fusion may well take place below the level at which representations of pitch per se are extracted from pure tones (as well as from complex tones). An analogous point was recently made by Borchert, Micheyl, and Oxenham (2011). In their study, listeners had to detect slight differences in pitch (fundamental frequency) between two complex tones which consisted of harmonics filtered into two separate, nonoverlapping spectral regions. When the tones were presented consecutively, performance was poor; listeners found the task difficult because of the large difference in timbre between the tones. However, when the tones were presented synchronously, performance was markedly better and the task was subjectively much easier, because it could then be performed by using a fusion cue rather than by explicit pitch comparisons.

How Can the Octave Be Recognized as a Simple Frequency Ratio?

In a very influential paper, Terhardt (1974) argued that the phenomenon of harmonic fusion originates from a learning process. He suggested that, early in life, humans initially perceive simultaneous pure tones forming a harmonic series as separate auditory entities, but that subsequently such tones are fused because of their frequent co-occurrence in the natural acoustic environment (and especially their systematic co-occurrence in vocal sounds). Shamma and Klein (2000) also took the view that harmonic fusion is learnt, and they put forth a physiologically based model whereby this learning could occur even in the absence of harmonic inputs. Although the spectral structure of the stimuli used here was always dissimilar to that of natural harmonic sounds (because the components of the latter sounds do not form only octave intervals), the frequency–ratio simplicity effect that we obtained with simultaneous tones could in principle be based on a learning process.

However, this is not necessarily the case. Interestingly, harmonicity is not a mandatory condition for the perceptual coherence of simultaneous pure tones, as shown by Roberts and his coworkers (Brunstrom & Roberts, 2000; Roberts & Bailey, 1996; Roberts & Brunstrom, 1998, 2001, 2003). When the elements of a harmonic series (e.g., 200, 400, 600, … 2000 Hz) are all shifted in frequency by the same amount in hertz (e.g., 50 Hz), their perceptual coherence is somewhat reduced but not dramatically, although they no longer form a harmonic series. Their constant frequency spacing is sufficient to produce perceptual coherence, as indicated by the fact that if a single element of the inharmonic set is slightly shifted in frequency, thus making the frequency spacing locally irregular, the shifted element tends to stand out perceptually. Given the rarity, in our acoustic environment, of inharmonic stimuli such as the one just described, their perceptual coherence is unlikely to originate from a learning process.⁴

As pointed out by Roberts and Brunstrom (2001), the perceptual coherence of these inharmonic stimuli, as well as harmonic fusion, may instead originate from the temporal coding of frequency by the auditory system. Because the successive action potentials elicited by a pure tone in an auditory-nerve fiber tend to occur at a particular phase of the tone, these successive neural spikes are generally separated by time intervals close to the period of the tone and its integer multiples (see, e.g., McKinney & Delgutte, 1999). This implies that simultaneous pure tones forming simple frequency ratios will produce, in separate auditory-nerve fibers, spikes separated by common time intervals. For two pure tones one octave apart, indeed, all the time intervals present in the neural response to the lower-frequency tone should also be present, approximately, in the neural response to the higher-frequency tone. Relations of that kind may be recognized at a higher level of the auditory system, perhaps after an autocorrelation of the peripheral neural responses (Licklider, 1951; Meddis & Hewitt, 1991, 1992; Patterson, Handel, Yost, & Datta, 1996; Yost, 1996; Cariani & Delgutte, 1996; Cariani, 2001; de Cheveigné, 2005). Such a mechanism can in principle explain harmonic fusion, as well as many aspects of pitch perception, including the perceptual affinity of consecutive tones one octave apart (Ohgushi, 1983; Hartmann, 1993; McKinney & Delgutte, 1999).

Therefore, the perceptual discrimination of an octave from slightly larger or smaller frequency ratios could rest upon the use of temporal information. Alternatively, this perceptual discrimination might be based on the use of spatial information. In the latter view, consistent with the fact that the auditory system has a tonotopic organization, an octave is perceptually defined as a specific distance between neural activations induced by pure tones. For simultaneous tones, our data would then imply, rather paradoxically, that deviations from this specific distance can be detected without being recognized as positive or negative deviations. Indeed, in the “simultaneous” condition of Experiment 1, the fact that performance decreased when the target frequency ratio was made larger than one octave implied that the (positive) sign of this mistuning from one octave could not be discriminated from the (negative) sign of the mistuning of the reference frequency ratio (0.97 octave).

Harmonic Versus Melodic Octaves: Is There a Perceptual Link?

As mentioned in the previous section of this Discussion, Terhardt (1974) has argued that harmonic fusion stems from a learning process. In his theory, two simultaneous pure tones one octave apart are fused merely because they co-occur in frequently heard sounds, such as the vowels of speech. Terhardt also suggested that, in consequence of our frequent exposition to vowels and other periodic complex tones, we acquire not only harmonic octave templates but also melodic octave templates. More generally, the learning process responsible for harmonic fusion would also account for the affinity perceived between successive pure tones forming simple frequency ratios, such as the octave. The results reported here do not support the latter hypothesis. If, as supposed by Terhardt, melodic and harmonic octaves were recognized by means of the same internal templates, then these templates should show similar properties in melodic and harmonic conditions. However, our results imply that the harmonic octave is recognized by a mechanism which is insensitive to the sign of deviations from the octave, whereas this is apparently not the case for the melodic octave.

To explain the “octave enlargement” phenomenon described in the introductory section of this article, Terhardt (1970, 1971, 1974; see also Terhardt, Stoll, & Seewann, 1982) argued that the harmonic complex tones typical of our auditory environment are such that their spectral components partially mask each other in the auditory periphery. As a result, the pitches evoked by these spectral components would be slightly different from those evoked by physically identical pure tones presented in isolation or successively. Partial masking, according to Terhardt, produces repulsive pitch shifts; this would account for the fact that, in general, a melodic octave is heard as optimally tuned for a physical frequency ratio slightly larger than 2:1.⁵ Here, we used complex tones composed of pure tones which did not mask each other significantly, as shown by Experiment 2. Thus, the pitch-shift effects invoked by Terhardt should not have occurred for these stimuli. In consequence, Terhardt’s theory predicted that maximum fusion would be obtained for frequency ratios slightly larger than one octave. Our results do not conform to this prediction: in the “simultaneous” condition of Experiment 1, all listeners but one (L6) performed better when the target frequency ratio was exactly one octave than when it was equal to 1.01 octave, as can be seen in Figure 3. Admittedly, the target frequency ratios may have been too coarsely sampled to reveal an octave-enlargement effect in the “simultaneous” condition: when listeners are required to set two successive tones one octave apart, only very small enlargement effects (<1%) are found at low frequencies, in spectral regions covered by the stimuli used here (cf. Figure 1 in McKinney & Delgutte, 1999).

Nevertheless, as pointed out above, our results clearly question the validity of Terhardt’s hypothesis on the origin of tonal affinity and the perception of the melodic octave. Two other problems for this hypothesis have been uncovered previously. First, Terhardt’s observations on the pitch shifts of components of harmonic complex tones are apparently difficult to replicate; it has been suggested that these pitch shifts do not really exist (Peters, Moore, & Glasberg, 1983; Hartmann & Doty, 1996). Second, the precision with which harmonic octave dyads can be identified becomes quite poor when the frequency of the lower tone exceeds about 1000 Hz, whereas this is not the case for melodic octave dyads (Demany & Semal, 1990; Demany et al., 1991); if sensitivity to melodic “octaveness” were derived from experience with harmonic complex sounds, how could it be more acute than sensitivity to harmonic octaveness? However, the latter objection applies only to the perception of melodic octaves at high frequencies. This is also largely true for the former objection, insofar as the octave enlargement effect is quite small and barely detectable at low frequencies. In contrast, the present research suggests that harmonic and melodic octaves are perceptually recognized as “special” frequency ratios by different processes even at low frequencies.

Appendix. Further Analysis of the Results of Experiment 1

Observer Models

The data collected in Experiment 1 were analyzed using decision-theoretic models of the sensory and decision processes involved in that experiment. These models, which were cast in the framework of equal-variance Gaussian signal detection theory (Green & Swets, 1966), are traditionally referred to as “observer” models. Four different observer models were considered. The first two models, Model A and Model B, are both based on the assumption that the discrimination between Oct_reference (0.97) and Oct_target (0.98, 0.99, … 1.04) depended on a single perceptual cue and was monotonically related to the difference (Δ, in octaves) between the two frequency ratios. These two models differ only in the form of the assumed relationship between d′ and Δ. In Model A, the relationship is assumed to be proportional,

$$d^{\prime }=\mathrm{\alpha }\mathrm{\Delta }.$$ (1)

The proportionality constant, α, is the only free parameter in Model A. This is therefore the most parsimonious of the four models; it is also the least flexible. In Model B, the relationship between d′ and Δ takes the form of a power law,

$$d^{\prime }=\mathrm{\alpha }{\mathrm{\Delta }}^{\mathrm{\beta }}.$$ (2)

Thus, Model B has two free parameters: the proportionality constant, α, and the exponent, β. This model is somewhat more flexible than Model A. It can accommodate concave and convex psychometric functions in addition to linear ones.

Models A and B reflect the idea that listeners’ judgments in Experiment 1 were only based on a perceptual cue which may be termed “spectral compactness.” By contrast, Models C and D assume that, in addition to the spectral compactness cue, listeners had access to a “consonance” cue,⁶ which was maximal when the presented frequency ratio was 1 octave and decreased as the distance of the presented frequency ratio to 1 octave increased, in either direction. Formally, this distance, denoted as δ, is defined as

$$\mathrm{\delta }=\mid f-1\mid ,$$ (3)

where f denotes the frequency ratio used in the current stimulus, in octaves (so that δ is also expressed in octaves). Specifically, Models C and D both assume that the magnitude of consonance, denoted ϕ, decays exponentially with the square of a quantity proportional to δ:

$$\mathrm{\varphi }=\mathrm{\gamma }{e}^{-\frac{1}{2}{\left(\frac{\mathrm{\delta }}{\mathrm{\sigma }}\right)}^2}.$$ (4)

The right-hand side of this equation can be recognized as the Gaussian function. The parameter γ governs the maximum value of consonance, whereas the parameter σ controls the rate at which consonance decreases as a function of the distance to 1 octave. It is assumed that listeners were able to compare frequency ratios with respect to consonance, and that on this basis discriminability was given by the following:

$$d^{\prime }=\mid {\mathrm{\varphi }}_{\text{target}}-{\mathrm{\varphi }}_{\text{reference}}\mid ,$$ (5)

where ϕ_target and ϕ_reference denote the ϕ values yielded by Oct_target and Oct_reference.

As mentioned above, Models C and D both assume that listeners had access not only to the consonance cue but also to the compactness cue. The only difference between these two models is that in Model C, as in Model A, the strength of the latter cue is simply proportional to the difference between the frequency ratios (equation 1), whereas in Model D, as in Model B, the two variables are related by a power law (equation 2). As a result, Model C has three free parameters, whereas Model D has four. The presence of two different cues for frequency-ratio discriminability in Models C and D raises the question of how the cues will be combined. The number of ways in which two sources of information can be combined is infinite. Here, it was assumed that the observer used a maximum-likelihood decision rule. This rule predicts that d′ based on both cues equals the square root of the sum of the squares of the d′′s based on each cue in isolation; formally:

$$d^{\prime }=\sqrt{{d^{\prime }}_{\mathit{compactness}}^2+{d^{\prime }}_{\mathit{consonance}}^2}.$$ (6)

To relate the predictions of the models to the psychophysical data, the d′ values computed using the above equations were transformed into probabilities of a correct response. The same functional relationship between d′ and the correct-response probability was assumed for all four models. Ignoring the possibility of attention lapses, the theoretical functional relationship between d′ and the probability of a correct response in the paradigm of Experiment 1 is as follows:

$$\mathrm{\Psi }(\mathrm{\Delta })=\mathrm{\Phi }(\sqrt{2}{d}^{\prime }(\mathrm{\Delta })),$$ (7)

where Ψ is the predicted correct-response probability with no attentional lapses, Φ denotes the cumulative standard normal function, and the functional dependence of Ψ and d′ on Δ is denoted explicitly. The probability of a correct response with attention lapses, π, was computed as follows:

$$\mathrm{\pi }(\mathrm{\Delta })=\mathrm{\lambda }0.5+(1-\mathrm{\lambda })\mathrm{\Psi }(\mathrm{\Delta }),$$ (8)

where λ is the attention-lapse rate (see, e.g., Wichmann & Hill, 2001; Dai & Micheyl, 2011). The lapse rate was treated as an additional free parameter.

The parameters of the four models were estimated by fitting each model separately to the data obtained from each listener in each condition, using a regularized maximum-likelihood fitting procedure. The procedure involved numerical minimization of a function of the form:

$$g=\sum _{i=1}^{7}ln\left(\frac{n!{\mathrm{\pi }}_i^{c_i}{(1-{\mathrm{\pi }}_i)}^{n-c_i}}{c_i!(n-c_i)!}\right)+\sum _{j=1}^{m}ln(f_i({\mathrm{\theta }}_j)),$$ (9)

where c_i is the number of correct responses measured for Δ_i (i.e., one of the seven Δ values used in the experiment) and n is the total number of trials per Δ value (n = 500). The first term on the right-hand side of this equation corresponds to the sum of the log-likelihood of the data under the model, assuming independent binomial observations. The second term is a regularization term, wherein f_j(θ_j) denotes the prior distribution of the jth model parameter. The support and form of the prior distributions were chosen so as to avoid aberrant fit results, for example, negative sigmas or lapse rates larger than 1, and the parameters of these distributions were determined using an empirical-Bayes approach (Gelman, Carlin, Stern, & Rubin, 2004).

Finally, the model fits were compared using the Bayesian information criterion (BIC) (Schwarz, 1978), which was computed as

$$\mathit{BIC}=-\sum _{i=1}^{7}ln\left(\frac{n!{\widehat{\mathrm{\pi }}}_i^{c_i}{(1-{\widehat{\mathrm{\pi }}}_i)}^{n-c_i}}{c_i!(n-c_i)!}\right)+mln(7),$$ (10)

where π̂_i denotes the best-fitting estimate of π_i and m is the number of free parameters in the considered model. The BIC provides a principled approach to comparing models that have different numbers of free parameters (Schwarz, 1978). It resolves the problem of overfitting, that is, the fact that models with more degrees of freedom generally provide a better fit to the data than models having fewer free parameters, by adding a penalty term (the second term on the right-hand side of equation 10) to the likelihood (the first term in equation 10).

Modeling Results

Table A1 displays the BIC obtained for each model and each listener in the two conditions of Experiment 1. In the “sequential” condition, the lowest BIC obtained for a given listener was always given by either Model A or Model B. For each listener, therefore, the most successful model in that condition was one of the two models assuming that the discrimination between Oct_reference and Oct_target was a monotonic function of their difference, in accordance with the idea that judgments were based on a single perceptual cue, spectral compactness. In the “simultaneous” condition, by contrast, the most successful model was Model D for five of the six listeners. In that condition, therefore, all listeners but one behaved as if they used two perceptual cues, compactness and consonance (fusion).

Table A1.

BICs for Models A, B, C, and D in the “Sequential” and “Simultaneous” Conditions of Experiment 1

	L1	L2	L3	L4	L5	L6
“Sequential” condition
A	57.8	95.0	62.9	54.8	63.5	52.8
B	60.8	54.0	58.1	56.8	61.7	54.7
C	62.2	98.6	69.4	59.8	69.5	55.2
D	64.8	58.4	68.0	62.6	71.5	55.7
“Simultaneous” condition
A	286.1	188.2	58.5	116.1	79.0	127.0
B	142.8	162.3	58.0	117.8	77.8	87.6
C	106.8	124.7	63.3	117.7	81.2	132.4
D	62.2	63.5	62.2	59.3	59.9	61.1

Note. Each column displays the results obtained for one of the six listeners (L1, L2, … L6). The lowest BIC within each column is indicated in bold.

In Figure 3, which shows the individual data of each listener, the curves represent best-fitting psychometric functions according to Model B for the “sequential” condition and Model D for the “simultaneous” condition. For the “sequential” condition, we chose Model B rather than Model A for two reasons: first, in the case of listener L2, the BIC of Model A was quite large (95.0), indicating that Model A was definitely inadequate; second, although Model A had the lowest BIC for three listeners, Model B had the second lowest BIC among the four models for each of these three listeners. In the “simultaneous” condition, the only listener for whom Model D was not the most successful of the four models was listener L3. It can be seen in Figure 3 that this was also the listener who had the poorest performance overall. In fact, as pointed out in the Discussion of Experiment 1, this listener may have been unable to perform the task as intended: instead of comparing frequency ratios, she may have simply compared frequencies.