Modeling the Etiology of Individual Differences in Early Reading Development: Evidence for Strong Genetic Influences

Abstract

We explored the etiology of individual differences in reading development from post-kindergarten to post-4^th grade by analyzing data from 487 twin pairs tested in Colorado. Data from three reading measures and one spelling measure were fit to biometric latent growth curve models, allowing us to extend previous behavioral genetic studies of the etiology of early reading development at specific time points. We found primarily genetic influences on individual differences at post-1^st grade for all measures. Genetic influences on variance in growth rates were also found, with evidence of small, nonsignificant, shared environmental influences for two measures. We discuss our results, including their implications for educational policy.

In the first years of formal schooling, learning to read is one of the major academic milestones children reach. A major goal of reading research, therefore, is to understand what factors underlie individual differences in this period of reading development. While most previous research has focused on predictors of early reading ability, either concurrently or longitudinally, researchers are increasingly exploring influences on the growth of reading (e.g., Morgan, Farkas, & Wu, 2011; Parrila, Aunola, Leskinen, Nurmi, & Kirby, 2005; Petrill et al., 2010; Sonnenschein, Stapleton, & Benson, 2010). The current study extends this work by using latent growth models in conjunction with behavioral genetic approaches (i.e., a biometric latent growth curve model, or biometric growth model, for short) to explore the etiology of individual differences in the rate of early reading growth.

Most previous studies of early reading development have used either phenotypic or behavioral genetic approaches separately. Previous phenotypic research has explored growth in emergent reading ability by using statistical techniques such as latent growth curve models, simplex models, or hierarchical linear modeling. These studies consistently show that growth on most early reading tests is nonlinear, with high rates of growth in the first year or two of instruction, which then decrease as children age (e.g., Bast & Reitsma, 1997; Francis, Shaywitz, Stuebing, Shaywitz, & Fletcher, 1996; Leppanen, Niemi, Aunola, & Nurmi, 2004; McCoach, O'Connell, Reis, & Levitt, 2006; Parrila et al., 2005; Sonnenschein et al., 2010). How much and at what stage of reading development the rate declines will vary, as Paris (2005) points out, depending on the reading skill being assessed as well as the items used. In addition, the exact timing of reading acquisition can also vary across orthographies; word reading accuracy, for example, is known to develop more quickly in orthographies that are more transparent than English (e.g., Landerl & Wimmer, 2008). Therefore, as Parrila et al. (2005) argue, models of reading development should not assume linearity. Assuming linearity could conceal variability in growth, as developing readers will grow and plateau along different trajectories depending on variance in their own ability, the orthography, and the reading skills being assessed.

Previous behavioral genetic studies of the etiology of individual differences in reading in kindergarten through 4^th grade have generally found primarily genetic influences and much lower estimates of environmental influences by the end of the first year of formal reading instruction (e.g., Byrne et al., 2007; 2009; Harlaar, Spinath, Dale, & Plomin, 2005; Taylor & Schatschneider, 2010). In addition, previous studies found strong genetic influences on the longitudinal stability of early reading development (e.g., Byrne et al., 2007; 2009).

An important extension of previous phenotypic and behavioral genetic studies is the use of biometric growth models. These models essentially combine phenotypic and behavioral genetic statistical approaches and are able to decompose the extent to which individual differences at a particular time point and in subsequent growth are driven by genetic and environmental factors. For early reading development, these models test whether the same genetic or environmental influences that make children different from each other as they start to learn to read affect how well they continue to learn to read.

To date, only one published study has applied biometric growth models to early reading development (Petrill et al., 2010). Petrill et al. used data from identical and fraternal twins on reading and reading-related tests. The twins were assessed at mean ages 6.07, 7.16, and 8.24 years, roughly matching up to the end of kindergarten, 1^st grade, and 2^nd grade. After fitting a linear biometric growth model to the data, Petrill et al. found mostly shared environmental influences and smaller but significant genetic influences for individual differences at the first wave (the intercept) for the three reading measures. Individual differences in the subsequent rate of growth on these tests, however, were driven only by shared environmental influences. In contrast, significant genetic influences for individual differences for growth were found for two reading-related skills, rapid naming and phonological awareness.

The biometric growth model results for the three reading measures in Petrill et al. (2010) appear inconsistent with previous behavioral genetic studies of reading development that routinely show strong genetic influences on both the longitudinal stability over this age range (e.g., Byrne et al., 2009; Petrill et al., 2007) as well as at each time point (e.g., Harlaar et al., 2005; Petrill et al., 2007; Samuelsson et al., 2007). Indeed, studies have shown primarily genetic influences at the end of first grade (Byrne et al., 2007; Taylor & Schatschneider, 2010). While it is certainly possible that the etiology of individual differences in the rate of growth could be different from the etiology at a particular time point, the conclusion that variation in rate of reading acquisition was due to only shared environmental influences seemed to be inconsistent with the current literature. Further evidence appears to be needed before concluding that there are no genetic influences on rate of growth.

Current Study

The current study was motivated by the fact that the etiology of individual differences in early reading development remains poorly understood with only one published study (Petrill et al., 2010). By fitting biometric growth models to our data collected from twins in Colorado, we are able to estimate the extent to which genetic and environmental factors influence variance in early reading growth amongst twins in our sample. In addition, our biometric growth models expand upon those used in Petrill et al. by: (a) fitting nonlinear functions, (b) allowing unique variances (i.e., residuals specific to each time point) to correlate in order to limit twin similarity not related to reading development, and (c) adding covariates to test potential sources of genetic and environmental influences. Taken together, our results extend previous research findings regarding the etiology of early reading development.

Methods

Participants

Participants in the current study are part of the ongoing International Longitudinal Twin Study (ILTS; Byrne et al., 2009) that includes twins from Australia, Colorado, and Scandinavia. Due to significant differences between countries in mean performance and reading education in kindergarten prior to the first testing wave (Samuelsson et al., 2008), only participants from Colorado with English as their first language, recruited based on birth records, are included in the present analyses. The Colorado sample at the end of kindergarten consisted of 225 monozygotic (MZ; i.e., identical) twin pairs and 262 same-sex dizygotic (DZ; i.e., fraternal) twin pairs for a total of 487 pairs. By post-4^th grade few pairs had been lost to attrition; the sample consisted of 210 MZ and 254 DZ pairs. Zygosity was determined from DNA collected via cheek swabs, or in a minority of cases from selected items from the Nichols and Bilbro (1966) questionnaire. Mean ages in years (standard deviation, range) were 6.27 (.31, 5.50–7.08), 7.42 (.32, 6.58–8.67), 8.45 (.31, 7.67–9.50), and 10.45 (.32, 9.67–11.67) for the post-kindergarten, post-1^st grade, post-2^nd grade, and post-4^th grade waves, respectively. T-tests corrected for twin non-independence revealed only one significant sex effect (p = .04 at post-4^th grade Passage Comprehension).

Procedure and Measures

The measures included in the present analyses are from larger test batteries that were administered in the ILTS in the summer after each school year. Testing at each time point was conducted in a single session lasting about 1 hour in the twins' homes. Two testers separately assessed each twin at the same time. For all measures, raw scores based on total number correct were used.

The Test of Word Reading Efficiency (TOWRE; Torgesen, Wagner, & Rashotte, 1999), Form A was administered post-kindergarten, post-1^st grade, post-2^nd grade, and post-4^th grade. In the Sight Word Efficiency subtest (Sight) children read a list of difficulty-ordered words as quickly as possible, with the score being the number correctly read in 45 seconds. The Phonemic Decoding Efficiency subtest (Decode) is a list of pronounceable nonwords administered in the same way. Test-retest reliability for children aged 6- to 9-years-old was reported as .97 for Sight and .90 for Decode.

The Woodcock Passage Comprehension subtest from the Woodcock Reading Mastery Test (Woodcock, 1987) was administered post-1^st grade, post-2^nd grade, and post-4^th grade. This test uses a cloze procedure; participants read short passages silently and are asked to provide the missing word that completes the sentence. Split-half reliability 1^st grade 1 is .94.

The Wide Range Achievement Test Spelling Production subtest (Spelling) (Jastak & Wilkinson, 1984) was administered post-1^st grade, post-2^nd grade, and post-4^th grade. Participants generate written spellings of orally presented words. The test consists of 45 items administered in increasing order of difficulty, and the test is discontinued after 10 consecutive spelling errors. The published alternate form reliability is .90.

The ILTS Colorado dataset also includes measures of parental education, the averaged maternal and paternal self-report of years of education and, for children attending public school, school literacy, the school average reading and writing scores from the Colorado Student Assessment Program (CSAP).

Analyses

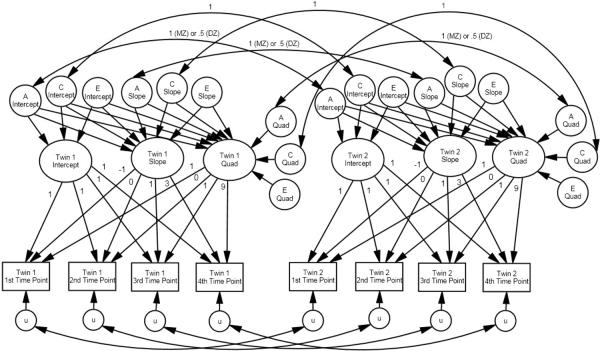
To assess genetic, shared environmental, and non-shared environmental influences on initial performance and on subsequent growth on the reading measures, we fitted biometric growth models (see McArdle, Prescott, Hamagami, & Horn, 1998; Reynolds et al., 2005) using the Mx software (Neale, Boker, Xie, & Maes, 2003). As shown in Figure 1, biometric growth modeling is a combination of latent growth curve modeling (Byrne & Crombie, 2003; Loehlin, 1998; Meredith & Tisak, 1990; Preacher, Wichman, MacCallum, & Briggs, 2008) and the standard twin model that decomposes phenotypic variance into independent genetic variance (a²), shared environmental variance (c²), and non-shared environmental variance (e²). The latent Intercept factor represents ability level at a particular time point, while the two growth latent factors, Slope and Quadratic, represent increases in scores over time (Slope) and either acceleration or deceleration in Slope over time (Quadratic). The loadings from Intercept are fixed to 1, while the loadings from Slope and Quadratic are scaled to the interval between time points. Not displayed in Figure 1, but present in our analyses, is a control for age at Time 1 modeled as a definition variable (Neale et al., 2003).

Figure 1.

Biometric quadratic growth model centered at second time point. Note that age at the 1^st time point has been controlled for as a definition variable in Mx and that correlations between unique variances (u's) at each time point have been constrained equal within zygosity.

The two TOWRE measures, Sight and Decode, were given at four time points, allowing us to fit them to biometric quadratic growth models. Passage Comprehension and Spelling were only given at three time points. Therefore we were unable to fit quadratic growth and, instead, fit the data to biometric unspecified growth models. Unspecified latent growth models (Byrne & Crombie, 2003; Duncan, Duncan, Strycker, Li, & Alpert, 1999; Preacher et al., 2008) refer to models wherein at least one loading from the growth latent factor is estimated in the model, rather than fixing all loadings a priori to a linear function.¹ In unspecified growth models, the growth factor is sometimes referred to as “Shape” to highlight that it is different from a fixed linear pattern (i.e., “Slope”). The biometric unspecified growth models fit to Passage Comprehension and Spelling are very similar to the model shown in Figure 1, but without the Quadratic factor and with the third time point loading estimated.

As in the twin model, the covariance between Twin 1 and Twin 2 on latent Intercept and the latent growth variables is a combination of genetic influences (A) and shared environmental influences (C). All Intercept, Slope, and Quadratic correlations between Twin 1 and Twin 2 for MZ twins are set to 1 as they share 100% of both their genes and shared environment (see Figure 1). For DZ twin pairs, the correlations between Twin 1 and Twin 2 for Intercept C, Slope C, and Quadratic C are also set to 1, as they also share 100% of shared environment. However the twin correlations for Intercept A and latent growth A are set to .5 as DZ twins share 50% of their segregating genes. There are no correlations between twins for non-shared environment (E), as that is independent for each member of the twin pair. The square of the resulting loadings from each A, C, and E factor onto Intercept, Slope, and Shape estimates the proportion of variance accounted for by genetic, shared environmental, and non-shared environmental influences.

Finally, unique variance, also known as time-point-specific error, is denoted by the small u's under each time point. The unique variances represent the extent to which each person's observed score at a time point varies from the score estimated by the latent growth model. As in any latent variable model, this variation can be caused by a variety of factors, most notably measurement error, that will make a person's score at one time point diverge from what would be expected based upon the other time points. Biometric growth models use pair-level data with unique variances for each twin in the pair. By not allowing correlations between the unique variances, all twin similarity in the model is assumed to be related to the latent intercept and growth factors. However, these residuals could include meaningful twin similarity that is unrelated to the latent factors due to poor fit or violation of model assumptions. It is also possible that the factors driving unique variances may be related within twin pair. Even in a well-fitting model, time-point-specific factors such as family disruptions (e.g., divorce, moving, or a new baby), motivation, and tester effects could cause errors to be related within-pair. In a model without unique variance correlations, therefore, the biometric estimates for intercept and growth will be a decomposition of variance related both to reading development and to other, time-point-specific, similarity. Depending on the magnitude and nature of the relation between the unique variances, this could lead to inaccurate genetic or shared environmental estimates for reading development. In line with other researchers who included unique variance correlations in their biometric growth models (e.g., McArdle & Plassman, 2009; Reynolds et al., 2005), we directly test the significance of these correlations in our models.²

Results

Descriptive Statistics and Univariate Heritability Estimates

Table 1 presents the means and standard deviations for the two TOWRE measures, Passage Comprehension, and Spelling. Note that the N's at each time point do not exactly match the 487 twin pairs (974 individuals) due to missing data. While we use raw scores to measure growth in the biometric growth models, the standard scores allow us to compare our sample to the standardizing population averages for the TOWRE measures, Passage Comprehension, and Spelling. The means for the standard scores show that our sample is very close to the standardizing population mean standard score of 100 at each of the time points. The standard score standard deviations on Sight, Decode, and Passage Comprehension are mostly lower than the standardizing population average of 15, especially post-kindergarten on Sight and Decode, suggesting a floor effect the consequences of which will be considered in the Discussion.

Table 1.

Descriptive and Univariate Statistics.

		SS		Raw		Univariate Estimates
	n	Mean	SD	Mean	SD	a 2	c 2	e 2
TOWRE Sight
Post-KG	973	96.99	10.54	12.85	12.63	.68* [.54, .85]	.22* [.05, .36]	.10* [.08,.12]
Post-1st	955	102.23	14.02	40.25	16.68	.84* [.66, .89]	.02 [.00, .20]	.14* [.11, .17]
Post-2nd	964	103.05	14.28	54.29	14.30	.73* [.56, .84]	.08 [.00, .24]	.19* [.15, .23]
Post-4th	926	102.39	12.16	68.95	11.11	.57* [.36, .76]	.15 [.00, .32]	.29* [.23, .36]
TOWRE Decode
Post-KG	973	102.13	8.37	5.51	6.32	.63* [.43, .79]	.12 [.00, .30]	.25* [.21, .31]
Post-1st	953	100.71	12.79	17.13	10.56	.82* [.70, .85]	.00 [.00,.11]	.18* [.15, .22]
Post-2nd	962	100.22	13.43	23.85	11.44	.75* [.56, .83]	.04 [.00, .22]	.21* [.17, .26]
Post-4th	926	102.76	13.60	35.11	11.09	.74* [.55, .82]	.03 [.00, .22]	.22* [.18, .28]
Woodcock Passage Comprehension
Post-1st	960	104.80	12.84	24.36	8.43	.71* [.53, .83]	.10 [.00, .26]	.20* [.16, .25]
Post-2nd	964	100.12	12.13	31.46	7.24	.59* [.39, .77]	.14 [.00, .31]	.27* [.22, .34]
Post-4th	928	98.52	13.79	39.68	7.14	.68* [.47, .77]	.04 [.00, .23]	.28* [.23, .35]
WRAT Spelling
Post-1st	960	100.14	15.44	12.71	5.23	.68* [.49, .81]	.10 [.00, .27]	.23* [.19, .28]
Post-2nd	964	97.28	15.91	17.93	5.80	.81* [.62, .85]	.00 [.00, .18]	.19* [.15, .23]
Post-4th	928	100.70	14.98	25.56	6.57	.77* [.59, .87]	.07 [.00, .24]	.16* [.13, .20]

Note: KG = Kindergarten; a² = proportion of variance due to genetic influences; c² = proportion of variance due to shared environmental influences; e² = proportion of variance due to nonshared environmental influences.

^*p < .05 determined using 95% confidence intervals, shown in brackets.

Also included in Table 1 are the results from univariate analyses that provide estimates of what proportion of variance at each time point is due to genetic (a²), shared environmental (c²), and non-shared environmental (e²) influences. Across all time points on the four tests, individual differences are driven primarily by genetic influences. Shared environmental influence is significant only at post-kindergarten on Sight. Non-shared environmental influences, including measurement error, are significant for all time points.

Biometric Growth Models

Quadratic growth

Table 2 presents the biometric quadratic growth modeling results for the Sight and Decode measures. For each measure, two different models were fit: one assuming that unique variances were correlated within twin pair (Correl.) and one assuming that unique variances were independent within twin pair (Indep.). Estimates of genetic (a²), shared environmental (c²), and non-shared environmental (e²) influences were obtained by squaring the loadings of latent Intercept, latent Slope, and latent Quadratic onto the A, C, and E factors (shown in Figure 1). Due to the large floor effect at the first time point (post-kindergarten) as well as to facilitate comparison with Passage Comprehension and Spelling, the quadratic function was centered at the second time point (post-1^st grade). The means, variances, and biometric estimates reported for Intercept reflect children's scores on the measure at the end of 1^st grade. In all cases the Quadratic is negative, suggesting that rates of growth declined over this period of reading development.

Table 2.

Estimates from Biometric Quadratic Growth Curve Models (Centered Post-l^st Grade) of Means, Variance, and Proportions of Variance in Intercept and Growth Due to Genetic and Environmental Influences.

		Intercept		Slope		Quadratic			Latent Intercept			Latent Slope			Latent Quadratic
Variable	Model	Mean	Var.	Mean	Var.	Mean	Var.	r Unique	a 2	c 2	e 2	a 2	c 2	e 2	a 2	c 2	e 2
TOWRE Sight KG – 4th	Indep.	38.24	184.20	21.12	29.66	−3.65	3.52	MZ = 0 DZ = 0	.85* [.68, .96]	.09 [.00, .27]	.05* [.03, .08]	.59* [.29, .87]	.33* [.06, .60]	.09* [.03, .16]	.72* [.41, .94]	.20* [.01, .49]	.08* [.03, .16]
	Correl.	38.23	182.91	21.10	26.62	−3.64	3.14	MZ = .53 DZ = .32	.83 * [.66, .93]	.09 [.00, .26]	.08 * [.06, .11]	.80 * [.46, .91]	.06 [.00, .37]	.14 * [.08, .23]	.86 * [.55, .93]	.01 [.00, .30]	.13 * [.07, .21]
TOWRE Decode KG – 4th	Indep.	16.21	81.04	9.39	16.60	−1.04	1.46	MZ = 0 DZ = 0	.90* [.73, .94]	.01 [.00, .18]	.08* [.06, .12]	.75* [.49, .92]	.15* [.002, .40]	.10* [.05, .17]	.79* [.50, .95]	.14* [.001, .41	.07* [.02, .16]
	Correl.	16.21	80.23	9.38	15.32	−1.03	1.27	MZ = .39 DZ = .14	.88 * [.69, .92]	.01 [.00, .19]	.11 * [.08, .15]	.79 * [.51, .92]	.08 [.00, .34]	.13 * [.08, .20]	.81 * [.55, .93]	.03 [.00, .29]	.15 * [.07, .26]

Note: Intercept is centered at the second time point (post-1^st grade). The four time points included: post-kindergarten, post-1^st, post-2^nd, and post-4^th. Indep. = Model without unique variances correlated; Correl. = Model with unique variance correlations, constrained within-zygosity; r_Unique = correlations for unique variances; MZ = monozygotic; DZ = dizygotic; a² = proportion of variance due to genetic influences; c² = proportion of variance due to shared environmental influences; e² = proportion of variance due to nonshared environmental influences. The endorsed final model, based on both better model fit and theoretical reasons, is shown in bold.

^*p < .05 determined using 95% confidence intervals, confidence intervals presented in brackets.

As discussed previously, our decision to test the correlations between the unique variances was motivated by the fact that factors driving unique variance may be related within the twin pair. The overall fit statistic for models using raw data in Mx, log likelihood (−2LL), is sensitive to the scale of the data and is not, on its own, interpretable. Given that the independent unique variances model is nested under the correlated unique variances model, we tested the significance of including the correlations by calculating the change in −2LL, which approximates a chi-square distribution. Assuming that the unique variances were not correlated significantly decreased the fit of the model for both TOWRE measures (Sight: Δ−2LL = 226.53, Δdf = 2, p < .01; Decode: Δ−2LL =76.36, Δdf = 2, p < .01). In addition, as shown in Table 2, the monozygotic (MZ) twin correlations were roughly twice the size of the dizygotic (DZ) twin correlations (Sight: r_Unique = .53 and .32; Decode: r_Unique = .39, .14). Not only were the unique variances significantly correlated, therefore, but the pattern of correlations (i.e., higher MZ correlations than DZ correlations) suggests that part of the reason they are correlated is due to genetic influences. Because of better model fit, as well as to account for twin similarity that is independent of the latent factors, we chose the correlated model as our final model and will focus all subsequent results and discussion on these results.

The biometric estimates for Sight and Decode at intercept show that variance at the end of 1^st grade was driven primarily by large genetic influences (a²_Intercept = .83 and .88 for Sight and Decode, respectively), with significant, but small, non-shared environmental influences (e²_Intercept = .08 and .11), and small, nonsignificant shared environmental influences (c²_Intercept = .09 and .01). Over 80% of the variance in post-1^st grade Sight and Decode scores, therefore, was due to genetic influences.

Similar patterns of biometric estimates, with large, significant genetic influences and small shared and non-shared environmental influences, were also found for linear Slope (Sight: a²_Slope = .80, c²_Slope = .06, e²_Slope = .14; Decode: a²_Slope = .79, c²_Slope = .08, e²_Slope = .13). Finally, the biometric estimates on the Quadratic factor also showed that deceleration in growth rates were also primarily influenced by genetic factors (Sight: a²_Quadratic = .86, c²_Quadratic = .01, e²_Quadratic = .13; Decode: a²_Quadratic = .81, c²_Quadratic = .03, e²_Quadratic = .15). Individual differences in development of fluent and accurate word reading (Sight) and nonword reading (Decode) in our sample, therefore, were driven largely by genetic influences.

Unspecified growth

In addition to the two TOWRE measures, our participants were tested on Passage Comprehension and Spelling. As discussed earlier, these two measures were given post-1^st grade, post-2^nd grade, and post-4^th grade; thus, we are unable to fit the data to a latent quadratic model. In order to capture the nonlinear pattern of growth shown in the raw variables (Table 1), these two measures were fit to biometric unspecified growth models. Table 3 shows the results of these models. Table 3 is very similar to Table 2, with one extra column (3^rd loading) showing the estimated loading from Shape to the third time point. This loading was estimated at 2.14 for Passage Comprehension and 2.45 for Spelling, showing that participants gained a little over half as many raw score points between 2^nd and 4^th grade as they did between 1^st and 2^nd grade.

Table 3.

Estimates from Biometric Unspecified Growth Curve Models of Means, Variance, and Proportions of Variance in Intercept and Growth Due to Genetic and Environmental Influences.

		Intercept		Shape		3rd Loading	r Unique	Latent Intercept			Latent Shape
Variable	Model	Mean	Var.	Mean	Var.			a 2	c 2	e 2	a 2	c 2	e 2
Passage Comp. 1st – 4th	Indep.	24.31	58.93	7.20	4.70	2.14	MZ = 0 DZ = 0	.80* [.59, .96]	.13 [.00, .32]	.07* [04, .12]	.68* [.09, 1.00]	.30 [.00, .76]	.02 [.00, .25]
	Correl.	24.32	58.85	7.17	4.63	2.14	MZ = .33 DZ = .14	.74 * [.53, .91]	.14 [.00, .33]	.12 * [.08, .18]	.27 * [.002, .82]	.35 [.00, .68]	.38 * [.15, .60]
WRAT Spelling 1st – 4th	Indep.	12.68	24.07	5.25	1.62	2.45	MZ = 0 DZ = 0	.80* [.59, .93]	.09 [.00, .29]	.11* [.07, .17]	.63* [.13, 1.00]	.31 [.00, .71]	.06 [.00, .25]
	Correl.	12.68	24.05	5.25	1.61	2.45	MZ = .31 DZ = .12	.75 * [.54, .89]	.10 [.00, .30]	.15 * [.11, .21]	.31 * [.07, .84]	.36 [.00, .64]	.32 * [.13, .50]

Note: Three time points included: post-1^st, post-2^nd, and post-4^th grade. Indep. = Model without unique variances correlated; Correl. = Model with unique variance correlations, constrained within-zygosity; 3^rd Loading = the loading from Latent Shape factor onto 3^rd time point; r_Unique= correlations for unique variances; MZ = monozygotic; DZ = dizygotic; a² = proportion of variance due to genetic influences; c² = proportion of variance due to shared environmental influences; e² = proportion of variance due to nonshared environmental influences. The endorsed final model, based on both better model fit and theoretical reasons, is shown in bold.

^*p < .05 determined using 95% confidence intervals, confidence intervals presented in brackets.

Identical to our approach with Sight and Decode, we tested whether the unique variances for Passage Comprehension and Spelling were significantly correlated within twin-pairs. As in the TOWRE models, allowing the unique variances to correlate significantly improved the fit of the models (Passage Comprehension: Δ−2LL = 30.84, Δdf = 2, p < .01; Spelling: Δ−2LL = 24.40, Δdf = 2, p < .01). The MZ twin correlations were, again, roughly twice the size of the DZ twin correlations (Passage Comprehension: r_Unique = .33 and .14; Spelling: r_Unique= .31, .12). This suggests that part of what the unique variance correlations are capturing is due to genetic influences. As with the TOWRE measures, we chose the correlated model as our final model and will focus all subsequent results and discussion on the results from this model.

Individual differences at post-1^st grade for Passage Comprehension and Spelling, like the TOWRE measures, were largely due to genetic influences (a²_Intercept = .74 and.75 for Passage Comprehension and Spelling, respectively). Shared and non-shared environmental influences were small (c²_Intercept = .14 and .10; e²_Intercept = .12 and .15). Unlike Sight and Decode, variance on growth rates (Shape) showed evidence of moderate, although not significant, shared environmental influences in addition to significant genetic and nonshared environmental influences (a²_Shape = .27 and .31; c²_Shape = .35 and .36; e²_Shape = .38 and .32). Individual differences in our sample for reading comprehension and spelling development from post-1^st grade through post-4^th grade, therefore, appear to be driven by both genetic and environmental factors.

Estimating overlap of biometric influences between latent Intercept and latent growth

In addition to estimating the proportion of variance in initial ability and growth due to genetic and environmental influences, the biometric growth model also estimates the extent to which the genetic and environmental influences on the latent Intercept were shared with the latent Shape (in the unspecified model) or with the latent Slope and Quadratic factors (in the quadratic model). In other words, are the factors that affect reading ability at the end of 1^st grade the same as the factors that affect reading growth through the end of 4^th grade?

The biometric correlations in Table 4 estimate how much the genetic and environmental influences overlap. For example, the genetic correlation between Intercept and Slope on Decode was large and significant at .90, suggesting that nearly all of the genetic influences on a child's rate of growth are shared with those influencing performance at Intercept. For Sight, the genetic correlation between Intercept and Slope was smaller but significant at .48, suggesting that some of the genetic influences on individual differences in Slope were shared with Intercept, with some independent genetic influences for Slope as well. The genetic correlations between Intercept and Quadratic were large and significant (−.74 for Sight and −.98 for Decode). As with the correlation between Intercept and Slope, the magnitude of correlation for Sight was significantly less than 1.00; thus, some genetic influences for rates of growth were independent of intercept. For both variables, the genetic correlations between Slope and Quadratic (i.e., how quickly growth rates declined) were large (−.94 for Sight and −.97 for Decode). The negative signs on the correlations with the Quadratic indicate that the genetic factors that made a child higher at the end of 1^st grade and have higher rates of growth resulted in more deceleration of growth rates. Finally, given that we found small and non-significant shared environmental estimates for Intercept, Slope, and Quadratic, it is not surprising that none of the shared environmental correlations were significant.

Table 4.

Genetic and Environmental Correlations between Intercept and Growth Latent Variables.

	Genetic		Shared Environment		Nonshared Environment
TOWRE Sight Kindergarten – 4th
	Intercept	Slope	Intercept	Slope	Intercept	Slope
Slope	.48* [.28, .63]		−.88 [−1.00, 1.00]		.95* [.77, 1.00]
Quad	−.74* [−.85, −.62]	−.94* [−.96, −.90]	.57 [−1.00, 1.00]	−.90 [−1.00, 1.00]	−.99* [−1.00, −.89]	−.98* [−1.00, −.91]
TOWRE Decode Kindergarten – 4th
	Intercept	Slope	Intercept	Slope	Intercept	Slope
Slope	.90* [.79, 1.00]		−.34 [−1.00, 1.00]		.94* [.79, 1.00]
Quad	−.98* [−1.00, −.92]	−.97* [−1.00, −.92]	.20 [−1.00, 1.00]	−.99 [−1.00, 1.00]	−.96* [−1.00, −.83]	−.79* [−.92, −.59]
Woodcock Passage Comprehension 1st – 4th
	Intercept		Intercept		Intercept
Shape	−.69* [−1.00, −.27]		−.86* [−1.00, −.47]		−.50* [−.68, −.18]
WRAT Spelling 1st – 4th
	Intercept		Intercept		Intercept
Shape	.82* [.18, 1.00]		−.74 [−1.00, .82]		−.35* [−.55, −.03]

Note: Unspecified model with three time points estimated for Passage Comprehension and Spelling: post-1^st, post-2^nd, and post-4^th grade. Quadratic model with four time points (including post-kindergarten) estimated for TOWRE Sight and Decode.

^*p <.05 determined using 95% confidence intervals, confidence intervals presented in brackets.

The pattern of genetic and environmental correlations between Intercept and Shape for Passage Comprehension tells a slightly different story. The genetic correlation was large and significant at −.69 as was the shared environmental correlation at −.86, but the negative sign suggests that the genetic and shared environmental influences that made a child higher at Intercept also made the child grow at a slower rate over time. Conversely, on Spelling, the genetic correlation between Intercept and Shape was significantly positive at .82. Genetic influences on intercept that were shared with rates of growth, therefore, made children higher both initially and on growth rates. The shared environmental correlation for Spelling was not significant.

Testing potential sources of biometric estimates

We separately included two covariates, parental education and school literacy. To the degree that parent education and school differences account for shared environmental variance, their inclusion as covariates should reduce the estimates of shared environment influence and increase estimates of genetic influence. As Table 5 shows, the covariates were significant predictors of individual differences in intercept and rates of growth in most cases, accounting for a maximum of 7 percent of the variance. While some of the biometric estimates differ between our main results reported in Tables 3 and 4 and the subsample with available CSAP scores in Table 5, the pattern of biometric estimates was similar with and without the covariates included, suggesting that our measures of parental education and school literacy scores fail to account for significant genetic or shared environmental influences on the reading and spelling measures.

Table 5.

Estimates from Biometric Growth Models with Covariates.

			Covariate Loading			Model Comp.		Intercept			Shape/Slope			Quadratic
	Covariate	N	Intercept	Shape/Slope	Quad.	Δ χ2	Δ df	a 2	c 2	e 2	a 2	c 2	e 2	a 2	c 2	e 2
TOWRE Sight KG – 4th	None	972	0	0	0	-	-	.82	.11	.08	.79	.07	.14	.84	.03	.13
	Parental Ed.	972	27**	.10*	−15**	15.99	18	.87	.05	.08	.76	.09	.14	.84	.03	.13
	None	784a	0	0	0	-	-	.84	.07	.09	.79	.06	.15	.85	.01	.14
	School Lit.	784a	17**	.07	−.09	23.37	18	.85	.06	.09	.78	.07	.15	.84	.02	.14
TOWRE Decode KG – 4th	None	972	0	0	0	-	-	.87	.02	.11	.78	.09	.13	.80	.04	.16
	Parental Ed.	972	.26**	.20**	−.19**	16.49	18	.88	.00	.12	.77	.09	.14	.80	.04	.16
	None	784a	0	0	0	-	-	.83	.07	.10	.54	.28	.18	.60	.16	.24
	School Lit.	784a	.18**	.13*	−.15*	11.00	18	.85	.05	.11	.54	.27	.19	.60	.15	.24
Passage Comp. 1st – 4th	None	972	0	0		-	-	.72	.16	.12	.27	.36	.37
	Parental Ed.	972	27**	.09		20.50	15	.76	.11	.13	.22	.39	.38
	None	784a	0	0		-	-	.80	.07	.13	.36	.19	.45
	School Lit.	784a	19**	.12*		20.51	15	.84	.03	.13	.32	.21	.47
WRAT Spelling 1st – 4th	None	972	0	0		-	-	.74	.11	.15	.32	.35	.32
	Parental Ed.	972	21**	25**		22.82	15	.75	.09	.16	.29	.36	.35
	None	784a	0	0		-	-	.80	.06	.14	.38	.30	.32
	School Lit.	784a	13**	17**		12.16	15	.81	.05	.14	.38	.29	.34

Note: Models analogous to the final models shown in Tables 2 and 3 and Figure 1, but were estimated in AMOS (Arbuckle, 2008) as Mx is unable to estimate loadings from the covariate onto the latent factors. Initial age in AMOS was controlled via covariate rather than definition variable. AMOS does not provide confidence intervals for the a², c², and e² estimates. Covariate Load. = Standardized regression loading; Model Comp. = Nested χ² model comparisons comparing model with covariate to model without covariate; a² = proportion of variance due to genetic influences; c² = proportion of variance due to shared environmental influences; e² = proportion of variance due to non-shared environmental influences; Parental Ed. = Average of Maternal and Paternal Education; School Lit. = Average of School Reading and Writing Scores from the CSAP.

^aOnly participants who attend public school have school literacy scores, leading to the lower N for those analyses.

^*p < .05,

^**p < .01

Discussion

The goal of the present study was to examine the etiology of individual differences in early reading development by fitting biometric growth models to longitudinal twin data. Our results suggest that individual differences in three measures of reading and one spelling measure at the end of 1^st grade as well as subsequent growth through the end of 4^th grade are driven primarily by genetic influences, with some differences arising from the measures used and assumptions underlying the modeling. These results are discussed as follows: (a) we briefly review the main findings; (b) we discuss how our results expand upon previous early reading development research; (c) we highlight limitations of the current methodology that should be taken into account for our study and all similar studies; finally, (d) we discuss the larger implications of our results.

Genetic and Environmental Influences on Early Reading

We tested our participants on two measures of fluent and accurate word reading and decoding, Sight and Decode, at the end of kindergarten, 1^st grade, 2^nd grade, and 4^th grade. In addition, our participants were tested on a measure of reading comprehension and a measure of spelling at the end of 1^st grade, 2^nd grade, and 4^th grade. Within our sample, genetic influences appear to be the primary source of variance both at the end of 1^st grade and on how quickly children continue to grow through the end of 4^th grade. For all four measures, estimates for intercept from the best-fitting biometric growth model (shown in Tables 2 and 3) showed the same pattern as the univariate results (Table 1) for post-1^st grade: strong genetic influences with small and nonsignficant shared environmental influences. The biometric growth models also tested the genetic and environmental influences on individual differences in rate of growth. Variance in growth (both Slope and Quadratic) on Sight and Decode was explained by strong genetic influences with small and nonsignificant shared environmental influences.

Passage Comprehension and Spelling showed a different pattern for variance on growth rates, with moderate genetic influences and, although not significant, also showed evidence for shared environmental influences. The lack of significance is partially due to the large confidence intervals on growth rates compared to Sight and Decode, a consequence of the smaller amounts of variance in growth rates for Passage Comprehension and Spelling than for Sight and Decode (see Tables 2 and 3). This lack of variance suggests that children in our sample grew at similar rates for Passage Comprehension and Spelling over this developmental window.

In addition to these variance differences, Sight and Decode differ from Passage Comprehension and Spelling because they are timed, fluency-and accuracy-based measures while Passage Comprehension and Spelling measure accuracy alone. This raises the possibility that timed measures could have larger heritability estimates for growth than untimed measures of reading. However, reading comprehension and spelling, as larger constructs, are different from speeded word reading and decoding in more ways than simply the speeded component. In addition, as shown in the univariate estimates, by the end of 4^th grade there are strong genetic influences for all measures. Given that individual differences in timed and untimed reading measures are equally heritable by the time the twins finished 4^th grade, it seems unlikely that the differences in genetic and environmental influences on growth rates for these measures is due primarily to the speed requirements.

Finally, the results from the latent intercept and growth correlations (Table 4) showed that genetic influences on individual differences in growth had significant overlap with genetic influences on individual differences at the end of 1^st grade. Given that our estimates of shared environmental influences on growth rates were close to zero for Sight and Decode and not significant for all of the measures, the shared environmental correlations between intercept and growth rates were generally also not significant. The one exception, the shared environmental correlation between Intercept and Shape for Passage Comprehension, was significant but negative (−.86). Combined with the significant negative genetic correlation between Intercept and Shape, it appears as though the genetic and shared environmental influences that resulted in higher comprehension performance at the end of 1^st grade are associated with lower growth rates through the end of 4^th grade, probably reflecting the nonlinear nature of reading comprehension development.

Extending Previous Research on the Etiology of Early Reading Development

Our results expand upon previous phenotypic studies of early reading development by exploring the etiology of individual differences in growth. In addition, they expand upon previous behavioral genetic studies of early reading by exploring growth instead of focusing on specific time points. Finally, our models incorporate two major modifications to the models presented in the only currently published biometric growth curve study of early reading (Petrill et al., 2010): using unspecified models to capture nonlinear growth, even with three time points, and allowing time-point-specific variances to correlate.

It is interesting that the current results contrast with Petrill et al. (2010) and show that individual differences in growth are not driven primarily by environmental factors, but by genetic factors. In addition to possible demographic and measure differences, we believe that the discrepancy in results is likely due to three main ways our samples and models differ. First, there was more uniformity in instructional exposure at each wave of our study. Our twins were tested during the summers following each school year, whereas the first wave in Petrill et al. included twins tested not just during kindergarten but also during 1^st grade; thus, their first wave included pairs with quite different amounts of shared environment for formal reading instruction during the period of most rapid reading development. Second, the present study used nonlinear growth models, in line with both our own raw descriptive statistics and evidence from previous phenotypic latent growth modeling (e.g., Bast & Reitsma, 1997; Francis et al., 1996; Parrila et al., 2005), whereas Petrill et al. assumed linear growth. Indeed, recent results from Dr. Petrill and colleagues using nonlinear growth models have indicated significant genetic influences on individual differences in reading growth (Logan & Petrill, 2012). Finally, our models go beyond Petrill et al. by including correlations between the unique variances. The fact that the unique variance correlations were significant for all four measures shows that the latent intercept and growth factors did not capture all of the twin similarity in our data. Including the unique variance correlations, therefore, allowed us to limit non-growth-related twin similarity in our biometric estimates.

Caveats for Biometric Growth Models of Early Reading Development

Biometric growth models share assumptions about the normality of the underlying variable distributions with many other statistical methods for studying developmental processes. As shown in Table 1, the descriptive statistics for the first wave, post-kindergarten, show a large floor effect for both Sight and Decode. Some of our participants were initially unable to do the tasks, due to the fact that they were non-readers at the end of kindergarten. While floor effects are common in studies of young readers (e.g., Catts et al., 2009) and are nearly impossible to avoid if one is interested in studying early reading ability, it is important to note that our estimates of individual differences in growth are limited by insensitivity of the measures to individual differences among pre-readers.

It is also important to keep in mind when interpreting analyses of individual differences in reading growth that variance in growth tends to be much smaller than variance at intercept (McCoach et al., 2006; Parrila et al., 2005; Phillips, Norris, Osmond, & Maynard, 2002; Sonnenschein et al., 2010). The idea that growth rates would be less variable than initial ability fits in with the consistent finding that children's reading ability relative to their peers is largely stable throughout elementary school (Butler, Marsh, Sheppard, & Sheppard, 1985; Francis et al., 1996; Juel, 1988; McNamara, Scissons, & Gutknecth, 2011; Morgan et al., 2011; Scarborough, 1998; Torgesen, Rashotte, & Alexander, 2001). This is not to say that reading growth is not happening, just that individual differences in growth rate are small. Therefore, saying that individual differences in growth in reading are driven primarily by either genetic or environmental factors may not have large practical implications if the magnitude of the effect is small.

Implications of Our Results

The finding that performance on our measures of early reading development is driven primarily by genetic factors has important implications for education policy. Specifically, these results refute the idea that differences amongst schools in general, and teachers in particular, are the primary influence on individual differences in early reading achievement. However, these results may be limited to populations with universal and relatively consistent reading instruction; estimates of genetic and environmental influences could differ in populations with more variation in instruction and reading practice. Of course children learn to read largely from reading instruction and practice in school, but this study suggests that variance in learning rates for reading in this environmental context is primarily due to genetic differences. Consistent with this result, Byrne et al. (2010) showed that twin pairs separated into different classrooms in kindergarten, 1^st grade, or 2^nd grade are only slightly less similar than twin pairs in the same classrooms. Classroom effects accounted for only 8% of the variance, consistent with the only large experimental study of classroom effects on early reading (Nye, Konstantopoulos, & Hedges, 2004).

It is important to note the types of conclusions that cannot be drawn from biometric growth models. These models estimate the average genetic and environmental etiology of individual differences for our sample and others like it, but they are not able to address the etiology of reading development for a particular child. Also, estimates of genetic and environmental influences are proportional and dependent on the amount of genetic and environmental variance being sampled: increased environmental variance, due to a broader sampling of socio-economic status, linguistic background, or differences in approaches to instruction, could yield different results. For example, Samuelsson et al. (2007) found low genetic and high shared environmental influences on reading at the end of kindergarten in Scandinavia, where letter-sound and reading instruction in school was delayed until 1^st grade. But by the end of 1^st grade, Samuelsson et al. found that individual differences in reading among the Scandinavian children were mostly due to genetic influences. This result is consistent with findings from other representative twin samples tested near the end of the first year of formal reading instruction from Australia, Colorado, the U.K., and Florida (Byrne et al., 2007; 2009; Harlaar et al., 2005; Taylor & Schatschneider, 2010).

Testing potential sources of genetic and shared environmental influences

While the current results offer insight into the etiology of early reading development, an important next step is to understand the sources of the genetic and shared environmental influences. Because our shared environment estimates were so low, and the main effects of the covariates were weak, although significant, we were unable to detect large changes in our pattern of genetic and environmental influences. Regardless, we encourage researchers to move from speculation regarding sources to data-supported claims by including potential genetic and environmental covariates.

Conclusion

Although we recognize that extreme environmental variation in early reading development may have large effects on individual and group differences, the small shared family and school environment influences on variation in our twins' early reading and spelling development seem inconsistent with current popular and political views in the United States, as illustrated by the No Child Left Behind Act (NCLB; 2008), that individual differences in children's early reading skills are primarily due to environmental differences related to family environment and/or teacher and school quality. While there is considerable evidence that intensive intervention can significantly ameliorate reading difficulties in some children, other children may still fall short of grade level due to their slower genetically influenced learning rates in reading and related skills (Byrne et al., 2008; Byrne et al., in press). Therefore, greater attention to the importance of genetic influences could lead to a more nuanced and realistic understanding of individual differences in children's early reading development.