Toward a Rational Design of Bioactive Glasses with Optimal Structural Features: Composition–Structure Correlations Unveiled by Solid-State NMR and MD Simulations

Abstract

The physiological responses of silicate-based bioactive glasses (BGs) are known to depend critically on both the P content (n_P) of the glass and its silicate network connectivity (N̅_BO^Si). However, while the bioactivity generally displays a nonmonotonic dependence on n_P itself, recent work suggest that it is merely the net orthophosphate content that directly links to the bioactivity. We exploit molecular dynamics (MD) simulations combined with ³¹P and ²⁹Si solid-state nuclear magnetic resonance (NMR) spectroscopy to explore the quantitative relationships between N̅_BO, n_P, and the silicate and phosphate speciations in a series of Na₂O–CaO–SiO₂–P₂O₅ glasses spanning 2.1 ≤ N̅_BO^Si ≤ 2.9 and variable P₂O₅ contents up to 6.0 mol %. The fractional population of the orthophosphate groups remains independent of n_P at a fixed N̅_BO-value, but is reduced slightly as N̅_BO^Si increases. Nevertheless, P remains predominantly as readily released orthophosphate ions, whose content may be altered essentially independently of the network connectivity, thereby offering a route to optimize the glass bioactivity. We discuss the observed composition-structure links in relation to known composition-bioactivity correlations, and define how Na₂O–CaO–SiO₂–P₂O₅ compositions exhibiting an optimal bioactivity can be designed by simultaneously altering three key parameters: the silicate network connectivity, the (ortho)phosphate content, and the n_Na/n_Ca molar ratio.

1. Introduction

Many melt-derived glasses of the Na₂O–CaO–SiO₂–P₂O₅ system, as well as other silicate-based analogues incorporating additional cations (e.g., Mg²⁺, Sr²⁺, Zn²⁺) and/or anions (e.g., F^–) are termed “bioactive”, as when subjected to body fluids, they spontaneously integrate with the tissue through a hydroxy-carbonate apatite (HCA) surface layer.¹⁻⁴ A few such bioactive glass (BG) options are widely exploited in orthopedic and periodontal surgery, e.g., the “45S5 Bioglass”.¹⁻³

Silicate-based glasses only exhibit bioactivity over a relatively narrow span of compositions. However, despite vast efforts being spent for improving and tailoring these materials, encompassing bioactivity assessments (i.e., the rate of HCA formation) both in vitro and in vivo,^2,3 very few quantitative composition/bioactivity relations are reported. The present insight thereof derives from empirical testing that typically involve systematic variations of the relative oxide contents, e.g., SiO₂ and P₂O₅.^2,3,5−9 Unfortunately, given the currently insufficient understanding of the underlying structure/composition relations that ultimately control the bioactivity, most empirically derived composition/bioactivity correlations have limited applicability to related BG formulations generated, for instance, by replacing glass modifier cations or by introducing additional glass network-forming elements, such as boron.

Considering the relatively modest progress made toward a rational design of BGs featuring optimal bioactivities via the relative oxide contents as direct variables, it is highly desirable to identify relatively simple descriptors¹⁰ that reasonably accurately capture the essential composition/bioactivity relations through the insight provided from the underlying structure/composition links. Two such parameters are employed,^5,11,12 although relatively sparsely and not nearly to their full potential:

• (i)One descriptor is the silicate network connectivity,¹¹⁻¹⁵ here denoted N̅_BO^Si and corresponding to the average number of bridging oxygen (BO) atoms per SiO₄ group in the structure. Q_Si labels a SiO₄ tetrahedron exhibiting n BO atoms and 4 – n nonbridging oxygen (NBO) ions. The negatively charged NBO species are balanced by the Na⁺/Ca²⁺ modifiers. The importance of the network connectivity for the bioactivity was first highlighted by Strnad;¹¹ this concept was subsequently developed further and applied by several groups.^{7,8,12,14−25} The exact limits of N̅_BO^Si required for bioactive glass compositions remain unsettled,^11,12,15,22 but ”favorable” values are commensurate with open structures primarily built by Q_Si and Q_Si³ groups that readily degrade when subjected to body fluids.
• (ii)The P content of the BG constitutes the second parameter for bioactivity predictions. Phosphorus is generally present as readily released orthophosphate anions (i.e., Q_P⁰ groups) dispersed across the glass matrix.^26,27 Numerous investigations conducted both in vitro and in vivo reveal that the presence of P boosts the bioactivity.^2,3,5−7,9 Dissolved Ca²⁺ and PO₄^3– species increase the supersaturation of the HCA constituents in the body fluid, thereby accelerating the phosphate formation at the glass surface.^2,3,5,28 The ion release also controls the local pH and avoids excessive acidity that inhibits bone bonding.²⁹ However, if the glass-modifier content is insufficient for fully balancing all negative charges of the orthophosphate species, Q_P and higher-polymerization Q_Pⁿ (n = 2, 3) phosphate moieties form. They are believed to diminish the bioactivity, owing to their lower mobility and the higher energetic cost associated with their release compared with the orthophosphate groups.^17,18 Yet, in modifier-rich BGs the existence and nature of the Q_P environments remains debated,^{14−19,30−35} in particular which compositional/structural parameters control their populations.

Given that the glass bioactivity is enhanced either by a relatively low silicate network polymerization or by large amounts of orthophosphate groups, designing BGs that combine these two beneficial features is an appealing perspective for optimizing the bioactivity. One option involves adding P to a base glass composition, while the silicate network connectivity is kept fixed at a “favorable” value. However, any potential bearings on N̅_BO^Si or the Q_P speciation by introducing high P contents must first be assessed. The extent to which additional P atoms enter the silicate network and distribute between ortho- and nonorthophosphate moieties dictates if the goal indicated above is practically feasible, i.e., whether it is possible to design low-connectivity BGs that feature substantial orthophosphate contents. To answer this key question, herein we quantitatively examine the relationships between the phosphate speciation, the silicate network connectivity, and the P content of the glass across wide compositional ranges.

Herein, we assess the structural alterations accompanying the variations of the P content and N̅_BO^Si by monitoring the sets of {Q_Si} and {Q_Pⁿ} populations that build each structure, as probed experimentally by magic-angle spinning (MAS) ²⁹Si and ³¹P nuclear magnetic resonance (NMR) spectroscopy, as well as by molecular dynamics (MD) simulations.³⁶ The observed composition–structure correlations are linked with composition–bioactivity relationships reported in the literature to advance the structure–bioactivity insight; we further suggest rational ways to combine the key descriptors toward an optimal bioactivity. The present direct comparison between the MD and NMR derived structural features is also the first attempt of its kind for a large set of BG samples (vide infra), which further span a wide range of (Na, Ca, Si, P) compositions. Our results confirm that both experimental and computational approaches reveal fully consistent qualitative trends. This mutual validation is also important for enabling discussions on specific MD-derived structural features that are not experimentally accessible.³⁶

2. Glass Series Design

To elucidate the structural changes resulting from variations of either the P content or the silicate network connectivity while the other parameter remains fixed, we prepared a set of 13 BG specimens from the quaternary Na₂O–CaO–SiO₂–P₂O₅ system, each labeled BG_p(N̅_BO^Si), with 0≤p≤6.0 representing the P₂O₅ content in mol % (see Table 1). Two glass series featuring nominal N̅_BO values of N̅_BO^Si(nom)=2.5 and N̅_BO(nom)=2.9, respectively, were derived by assuming that P is present solely as orthophosphate groups (Q_P⁰) in each glass structure, thereby requiring a known net amount of the Na⁺/Ca²⁺ network modifiers for charge balance. Both BG families exhibit a constant molar ratio n_Na/n_Ca = 1.54, and the modifier reservoir consistently remains sufficiently large for simultaneously arranging the desired N̅_BO-value together with the sole presence of Q_P⁰ groups. This BG design strategy, employed in a few recent studies,^14,22,31 implies that the total n_Na+n_Ca amount increases concurrently with n_P across each BG(2.5) and BG(2.9) series, while that of Si decreases, approximately amounting to a net Si→P stoichiometric replacement (see Table 1).

Table 1. BG Sample Compositions^a.

label	N̅BOSi(nom)b	aNa2O (mol %)	bCaO (mol %)	cSiO2 (mol %)	dP2O5 (mol %)	stoichiometric formula	y(CaO)c	nNa/nCad	ρ (g cm–3)e
BG2.6(2.1)	2.11	0.244 (0.229)	0.269 (0.255)	0.461 (0.486)	0.026 (0.030)	Na0.384Ca0.212Si0.363P0.041O1.233	0.52	1.81	2.704
BG6.0(2.1)	2.15	0.221 (0.207)	0.324 (0.315)	0.395 (0.412)	0.060 (0.065)	Na0.345Ca0.253Si0.308P0.094O1.325	0.59	1.36	2.743
BG0(2.5)	2.50	0.186 (0.178)	0.242 (0.231)	0.572 (0.591)	0.000 (0.000)	Na0.314Ca0.204Si0.482P0.000O1.325	0.57	1.54	2.673
BG1.0(2.5)	2.50	0.192 (0.181)	0.249 (0.250)	0.549 (0.559)	0.010 (0.010)	Na0.319Ca0.207Si0.457P0.017O1.322	0.57	1.54	2.685
BG2.0(2.5)	2.50	0.197 (0.191)	0.257 (0.258)	0.526 (0.527)	0.020 (0.024)	Na0.324Ca0.211Si0.432P0.033O1.320	0.57	1.54	2.691
BG4.0(2.5)	2.50	0.209 (0.193)	0.271 (0.254)	0.480 (0.509)	0.040 (0.044)	Na0.334Ca0.217Si0.385P0.064O1.314	0.57	1.54	2.693
BG6.0(2.5)	2.50	0.219 (0.201)	0.287 (0.274)	0.434 (0.460)	0.060 (0.065)	Na0.343Ca0.223Si0.340P0.094O1.310	0.57	1.54	2.707
BG2.6(2.7)	2.74	0.202 (0.194)	0.222 (0.214)	0.550 (0.560)	0.026 (0.032)	Na0.329Ca0.181Si0.448P0.042O1.347	0.52	1.81	2.635
BG0(2.9)	2.93	0.151 (0.143)	0.197 (0.183)	0.652 (0.674)	0.000 (0.000)	Na0.262Ca0.171Si0.566P0.000O1.435	0.57	1.53	2.600
BG2.0(2.9)	2.93	0.165 (0.151)	0.215 (0.206)	0.600 (0.623)	0.020 (0.020)	Na0.278Ca0.182Si0.506P0.034O1.418	0.57	1.53	2.624
BG3.0(2.9)	2.93	0.172 (0.161)	0.224 (0.226)	0.574 (0.583)	0.030 (0.030)	Na0.286Ca0.187Si0.477P0.050O1.409	0.57	1.53	2.625
BG4.0(2.9)	2.93	0.179 (0.162)	0.233 (0.226)	0.548 (0.572)	0.040 (0.040)	Na0.294Ca0.191Si0.449P0.066O1.401	0.57	1.53	2.639
BG6.0(2.9)	2.93	0.193 (0.172)	0.252 (0.244)	0.495 (0.524)	0.060 (0.060)	Na0.308Ca0.201Si0.396P0.096O1.385	0.57	1.53	2.661

^a{a, b, c, d} specify the nominally batched aNa₂O–bCaO–cSiO₂–dP₂O₅ oxide equivalents with a + b + c + d = 1; they were used for obtaining the stoichiometric formulae. Values within parentheses correspond to EDX-analyzed compositions.

^bThe silicate network connectivity, i.e., average number of bridging oxygen atoms per SiO₄ tetrahedron, calculated by accounting for the modifier cation-consumption of the orthophosphate species in each batched glass composition, according to the procedure of Edén.^15,23

^cMolar fraction of CaO out of the glass modifier oxides; y(CaO) = n(CaO)/[n(CaO) + n(Na₂O)].

^dMolar ratio between Na⁺ and Ca²⁺ cations.

^eDensities (accurate within ±0.003 g cm^–3) were determined by the Archimedes method in water at 22 °C.

Besides each BG(2.5) and BG(2.9) branch (where we drop the p subscript when collectively referring to all its members), two additional samples—BG_2.6(2.1) and BG_2.6(2.7)—form a set of glasses exhibiting roughly constant P₂O₅ contents (2–3 mol %), but with N̅_BO^Si increasing from 2.1 to 2.9. This series enables us to selectively probe the structural changes resulting when solely the silicate network-connectivity varies. Note that the BG_2.6(2.1) specimen corresponds to the widely utilized “45S5 Bioglass”.¹⁻³

The primary aim of the present work is to enhance the structure–bioactivity insight by exploring the phosphate and silicate speciations of both bioactive and nonbioactive glass compositions that are selected based on the following hypotheses, inferred and discussed by Edén¹⁵ on the basis of in vitro bioactivity tests reported in the literature:^6,7 (A) A silicate network connectivity conforming to the range 2.0 ≲ N̅_BO^Si ≲ 2.7 is a prerequisite for bioactivity; it is optimized for values around 2.5–2.6.¹⁵ (B) Provided that requirement A is fulfilled, the bioactivity grows monotonically with the net orthophosphate content

1

where n_P is the stoichiometric amount of P (see Table 1). Here and onward, x_Pⁿ and x_Si denote the fractional population of Q_Pⁿ and Q_Si groups out of the total {Q_Pⁿ} and {Q_Si} speciation, respectively. In this work, we examine and discuss hypotheses A and B further.

3. Materials and Methods

3.1. Sample Preparations and Characterization

The BGs were prepared from precursors of NaH₂PO₄ (99.99%; Merck), and Na₂CO₃ (99.9%), CaCO₃ (99.9%), and SiO₂ (99.99%) from ChemPur. To accelerate spin–lattice relaxation for the NMR experimentation, 0.1 wt % of Fe₂O₃ was added to each batch. Each precursor-mixture (6.0 g) was ball-milled for 12 h and subsequently placed in a Pt crucible that was heated for 4 h in an electric furnace at 950 °C for CO₂ removal. The temperature was set to a final value in the range of 1350–1620 °C, with the highest temperatures required by compositions exhibiting a large P-content and/or high N_BO^Si-value. Each melt was held for 4 h prior to its quenching by immersing the bottom of the crucible in water.

Powder X-ray diffraction with a PANalytical X’pert PRO MPD diffractometer and Cu Kα₁ radiation revealed no crystalline phases (detection limit ≲1%). Here, 2θ ranged between 10° and 70°. Scanning electron microscopy (SEM) with a JSM 7000F (JEOL) microscope in backscatter electron imaging mode (20 kV acceleration voltage) evidenced that each specimen constitutes a homogeneous glass phase, except for BG_6.0(2.9) that manifested tendencies of amorphous phase-separation. Cation contents were estimated by a LINK INCA (Oxford instruments) energy-dispersive X-ray (EDX) detector. Each reported composition resulted from averaging over ten analyses from distinct fragments, with the respective O content calculated to charge-balance the cations. The nominal and EDX-analyzed glass compositions agree overall well (see Table 1), where the deviations remain within the uncertainty of the analysis. Hence, the sample nomenclature and structural analysis assume the nominal glass compositions. See Mathew et al.²⁵ for further synthesis/characterization details.

3.2. Solid-State NMR Experiments

All MAS NMR experimentation utilized a Bruker Avance-III spectrometer operating at 9.4 T; i.e., the ³¹P and ²⁹Si Larmor frequencies are −162.0 MHz and 79.47 MHz, respectively. Finely ground glass powders were packed in 7 mm zirconia rotors and spun at 7.00 kHz. The NMR acquisitions utilized single pulses with flip angles, rf nutation frequencies, and relaxation delays of {70°, 62.5 kHz, 120 s} and {90°, 81 kHz, 40 s} for ²⁹Si and ³¹P, respectively, with the corresponding number of accumulated signal transients depending on the content of the detected nucleus and ranging over 400–900 and 256–640. Separate T₁ relaxation measurements verified that these relaxation delays provide quantitative NMR spectra. No signal apodization was employed in the data processing. ³¹P and ²⁹Si chemical shifts are quoted relative to 85% H₃PO₄(aq) and neat tetramethylsilane (TMS), respectively.

3.3. Molecular Dynamics Simulations

Classical MD simulations were performed with the DLPOLY3 package^37,38 for NVT ensembles, where 6000–12000 {Na, Ca, Si, P, O} atoms were placed in a cubic box with periodic boundary conditions and a size within 4.2–5.1 nm; these numbers varied slightly to match each nominal BG composition and experimental density (see Table 1 and the Supporting Information). The melt-quench simulation started from a random atom configuration, equilibrated for 100 ps at 3500 K, followed by a 10 K/ps cooling procedure down to 300 K. A final NVT run at 300 K was then performed for 200 ps, of which the last 150 ps were used for the structural analysis. For each glass composition, this protocol was completed 2–4 times with different initial configurations (see the Supporting Information). The average value and uncertainty of each reported structural parameter were derived from these independent samples.

A polarizable shell-model potential, developed for modeling multicomponent glasses,^17−19,39 was employed throughout. Each cation carries its full formal charge. O^2– species are represented as core (O_C) and shell (O_S) units coupled by a 300 THz harmonic oscillator and bearing charges of z_C = 0.8482e and z_S = −2.8482e, respectively (i.e., z_C + z_S = −2e constitutes the formal charge). The short-range O_S–O_S and cation–O_S interactions were parametrized by a Buckingham potential,^17−19,39 evaluated for all pairs up to 0.8 nm. Long-range Coulombic interactions among all charged particles were calculated by a smoothed particle mesh Ewald summation³⁸ with a 1.2 nm real-space cutoff and an accuracy of 10^–6. The intratetrahedral O–Si–O and O–P–O bond angles were constrained by using three-body truncated harmonic potentials.³⁸ The equations of motion were integrated in time-steps of 0.2 fs by the velocity Verlet integrator approach. The temperature was controlled by a Berendsen thermostat with a 1.0 ps relaxation time constant. See refs (17−19 and 39) for further details on the simulation procedures, and the Supporting Information for additional discussions on the convergence of the MD data with respect to the system size and the cooling rate of the simulation.

4. Results

4.1. ³¹P NMR

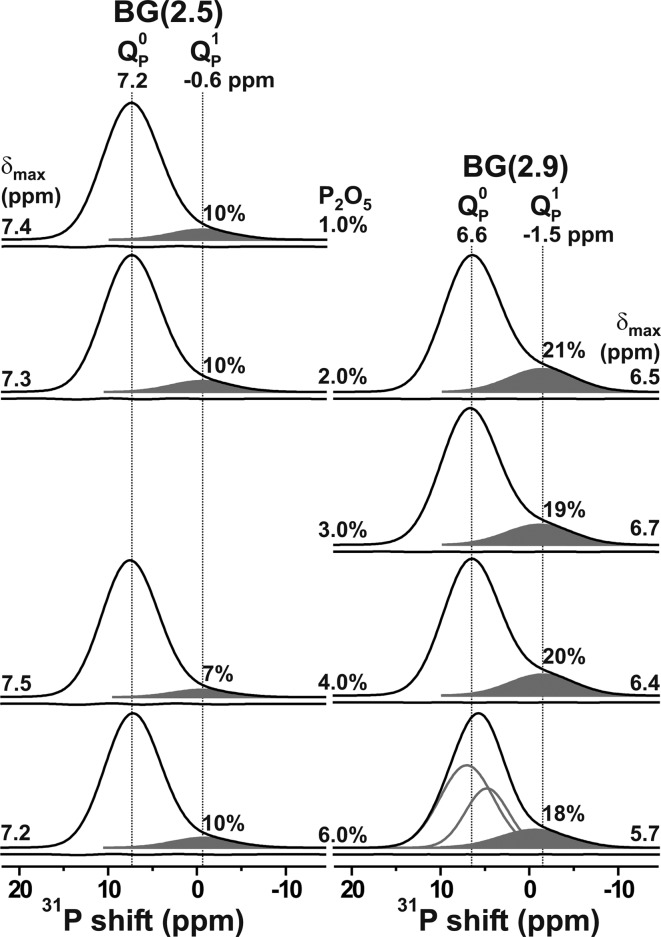
The ³¹P MAS NMR spectra recorded from the BG(2.5) and BG(2.9) series are displayed in Figure 1. All are representative of phosphate groups in strongly disordered structures, as reflected by NMR signals associated with 7.5–8.0 ppm full-width at half-maximum (fwhm) height. Onward disregarding the BG_6.0(2.9) sample that is not fully homogeneous (see section 3.1), all specimens within each fixed-N̅_BO^Si series exhibit essentially equal ³¹P NMR peak maxima (δ_max) and fwhm values, regardless of the P content. The observed peak maxima in the range 6–9 ppm are consistent with Q_P (orthophosphate) environments charge-balanced by both Na⁺ and Ca²⁺.^26,27,40

Figure 1.

Experimental ³¹P MAS NMR spectra recorded from Na₂O–CaO–SiO₂–P₂O₅ glasses, where the BG(2.5) and BG(2.9) series are displayed in the left and right columns, respectively, and ordered according to increasing P₂O₅ contents from top to bottom. The peak maximum is specified at the outermost portion of each spectrum; it is mainly dictated by the ³¹P resonances from Q_P⁰ groups, whose traces are not indicated, except for the NMR spectrum from BG_6.0(2.9) that required deconvolutions into two distinct ³¹P signals. Shaded areas mark signal contributions from Q_P moieties, whose relative populations (in %) are indicated. The curve beneath each spectrum reveals the difference between the experimental and best-fit spectra.

The NMR peakshape recorded from each BG(2.5) glass is nearly Gaussian, but it becomes progressively more asymmetric when the silicate-network connectivity increases: this growing “tail” stems from Q_P¹ groups.^{16,20,25−27,31−33,41,42} A main goal of the present work is to quantify these populations and rationalize their dependence on the silicate network connectivity and P content of the BG. The Supporting Information discusses the problems of detecting low amounts of Q_P groups by solid-state ³¹P NMR on BGs (such as the most thoroughly studied “45S5” composition; e.g., see Pedone et al.³⁰), as well as highlighting their assisted probing by exploiting information from the spinning sidebands in the NMR spectrum. While we for brevity denote the n ≥ 1 phosphate moieties by Q_Pⁿ, their BO atoms all involve linkages to Si rather than P, as highlighted previously in numerous MD studies,^17−19,30 as well as experimentally by through-space and through-bond coupling-based NMR techniques.^33,41 We note that standard ³¹P MAS NMR experimentation cannot discriminate between ³¹P in Si–O–P and P–O–P motifs.^33,41 The MD-derived fractions of P–O–P bonds in the present glasses remain very low (≲ 3% out of all P–O–Si and P–O–P motifs) and are only present in the P-richest samples featuring ≥4 mol % P₂O₅.

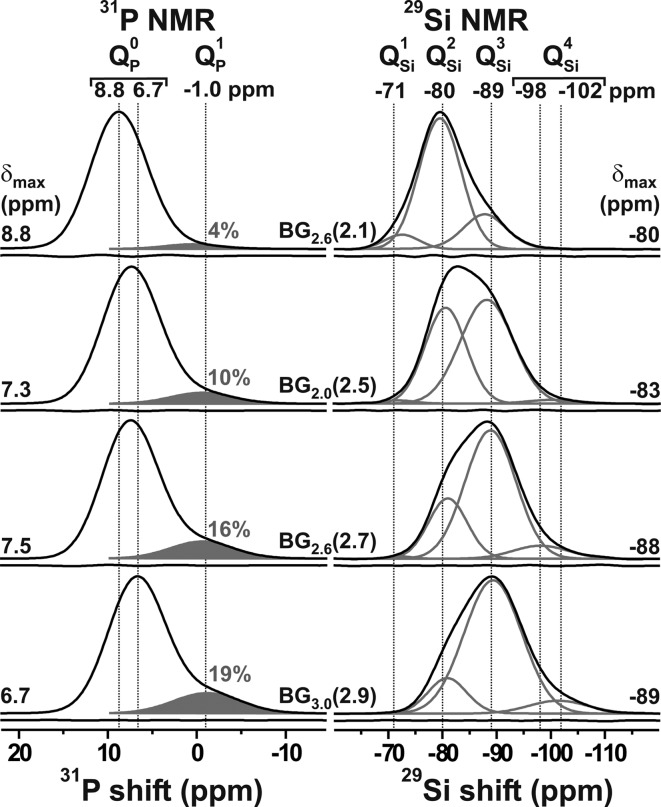
The ³¹P NMR results of Figure 2 from glasses featuring a nearly constant P content (2–3 mol % P₂O₅) but variable N̅_BO^Si values between 2.1 and 2.9, suggest a strict relationship between the fraction of Q_P groups in the BG structure and its silicate network connectivity. To quantify these relationships further, we deconvoluted each ³¹P NMR signal into two Gaussian peak components stemming from Q_P⁰ and Q_P species by constrained iterative fitting (see the Supporting Information). Each peak is represented by the parameter-triplet (δ_Pⁿ, W_P, x_Pⁿ), corresponding to the mean ³¹P chemical shift, the fwhm, and the fractional population, respectively, of the given Q_P species. The best-fit results are listed in Table 2. They reveal no significant variations across the set of BGs, as anticipated from the very similar experimental ³¹P NMR spectra. Owing to the higher ³¹P shielding resulting from Qⁿ → Qⁿ⁺¹ conversions, the chemical shifts associated with Q_P⁰ and Q_P groups are separated by ≈8 ppm, with those from Q_P⁰ moieties appearing within a narrow window of 6.4–8.7 ppm, whereas their Q_P counterparts span between −1.7 ppm and 0.4 ppm. As discussed further in section 4.3, the results from BGs associated with four distinct N̅_BO^Si-values evidence a concurrent growth of the relative fraction of the Q_P environments from ≈0.05 to ≈0.20 when N̅_BO^Si is increased between 2.1 and 2.9, whereas the x_P values are independent of the P content within each BG(N̅_BO^Si) series.

Figure 2.

Experimental ³¹P (left column) and ²⁹Si (right column) NMR spectra, plotted with black traces and acquired from the as-indicated BG_p(N̅_BO^Si) samples. The spectra are listed according to increasing silicate network connectivity from top to bottom. Each ³¹P NMR contribution from the Q_P groups is marked by a shaded area (left column), with the respective population (in %) specified. The gray traces in the right column represent ²⁹Si NMR peaks stemming from the various Q_Siⁿ groups, as obtained by spectral deconvolution. The curve beneath each NMR spectrum represents the difference between the experiment and its respective best-fit.

Table 2. ³¹P NMR Results^a.

	net peak		QP0			QP1
label	δmax (ppm)	W (ppm)	δ0 (ppm)	W0 (ppm)	x0	δ1 (ppm)	W1 (ppm)	x1	N̅BOSi(nom)	N̅BOSi(NMRP)b
BG2.6(2.1)	8.8	7.51	8.7	7.4	0.959	0.4	7.3	0.041	2.11	2.11
BG6.0(2.1)	7.3	7.48	7.3	7.4	0.955	–0.8	7.4	0.045	2.15	2.14
BG0(2.5)	–	–	–	–	–	–	–	–	2.50	2.50
BG1.0(2.5)	7.4	7.77	7.4	7.6	0.899	–0.6	8.1	0.101	2.50	2.50
BG2.0(2.5)	7.3	7.72	7.4	7.5	0.896	–0.6	8.3	0.104	2.50	2.50
BG4.0(2.5)	7.5	7.57	7.5	7.4	0.931	–0.6	7.9	0.069	2.50	2.49
BG6.0(2.5)	7.2	7.55	7.2	7.4	0.902	–0.8	8.2	0.098	2.50	2.48
BG2.6(2.7)	7.5	7.72	7.5	7.4	0.838	–0.6	8.4	0.162	2.74	2.73
BG0(2.9)	–	–	–	–	–	–	–	–	2.93	2.93
BG2.0(2.9)	6.5	7.96	6.4	7.5	0.795	–1.7	8.6	0.205	2.93	2.92
BG3.0(2.9)	6.7	7.97	6.8	7.5	0.814	–1.2	8.9	0.186	2.93	2.91
BG4.0(2.9)	6.4	7.85	6.5	7.4	0.805	–1.5	8.7	0.195	2.93	2.90
BG6.0(2.9)c	5.7	7.47	7.0	7.1	0.549	–0.6	9.2	0.179	2.93	2.89
			4.8	5.7	0.272

^aThe data involves the net NMR chemical shift (δ_max; uncertainty ±0.1 ppm) and fwhm height (W; ±0.15 ppm) of the ³¹P NMR signal, as well as the chemical shift (δⁿ; ±0.3 ppm), fwhm height (Wⁿ; ±0.5 ppm), and fractional population (xⁿ; ±0.02) of each Q_Pⁿ contribution extracted by spectra deconvolution.

^bVaules corrected for the NMR-derived minor Q_P¹ contributions.

^cThis sample exhibits phase separation and its ³¹P NMR spectrum required two Q_P⁰ signals for deconvolution.

For a fixed number of NBO ions at the phosphate group, its ³¹P chemical shift is dictated mainly by the nature and location of the surrounding glass-modifier cations.^16,27,31,40 Previous ³¹P NMR reports on Na–Ca–Si–P–O glasses^{16,25,27,30−32,43} observed δ_P⁰ values that are intermediate of the shifts associated with the orthophosphate groups present in polymorphs of Na₃PO₄ and Ca₃(PO₄)₂ that resonate around 12–15 ppm and 0–3 ppm, respectively. A linear relationship between δ_P and y(CaO) = n(CaO)/[n(CaO) + n(Na₂O)] is reported for Na₂O–CaO–SiO₂–P₂O₅ glasses.^16,27,31 The present ³¹P NMR results for BGs featuring a nearly constanty(CaO) value accord with those findings: the following weighted average,

2

with y(CaO) = 0.57 for the BG(2.5) and BG(2.9) series (see Table 1), predicts a chemical-shift range of 5.2 ≤ (δ̅_P⁰/ppm) ≤ 8.2 for the Q_P groups when δ_A and δ_B are selected over the typical shift-spans of crystalline Na and Ca based orthophosphates, i.e., 12–15 ppm and 0–3 ppm, respectively. Consequently, our observed δ_P⁰ values in the range of 6.5–7.5 ppm are overall consistent with earlier NMR work reporting an essentially statistical Na/Ca distribution around the orthophosphate species;^16,27,31,43 see the Supporting Information for further discussions.

The present NMR analysis cannot discriminate between a strict statistical (Na,Ca)–P association and minor preferences of either cation to charge-balance the phosphate moieties. A more accurate ¹⁷O NMR analysis applied to the 45S5 BG, revealed a slight depletion of Na⁺–PO₄^3– contacts,³⁰ while previous MD simulations also suggested a strong preference for Ca²⁺–PO₄^3– rather than Na⁺–PO₄^3– associations,^17,44−46 as also observed in our modeled BG_2.6(2.1) structure. The MD-derived Na/Ca partitioning among Si/P for the entire glass series will be presented together with those from a more extended NMR study in a forthcoming paper.

4.2. ²⁹Si NMR

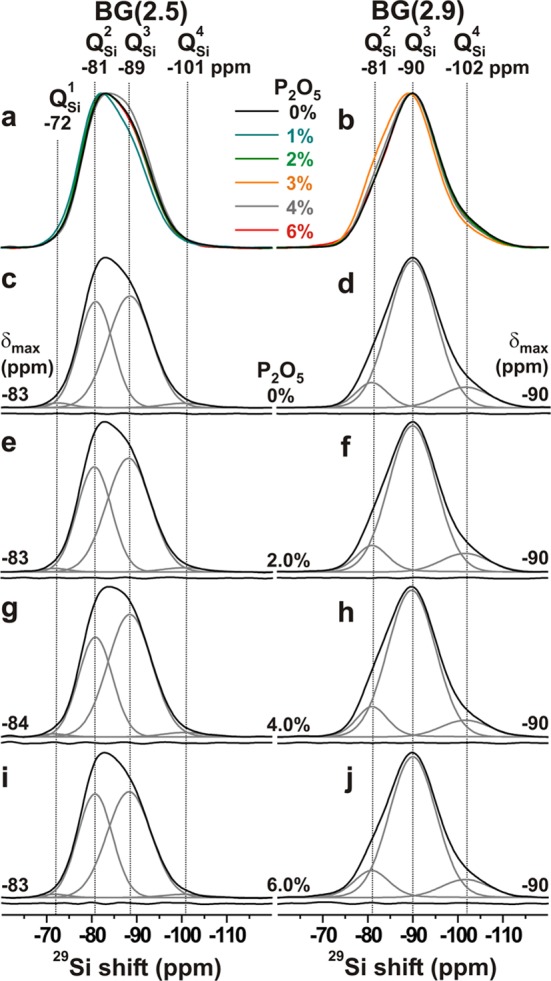
For Na–Ca–Si–P–O glasses, the mean ²⁹Si chemical shift (δ_Siⁿ) of a Q_Si species depends principally on the same structural factors as ³¹P, i.e., the number of BO atoms (n) at the SiO₄ tetrahedron, and the Na⁺/Ca²⁺ constellation for local charge-balance.^{16,27,40,47,48} All glasses within a given BG(N̅_BO^Si) branch exhibit a constant n_Na/n_Ca ratio. Consequently, the center-of-gravity shift (δ_CG) of the ²⁹Si NMR peak and the accompanying peakshape are expected to depend predominantly on the precise set of fractional populations {x_Si} and their associated {δ_Siⁿ} values, where ²⁹Si nuclei of Q_Si moieties typically resonate in the range from −112 ppm to −100 ppm and the shift increases by roughly 7–12 ppm per Q_Siⁿ → Q_Si conversion.^40,47,48 Hence, for the present glasses, identical ²⁹Si NMR responses are expected throughout a given BG(N̅_BO^Si) series, whereas a gradual net displacement toward more negative shifts should occur when N̅_BO increases. The latter trend is witnessed by the ²⁹Si MAS NMR spectra presented in Figure 2. In contrast, very similar spectra are observed across each BG(2.5) and BG(2.9) branch, regardless of the P content of the BG; see the top row of Figure 3. Furthermore, Table 3 reveals very similar sets of ²⁹Si NMR best-fit parameters {δ_Siⁿ, W_Si, x_Siⁿ} within each N̅_BO-branch.

Figure 3.

²⁹Si MAS NMR spectra obtained from the BG(2.5) (left column) and BG(2.9) (right column) series of glasses. (a, b) Superimposed NMR spectra associated with the as-indicated glasses. (c–j) Experimental spectra (black traces) displayed together with deconvoluted peak-components (gray traces). They are assigned at the top of each column. The curves beneath the spectra constitute differences between experiments and best-fits.

Table 3. ²⁹Si NMR Results^a.

	net NMR peak			QSi1			QSi2			QSi3			QSi4
label	–δmax (ppm)	–δCG (ppm)	W (ppm)	–δ1 (ppm)	W1 (ppm)	x1	–δ2 (ppm)	W2 (ppm)	x2	–δ3 (ppm)	W3 (ppm)	x3	–δ4 (ppm)	W4 (ppm)	x4	N̅BOSi(nom)	N̅BOSi(NMRSi)
BG2.6(2.1)	79.5	81.0	11.12	72.5	7.5	0.066	79.5	9.1	0.724	87.8	9.3	0.210	–	–	–	2.11	2.14
BG6.0(2.1)	80.9	81.7	13.66	73.4	7.1	0.056	80.2	9.2	0.658	87.5	11.0	0.286	–	–	–	2.15	2.20
BG0(2.5)	83.0	85.3	15.68	72.5	7.0	0.015	80.9	8.9	0.409	88.5	11.5	0.555	100.5	11.0	0.021	2.50	2.58
BG1.0(2.5)	82.1	84.0	15.12	72.4	7.0	0.017	80.5	9.1	0.455	88.0	11.5	0.512	100.5	11.0	0.016	2.50	2.53
BG2.0(2.5)	82.9	85.1	15.80	71.8	7.0	0.012	80.6	8.9	0.405	88.2	11.5	0.563	100.5	11.0	0.020	2.50	2.59
BG4.0(2.5)	84.0	85.6	15.83	71.6	7.0	0.010	80.8	8.9	0.372	88.5	11.5	0.598	100.5	11.0	0.020	2.50	2.63
BG6.0(2.5)	82.8	85.0	15.75	71.9	7.0	0.010	80.7	9.0	0.423	88.3	11.5	0.551	100.5	11.0	0.016	2.50	2.57
BG2.6(2.7)	88.2	87.6	15.56	72.3	5.2	0.006	81.0	8.4	0.242	88.9	11.0	0.677	98.1	12.0	0.075	2.74	2.82
BG0(2.9)	89.8	90.1	14.70	–	–	–	80.9	8.2	0.094	89.9	12.5	0.793	101.7	12.8	0.113	2.93	3.02
BG2.0(2.9)	89.9	90.1	14.57	–	–	–	81.0	8.2	0.108	89.9	12.4	0.791	101.6	12.5	0.101	2.93	2.99
BG3.0(2.9)	89.2	89.0	15.53	–	–	–	80.9	8.4	0.144	89.3	12.5	0.779	101.4	12.9	0.077	2.93	2.93
BG4.0(2.9)	89.7	89.9	14.46	–	–	–	81.0	8.1	0.118	89.7	12.5	0.791	101.7	12.7	0.091	2.93	2.97
BG6.0(2.9)	90.0	90.1	14.41	–	–	–	80.8	8.1	0.121	90.0	12.2	0.778	101.7	12.6	0.101	2.93	2.98

^aThe data involve the peak maximum (δ_max; uncertainty ±0.2 ppm), the center-of-gravity shift (δ_CG; ±0.3 ppm) and the fwhm height (W; ±0.3 ppm) of the net ²⁹Si NMR signal, and the chemical shift (δⁿ), fwhm height (Wⁿ), and fractional population (xⁿ) of each Q_Siⁿ peak contribution resulting from spectral deconvolution. N̅_BO(nom) and N̅_BO^Si(NMR_Si) represent the silicate network connectivity obtained from the BG composition and by eq 3, respectively.

The net NMR responses derive from superimposed signals centered at the chemical shifts {δ_Si⁴, δ_Si, δ_Si², δ_Si} that appear around {−101, −88, −81, −72} ppm, respectively (see Figures 2 and 3). However, typically only three components are significant across the entire N̅_BO^Si-span of the present glasses, of which two moieties dominate: Q_Si and Q_Si³. The networks of the BG(2.9) glasses are primarily built by Q_Si groups (≈78% out of the total SiO₄ speciation), as expected, with the remaining constituting roughly equal amounts ≈10% of Q_Si⁴ and Q_Si groups. While minor Q_Si² contributions must be present because N̅_BO < 3.0, the NMR spectra unambiguously also reveal the presence of Q_Si⁴ groups. This feature stems from disproportionation equilibria, such as 2Q_Si ↔ Q_Siⁿ⁺¹ + Q_Si.^40,47,48 They produce deviations from a strict binary distribution that predicts the coexistence of only two tetrahedral species, Q_Siⁿ and Q_Si, except when N̅_BO^Si equals any member of the set {0, 1, 2, 3, 4}, when one sole Q_Si group associated with n = N̅_BO^Si results. A similar trend is observed for the BG(2.5) series for which a binary distribution predicts equal {x_Si, x_Si³} values, whereas the NMR-derived Q_Si populations (Table 3) reveal higher (≈0.55) and lower (≈0.41) x_Si³ and x_Si fractions, respectively; those NMR spectra further comprise weak signals from Q_Si⁴ and Q_Si tetrahedra (x_Siⁿ ≲ 0.02).

From each set {x_Siⁿ}, we calculated the ²⁹Si NMR-derived value N̅_BO(NMR_Si), according to

3

Table 4 compares these results with their nominal counterparts [N̅_BO^Si(nom)], as well as those obtained by correcting the latter values for the observed non-negligible amounts of Q_P groups (whose presence releases Na⁺/Ca²⁺ modifiers that become available for depolymerizing the silicate glass network), which provides a set of ³¹P NMR-derived values, denoted {N̅_BO^Si(NMR_P)}. Owing to the overall low amounts of P, each of N̅_BO(NMR_P) remains close to its N̅_BO^Si(nom) analogue (within ≤1% deviation throughout). Whereas the N̅_BO(NMR_Si) values stay fairly constant across each BG(2.5) and BG(2.9) branch, they are consistently 2–4% larger than their nominal counterparts. Yet, it is gratifying that the deviations between the respective N̅_BO^Si data obtained by ³¹P and ²⁹Si NMR typically only amount to ≈3%, with the largest discrepancy (≈5%) observed for the BG_4.0(2.5) glass.

Table 4. Fractional populations of Q_Siⁿ Groups derived by MD simulations and NMR^a.

	xPn populationsb		xSin populationsb				silicate network connectivity
label	QP0	QP1	QSi1	QSi2	QSi3	QSi4	N̅BOSi(nom)	N̅BOSi(NMRP)c	N̅BOSi(NMRSi)d	N̅BOSi(MD)e
BG2.6(2.1)	0.834 (0.959)	0.166 (0.041)	0.186 (0.066)	0.517 (0.724)	0.266 (0.210)	0.021 (0.000)	2.11	2.11	2.14	2.10
BG6.0(2.1)	0.798 (0.955)	0.200 (0.045)	0.197 (0.056)	0.514 (0.658)	0.252 (0.286)	0.027 (0.000)	2.15	2.14	2.20	2.09
BG0(2.5)	–	–	0.068 (0.015)	0.428 (0.409)	0.425 (0.555)	0.076 (0.021)	2.50	2.50	2.58	2.50
BG1.0(2.5)	0.670 (0.899)	0.318 (0.101)	0.073 (0.017)	0.426 (0.455)	0.435 (0.512)	0.065 (0.016)	2.50	2.50	2.53	2.49
BG2.0(2.5)	0.721 (0.896)	0.267 (0.104)	0.080 (0.012)	0.418 (0.405)	0.440 (0.563)	0.060 (0.020)	2.50	2.50	2.59	2.48
BG4.0(2.5)	0.622 (0.931)	0.364 (0.069)	0.084 (0.010)	0.443 (0.372)	0.409 (0.598)	0.063 (0.020)	2.50	2.49	2.63	2.45
BG6.0(2.5)	0.690 (0.902)	0.304 (0.098)	0.087 (0.010)	0.457 (0.423)	0.392 (0.551)	0.062 (0.016)	2.50	2.48	2.57	2.42
BG2.6(2.7)	0.517 (0.838)	0.475 (0.162)	0.041 (0.006)	0.336 (0.242)	0.507 (0.677)	0.115 (0.075)	2.74	2.73	2.82	2.70
BG0(2.9)	–	–	0.016 (0.000)	0.225 (0.094)	0.571 (0.793)	0.189 (0.113)	2.93	2.93	3.02	2.93
BG2.0(2.9)	0.417 (0.795)	0.553 (0.205)	0.017 (0.000)	0.246 (0.108)	0.553 (0.791)	0.183 (0.101)	2.93	2.92	2.99	2.90
BG3.0(2.9)	0.444 (0.814)	0.528 (0.186)	0.020 (0.000)	0.252 (0.144)	0.562 (0.779)	0.166 (0.077)	2.93	2.91	2.93	2.87
BG4.0(2.9)	0.440 (0.805)	0.554 (0.195)	0.022 (0.000)	0.269 (0.118)	0.539 (0.791)	0.169 (0.091)	2.93	2.90	2.97	2.86
BG6.0(2.9)	0.460 (0.821)	0.527 (0.179)	0.028 (0.000)	0.295 (0.121)	0.529 (0.778)	0.149 (0.101)	2.93	2.89	2.98	2.79

^aValues within parentheses correspond to the populations obtained by NMR. Typical standard deviations of the MD-generated x_Pⁿ and x_Si populations are σ = 0.034 and σ = 0.011, respectively, as estimated from all simulations that involved ≈6000 atoms (see the Supporting Information).

^bThe MD-derived structures also comprise minor amounts of Q_P² (x_P ≲ 0.03) and Q_Si⁰ (x_Si ≲ 0.01) groups that are not listed.

^cCorrected for the NMR-derived minor Q_P¹ contributions.

^dObtained from the ²⁹Si NMR-derived {x_Siⁿ} sets via eq 3.

^eObtained from the MD data.

4.3. Silicate and Phosphate Speciations: MD Simulations versus NMR

Here, we present the MD-modeled {Q_Siⁿ} and {Q_P} speciations and contrast their predictions with the experimental data obtained by MAS NMR.

4.3.1. NBO Distribution among Phosphate Groups

Some of the sparse experimental reports on (semi)quantitative {x_P⁰, x_P} populations of Na₂O–CaO–SiO₂–P₂O₅ structures concluded that the Q_P¹ groups generally increase with the P₂O₅ content.^16,26,32 In contrast, Grussaute et al.³¹ reported that the Q_P populations are independent thereof, at least for x(P₂O₅) ≤ 2.4 mol % and high silicate network connectivities (2.65–3.0). However, inspection of their ³¹P NMR data reveals a clear growth of x_P¹ when N̅_BO increases, but this trend was not commented. Mercier et al.³² highlighted a dependence of the Q_P¹ fraction on the SiO₂ content of the glass, further inferring that it increased concomitantly with the silicate network polymerization; yet, their glass-series design did not allow for reaching a quantitative x_P/N̅_BO^Si correlation. Such a relationship is established herein.

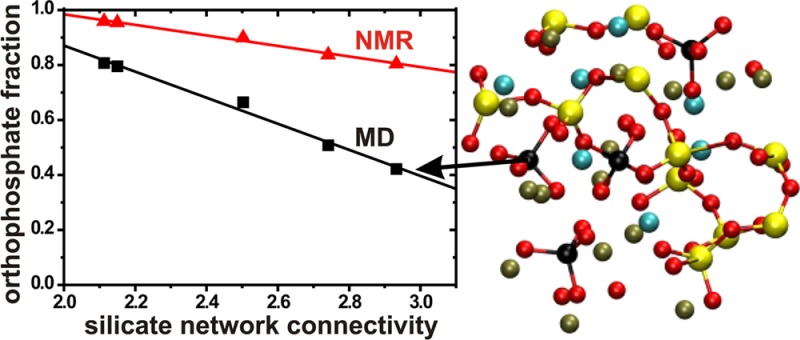
Table 4 lists the sets of MD-generated {x_P⁰, x_P} populations for the present structures. It is gratifying that the following qualitative trends fully accord with the experimental results of section 3.1: (i) The Q_P¹ population grows steadily as N̅_BO increases, with the extreme values of x_P¹ =0.17 and x_P ≈0.55 observed for the BG_2.6(2.1) and BG(2.9) structures, respectively. (ii) At a fixed silicate network connectivity, the Q_P¹ population remains essentially constant when the P content varies (Table 4). The primary discrepancy between the {x_P} sets obtained from ³¹P NMR and the MD calculations is the significantly lower orthophosphate populations in the modeled structures, whereas the Q_P¹ contributions are consistently 2.5–3 times higher than their experimental counterparts. Noteworthy, the deviations constitute a straightforward scaling, essentially independent of the N̅_BO value. Previous MD studies of the Na₂O–CaO–SiO₂–P₂O₅ system have focused almost exclusively on the “45S5” composition [i.e., BG_2.6(2.1)], where consistently higher x_P¹ values were observed^{17,18,44−46,49,50} compared to those (≈0) estimated by ³¹P NMR.^24,30,43 This discrepancy likely reflects slight x_P overestimations in MD simulations, and a corresponding potential underestimation by ³¹P MAS NMR whenever the Q_P¹ population is at the detection level of the technique, such as for 45S5 (see the Supporting Information). The present MD-generated phosphate speciation of BG_2.6(2.1) confirm previously modeled results on 45S5,^{17,18,46,49,50} while our remaining specimens complement the very few MD reports from other Na–Ca–Si–P–O compositions^17,18 by systematically exploring a significantly wider compositional range than previously considered.

Because the NMR-derived phosphate speciations solely comprise Q_P⁰ and Q_P groups, there is a direct mapping between x_P¹ and N̅_BO (i.e., the average number of BO atoms per PO₄ tetrahedron), whereas the modeled counterparts additionally comprise minor x_P² populations (≲0.03; see the Supporting Information). To gain quantitative insight into the relationship between the Q_P population and the silicate network polymerization, being of direct concern for designing BG specimens with optimal bioactivity, we fitted the {N̅_BO^P} set against {N̅_BO}. For both the NMR and MD generated data, Figure 4 reveals an approximately linear relationship over the present parameter space {2.1 ≤ N̅_BO^Si ≤ 2.9; p ≤ 6.0}. This trend persists regardless of whether each NMR/MD derived set {N̅_BO} is correlated with the composition-dictated N̅_BO^Si(nom) values, or with those obtained from either of ²⁹Si NMR [N̅_BO(NMR_Si)] or MD simulations [N̅_BO^Si(MD)] (the latter are discussed below). As phase separation tendencies were observed for the BG_6.0(2.9) glass (see section 3.1), the linear N̅_BO/N̅_BO^Si correlation likely breaks down for higher values of N̅_BO and/or x(P₂O₅).

Figure 4.

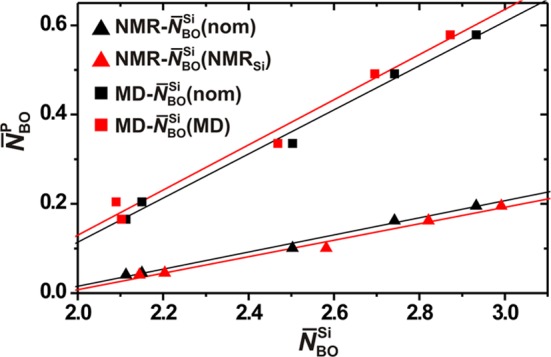
Average number of BO atoms at the phosphate groups (N̅_BO^P) in the BG structures, plotted against its Si analogue (N̅_BO), as obtained either by ²⁹Si NMR experiments [N̅_BO^Si(NMR_Si)], or by MD simulations [N̅_BO(MD)]. Averages were taken over all N̅_BO^P-values within each series of constant N̅_BO(nom). Given that the experimental and modeled N̅_BO^Si values generally differ slightly from their nominal counterparts [N̅_BO(nom)], the results of correlating the {N̅_BO^P(NMR)} and {N̅_BO(MD)} set with N̅_BO^Si(nom) are also provided (red symbols). Straight lines represent best-fit results of each N̅_BO/N̅_BO^Si correlation and method {MD-N̅_BO(nom), MD-N̅_BO^Si(MD), NMR-N̅_BO(nom), NMR-N̅_BO^Si(NMR_Si)}; they are associated with the respective R² correlation coefficients of {0.988, 0.977, 0.989, 0.981}.

4.3.2. NBO Distribution among Silicate Groups

We now focus on the BO/NBO partitioning among the network-forming SiO₄ groups, i.e., the n-distribution of {Q_Siⁿ}. The MD-derived {Q_Si} speciations are contrasted with their experimental counterparts in Table 4. As required and also in full accordance with ²⁹Si NMR, the modeled structures manifest essentially equal {Q_Siⁿ} sets within each glass family of constant N̅_BO(nom)-value (regardless of the P content), whereas the Q_Siⁿ distribution shifts progressively toward higher n for increasing silicate network polymerization. For each silicate network, its average number of BO atoms, N̅_BO(MD), was calculated according to eq 3. The {N̅_BO^Si(MD)} set accords well with its nominal {N̅_BO(nom)} counterpart, besides a slight but consistent decrease of the MD-generated results when the P content increases; this is readily explained by the presence of significant fractions of Q_P¹ groups that release some Na⁺/Ca²⁺ cations relative to the as-assumed scenario of solely orthophosphate species when the present glass compositions were devised (see section 2). However, owing to the overall low P₂O₅ contents (≤6 mol %), the observed reduction of N̅_BO remains very minor.

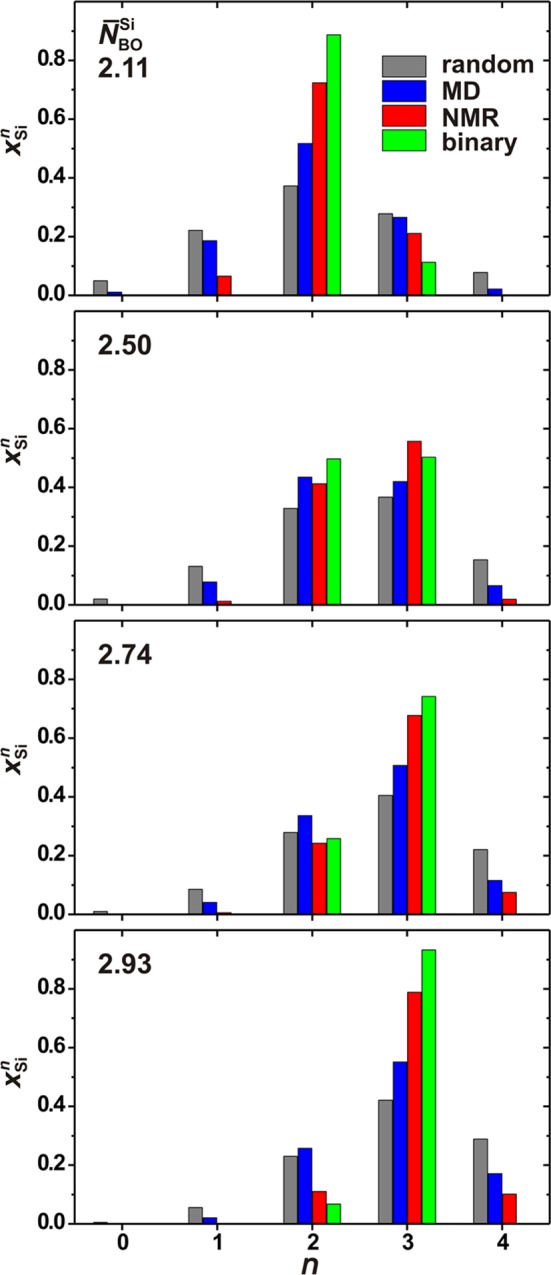
The major distinction between the experimental and modeled data is the significantly wider {Q_Siⁿ} distributions observed from the latter (Table 4). The NMR/MD derived {Q_Si} sets are displayed in Figure 5, which also includes results by assuming either a “binary” or “random” (statistical) BO/NBO distribution among the SiO₄ groups. The ²⁹Si NMR-derived silicate speciation generally comprises three terms, {Q_Si^n–1, Q_Si, Q_Siⁿ⁺¹}, in agreement with some recent NMR reports on BGs,^30,32,33 although earlier studies generally employed spectra deconvolutions into two signals.^16,24,27,43 The modeled/experimental {Q_Si} populations and the binary/random distribution scenarios are next compared by their respective distribution widths σ. As very similar σ-values are observed among the various glass structures for a given distribution type (“NMR/MD/random”; except for the binary scenario that anyway obeys σ ≤ 0.5), only averages over the entire set of samples are considered, which compare as follows:

4

with their (approximate) values given within parentheses.

Figure 5.

Q_Siⁿ fractional populations determined either by ²⁹Si NMR or MD simulations and plotted versus the number of BO atoms (n) at the SiO₄ group. For the glass series BG(2.5) and BG(2.9) that comprise several samples, the {x_Si} values represent averages over all members within the series. The results are compared with the predictions from binary and random NBO/BO distributions (calculated from the expressions of ref (21)) for each as-indicated N̅_BO^Si(nom) value.

We conclude that the experimentally determined {x_Siⁿ} sets, typically comprising three (significant) contributions, is slightly wider than a binary n-distribution, whereas the MD-derived counterpart is intermediate between the two limiting models, meaning that it is significantly wider than the scenarios of either a binary distribution or that estimated by NMR, but markedly more ordered than predicted from a statistical BO/NBO partitioning among the SiO₄ groups.

5. Discussion

5.1. Orthophosphate Content versus Silicate Network Connectivity

For a wide range of Na₂O–CaO–SiO₂–P₂O₅ glass compositions, the present experimental and modeling results (Table 4) firmly establish and extend the inferences by Grussaute et al.³¹ that for a constant network polymerization, the Q_P¹ population is independent of the P₂O₅ content of the glass (provided that y(CaO) is fixed³¹). Hence, the total orthophosphate population [n_P; see eq 1] is directly proportional to the net stoichiometric amount of P in the structure, as evidenced by Figure 6 that plots each experimental and modeled number density, ρ_N and ρ_N⁰ of the P atoms and the Q_P species, respectively, against the P₂O₅ content of the glass. Two important inferences may be made, both having bearings on future BG glass design:

• (i)Considering previous demonstrations that the bioactivity increases with the P content of the BG,^6,7,9,22 our present results evidence a direct correlation between the bioactivity and the orthophosphate content of the structure. Further, from the direct n_P/bioactivity correlation inferred in refs (15 and 22) follows that the bioactivity increases monotonically with n_P⁰ [see eq 1], thereby establishing the validity of hypothesis B in section 2.
• (ii)One may readily design a BG_p(N̅_BO^Si) composition that combines a favorable silicate network polymerization with a high P content, at least for p ≤ 6.0. Hence, for the range of suitable silicate network connectivities 2.0 ≲ N̅_BO ≲ 2.6 (discussed further in section 5.2), an optimal bioactivity is attained by arranging the highest possible P content, without altering the N̅_BO^Si-value significantly, as the majority of the phosphate species are not forming bonds to other SiO₄ or PO₄ groups, but enter the structure as isolated orthophosphate ions (provided that the glass modifier content is increased accordingly; see section 2 and Table 1).

Figure 6.

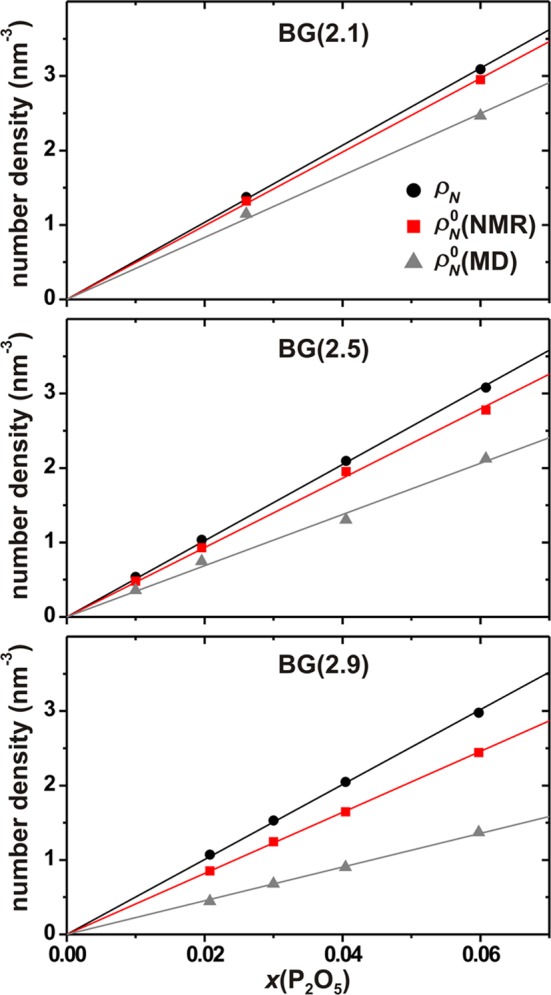
Number density (number of species per nm³) of P atoms (ρ_N) and orthophosphate groups (ρ_N⁰), plotted against the molar fraction of P₂O₅ for the as-indicated BG(N̅_BO) series of glasses. ρ_N was obtained from the stoichiometric glass composition and its accompanying experimental density ρ (see Table 1), whereas ρ_N⁰ = x_Pρ_N involves the fractional population x_P⁰ obtained either by ³¹P NMR or by MD simulations. Straight lines represent best-fit results.

5.2. Bioactivity versus Silicate Network Connectivity

Early work concluded that a bioactive glass composition required a “network connectivity <3”.^11,12 This originated from the incorrect assumption of a nonpreferential BO/NBO distribution among Si and P; because P is mainly present as orthophosphate ions, their Na⁺/Ca²⁺ consumption then leads to a higher than predicted N̅_BO^Si-value; to avoid such confusions, we refer specifically to the silicate network connectivity, i.e., N̅_BO.¹⁵ Yet, the precise N̅_BO^Si-range that optimizes the bioactivity remains unsettled in the current absence of a systematic investigation.

On the basis of published data from a large series of Na₂O–CaO–SiO₂–P₂O₅ compositions,⁶ we proposed N̅_BO^Si ≲ 2.7 as a necessary criterion for bioactivity, with optimal N̅_BO values predicted at the upper range of 2.5–2.6, beyond which the bioactivity diminishes rapidly.¹⁵ According to these predictions, the bioactivity increases from the BG(2.1) to the BG(2.5) glass branch—with the fastest HCA growth expected from the BG_6.0(2.5) specimen due to its highest P content—whereas BG_2.6(2.7) is anticipated to display a low bioactivity and no member of the BG(2.9) series should give physiological responses. While bioactivity testing is underway for the current glasses, the hypothesis that N̅_BO^Si ≈ 2.55 provides optimum conditions is supported further by the very recent work of Duée et al.⁹ They employed “mixture designs” to identify optimal BG candidates with x(P₂O₅)≤0.05; it amounted in two “best” glass compositions, both incidentally exhibiting N̅_BO = {2.56; 2.60}, despite that the silicate network connectivity was not a targeted parameter in their assessments. Noteworthy, the “D47” composition⁹ (0.215Na₂O–0.265CaO–0.470SiO₂–0.050P₂O₅) is almost identical to a “BG_5.0(2.5)” glass in our nomenclature, i.e., 0.214Na₂O–0.278CaO–0.458SiO₂–0.050P₂O₅. The onset of HCA formation from D47 was twice as rapid as for the “45S5 Bioglass”,⁹ hence providing further support for our stated optimal N̅_BO^Si-range.

Another question is if the bioactivity-increase across the range 2.0 ≲ N̅_BO^Si ≲ 2.6 and its sharp reduction as N̅_BO grows further can be rationalized from a structural viewpoint. The {Q_Siⁿ} speciations of Table 3 reveal that the most bioactive glasses exhibit structures built primarily by Q_Si and Q_Si³ groups, i.e., representing interconnected chain/ring motifs with a significant cross-linking: if the latter is negligible, then the BG degrades too rapidly in its contact with body fluids, thereby preventing significant HCA formation.^6,9 In contrast, a too high polymerization of the network impedes its degradability in solutions due to the large number of Si–O–Si bonds requiring hydrolysis, coupled with a diminished Na⁺/Ca²⁺ reservoir and accompanying reduced ion dissolution associated with the (too) Si-rich composition. Apparently, the best compromise between these two limits occurs when the Q_Si and Q_Si³ populations are nearly matched, i.e., when N̅_BO≈2.5 (see Table 4), as opposed to the (perhaps more intuitive) scenario of N̅_BO^Si ≈ 2.0 that reveals predominantly Q_Si moieties. This is one reason why the link between the glass solubility and the bioactivity is not strict.

As the network polymerization increases across the range 2.1–2.9, the Q_Si³ population grows steadily at the expense of its Q_Si counterpart; while this effect alone cannot explain the nonmonotonic dependence of the bioactivity on N̅_BO^Si, the bioactivity might reduce when Q_Si reaches above some ”critical” level (≥70%, according to Table 3). Yet, the emergence of Q_Si⁴ structural groups is apparently a more accurate indicator for the onset of “non-bioactivity”. While Q_Si motifs are essentially absent in the BG structures associated with N̅_BO^Si ≤ 2.5, their population increases steeply for more polymerized networks; they constitute ≈10% out of the total SiO₄ speciation for the nonbioactive BG(2.9) compositions (Table 3). The loss of bioactivity may be understood from the significantly higher cross-linking invoked by the Q_Si groups and the accompanying local depletion of glass modifier ions; altogether these features create structural portions that more strongly resists degradation in aqueous medium compared to the chain/sheet-like motifs prevailing in the bioactive glass structures. These inferences were made from the NMR-derived {Q_Siⁿ} speciations; however, as in the case of the Q_P populations, this trend is also mirrored by the modeled structures (Table 4).

5.3. The Roles of Na and Ca

Once fixating both the P content and silicate network connectivity, the n_Na/n_Ca molar ratio constitutes the remaining free parameter for a given Na₂O–CaO–SiO₂–P₂O₅ glass formulation. Despite influencing the bioactivity to a lesser extent than the {N̅_BO^Si, n_P} pair, the relative Na/Ca content is worth discussing as its bearing on the bioactivity yet remains to be systematically assessed, particularly considering indications that the bioactivity-boost for increasing P content may be strictly monotonic only over a range of relative Na/Si amounts within 0.8 ≲ n_Na/n_Si ≲ 1.2.¹⁵

Keeping either a large Na or Ca content has both its pros and cons. Large amounts of Ca are beneficial for primarily three reasons: (i) Being a component of HCA, higher dissolution rates of Ca improves the apatite supersaturation.^2,3,5 (ii) The {x_P⁰, x_P} values depend to some extent on the n_Na/n_Ca ratio, with the desirable orthophosphate fraction increasing concurrently with the Ca content.³¹ (iii) Large amounts of Na⁺ ions induces cytotoxicity.^9,51 In contrast, arranging a large Na content is favorable for (i) facilitating the preparation of P-rich glasses by lowering the melting temperature, and particularly, (ii) enhancing the glass solubility; the higher Na⁺ mobility relative to Ca²⁺ overall accelerates the surface reactions and elevates the local pH, altogether stimulating the calcium phosphate formation.^2,3,5,29

Noteworthy, as both the Ca²⁺ and PO₄^3– ions are dispersed throughout the glass matrix,²⁴⁻²⁷ an increased glass degradation also facilitates their release (vide infra). We therefore hypothesize that a relatively high n_Na/n_Ca ratio within 1.0–2.0 (i.e., 0.3≤y(CaO)≤0.5) may release an otherwise stricter lower bound on the N̅_BO^Si-value, thereby allowing the combination of a high bioactivity with a relatively condensed silicate network exhibiting N̅_BO ≈2.5 (see section 5.2). Furthermore, given that each Na⁺ and Ca²⁺ species associate with both Si and P (section 4.1), altering the n_Na/n_Ca ratio offers a route to tune the glass–surface reactivity, and thereby the BG degradation, without any significant bearings on the N̅_BO^Si-value. Note, however, that increasing the relative amount of Ca (i.e., decreasing n_Na/n_Ca) may be favorable as it elevates x_Pslightly,³¹ and thereby the net orthophosphate content [see eq 1].

5.4. Recommendations for Bioactivity Optimizations

The present results suggest that future bioactivity-composition assessments should target the parameter-triplet {N̅_BO^Si, n_P, n_Na/n_Ca} in the search for optimal BG compositions. Our suggested {N̅_BO, n_P, n_Na/n_Ca} parametrization of the glass composition provides more transparent insight into the composition-bioactivity relationships compared with the standard formulations expressed as oxide equivalents. The bioactivity is mainly dictated by the {N̅_BO^Si, n_P} pair, and to a lesser extent by the exact n_Na/n_Ca ratio. Hence, it is expected to be optimized at the highest incorporable P₂O₅ content around the parameter space {N̅_BO ≈ 2.55, 1 ≲ n_Na/n_Ca ≲ 2}.¹⁵ The feasibility of preparing P-richer compositions than x(P₂O₅) > 0.06 needs to be tested. Future work must also more quantitatively define our suggested weak interdependence between these bioactivity descriptors. Additionally, the “optimal parameter-spaces” stated herein are strictly only applicable to Na–Ca–Si–P–O glasses (and limiting systems thereof), and their transferability to related M–M′–Si–P–O glasses remains to be explored.

6. Conclusions

The alterations of the Q_Siⁿ and Q_P speciations in a series of 13 glasses were for the first time explored systematically over a wide compositional range within the Na₂O–CaO–SiO₂–P₂O₅ system, by using a combination of atomistic MD simulations and ³¹P/²⁹Si solid-state NMR experiments; both techniques generally revealed equivalent qualitative trends. Our glass series design allowed for an independent probing of the structural changes accompanying a variation in either the P content of the BG or its silicate network connectivity; the series encompassed both bioactive (2.1 ≤ N̅_BO^Si ≤ 2.5) and nonbioactive glass compositions (N̅_BO > 2.7). When N̅_BO^Si increases from 2.1 to 2.9, both the MD/NMR-derived {Q_Si} speciations reveal net Q_Si² → Q_Si conversions (as expected). However, despite that the network polymerization increases accordingly throughout the entire range of bioactive glass compositions (N̅_BO^Si ≲ 2.7), the progressive formation of Q_Si groups itself does not obviously correlate with the transition from bioactive to nonbioactive compositions, which merely coincides with the emergence of non-negligible (≳10%) contributions of Q_Si⁴ groups; the accompanying markedly enhanced structural cross-linking from four BO atom per SiO₄ tetrahedron (as opposed to 1–3 BO) together with a local depletion of readily released Na⁺/Ca²⁺ cations strongly diminishes the glass degradation in aqueous media.

If the silicate network connectivity of the BG remains constant, the {Q_P⁰, Q_P} fractional populations are independent of the amount of P₂O₅ (at least for x(P₂O₅) ≤ 0.06), thereby providing a direct link between the orthophosphate content and n_P. In contrast, if n_P remains constant, the fraction of Q_P⁰ species decreases linearly as N̅_BO increases. Fortunately, for the network connectivity-range 2.0 ≲ N̅_BO^Si ≲ 2.6 that encompasses nearly all bioactive glass compositions, Q_P moieties constitute ≳80% of the total phosphate speciation, thereby rationalizing earlier statements^15,22 that the bioactivity increases monotonically with the P content of the BG (provided that the glass modifier reservoir is sufficiently large to charge-balance all Q_P⁰ groups). By showing that the Q_P concentration increases with the P₂O₅ molar fraction for a fixed silicate network connectivity, the present results prove it possible to design highly bioactive glasses that combine a favorable network connectivity with large amounts of readily released orthophosphate ions, thereby promoting both a rapid degradation of the glass network and a fast dissolution of biologically active ions.^52,53 The structural role of P is the key factor: the majority of all P species enter the structure as orthophosphate groups detached from the glass network; their fast dissolution enhances the bioactivity relative to a glass with the same network connectivity but a lower P content.

Future composition/bioactivity assessments/optimizations should target the parameter-set {N̅_BO^Si, n_P, n_Na/n_Ca}. Each such triplet translates into a unique Na₂O–CaO–SiO₂–P₂O₅ glass composition, whose bioactivity may be roughly assessed by inspection, as each parameter influences the glass bioactivity in a predictable manner, while their effects may be tuned almost independently from each other. However, future studies must better quantify the expectedly weak correlation between the {x_P, x_P¹} populations and the n_Na/n_Ca ratio,³¹ as well as exploring the degree of correlation between the bioactivity of the glass and its solubility. As the latter may be changed by varying either the silicate network connectivity or the Na content of the BG, whose effects are likely synergetic, the N̅_BO-range providing high bioactivities is presumably not completely decoupled from the n_Na/n_Ca ratio: rather, we suggest that the increased solubility associated with Na-rich BGs may (slightly) alter the N̅_BO^Si-values defining each transition between high/low/nonbioactive compositions. These ideas are currently being explored.

Supporting Information Available

Further information about the NMR spectra and the deconvolution procedures, discussion about the detection of Q_P¹ groups by ³¹P NMR, as well as additional MD data and discussions thereof. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.