Automated identification of RNA 3D modules with discriminative power in RNA structural alignments

Abstract

Recent progress in predicting RNA structure is moving towards filling the ‘gap’ in 2D RNA structure prediction where, for example, predicted internal loops often form non-canonical base pairs. This is increasingly recognized with the steady increase of known RNA 3D modules. There is a general interest in matching structural modules known from one molecule to other molecules for which the 3D structure is not known yet. We have created a pipeline, metaRNAmodules, which completely automates extracting putative modules from the FR3D database and mapping of such modules to Rfam alignments to obtain comparative evidence. Subsequently, the modules, initially represented by a graph, are turned into models for the RMDetect program, which allows to test their discriminative power using real and randomized Rfam alignments. An initial extraction of 22 495 3D modules in all PDB files results in 977 internal loop and 17 hairpin modules with clear discriminatory power. Many of these modules describe only minor variants of each other. Indeed, mapping of the modules onto Rfam families results in 35 unique locations in 11 different families. The metaRNAmodules pipeline source for the internal loop modules is available at http://rth.dk/resources/mrm.

INTRODUCTION

About a decade ago, the International Human Genome Sequencing Consortium established that only ∼1.2% of the genome encodes for proteins (1). Later the ENCODE projects (2,3) revealed that almost the entire genome is transcribed as well as thousands of non-coding RNAs (ncRNAs). Thus, non-coding DNA, previous labeled as ‘junk’, often contains transcripts for functional RNA, which play a major role in various cellular processes from gene regulation to catalytic functions. The exact number of ncRNA encoded in the genome is still unknown as well as the functionality of many of them, but various kinds of ncRNAs have been identified so far including the well-known transfer RNA (4), ribosomal RNA (5) and long ncRNAs (6).

Many ncRNAs are structured, and their particular spatial structure enables them to accomplish a broad range of tasks. Secondary structural motifs, like hairpins, augmented by tertiary interactions fold into complex 3D architectures. Recurring building blocks within these structures are referred to as ‘modules’, which can be distinguished by the number and types of the involved base pairs. More than 20 different types of modules have been identified until now. For an overview, see (7). Although helices of the secondary structure are composed of cis-Watson–Crick type base pairs between A-U, U-A, G-C, C-G, G-U or U-G, tertiary interactions additionally include non-Watson–Crick base pairs in both cis and trans orientation. This has been revealed by crystal structures for the past 20 years (8,9). Previous studies (10,11) systematically analyzed those base pairs and introduced a nomenclature to circumvent the ambiguous and confusing notations that have been invented over the years. The 3D modules show up as recurring building blocks to gain similar functions in different molecules, and they are conserved throughout all kingdoms of life showing the universality of the concept. They serve as protein and ligand binding sites [for an overview see (12)], support catalysis reactions (13) or organize and stabilize the architectural composition (14–16).

The functionality of an RNA molecule depends more on its structure rather than sequence. As a consequence, structure is often highly conserved while sequences evolve quickly. Compensatory base pair changes (e.g. G-C changes to A-U in another sequence) and neutral mutations allow to maintain the structure and conserve the function while sequences evolve.

A fundamental understanding of folding and structure sheds light on how RNA molecules can fulfill substantial functions. Especially 3D modules can deliver valuable information about the spatial folding behaviour. The assignment of such 3D information to 2D structures can improve structure prediction, limits the number of false positives, assigns functions to unknown ones and helps to find new modules as well as classifying transcripts as ncRNAs. Moreover, the discovery of non-canonical base pairs supports the explanation of more-and-more upcoming structure probing experiments. The main experimental methods for 3D determination on atomic resolution level, Nuclear Magnetic Resonance and X-ray diffraction, have been applied successfully for >20 years, but they are difficult for structurally flexible or highly charged molecules, not to mention general difficulties in the crystallization procedure. For these reasons, methods for computer-aided structure elucidation are much sought after. In recent years, many approaches have been developed addressing structure prediction.

There are knowledge-based approaches predicting the global RNA structure, e.g. the MC-Fold/MC-Sym pipeline (17). This is a software package that models the 3D structure on a full-atomic level using a library of fragments (cyclic motifs). These are included into the secondary structure, which is derived in a first step by free energy minimization. Such tools are restricted to smaller molecules (50 nt) and single sequences. To circumvent this drawback, Jonikas et al. (18) developed the nucleic acid simulation tool, which is based on a coarse-grained model. That means, each nucleotide is represented by its C3′ atom. They apply an energy function that incorporates statistics, like distances and angles of atoms, derived from known ribosomal structures, to sample the conformational space. It requires secondary structure and tertiary contact information. Other tools are graphic based and require user-guided manipulation of the architecture. MANIP (19) allows the user to assemble secondary structural motifs into a 3D conformation. The architectures are automatically constrained by biological and stereochemical rules of RNA structures. A final refinement step verifies all atom contacts and refines the base pairs including non-canonical base pairs. Such tools are only applicable for a limited number of models. Another promising approach is to use evolutionary information to predict the molecular structure. For example, ModeRNA from Rother et al. (20) is a comparative 3D prediction tool. It requires the 3D structure of a homologous molecule and a pairwise alignment consisting of the template and the target sequence. The 3D coordinates of the known structure serve as template for invariant residues of the target model. By means of the alignment they introduce substitutions for varying residues, they process insertions and deletions and they add structural fragments in short regions without structural information. For an overview of several prediction tools, see (21).

As the mentioned tools have their drawbacks, for example, limitation to small molecules or necessity of expert knowledge some tools focus on the prediction of recurring RNA building blocks that constitute the 3D structure. For example, Djelloul et al. (22) identify and classify so-far unknown RNA modules. They represent modules as topological graphs with vertices for each nucleotide and edges for base interactions. In a three-step approach, they extract bulges, internal, junction and terminal loops and the corresponding non-canonical interactions of an input structure. Then they compute a pairwise similarity measure for all modules based on the largest common non-canonical subgraph. Subsequently, they cluster the structural elements according to their similarity. Djelloul et al. tested their approach on the ribosomal RNA of three organisms and found 10 known and four putative new modules. The advantage of this method is that the size of the input structure is not restricted. It is also possible to give a set of input structures, which increases the possibility of significant clusters. A disadvantage is that the method ignores sequence information, which means exclusion of isostericity information. It also ignores variations of base pair interactions because of the isomorphism restrictions of the algorithm.

RNAMotifScan, an approach developed by Zhong et al. (23), circumvents these drawbacks. It takes base pair isostericity, crossing base pairs, and multi-pairing into account. Zhong et al. use annotation programs to identify base-pairing patterns within 3D structures. With a dynamic programming procedure, they compute the similarity between a query module and structural segments to find similar occurrences. In a newer version (24), they introduce a statistical framework to measure the significance of the similarity. Furthermore, they cluster the identified instances based on a P-value. They apply their elaborated tool on data sets for hairpins as well as internal loops resulting in the identification of known modules and new occurrences.

Cruz and Westhof developed RMDetect (25), a sequence-based approach. They use graph-based statistical models for kink-turns, G-bulges, C-loops and tandem GA loops to scan single sequences as well as alignments for further occurrences of these known modules. Each model has been generated by merging several instances of a known module into an interaction network. The statistics are obtained from a compilation of many instance sequences from different alignments.

The identification of such RNA 3D modules suggests to include the gained knowledge into the computationally less costly secondary structure prediction. For example, (26) enhances the 3D structure prediction of large RNAs by inserting 3D modules into the secondary structure. Their program, called RNA-MoIP, uses an integer programming framework to remove canonical base pairs from secondary structures to make room for 3D modules (e.g. k-way junctions), which serve as a template for creating a 3D structure. These approaches are promising and important on the way to RNA global structure prediction.

We show that models for known and also for new modules can be generated without extensive expert knowledge. Our approach combines the automated generation of stochastic models with exploitation of evolutionary data. Our pipeline, called metaRNAmodules, maps short modules on alignments and subsequently creates a model using RMBuild from the RMDetect package. We test our models on RNA alignments as well as randomized alignments to show that those models have statistical discriminative power, i.e. the score distributions are well-separated. These models can be used to search RNA sequences or alignments for further occurrences of the modules.

MATERIALS AND METHODS

metaRNAmodules

metaRNAmodules is a pipeline that builds models of known as well as unknown modules in an automated way. It maps a putative module, extracted from FR3D, on a particular Rfam 10.1 sequence, which belongs almost always to the full alignment. The sequence is aligned to the corresponding seed alignment. A Bayesian Network (BN) model of the module features is generated where we interpret all bases of the module as nodes and all base pairs as connections between nodes, i.e. the respective pairing partner. The model is trained and evaluated using a 5-fold cross-validation. Furthermore, we test the model on a randomized alignment to get a background distribution (see ‘Materials and Methods’ section for the individual steps). We compare the score distributions of the validation data and the randomized data set to see whether we can separate them to distinguish between true and false positives. For a visualization of the pipeline see Figure 1.

Figure 1.

The Figure shows on overview of the metaRNAmodules pipeline. metaRNAmodules extracts putative modules from FR3D, a database derived from PDB (A). During the mapping step on modified Rfam alignments (B), a large fragment of the modules is filtered out. The training of the new models (C) filters out further modules. The remaining modules are filtered and ranked according to 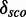(D).

Data extraction and preprocessing

Ultimately, we want to discover, both, known modules as well as currently not classified but statistically likely new (candidate) modules in sequences. This is done via the ability of a BN model built from a candidate module to successfully discriminate between random RNA sequences and those containing the module. To this end, we make use of a number of databases and tools that we describe in more detail later in the text.

The FR3D database (27) is derived from the PDB database (28) of crystal and Nuclear Magnetic Resonance structures of (bio-)molecules. It analyses the structure files to classify base pair and base stacking interactions according to the Leontis–Westhof annotation. The results are used to find geometrically similar instances of these modules.

From this database structurally complex (as defined later in the text), putative modules are extracted. Structures are clustered by similarity, without reference to their actual 3D coordinates. Although 3D coordinates would improve the initial structural clustering, we are ultimately interested in a 2D graph-like representation. For this FR3D is ideal, as every base pair is annotated according to the Leontis–Westhof notation (10), including possible base pairs that fall outside that classification. Special cases like interactions that fall between two groups, or are otherwise not completely determined are currently ignored. See Figure 1A for the extraction part of the pipeline.

For the automated module detection, our definition of structurally non-trivial RNA modules follows the established notion in (25). These modules are in some sense local as they generally are of 20 or fewer nucleotides in size. They are structurally non-trivial as they are composed of ‘sets of ordered non-Watson-Crick base pairs embedded between Watson-Crick pairs’ (25). Here, a Watson–Crick base pair is a 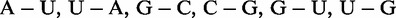pair in cis-Watson–Crick conformation.

Given the two Watson–Crick pairs and , (w.l.o.g. 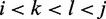), represented by their indices, a module is admissible if its total size is constrained similar to how modern RNA folding programs (29) handle interior loops. The total size of the left loop k – i, as well as the right loop j – l is restricted to no more than 30 nt for a maximal module size of 60 nt. In addition, for each pair 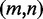with 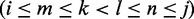, the pair 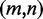either is of a non-Watson–Crick type or part of a local base pair crossing (a small pseudoknot structure entirely contained within the outer Watson–Crick pairs).

This definition disallows any RNA module candidate that can be subdivided by a non-crossing Watson–Crick base pair. Succinctly, all base pairs between the two outermost ones are either non-canonical, part of a base pair triplet (forming a zig-zag pattern) or crossing. Two distinct RNA modules may share an outermost canonical base pair in an RNA structure but remain separate entities.

General pseudoknotted structures, like kissing hairpins, triple helices or more complicated structures, are excluded. These are not local structures according to our definition. In addition, we exclude multi-branched structures. There are fewer instances of multi-branched loops in the available data (PDB, resp. FR3D databases). In addition, they are computationally more demanding in that they have three or more exiting helices. Finally, structural multiple alignments in multi-branched regions have to be investigated for accuracy before automated detection of RNA module candidates should be performed.

As hairpin structures may themselves be structurally interesting modules, we admit such structures, not containing the inner 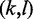base pair, but otherwise defined analogously, too.

Two candidates are structurally equal if their base pair pattern is identical and base pairs mapped onto each other are isosteric to each other. This allows us to group many candidates with different sequence patterns that will likely form the same tertiary structure based on isostericity (10). The two most well-known base pair isostericity classes are formed by canonical cis-Watson–Crick base pairs. The four pairs A-U, U-A, G-C, C-G are isosteric (in class I₁), i.e. can be replaced with each other without disturbing the tertiary structure. The complete classification of base pairs according to their constituent nucleotides and the participating nucleotide edges forming the actual bond can be found in (10). From this classification, we derive the previously mentioned equality condition for grouping of candidate modules.

Modeling of such modules and their prediction is necessarily restricted to those structural features that can be described in terms of Watson–Crick and non-Watson–Crick base pairs and their spatial relationship when transformed to small graphs. This does exclude other structures that have been of recent interest, like G-quadruplexes (30,31). Such structural features of RNA require the introduction of a novel ‘feature’ in the language of RNA structures (32,33), while RNA 3D modules can, at least in principle, be completely described with a secondary structure graph (sometimes extended to allow crossing base pairs).

In the following, we write a putative module sequence as ACAAU AU and the corresponding dot bracket notation of the base pairs as (..((&)> where is a separator of the two module regions. Hairpin modules lack the separator. ‘’ denote single base pairs of canonical or non-canonical pairing type, whereas ‘’ denote bases which pair to two nucleotides of type ‘’ or ‘’, whereas ‘.’ marks unpaired bases [see (34)].

Rfam mapping and extraction

Now that we have extracted putative modules, we prepare the alignments for the mapping and training step before we generate new models (see Figure 1B).

We map the putative modules onto alignments to exploit base variance information for each column during the training procedure. As the results always depend on the reliability of the alignments, we use Rfam 10.1 seed alignments (35). Even though these alignments are hand-curated and contain representative members of the ncRNA family, they exhibit redundant sequences that influence the computation of the conditional probabilities of the BN. The count of the bases of a column is biased towards the redundant sequences. To avoid this issue, we clean the seed alignments of Rfam and remove sequences with >95% pairwise sequence identity. Alignments modified in such a way are referred to as Rfam_clean. Additionally, we demand that each Rfam_clean alignment contains >30 sequences to get a reasonable amount of data to start with.

The mapping procedure comprises two steps. First, we map a putative module on an Rfam sequence using Rfam structure tables provided by Rfam. Those tables contain, for sequences with a corresponding PDB database entry, a mapping between the Rfam, EMBL and PDB coordinate systems. We filter the tables for Rfam sequences by means of the PDB identifier (PDBid) that are assigned to each putative module. We require that the Rfam sequence and the putative module are located on the same strand, the positions in the EMBL coordinate system overlap and both refer to the same molecule in cases where a PDB entry consists of several chains. To determine the accurate position of the module in the Rfam sequence, we globally align the FR3D sequence to the ungapped Rfam sequence using Clustal W (36). With that we want to make sure that the module sequence is identical to the corresponding Rfam region. In some cases, the sequence versions vary, i.e. one or more nucleotides differ because of insertions or deletions. We only want to use modules where we are sure that we identify the module in the reference sequence correctly. In >90% of the cases, the Rfam sequence that is linked to the 3D structure via the Rfam structure tables belongs to the full alignment and is not part of the seed. As we have more trust in the seed alignment, we align in a second step that particular sequence to Rfam_clean using cmalign v1.0.2 (37).

During this aligning process, cmalign inserts gaps in the alignment. This is not desirable in cases where gaps are inserted within the module region because it artificially increases the module length. It denotes additional nodes for gaps in the interaction network. That is why we remove alignment columns that are located in the module region, but not belonging to the module. Those columns deliver no additional information and thus will not decrease the information content of the BN. We also dismiss sequences containing the characters ‘S,M,Y,W,N,V,K,R,I’. They cannot be handled by RMDetect (see ‘Model construction and testing’ section). Furthermore, we delete sequences that have a ‘.’ or ‘-’ at positions that are assigned as paired in the module. Such modified alignments we refer to as Rfam_cm.

Model construction and testing

After pre-processing the data, we are prepared to build the new models (see Figure 1C). For this step, we use RMDetect (25), a tool that searches sequences for RNA 3D modules based on sequence information only. Version 0.0.3 includes four hand-curated models for Kink-turns, G-bulges, C-loops and tandem GA loops as well as a model developed in an automated way for the AA-rich module. The developers interpret a 3D module as a BN (38). A BN is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph. Each base of a module corresponds to a node and each base pair or statistical correlation corresponds to an edge. Using such a system, Cruz et al. are able to model all base dependencies of a module including base-, edge- and stacking-interactions. RMDetect searches single RNA sequences as well as RNA alignments for independent occurrences of modules. A potential candidate is evaluated by means of a score based on the probability of the sequence, given the individual model and the probability of a sequence, given a null model where the four bases and the gap are uniformly distributed.

The RMDetect package further contains a tool, called RMBuild, which is able to build BN models for modules. Given a PDB file, the coordinates of a particular module and an alignment, RMBuild analyses the PDB sequence and generates a BN model for the region of interest. RMBuild uses MC-Annotate (17), which identifies amongst other things all base pairs/triples and interacting structural elements. These features are modeled in the BN. As we already have the concrete FR3D module features that we want to model, we do not apply MC-Annotate. Instead, we automatically generate an interaction network file with all FR3D features, i.e. all nodes and edges, and feed it together with Rfam_cm into RMBuild, which computes the conditional probabilities for each node.

The annotated base pairs extracted from the FR3D database yield the edges—which then model pairing information—in the BN. At this stage, we model each putative module independently and do not distinguish between putative modules that exhibit the same structure or map to the same position on Rfam_cm. Our goal is to automate the mapping and model generation so we can give each putative module instance individually as input resulting in a BN model. A new model based on Rfam_cm and FR3D we call .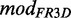

For our purpose, we run RMDetect with a minimum score of 0.0 and a minimum base pair probability of 0.0001 to fetch all possible candidates. We compare the RMDetect score distributions of a validation data set and a randomized data set to find modules with discriminative power by means of the score distribution discrimination measurement (see ‘Score distribution discrimination measurement’ section). We use the score distribution of the validation data to establish score cutoffs for each module individually. To generate the hairpin modules, we modified RMDetect in a way that it is able to handle only one region.

To estimate the performance of the models, we use a 5-fold cross-validation. The 5-fold cross-validation is splitting Rfam_cm into five subsets, selecting each in turn as the validation set, called 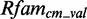, whereas the remaining four form the training set, called .

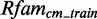To estimate the statistical significance of our models, we need a good and reliable null model. For that reason, we shuffle Rfam_cm 100 times with Multiperm v0.9.3 (39). Multiperm is an algorithm that preserves the gap and local conservation structure and also the approximate dinucleotide frequencies. A shuffled alignment we call 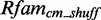. Applying RMDetect with a particular model on 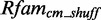yields a background score distribution, which we compare with the score distribution of the model applied on .

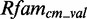Evaluation

To decide whether the new models have discriminative power, we define a score distribution discrimination measurement 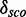as follows: We compute the restricted mean 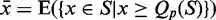of all RMDetect scores S, which are greater or equal than the P-quantile value Q_p, where P is a real number between 0 and 1 (usually taken in the range between 0.8 and 0.95), for the validation data score distribution as well as the mean 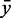of all scores, which are greater or equal than the P-quantile value Q_p for the null model distribution. The difference of the means 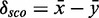gives a strong hint on how well the two distributions are separated. A positive score indicates that the model scores candidates belonging to 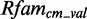alignments higher than candidates drawn from random background sequences. A score close to zero points towards RNA modules for which our way of generating a model does not result in a strongly discriminating model (see Figure 1D).

RESULTS

Mapping modules onto Rfam_clean

The analysis of the FR3D database results in 15 290 putative interior loop modules with 569 unique PDB identifiers and 1696 different secondary structures. After the mapping, including all filtering steps described in the ‘Materials and Method’ section, 3022 putative modules with 384 unique secondary structures and 237 unique PDB identifiers are left. They map on 18 Rfam families, mainly on ribosomal RNA and riboswitches (91.3 and 1.99%, respectively), and can be clustered into 84 modules (see Supplementary Table S2 for an overview). In all, 119 putative modules have no sequences left in 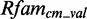and only three sequences in 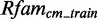(see Supplementary Figures S1 and S2). Owing to the lack of data, we exclude those from further evaluation. The remaining putative modules contain 5–637 sequences in 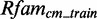and 1–160 sequences in 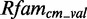. The modules have a length, i.e. the sum of nucleotides, from 5 to 46 nt (see Supplementary Figures S3 and S4).

In addition to the interior loop modules, we extract 7205 putative hairpin modules with 681 unique PDBids and 425 secondary structures. As an example, we build models for hairpin candidates with 3 bp. In all, 73 of 120 new models deliver a sufficient amount of data after scanning 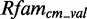and 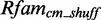. However, 12 models find no candidates in 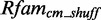These 12 have the highest score distribution discrimination measurement 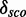for different Q_p values (see Supplementary Figure S17 and Supplementary Table S3). In total, 17 models have a 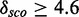(see next subsection). Clustering the modules according to position and family, they map on results in seven cluster representatives. Supplementary Figure S20 shows the absolute score counts and the kernel density estimate for the cluster representatives. Table 2 shows an overview of the families and the cluster representatives. The number of bases of the modules varies from 8 to 18 nt and the complexity ranges from 0.17 to 0.4 as Supplementary Figures S18 an S19 show. As complexity, we define the number of all base pairs divided by the number of nucleotides of a module. A base pair triplet is counted as 2 bp. For example, the module ACAAU AU with the structure (..((&)> has a complexity of 0.43.

Table 2.

Rfam families and cluster representatives

Family	No. of modules	PDB res.	Rep.	Alignment+ pos.	Fit
5S rRNA	3	9:23-30/54-60	2GYC	36-68/112-136	***
		9:32-37/43-48	3CCQ	73-87/99-105	**
		A:71-79/97-105	2QBE	154-168/193-211	**
U4 snRNA	1	F:28-34/42-45	2OZB	30-36/46-49	****
SR77777P RNA	2	A:181-187/212-216	2J37	254-261/286-290	**
		B:190-194/205-209	1L9A	264-268/279-283	****
TPP riboswitch	1	X:59-63/76-80	2GDI	272-277/290-295	**
SAM riboswitch	1	A:17-21/31-38	2GIS	18-22/35-42	***
Purine riboswitch	1	X:22-25/45-52	1Y26	28-31/52-60	****
Bact. SRP RNA	1	A:14-18/29-33	1CQ5	49-53/65-69	****
Bact. SSU rRNA	16	A:1124-1132/1142-1149	1XNQ	1241-1249/1270-1278	**
		A:147-153/168-175	1N36	160-166/181-188	**
		A:1246-1253/1284-1291	2UXD	1377-1384/1415-1423	***
		A:1303-1307/1330-1334	1HNW	1435-1439/1462-1466	***
		A:1384-1387/1475-1479	2HHH	1534-1537/1646-1650	**
		A:1429-1436/1465-1471	2VHO	1562-1569/1614-1620	**
		A:242-247/277-284	2QPO	298-303/334-343	***
		A:409-417/426-433	1VOV	468-476/487-494	***
		A:446-455/477-488	1N36	507-516/535-564	****
		A:502-512/539-543	2B64	579-589/616-620	*
		A:515-522/527-536	2QBF	592-599/604-613	***
		A:682-688/699-708	2GY9	761-767/778-788	***
		A:63-69/99-103	2HGR	63-70/106-113	*
		A:779-783/799-803	2B9M	861-865/881-885	***
		A:826-829/857-874	1HRO	908-911/942-959	***
		A:887-894/905-910	2QB9	972-979/990-995	***
PK-G12 23S rRNA	1	B:2295-2299/2317-2337	3BBX	14-18/36-68	*
Arch. SRP RNA	1	B:193-199/208-214	1QZW	254-260/269-275	**
5S rRNA	1	9:33-49	2GYC	73-105	***
tRNA	1	C:912-926	1WZ2	15-31	***
Purine riboswitch	1	X:31-39	1Y26	37-46	****
Bact. SSU rRNA	70	A:507-524	1IBM	584-601	****
		A:320-333	2J02	379-392	****
		A:341-348	1N36	400-407	****
		A:689-698	1VS7	770-779	****

The Table presents Rfam families and the number of 3D modules for each family after merging the modules depending on family and position. Ten families on top represent internal loop modules, four families below represent hairpin modules. For each merged cluster, a representative, namely, the model with maximal 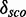, is shown. Columns three and four denote the chain and residue numbers of the PDB sequence as well as the PDBid where the representative is extracted. ‘Alignment pos.’ indicates the position of the module in Rfam_clean with the aligned full sequence. The last column shows how good the representative fits into the consensus secondary structure of Rfam.

****means the module is located in a single stranded region, i.e. it fits very well in the consensus secondary structure.

***indicates a fairly well fit overlapping no more than two paired bases of the consensus structure.

**denotes representatives which fit less well because the paired bases of the modules overlap between three and five base pairs of stem regions of the consensus structure.

*imply that more than half of the paired bases match an already paired base of the consensus structure.

As the number of hairpin modules is so much smaller than the number of interior loop modules, we will restrict our discussion to interior loops in the following.

Automated model generation

We start to generate models in an automated way for 2903 putative modules. In all, 223 models are problematic: they cause problems while running on 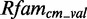and 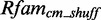because the putative modules are rather short and contain not enough information content so that they deliver thousands of arbitrary candidates. Thirteen models deliver no data at all, e.g. six putative modules mapping on Rfam family RF00050. These modules are rather long with >40 nt. We exclude them from further analysis. 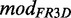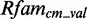Of the remaining 2667 new models, 685 deliver an insufficient amount of candidates (<1) applying on and 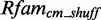. As we cannot generate score distributions for them, we exclude these models. The remaining 1982 new models produce sufficient data that we can analyze.

Score distribution discrimination measurement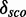

The score distribution discrimination measurement 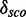is used to filter for models with discriminative power against random sequences. See Figure 2 as an example showing the absolute count and the density plots including 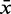and 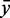for a kink-turn model. We choose different values for P from 0.8 to 0.95 to see how the models perform at varying significance levels (see Table 1 and Supplementary Figure S10). After a visual inspection of the distribution plots, it shows that a cutoff of 4.6 for 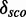is appropriate to discriminate between overlapping and separated distributions for all quantile values. For that reason, the following numbers refer to P = 0.8. In all, 977 models have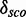 4.6. They have 172 different structures, map on 10 Rfam families and have 200 unique PDBids. In all, 1005 models (50.71%) have less well-distinguishable score distributions (<4.6). There is no tendency towards an increasing 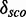with increasing the number of nucleotides of a module. We check whether there is a correlation between 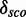and the complexity of a module. See Supplementary Figure S11 for a distribution of the complexity values and Supplementary Figure S12 for a distribution of the number of base pairs of the putative modules. Supplementary Figures S5 and S6 show that there is a correlation (∼0.75) between 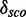and the number of nucleotides and a weak negative correlation (approximately –0.48) between the complexity and 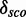. Many of these 977 modules map on the same families and have overlapping positions (see Supplementary Table S1), even if they have varying structures. We cluster the modules generated by our pipeline depending on family and positions in the gapped alignment and get 28 3D modules on 10 Rfam families. Table 2 shows an overview of the families, the number of modules and for each cluster a representative that is the candidate with maximal 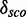. The table also shows cluster representatives for the hairpin modules (bottom entries). Supplementary Figure S9 shows a histogram of the absolute score counts and the density estimate for each representative. More than half of the 28 modules (57.1%) map on the bacterial SSU (RF00177) and 10.7% map on the 5S rRNA (RF00001). Of the 28 representatives, 16 (57.1%) fit very well in the consensus secondary structure of Rfam. They are located within single-stranded regions, and their cis-Watson–Crick type base pairs overlap with an opening or closing base pair of stem regions in the consensus secondary structure (see Figure 3). Seven fit fairly well in the consensus structure overlapping no more than two paired bases of the consensus structure. Three fit less well because the paired bases of the modules overlap between three and five base pairs of the stem regions of the consensus structure. Two representatives do not blend in. More than half of their paired bases match an already paired base of the consensus structure. Such observations help to improve the secondary structure prediction.

Figure 2.

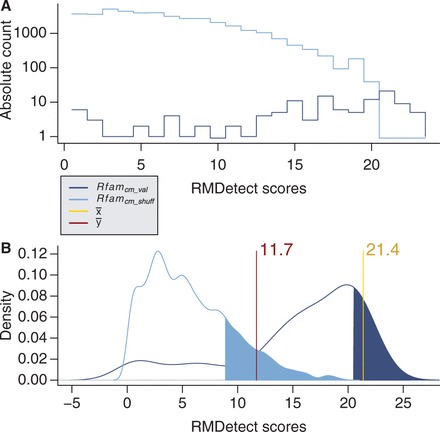
The Figure shows the absolute score distributions (‘A’) and density plots (‘B’) for the FR3D model of the U4 spliceosomal RNA kink-turn with structure (…(((&)))) on 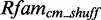and 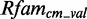. The coloured right tails show 1- 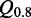, i.e. all values the 80% quantile values (8.7 and 20.5, respectively), of each distribution. 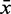and 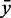show the mean of each coloured region and 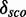= 9.7.

Table 1.

Minimal and maximal 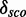for different quantile values

P	Min.	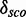max.		%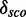
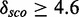	Internal loop modules
0.80	–7.23	33.66	977	49.3
0.85	–9.57	33.76	958	48.3
0.90	–11.99	35.32	832	42.0
0.95	–11.99	35.45	572	28.9

Minimal and maximal 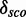for different quantile values P as well as the number of models with 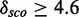and the percentage of 1982 models.

Figure 3.

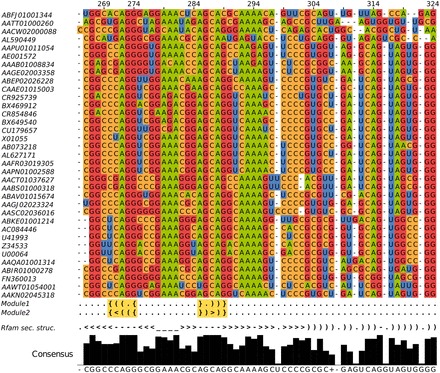
Rfam alignment with mapped modules. Two modules (Module 1 and Module 2) with different structures map on Rfam SRP family (RF00017_cm) at position 270–274/285–289. Highlighted regions below the alignment show the module base pairs.’’ are single base pairs of canonical or non-canonical pairing type, whereas ‘’ denote bases pairing twice, i.e. to two nucleotides of type ‘’ or ‘’ [see (34)]. Rfam sec. struc. is the consensus secondary structure of Rfam. ‘’ are used for ‘internal’ helices enclosing a multi-furcation of all terminal stems, ‘’ show simple terminal stems, ‘’ and ‘’ denote unpaired bases of a hairpin loop and a bulge loop, respectively, and ‘.’ are insertions relative to a known structure. The histogram below shows the level of conservation of the alignment bases. The modules fit very well in the consensus secondary structure. Covariation information for model training can be obtained for four columns (270, 271, 285 and 290). The other columns are highly conserved. The consensus barplot below means the higher a bar the more conserved.

General observations

We would expect that two modules derived from fairly similar organisms with different PDBids, but the same secondary structure, would map on the same Rfam family at the same position. What we observe is that they usually do map onto the same positions in the alignment. Furthermore, we expect those modules to perform roughly equal in terms of 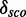and numbers of candidates. We see that there are only slight differences in the performances. For example, the molecules 1HR0, 1I96 and 1XMO contain a putative module (residue numbers 805–808/830–847, 808–811/833–850 and 805–808/830–847, respectively) with the same structure (<((&)))…………).), which map on Rfam family RF00177 at position 908–911/942–959. These positions (as well as the following) refer to the gapped seed alignment with additionally aligned reference sequence where gaps only columns in the original alignment part are ignored. Their 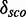varies from 29.8 to 18.4. It shows that the number of candidate scores used for the computation of 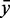differ owing to different sequences in the sets. Furthermore, the scores vary due to slightly different conditional probabilities computed from 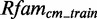. For example, the 1HRO model finds a candidate with a score of 30.48, whereas the same candidate has a score of 29.61 given the 1XMO model.

Another observation is that some new models define the same module. For example, there are two BNs, which model the U4 kink-turn mapping on the U4 spliceosomal RNA (RF00015) at position 30–36/46–49. Both putative modules are extracted from PDBid 2OZB at the same position, but from different chains. Their secondary structures look as follows (…(((&)))) and ((..(((&))>). Both of them are able to predict the real U4 kink-turn, but 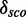of the module without the base pair triplet is slightly higher with 9.98 compared with 9.37. This shows that an additional base pair, even if not a triplet, leads to better results. We use strict filter mechanisms, e.g. both module regions have to be located on the same chain. This excludes many potential modules. Molecule 1SA9 is a good example: we extract a putative module where one region is located at chain C and the other one at chain D, position 3 and 6, respectively. The PDB entry is described as ‘Structures of two RNA octamers containing tandem G.A base pairs’ (40). With our filter mechanisms, we exclude such inter-molecular modules.

Prediction accuracy assessment

metaRNAmodules aims to generate models automatically for known as well as new modules. The FR3D database from where we extract the putative modules contains no name annotations; that is why we could not easily distinguish between new and known modules. Furthermore, there is no comprehensive database that lists all PDB structures and their recurring building blocks and positions. There is also no corresponding FR3D, PDB and Rfam coordinate system so that no easy comparison is possible. Currently, a lot of manual work is necessary to compare our automatically generated modules with those reported in the literature, especially comparing the positions. Here, we show some results for known modules that have been mentioned in the literature before. Position annotations are for the gapped seed alignment. metaRNAmodules is able to model and predict the SAM I Riboswitch kink-turn with PDBid 2GIS (41). The module maps on Rfam family RF00162 at position 18–22/35–42. Our pipeline also models and predicts the U4 small nuclear RNA kink-turn with PDBid 2OZB (42), which maps on the U4 spliceosomal RNA family (RF00015) at position 30–36/46–49. The Lysine G-bulge (also called Loop E motif) with PDBid 3DIG (43) is mentioned in the literature at position 26–28/65–66,28 in the PDB sequence. metaRNAmodules generates a model for this position, based on the Lysine riboswitch alignment RF00168 at position 28–39/85–92. This model includes not only the 3 G-bulge base pairs but also additionally three non-/canonical base pairs around the G-bulge. Our pipeline is able to predict the correct position.

Some of the prominent known modules could not be modeled and/or predicted by metaRNAmodules. For example, the pipeline is able to model all base pairs of C-loop C15 with PDBid 1J5E (44). It maps on the 16S rRNA (RF00177) at position 430–434/448–449. However, the module could not be found in 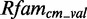. The score distributions have no discriminative power.

The 16S rRNA of Thermus thermophilus contains in an internal loop of helix 17 a sarcin-ricin motif at position 446–450/484–488 based on the annotation in (45) (PDBid 1J5E). Another module is located directly in its neighbourhood, only separated by a Watson–Crick/Watson–Crick base pair, at position 451–455/477–482. metaRNAmodules models the sarcin-ricin module correct, except for the G485-U486 trans-Sugar/Hoogsteen base pair, and is able to find the module in 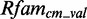, but with a low 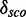of 4.3. The other module is also modeled correct, except for the C454-A478 trans-Hoogsteen/Watson–Crick base pair and metaRNAmodules is able to find the module in 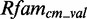. The discriminative power is also low ( 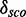= 4.1). We model these putative modules separately according to our definition described in the ‘Materials and Method’ section that does not allow Watson–Crick/Watson–Crick base pairs within the module region. To see whether we can improve the prediction, we merge the two putative modules into one including the Watson–Crick/Watson–Crick base pair, now spanning position 446–455/477–488. We find the module in ∼64% of the validation sequences and 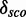= 14.4.

Comparison with original RMDetect models

As we use the RMDetect software package for our pipeline, we want to compare our results with the Cruz models and results. In general, a direct comparison of the models is difficult for several reasons. One difficulty is that our modules have no labels, which identifies them as, say, a kink-turn or a C-loop. Each putative module has to be identified as a well-known module by means of the PDBid and position. Furthermore, the models are generated and trained by varying data. The Cruz et al. C-loop model is a consensus model of seven C-loop instances and is trained on a single alignment of 16S rRNA and 23S rRNA sequences. The G-bulged model is a consensus of 11 G-bulged modules and is compiled on a consensus alignment of 16S rRNA, 23S rRNA and lysine riboswitch sequences. The kink-turn is a consensus model of 14 kink-turn instances and is compiled on 16S rRNA, 23S rRNA, SAM riboswitch and U4 sequences. Their BN topology follows established networks given in the literature. Cruz et al. added some additional edges based on expert knowledge. The tandem GA/AG loop model is based on one instance. The network parameters are computed in a particular way [for details, see (25)].

We model each putative module separately only based on nodes and edges given by the FR3D analysis. We do not include any further knowledge. We furthermore train the models only on a single alignment. This results in deviating model parameters and influences the candidate search. Also the validation sets vary. Disregarding these differences, we report in the following on some examples that have been used for the Cruz work in comparison with our work: Cruz et al. modeled and trained the AA-rich module on the PDB sequence 3OWI, the crystal structure of a glycine riboswitch. metaRNAmodules can neither extract a putative module from this molecule nor create a model because our version of the FR3D database does not contain an entry for 3OWI. PDB contains several entries for glycine riboswitches, e.g. 3OX* or 3OW* where ‘*’ is an arbitrary letter, but searching FR3D for these molecules delivers no results.

The tandem GA/AG loop has been found for example in the crystal structure of the RNA octamer ‘GGCGAGCC’ (PDBid 1SA9). metaRNAmodules extracts the relevant module, but during the mapping process, it is filtered out because it is located on two chains. Another tandem GA/AG instance is located in the 16S rRNA (PDBid 1J5E) at sequence position 1394–1397/1454–1457. It is used to train the Cruz model. We also modeled this module, and we find it in the validation data. An instance of the G-bulged module can be found in the lysine riboswitch at PDB sequence position 25–29/64–67 (3DIL). Our pipeline is able to model the correct module, except the base pair G27-U28 and maps it on RF00168 (lysine riboswitch family). The search in the validation data (10 sequences) results in a single candidate. The PDB database contains several entries for a lysine riboswitch, e.g. 3DIZ, 3DIG, 3DIM. We create models for all of them, but they perform equally bad when searching the validation data. A C-loop instance can be found in molecule 1J5E at sequence position 362–367/387–390. metaRNAmodules extracts a putative module and maps it on the bacterial small subunit ribosomal RNA (RF00177). However, our module misses two base pairs compared with the Cruz model.

A prominent kink-turn instance can be found in the SAM riboswitch (PDBid 2GIS) at position 17–21/31–38. The pipeline maps the putative module on the correct family (RF00162), but our model contains one additional base pair at A20-G32. Despite these different models, we also find the correct candidates. Supplementary Figures S7 and S8 show two examples of the RMDetect score distributions using our kink-turn model in comparison with the Cruz et al. kink-turn model. Supplementary Figures S13–16 show scatterplots of RMDetect scores from the Cruz kink-turn model against our kink-turn models. Depending on the scanned alignment, there is a tendency that the Cruz model finds more candidates and also scores them higher than our models.

Runtime to train and test models

We generated 3022 new models and each of them is subjected to a 5-fold cross-validation. It takes 26 Central Processing Unit (CPU) years for model generation and testing on validation- and randomized data. This has been accomplished in ∼30 days on a linux cluster consisting of Intel(R) Xeon(R) X5570 CPUs @2.93GHz.

DISCUSSION

RNA structural modules form a recurrent and important building block in all kingdoms of life. Their importance has therefore been recognized, and the modules have been investigated in various forms from global 3D structure prediction to their function in RNA. As they are recurrent, it seems to be appropriate to simplify the search for such modules in varying sequences. Given that substantial labour and experience are needed to manually design these models, we here addressed the problem of automating the process of extracting known as well as unknown modules.

We successfully constructed a pipeline for this, metaRNAmodules, and we showed that putative modules can be mapped onto alignments exploiting evolutionary nucleotide exchanges during module construction. New models with discriminative power (over background) are generated in an automated way so that a large number of putative modules readily can be modeled without requiring expert knowledge.

In general, the statistical power of the BNs we have constructud here, seems to be limited by base pairing (or single nucleotide) information. We shall need to investigate in the future if a more principled construction of statistical models may incorporate sequence signals beyond this. Based on the structural information encoded by Cruz and Westhof (25) in their models, such an extension seems promising.

In addition, as the initial base pairing information extracted from 3D structural (PDB) data is itself based on computational methods, we will need to explore different methods for this task. Currently, our pipeline is based on FR3D, whereas the original RMDetect work is based on MC-Annotate.

The comparison with the Cruz and Westhof models (25) indicates that putative modules of a certain complexity and length can be modeled in an automated process, and enables them to perform as well as models generated by time-consuming manual model building.

We did not expect to generate ‘these exact’ models automatically, as they imply a certain amount of expert knowledge beyond formal elucidation. This for example includes the exact boundaries of a module and sterically, but not statistically, important information.

In this work, we restricted automatically discovered RNA modules to those forming part of a stem. Canonical multi-branched loops form a future avenue of investigation but are, by their very definition, more complicated. These complications range from the fewer number of instances of multi-branched loops in PDB structures to questions about the quality of multiple alignments in these loop regions. However, in the future, we plan to examine multi-branched structures, as better predictions of modules in these regions are likely to result in more accurate predictions of the 3D conformation of the RNA structure. Another open question is how to include RNA 3D modules in structure prediction algorithms. Currently, inclusion of RNA modules happens in most cases when initial structural predictions on the level of secondary structures have been completed or when only a limited number of modules is included. Including RNA 3D modules in secondary structure prediction algorithms cause additional problems to be overcome. Although the algorithms themselves are easily adapted, the relevant parameters, e.g. thermodynamic energy values or probabilities, are hard to determine.

CONCLUSION

We presented metaRNAmodules, a new pipeline for automated putative module extraction and model generation. It filters the FR3D database for putative (known and unknown) modules that are subsequently mapped on Rfam alignments. These are used to train the BN models exploiting evolutionary base exchange information. metaRNAmodules is capable to find well-known modules and performs equally well in comparison with manually created models. The procedure leaves room for improvements, for example, by further investigation of known modules and using improved alignments.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online, including [41,43,46].

FUNDING

The Danish Center for Scientific Computing (DCSC, DeiC) and the Danish Council for Strategic Research (Programme Commission on Strategic Growth Technologies); Austrian FWF, project ‘SFB F43 RNA regulation of the transcriptome’. Funding for open access charge: Danish Council for Strategic Research (Programme Commission on Strategic Technologies).

Conflict of interest statement. None declared.