Abstract
Dynamic DNA nanotechnology often uses toehold-mediated strand displacement for controlling reaction kinetics. Although the dependence of strand displacement kinetics on toehold length has been experimentally characterized and phenomenologically modeled, detailed biophysical understanding has remained elusive. Here, we study strand displacement at multiple levels of detail, using an intuitive model of a random walk on a 1D energy landscape, a secondary structure kinetics model with single base-pair steps and a coarse-grained molecular model that incorporates 3D geometric and steric effects. Further, we experimentally investigate the thermodynamics of three-way branch migration. Two factors explain the dependence of strand displacement kinetics on toehold length: (i) the physical process by which a single step of branch migration occurs is significantly slower than the fraying of a single base pair and (ii) initiating branch migration incurs a thermodynamic penalty, not captured by state-of-the-art nearest neighbor models of DNA, due to the additional overhang it engenders at the junction. Our findings are consistent with previously measured or inferred rates for hybridization, fraying and branch migration, and they provide a biophysical explanation of strand displacement kinetics. Our work paves the way for accurate modeling of strand displacement cascades, which would facilitate the simulation and construction of more complex molecular systems.
INTRODUCTION
Recent advances in DNA nanotechnology have enabled the construction of 2D and 3D nanoscale structures (1–7). Nucleic acids have predictable double-helical structure and generally well-understood thermodynamic (8–11) and mechanical (12) properties, which makes them excellent engineering materials. In addition to static structures, dynamic nanoscale devices such as circuits (13–16), catalysts (17,18), autonomous molecular motors (19–22) and reconfigurable nanostructures (18,23–25) have been engineered using DNA. Inspired by experimental advances, theoretical schemes have been proposed (26,27) to engineer arbitrarily complex chemical dynamics using DNA. If successful, such efforts could enable dynamic DNA circuits to actively control nanoscale devices.
Unfortunately, the biophysical understanding of key kinetic phenomena remains underdeveloped relative to our knowledge of static properties, limiting the development of dynamic DNA nanotechnology. Here, we study the biophysical basis of a molecular mechanism called toehold-mediated strand displacement, which is central to many dynamic DNA devices built to date. Toehold-mediated strand displacement enables control over the kinetics of molecular rearrangement, allowing the engineer to program when and where specific steps take place in a molecular machine.
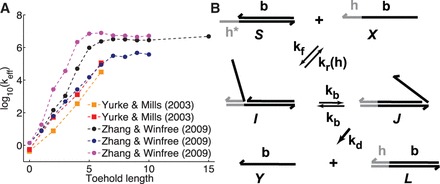
Figure 1 illustrates strand displacement using domain notation. A domain is a set of contiguous nucleotides designed to be either fully bound or fully unbound in stable configurations. Our system initially comprises a two-stranded complex (S) and a single-stranded ‘invader’ (X). S consists of an ‘incumbent’ strand (Y) bound to a ‘substrate’ strand, which has a single-stranded overhang called a ‘toehold’. The invader is fully Watson–Crick complementary to the substrate and may bind reversibly to it using the toehold domain (h). This binding is reversible because the toehold may ‘fray’ and eventually dissociate. (We use the term ‘fraying’ to describe the disruption of base pairs at the end of a duplex; if all base pairs fray, the duplex melts or dissociates. Conversely, ‘zippering’ refers to when a new base pair forms at the end of an existing duplex.) Once the toehold is bound, the ‘overhanging’ branch migration domain (b) of the invader may compete with the incumbent for binding with the substrate. As the incumbent and invader exchange base pairs with the substrate, the branch point of the three-stranded complex moves back and forth. This ‘three-way branch migration’ (henceforth, ‘branch migration’) process has previously been modeled as an unbiased random walk (28–30), as each step causes no net change in base pairing. Eventually, the incumbent may dissociate, completing strand displacement. Overall, displacement is thermodynamically driven forward by the net gain in base pairs due to the toehold.
Figure 1.
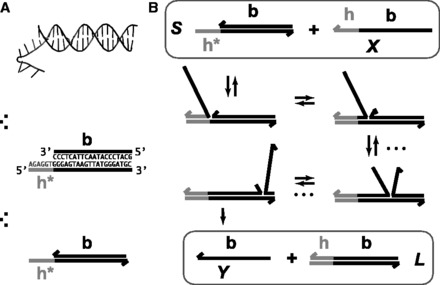
(A) Domain notation. Arrows indicate 3′-ends; Asterisk indicates Watson–Crick complementarity. (B) Toehold h mediates the displacement of the incumbent (Y) by the invader (X). Dots indicate branch migration intermediates, which are not shown.
Although it is known that bimolecular rate constants for strand displacement can vary a million-fold depending on the length of the toehold, little is known about the underlying biophysics or how to generalize the results to other reaction conditions or molecular modifications. For example, what are the mechanisms and intermediate states involved in a single step of branch migration? How do the kinetics of strand displacement depend on the length of the branch migration domain or on the temperature and buffer conditions? How different is strand displacement in RNA and DNA? What is the effect of sequence mismatches at different positions along the branch migration domain? To begin answering these questions, a fundamental biophysical understanding is necessary.
However, the commonly accepted view of strand displacement biophysics appears at odds with kinetic measurements (30,31). Consider strand displacement with a 1-base toehold and a 20-base branch migration domain. Let us assume that the rate constant for the formation of the toehold base pair is on the order of 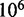 /M/s. [This value for 1-nt association is within a factor of two of experimental values for 6-, 10-, 15-, and 20-mer hybridization rates (30,32), after accounting for the linear length-dependence for short oligonucleotides (33).] Once the toehold has bound, there are two possibilities: (i) the toehold base pair could dissociate, leading to the dissociation of the invader or (ii) the nearest base pair of the substrate-incumbent complex could fray, allowing the invader to compete to replace that base pair and complete the first step of branch migration. Assuming, as may seem reasonable, that the rate at which either base pair frays is similar, process (ii) should be approximately half as fast as process (i). This is because, once the substrate-incumbent base pair frays, there is a 50% chance of the invader replacing the frayed base pair, and a 50% chance of returning to the initial step. Once the first step of branch migration is complete, subsequent forward and backward steps are assumed to occur at the same rate. Therefore, the probability of successfully completing the remaining steps of branch migration before going back to the toehold-only-bound state is 1/20, from the gambler’s ruin analysis [see Section 14.2 of Feller (34)]. The lifetime of the three-stranded intermediate should be independent of concentration. Therefore, at low enough concentrations, the overall reaction can be modeled as an instantaneous second-order process, as reported by Zhang and Winfree (30). Under these conditions, the overall effective rate constant (
/M/s. [This value for 1-nt association is within a factor of two of experimental values for 6-, 10-, 15-, and 20-mer hybridization rates (30,32), after accounting for the linear length-dependence for short oligonucleotides (33).] Once the toehold has bound, there are two possibilities: (i) the toehold base pair could dissociate, leading to the dissociation of the invader or (ii) the nearest base pair of the substrate-incumbent complex could fray, allowing the invader to compete to replace that base pair and complete the first step of branch migration. Assuming, as may seem reasonable, that the rate at which either base pair frays is similar, process (ii) should be approximately half as fast as process (i). This is because, once the substrate-incumbent base pair frays, there is a 50% chance of the invader replacing the frayed base pair, and a 50% chance of returning to the initial step. Once the first step of branch migration is complete, subsequent forward and backward steps are assumed to occur at the same rate. Therefore, the probability of successfully completing the remaining steps of branch migration before going back to the toehold-only-bound state is 1/20, from the gambler’s ruin analysis [see Section 14.2 of Feller (34)]. The lifetime of the three-stranded intermediate should be independent of concentration. Therefore, at low enough concentrations, the overall reaction can be modeled as an instantaneous second-order process, as reported by Zhang and Winfree (30). Under these conditions, the overall effective rate constant (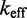 ) is given by a hybridization rate constant for the toehold, multiplied by a success probability of displacement once the toehold is bound. Even though the time spent in the three-stranded intermediate is small,
) is given by a hybridization rate constant for the toehold, multiplied by a success probability of displacement once the toehold is bound. Even though the time spent in the three-stranded intermediate is small, 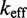 depends strongly on the probability of displacement once bound:
depends strongly on the probability of displacement once bound: 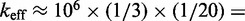
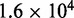 /M/s for a one-base toehold. This is over three orders of magnitude larger than the 8/M/s value measured by Zhang and Winfree (30). This is a large unexplained discrepancy, despite the approximate nature of our calculation.
/M/s for a one-base toehold. This is over three orders of magnitude larger than the 8/M/s value measured by Zhang and Winfree (30). This is a large unexplained discrepancy, despite the approximate nature of our calculation.
We now summarize the experimental evidence for the exponential acceleration in 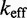 with toehold length, which was first reported by Yurke and Mills (31). Zhang and Winfree (30) further characterized this exponential acceleration and confirmed that it saturates in the long-toehold limit. Relevant data from both studies (Figure 2A) suggest that the exponential acceleration in itself is not an artifact of particular sequences, although details may well depend on the experimental system (sequences, modifications for read-out, etc.) or conditions (salt, temperature, etc.). The kinetics of zero-toehold (‘blunt end’) strand displacement was investigated by Reynaldo et al. (35), whose measurement of 3.6/M/s at 30°C is similar to the 1.4/M/s at 25°C reported by Zhang and Winfree (30).
with toehold length, which was first reported by Yurke and Mills (31). Zhang and Winfree (30) further characterized this exponential acceleration and confirmed that it saturates in the long-toehold limit. Relevant data from both studies (Figure 2A) suggest that the exponential acceleration in itself is not an artifact of particular sequences, although details may well depend on the experimental system (sequences, modifications for read-out, etc.) or conditions (salt, temperature, etc.). The kinetics of zero-toehold (‘blunt end’) strand displacement was investigated by Reynaldo et al. (35), whose measurement of 3.6/M/s at 30°C is similar to the 1.4/M/s at 25°C reported by Zhang and Winfree (30).
Figure 2.
(A) Dependence of 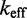 on toehold length, measured by Yurke and Mills (31) (at 20°C, 1 M Na+) and Zhang and Winfree (30) (at 25°C, 12.5 mM Mg++). Each curve is from a different toehold sequence. (B) The phenomenological model of Zhang and Winfree (30). kd is assumed to be large relative to other rate constants.
on toehold length, measured by Yurke and Mills (31) (at 20°C, 1 M Na+) and Zhang and Winfree (30) (at 25°C, 12.5 mM Mg++). Each curve is from a different toehold sequence. (B) The phenomenological model of Zhang and Winfree (30). kd is assumed to be large relative to other rate constants.
Zhang and Winfree (30) built a phenomenological model for predicting 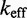 from toehold sequence (Figure 2B). They modeled branch migration using two macro-states I and J, containing the first and second half of the isoenergetic branch migration intermediates, respectively, which are connected by a simple transition with rate constant kb (see Supplementary Figure S1 and Supplementary Section S1 for more details). Their model fits the data, but it is hard to physically interpret the transition between I and J. Branch migration is generally thought of as a random walk through many isoenergetic states, rather than a single reversible transition characterized by a first-order rate constant. Without a more nuanced understanding of the process, it is unclear whether the fitted value of
from toehold sequence (Figure 2B). They modeled branch migration using two macro-states I and J, containing the first and second half of the isoenergetic branch migration intermediates, respectively, which are connected by a simple transition with rate constant kb (see Supplementary Figure S1 and Supplementary Section S1 for more details). Their model fits the data, but it is hard to physically interpret the transition between I and J. Branch migration is generally thought of as a random walk through many isoenergetic states, rather than a single reversible transition characterized by a first-order rate constant. Without a more nuanced understanding of the process, it is unclear whether the fitted value of 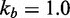 /s can be justified on more fundamental biophysical grounds.
/s can be justified on more fundamental biophysical grounds.
In this work, we model branch migration at a more detailed level that explicitly includes intermediates, thereby highlighting important thermodynamic and kinetic features of the process that are not evident from the phenomenological approach.
First, we analyze a 1D (single-pathway) model of toehold-mediated strand displacement called the intuitive energy landscape (IEL) model. Systematically exploring the parameter space of this simple model suggests that some combination of two factors could explain the dependence of strand displacement rate on toehold length: (i) the branch migration process is not isoenergetic and contains a free energy penalty for intermediate states and (ii) branch migration is slow relative to fraying of the toehold.
To verify that these factors are not already implicit features of more detailed models of DNA secondary structure thermodynamics, we simulated the experiments of Zhang and Winfree (30) using a secondary structure kinetics (SSK) simulator called Multistrand (36). Multistrand incorporates extensive thermodynamic information—from state-of-the-art nearest-neighbor (NN) thermodynamic models of DNA secondary structure (8–11)—combined with a minimally parameterized rate model. Multistrand predicts that 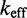 would increase by a factor of
would increase by a factor of 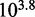 , as toehold length increases from 0 to 15, in contrast to the experimentally observed factor of
, as toehold length increases from 0 to 15, in contrast to the experimentally observed factor of 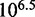 . This quantitative discrepancy confirms that factors (i) and (ii) suggested by the IEL analysis are not already implicitly incorporated in more detailed models of DNA secondary structure thermodynamics.
. This quantitative discrepancy confirms that factors (i) and (ii) suggested by the IEL analysis are not already implicitly incorporated in more detailed models of DNA secondary structure thermodynamics.
We then experimentally investigate possibility (i) suggested by the IEL, by measuring the relative stability of complexes that mimic the geometric structure of branch migration intermediates. Our experiments provide evidence in support of a free energy penalty for branch migration intermediates that is not predicted by the NN models of DNA.
Finally, we use a recently proposed coarse-grained molecular model of DNA (oxDNA) (37–39), which incorporates more physical detail, including geometric and steric effects. In addition to correctly predicting the length-dependence of toehold-mediated strand displacement rates, oxDNA independently predicts the thermodynamic penalty for branch migration intermediates, suggesting it arises from local steric effects between single-stranded overhangs around the branch point. Further, oxDNA predicts that branch migration is slower than fraying of the toehold, as it is geometrically more complex and necessarily involves more thermodynamically unfavorable steps.
MATERIALS, METHODS AND RESULTS
Intuitive Energy Landscape model
Through a simple approximate calculation, we argued that the current view of strand displacement biophysics is at odds with kinetic measurements (30,31). We now perform a more rigorous intuitive analysis by building a simple single-pathway model called the IEL model. The IEL is simple enough that its kinetic predictions may be analytically or numerically calculated, for a given parameterization. We systematically explore the IEL’s parameter space to obtain biophysical intuition and identify key thermodynamic and kinetic features essential for predictions to match experimental data.
State space
The IEL considers an invading strand and a substrate-incumbent complex contained in a virtual box of volume V in solution, which defines a concentration u of one molecule per volume V. The state space of the IEL is illustrated in Figure 3. State A corresponds to the invader being unattached to the substrate-incumbent duplex. State B represents the formation of a first base pair within the toehold. For each additional toehold base pair that zips up, we define a new state, with state C indicating the fully formed toehold. From here, each step of branch migration involves replacing an incumbent-substrate base pair with an invader-substrate base pair. We describe the stepping between these intermediates using a simple model in which the system must pass though a single effective transition state of raised free energy, so each complete branch migration step is shown as a single tooth of the ‘sawtooth’ pattern between states C and D. This unknown effective transition state could be potentially as simple as a frayed substrate-incumbent base pair, but could also be more complex. The final stage of successful displacement involves the dissociation of the incumbent (state E) followed by the formation of the final base pair between invader and substrate (state F). Subtleties relating to the zero-toehold case are discussed in Supplementary Section S2 (see Supplementary Figure S2).
Figure 3.
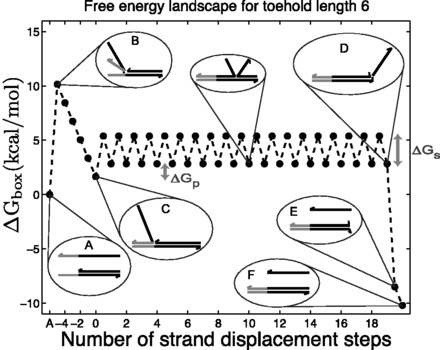
Free energy landscape of the IEL at 25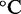 for a six base toehold. States A–F and the sawtooth amplitude (
for a six base toehold. States A–F and the sawtooth amplitude (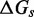 ) and plateau height (
) and plateau height (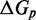 ) parameters are described in the text.
) parameters are described in the text. 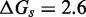 kcal/mol and
kcal/mol and 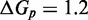 kcal/mol are used for illustration.
kcal/mol are used for illustration.
Energy model
The IEL models the free energy of the virtual box (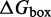 ) relative to state A.
) relative to state A. 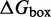 is defined as in Figure 3. Initial binding (state A to B) incurs a free energy penalty of
is defined as in Figure 3. Initial binding (state A to B) incurs a free energy penalty of 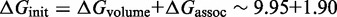 kcal/mol (11) (at concentration
kcal/mol (11) (at concentration 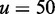 nM) due to the reduction in the entropy of the box caused by lost translational and orientational degrees of freedom.
nM) due to the reduction in the entropy of the box caused by lost translational and orientational degrees of freedom. 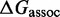 is the free energy cost of association at a standard concentration of
is the free energy cost of association at a standard concentration of 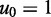 M, and
M, and 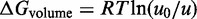 is a correction for the actual concentration, where R is the universal gas constant and T is the temperature in Kelvin. Figure 3 shows the first base pair of the toehold adjacent to the helix, where it interacts favorably with the adjacent duplex end. For simplicity, we neglect sequence-dependent interaction strengths and use the average value
is a correction for the actual concentration, where R is the universal gas constant and T is the temperature in Kelvin. Figure 3 shows the first base pair of the toehold adjacent to the helix, where it interacts favorably with the adjacent duplex end. For simplicity, we neglect sequence-dependent interaction strengths and use the average value 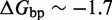 kcal/mol for this and all other base pairs, as taken from the NN model (8–10) of DNA secondary structure thermodynamics. Formation of each successive base pair in the toehold therefore contributes
kcal/mol for this and all other base pairs, as taken from the NN model (8–10) of DNA secondary structure thermodynamics. Formation of each successive base pair in the toehold therefore contributes 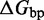 . Our effective transition states, which are local free energy maxima along the sawtooth, are raised
. Our effective transition states, which are local free energy maxima along the sawtooth, are raised 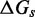 above the branch migration intermediates with fully paired substrate. As the physical details of branch migration steps are not well-understood, the effective ‘sawtooth amplitude’ (
above the branch migration intermediates with fully paired substrate. As the physical details of branch migration steps are not well-understood, the effective ‘sawtooth amplitude’ (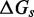 ) is an adjustable parameter. Changing
) is an adjustable parameter. Changing 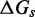 allows branch migration and toehold melting rates to be independently modulated; for
allows branch migration and toehold melting rates to be independently modulated; for 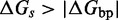 , branch migration is slow relative to fraying.
, branch migration is slow relative to fraying.
We also introduce a final parameter, a plateau height 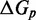 , which captures how the free energy of branch migration intermediates could vary with the structure of the branch migration junction. In particular, there is an asymmetry between state C and all other intermediates of branch migration: only one single-stranded overhang is present at the junction in state C, whereas an overhang protrudes from both sides for all other intermediates. We thus introduce a parameter
, which captures how the free energy of branch migration intermediates could vary with the structure of the branch migration junction. In particular, there is an asymmetry between state C and all other intermediates of branch migration: only one single-stranded overhang is present at the junction in state C, whereas an overhang protrudes from both sides for all other intermediates. We thus introduce a parameter 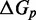 that accounts for a possible free energy penalty due to the additional overhang, which could conceivably arise from entropic or electrostatic effects. Henceforth, IEL (
that accounts for a possible free energy penalty due to the additional overhang, which could conceivably arise from entropic or electrostatic effects. Henceforth, IEL (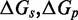 ) denotes a sawtooth amplitude of
) denotes a sawtooth amplitude of 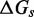 and a plateau height of
and a plateau height of 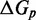 (both in kcal/mol).
(both in kcal/mol).
In an intuitive model like the IEL, one could consider a range of alternative perturbations to the current biophysical understanding of strand displacement. 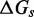 and
and 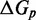 , however, parameterize in a simple way aspects of the branch migration process that are known to be poorly characterized. Furthermore, as we show later, experiments and more detailed modeling provide physical justification for the effects that these parameters represent.
, however, parameterize in a simple way aspects of the branch migration process that are known to be poorly characterized. Furthermore, as we show later, experiments and more detailed modeling provide physical justification for the effects that these parameters represent.
Rate model
The system may undergo a transition to either of its neighboring states on the 1D landscape. To ensure that stochastic simulations will eventually converge to the thermodynamic (Boltzmann) equilibrium over the states, transition rates must satisfy detailed balance, i.e.
| (1) |
Here kij is the transition rate from i to j. Equation (1) only fixes the relative rates; in principle, for each pair of adjacent states i and j, an independent scaling factor could be chosen. Consequently, the number of candidate rate models is enormous. In the spirit of minimal parameterization to avoid over-fitting the data, we use only two independent scaling factors: 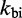 for all bimolecular and
for all bimolecular and 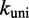 for all unimolecular transitions.
for all unimolecular transitions.
For unimolecular transitions (all except A 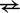 B and D
B and D 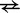 E in Figure 3), we use a model in which all energetically downhill steps have a constant rate
E in Figure 3), we use a model in which all energetically downhill steps have a constant rate 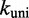 . This is a sensible first approximation, given that these steps involve forming a base pair at the end of a duplex or stepping down from the transition states of branch migration, which may resemble forming a base pair at the junction. In other words, for
. This is a sensible first approximation, given that these steps involve forming a base pair at the end of a duplex or stepping down from the transition states of branch migration, which may resemble forming a base pair at the junction. In other words, for 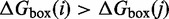 ,
,
| (2) |
and therefore,
| (3) |
This model is a continuous-time variant of the Metropolis (40) scheme for calculating thermodynamic averages.
For bimolecular transitions (A 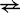 B or D
B or D 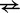 E), the IEL assumes that complexes join at the constant rate
E), the IEL assumes that complexes join at the constant rate 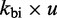 , and calculates the reverse rate by detailed balance. If i to j is a join step,
, and calculates the reverse rate by detailed balance. If i to j is a join step,
| (4) |
and
| (5) |
We choose 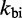 to be
to be 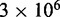 /M/s, based on the hybridization rate constant fitted by Zhang and Winfree (30). For simplicity, we choose
/M/s, based on the hybridization rate constant fitted by Zhang and Winfree (30). For simplicity, we choose 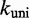 such that the dissociation rate of the last base pair of the toehold (state B to A) is approximately equal to the fraying rate for every other base pair of the toehold (steps from state C toward B). This yields
such that the dissociation rate of the last base pair of the toehold (state B to A) is approximately equal to the fraying rate for every other base pair of the toehold (steps from state C toward B). This yields 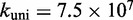 /s (see Supplementary Section S2 for details). This choice of
/s (see Supplementary Section S2 for details). This choice of 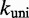 , at the very least, ensures that two somewhat similar processes have similar rates.
, at the very least, ensures that two somewhat similar processes have similar rates.
Analytic and numerical calculations
We use an analytic formula for calculating absorption probabilities for a 1D random walk with absorbing boundaries (41) to calculate 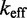 as a function of toehold length h for various values
as a function of toehold length h for various values 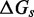 and
and 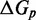 (Figure 4A). (For details, see Supplementary Section S2.) To quantify the extent of control provided by toeholds, we define
(Figure 4A). (For details, see Supplementary Section S2.) To quantify the extent of control provided by toeholds, we define
| (6) |
to be the orders of magnitude acceleration in 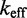 as toehold length increases from h1 to h2. We will be most interested in
as toehold length increases from h1 to h2. We will be most interested in 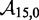 , which corresponds to the difference between the leak rate and the maximal rate measured in Zhang and Winfree (30). [We choose 15 rather than
, which corresponds to the difference between the leak rate and the maximal rate measured in Zhang and Winfree (30). [We choose 15 rather than 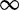 because the length-dependence of hybridization rates (33) suggests that experimental values for
because the length-dependence of hybridization rates (33) suggests that experimental values for 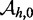 may not be bounded, but for our purposes there is insignificant change past length 15.] The experimental results of Zhang and Winfree (30) can be matched by the IEL, but only with surprisingly large values of
may not be bounded, but for our purposes there is insignificant change past length 15.] The experimental results of Zhang and Winfree (30) can be matched by the IEL, but only with surprisingly large values of 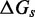 and
and 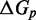 . IEL(2.6, 0), with a plausible value of
. IEL(2.6, 0), with a plausible value of 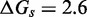 kcal/mol (∼1.5 base pair stacks) and an a priori choice of
kcal/mol (∼1.5 base pair stacks) and an a priori choice of 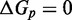 kcal/mol, predicts
kcal/mol, predicts 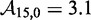 . This is 3.4 orders of magnitude smaller than the experimentally observed value of 6.5. Increasing either
. This is 3.4 orders of magnitude smaller than the experimentally observed value of 6.5. Increasing either 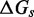 or
or 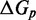 serves to increase the predicted
serves to increase the predicted 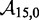 , as shown by the contour plot in Figure 4B. The slope of contour lines suggests that
, as shown by the contour plot in Figure 4B. The slope of contour lines suggests that 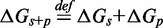 is the key quantity. Indeed, a scatter plot of the dependence on
is the key quantity. Indeed, a scatter plot of the dependence on 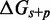 (Figure 4C) using all the data in Figure 4B produces almost no vertical spread.
(Figure 4C) using all the data in Figure 4B produces almost no vertical spread. 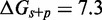 kcal/mol matches the experimentally observed value of
kcal/mol matches the experimentally observed value of 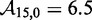 .
.
Figure 4.
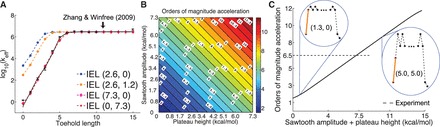
(A) Predictions of IEL ( ) for different values of the sawtooth amplitude
) for different values of the sawtooth amplitude  and plateau height
and plateau height 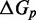 .
. 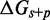 needs to be as high as 7.3 kcal/mol (>4 base-pair stacks) to match experiment (30). (B) Contour plot of orders of magnitude acceleration (
needs to be as high as 7.3 kcal/mol (>4 base-pair stacks) to match experiment (30). (B) Contour plot of orders of magnitude acceleration (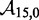 ) as a function of (
) as a function of (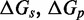 ) for
) for 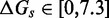 kcal/mol and
kcal/mol and 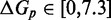 kcal/mol. (C) Scatter plot of
kcal/mol. (C) Scatter plot of 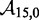 versus
versus 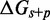 using all the data in (B). The points plotted show almost no vertical spread, meaning that all points lie on a line. This indicates that
using all the data in (B). The points plotted show almost no vertical spread, meaning that all points lie on a line. This indicates that 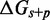 is the predictive quantity. Inset: IEL (1.3, 0) and IEL (5.0, 5.0) for a 1-base toehold. The bimolecular initial binding step, which is identical in both landscapes, is marked in orange to highlight the contrast between the landscapes.
is the predictive quantity. Inset: IEL (1.3, 0) and IEL (5.0, 5.0) for a 1-base toehold. The bimolecular initial binding step, which is identical in both landscapes, is marked in orange to highlight the contrast between the landscapes.
Other perturbations of the IEL model were unable to match the experiments. For example, we considered an alternative to the Metropolis method for setting unimolecular rates, the Kawasaki (42) method, which scales both uphill and downhill transition rates based on the corresponding change in 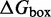 . After rescaling
. After rescaling 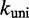 so that dissociation of the last toehold base pair still occurs at the same rate as fraying, the Kawasaki method predicts a value for
so that dissociation of the last toehold base pair still occurs at the same rate as fraying, the Kawasaki method predicts a value for 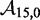 within 10% of the Metropolis method (see Supplementary Figure S3). Going further, and considering that
within 10% of the Metropolis method (see Supplementary Figure S3). Going further, and considering that 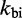 and
and 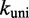 may not be chosen ideally, we first note that logically, a uniform change to both rates will cancel and thus have no effect on
may not be chosen ideally, we first note that logically, a uniform change to both rates will cancel and thus have no effect on 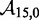 . In contrast, IEL predictions do depend on the ratio
. In contrast, IEL predictions do depend on the ratio 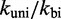 , which substantially affects the probabilities that initial contacts lead to successful zippering of the toehold and to successful branch migration before dissociation (see Supplementary Figure S4 and Supplementary Section S2). However, even implausibly low values of
, which substantially affects the probabilities that initial contacts lead to successful zippering of the toehold and to successful branch migration before dissociation (see Supplementary Figure S4 and Supplementary Section S2). However, even implausibly low values of 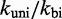 cannot account for the data without a large value of
cannot account for the data without a large value of 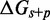 .
.
These features of the IEL can be understood through simple analytical approximations. Conceptually, we can split the strand displacement process into an attachment step (A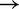 B), followed by success or failure of zipping up the toehold, followed by either dissociation of the toehold or successful displacement. We first treat the case of long toeholds, for which in the IEL model
B), followed by success or failure of zipping up the toehold, followed by either dissociation of the toehold or successful displacement. We first treat the case of long toeholds, for which in the IEL model 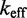 saturates at
saturates at
| (7) |
with 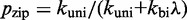 and
and 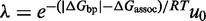 giving the approximate probability that after making the first base pair, the invader does not dissociate and the remaining toehold bases zip up. (For long toeholds successful displacement is guaranteed once the toehold is formed.) For shorter toeholds that do not saturate
giving the approximate probability that after making the first base pair, the invader does not dissociate and the remaining toehold bases zip up. (For long toeholds successful displacement is guaranteed once the toehold is formed.) For shorter toeholds that do not saturate 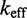 , the probability of toehold dissociation before branch migration dominates, and we can derive
, the probability of toehold dissociation before branch migration dominates, and we can derive
| (8) |
for 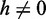 and, there being two ends where branch migration could start, twice the given value for h = 0.
and, there being two ends where branch migration could start, twice the given value for h = 0.
We clearly see that the slope in Figure 4A is governed by 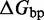 , while the role of b (Supplementary Figure S5) and
, while the role of b (Supplementary Figure S5) and 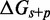 in determining
in determining
| (9) |
is immediate from their influence on 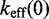 . The more subtle effect of changing
. The more subtle effect of changing 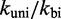 results partly from effects on
results partly from effects on 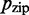 ; a slightly more accurate approximation can explain the behavior seen in Supplementary Figure S4. Details on this and other derivations are given in Supplementary Section S2.
; a slightly more accurate approximation can explain the behavior seen in Supplementary Figure S4. Details on this and other derivations are given in Supplementary Section S2.
Matching both strand displacement and branch migration rates
The IEL analysis suggests that we can reconcile kinetic models of displacement at the base pair level with the experimental measurements of Zhang and Winfree (30) by incorporating a thermodynamic penalty for initiating branch migration (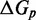 ) and/or slowing down the rate of branch migration through a relatively large sawtooth amplitude (
) and/or slowing down the rate of branch migration through a relatively large sawtooth amplitude (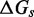 ) associated with each step of branch migration. Although
) associated with each step of branch migration. Although 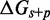 is constrained to be at least 7.3 kcal/mol to match the data, the individual contributions of
is constrained to be at least 7.3 kcal/mol to match the data, the individual contributions of 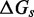 and
and 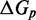 are not determined by the analysis.
are not determined by the analysis.
To compare the inferences of the IEL analysis with experimental measurements, we need to account for the increase in initial binding rate (A B) with toehold length, as observed for short oligonucleotide hybridization (33). (For simplicity, the IEL assumes that the initial binding rate is independent of toehold length.) To this end, we also explored a variant of the IEL, called the Augmented Energy Landscape (AEL) model, that includes the linear increase in the formation rate of the first base pair (see Supplementary Section S3). For the AEL, we find that a smaller value of
B) with toehold length, as observed for short oligonucleotide hybridization (33). (For simplicity, the IEL assumes that the initial binding rate is independent of toehold length.) To this end, we also explored a variant of the IEL, called the Augmented Energy Landscape (AEL) model, that includes the linear increase in the formation rate of the first base pair (see Supplementary Section S3). For the AEL, we find that a smaller value of 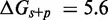 kcal/mol is required owing to the contribution of the binding rate to the overall acceleration. A good fit to the experimental data shown in Figure 4 is obtained for
kcal/mol is required owing to the contribution of the binding rate to the overall acceleration. A good fit to the experimental data shown in Figure 4 is obtained for 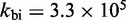 /M/s and
/M/s and 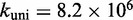 /s (Supplementary Table S1).
/s (Supplementary Table S1).
We have not yet presented evidence to suggest that the plateau height 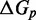 is non-zero. However, if
is non-zero. However, if 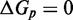 , a sawtooth amplitude of 7.3 kcal/mol (5.6 for the AEL) would be required to account for the data, which implies an average branch migration step time of
, a sawtooth amplitude of 7.3 kcal/mol (5.6 for the AEL) would be required to account for the data, which implies an average branch migration step time of 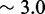 ms (
ms (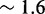 ms for the AEL). This is much slower than experimentally inferred step times on the order of 12–20 μs (28,29). Therefore, simultaneously matching both measured branch migration and strand displacement rates requires a significant thermodynamic penalty to initiating branch migration.
ms for the AEL). This is much slower than experimentally inferred step times on the order of 12–20 μs (28,29). Therefore, simultaneously matching both measured branch migration and strand displacement rates requires a significant thermodynamic penalty to initiating branch migration.
The IEL analysis raises two important questions. First, could the necessary values of 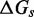 and
and 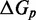 represent features missing in the IEL’s simplified thermodynamic landscape that are implicitly already present in more detailed models? If this is not the case, are
represent features missing in the IEL’s simplified thermodynamic landscape that are implicitly already present in more detailed models? If this is not the case, are 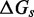 and
and 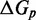 purely phenomenological parameters used to fit the data or do they represent real physical effects that arise from the molecular properties of DNA?
purely phenomenological parameters used to fit the data or do they represent real physical effects that arise from the molecular properties of DNA?
Secondary Structure Kinetics model
As a first step toward answering these questions, we use a SSK simulator called Multistrand (36) to study strand displacement as a random walk on a more complex energy landscape, the NN secondary structure model (8–11), that incorporates a wealth of existing thermodynamic knowledge. Multistrand extends the Kinfold simulator (43) from single-strand landscapes to landscapes for multiple interacting nucleic acid molecules. Code implementing the Multistrand model is available for public download (see Supplementary Section S4 for details).
State space
Multistrand considers a set of strands in a virtual box of volume V in solution, which defines a concentration u of one molecule per volume V. The state space consists of all possible sets of Watson–Crick base pairs (such as states in Figure 5A), with two restrictions: (i) no base can have more than one pairing interaction and (ii) secondary structures containing pseudo knots are not allowed. Structures without pseudo knots are tree-like and have nested base pairing (11). The size of Multistrand’s state space grows exponentially in the number of bases (11).
Figure 5.
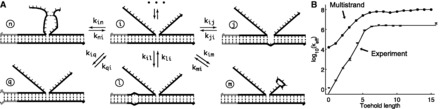
(A) Example states and elementary steps in Multistrand (36), a SSK simulator. States illustrated are each adjacent to state i, as they differ from i by only one base pair. Transition rates are chosen to obey detailed balance. Dots and arrows at the top indicate other possible elementary steps from state i (not shown). (B) Multistrand predictions of experimentally measured (30) strand displacement rates as a function of toehold length. Experimental data points and error bars are from Zhang and Winfree (30); the fitted line is their phenomenological model. Standard errors for Multistrand simulations are under 1% (not shown).
Energy model
Let 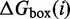 be the free energy of the virtual box in state i, relative to a completely unstructured state with no base pairs.
be the free energy of the virtual box in state i, relative to a completely unstructured state with no base pairs. 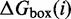 is the sum of free energies of each isolated complex
is the sum of free energies of each isolated complex 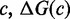 , in state i. The free energy of each complex is estimated using the NN model (8–10), which has been extended to multiple interacting nucleic acid strands (11). NN parameters were measured (9,10) in 1 M Na+, which is roughly thermodynamically equivalent to the 12.5 mM Mg++ used by Zhang and Winfree (30), according to salt corrections (44,45) to the NN model. The NN model assumes that the free energy contribution of each base pair is dependent only on the identity and orientation (5′ or 3′) of its nearest neighbors on either side and calculates
, in state i. The free energy of each complex is estimated using the NN model (8–10), which has been extended to multiple interacting nucleic acid strands (11). NN parameters were measured (9,10) in 1 M Na+, which is roughly thermodynamically equivalent to the 12.5 mM Mg++ used by Zhang and Winfree (30), according to salt corrections (44,45) to the NN model. The NN model assumes that the free energy contribution of each base pair is dependent only on the identity and orientation (5′ or 3′) of its nearest neighbors on either side and calculates 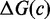 by summing contributions from each sub-structure (‘loop’) closed by a base-paired section; where
by summing contributions from each sub-structure (‘loop’) closed by a base-paired section; where
| (10) |
L is the number of strands in complex c and 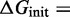
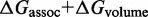 is, like in the IEL, the free energy cost of bringing two separate strands together. Stabilizing contributions to
is, like in the IEL, the free energy cost of bringing two separate strands together. Stabilizing contributions to 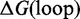 mainly arise from base-pair stacks, and destabilizing contributions arise from the entropic cost of closing loops. At duplex ends in either interior or exterior loops, the first overhanging nucleotide contributes a ‘dangle’ energy term (46). When two duplex ends abut, as at a nick, the duplexes are known to ‘coaxially stack’ onto each other (47–50), thereby stabilizing the structure; this interaction is not explicitly incorporated into Multistrand, although in some cases dangle energy terms partially account for it. Multistrand’s energy model is identical to that used in NUPACK (51) and is thus similar to those in Vienna RNA (52) and Mfold (53).
mainly arise from base-pair stacks, and destabilizing contributions arise from the entropic cost of closing loops. At duplex ends in either interior or exterior loops, the first overhanging nucleotide contributes a ‘dangle’ energy term (46). When two duplex ends abut, as at a nick, the duplexes are known to ‘coaxially stack’ onto each other (47–50), thereby stabilizing the structure; this interaction is not explicitly incorporated into Multistrand, although in some cases dangle energy terms partially account for it. Multistrand’s energy model is identical to that used in NUPACK (51) and is thus similar to those in Vienna RNA (52) and Mfold (53).
Rate model
Multistrand allows transitions between states i and j if they differ by a single base pair. The rate models we have explored for Multistrand are identical to the IEL, except for scaling factors. Like the IEL, Multistrand’s predictions are not particularly sensitive to the choice between standard unimolecular rate models: The predicted orders of magnitude acceleration in 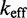 between toeholds 0 and 15 differ by less than 3% between Metropolis and Kawasaki (Supplementary Figure S6B). For Metropolis,
between toeholds 0 and 15 differ by less than 3% between Metropolis and Kawasaki (Supplementary Figure S6B). For Metropolis, 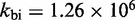 /M/s and
/M/s and 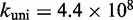 /s were calibrated (36) by fitting Multistrand simulations to experimentally measured DNA–DNA hybridization (32) and zippering (33) rates, respectively. Given the rate model, energy model and current state, the choice and timing of the next transition is determined using a Gillespie algorithm (54). Multistrand allows any initial first pair of nucleotides to interact, each at the standard bimolecular rate, resulting in an increase in hybridization rates with increasing toehold lengths.
/s were calibrated (36) by fitting Multistrand simulations to experimentally measured DNA–DNA hybridization (32) and zippering (33) rates, respectively. Given the rate model, energy model and current state, the choice and timing of the next transition is determined using a Gillespie algorithm (54). Multistrand allows any initial first pair of nucleotides to interact, each at the standard bimolecular rate, resulting in an increase in hybridization rates with increasing toehold lengths.
In principle, each i to j transition could have both forward and reverse rates scaled arbitrarily but equally, thus obtaining a distinct kinetic model that still satisfies detailed balance. However, doing so would amount to treating the microscopic barriers that impede transitions between the states of the NN model as different in every case. In the absence of additional information justifying such differences, the Metropolis approach constitutes a minimally parameterized rate model in which microscopic barriers associated with downhill processes (which typically involve base-pair formation) are assumed to be uniform, and their effects are incorporated in the value of 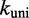 . As such, the Metropolis approach allows us to ask whether the free-energy landscape given by the NN model is sufficiently accurate and precise that it captures the factors that determine relative kinetics, and that finer details are only important in setting an overall rate constant
. As such, the Metropolis approach allows us to ask whether the free-energy landscape given by the NN model is sufficiently accurate and precise that it captures the factors that determine relative kinetics, and that finer details are only important in setting an overall rate constant 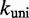 .
.
Comparing Multistrand predictions with data
We simulated the ‘average strength toehold’ experiments of Zhang and Winfree (30) and calculated 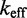 as a function of toehold length. For technical details regarding the simulations, see Supplementary Section S4 and Supplementary Table S2. Multistrand captures the qualitative dependence of
as a function of toehold length. For technical details regarding the simulations, see Supplementary Section S4 and Supplementary Table S2. Multistrand captures the qualitative dependence of 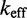 on toehold length, despite its minimally parameterized rate model. However, Multistrand predictions quantitatively diverge from experiment in two ways (Figure 5B): (i) the saturation value of
on toehold length, despite its minimally parameterized rate model. However, Multistrand predictions quantitatively diverge from experiment in two ways (Figure 5B): (i) the saturation value of 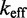 for toeholds longer than five bases is roughly 20 times larger and (ii) increasing toehold length from 0 to 15 increases
for toeholds longer than five bases is roughly 20 times larger and (ii) increasing toehold length from 0 to 15 increases 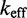 by a factor of
by a factor of 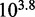 , in contrast to
, in contrast to 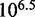 observed in experiment.
observed in experiment.
The first issue could be addressed by uniformly decreasing both 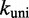 and
and  , which would shift the predicted curve down to match the data for toeholds longer than five bases. Indeed, this re-scaling is also physically reasonable, as there is considerable variation among hybridization and fraying rates in the literature for nucleic acids (32, 33,55–60).
, which would shift the predicted curve down to match the data for toeholds longer than five bases. Indeed, this re-scaling is also physically reasonable, as there is considerable variation among hybridization and fraying rates in the literature for nucleic acids (32, 33,55–60).
Scaling 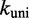 and
and 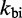 uniformly would not resolve the second challenge. However, like the IEL, Multistrand is particularly sensitive to the ratio
uniformly would not resolve the second challenge. However, like the IEL, Multistrand is particularly sensitive to the ratio 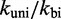 . Decreasing
. Decreasing 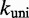 slows down all unimolecular transitions—which brings the branch migration rate closer to experimentally inferred values but makes fraying too slow. Two parameters,
slows down all unimolecular transitions—which brings the branch migration rate closer to experimentally inferred values but makes fraying too slow. Two parameters, 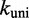 and
and 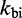 , are simply not enough (36) to simultaneously match the four distinct time scales involved: rates of hybridization, fraying, branch migration and branch migration initiation. Therefore, even unrealistically low choices of
, are simply not enough (36) to simultaneously match the four distinct time scales involved: rates of hybridization, fraying, branch migration and branch migration initiation. Therefore, even unrealistically low choices of 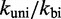 are unable to match observed acceleration in strand displacement rates due to toehold length (see Supplementary Figure S7).
are unable to match observed acceleration in strand displacement rates due to toehold length (see Supplementary Figure S7).
The SSK analysis confirms that understanding what the IEL’s 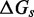 and
and 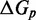 represent requires examining features not present in the NN model. Multistrand models branch migration as a fray–and–replace process and interprets the IEL’s sawtooth transition state as one in which the substrate-incumbent base pair at the junction is frayed. This choice, when coupled with a
represent requires examining features not present in the NN model. Multistrand models branch migration as a fray–and–replace process and interprets the IEL’s sawtooth transition state as one in which the substrate-incumbent base pair at the junction is frayed. This choice, when coupled with a 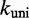 calibrated to match fraying rates (33), results in a branch migration rate that is much faster than experimentally inferred step times (28,29).
calibrated to match fraying rates (33), results in a branch migration rate that is much faster than experimentally inferred step times (28,29).
Indeed, the thermodynamics of the branch migration junction, e.g. states i and j in Figure 5A, is not well characterized in the standard NN secondary structure model, as it involves overhangs, dangles and coaxial stacking. Reflecting the lack of consensus, tools like NUPACK (51), Vienna RNA (52) and Mfold (53) offer several ways of treating dangle contributions; however, none of the three ‘dangle options’ in the NUPACK energy model (11) improved Multistrand predictions (Supplementary Figure S6A).
Measuring relative stability of branch migration intermediates
For the IEL to match measured hybridization, fraying and branch migration rates, and hence strand displacement rates, a non-zero plateau height (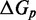 ) was necessary. We hypothesized that the initiation of branch migration incurs a thermodynamic cost due to the second overhang it engenders at the junction, even though the nearest neighbor model for DNA secondary structure thermodynamics predicts no such effect. We now present experimental evidence in support of this hypothesis by investigating the free energy landscape of branch migration. The biggest experimental challenge in measuring the relative stability of branch migration intermediates is that they cannot be easily isolated. Indeed, they are interchangeable as branch migration proceeds back and forth, with individual step times just tens of microseconds (28,29).
) was necessary. We hypothesized that the initiation of branch migration incurs a thermodynamic cost due to the second overhang it engenders at the junction, even though the nearest neighbor model for DNA secondary structure thermodynamics predicts no such effect. We now present experimental evidence in support of this hypothesis by investigating the free energy landscape of branch migration. The biggest experimental challenge in measuring the relative stability of branch migration intermediates is that they cannot be easily isolated. Indeed, they are interchangeable as branch migration proceeds back and forth, with individual step times just tens of microseconds (28,29).
System description
To overcome this issue, we designed immobile complexes Xi:Yj comprising hairpin Xi and strand Yj (Figure 6). Xi and Yj have poly-T overhangs of length i and j, respectively. Varying 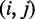 from
from 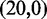 to
to 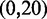 with
with 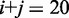 yields complexes that are ‘frozen snapshots’ of branch migration, with no expected branch migration possible. X20:Y00 mimics the binding of the invader by the toehold, and X19:Y01 represents the displacement of 1 base, and so on. X10:Y10 represents the ‘half way stage’ of branch migration and X00:Y20 captures nearly successful displacement. Measuring the relative stability of these frozen snapshots is expected to be indicative of the relative free energies of branch migration intermediates. Experiments involving these complexes will henceforth be referred to as the ‘strand displacement snapshot’ study. To investigate the consequences of short overhangs at the junction, we designed complexes Xi:Yi (for i = 0, 1, 2, 5 and 10). These experiments will be referred to as the ‘local overhang’ study. All our complexes have the same base pairs at the junction and poly-T overhangs, whereas branch migration typically involves different bases at each step. We can therefore study the thermodynamic consequences of junction geometry, without the complication of sequence dependence.
yields complexes that are ‘frozen snapshots’ of branch migration, with no expected branch migration possible. X20:Y00 mimics the binding of the invader by the toehold, and X19:Y01 represents the displacement of 1 base, and so on. X10:Y10 represents the ‘half way stage’ of branch migration and X00:Y20 captures nearly successful displacement. Measuring the relative stability of these frozen snapshots is expected to be indicative of the relative free energies of branch migration intermediates. Experiments involving these complexes will henceforth be referred to as the ‘strand displacement snapshot’ study. To investigate the consequences of short overhangs at the junction, we designed complexes Xi:Yi (for i = 0, 1, 2, 5 and 10). These experiments will be referred to as the ‘local overhang’ study. All our complexes have the same base pairs at the junction and poly-T overhangs, whereas branch migration typically involves different bases at each step. We can therefore study the thermodynamic consequences of junction geometry, without the complication of sequence dependence.
Table 1.
Sequences for domains from Figure 6, listed 5′–3′
| Domain | Sequence | Length |
|---|---|---|
| d | CCTCATCATACTACG | 15 |
| e | CTCCATGTCACTTC | 14 |
Figure 6.
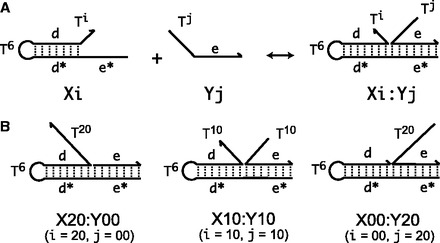
(A) Complex Xi:Yj comprises hairpin Xi and strand Yj, with poly-T overhangs of length i and j respectively. Domains d and e are designed to be orthogonal to each other and the overhangs (sequences in Table 1). (B) Varying (i, j) from 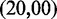 to
to 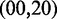 with
with 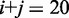 mimics the geometry branch migration intermediates [X20:Y00 (start), X10:Y10 (middle) and X00:Y20 (end), respectively]. No branch migration is intended in these complexes.
mimics the geometry branch migration intermediates [X20:Y00 (start), X10:Y10 (middle) and X00:Y20 (end), respectively]. No branch migration is intended in these complexes.
Temperature dependent absorbance experiments
We measure the UV absorbance (at 260 nm) of each complex between 20 and 90°C, at four different concentrations. As the absorbance of single-stranded DNA (ssDNA) is higher than that of double-stranded DNA, and the fraction of ssDNA is dependent on the temperature, a temperature-dependent absorbance curve is obtained at each concentration (Supplementary Figure S8). Each complex Xi:Yj exhibits two transitions: the bimolecular, lower temperature transition and the unimolecular, higher temperature transition due to the hairpin in Xi closing or opening. The unimolecular transition was identified both by it being independent of concentration and by control melts involving the hairpins only (data not shown). At the concentrations chosen, the bimolecular and unimolecular transitions are distinct.
For each complex, we infer the enthalpy (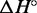 ) and entropy (
) and entropy (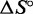 ) of formation by fitting the smoothed and normalized temperature-dependent absorbance curves (Figure 7) to a two-state model (61):
) of formation by fitting the smoothed and normalized temperature-dependent absorbance curves (Figure 7) to a two-state model (61):
| (11) |
where 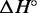 and
and 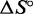 are assumed to be temperature independent. We perform this fitting using a Bayesian analysis and confirm our findings using a simpler descriptive ‘leave-one-concentration-out’ approach. Details are provided in Supplementary Section S5; see Supplementary Figure S9 and Supplementary Tables S3–S5.
are assumed to be temperature independent. We perform this fitting using a Bayesian analysis and confirm our findings using a simpler descriptive ‘leave-one-concentration-out’ approach. Details are provided in Supplementary Section S5; see Supplementary Figure S9 and Supplementary Tables S3–S5.
Figure 7.
Smoothed and normalized UV absorbance data while annealing (at 200 nM). The lower temperature transition is the (bimolecular) formation of the complex, whereas the higher temperature transition is the (unimolecular) formation of the hairpin. The mean absorbance between  and 35°C is normalized to 0 and that between
and 35°C is normalized to 0 and that between 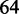 and 66°C (indicated by vertical lines) to 1. The temperature range whose mean absorbance is normalized to 1 is concentration-dependent (Supplementary Table S3). Data acquired by annealing and melting are essentially superimposable. The dashed line indicates the halfway point of the bimolecular transition.
and 66°C (indicated by vertical lines) to 1. The temperature range whose mean absorbance is normalized to 1 is concentration-dependent (Supplementary Table S3). Data acquired by annealing and melting are essentially superimposable. The dashed line indicates the halfway point of the bimolecular transition.
From 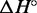 and
and 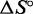 , we can calculate the free energy of formation,
, we can calculate the free energy of formation, 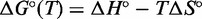 . By comparing the free energies of different complexes, we infer the contribution of the poly-T overhangs. Our two-state assumption means that
. By comparing the free energies of different complexes, we infer the contribution of the poly-T overhangs. Our two-state assumption means that 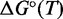 is assumed to be linear in T—deviations from linearity limit the accuracy of extrapolation from values around the melting temperature of the complexes. Values of
is assumed to be linear in T—deviations from linearity limit the accuracy of extrapolation from values around the melting temperature of the complexes. Values of 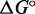 at 55°C, which is closer to the melting temperature, are plotted in Supplementary Figure S10.
at 55°C, which is closer to the melting temperature, are plotted in Supplementary Figure S10.
Second overhang causes de-stabilization due to a local effect
Unlike the predictions of NN thermodynamic models (9,11) of DNA, the immobile complexes we designed are not all of equal free energy; a second overhang at the junction causes a thermodynamic penalty (Figure 8A). At 25°C, we infer a free energy penalty of 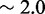 kcal/mol (3.4 RT) as branch migration proceeds from 0 to 10 steps (X20:Y00 versus X10:Y10), with the majority (
kcal/mol (3.4 RT) as branch migration proceeds from 0 to 10 steps (X20:Y00 versus X10:Y10), with the majority (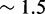 kcal/mol) arising from the first step (X20:Y00 versus X19:Y01). An approximately symmetric decrease is inferred for steps 11 to 20 (X10:Y10 versus X00:Y20).
kcal/mol) arising from the first step (X20:Y00 versus X19:Y01). An approximately symmetric decrease is inferred for steps 11 to 20 (X10:Y10 versus X00:Y20).
Figure 8.
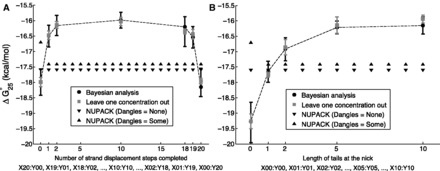
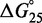 of formation for complexes in the ‘strand displacement snapshot’ study (A) and the ‘local overhang’ study (B). Black error bars indicate Bayesian posterior means and 99% confidence intervals, whereas gray error bars indicate means and standard deviations of leave-one-concentration-out least square fits. NUPACK predictions with dangles options ‘some’ and ‘none’ are provided for comparison.
of formation for complexes in the ‘strand displacement snapshot’ study (A) and the ‘local overhang’ study (B). Black error bars indicate Bayesian posterior means and 99% confidence intervals, whereas gray error bars indicate means and standard deviations of leave-one-concentration-out least square fits. NUPACK predictions with dangles options ‘some’ and ‘none’ are provided for comparison.
As the de-stabilization due to an additional overhang plateaus so quickly, we suspect that the penalty is due to local effects at the junction, which is supported by the ‘local overhang’ study (Figure 8B). Two one-base overhangs on either side of the junction (X01:Y01) result in a penalty of 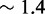 kcal/mol relative to no-overhangs (X00:Y00). Lengthening the overhangs increases this penalty, but each additional base contributes progressively less, with an overall penalty of 3.0 kcal/mol and 3.2 kcal/mol, respectively, for 5-base (X05:Y05) and 10-base (X10:Y10) overhangs.
kcal/mol relative to no-overhangs (X00:Y00). Lengthening the overhangs increases this penalty, but each additional base contributes progressively less, with an overall penalty of 3.0 kcal/mol and 3.2 kcal/mol, respectively, for 5-base (X05:Y05) and 10-base (X10:Y10) overhangs.
Our experiments suggest that current NN models of DNA do not capture the free energy landscape of strand displacement accurately enough to capture the kinetics of branch migration. This explains in part the inability of SSK models like Multistrand to match experimentally observed toehold-mediated acceleration.
Coarse-grained molecular modeling
A 3D model of DNA at the nucleotide level
Although it is possible to tune the IEL to agree with experimental data, and, moreover, the observed destabilisation of duplexes by ssDNA overhangs appears to support a plateau during displacement, a physical explanation of the parameters required is important. Atomically detailed or coarse-grained molecular models have the potential to provide this kind of insight (62). Here, we consider a recently proposed coarse-grained molecular model of DNA (oxDNA) (37–39), specifically the parameterization of Ouldridge (39). Code implementing the model is available for public download (see Supplementary Section S6). In this model, illustrated in Figure 9, each nucleotide is a 3D rigid body so that the state space of N model nucleotides has 6N spatial dimensions and 6N momenta. Pairs of nucleotides interact through a number of pairwise effective interactions (shown in Supplementary Figure S11), representing chain connectivity, excluded volume, hydrogen-bonding and stacking interactions between bases. The combination of nearest-neighbor stacking within a strand and hydrogen-bonding between complementary bases drives the formation of helical duplexes. We note here that oxDNA explicitly considers stacking interactions between pairs of bases. This is distinct from the base-pair stacks and coaxial stacks that appear in typical NN models, which involve four bases (two from each strand). Multiple interactions in oxDNA then contribute to the effective strength of base-pair and coaxial stacking, when the model is compared with NN descriptions.
Figure 9.
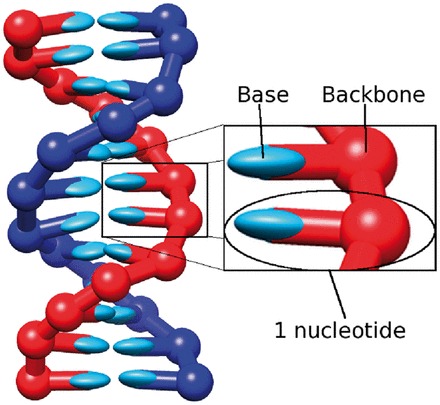
A 12-bp DNA duplex as represented by oxDNA. The enlarged section shows two rigid nucleotides, highlighting the backbone and base parts. The planarity of bases is captured through the orientational dependence of interactions. Image reproduced from Ouldridge et al. [90].
oxDNA captures the thermodynamic and mechanical changes associated with the formation of duplexes from single strands, under high salt conditions. Specifically, it quantitatively reproduces the oligomer length-dependence of melting temperatures for the duplex transition, the widths of transitions, the elastic moduli of duplexes and the short persistence length of single strands. oxDNA includes the Watson–Crick rules of complementary base pairing, but no further sequence dependence. Duplex formation was therefore fitted to the behavior of SantaLucia’s NN model (10) when averaged over sequence, and we can only compare directly with the average-strength toehold data of Zhang and Winfree (30). oxDNA was fitted at 0.5 M [Na+], where electrostatic interactions are strongly screened—the repulsion of phosphates is therefore incorporated into the backbone excluded volume for simplicity. The experiments of Zhang and Winfree (30) were performed in a buffer of 12.5 mM 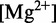 , which is known to result in similar duplex formation thermodynamics to high monovalent salt buffers (10). It is plausible that kinetics of strand displacement might be significantly different in these two buffers—the migration of Holliday junctions, for example, is known to vary between magnesium and sodium buffers (63,64). Given that oxDNA was fitted only to the duplex formation thermodynamics, however, there is no reason to assume that its kinetics and the representation of transition intermediates are more suited to one buffer than the other.
, which is known to result in similar duplex formation thermodynamics to high monovalent salt buffers (10). It is plausible that kinetics of strand displacement might be significantly different in these two buffers—the migration of Holliday junctions, for example, is known to vary between magnesium and sodium buffers (63,64). Given that oxDNA was fitted only to the duplex formation thermodynamics, however, there is no reason to assume that its kinetics and the representation of transition intermediates are more suited to one buffer than the other.
Although oxDNA contains many parameters, none were adjusted from those presented previously (39) for the purposes of this particular study. The parameter values used have been seen to produce physically reasonable behavior for a range of systems. Such systems include DNA tweezers (39), a DNA walker (65) and the interaction of kissing hairpins (66) and overstretching of DNA under tension (67). Two of these systems, the tweezers and the walker, depend on strand displacement, and so oxDNA has previously been shown to reproduce this phenomenon. Furthermore, a barrier to initiating branch migration was predicted when studying the tweezers (39), although it was not studied in great detail.
Simulation techniques
We provide a concise summary of our simulation techniques here; for details, see Supplementary Section S6. We use two algorithms to simulate oxDNA: the ‘Virtual Move Monte Carlo’ (VMMC) algorithm of Whitelam et al. (68,69) and the rigid-body Langevin Dynamics (LD) algorithm of Davidchack et al. (70). The first approach randomly attempts and accepts moves of clusters of nucleotides (illustrated in Supplementary Figure S12) in a manner that ensures the system samples from a Boltzmann distribution. The second incorporates noise and damping terms into Newton’s equations in a self-consistent manner, thereby generating states drawn from the canonical ensemble. The sampling of states is more efficient with VMMC, and so it is used for all thermodynamic averages. Langevin algorithms, however, are explicitly dynamical, so they naturally give kinetic information that is harder to infer from VMMC. Consequently, all kinetic results quoted in this work use the LD algorithm.
Processes like strand displacement are computationally demanding to simulate, and thus they require enhanced sampling techniques. We use umbrella sampling (71) to improve equilibration of thermodynamic averages in VMMC simulations. This method involves applying an artificial bias to lower free-energy barriers, thereby accelerating the transitions between (meta)stable states. For LD simulations of kinetics, we use forward flux sampling (72,73) to obtain accurate estimates of the relative rates of strand displacement for different lengths of toehold, as shown in Supplementary Figure S13.
oxDNA’s energy, mass and length scales imply a time scale. Results in this section are quoted in terms of this time scale for completeness. As we are using a coarse-grained model with an approximate model of dynamics, however, the absolute times and rates reported should not be overinterpreted. We focus on relative rates, which should be affected in a similar manner by the approximations in oxDNA and the algorithms used to simulate it.
Kinetic simulations of displacement
We consider a slightly truncated system (Supplementary Table S6) based on that used by Zhang and Winfree (30). For computational simplicity, we removed the majority of the tail of the incumbent strand, which was used to interact with a reporter. Further, to simplify the order parameter for displacement, we use an approach in which only the expected (native) base pairs between the incumbent and the substrate or the invading strand and the substrate are given a non-zero binding strength. This simplification is reasonable because the sequences were designed to exhibit minimal secondary structure and cross-interactions when single-stranded. Additional simulations of toehold association were also performed to explore the consequences of this simplification: for further details, see Supplementary Section S6. Simulations of the three strands were performed in a periodic cell of volume 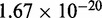 L for toehold lengths between 0 and 7 bases. We initialized the system at 25°C with the incumbent fully bound to the substrate and the invading strand separate and measured the overall rate of displacement using forward flux sampling. Order parameters and detailed results are given in Supplementary Tables S7–S10.
L for toehold lengths between 0 and 7 bases. We initialized the system at 25°C with the incumbent fully bound to the substrate and the invading strand separate and measured the overall rate of displacement using forward flux sampling. Order parameters and detailed results are given in Supplementary Tables S7–S10.
Figure 10 reports the measured relative rates of displacement for different toehold lengths in simulation (30). oxDNA agrees remarkably well with the experimental data: in particular, it shows the same exponential dependence on toehold length for short toeholds followed by a plateau for longer ones. The overall acceleration from 0- to 7-base toehold is 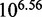 , close to the experimental value of
, close to the experimental value of 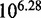 . It would be unwise to put excessive emphasis on this agreement, but the base-pairing energies of oxDNA are fitted to the same secondary-structure free energies underlying the thermodynamics of Multistrand and the IEL, and therefore the predictions of these discrete models should be equally applicable to oxDNA as to real DNA. By analyzing oxDNA’s representation of displacement, we now aim to physically justify the parameters used in the IEL.
. It would be unwise to put excessive emphasis on this agreement, but the base-pairing energies of oxDNA are fitted to the same secondary-structure free energies underlying the thermodynamics of Multistrand and the IEL, and therefore the predictions of these discrete models should be equally applicable to oxDNA as to real DNA. By analyzing oxDNA’s representation of displacement, we now aim to physically justify the parameters used in the IEL.
Figure 10.
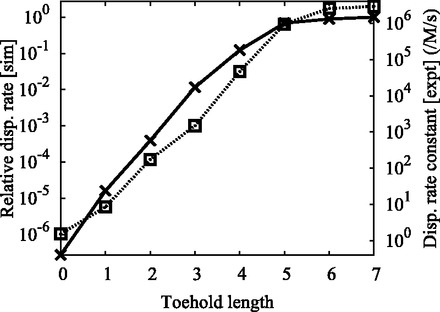
Rate of displacement, as a function of toehold length, observed in simulations (crosses, left axis). Details on the measurement errors of these values are provided in Supplementary Section S6. Also shown (squares, right axis) are the experimental data for the bimolecular rate constant of strand displacement for an average-strength toehold of varying length, taken from Figure 3b of Zhang and Winfree (30). The logarithmic scales of both axes are identical up to a constant normalizing offset.
Free-energy profile of displacement
We measure the free-energy profile of displacement to see whether oxDNA reproduces the experimental tendency of two ssDNA overhangs to destabilize a branch point and provides a physical explanation for it. We show the free energy of the three-stranded displacement complex as a function of the progress of branch migration, as measured by the identity of the base pair between invading and substrate strands closest to the  -end of the substrate, in Figure 11. We observe an increase in free energy of ∼1.3 kcal/mol as branch migration is initiated, similar to the plateau height introduced to improve the IEL. Furthermore, as suggested by our strand displacement snapshot experiment, this barrier appears to saturate quickly: once a second ssDNA overhang of three or four bases has been created, there is negligible further increase in the destabilization. When the invading strand’s single-stranded overhang is reduced to a few bases toward the end of branch migration, the free-energy penalty decreases (as in experiment).
-end of the substrate, in Figure 11. We observe an increase in free energy of ∼1.3 kcal/mol as branch migration is initiated, similar to the plateau height introduced to improve the IEL. Furthermore, as suggested by our strand displacement snapshot experiment, this barrier appears to saturate quickly: once a second ssDNA overhang of three or four bases has been created, there is negligible further increase in the destabilization. When the invading strand’s single-stranded overhang is reduced to a few bases toward the end of branch migration, the free-energy penalty decreases (as in experiment).
Figure 11.
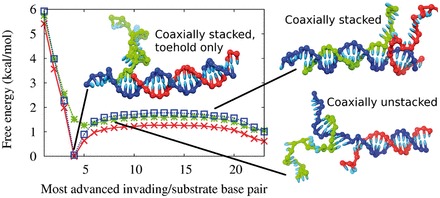
Free energy profile of displacement for a 4-base toehold. The red crosses show the free energy as a function of the index of the most advanced base pair between the invading strand and the substrate (base pair 1 is the base pair in the toehold furthest from the incumbent). These macrostates can be subdivided into those that involve coaxial stacking at the branch point (blue squares) and those that do not (green stars). The definition of which states are defined as stacked and which as unstacked is given in Supplementary Section S6. The simulation snapshots illustrate typical configurations of the macrostates indicated. In each of these images, the blue strand is the substrate, the red is the incumbent and the green is the invading strand.
The fact that the penalty saturates after around four bases suggests that the cause is local to the branch point. From looking at the branch migration intermediate in Figure 11 in which the helices are coaxially stacked at the junction, one can see that the branch point is densely packed with nucleotides. To maintain coaxial stacking of helices at the junction, the two single-stranded overhangs must both take evasive action, unstacking and bending away from each other. The system can also reduce the overcrowding by breaking the coaxial stacking at the branch point, as in the coaxially unstacked image in Figure 11, but this carries a penalty itself. This overcrowding is worse with two ssDNA overhangs than one, resulting in a free-energy penalty for initiating branch migration and creating a second overhang.
Figure 11 also shows separate free-energy profiles for systems restricted to coaxially stacked or unstacked states (definitions of these states are provided in Supplementary Section S6). The existence of the overcrowding penalty makes the coaxially unstacked state (which is initially unfavorable, but involves minimal overcrowding) relatively more probable at later stages of branch migration. In the absence of coaxial stacking, the plateau height is minimal, consistent with our diagnosis of overcrowding.
To complete the comparison between simulation and experiment, we have estimated the destabilizing effect of single-stranded overhangs on duplex formation within oxDNA. The systems are analogous to those used in our experimental studies and illustrated in Figure 6, but the hairpins have shorter stems of length 12 base pairs. Furthermore, to make comparisons at 25 and 55°C for the chosen simulated concentration, we use complementary lengths for interstrand binding of six and eight bases, respectively, ( can be inferred most accurately from experiments at
can be inferred most accurately from experiments at  C, where the complexes melt, but we are most interested in the value at ∼25°C). The contribution of the single-stranded overhangs to the free energy of association
C, where the complexes melt, but we are most interested in the value at ∼25°C). The contribution of the single-stranded overhangs to the free energy of association 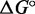 is expected to be independent of the length of the duplexes, however, allowing a direct comparison of this property to be made. The sequences used are given in Supplementary Table S11, and further details are provided in Supplementary Section S6.
is expected to be independent of the length of the duplexes, however, allowing a direct comparison of this property to be made. The sequences used are given in Supplementary Table S11, and further details are provided in Supplementary Section S6.
The results of the hybridization simulations are reported in Table 2. The presence of two long ssDNA overhangs is destabilizing by ∼1.3 and 0.75 kcal/mol at 25 and 55°C, respectively, relative to the case with one single-stranded overhang. We conclude that oxDNA has a plateau height comparable with (but slightly smaller than) that found in experiment, with the caveat that we have not measured sequence-dependent effects at the branch point.
Table 2.
Destabilizing 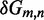 due to dangling ssDNA sections, as found in simulations
due to dangling ssDNA sections, as found in simulations
| Duplex length | T/°C | m | n |
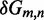 (kcal/mol) (kcal/mol) |
|---|---|---|---|---|
| 6 | 25 | 10 | 0 | 1.46 [1.2] |
| 0 | 10 | 1.38 [1.0] | ||
| 10 | 10 | 2.72 [3.2] | ||
| 8 | 55 | 10 | 0 | 0.87 [0.60] |
| 0 | 10 | 0.94 [0.78] | ||
| 10 | 10 | 1.65 [1.79] |
m is the length of the excess ssDNA attached to the hairpin, and n the length attached to the shorter strand. Values for 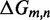 , the free energy of formation of the duplex, are extracted from simulations. The reported value,
, the free energy of formation of the duplex, are extracted from simulations. The reported value, 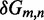 , is given by
, is given by 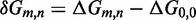 .
. 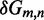 is then the destabilization of the duplex due to the ssDNA overhangs. The values in square brackets correspond to values inferred from our experimental studies for the closest equivalent lengths of dangling ssDNA. Note that
is then the destabilization of the duplex due to the ssDNA overhangs. The values in square brackets correspond to values inferred from our experimental studies for the closest equivalent lengths of dangling ssDNA. Note that 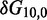 and
and 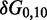 found here are compared to
found here are compared to 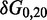 and
and 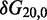 from experiment – the local nature of the destabilisation makes this reasonable.
from experiment – the local nature of the destabilisation makes this reasonable.
Kinetics of branch migration and fraying
Here, we examine oxDNA’s representation of the mechanism of branch migration in detail. Consistent with the literature (28,29,33), oxDNA predicts that branch migration is slow compared to the rate at which base pairs in the toehold fray and provides a mechanistic explanation for this difference.
Typical branch migration steps observed in oxDNA are shown in Figure 12. Two types of process occur most commonly:
Invading and incumbent duplexes remain coaxially stacked at the branch point, and a single-stranded base from the invading strand enters the duplex region, competes for base-pairing to the substrate with a base from the incumbent, and eventually displaces it. This process is illustrated in Figure 12A. We refer to this process as ‘branch migration via invasion’.
Invading and incumbent duplexes coaxially unstack at the branch point, and a base in the substrate is transferred from one duplex to the other. In this process, one base pair must fully break before the other forms some time later. An example of such a step is shown in Figure 12B. We refer to this process as ‘branch migration via sequential disruption and formation of bonds’.
Figure 12.
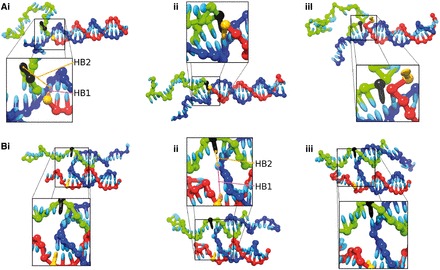
Typical branch migration steps as represented by oxDNA, for a toehold length of three bases. In each case, the nucleotide colored black displaces the nucleotide colored gold. (A) Displacement via invasion: a base from the invading strand enters the incumbent/substrate duplex and competes with a base from the incumbent for base pairing. (i) Initial state, with the gold-colored base on the incumbent bound to the substrate and the black-colored base on the invading strand unbound. (ii) Metastable intermediate with both the gold and black bases competing for base pairing with the substrate. (iii) Final state, with the black base bound to the substrate and the gold base unbound. (B) Displacement via sequential disruption and formation of bonds: a base pair in the incumbent/substrate duplex breaks and the substrate base unstacks and moves across to the invading/substrate duplex. (i) Coaxially unstacked initial state, with the gold-colored base on the incumbent bound to the substrate and the black-colored base on the invading strand unbound. (ii) Metastable intermediate state, in which the base pair involving the gold base has broken, and the base from the substrate strand has unstacked. (iii) Final state, with the substrate base now bound to the black base in the invading strand. Labeled distances between hydrogen-bonding sites are used as coordinates to monitor branch migration steps in detail later in Figure 13.
Invasion is dominant at the start of branch migration, when the majority of systems are coaxially stacked. Branch migration via sequential disruption and formation of bonds becomes more relevant at intermediate stages, when coaxial stacking is less prevalent. The two mechanisms differ in whether the duplexes are coaxially stacked during branch migration, and whether the displacing base invades the duplex before disruption of the initial base pairing. Invasion is geometrically infeasible from an unstacked state. However, the substrate strand could remain stacked at the branch point whilst ‘flipping out’ a base from the incumbent and only then replacing it with a base from the invader. This third type of process is rarer than the alternatives in oxDNA, but cannot be ruled out for real DNA. Importantly, all three processes require the disruption of favorable stacking interactions between neighboring bases and considerable structural rearrangement, for each step of branch migration.
We also note that the branch migration pathways have relatively long-lived metastable intermediates (states represented by Figure 12A.ii and B.ii. These intermediates can be clearly identified on free-energy landscapes for individual steps of the branch migration process that are plotted in Figure 13A and B. Typical trajectories of branch migration are shown in Figure 13C and D. Figure 13C, taken from the start of branch migration, clearly shows the system moving from one base-pairing configuration to another via a metastable intermediate in which both invading and incumbent bases are close to the substrate base (branch migration via invasion). Figure 13D, taken from a later stage of branch migration, shows a change in base pairing occurring via the diffuse metastable intermediate in which both invading and incumbent bases are distant from the substrate base (branch migration via sequential disruption and formation of bonds). We note that trajectories of both types are possible at each stage, but that invasion is particularly dominant for the first step of branch migration. The fact that the intermediates are metastable, despite their high free energy, indicates that they are not easily accessible from the typical configurations of the system.
Figure 13.
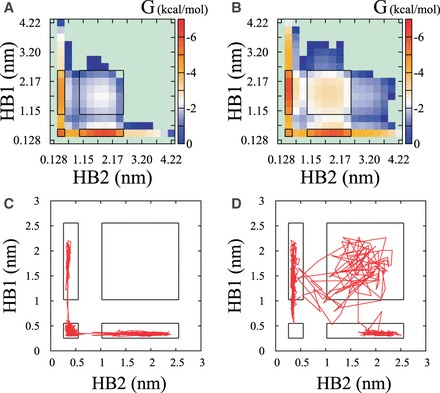
(A) The free-energy landscape of the first branch migration step (for a three-base toehold) as a function of the separation of hydrogen-bonding sites involved, obtained from umbrella sampling simulations. The distances HB1 and HB2 between hydrogen-bonding sites of nucleotides are illustrated in Figure 12A.i. In essence, they are distances of the competing bases in the invading (HB2) and incumbent (HB1) strands from their complement in the substrate. In these figures, the black rectangles and squares highlight the same regions in each graph, roughly corresponding to the initial, final and intermediate states involved in branch migration. Free energy landscapes are measured in bins of 0.255 nm—the labels indicate the values of HB1 and HB2 at the center of the bins. The arbitrary offset of G is chosen so that the most probable bin has a free energy 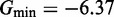 kcal/mol. All bins with a free energy greater than zero on this scale are shown in light green. (B) An equivalent landscape to (A), but obtained at a later stage (step 11) of migration when branch migration via sequential disruption and formation of bonds is more common. (C) An example trajectory showing the first step of branch migration occurring via invasion. (D) An example trajectory from the 11th step showing branch migration via sequential disruption and formation of bonds.
kcal/mol. All bins with a free energy greater than zero on this scale are shown in light green. (B) An equivalent landscape to (A), but obtained at a later stage (step 11) of migration when branch migration via sequential disruption and formation of bonds is more common. (C) An example trajectory showing the first step of branch migration occurring via invasion. (D) An example trajectory from the 11th step showing branch migration via sequential disruption and formation of bonds.
By contrast, the fraying of a few base pairs in the toehold and the subsequent detachment of the invading strand can occur relatively easily. As illustrated in Figure 14A–C, it is not necessary to disrupt at least one stacking interaction for every base pair that is broken (as it is in branch migration). Further, transition states in fraying are much closer in configuration space to the typical states of the system than they are for branch migration, making them easier to access. This finding is corroborated by Figure 14D, which shows that the coordinates of the system do not have to deviate far from their typical values before detachment occurs. For comparison with Figure 13, Figure 15A shows a free-energy landscape as a function of the separation of the base pairs in a two base-pair toehold. The minimum in the bottom left corresponds to the fully bound state, and the trajectory shown in Figure 15B is the same as that in Figure 14, illustrating both base pairs breaking in quick succession and the system leaving the bound state.
Figure 14.
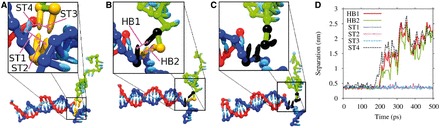
An example of melting for a 2-base toehold. As before, the blue strand is the substrate, the red is the incumbent and the green is the invading strand. (A) Both base pairs of the toehold (shown in gold) are formed. (B) One base pair (shown in black) is broken, and one (gold) remains. (C) Both base pairs (black) are broken. (D) Plots of hydrogen bonding and stacking site separation during this detachment, demonstrating the relatively minor disruption of interstrand stacking (only the stacking between incumbent and invading strand is disrupted) and rearrangement of structure necessary, and the proximity of the transition state to the fully bound state. The relevant distances for the stacking interactions are shown in (A), and for the hydrogen-bonding in (B). (A), (B) and (C) correspond to times of 175, 204 and 210 ps on the trajectory shown in (D). In this case, the system first breaks the intrastrand stack ST4, followed by base pairs HB1 and HB2. Trajectories with different orders are also observed.
Figure 15.
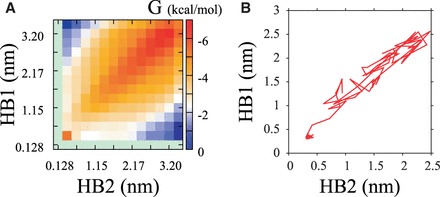
(A) Free-energy landscape of a system with a two base-pair toehold, with the system prevented from forming other base pairs between invader and substrate and also prevented from having either base pair separation exceed 3.7 nm. HB1 and HB2 are the base-pair separations defined in Figure 14B. The free energy landscape is measured in bins of 0.255 nm—the labels indicate the values of HB1 and HB2 at the center of the bins. The arbitrary offset of G is chosen so that the most probable bin has a free energy 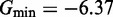 kcal/mol. All bins with a free energy greater than zero on this scale are shown in light green. (B) The melting trajectory from Figure 14 projected onto the HB1, HB2 space.
kcal/mol. All bins with a free energy greater than zero on this scale are shown in light green. (B) The melting trajectory from Figure 14 projected onto the HB1, HB2 space.
Although the fine details of branch migration processes will be sensitive to detailed chemistry neglected by oxDNA, the conclusion that each step of branch migration necessarily involves the breaking of more stacking interactions and a greater structural rearrangement than fraying of base pairs in the toehold is likely to be a robust one. As a result, if toehold melting and branch migration are to be simultaneously characterized by the IEL, the sawtooth amplitude of branch migration should be larger than the cost of fraying a base pair. We have not directly attempted to infer rates or transition free energies for processes that would correspond to elementary steps in the IEL with oxDNA. As we have discussed, such elementary processes can be relatively complex in oxDNA, involving effects that cannot be captured at the secondary structure level, making the precise definition of rate constants difficult. Nonetheless, understanding the process at an effective secondary structure level is helpful: oxDNA then justifies tuning the IEL to use an effective sawtooth amplitude significantly larger than the free energy of a single base-pair stack to slow the rate of branch migration.
DISCUSSION
We have argued that the kinetics of strand displacement can be explained by the destabilizing effect of single-stranded overhangs at the branch migration junction, and the relative slowness of branch migration compared to the fraying of a base pair in the toehold. How consistent are our findings and interpretations with the literature?
Our experiments infer two de-stabilizations: one due to the first ssDNA overhang at the junction (X20:Y00 versus X00:Y00; 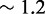 kcal/mol at 25°C) and another due to the addition of the second overhang (X10:Y10 versus X20:Y00;
kcal/mol at 25°C) and another due to the addition of the second overhang (X10:Y10 versus X20:Y00; 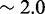 kcal/mol). We have not investigated the sequence dependence of these effects. Vasiliskov et al. (50) have measured the destabilization due to a single base overhang (analogous to X01:Y00 versus X00:Y00, which we did not measure) by immobilizing DNA oligonucleotides in 3D polyacrylamide gel microchips. Most of their sequence-dependent values lie between 0.5 and 1.0 kcal/mol at 37°C, which is similar to our temperature-extrapolated destabilization of 0.9 kcal/mol for X20:Y00 relative to X00:Y00. We would expect the destabilization to be slightly less for X01:Y00 than X20:Y00 from the intuition derived from our experimental studies of two overhangs, which indicate that the destabilization is not fully saturated by a single-base overhang.
kcal/mol). We have not investigated the sequence dependence of these effects. Vasiliskov et al. (50) have measured the destabilization due to a single base overhang (analogous to X01:Y00 versus X00:Y00, which we did not measure) by immobilizing DNA oligonucleotides in 3D polyacrylamide gel microchips. Most of their sequence-dependent values lie between 0.5 and 1.0 kcal/mol at 37°C, which is similar to our temperature-extrapolated destabilization of 0.9 kcal/mol for X20:Y00 relative to X00:Y00. We would expect the destabilization to be slightly less for X01:Y00 than X20:Y00 from the intuition derived from our experimental studies of two overhangs, which indicate that the destabilization is not fully saturated by a single-base overhang.
oxDNA suggests that the destabilization due to overhangs arises from steric interference, which can be relieved by breaking coaxial stacking at the junction. This suggests that 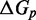 (and the free energy cost of introducing two overhangs to an overhang-free system) should not be significantly larger than the
(and the free energy cost of introducing two overhangs to an overhang-free system) should not be significantly larger than the 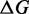 associated with the coaxial stacking transition in a nicked duplex. Several attempts to measure this quantity (48,50,74) have inferred values of
associated with the coaxial stacking transition in a nicked duplex. Several attempts to measure this quantity (48,50,74) have inferred values of 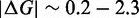 kcal/mol at 37°C and
kcal/mol at 37°C and 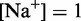 to 15 mM. Increasing
to 15 mM. Increasing 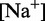 to 100 mM was observed to increase stability of coaxial stacks by ∼0.4 kcal/mol. We therefore conclude that our temperature-extrapolated destabilization of 2.8 kcal/mol between X10:Y10 and X00:Y00 at 37°C (and in high salt conditions) is not inconsistent with these data.
to 100 mM was observed to increase stability of coaxial stacks by ∼0.4 kcal/mol. We therefore conclude that our temperature-extrapolated destabilization of 2.8 kcal/mol between X10:Y10 and X00:Y00 at 37°C (and in high salt conditions) is not inconsistent with these data.
What do our findings imply for RNA? Walter et al. (75) have measured de-stabilization due to a single base overhang at a junction of duplexes as well as two single base overhangs on either side of a junction for RNA. They report a 2.8 kcal/mol de-stabilization for their analog of X01:Y01 versus X00:Y00 at 37°C, which is much higher than our extrapolation of 1.4 kcal/mol for DNA. As the geometry (A-form helix) and thermodynamics of RNA are significantly different from that of DNA, we would not expect analogous measurements for RNA to be quantitatively similar. For DNA, we find that X20:Y01 is significantly less stable than X01:Y01, and if this holds true for RNA, we would expect 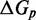 for RNA to be significantly higher than the 2.0 kcal/mol at 25°C we infer for DNA. However, efn2, a NN thermodynamics model for RNA that has been expanded to include experimentally measured terms for coaxial stacking and 1– and 2-nt overhangs at junctions (76,77), does not predict a free energy penalty similar to that which we infer for DNA strand displacement (see Supplementary Section S7 and Supplementary Figure S14), possibly due to incorporating these terms only in ‘interior loops’.
for RNA to be significantly higher than the 2.0 kcal/mol at 25°C we infer for DNA. However, efn2, a NN thermodynamics model for RNA that has been expanded to include experimentally measured terms for coaxial stacking and 1– and 2-nt overhangs at junctions (76,77), does not predict a free energy penalty similar to that which we infer for DNA strand displacement (see Supplementary Section S7 and Supplementary Figure S14), possibly due to incorporating these terms only in ‘interior loops’.
Is the IEL’s inferred value of 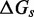 consistent with measured branch migration rates? Using the experimentally measured plateau height
consistent with measured branch migration rates? Using the experimentally measured plateau height 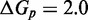 kcal/mol and the corresponding inferred values of
kcal/mol and the corresponding inferred values of 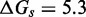 kcal/mol for the IEL and
kcal/mol for the IEL and 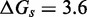 kcal/mol for the AEL, these models predict branch migration step times of ∼103 and ∼53 μs, respectively. These values are now more in line with previous experimental measurements: Radding et al. (28) report an average branch migration step time of 12 μs at 37°C in 10 mM Na+ and Green and Tibbetts (29) estimate an upper limit of 20 μs at 65°C in 0.3 M Na+. Our estimates are therefore somewhat larger, although it would be expected that the low temperature high salt conditions of Zhang and Winfree (30), which stabilize helices, would reduce branch migration rates. Indeed, such an effect is reported by Radding et al. (28). Finally, we note that Zhang and Winfree (30) infer a branch migration step time of ∼2.5 ms from their phenomenological model, ∼12–24 times larger still than our estimates. We attribute this difference to the absence in their model of a free energy penalty for initiating branch migration, i.e. what we here call
kcal/mol for the AEL, these models predict branch migration step times of ∼103 and ∼53 μs, respectively. These values are now more in line with previous experimental measurements: Radding et al. (28) report an average branch migration step time of 12 μs at 37°C in 10 mM Na+ and Green and Tibbetts (29) estimate an upper limit of 20 μs at 65°C in 0.3 M Na+. Our estimates are therefore somewhat larger, although it would be expected that the low temperature high salt conditions of Zhang and Winfree (30), which stabilize helices, would reduce branch migration rates. Indeed, such an effect is reported by Radding et al. (28). Finally, we note that Zhang and Winfree (30) infer a branch migration step time of ∼2.5 ms from their phenomenological model, ∼12–24 times larger still than our estimates. We attribute this difference to the absence in their model of a free energy penalty for initiating branch migration, i.e. what we here call 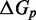 .
.
Are the IEL’s values for 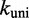 and
and 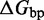 compatible with measured fraying rates? Wetmur and Davidson (33) have inferred fraying rates from temperature-jump experiments. They predict 0.04 μs for fraying of a base pair at 25°C, which is faster than our values (0.2 μs for the IEL, 2 μs for AEL) and consistent with fraying being at least an order of magnitude faster than branch migration steps. We note, however, that these reported values were not directly measured in experiments and required modeling to extract. Furthermore, related measurements of the kinetics of RNA base pair fluctuations found significantly slower rates, with fraying times on the order of microseconds at 25°C (55–57). We therefore conclude that our parameterization is not inconsistent with well-established kinetic properties of nucleic acids.
compatible with measured fraying rates? Wetmur and Davidson (33) have inferred fraying rates from temperature-jump experiments. They predict 0.04 μs for fraying of a base pair at 25°C, which is faster than our values (0.2 μs for the IEL, 2 μs for AEL) and consistent with fraying being at least an order of magnitude faster than branch migration steps. We note, however, that these reported values were not directly measured in experiments and required modeling to extract. Furthermore, related measurements of the kinetics of RNA base pair fluctuations found significantly slower rates, with fraying times on the order of microseconds at 25°C (55–57). We therefore conclude that our parameterization is not inconsistent with well-established kinetic properties of nucleic acids.
We argue that the slowness of branch migration initiation relative to fraying is a key aspect in understanding strand displacement. In contrast, Reynaldo et al. (35) explained the low rate constant of zero-toehold displacement by positing that a certain number of base pairs, n = 3 or 4, are necessary to form a stable duplex, and thus shorter duplexes can be ignored or assumed to detach instantly. Our models differ by assigning favorable and increasingly strong thermodynamic energies for toeholds attaching by 1, 2 or more base pairs; there is no penalty for short duplexes. Instead, we can reinterpret their n as the value for which the rate of fraying n base pairs (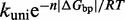 ) equals that of initiating branch migration (
) equals that of initiating branch migration (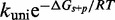 ), which for the IEL gives
), which for the IEL gives 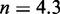 . A similar calculation for the AEL gives
. A similar calculation for the AEL gives 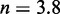 .
.
CONCLUSIONS
We explain the dependence of strand displacement kinetics on toehold length using two factors: (i) the physical process by which a single step of branch migration occurs is significantly slower than the fraying of a single base pair and (ii) initiating branch migration incurs a thermodynamic penalty, not captured by state-of-the-art nearest neighbor models of DNA, due to the additional overhang it engenders at the junction. The slowness of branch migration relative to fraying is captured in the IEL by a sawtooth amplitude 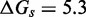 kcal/mol, which is significantly larger than a single base-pair stack (
kcal/mol, which is significantly larger than a single base-pair stack (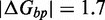 kcal/mol). oxDNA provides physical justification for this by suggesting that branch migration steps are slower than fraying as each stage necessarily involves greater structural rearrangement and disruption of favorable stacking interactions. Initiating branch migration is slower than the average branch migration step because of the free energy penalty (
kcal/mol). oxDNA provides physical justification for this by suggesting that branch migration steps are slower than fraying as each stage necessarily involves greater structural rearrangement and disruption of favorable stacking interactions. Initiating branch migration is slower than the average branch migration step because of the free energy penalty ( ) incurred; from our experiments we infer
) incurred; from our experiments we infer 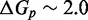 kcal/mol. oxDNA reproduces this penalty and suggests that it arises from steric interference of the single strands and duplexes at the branch migration junction. Specifically, the presence of an extra single-stranded overhang after the first step of branch migration causes additional disruption of (coaxial) stacking and reduction of conformational freedom as the strands are forced to bend away from each other.
kcal/mol. oxDNA reproduces this penalty and suggests that it arises from steric interference of the single strands and duplexes at the branch migration junction. Specifically, the presence of an extra single-stranded overhang after the first step of branch migration causes additional disruption of (coaxial) stacking and reduction of conformational freedom as the strands are forced to bend away from each other.
Our work shows that toehold-mediated strand displacement involves four distinct time scales—rates of hybridization, fraying, branch migration and branch migration initiation—coupled with the energetics of base pairing in the toehold. The IEL model captures these rates via the parameters 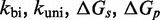 and
and 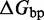 . Presuming that these rates and energies are the essential determinants of strand displacement kinetics, the IEL analysis provides a framework for making kinetic predictions about different strand displacement-based systems. For example, the IEL predicts that for short toeholds,
. Presuming that these rates and energies are the essential determinants of strand displacement kinetics, the IEL analysis provides a framework for making kinetic predictions about different strand displacement-based systems. For example, the IEL predicts that for short toeholds, 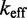 scales as ∼
scales as ∼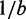 , where b is the branch migration domain length (see Supplementary Section S2 and Supplementary Figure S15). However, the dependence of
, where b is the branch migration domain length (see Supplementary Section S2 and Supplementary Figure S15). However, the dependence of 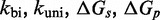 and
and 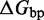 on reaction conditions (e.g. salt concentrations and temperature) are only partially understood, impeding quantitative predictions for differing reaction conditions. Nonetheless, our current understanding does suggest that determining just those five parameters should be sufficient to predict toehold-mediated strand displacement under new conditions.
on reaction conditions (e.g. salt concentrations and temperature) are only partially understood, impeding quantitative predictions for differing reaction conditions. Nonetheless, our current understanding does suggest that determining just those five parameters should be sufficient to predict toehold-mediated strand displacement under new conditions.
We expect that the IEL framework is also suitable for describing other nucleic acids. Toehold-mediated strand displacement has been demonstrated with RNA (78,79), but the dependence of kinetics on toehold length has not been characterized. Although several experimental studies have reported hybridization and fraying rates for RNA that are within the range observed for DNA (55,57,80–82), branch migration and branch migration initiation rates are not well understood. There is, however, some evidence that with 1-nt toeholds, strand displacement rates for RNA are considerably slower than those for DNA (83), whereas the average base pairing energy is stronger (76); these observations are enough to predict that a plot of 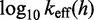 for RNA would have a lower y-intercept but higher initial slope than that for DNA. Broadly, then, we would expect the qualitative features of RNA strand displacement kinetics to be similar to that of DNA; quantitative understanding will require further experiments.
for RNA would have a lower y-intercept but higher initial slope than that for DNA. Broadly, then, we would expect the qualitative features of RNA strand displacement kinetics to be similar to that of DNA; quantitative understanding will require further experiments.
Similarly, the effect of structural variations of toehold-mediated strand displacement, such as associative and remote toeholds (84,85), or initial mismatches in the branch migration domain (86) could be understood in terms of their effects on the fundamental rates and energies. These particular variants are likely to slow down branch migration initiation and hence increase 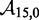 , which could in turn permit greater design flexibility while engineering nucleic acid devices and systems.
, which could in turn permit greater design flexibility while engineering nucleic acid devices and systems.
Although the IEL provides a simple framework for understanding strand displacement, it does not predict or explain the underlying biophysical mechanisms, nor can it easily be adapted to handle more complex structural variants or explain sequence-dependent behavior in larger strand displacement cascades and dynamic DNA nanotechnology (24), where the kinetics of both on- and off-pathway reactions (such as ‘leak’ reactions analogous to zero-toehold strand displacement) are of great current interest. oxDNA is well suited to studying the underlying biophysical mechanisms and behaviors of structural variants, but it is computationally expensive for larger systems.
Efficient quantitative simulation of sequence-dependent kinetics for both desired and spurious strand displacement pathways would facilitate design and optimization of large systems in silico. SSK models based on NN thermodynamics, such as Multistrand, would be well-suited for such purposes, but as found here, current implementations require adjustment to match critical thermodynamic and kinetic features. Thermodynamically, accurate coaxial stacking terms and penalties for overhanging single-stranded sections of DNA at junctions should be incorporated into the model. Incorporating the relative rates of fraying and branch migration within the Multistrand model faces several challenges. Because every secondary structure state has a well-defined free energy, branch migration intermediates at the ‘top of the sawtooth’ (frayed junctions with two tails) cannot simply be pushed to higher energies, as was done for the IEL using 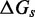 . Moreover, Multistrand currently incorporates only one of the two possible branch migration mechanisms suggested by oxDNA (sequential disruption and formation of bonds). Three independent approaches could conceivably be pursued to better capture branch migration kinetics. First, an additional unimolecular rate constant parameter could be used for transitions local to the junction. Second, new transitions, such as ‘shift’ moves in Kinfold (43,87), could be incorporated to model alternative branch migration pathways. Third, Multistrand’s state space could be augmented, possibly by including features such as non-base-pair stacking interactions.
. Moreover, Multistrand currently incorporates only one of the two possible branch migration mechanisms suggested by oxDNA (sequential disruption and formation of bonds). Three independent approaches could conceivably be pursued to better capture branch migration kinetics. First, an additional unimolecular rate constant parameter could be used for transitions local to the junction. Second, new transitions, such as ‘shift’ moves in Kinfold (43,87), could be incorporated to model alternative branch migration pathways. Third, Multistrand’s state space could be augmented, possibly by including features such as non-base-pair stacking interactions.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online, including [88–91].
FUNDING
National Science Foundation [CCF-0832824]; the Engineering and Physical Sciences Research Council [EP/I001352/1]; the Gordon and Betty Moore Foundation through the Caltech Programmable Molecular Technology Initiative; the Scatcherd European Trust; and University College, Oxford. Funding for open access charge: ‘Caltech Programmable Molecular Technology Initiative’, through the Gordon and Betty Moore Foundation.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Zhen-Gang Wang, Andrew J. Turberfield, David Yu Zhang, Niles A. Pierce, Brian R. Wolfe, David Soloveichik and Georg Seelig for helpful discussions. The authors thank the anonymous referees for feedback, which significantly improved this work.
REFERENCES
- 1.Kallenbach NR, Ma RI, Seeman NC. An immobile nucleic acid junction constructed from oligonucleotides. Nature. 1983;305:829–831. [Google Scholar]
- 2.Winfree E, Liu FR, Wenzler LA, Seeman NC. Design and self-assembly of two-dimensional DNA crystals. Nature. 1998;394:539. doi: 10.1038/28998. [DOI] [PubMed] [Google Scholar]
- 3.Rothemund PWK. Folding DNA to create nanoscale shapes and patterns. Nature. 2006;440:297–302. doi: 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
- 4.He Y, Ye T, Su M, Zhang C, Ribbe A, Jiang W, Mao C. Hierarchical self-assembly of DNA into symmetric supramolecular polyhedra. Nature. 2008;452:198–201. doi: 10.1038/nature06597. [DOI] [PubMed] [Google Scholar]
- 5.Seeman NC. An overview of structural DNA nanotechnology. Mol. Biotech. 2007;37:246–257. doi: 10.1007/s12033-007-0059-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pinheiro AV, Han D, Shih WM, Yan H. Challenges and opportunities for structural DNA nanotechnology. Nat. Nanotechnol. 2011;6:763–772. doi: 10.1038/nnano.2011.187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wei B, Dai M, Yin P. Complex shapes self-assembled from single-stranded DNA tiles. Nature. 2012;485:623–627. doi: 10.1038/nature11075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.SantaLucia J, Jr, Allawi HT, Seneviratne PA. Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry. 1996;35:3555–3562. doi: 10.1021/bi951907q. [DOI] [PubMed] [Google Scholar]
- 9.SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA. 1998;17:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.SantaLucia J, Jr, Hicks D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 11.Dirks RM, Bois JS, Schaeffer JM, Winfree E, Pierce NA. Thermodynamic analysis of interacting nucleic acid strands. SIAM Rev. 2007;49:65–88. [Google Scholar]
- 12.Hagerman PJ. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 13.Stojanovic MN, Semova S, Kolpashchikov D, Macdonald J, Morgan C, Stefanovic D. Deoxyribozyme-based ligase logic gates and their initial circuits. J. Am. Chem. Soc. 2005;127:6914–6915. doi: 10.1021/ja043003a. [DOI] [PubMed] [Google Scholar]
- 14.Penchovsky R, Breaker RR. Computational design and experimental validation of oligonucleotide-sensing allosteric ribozymes. Nat. Biotechnol. 2005;23:1424–1433. doi: 10.1038/nbt1155. [DOI] [PubMed] [Google Scholar]
- 15.Seelig G, Soloveichik D, Zhang DY, Winfree E. Enzyme-free nucleic acid logic circuits. Science. 2006;314:1585–1588. doi: 10.1126/science.1132493. [DOI] [PubMed] [Google Scholar]
- 16.Qian L, Winfree E. Scaling up digital circuit computation with DNA strand displacement cascades. Science. 2011;332:1196–1201. doi: 10.1126/science.1200520. [DOI] [PubMed] [Google Scholar]
- 17.Zhang DY, Turberfield AJ, Yurke B, Winfree E. Engineering entropy-driven reactions and networks catlayzed by DNA. Science. 2007;318:1121–1125. doi: 10.1126/science.1148532. [DOI] [PubMed] [Google Scholar]
- 18.Yin P, Choi HM, Calvert CR, Pierce NA. Programming biomolecular self-assembly pathways. Nature. 2008;451:318–323. doi: 10.1038/nature06451. [DOI] [PubMed] [Google Scholar]
- 19.Yurke B, Turberfield AJ, Mills AP, Simmel FC, Neumann J. A DNA-fueled molecular machine made of DNA. Nature. 2000;406:605–608. doi: 10.1038/35020524. [DOI] [PubMed] [Google Scholar]
- 20.Dirks RM, Pierce NA. Triggered amplification by hybridization chain reaction. Proc. Natl Acad. Sci. USA. 2004;101:15275–15278. doi: 10.1073/pnas.0407024101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pei R, Taylor SK, Stefanovic D, Rudchenko S, Mitchell TE, Stojanovic MN. Behavior of polycatalytic assemblies in a substrate-displaying matrix. J. Am. Chem. Soc. 2006;128:12693–12699. doi: 10.1021/ja058394n. [DOI] [PubMed] [Google Scholar]
- 22.Green SJ, Bath J, Turberfield AJ. Coordinated chemomechanical cycles: a mechanism for autonomous molecular motion. Phys. Rev. Lett. 2008;101:238101. doi: 10.1103/PhysRevLett.101.238101. [DOI] [PubMed] [Google Scholar]
- 23.Bath J, Turberfield AJ. DNA nanomachines. Nat. Nanotechnol. 2007;2:275–284. doi: 10.1038/nnano.2007.104. [DOI] [PubMed] [Google Scholar]
- 24.Zhang DY, Seelig G. Dynamic DNA nanotechnology using strand-displacement reactions.’ Nat. Chem. 2011;3:103–113. doi: 10.1038/nchem.957. [DOI] [PubMed] [Google Scholar]
- 25.Krishnan Y, Simmel FC. Nucleic acid based molecular devices. Angew. Chem. Int. Ed. 2011;50:3124–3156. doi: 10.1002/anie.200907223. [DOI] [PubMed] [Google Scholar]
- 26.Soloveichik D, Seelig G, Winfree E. DNA as a universal substrate for chemical kinetics. Proc. Natl Acad. Sci. USA. 2010;107:5393–5398. doi: 10.1073/pnas.0909380107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cardelli L. Two domain DNA strand displacement. Math. Struct. Comput. Sci. 2013;23:247–271. [Google Scholar]
- 28.Radding CM, Beattie KL, Holloman WK, Wiegand RC. Uptake of homologous single-stranded fragments by superhelical DNA. J. Mol. Biol. 1977;116:825–839. doi: 10.1016/0022-2836(77)90273-x. [DOI] [PubMed] [Google Scholar]
- 29.Green C, Tibbetts C. Reassociation rate limited displacement of DNA strands by branch migration. Nucleic Acids Res. 1981;9:1905–1918. doi: 10.1093/nar/9.8.1905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhang D, Winfree E. Control of DNA strand displacement kinetics using toehold exchange. J. Am. Chem. Soc. 2009;131:17303–17314. doi: 10.1021/ja906987s. [DOI] [PubMed] [Google Scholar]
- 31.Yurke B, Mills A. Using DNA to power nanostructures. Genet. Prog. Evol. Mach. 2003;4:111–122. [Google Scholar]
- 32.Morrison LE, Stols LM. Sensitive fluorescence-based thermodynamic and kinetic measurements of DNA hybridization in solution. Biochemistry. 1993;30:3095–3104. doi: 10.1021/bi00063a022. [DOI] [PubMed] [Google Scholar]
- 33.Wetmur JG, Davidson N. Kinetics of renaturation of DNA. J. Mol. Biol. 1968;31:349–370. doi: 10.1016/0022-2836(68)90414-2. [DOI] [PubMed] [Google Scholar]
- 34.Feller W. An Introduction to Probability Theory and its Applications. Vol. 1. New York: Wiley and Sons; 1968. [Google Scholar]
- 35.Reynaldo LP, Vologodskii AV, Neri BP, Lyamichev VI. The kinetics of oligonucleotide replacements. J. Mol. Biol. 2000;297:511–520. doi: 10.1006/jmbi.2000.3573. [DOI] [PubMed] [Google Scholar]
- 36.Schaeffer JM. Ph.D. Thesis. California Institute of Technology; 2013. Stochastic simulation of the kinetics of multiple interacting nucleic acid strands. [Google Scholar]
- 37.Ouldridge TE, Louis AA, Doye JPK. DNA nanotweezers studied with a coarse-grained model of DNA. Phys. Rev. Lett. 2010;104:178101. doi: 10.1103/PhysRevLett.104.178101. [DOI] [PubMed] [Google Scholar]
- 38.Ouldridge TE, Louis AA, Doye JPK. Structural, mechanical and thermodynamic properties of a coarse-grained DNA model. J. Chem. Phys. 2011;134:085101. doi: 10.1063/1.3552946. [DOI] [PubMed] [Google Scholar]
- 39.Ouldridge TE. Ph.D. Thesis. University of Oxford; 2011. Coarse-grained modelling of DNA and DNA nanotechnology. [Google Scholar]
- 40.Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculation by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 41.Rudolph G. Technical report. Collaborative Research Center ‘Computational Intelligence’ CI-75, University of Dortmund; 1999. The fundamental matrix of the general random walk with absorbing boundaries. [Google Scholar]
- 42.Kawasaki K. Diffusion constants near the critical point for time-dependent Ising models. Phys. Rev. 1966;145:224–230. [Google Scholar]
- 43.Flamm C, Fontana W, Hofacker IL, Schuster P. RNA folding at elementary step resolution. RNA. 2000;6:325–338. doi: 10.1017/s1355838200992161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.von Ahsen N, Wittwer CT, Schutz E. Oligonucleotide melting temperatures under PCR conditions: nearest-neighbor corrections for Mg2+, deoxynucleotide triphosphate, and dimethyl sulfoxide concentrations with comparison to alternative empirical formulas. Clin. Chem. 2001;47:1956–1961. [PubMed] [Google Scholar]
- 45.Owczarzy R, Moreira BG, You Y, Behlke MA, Walder JA. Predicting stability of DNA duplexes in solutions containing magnesium and monovalent cations. Biochemistry. 2008;47:5336–5353. doi: 10.1021/bi702363u. [DOI] [PubMed] [Google Scholar]
- 46.Bommarito S, Peyret N, SantaLucia J., Jr Thermodynamic parameters for DNA sequences with dangling ends. Nuclei Acids Res. 2000;28:1929–1934. doi: 10.1093/nar/28.9.1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Peyret N. Ph.D. Thesis. Wayne State University; 2000. Prediction of nucleic acid hybridization: parameters and algorithms. [Google Scholar]
- 48.Protozanova E, Yakovchuk P, Frank-Kamenetskii MD. Stacked-unstacked equilibrium at the nick site of DNA. J. Mol. Biol. 2004;342:775–785. doi: 10.1016/j.jmb.2004.07.075. [DOI] [PubMed] [Google Scholar]
- 49.Pyshnyi DV, Ivanova EM. Thermodynamic parameters of coaxial stacking on stacking hybridization of oligodeoxyribonucleotides. Russ. Chem. B. 2002;51:1145–1155. [Google Scholar]
- 50.Vasiliskov VA, Prokopenko DV, Mirzabekov AD. Parallel multiplex thermodynamic analysis of coaxial base stacking in DNA duplexes by oligodeoxyribonucleotide microchips. Nucleic Acids Res. 2001;29:2303–2313. doi: 10.1093/nar/29.11.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zadeh JN, Steenberg CD, Bois JS, Wolfe BR, Pierce MB, Khan AR, Dirks RM, Pierce NA. NUPACK: analysis and design of nucleic acid systems. J. Comput. Chem. 2011;32:170–173. doi: 10.1002/jcc.21596. [DOI] [PubMed] [Google Scholar]
- 52.Hofacker IL. Vienna RNA secondary structure server. Nuclei Acids Res. 2003;31:3429–3431. doi: 10.1093/nar/gkg599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nuclei Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 55.Craig ME, Crothers DM, Doty P. Relaxation kinetics of dimer formation by self-complementary oligonucleotides. J. Mol. Biol. 1971;62:383–401. doi: 10.1016/0022-2836(71)90434-7. [DOI] [PubMed] [Google Scholar]
- 56.Pörschke D, Uhlenbeck OC, Martin FH. Thermodynamics and kinetics of the helix-coil transition of oligomers containing GC base pairs. Biopolymers. 1973;12:1313–1335. [Google Scholar]
- 57.Pörschke D. A direct measurement of the unzippering rate of a nucleic acid double helix. Biophys. Chem. 1974;2:97–101. doi: 10.1016/0301-4622(74)80029-3. [DOI] [PubMed] [Google Scholar]
- 58.Kuhn H, Demidov VV, Coull JM, Fiandaca MJ, Gildea BD, Frank-Kamenetskii MD. Hybridization of DNA and PNA molecular beacons to single-stranded and double-stranded DNA targets. J. Am. Chem. Soc. 2002;124:1097–1103. doi: 10.1021/ja0041324. [DOI] [PubMed] [Google Scholar]
- 59.Tsourkas A, Behlke MA, Rose SD, Bao G. Hybridization kinetics and thermodynamics of molecular beacons. Nuclei Acids Res. 2003;31:1319–1330. doi: 10.1093/nar/gkg212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gao Y, Wolf LK, Georgiadis RM. Secondary structure effects on DNA hybridization kinetics: a solution versus surface comparison. Nuclei Acids Res. 2006;34:3370–3377. doi: 10.1093/nar/gkl422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Albergo DD, Marky LA, Breslauer KJ, Turner DH. Thermodynamics of (dG-dC)3 double-helix formation in water and deuterium oxide. Biochemistry. 1981;20:1409–1413. doi: 10.1021/bi00509a001. [DOI] [PubMed] [Google Scholar]
- 62.Elber R, Kirmizialtin S. Molecular machines. Curr. Opin. Struct. Biol. 2013;23:206–211. doi: 10.1016/j.sbi.2012.12.002. [DOI] [PubMed] [Google Scholar]
- 63.Panyutin IG, Hsieh P. The kinetics of spontaneous DNA branch migration. Proc. Natl Acad. Sci. USA. 1994;91:2021–2025. doi: 10.1073/pnas.91.6.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Joo C, McKinney SA, Lilley DM, Ha T. Exploring rare conformational species and ionic effects in DNA Holliday Junctions using single-molecule spectroscopy. J. Mol. Biol. 2004;342:739–751. doi: 10.1016/j.jmb.2004.06.024. [DOI] [PubMed] [Google Scholar]
- 65.Ouldridge TE, Hoare RL, Louis AA, Doye JPK, Bath J, Turberfield AJ. Optimizing DNA nanotechnology through coarse-grained modelling: a two-footed DNA walker. ACS Nano. 2013;26:2479–2490. doi: 10.1021/nn3058483. [DOI] [PubMed] [Google Scholar]
- 66.Romano F, Hudson A, Doye JPK, Ouldridge TE, Louis AA. The effect of topology on the structure and free energy landscape of DNA kissing complexes. J. Chem. Phys. 2012;136:215102. doi: 10.1063/1.4722203. [DOI] [PubMed] [Google Scholar]
- 67.Romano F, Chakraborty D, Doye JPK, Ouldridge TE, Louis AA. Coarse-grained simulations of DNA overstretching. J. Chem. Phys. 2013;138:085101. doi: 10.1063/1.4792252. [DOI] [PubMed] [Google Scholar]
- 68.Whitelam S, Geissler PL. Avoiding unphysical kinetic traps in Monte Carlo simulations of strongly attractive particles. J. Chem. Phys. 2007;127:154101. doi: 10.1063/1.2790421. [DOI] [PubMed] [Google Scholar]
- 69.Whitelam S, Feng EH, Hagan MF, Geissler PL. The role of collective motion in examples of coarsening and self-assembly. Soft Matter. 2009;5:1251–1262. doi: 10.1039/b810031d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Davidchack RL, Handel R, Tretyakov MV. Langevin thermostat for rigid body dynamics. J. Chem. Phys. 2009;130:234101. doi: 10.1063/1.3149788. [DOI] [PubMed] [Google Scholar]
- 71.Torrie GM, Valleau JP. Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. J. Comp. Phys. 1977;23:187–199. [Google Scholar]
- 72.Allen RJ, Warren PB, ten Wolde PR. Sampling rare switching events in biochemical networks. Phys. Rev. Lett. 2005;94:018104. doi: 10.1103/PhysRevLett.94.018104. [DOI] [PubMed] [Google Scholar]
- 73.Allen RJ, Valeriani C, ten Wolde PR. Forward flux sampling for rare event simulations. J. Phys. Condens. Matter. 2009;21:463102. doi: 10.1088/0953-8984/21/46/463102. [DOI] [PubMed] [Google Scholar]
- 74.Yakovchuk P, Protozanova E, Frank-Kamenetskii MD. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res. 2006;34:564–574. doi: 10.1093/nar/gkj454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Walter AE, Turner DH, Kim J, Lyttle MH, Muller P, Mathews DH, Zuker M. Coaxial stacking of helixes enhances binding of oligoribonucleotides and improves predictions of RNA folding. Proc. Natl Acad. Sci. USA. 1994;91:9218–9222. doi: 10.1073/pnas.91.20.9218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Mathews DH, Sabina J, Zuker M, Turner DH. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- 77.Mathews DH, Disney MD, Childs JL, Schroeder SJ, Zuker M, Turner DH. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl Acad. Sci. USA. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Choi HMT, Chang JY, Trinh LA, Padilla JE, Fraser SE, Pierce NA. Programmable in situ amplification for multiplexed imaging of mRNA expression. Nat. Biotechnol. 2010;28:1208–1212. doi: 10.1038/nbt.1692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Callura JM, Dwyer DJ, Issacs FJ, Cantor CR, Collins JJ. Tracking, tuning, and terminating microbial physiology using synthetic riboregulators. Proc. Natl Acad. Sci. USA. 2010;107:15898–15903. doi: 10.1073/pnas.1009747107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Wetmur JG. Hybridization and renaturation kinetics of nucleic acids. Annu. Rev. Biophys. Bioeng. 1976;5:337–361. doi: 10.1146/annurev.bb.05.060176.002005. [DOI] [PubMed] [Google Scholar]
- 81.Pörschke D. Elementary steps of base recognition and helix-coil transitions in nucleic acids. Mol. Biol. Biochem. Biophys. 1977;24:191–218. doi: 10.1007/978-3-642-81117-3_5. [DOI] [PubMed] [Google Scholar]
- 82.Lima WF. Implication of RNA structure on antisense oligonucleotide hybridization kinetics. Biochemistry. 1992;31:12055. doi: 10.1021/bi00163a013. [DOI] [PubMed] [Google Scholar]
- 83.Homann M, Nedbal W, Sczakiel G. Dissociation of long-chain duplex RNA can occur via strand displacement in vitro: biological implications. Nucleic Acids Res. 1996;24:4395–4400. doi: 10.1093/nar/24.22.4395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Chen X. Expanding the rule set of DNA circuitry with associative toehold activation. J. Am. Chem. Soc. 2011;134:263–271. doi: 10.1021/ja206690a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Genot AJ, Zhang DY, Bath J, Turberfield AJ. Remote toehold: a mechanism for flexible control of DNA hybridization kinetics. J. Am. Chem. Soc. 2011;133:2177–2182. doi: 10.1021/ja1073239. [DOI] [PubMed] [Google Scholar]
- 86.Zhang DY, Winfree E. Robustness and modularity properties of a non-covalent DNA catalytic reaction. Nucleic Acids Res. 2010;38:4182–4197. doi: 10.1093/nar/gkq088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Pörschke D. Model calculations on the kinetics of oligonucleotide double helix coil transitions. Evidence for a fast chain sliding reaction. Biophys. Chem. 1974;2:83–96. doi: 10.1016/0301-4622(74)80028-1. [DOI] [PubMed] [Google Scholar]
- 88.Puglisi JD, Tinoco IT., Jr Absorbance melting curves of RNA. Methods Enzymol. 1989;180:304–325. doi: 10.1016/0076-6879(89)80108-9. [DOI] [PubMed] [Google Scholar]
- 89.Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. Boca Raton, Florida: CRC Press; 2004. [Google Scholar]
- 90.Ouldridge TE, Šulc P, Romano F, Doye JPK, Louis AA. DNA hybridization kinetics: zippering, internal displacement and sequence dependence. Nucleic Acids Res. 2013;41:8886–8895. doi: 10.1093/nar/gkt687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Ferrenberg AM, Swendsen RH. New Monte Carlo technique for studying phase transitions. Phys. Rev. Lett. 1988;61:2635–2638. doi: 10.1103/PhysRevLett.61.2635. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


