Exploring the Latent Structures of Psychological Constructs in Social Development Using the Dimensional—Categorical Spectrum

Abstract

This paper provides an introduction to a recently developed conceptual framework—the dimensional–categorical spectrum—for utilizing general factor mixture models to explore the latent structures of psychological constructs. This framework offers advantages over traditional latent variable models that usually employ either continuous latent factors or categorical latent class variables to characterize the latent structure and require an a priori assumption about the underlying nature of the construct as either purely dimension or purely categorical. The modeling process is discussed in detail and then illustrated with data on the delinquency items of Achenbach’s child behavior checklist from a sample of children in the National Adolescent and Child Treatment Study.

Introduction

In the behavioral sciences in general, and in developmental psychology more specifically, statistical modeling that makes use of latent variables (LVs) has come to be widely accepted as a valid analytic approach for empirical investigations of substantive research questions. There are various reasons for the increased use of these models, none more important than the fact that many constructs of interest to researchers cannot be directly observed or measured (Bartholomew & Knott, 1999; Heinen, 1996). In order to make inferences regarding a LV, observations are made on variables believed to be influenced by or manifestations of the LV. These observable variables are termed manifest variables and are supposed to be imperfect, indirect observations of the LV.

Manifest variables may have a variety of measurement modalities or measurement scales, including interval and ratio scales of measures, censored interval scales, count scales, ordinal or Likert scales, binary or multinomial responses, etc. LVs may also have different scales, although they are usually limited to interval or multinomial. The conventional classification scheme for LV models that exists in the literature is based on distinctions between the types of manifest variables and LVs (Heinen, 1996); for example, traditional factor analysis models are delineated by continuous (interval scale) manifest variables and one or more continuous (interval scale) LVs. Within the last decade, advances in LV modeling have quickly made these more standard model distinctions obsolete (De Boeck, Wilson, & Acton, 2005; Lubke & Muthén, 2005). Recent advances in maximum likelihood estimation using complex algorithms in a general LV modeling framework (Asparouhov & Muthén, 2004; Skrondal & Rabe-Hesketh, 2004) allow for indicators of a single LV (either continuous or categorical) to be of mixed measurement modalities, while also providing a wider selection of error distributions. Most recently, the boundary between categorical and continuous LVs has been essentially eliminated by the development of hybrid or factor mixture models (FMMs), which include both continuous and categorical LVs in the same model (Arminger, Stein, & Wittenburg, 1999; Dolan & van der Maas, 1998; Muthén, 2008; Muthén & Shedden, 1999; Yung, 1997). These models combine features from both conventional factor analysis and latent class analysis.

Despite the present ubiquity of the known variety of standard LV models in behavioral research and the emergence of these hybrid LV models, the most fundamental question regarding the latent structure of psychological constructs often goes largely unasked in applied settings. That is, the question pertaining to the ontological status of a construct, usually posed in some variation of the form: 'Is this latent construct a discrete entity, reflecting between individuals a difference in kind or, rather, is this latent construct a dimensional quantity, reflecting between individuals a difference in degree?' The answer to this question of latent structure is often presupposed in modeling applications. That is, when utilizing a factor analytic approach, researchers necessarily presuppose a dimensional or continuous latent structure, and when utilizing a latent class approach, researchers necessarily presuppose a categorical or discrete latent structure. With the development of factor mixture models, researchers are no longer forced to choose between continuous or categorical LV conceptualizations—we can use both at once to model the latent structure (Kuo, Aggen, Prescott, Kendlet, & Neale, 2008; Muthén & Asparouhov, 2006a; Muthén, Asparouhov, & Rebollo, 2006). The categorical vs. continuous latent structure dichotomy becomes artificial in light of these hybrid models. What remains obscured, however, is the interpretation and understanding of latent structure when both continuous and categorical LVs simultaneously apply. Modeling data in such a manner necessarily raises such questions as: What does it mean for a latent structure to be at once both categorical and continuous? The purpose of this paper is to present the dimensional–categorical spectrum (DCS), a new overarching methodological framework, based on general factor mixture modeling, intended for the exploration the latent structures of psychological constructs that helps to answer that very question. The presentation also includes an example of the DCS framework applied to measures of delinquency from a study of youth with serious emotional disturbance (SED). We do not intend to reach substantive conclusions on the basis of this analysis but rather to illustrate use of the DCS. The presentation of the models within the DCS framework is non-technical, relying primarily on path diagrams, probability distribution function illustrations, the hypothetical example of conduct disorder, and the data illustration. For a complete technical treatment of the DCS, readers are referred to Masyn, Henderson, Marcus, and Edens (2009).

The remainder of this article contains a description of the general factor mixture model, followed by an explanation of the different models along the DCS—all special cases of the general factor mixture model. A procedure for model specification, comparison, and selection is presented, followed by the data illustration.

The General Factor Mixture Model

In this section, the unconditional factor mixture model is described in its most general form for continuous observed response variables (although the specification of the model in a generalized LV framework does accommodate a variety of measurement scales and modalities for the manifest variables). The section also includes a brief explanation of how the model may be expanded to incorporate antecedent and consequent observed variables.

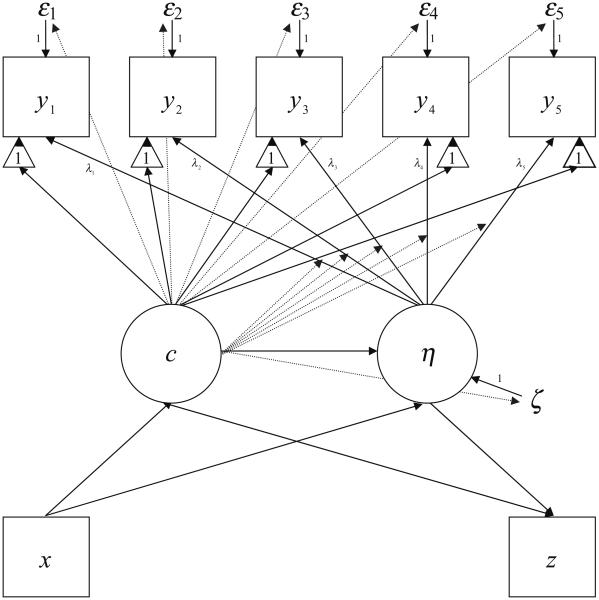
Figure 1 displays a path diagram for a hypothetical general factor mixture model with five continuous response variables, y₁ . . ., y₅. Each individual in the sample has observed values for one or more of these variables (missing data is permitted with these models using maximum likelihood estimation under the missing-at-random (MAR) assumption) and these observed or manifest variables are considered to be indicators of the underlying latent structure. In the most general factor mixture model, the observed responses may be characterized as manifestations of both a K-class multinomial LV, c, and one or more continuous LVs (factors), η. The error terms, also referred to as random disturbances or unique factors, on the observed variables, denoted in the diagram by ε₁, . . ., ε₅, represent the variability in the ys not explained by or associated with the underlying latent structure. Typically, the probability distribution for η is assumed to be normal, and the probability distribution for ε is usually assumed to be from the exponential family of distributions, most commonly, multivariate normal, although other distributions can be specified depending on the measurement scales for the y’s. In the general factor mixture model, the observed response, y_mi, to item m, for individual i, in latent class k, with latent factor value η_i, is expressed by

$$y_{mi}={\mu }_{y_{m}i}+{\epsilon }_{mi},$$

$${\mu }_{y_{m}i}=E[y_{mi}\mid c_i=k,{\eta }_i]={\nu }_k+{\lambda }_{mk}{\eta }_i$$

$${\eta }_i={\mu }_{\eta i}+{\varsigma }_i$$

$${\mu }_{\eta i}=E[{\eta }_i\mid c_i=k]={\alpha }_k,$$

where, typically,

$${\epsilon }_{mi}\sim N(0,{\theta }_{mk}),$$

$${\varsigma }_i\sim N(0,{\Psi }_k).$$

Figure 1.

Path Diagram of a Hypothetical General Factor Mixture Model

In the case of continuous y’s, the parameters related to the measurement model for the η’s include intercepts (v in previous equations; represented in Figure 1 by the arrowheads pointing from the constant ‘1’ in triangles to the ys), residual variances for the observed response variables (θ; the variances of the unique factors represented by ε’s), and factor loadings (λ; the paths from η to the ys). The parameters related to the measurement model for the latent class variable can include class-specific intercepts (v_k; the paths from c to the constant ‘1’in triangles), class-specific residual variances for the observed response variables (θ_k; the paths from c to the εs), class-specific factor loadings (λ_k; the paths from c to the paths from η to the ys), class-specific factor means (α_k; the path from c to η), and class-specific factor variances/ covariances (ζ_k; the path from c to the factor error term, ζ). The values of the paths from each of the random disturbances to the observed variables and latent factors are fixed at unity and the means of those disturbances are fixed at zero. Notice that for the latent class variable, the latent factor(s) and unique factors (error terms), as well as the observed variables, may serve as latent class indicators. In fact, indicators for the latent class variable include any variables, observed or latent, that differ in values between individuals in the population due to latent class membership, as well as model parameters that are permitted to be class-specific (i.e., random effects). The latent classes are then characterized by the class-specific joint distribution of all those variables and random effects and are empirically based on the overall joint distribution in the sample. Thus, the resultant classes from the model estimation will depend on: (a) which variables and random effects are included as latent class indicators, and (b) the specification of the within-class joint distribution of those latent class indicators. This is analogous to selecting the attribute space and the resemblance coefficient in a cluster analysis. For example, if we specified a latent class model in which the classes differed only with respect to their mean structure, we may extract different classes (number, size, and class-specific parameters estimates) than a model in which the classes differed with respect to both their mean and variance-covariance structure.

The distribution of the latent classes is a discrete probability distribution described by the (mixing) proportion or relative frequency of each latent class in the overall population, denoted by π₁, . . ., π_k, such that,

$$\mathrm{Pr}(c=k)={\pi }_k.$$

The overall probability distribution for y, f(y), is then defined by a mixture distribution as follows:

$$\sum _{k=1}^k({\pi }_k\cdot f(y\mid c=k)).$$

We have focused, thus far, on how to characterize one or more LVs on the basis of the observed mean and variance–covariance structure of a set of manifest variables using a general factor mixture model. Often it is of interest to relate the underlying latent phenomenon, once satisfactorily characterized, to one or more observed antecedent and consequent variables, that is, variables that predict or influence the latent phenomenon and variables that are influenced by the latent phenomenon. Antecedent variables are those that explain or predict individual differences in the latent construct, represented by x in Figure 1. The paths from x to c and η indicate that both probability of latent class membership and individual values on η may be influenced by x. Consequent variables are proximal or distal outcomes or sequelae that are predicted by individual differences in the latent construct, represented by z in Figure 1. The paths from c and η to z indicate that z may be influenced by individual values for both the latent class variable and latent factor(s). For the empirical example, there is an x-variable but no z-variable included in the analysis.

Models on the DCS

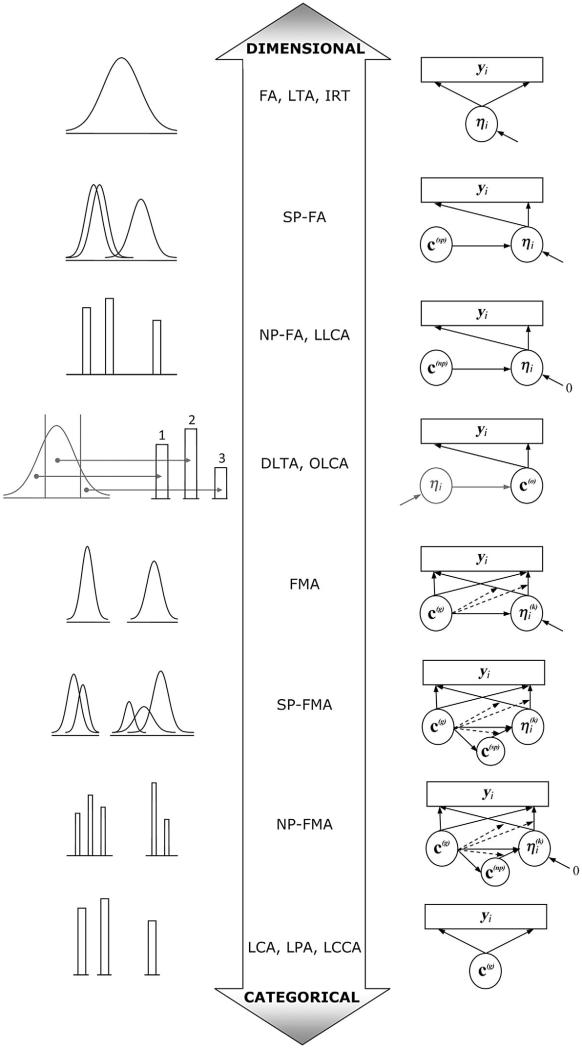
In this section, each of the specific models on the dimensional–categorical spectrum are briefly described as special cases of the general factor mixture model and are explained in terms of how the difference between any two individuals on the latent level is characterized as well as how variability across all individuals is characterized. The hypothetical example of conduct disorder is provided to further elucidate model interpretation. All primary models on the DCS are depicted in a broad format in Figure 2, and for the sake of space and clarity of presentation, all factor distributions on the left panel of Figure 2 are shown in a single dimension.

Figure 2.

Schematic of the Dimensional–Categorical Spectrum (DCS; adapted from Masyn et al., 2009)

Factor Analysis

Factor analysis (FA; also known, in the case of binary or ordinal manifest variables, as latent trait analysis (LRT) or item response theory (IRT)) models reside at the fully dimensional end of the DCS. As shown in the path diagram in Figure 2 on the right-hand side corresponding to the FA point on the DCS, there is no categorical LV involved in the model specification; that is, the latent structure manifest by the observed y’s is entirely characterized by one or more continuous latent factors, η. We can think of the FA model as a special case of the general factor mixture model for which there is only one latent class, that is, K = 1, and every individual’s probability of membership in that class is unity.

If this were the representation of the underlying latent structure for conduct disorder (CD), most consistent with the observed data, then we would interpret CD as a (multi)dimensional characteristic in the population, for which all individuals could be placed along a continuum, as shown on the left-hand side of the DCS, across from the FA path diagram, and any delineation of conduct patterns would simply represent artificial cut-points placed along that continuum of behavior disturbance. Any two randomly selected children, i and j, could be compared according to their scores on the underlying latent factors. In that case, not only could we determine whether child i had more or less behavior disturbance than child j, we could also quantify how much more or how much less. Overall population variability or heterogeneity in the latent structure could be summarized by the variance–covariance of η.

Semi-parametric Factor Analysis (SP-FA)

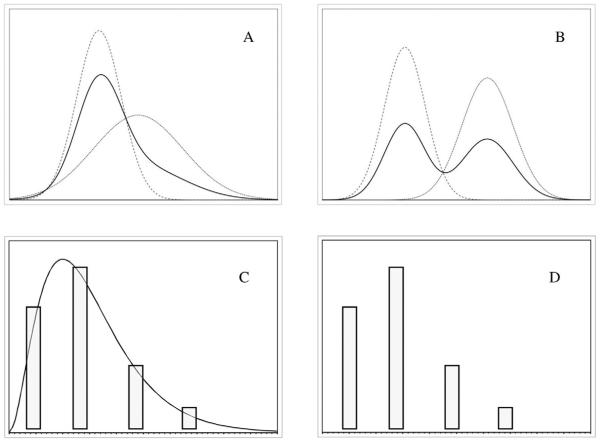
Semi-parametric factor models fall just beyond traditional factor models on the DCS. SP-FA can be viewed as an approach that relaxes the conventional multivariate normality assumption for the latent factors in a standard FA, wherein latent classes of normal distributions are used to approximate, when ‘mixed’ together, some nonspecific continuous distribution (first described in Pearson, 1894, 1895; see also Bauer & Curran, 2003; McLachlan & Peel, 2000). The top row of Figure 3 gives two illustrations of two normally distributed subpopulations (indicated by dashed lines) that, when combined, result in an overall population distribution of values (indicated by the solid line) that is non-normal. Notice that with the overlap of the two normal distributions in Plot A of Figure 3, the two classes do not represent distinct groups of individuals, quantitatively or qualitatively (referred to by De Boeck et al., 2005, as ‘smooth’ differences). In Plot B of Figure 3, the two classes are more separate, resulting in an overall population distribution that is bimodal (referred to by De Boeck et al., 2005 as ‘abrupt’ differences). In both cases, all individuals can be compared with respect to their η values, irrespective of class membership, because members of all latent classes fall along the same latent metric scale. This equivalence of latent scale across (latent) subgroups is referred to as strict factorial invariance in the psychometric literature (Meredith, 1993).

Figure 3.

Top Row: Finite Mixtures of Normal Distributions; A: ‘Smooth’ Differences in Mixture Components; B: ‘Abrupt’ Differences in Mixture Components. Bottom Row: Finite Mixtures of Mass Points; C: Mass Point Approximation of a Continuous Probability Density Distribution; D: Probability Mass Function of a Discrete Probability Distribution

Reflecting on class separation in these models raises an important point. It is necessary to distinguish between the nature of the latent structure and the corresponding distribution of latent values in the population. In the DCS framework, the distinctions between purely dimensional and purely categorical latent structures (and all those in between) are not made exclusively on the basis of the population distribution of values at the latent level (e.g., a multimodal distribution of a continuous LV is not necessarily ‘less’ dimensional than a normal distribution of a continuous LV). Further, if latent classes are used to characterize (part of) the heterogeneity in the population, that does not necessarily imply the data have a categorical latent structure. However, even while individuals fall along the same latent continuum, as the latent classes become more distinct from one another (i.e., there is less overlap), and the variability within the latent classes decreases such that individuals within classes are more homogeneous than individuals between classes, discontinuities in the overall population distribution become more evident (De Boeck et al., 2005). These discontinuities, in turn, lead to a more discretized understanding of individual differences at the latent level (represented by models toward the categorical end of the DCS at the bottom of Figure 2).

At the SP-FA point of the DCS, the latent classes are used to characterize non-normal interindividual heterogeneity at the latent level. Thus, the latent class variable, c, is superscripted by (sp) to indicate that the latent class variable is being used to obtain a semi-parametric approximation for the distribution of the underlying factors (‘semi’ because a multivariate normal distribution is assumed for the factors within class). In terms of model specification, since only parameters related to the distribution of the latent factors vary across the latent classes, there is strict factorial invariance, and all individuals can be compared with respect to their η values, irrespective of class membership. Thus, for the hypothetical conduct disorder example, the interpretation of the latent structure of CD under the SP-FA model would be essentially the same as that for the FA model; that is, as a (multi)dimensional characteristic in the population, for which all individuals could be placed along a continuum of behavior disturbance, as shown on the left-hand side of the DCS, across from the SP-FA path diagram. Individual differences in the latent construct across the entire population would be summarized by the overall variance–covariance of η, calculated as the variance–covariance of the remixed population distribution for η.

Non-parametric Factor Analysis (NP-FA)

Non-parametric factor models fall below semi-parametric factor models on the DCS. Instead of using mixtures of (multivariate) normal distributions to approximate the overall population distribution of h, as in the case of SP-FA, a mixture of mass points is used, in which the number of mass points is equal to the number of latent classes, the locations of the mass points are given by the factor means for the corresponding classes, and the weights of the mass point are given by the corresponding class proportions. Plot C of Figure 3 displays a non-normal population distribution modeled by a series of four mass points (shown as bars in the diagram). Plot D of Figure 3 displays a series of mass points placed along a continuum without the overlying continuous population distribution. This represents the other possible ‘reality’ for this model: that the overall population distribution of η is truly discrete with a common metric across the discrete outcomes. This is also known as a located latent class analysis (LLCA), in which the population is composed of a finite number of homogeneous unobserved subpopulations (latent classes) with each subpopulation ‘located’ at a different point on the same underlying latent continuum. It is important to note that even though all members of a latent class are the same with regard to their scores on the latent factors, this does not imply that they will have the same observed values on the y’s because the relationship between η and the y’s remains stochastic. That is, homogeneity at the latent level does not imply homogeneity at the level of the observed variables.

For these models in Figure 2, the latent class variable, c, is superscripted by (np), to indicate that the latent class variable is being used for a non-parametric approximation for the distribution of the underlying factors. In terms of model specification, there is no variability on the latent factors within class, indicated by a ‘0’ pointing to η in place of a random error term and, as with the SP-FA, strict factorial invariance is imposed. NP-FA models can be viewed as a special case of SP-FA models with ψ_k = 0, ∀_pk.

If this were the representation of the underlying latent structure for CD most consistent with the data, then we could interpret the results similar to FA and SP-FA and make the same comparisons between children on the latent level; that is, comparing scores on the scale of η. However, in this specification, all members of a given latent class would have the same scores for η. Thus, describing the means and mean differences between the classes exactly describes all individual differences at the latent level of conduct problems.

Alternatively, we could interpret the distribution of latent values of behavior disturbance as truly discrete—that at the latent level, there exist a finite number of subpopulations of individuals who are the same with respect to their level of behavior disturbance with the subpopulations differing from each other with regards to their level of conduct problems. Essentially, children within a given class are all the same with respect to latent behavior disturbance, and any two individuals from two given classes would have the same difference in latent scale scores.

The NP-FA may be viewed as the midpoint of the DCS, in which the latent structure is really both dimensional and categorical: The latent structure and the population distribution of values is characterized by homogeneous subgroups of individuals (the categorical part) but differences between those groups can be quantified on a given factor metric (the dimensional part).

Ordered Latent Class Analysis (OLCA)

Ordered latent class models fall just past the midpoint of the DCS where the underlying latent structure could be considered more categorical than dimensional. Here, the underlying latent structure is characterized by a set of K ordered latent classes. The classes are ordered or ranked with respect to an underlying continuum, but unlike the LLCA, the distances between the classes, as well as the differences between individuals across those classes, cannot be quantified according to a common metric. OLCA is a form of discretized latent trait analysis (DLTA), for which the latent ordinal variable is conceptualized as arising from an underlying continuous LV (or trait), η, that has been discretized. For a single underlying dimension, the K ordinal latent classes wouldbe created by grouping individuals based on K – 1 cut-points (or thresholds) made along the scale of η. For these models in Figure 2, the latent class variable, c, is superscripted by (o), to indicate that the latent class variable is ordinal rather than multinomial (as in the other models). In the OLCA path diagram, η is shown pointing to c^(o) to indicate that membership in the ordered latent classes depends upon the underlying η values.

If this were there presentation of the underlying latent structure for conduct disorder most consistent with the observed data, then we could interpret this in a similar way as the factor analysis, SP-FA, and NP-FA. However, the latent population distribution of behavior disturbance is already discretized into the ordered latent classes. Any two randomly selected children, i and j, from the overall population can be compared in a relative way, rather than absolute, according to latent class membership. In this setting, we can only determine whether child i has more or less behavior disturbance than child j, and only if they are not in the same class.

Alternatively, we could interpret the distribution of latent values of behavior disturbance as truly discrete—that at the latent level, there exist a finite number of subpopulations of individuals who are the same with respect to their level of behavior disturbance but that these subpopulations differ from each other with regard to their relative level of conduct problems.

Unlike the LLCA, we cannot quantify the differences between the classes or rank the relative distances between the classes.

Factor Mixture Analysis (FMA)

At this point, along the DCS, the nature of the latent structure is primarily categorical, with dimensional qualities within discrete and mutually exclusively groups. Although all of the models on the DCS are special cases of the general factor mixture model, we reserve the term FMA for the special case in which there is not factorial invariance across the latent classes and, as a result, the factor metrics from one latent class to another are not comparable.

For these models in Figure 2, the latent class variable, c, is superscripted by (g), to indicate that the latent class variable represents qualitatively different subgroups of individuals whose differences on the latent factors cannot be quantified across class. Additionally, η is superscripted by (k) to indicate that the latent factors are not the same, that is, they are not being measured the same way across the latent classes. On the left side of the DCS corresponding to FMA, the lack of factorial invariance is represented by space between the horizontal lines representing the class-specific latent dimensions. FMA models without configural invariance could have a different number of factors within each latent class, as well as different patterns of factor loadings. In terms of model specification, differing degrees of factorial (non-)invariance can be imposed across the latent classes (comparable to types of factorial invariance across observed groups described by Meredith, 1993). Without strict factorial invariance, the latent classes cannot be compared with respect to the factor structure (see Lubke & Dolan, 2003, for a defense of the strict measurement invariance requirement over the strong measurement invariance requirement typically maintained as sufficient for subpopulation comparisons, for example, Widaman & Reise, 1997). Furthermore, individuals from different latent classes cannot be compared on their factor scores.

If the FMA were the representation of the underlying latent structure for conduct disorder most consistent with the observed data, then we would interpret conduct disorder as a discrete, categorical construct implying that at the latent level the population can be divided into K qualitatively distinct behavior subgroups. Within each of these K subgroups, the manifest observed variables also measure an underlying trait, η^(k), different in meaning for each class. For example, we might obtain a three-class solution, where we would interpret one class as a subpopulation of individuals without any clinical level of behavior disturbance with an underlying trait of social competence; one class as a subpopulation of individuals with conduct disorder with an underlying trait of aggression; and one class as a subpopulation of individuals with conduct disorder with an underlying trait of deceitfulness. Without strict factorial invariance, only two randomly selected individuals from the same latent class can be compared according to their scores on the underlying class-specific latent factors. All that could be said about two individuals from different latent classes is simply that they are from different classes, and their differences can only be described in terms of the qualitative differences between their respective classes, informed by the expected responses on the manifest variables. The population distribution on the latent level can be described by listing the relative frequencies (π_k) of the classes and then the class-specific means and variance–covariances of the class-specific latent factors.

Just as the SP-FA and NP-FA models can be viewed as approaches for relaxing the normality assumption for η in a traditional factor analysis, the FMA models can be viewed as approaches for relaxing the conditional independence assumption for the y’s within c^(g) usually imposed in a traditional latent class analysis. By including a factor structure within each of the latent classes, the manifest variables are permitted to have shared variance above and beyond that which is explained by the latent class variable.

Semi-parametric and Non-parametric Factor Mixture Analysis (SP-FMA and NP-FMA)

Semi-parametric and non-parametric factor mixture models represent a combination of the FMA models described above and the SP-FA and NP-FA models at the other end of the DCS such that the distribution of factor scores within each of the latent classes is characterized by a finite mixture of normal distributions, in the case of SP-FMA, or by a finite mixture of mass points, in the case of NP-FMA. To accomplish this, a second latent class variable, c^(sp), in the case of SP-FMA, or c^(np), in the case of NP-FMA, is included. Therefore, there is a K-class multinomial latent variable, c^(g), with K qualitatively distinct latent classes across which there is not strict factorial invariance; and a S-class multinomial latent variable, c^(sp) or c^(np), with S mixing components (normally distributed components for c^(sp) or discrete mass points for c^(np) within each of the K classes, for which there is strict factorial invariance.

If the SP-FMA or NP-FMA were the representation of the underlying latent structure for conduct disorder most consistent with the observed data, then we would interpret CD in a similar manner as with the FMA; that is, as a discrete, categorical attribute. That, at the latent level, the population can be divided into K qualitatively distinct subgroups. Within each of these K subgroups, the manifest observed variables also measure an underlying trait, where η^(k) represents the underlying latent factors manifest by the y’s in Class k.

Latent Class Analysis (LCA)

Latent class analysis (LCA; also known as latent profile analysis or latent class cluster analysis) models reside at the fully categorical end of the DCS. As illustrated in Figure 2, there is no continuous LV involved in the model specification; that is, the latent structure manifest by the observed y’s is entirely characterized by a categorical LV, c^(g). We can think of these latent class models as a special case of the general factor mixture model for which the factor means and variance–covariances are all zero.

If the LCA were the representation of the underlying latent structure for conduct disorder most consistent with the observed data, then we would interpret conduct disorder as a purely discrete, categorical construct implying that at the latent level the population can be divided into K qualitatively distinct, homogeneous subgroups with respect to behavior disturbance profiles. The latent classes can be understood by examining the expected responses on the observed outcome variables for each latent class. Any two randomly selected children, i and j, from the overall population are either the same or different depending on whether or not they come from the same class. The population distribution on the latent level can be described by simply listing the relative frequencies (π_k) of the classes.

Model Comparisons Using the DCS

Now that we have fully explained all the models along the DCS, we turn to the strategy for how these models and the overarching framework of the DCS can be used with real data to empirically explore the latent structure of a psychological construct as manifest by a select set of observed variables. The approach recommended herein is to begin with model fitting and testing to select the ‘best’candidate model at each point along the DCS. Because the exercise of investigating latent structure is inherently exploratory, model building and selection at each point of the DCS should proceed accordingly. Then, comparisons are made between the candidate models across the DCS. All DCS models can be estimated using maximum likelihood estimation implemented via one or more complex algorithms (for more on model estimation, see Asparouhov & Muthén, 2004; McLachlan & Peel, 2000; and Muthén & Shedden, 1999).

Candidate model selection should begin with the two opposite ends of the DCS. Model selection at the factor analysis (FA; LTA; IRT) end of the DCS can follow standard procedures for either confirmatory or exploratory factor analysis (Bartholomew & Knott, 1999; Fabrigar, Wegener, MacCallum, & Strahan, 1999; Jöreskog, 1969, 1971; Muthén, 1989). Modeling at the latent class analysis end of the DCS (LCA; LTA, LCCA) also follows standard procedures (LCA: Goodman, 2002; Lazarsfeld & Henry, 1968; McCutcheon 1987. LTA: Embretson and Reise 2000; Langeheine and Rost 1988; Vermunt and Magidson 2005. LCCA: McLachlan and Peel 2000; Vermunt and Magidson 2002.) As with factor analysis, unless there are compelling reasons to do otherwise, deciding on the number of classes (class enumeration) for the categorical latent variable is driven by both substantive and empirical considerations. Once selected, the candidate models for the FA and LCA ends of the DCS can then be used to guide the model specifications for all points in between.

For the OLCA/DLTA models, the process of model specification, class enumeration, and candidate model selection should proceed in the same manner as for LCA models but with the appropriate parameters constraints made across the classes to achieve the desired ordering (Croon, 1990, 2002; Heinen, 1996). For all other points on the DCS, model specification involves both latent factors and latent classes. For the mid-points along the DCS, for example, SP-FA, FMA, etc., the within-class model that must be specified before beginning the class enumeration now involves a factor structure. As with any mixture model, the cost to model parsimony and stability can be great when allowing too many differences in the within-class structure. Often times, a compromise is brokered between flexibility and parsimony; an example of this would be an FMA model with a within-class factor configuration matching either the FA candidate model and/or the SP-FA candidate model and with weak factorial invariance imposed across the classes.

Because all models on the DCS (except FA models) involve a latent class variable, certain approaches for model estimation and fit comparisons related to finite mixture modeling are applicable. For instance, the use of multiple starts from random locations in the parameter space can improve chance of convergence to global maxima (Hipp & Bauer, 2006; McLachlan & Peel, 2000). Furthermore, the standard chi-square difference test (likelihood ratio test; LRT) cannot be used for comparing mixture models with different numbers of classes, because regularity conditions of the test are violated (McLachlan & Peel, 2000). For discriminating between models at the same point on the DCS with different numbers of classes, two alternatives to the standard chi-square difference test are available: (a) the Vuong-Lo-Mendell-Rubin test (VLMR-LRT; Lo, Mendell, & Rubin, 2001), an analytic approximation to the LRT distribution; and (b) the parametric bootstrapped LRT (BLRT; McLachlan, 1987; McLachlan & Peel, 2000), an empirical derivation of the sampling distribution of the LRT statistic using parametric bootstrapping. AAs implemented in Mplus, both tests yield a p value for the comparison of a (k-1)-class model (the null model) to the specified k-class model (the alternative model).

For comparing models both within and between points on the DCS, other information-heuristic, likelihood-based indices, such as the Bayesian information criterion (BIC; Schwarz, 1978) are used in model selection. This index and similar ones are computed as a function of the log likelihood with a penalty for model complexity (e.g., the number of parameters estimated relative to the sample size). In general, a lower value on an information criterion indicates a better model. Sometimes, the BIC may not reach a minimum and continue to decrease with added classes until the models fail to converge due to analytic or empirical non-identification. In these cases, we can loosely explore the diminishing gains in model fit according to these indices with the use of ‘elbow’ plots (Petras & Masyn, 2010).

In addition to the previously discussed statistical criteria, it is also useful to assess the value and utility of the resultant classes themselves. One measure that can be used for this objective is entropy (Ramaswamy, Desarbo, Reibstein, & Robinson, 1993). Entropy summarizes the degree to which the latent classes are distinguishable and the precision with which individuals can be placed into classes. It is a function of the individual estimated posterior class probabilities and ranges from 0 to 1 with higher values indicating clearer class separation. For models with ‘abrupt’ class separation, we would expect higher entropy values than models with ‘smooth’ class separation. It may also be worthwhile noting class size and proportions since an overextraction of classes might be revealed through particularly small and non-distinct classes emerging at higher enumerative values.

Once a candidate model has been selected for each point on the dimensional– categorical spectrum, the models are then compared across the DCS using similar criteria to those used to originally select the candidate models. Other details are taken into account, such as model goodness-of-fit residual diagnostics (if available), graphical data exploration (as suggested by Lubke & Spies, 2008), and conceptual interpretation.

Unfortunately, for the applied researcher, there is no single method for comparing models with differing numbers of latent classes or different latent structures that is widely accepted as best (Muthén & Asparouhov, 2006b; Nylund, Asparouhov, & Muthén, 2007); but by careful and systematic consideration of a set of plausible models, and utilizing a combination of statistical and substantive model checking (Muthén, 2003), researchers can improve their confidence in the tenability of their resultant model selection. In other words, in addition to utilizing the measures described earlier, it is also important to make some qualitative evaluations of the usefulness and validity of the primary candidate models can also be done. For example, auxiliary information, potentially derived from substantive theory, in the form of antecedent and consequent variables of the latent construct can be examined to evaluate the concurrent and prognostic validity of the latent structure as specified in a given model (Muthén, 2003).

It is important to keep in mind that the aim of this entire process is to explore the underlying latent structure of a particular construct as manifest by a set of observed variables. And although there are many different models across the DCS to consider, many of the adjacent points on the DCS offer consistent representations of the latent structure with respect to how individual differences can be understood (e.g., FA and SP-FA). Even candidate models at non-adjacent points of the DCS may lead to the same inference regarding the latent structure. For example, the unrestricted candidate LCA model could yield classes that closely match those obtained by the candidate OLCA model; or an FMA candidate model with a small degree of partial factorial non-invariance may actually lead to the same inference as the SP-FA candidate model with strict factorial invariance. This exploratory process of considering such a wide range of models is intended to result in a model-based, empirical junction at the latent structure most consistent with the data and, hopefully, congruous with the true ontological nature of the construct being measured.

Data Example

Study Description

We analyzed data from the National Adolescent and Child Treatment Study (NACTS), a comprehensive four-wave, 7-year longitudinal study of children and adolescents with serious emotional disturbance (SED; see Greenbaum, Dedrick, Friedman, Kutash, Brown, Lardieri, & Pugh, 1996 for details on sampling, procedures, and study design). Because the current study focused on adolescent delinquency, a subsample of NACTS participants was used. This subsample consisted of 569 young adolescents with SED who were 12–18 years of age at entry to the study. This sample was primarily White (73%) and male (76%), with 56% from two-parent households and 34% from single-parent households.The modal family income category was over $15 000, but less than $20 000 (15% were in this category and 66% of the sample earned the mode or less).

Measures

Delinquency

Delinquency was measured by the delinquency scale of the child behavior checklist (CBCL; Achenbach, 1991). The delinquency scale of the CBCL is the sum of 13 items. Items in the CBCL use a 3-point response scale (0 = Not true, 1 = Somewhat or sometimes true, and 3 = Very or often true). Internal consistency reliabilities for the delinquency scale, as measured by Cronbach’s alpha, were .81 and .99 for Wave 1 and Wave 4, respectively. Normalized T-scores above 66 are considered in the clinical range (Achenbach, 1991). Wave 1 delinquency scores ranged from 50 to 93 (M = 68.27, SD = 10.53); Wave 4 delinquency scores ranged from 50 to 93 (M = 63.98, SD = 9.41). The percentages of the sample that were in the clinical range (>66) for Wave 1 and Wave 4 were 58% and 40%, respectively. For this analysis, separate responses for the 13 items of the delinquency scale in Waves 1 and 4 were used. A parent or parent surrogate completed the CBCL/4–18 for the child during Waves 1 and 4 of NACTS. During Wave 1, 71% percent of the CBCLs were completed by biological mothers, 11% by biological fathers, 18% by adopted, stepparents, and other adult caretakers. During Wave 4, 74% percent of the CBCLs were completed by biological mothers, 12% by biological fathers, and 14% by adopted, stepparents, and other adult caretakers.

Covariate

During child interviews at Waves 1 and 4, adolescents were asked to indicate on a 5-point scale to what extent they perceived difficulty with their involvement in their family system (1 = definitely not a problem to 5 = very big problem). Waves 1 and 4 mean scores for this measure were 2.77 (SD = 1.56) and 2.23 (SD = 1.38), respectively. Wave 1 reports were used for this analysis.

Analysis Plan

For the purposes of this analysis, the data on the observed responses for the 13 items from the CBCL collected in Waves 1 and 4 were restructured into three age-grouped time intervals: 12–14 years (N = 278); 15–17 years (N = 499); and 18–20 years (N = 264). No subject contributed more than one set of observations per each age-grouped time interval. To facilitate the reader’s understanding, we present in detail our recommended sequence for exploration along the dimensional–categorical spectrum for the 15–17 age-grouped interval.

All analysis models were estimated using full-information maximum likelihood (FIML) with robust standard errors (MLR) as implemented in Mplus V5.1 (Muthén & Muthén, 1998–2009).¹ FIML utilizes all of the available data under the missing-at-random (MAR) assumption as defined by Little and Rubin (2002). For each model, a high number of sets of random start values drawn from random locations in the parameter space relative to an initial start value set were utilized.

Results

Table 1 displays the observed proportions in the 15–17 year age-grouped interval corresponding to each response category for the 13 items of the CBCL used for this analysis. It is clear from this table that there was a good deal of heterogeneity between individuals and between items.

Table 1.

Observed Proportions for Response Categories for CBCL Narrowband Delinquency Items, Ages 15–17 (N = 499)

Response Category	Item 26	Item 39	Item 43	Item 63	Item 67	Item 72	Item 81	Item 82	Item 90	Item 96	Item 101	Item 105	Item 106
Not true	.36	.40	.30	.47	.71	.91	.62	.67	.27	.68	.62	.72	.79
Somewhat or  sometimes true	.38	.27	.39	.24	.16	.06	.22	.20	.37	.19	.16	.16	.11
Very or often true	.26	.33	.31	.29	.14	.03	.16	.13	.36	.14	.22	.12	.10

Note: Item 26 = ‘Doesn’t seem to feel guilty after misbehaving’; Item 39 = ‘Hangs around with others who get in trouble’; Item 43 = ‘Lying or cheating’; Item 63 = ‘Prefers being with older kids’; Item 67 = ‘Runs away from home’; Item 72 = ‘Sets fires’; Item 81 = ‘Steals at home’; Item 82 = ‘Steals outside the home’; Item 90 = ‘Swearing or obscene language’; Item 96 = ‘Thinks about sex too much’; Item 101 = ‘Truancy, skips school’; Item 105 = ‘Uses drugs for nonmedical purposes’; Item 106 = ‘Vandalism’.

For all models estimated, we recorded the following: log likelihood values, number of free parameters, and BIC. For models with latent classes (K ≥ 2), we also recorded entropy, the p-value for the VLMR-LRT, the p-value for the BLRT, and the estimated frequency (f) and relative frequency (rf) of the smallest class (Petras & Masyn, 2010). For the factor analysis models, we elected to specify a single-factor confirmatory model rather than follow EFA procedures for two reasons; (a) the delinquency subscale composed of these items is conceptualized and previously derived as unidimensional and therefore treated as such in most analyses, and (b) the conventional criteria for adequate overall goodness-of-fit of the single-factor model to the data as measured by the CFI, TLI, and RMSEA, were all met. For the SP-FA models, two-, three-, and four-class, one-factor models were specified; in one set of models, the factor variance was constrained to be equal across class and in another set of models, the factor variance was permitted to vary across the latent classes. Comparing the models with and without class-varying factor variance, there appeared to be very little improvement in overall fit for a given number of classes for the former over the latter. Overall, the one-factor CFA model, equivalent to the one-class, one-factor SP-FA model, had the best (i.e., lowest) BIC value and a log likelihood of comparable value compared to all the other SP-FA models. Thus, the one-factor CFA was selected as the candidate model for both the FA and SP-FA points on the DCS with fit indices recorded in Table 2.

Table 2.

Fit Indices for DCS Candidate Models, Ages 15–17

DCS location	Candidate model	Log likelihood	No. of est. parameters	BIC	Entropy	VLMR- LRT(p)	BLRT (p)	f (rf) of smallest class
FA	1-Factor CFAa	–4987.98	39	10 218.24	n/a	n/a	n/a	499 (1.00)
SP-FA	1-Class, 1-Factor  SP-FAa	–4987.98	39	10 218.24	n/a	n/a	n/a	499 (1.00)
NP-FA	4-Class, 1-Factor    NP-FA	–4992.15	44	10 257.66	.75	.01	<.001	39 (.08)
OLCA	3-Class OLCA	–4971.18	80	10 439.37	.83	c	c	105 (.21)
FMA	2-Class, 1-Factor  FMAb (weak  invariance)	–4885.54	67	10 187.31	.77	.05	<.001	115 (.23)
SP-FMA	2-C(g) x l-C(sp),  1-Factor SP-FMAb  (weak invariance)	–4885.54	67	10 187.31	.77	c	c	115 (.23)
NP-FMA	2-C(g) x 2-C(np),  1-Factor NP-FMA  (weak invariance)	–4940.26	69	10 309.19	.79	c	c	61 (.12)
LCA	3-Class LCA	–4970.65	80	10 438.30	.83	.11	<.001	102 (.20)

^aEquivalent models.

^bEquivalent models.

^cNot available from Mplus V5.1 for this model specification.

For the next point on the DCS, the four-class, one-factor NP-FA model had the best BIC value. Additionally, the VLMR-LRT failed to reject the four-class model over the five-class model, and the five-class model produced a very small class (only 1% of the total sample) with parameters that were not likely to be reliably estimated. For the OLCA models, the estimation algorithm failed to converge with more than three latent classes. Of the models that could be estimated, the three-class model had the best BIC value. For the FMA point on the DCS, we considered models with both configural and weak factorial invariance. For the set of models with only configural variance, the one-class, one-factor FMA, equivalent to the one-class, one-factor SP-FA and the one-factor CFA, was selected as the candidate model. Among the FMA models with weak factorial invariance, the two-class, one-factor FMA model was selected. For the SP-FMA models with configural and weak factorial invariance within each of the c^(g) classes, the candidate models selected based on these results were the same models as were selected from the FMA model sets. For the NP-FMA models with configural and weak factorial invariance within each of the c(g) classes, the (S = 2, K = 2) NP-FA models were selected as the candidate models in both cases and the model with weak factorial invariance had the best BIC of the two. For the latent class models, the three-class LCA model was selected as the candidate model.

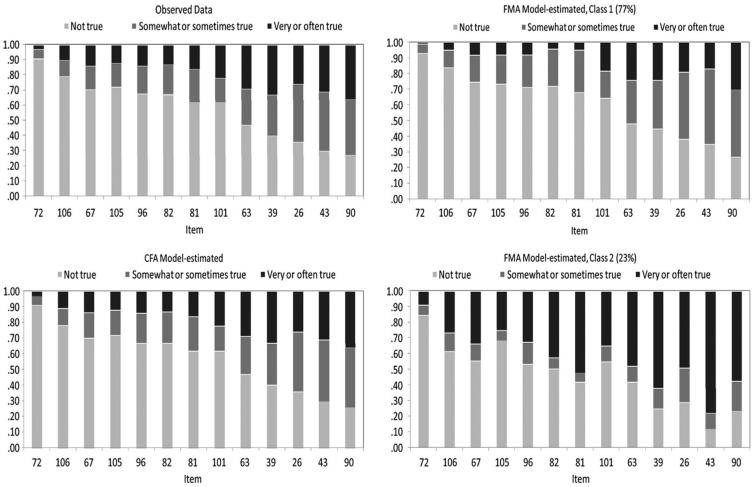
Table 2 presents the candidate models from along the DCS spectrum, based on the results discussed in the previous paragraph. The fit of the three-class LCA was almost identical to the three-class OLCA, suggesting that constraining the classes to be ordered does not result in any meaningful decrement of model fit. Closer examination of the parameter estimates from the two models revealed that the unconstrained LCA yielded parameter estimates very similar to those from the OLCA model. The best BIC value corresponded to the two-class, one-factor FMA models with weak factorial invariance, followed by the one-factor CFA model. When comparing the sample response category proportions for each item to the class-specific model-estimated proportions from the one-factor CFA and the two-class, one-factor FMA, as shown by stacked bar charts in Figure 4, it can be seen that the two latent classes from the FMA are ordered with respect to their item response probabilities, both following, with a few exceptions for class 2, the general item pattern as the overall sample. This suggests that an underlying continuum may indeed be a more parsimonious way of describing the latent structure. Neither model had any significant univariate standardized Pearson residuals and the one-factor CFA had only a few more significant bivariate standardized Pearson residuals than the two-class, one-factor model. In examining the association with the covariate, family problems, the results were similar for the one-factor CFA and the two-class, one-factor FMA (with weak factorial invariance). For both models, higher levels of family problems corresponded to significantly higher levels of delinquency in the CFA model (β = .20, p < .001), and a significantly higher probability of membership in the higher of the two classes in the FMA model (OR = 1.32, p = .05). Given the comparable residual analysis, the parsimony of the one-factor CFA model, the closeness of the unconstrained LCA to the OLCA, and the fact that the results of the two-class, one-factor FMA do not seem to be inconsistent with a dimensional interpretation, we settled on the one-factor CFA as the final model for the 15–17 year age range.

Figure 4.

Stacked Bar Charts of Item Response Categories Proportions for the Observed Data and Model-Estimated Proportions for the CFA Model and for Each of the Two Latent Classes from the 2-Class, 1-Factor FMA Model with Weak Invariance. Items for all Plots are Ordered from Highest to Lowest Observed Proportions of the ‘Not True’ Category

Based on these results, we would make the tentative inference that the latent construct of delinquency for the 15–17 year old population represented by this sample, as measured by the items on this subscale of the CBCL and manifest in this sample, has a (uni)dimensional structure. Further investigations are needed on larger and more diverse groups of subjects, with different item assessments, to be able to generalize beyond the CBCL and the particular population of SED children represented by this sample.

Discussion

In this article, we have presented a unifying framework for utilizing general factor mixture models to explore the latent structure of psychological constructs. In the data illustration of this approach, we found that a dimensional latent structure for delinquency was most consistent with the narrowband delinquency items on the CBCL as manifest in the sample. However, as with any analysis, it is important to recognize that the results are inextricably linked to the variable set used for the analysis and the sample from which the values on those variables are drawn. If the sample is not population-based, then the inferences regarding the latent structure may not be valid for the whole population. Furthermore, the inferences regarding the latent structure are always inferences regarding the latent structure as manifest by the observed variables in the model. In an ideal setting, observations from multiple instruments, multiple reporters, and multiple domains would be used. There is an opportunity here for future research to investigate the sensitivity of these models and the inference regarding latent structure to item set and the presence of shared variance (observed or unobserved) amongst the manifest variables not associated with the latent structure.

In general, the application of the hybrid factor mixture models utilized in the DCS framework is still in its infancy as there remains much work to be done methodologically with respect to ‘best practices’ for model specification, goodness-of-fit testing, inference, diagnostics, and validation so that we have the most reliable and accurate means available for selecting the candidate models and for selecting among the candidate models (but see recent articles by Allua, Stapleton, & Beretvas, 2008; Kuo et al., 2008; Lubke & Muthén, 2007; Lubke & Neale, 2006; Wang, Brown, & Bandeen-Roche, 2005). This does not, however, lessen enthusiasm for the potential of these models to provide a practical and useful union between the latent factor and latent class modeling traditions, overcoming limitations inherent in the two more conventional approaches (Muthén, 2006). Most importantly, the expansion of the ways in which individual differences in the latent construct can be characterized in the general factor mixture modeling framework have implications not just for the representation and interpretation of the nature of the latent construct itself but for how the role of latent phenomenon in a larger system of variables can be understood and, analytically-speaking, parameterized.

The DCS framework may also offer particular advantages over more conventional approaches when applied in longitudinal studies. Typically, in such studies, the modeling approach assumes that the latent structure itself is stable across time while allowing for the possibility that the relationship between the underling latent structure and the manifest variables could change; that is, assuming structural invariance but allowing for measurement non-invariance. However, even a construct that is considered ‘crystallized’ in a non-developmental sense for, say, adult populations, may initially involve a more dynamic organization of covariations (Zucker, Fitzgerald, & Moses, 1994). Further, some developmental phenomena may be characterized not by a particular latent structure but by change in the latent structure itself over time (Beauchaine, 2003; Eaton, 2002). In view of the possibility of impermanence in a latent structure with respect to development, there is a clear need for an empirical methodology, such as the conceptual system of models presented here as the DCS, to explore stability and change in the latent structure of a construct over time that is flexible and broad enough with respect to the set of models under consideration to successfully detect and characterize such change, if present.

The methodological opportunity provided by this framework to investigate the invariance of the latent structures across time also presents a methodological challenge. As mentioned before, most longitudinal models for latent constructs are predicated on stability in the latent structure, for example, latent transition models, higher order growth models, etc. Advances in longitudinal analysis techniques are necessary to permit the modeling of intra-individual change over time in a construct when the latent structure of the construct itself is changing and evolving as well.

In addition to many future directions for methodological research related to the models of the DCS, there are also a multitude of substantive opportunities to examine or re-examine the latent structure of familiar as well as unfamiliar phenomenon using the DCS framework where previously researchers may have presupposed one type of latent structure, or experienced a methodological ‘forced choice’ of a single dimension or a two-category taxonomy. For example, in the current infant attachment literature, attachment behaviors are most often discussed and evaluated relative to a theoretical typology of four primary ‘patterns’ of attachment behaviors: secure, avoidant, ambivalent, and disorganized/disoriented. These attachment profiles have been developed through an iterative process of theory-generation, measurement-development, measurement-validation, and theory-testing. Although there is acknowledgement of possible dimensionality within these profiles, for example, one infant more be more securely attached than another, the attachment categories are predominant. Recently, however, a study by Fraley and Spieker (2003) was done using taxometric methods to examine the latent structure of infant attachment behaviors as measured by the strange situation. They found evidence to suggest that attachment is dimensional rather than categorical. The DCS approach could be used to further explore this issue. It could also be used to explore the consistency in the latent structure of attachment across the lifespan, for example, investigating whether the latent structure of infant attachment behaviors is similar to the latent structure of adult attachment behaviors.

As another example, consider a key concept in socio-emotional development research: social competence. Although this is a key concept, it is also equivocal in definition as it involves several different skill sets, including social skills, social awareness, and self-confidence, with the manifestations of these skills shifting through development as well as across different social contexts. The DCS approach has the flexibility for exploring the latent structure of social competence using different measures for different skills across different ages and contexts. A more complex but consistent model for the latent structure of social competence could then allow for a more effective examination of the predictors and correlates of social competence at a given developmental phase as well as a more nuanced description of individual-level change in social competence across the lifespan. In a similar vein, an exploration of latent structure could be done at the level of social relationships. For example, there has been some empirical work done (Haslam, 1994) to evaluate Fiske’s (1992) theory of sociality as composed of four discrete profiles of social relations. The DCS approach could be used to investigate the underlying latent structures of different social relationships at different levels of social organization, for example, dyadic relationships, peer groups, etc.

As a final example of opportunities for the application of DCS in social development, consider constructs related to personality and temperament. In personality psychology, much of the debate around broad personality traits has related to the number of traits but the prevailing assumption is that these traits are continuous dimensions. Although there has been some empirical work that has called into question that assumption with regards to specific traits such as self-monitoring and expression regulation, there has been little to no work exploring the assumed dimensional latent structure of broad personality traits, such as the Big Five.

The examples above represent a small portion of the prospective applications for the DCS approach. The most fundamental motivation for its use is that the way in which a latent structure is modeled has implications for not only how individual differences at the latent level are understood but also for how those differences are modeled in terms of trajectories, antecedents, and consequences. It is through these more flexible and expansive empirical explorations of the latent structures of social developmental phenomena—enabled by this framework—that we can gain deeper insight into developmental pathways of these phenomena, including the internal mechanisms and external influences that govern their developmental courses across the lifespan.