Discrete-Time Survival Factor Mixture Analysis for Low-Frequency Recurrent Event Histories

Abstract

In this article, the latent class analysis framework for modeling single event discrete-time survival data is extended to low-frequency recurrent event histories. A partial gap time model, parameterized as a restricted factor mixture model, is presented and illustrated using juvenile offending data. This model accommodates event-specific baseline hazard probabilities and covariate effects; event recurrences within a single time period; and accounts for within- and between-subject correlations of event times. This approach expands the family of latent variable survival models in a way that allows researchers to explicitly address questions about unobserved heterogeneity in the timing of events across the lifespan.

INTRODUCTION

In the study of human development, research questions around specific life course events, such as initiation of sexual activity, onset of alcohol use, incidents of felony arrest, transitions to parenthood, retirement, or assisted-living, and so on, are often concerned with the “whether” and “when” of event occurrence. For example, it may be of interest to investigate not only the risk factors that influence whether an adolescent chooses to engage in underage drinking, but also which of those factors influence when or at what age such a behavior begins. Furthermore, the timing of first alcohol use in adolescence may itself be a critical predictor of negative drinking behaviors and alcohol use disorders in adulthood. Historically, event data in social research was more likely to be treated without regard to event timing, using such modeling techniques as logistic regression, which allows an investigator to explore the relationship between the probability of event occurrence and covariates of interest, including perhaps a preventive intervention or treatment. More recently, there has been an increased interest in and use of event history analysis, also known as survival analysis—the general set of statistical methods developed specifically to model the timing of events.

Survival analysis techniques are usually divided into two categories: (1) those dealing with event times measured in a discrete-time metric and (2) those dealing with event times measured in a continuous-time metric. This distinction is made because the methods applied to one type of time metric do not necessarily apply to the other, just as regression techniques for continuous outcome variables do not apply directly to categorical outcomes. For continuous-time event histories, it is assumed that the timing of each observed event is known exactly and that no two individuals share the same event time. For discrete-time event histories, event occurrence is only recorded within a small number (relative to the sample size) of time intervals such that multiple individuals may experience the event during any given time interval.

Discrete-time survival methods have been in use for as long as continuous-time methods but have not enjoyed the same visibility in the technical and applied literature until recently. The most common approach to modeling discrete-time events, utilizing a logistic regression framework, was suggested by Cox in his seminal 1972 paper. The adaptation of logistic regression for discrete-time survival has been studied further by Singer and Willett (1993, 2003; Willett & Singer, 1993, 1995) as well as many others including Prentice and Gloeckler (1978), Laird and Oliver (1981), and Allison (1982). There are several competing approaches currently in use including multilevel ordered multinomial regression (Hedeker, Siddiqui, & Hu, 2000), mixed Poisson models (Nagin & Land, 1993), log linear models (Vermunt, 1997), and discrete-time Markov chain models (Masyn, 2008; Van de Pol & Langeheine, 1990). The methodology developments presented in this article advance discrete-time survival analysis somewhat differently by extending a previously established latent class analysis approach for single event processes into a finite mixture modeling framework. This approach is analytically equivalent to the logistic regression survival model in the most basic setting with a single, nonrecurring event and observed covariates (Masyn, 2003; Muthén & Masyn, 2005).

Often for settings in which event history analysis is applied, the types of events that are considered are single, nonrepeatable events. For individuals who experience the event, their end state is, in the language of Markov models, absorbing; that is, once an individual has had the event, there is no further risk of the event for that individual—the individual cannot experience a repeat occurrence of the event. Given the historical development of survival models in the area of life table analysis, it is not surprising that the main focus for methods development has been around single, terminating events, such as death. However, there are many event history processes in developmental research that do not fit the single event model. Most generally, data from such processes can be referred to as multivariate survival or event history data.

The purpose of this article is to extend the latent class analysis formulation developed for single events to a latent class factor model (factor mixture model) for low-frequency, recurrent events that allows for event-specific survival processes and accounts for observed and unobserved shared variance between processes. This extension is applied to the example of recurrent juvenile offending during ages 6 through 17 using data drawn from the first cohort of the Philadelphia Cohort Study (Wolfgang, Figlio, & Sellin, 1972, 1994). The purpose of the example analysis is not to reach substantive conclusions but rather to illustrate use of the modeling approach. The presentation of the models in this article intentionally omits most of the technical details of model specification, identification, and estimation, relying primarily on path diagrams and the data illustration.

The remainder of the article provides a description of the data used for the analysis example followed by: an overview of single, nonrecurring event history processes specified in a latent variable framework; an explanation of the modeling extension for low-frequency recurrent event history processes; a description of the recommended model building sequence; the demonstration of the model building procedure and presentation of the analysis results from the data example; and a discussion of the limitations of and future directions for this work.

DATA EXAMPLE DESCRIPTION

The data used for analysis illustrations come from the first cohort of the Philadelphia Cohort Study (Wolfgang, Figlio, & Sellin, 1972, 1994). Information was collected in 1964 on a sample of 9,944 boys born in 1945 who lived in Philadelphia, Pennsylvania, from the ages of 10 through 18. The purpose of the original study was to investigate the history of juvenile delinquency in a birth cohort with particular attention to the onset and persistence or desistance of delinquent behavior. Records from public, private, and parochial schools and from the Philadelphia Police Department’s Juvenile Aid Division were used to gather basic demographic information as well as juvenile offense details including the age of each offense, the type of crime committed, and the offense disposition. The subsample of 9,681 used for the analyses herein consists of offense data on the first, second, and third offenses of record from the youngest age of offending, age 6, through age 17, for all boys with complete demographic information.

The sample was primarily White (72%), and there was a nearly even distribution of income levels above and below the national median income of $5,620 for all families in 1960 (U.S. Census Bureau, 2008): 15% at less than $4,501, 30% between $4,501 and $5,783, 30% between $5,784 and $6,779, and 24% greater than $6,779. Of the 3,405 (35% of total) boys who had at least one juvenile offense on record, 1,813 (19% of total, 53% of offenders) recidivated at least once and 1,172 (12% of total, 34% of offenders, and 65% of recidivators) recidivated two or more times.

Table 1 displays the frequencies and relative frequencies for variables corresponding to the first offense of record among those boys with one or more juvenile offenses prior to age 18. Of those with at least one offense, nearly 74% had their first offense after the age of 12, and the ages of 15 and 16 had the highest frequencies, consistent with the adolescent peak typically observed in population age-crime curves. About one half of the first offenses (51%) were nonindex, noncurfew offenses, with nonindex offenses overall accounting for nearly 75% of the first offenses. Most (78%) of the first offenses were disposed of with a remedial action.

TABLE 1.

Descriptives Corresponding to the First, Second, and Third Offenses of Record

Offense (n = number of events in sample)	Variable	Values	f	%
	Age at 1st offense	6–9 years	198	5.8
		10	178	5.2
		11	229	6.7
		12	292	8.6
		13	401	11.8
		14	478	14.0
		15	585	17.2
		16	705	20.7
		17	339	10.0
1st offense  (n = 3405)	1st offense type (Injury: assault, personal  injury; Theft: robbery, burglary,  [auto]theft; Damage: violent property  damage; Combination: combination of  index offenses at police contact;  Non-index offenses: less serious crimes  not included in the index crimes, e.g.,  malicious mischief, trespassing,  common law vice, etc. Curfew-only,  non-index offenses are distinguished  here from non-curfew non-index  offenses.)	Nonindex,  curfew	502	14.7
		Nonindex,  noncurfew	1727	50.7
		Injury	263	7.7
		Theft	471	13.8
		Damage	249	7.3
		Combination	193	5.7
	1st offense disposition (Remedial:  unofficial action by the police; Arrest:  official action by the police; Adjustment:  Case adjusted or discharged either  before or at a court hearing; Court  penalty: severe penalty was imposed,  such as probation, fine, or incarceration.)	Remedial	2653	77.9
		Arrest	50	1.5
		Adjustment	402	11.8
		Court  penalty	300	8.8
2nd offense  (n = 1813)	Age difference between 1st and 2nd  offense	0 years	578	31.9
		1	565	31.2
		2	288	15.9
		3	173	9.5
		4–5	160	8.8
		6–9	49	2.7
3rd offense  (n = 1171)	Age difference between 2nd and 3rd  offense	0 years	521a	44.5
		1	425	36.3
		2	128	10.9
		3	58	4
		4–5	39	3.3

^a151 of these third offenses occurred in the same time period as both the first offense and second offense.

OVERVIEW OF DISCRETE-TIME SURVIVAL ANALYSIS FOR SINGLE EVENT HISTORIES

Characterizing the Single Event History Process

To understand and model any event history process, one must first answer three basic questions: “Who?” “What?” and “When?” The whole of a survival analysis is predicated on three primary elements corresponding to the follwoing cogent questions: (1)Q: Who is at risk? A: The risk set. (2)Q: For what event are they at risk? A: The target event. (3)Q: When are they at risk and when do the events occur? A: Time-at-risk and event times are recorded according to the time metric and scale on which the event history unfolds (either actual or measured). Elements (1) and (2) are inherently linked. Delineation of the risk set, that is, the set of all individuals at risk for the target event in a given time period, should follow from careful definition and characterization of the target event. For single, nonrecurring event processes, the target event must be such that once an individual experiences the target event, he or she is not longer at risk for the event. For the study of juvenile offending event histories, one may define the target event as the first delinquent offense of record. For a given time period, all individuals younger than age 18 who did not yet have a delinquent offense of record at the beginning of the time period would be at risk for the target event during that time period and, therefore, part of the risk set for the event in that time period. Individuals who had already offended by the beginning of a given time period would not be in the risk set for that time period or any subsequent time periods. Individuals who had not offended by the beginning of a given time period but were not observed for the whole of that time period or any later time periods are considered right-censored. Right-censoring is the most common form of missingness in event history data and is the most straightforward to accommodate in the data analysis. In some cases, the only right-censoring of individuals that occurs is at the end of the study, that is, there are some individuals who will be under observation for the whole of a study but will not have experienced the event by the study’s inevitable conclusion. The censoring mechanisms are usually assumed to be noninformative, meaning that the distribution of censoring times is independent of event times, conditional on all observed data. This assumption is analogous to the missing-at-random (MAR) assumption (Little & Rubin, 2002). For this article, treatment of missing event time data is limited to noninformative right-censoring.

Measuring the Single Event History Process

Once decisions have been made regarding the three above-mentioned elements, then the actual event history data collected on each individual in a sample can be translated into event history outcome measures that reflect the careful and precise definitions of target event, risk set, and time metric. For each individual in a sample, event history data, regardless of the study design and collection methods, can usually be summarized by the following information: (1) The final time period, A_i, during which individual i was observed to be at risk for the target event, and (2) an event indicator, δ_i, for whether individual i experienced the target event during A_i. Suppose a₁ is defined at the first discrete time period during which an individual could be at risk for the event and suppose there are a maximum of J time periods, (a₁,a₂,. . .,a_J) during which any single individual is observed to be at risk. A series of event indicators can be constructed, one for each of the J time periods, that reflect each individual’s membership in the risk set for each time period and his or her outcome for the time period (event vs. no event). Let e_iaj be the event indicator for individual i in time period a_j defined by

$$e_{i{a}_j}=\{\begin{array}{cc}1\text{if}\hfill & A_i=a_j,{\delta }_i=1\hfill \\ 0\text{if}\hfill & A_i=a_j,{\delta }_i=0\text{or}{A}_i>a_j\hfill \\ •\text{if}\hfill & A_i<a_j\hfill \end{array}\phantom{\}}$$

where • indicates a missing value code. The values of 0 and 1 indicate membership in the risk set for period a_j whereas • indicates exclusion from the risk set (either due to prior event occurrence or right-censoring). For the juvenile offending example, records are only available for children ages 6 to 17. Twelve event indicators, one for each age, could be created: (e₆,e₇, . . .,e₁₇). An individual with a first event at age 10 would have A_i = 10 and δ_i = 1 with the following values for the event indicators:

$$\begin{array}{cccccccccccc}\hfill e_6& \hfill e_7\hfill & \hfill e_8\hfill & \hfill e_9\hfill & \hfill e_{10}\hfill & \hfill e_{11}\hfill & \hfill e_{12}\hfill & \hfill e_{13}\hfill & \hfill e_{14}\hfill & \hfill e_{15}\hfill & \hfill e_{16}\hfill & \hfill e_{17}\\ \hfill (0& \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •)\end{array}$$

An individual with A_i = 10 and δ_i = 0 would have the following values for the event indicators:

$$\begin{array}{cccccccccccc}\hfill e_6& \hfill e_7\hfill & \hfill e_8\hfill & \hfill e_9\hfill & \hfill e_{10}\hfill & \hfill e_{11}\hfill & \hfill e_{12}\hfill & \hfill e_{13}\hfill & \hfill e_{14}\hfill & \hfill e_{15}\hfill & \hfill e_{16}\hfill & \hfill e_{17}\\ \hfill (0& \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •\hfill & \hfill •)\end{array}$$

And, an individual with A_i = 17 and δ_i = 0 would have the following values for the event indicators:

$$\begin{array}{cccccccccccc}\hfill e_6& \hfill e_7\hfill & \hfill e_8\hfill & \hfill e_9\hfill & \hfill e_{10}\hfill & \hfill e_{11}\hfill & \hfill e_{12}\hfill & \hfill e_{13}\hfill & \hfill e_{14}\hfill & \hfill e_{15}\hfill & \hfill e_{16}\hfill & \hfill e_{17}\\ \hfill (0& \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0)\end{array}$$

Notice that for the two right-censored individuals above, with δ_i = 0, information about their event processes can still be included even if the exact event times are unknown. For example, for the individual with A_i = 10 and δ_i = 0, it is known that the individual was at risk, that is, in the risk set, for the target event for ages 6 to 10 but remained event free. The event indicator coding indicates what is known about the event time, T, for that individual: T > 10. In general, through the construction of these event indicators, the a priori definitions of target event, risk set, and time metric and scale are hard-coded into the data, and it is these event indicators that will serve as the dependent variables in the discrete-time survival model.

Quantifying the Single Event History Process

There are two main quantities of interest when describing a discrete-time event history process: (1) the survival probability and (2) the hazard probability. The survival probability corresponding to time period a_j is defined as the probability of an individual “surviving” beyond a_j; that is, remaining event-free through time period a_j. Define the survival probability, P_s(a_j), such that

$$P_s\left(a_j\right)=P_r(T>a_j).$$ (1)

where T is the time period of event occurrence.

The hazard probability, although perhaps less intuitive than the survival probability, is the quantity that is dealt with most often in survival analyses as the majority of discrete-time event history models are specified in terms of the hazard probabilities. The hazard probability corresponding to time period a_j is defined as the probability of an individual experiencing the event in time period a_j given that he or she had not experienced the event prior to time period a_j. Define the hazard probability, P_h(a_j), such that

$$P_h\left(a_j\right)=P_r(T=a_j\mid T\ge a_j).$$ (2)

It is useful to examine the survival and hazard probabilities for the time periods under study. Although the survival probability describes who, among the original risk set, are still at risk beyond a given time period (reflecting the cumulative impact of risk on the population), the hazard probability assists in identifying particularly risky time periods for event occurrence and characterizes how risk for the event changes over time among those who remain in the risk set.

Modeling the Single Event History Process in a Latent Variable Framework

To fit discrete-time survival models into a general latent variable framework, such as the one formulated by Muthén and Shedden (1999), involving categorical and continuous latent variables with maximum likelihood estimation carried out using the expectation-maximization (EM) algorithm, one must only observe that the maximum likelihood estimates for the event indicator means based on a (K = 1) latent class model with (e_a1,e_a2 ,..., e_aj ) as binary class indicators are equal to the maximum likelihood estimates for the hazard probabilities (Masyn, 2003; Muthén & Masyn, 2005). That is,

$${\widehat{P}}_r(e_{a_j}=1)={\widehat{P}}_h\left(a_j\right).$$ (3)

As with a traditional latent class analysis (e.g., McCutcheon, 1987), the probabilities for the binary indicators can be associated with observed covariates by means of a logistic regression. Because the binary latent class indicators are the event indicators, and the probabilities of the event indicators are the hazard probabilities for the corresponding time periods, this functional association between the event indicators and covariate is termed the logistic or logit hazard model. In its most general form, the conditional logit hazard model is given by

$$\log \left(\frac{P_r(e_{a_j}=1\mid x)}{1-P_r(e_{a_j}=1\mid x)}\right)=\mathrm{logit}\left(P_h(a_j\mid x)\right)={\nu }_j+{\beta }_{j}x,$$ (4)

where x is one or more covariates associated with the event process. The x-variables may be either time-invariant (x) or time-varying (x_j) . β_j represents the change in the logit hazard probability for a one unit increase in x. Thus, exp(β_j) is the hazard odds ratio (hOR) associated with x. By dropping the subscript j from β_j, equivalent to constraining all paths from x to the event indicators, (e_a1,e_a2, . . .,e_aj), to be equal, the effects of x are constrained to be equal across all time periods, that is, time-invariant. This is referred to as the proportional hazard odds model because the hOR associated with x is constant across time. The intercept parameter, v_j, is the logit of the baseline hazard probability; that is, the log hazard odds for time period a_j when x = 0.

Example

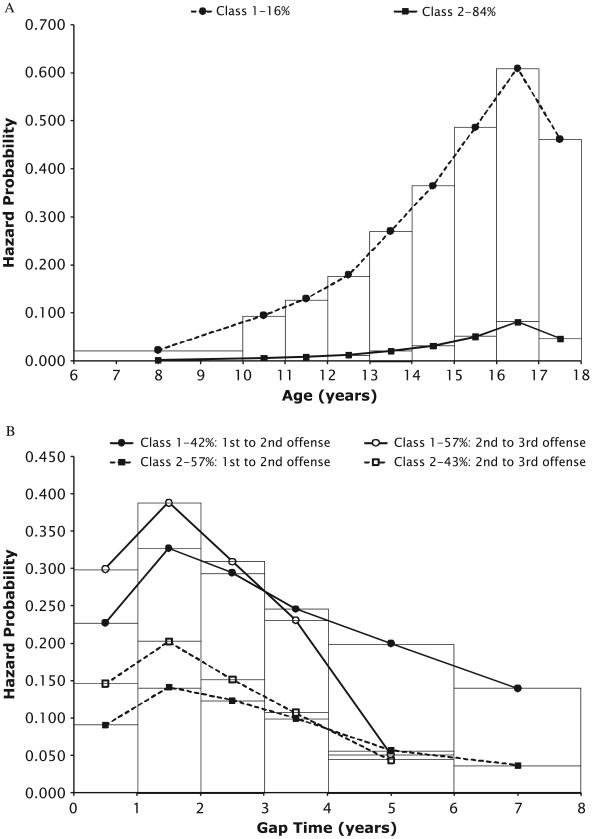
Figure 1A displays a plot of the unconditional sample hazard probabilities, each calculated as the ratio of the number of first offenses during a given time period to the number of boys at risk for a first offense in that time period. For example, for the age 11 time period 9,305 boys were at risk for a first offense and 229 of those boys committed their first offense of record at age 11, yielding an estimated hazard probability of 229/₉₃₀₅ = .03. The plot shows a pattern of steadily increasing risk for first offense among those in the risk set, with a peak hazard probability at age 16 and a sharp decline at age 17.

FIGURE 1.

Sample-based hazard probabilities by (A) grouped-age intervals for first, second, and third offenses and (B) gap time intervals for second and third offenses.

Note. Estimated hazard probabilities in figures corresponding to time intervals greater than one year are plotted as an approximation of the within-interval, 1-year hazard probability at the center of the interval. Full details of these calculations are available in a technical appendix upon request from the author.)

DISCRETE-TIME SURVIVAL ANALYSIS FOR RECURRENT EVENT HISTORIES

Recurrent event processes, also termed repeatable events or multiple spell models, yield a particular kind of multivariate survival data. In contrast to single-event processes (which yield univariate survival data), the target event of interest is nonterminating; that is, after an individual’s first occurrence of the given event, he or she returns to an at-risk status for a subsequent occurrence. Examples of recurrent events include pregnancies, hospitalizations, work absences, and school suspensions. Hougaard (2000) made the usefully distinction between recurrent event processes with high and low enumerations. That is, some recurrent event processes have a small number of maximum events that are ever observed for a single subject, such as pregnancies, career transitions, or age- and illness-related deaths of immediate family members. Other recurrent event processes may have such a large number of recurrences for some subjects, such as school truancies, work absences, or age-related losses of function, that enumerating them becomes impractical. For the purposes of this article, only recurring event processes of the low enumerative kind, termed here low-frequency recurrent event histories will be considered.

Characterizing the Recurrent Event History Process

Just as with a single, nonrecurring event process, the three basic questions must be answered to properly specify the event history model: “Who?” “What?” and “When?” In the case of recurrent event processes, these questions must be answered for each event enumeration. Suppose that M is the maximum number of event occurrences to be modeled for any single individual during the time span of observation. Often, the formulation for the first event occurrence (m = 1) parallels that for a single event occurrence (as described in the previous section). For the recurrent event processes dealt with in this article, assume (1) an individual may only be at risk for one event at a time; (2) an individual may not be at risk for the m^th event until he or she has experienced the (m – 1)^th event for m > 1; and (3) more than one event occurrence for an individual can occur in the same discrete time period.

There are two ways view the timing of risk for event recurrence. One way is to record all event recurrences on the same time scale as the first event occurrence, for example, age in years. Another approach is to rescale the timing of a recurrence with respect to the occurrence of the previous event. This is referred to in the literature as the gap time (GT) formulation (Kelly & Lim, 2000). A distinction here is made between what will be termed full-GT and partial-GT formulations. With the partial-GT formulation, the time scale of the first event is different from the time scale for all subsequent events. For example, using age (in years) as the time scale for the first offense occurrence and then time (in years) since offense (m – 1) as the time scale for all events m > 1. Essentially, the event clock resets to zero after each event. Usually, the time metric, for example, discrete time with one-year time intervals, remains the same across event enumerations. If the set of events under consideration are all recurrences, such that the first time period for the whole of the event processes under investigation is marked by the first occurrence, rather than by first risk of the first occurrence, then a full-GT formulation can be used with all event times on the same gap time scale. The remainder of this article deals with the partial-GT approach.

Example.

Figure 1A displays plots of the sample-based hazard probabilities for the second and third offenses, showing that on the age-time scale, the hazard patterns for the second and third offenses are progressively more elevated compared to the first offense, but the shapes of the patterns are comparable across the age span, with the peak hazards at slightly younger ages. Figure 1B displays the plots of the sample-based hazard probabilities for the second and third offenses in gap time. Comparing the patterns of hazard probabilities for recurrent events across the two time scales in Figures 1A and 1B, it is clear that, for example, the pattern for the second offense in Figure 1A is reflecting the pattern of first offense hazard and the high hazard probability for recurrence in shorter time frames following first offense. This suggests that in modeling the time to recurrent events using the gap time formulation, it may be constructive to include information related to the actual age of first offense.

Table 1 displays the frequencies and relative frequencies for variables corresponding to the timing of the second and third offenses for recidivating offenders. In terms of the age difference between offenses, the frequencies are highest for the shorter gap times and decrease with increasing gap times. The skew is more evident for the gap time between the second and third offense than between the first and second, suggesting that the time between offenses may shorten as the event enumeration increases for those who are more persistent offenders.

Measuring the Recurrent Event History Process

To extend the single event history process definitions to recurrent event processes, additional event indicators corresponding to each of the enumerated events are needed. Instead of a single set of event indicators, a series of event indicators sets are constructed, with one set for each of the M event enumerations that reflect each individual’s membership in the m^th event risk set for each time period and his or her outcome for the time period (m^th event vs. no m^th event), conditional on risk set membership. The creation of event indicators set of for the first, second, and third juvenile offense using the partial-GT formulation for the data example is detailed below.

Example

For the Philadelphia Cohort Study data, the timing of the first offense was measured by age in years. Due to the large sample size, even though rates of offending are relatively low in the overall population, there was a sufficient number of individuals at risk for the first offense at each age and a sufficient number of events observed at each age to make creating event indicators corresponding to one-year time intervals practical; the exception being the ages before 10 years that were grouped into a single 4-year interval corresponding to ages 6 through 9. For the second and third offenses, the gap time scale (in years) was used for the construction of the event indicators. Thus, there were event indicators for 0, 1, 2, 3, 4–5, and 6–7 years from first to second offense occurrence and event indicators for 0, 1, 2, 3, and 4–5 years from second to third offense occurrence. (Guidelines for what constitutes adequate sample of at-risk individuals and observed events for each time period are the same as those for logistic regression and latent class analysis.)

Table 2 displays example coding for the event indicators of six individuals. Person 1 did not offend prior to the age of 18 years. This individual was at risk for a first offense but event-free during the entire age span under consideration, reflected by the 0 values for all the first-offense event indicators. Because Person 1 did not have a first offense, he was never at risk for a second or third offense, reflected by the • missing value indicator. Person 2 had his first offense at age 15 and was not observed recidivating. For this individual, the event indicators prior to age 15 have a value of 0 and then the event indicator for age 15 has a value of 1, reflecting that the individual was at risk for a first offense prior up through age 15 the event occurred at age 15. Person 2 is coded as missing for the remaining two event indicators for the first offense, corresponding to ages 16 and 17, because after his first offense at the age of 15, he was no longer in the first offense risk set. Because data was restricted to juvenile offending, occurring before the age of 18, Person 2 was only at risk for a second offense at ages 15, 16, and 17, corresponding to gap times of 0, 1, and 2. Because Person 2 did not recidivate, the gap time event indicators for the second offense for 0, 1, and 2 years are coded as 0. The remaining gap time indicators for the second offense corresponding to 3 through 6–7 years are coded as missing since the offender was right-censored after age 17. Because Person 2 did not recidivate, he has missing values for all third-offense event indicators. Persons 3 through 6 all had their first offense at age 15 and, thus, all have the same event indicator coding as Person 2 for those indicators corresponding to the first event. Person 3 had his second offense at age 16 (corresponding to a gap time of 1 year) and no third offense. Because the second offense occurred at age 16, Person 3 was only at risk for a third offense at ages 16 and 17, corresponding to gap times of 0 and 1 year. Thus, Person 3 is coded as missing for third offense gap time event indicators beyond a gap time of 1 year. Person 4 matches Person 3 for first and second event indicator coding. However, Person 3 has a third offense at age 17, indicated by a 1 value for the 1-year gap time event indicator for the third offense. Persons 5 and 6 were observed to have three offenses. Their ages of first offense were the same, and their gap times between the second and third offenses were zero. Thus, their coding is identical for the first and third offense event indicators. However, Person 5 has a gap time of 1 year between his first and second offense while Person 6 has a gap time of 0 years. For the 0-year gap time indicator of the second offense, only one other offense, the first, could have occurred in the same time interval. However, for the zero gap time indicator of the third offense it is possible that either the first and second offenses share the same time interval of occurrence as the third offense (as with Person 6) or only the second offense shares the same time interval of occurrence with the third (as with Person 5). To account for this difference in the actual analysis, a covariate indicating the number of prior events sharing the same time period as the event in question should be used as an adjustment variable with a direct path to the 0-year gap time event indicator.

TABLE 2.

Examples of Partial Gap Time Data Coding

	Age (Yrs) at Offense # —			Event Indicators for Ist Offensea					Event Indicators for 2nd Offenseab				Event Indicators for 3rd Offense,ab
i	1	2	3	e(1)6 –9– e(1)13	e(1)14	e(1)15	e(1)16	e(1)17	egt(2)0	egt(2)1	egt(2)2	egt(2)3 – egt(2)6 –7	egt(2)0	egt(2)1	egt(2)2	egt(2)3 – egt(2)4 –5
1	n/a	n/a	n/a	0	0	0	0	0	•	•	•	•	•	•	•	•
2	15	n/a	n/a	0	0	1	•	•	0	0	0	•	•	•	•	•
3	15	16	n/a	0	0	1	•	•	0	1	•	•	0	0	•	•
4	15	16	17	0	0	1	•	•	0	1	•	•	0	1	•	•
5	15	16	16	0	0	1	•	•	0	1	•	•	1	•	•	•
6	15	15	15	0	0	1	•	•	1	•	•	•	1	•	•	•

^•indicates a missing value code.

^a“(_)” superscirpt indicates the event enumeration, e.g., (1) for the first offense.

^b“gt” superscript indicates that the event indicators correspond to intervals on a gap time scale.

As a side note, it is worth mentioning that in the coding described above, it is assumed that an individual who commits his m^th offense is immediately at risk for the (m + 1)^th offense. This would not be a reasonable assumption for offending populations in which individuals are usually incarcerated and, therefore, incapacitated until their release. The coding scheme can be adjusted to accommodate these situations such that incarcerated individuals would not enter the risk set for the (m + 1)^th offense until the time of their release and the time of incarceration would be included as a predictor in the hazard model for the (m +1)^th offense. In this particular sample of juvenile offending however, incarceration in a correctional institution for the early offenses is infrequent (e.g., only 1% of first offenses have an incarceration disposition) and the assumption of immediate entry to the subsequent event risk set is quite practical.

Quantifying the Recurrent Event History Process

Similar to the single event history process, the main quantities of interest are the hazard and survival probabilities. Because there are separate sets of event indicators for each event enumeration (J⁽¹⁾ event indicators for the first event process, J⁽²⁾ event indicators for the second event process, etc.), it is also possible to allow fully event-specific hazard probabilities. Let T^(m) be the time period (in age- or gap time) during which the m^th event occurs. The hazard probability for the first event, corresponding to time period aj⁽¹⁾, is defined as before with the only change being additional notation to indicate correspondence to the first event process:

$$P_h^{\left(1\right)}\left(a_j^{\left(1\right)}\right)=P_r(T^{\left(1\right)}=a_j^{\left(1\right)}\mid T^{\left(1\right)}\le a_j^{\left(1\right)}).$$ (5)

The hazard probability for the m^th event (m > 1), corresponding to time period aj^(m), is given by

$$P_h^{\left(m\right)}\left(a_j^{\left(m\right)}\right)=P_r(T^{\left(m\right)}=a_j^{\left(m\right)}\mid T^{\left(m\right)}\ge a_j^{\left(m\right)},{\delta }^{(m-1)}=1),$$ (6)

where δ^(m–1)= 1 if T^(m–1) is observed, that is, if the (m – 1)^th event occurred while the individual was under observation.

Modeling the Recurrent Event History Process in a Latent Variable Framework

The modeling approach for a single event history process presented earlier can be extended to accommodate recurrent events. It is in this multivariate survival setting that one of the primary advantages of conducting survival analysis within a more general latent variable framework becomes most evident: the ability to explicitly account for the influence of unobserved heterogeneity through the use of latent variables.

As with any case of repeated measures on individuals within a sample, it is unlikely that the event times for the different event enumerations observed for each individual are independent. If this shared variance across event enumerations, not explained by observed covariates, is ignored, not only will the standard errors on parameters be underestimated, but also the estimates of the hazard probabilities and covariate effects will themselves be biased (Kelly & Lim, 2000; Vaupel, Manton, & Stallard, 1979). Furthermore, the bias for the estimated covariate effects occurs even if the sources of unobserved heterogeneity have no associations with the covariates. Approaches such as using the time of prior occurrence as a covariate or robust variance estimates have been shown to not adequately correct these biases (Allison, 1995; Kelly & Lim, 2000). Another approach to dealing with the within-subject correlations is to characterize the shared variance as unobserved heterogeneity in the form of a latent variable. This is easily accomplished from within the chosen modeling framework.

There are two primary techniques within this framework to account for unobserved heterogeneity in multivariate survival processes such as recurrent event histories. The first is probably the more common, utilizing a continuous latent variable as a random effect as is done with other types of repeated measures or multilevel data (see, e.g., Hedeker et al., 2000; Steele, Goldstein, & Brown, 2004). To specify a model with a continuous, underlying latent variable (often referred to as a frailty in the survival literature) in the general modeling framework, the event indicators would be used as indicators of a latent factor, as in a categorical factor analysis. Although this may be the most straightforward and intuitive specification for shared variance, it has been shown that the parameter estimates for the baseline hazard probabilities as well as for the observed covariate effects are very sensitive to the distributional assumptions made for the latent factor and are subject to bias in the case of distribution misspecification (Heckman & Singer, 1984a, 1984b; Land, Nagin, & McCall, 2001).

The alternate technique for incorporating unobserved heterogeneity is to specify a model with a categorical latent variable. Heckman and Singer (1984a) originally suggested this approach to avoid the pitfalls of misspecifying the frailty distribution (see also Vermunt, 2002). The overall survival distribution in the population is described by a “mixing” of a finite number of subpopulations (i.e., latent classes of individuals) with distinct, class-specific survival distributions. The shared variance between event times, not explained by the observed covariate in the model, is attributed to latent class membership. One method for implementing this nonparametric frailty concept in the general modeling framework for discrete-time event processes is to include all the event indicators for all the recurrent event enumerations under consideration as latent class indicators and increase the number of categories for the latent class variable to two or more, as in a traditional latent class analysis. The primary disadvantage to this method is that the model can quickly become parameter laden and unparsimonious with each additional latent class if allowing all baseline hazard probabilities for all time periods across all event enumerations to be class-specific.

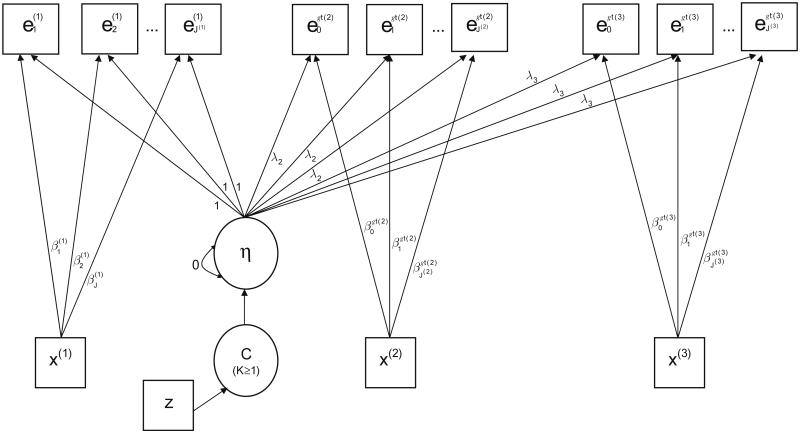
The recurrent event history model proposed in this article draws strengths from the two methods described above by parameterizing the unobserved heterogeneity using a latent class and latent factor variable, similar to the implementation of the Heckman–Singer model in continuous-time settings. The model, represented by a path diagram in Figure 2, characterizes the shared variance across event enumerations, not accounted for by the observed x-variables, using a restricted factor mixture latent structure. There is an underlying “continuous” frailty variable, denoted by η. However, instead of specifying a parametric distribution for the values of η in the population, the distribution of η is characterized by a set K weighted mass points where K is the number of categories fo characterized by a set K weighted mass points where K is the number of categories for the latent class variable, C; the weights of the mass points are the latent class proportions (or mixing proportions); and the locations of the mass points are the class-specific means of η. These correspondences between the distribution of η and the latent class variable, C, is represented in the path diagram by the arrow pointing from C to η. Within each latent class, the variance of η is fixed at zero. The restricted factor mixture model described here is sometimes referred to as a latent class factor analysis or a located latent class analysis model.

FIGURE 2.

Path diagram for a low-frequency, recurrent event history process in a factor mixture framework.

The factor loadings for the first set of event indicators are fixed to one. The factor loadings for the second set of event indicators are constrained to be equal but are freely estimated as are the factor loadings for the sets of event indicators for all other event enumerations. This specification implies that the underlying frailty has a time-invariant or proportional effect on the hazard odds for a given event time process but that the influences of that frailty may vary according to the event enumeration. This provides a much more flexible and tenable model for unobserved heterogeneity than the standard random effects frailty models but provides a greater degree of parsimony than the completely unrestricted latent class models.

In terms of the functional form of the associations between the event indicator probabilities and the observed and unobserved sources of variance, the same logistic regression formulation is used as previously described, with the inclusion of the latent class variable, C. That is,

$$\log \left(\frac{P_r(e_{a_j^{\left(m\right)}}^{\left(m\right)}=1\mid x,C=k)}{1-P_r(e_{a_j^{\left(m\right)}}^{\left(m\right)}=1\mid x,C=k)}\right)=\mathrm{logit}\left(P_h^{\left(m\right)}(a_j^{\left(m\right)}\mid x,C=k)\right)={\nu }_j^{\left(m\right)}+{\beta }_j^{\left(m\right)}{x}^{\left(m\right)}+{\lambda }_m{\alpha }_k,$$ (7)

where x^(m) is one or more covariates associated with the m^th event process. As before, the x-variables may be either time-invariant (as depicted in Figure 2) or time-varying. β_j represents the log hOR for the m^th event at time period a j^(m) associated with a one unit increase in x^(m). The intercept parameter, v_j^(m), is the logit of the baseline hazard probability for the m^th event for time period a_j^(m). λ_m is the frailty factor loading for the m^th event indicators, and represents the log hOR for the m^th event corresponding to a one unit increase on the scale of η. α_k is the mean of η in Class k, that is, E(η|C = k) = α_k. Thus, λ_mα_k represents the difference in the logit hazard probabilities between Class k and Class 1, associated with the m^th event, accounting for the effects of the observed covariates, x^(m). For identification, α₁ = 0 and λ₁ = 1.

Correlates and predictors of the unobserved frailty, represent by z in Figure 2, can be investigated by examining their associations with latent class membership through a multinomial regression given by

$$P_r(C=k\mid z)=\frac{\exp ({\pi }_{0k}+{\pi }_{1k}z)}{{\sum }_{g=1}^K\exp ({\pi }_{0g}+{\pi }_{1g}z)},$$ (8)

where Class K serves as the references class with π_0k = π_1K = 0 for identification.

MODEL BUILDING

This section describes the model building process as a recommended series of steps and is followed by a section that illustrates the application of these steps to the example data.

STEP 0) Assemble all variables of interest and construct all necessary event indicators.

STEP 1A) Fit separate unconditional single event models for each event occurrence process.

STEP 1B) For each separate model, add event-specific covariates (corresponding to the x-variables in Figure 2), investigating significance of effects and evidence of nonproportionality of the hazard odds (i.e., time-varying effects).

STEP 2A) Combine each of the final models from (1B) into a single, one-class, partial gap time model without the latent factor.

STEP 2B) Add the frailty factor specification and estimate a series of factor mixture models (corresponding to Figure 2) with an increasing numbers of latent classes (beginning with a two-class model) to determine the minimum number of latent classes needed to effectively account for the shared variance across the event processes due to unobserved heterogeneity. This step in the modeling process—deciding on the appropriate number of classes—can prove challenging, particularly because there is no single method for comparing models with differing numbers of latent classes that is widely accepted as best (Nylund, Asparouhov, & Muthén, 2007). The standard chi-square difference test (likelihood ratio test [LRT]) cannot be used in this setting. However, two alternatives, as implemented in the Mplus V5.2 software (Muthén & Muthén, 1998–2008a), are available: (1) the Vuong-Lo-Mendell-Rubin (VLMR-LRT; Lo, Mendell, & Rubin, 2001) analytic approximation to the LRT, and (2) the parametric bootstrapped LRT (BLRT) empirical approximation to the LRT, recommended by McLachlan and Peel (2000). In addition to these tests, likelihood-based information indices, such as the Bayesian Information Criterion (BIC: Schwarz, 1978) are used in model selection. Besides these statistical criteria, it is also useful assess the value and utility of the resultant classes themselves. One measure which can be used for this purpose is entropy (Ramaswamy, Desarbo, Reibstein, & Robinson, 1993) that summarizes the degree to which the latent classes are distinguishable. Furthermore, it is important to make some qualitative evaluations of the usefulness and face validity of the latent class extractions by examining and interpreting the estimates and corresponding plots of the model-implied mean class-specific hazard probabilities for different models. Although there is no universally prescribed or singular method for model selection at this step of class enumeration, by careful and systematic consideration of a set of plausible models, and by utilizing a combination of statistical and substantive model checking (Muthén, 2003; see Read and Cressie, 1988, for more on goodness-of-fit statistics for discrete multivariate data), researchers can improve their confidence in the soundness of their resultant model selection. There is an ever-growing volume of work on finite mixture model specification and latent class enumeration, and much of the work done in the context of one type of mixture modeling can be generalized to other types. For more details on mixture specification in growth modeling, see Grimm and Ram (this issue).

STEP 3) Using the final model from (2B), add auxiliary information in the form of predictors of latent class membership (corresponding to the z-variables in Figure 2).

STEP 4) Using the final model from (3), add auxiliary information, in the form of consequents or distal outcomes of latent class membership. The results of this step and Step 3 can be examined to evaluate the concurrent and prognostic validity of the latent class structure as specified in a given model (Muthén, 2003). The inclusion of consequent variables or distal outcomes is not discussed further in this article.

The next section summarizes, in brief, the results of modeling Steps 1 through 3 applied to the Philadelphia Cohort Study data and then presents a detailed description of the final resultant model.

All analysis models were estimated using full-information maximum likelihood (FIML) with robust standard errors (MLR) as implemented in Mplus V5.2 (Muthén & Muthén, 1998-2008b; the corresponding Mplus syntax for all models is available as a technical appendix upon request from the author). FIML utilizes all of the available data under the missing-at-random (MAR) assumption as defined by Little and Rubin (2002) and corresponds for all event processes to the assumption of noninformative censoring given the previously described data coding. For each model, a high number of sets of random start values drawn from random locations in the parameter space relative to an initial start value set were utilized.

DATA EXAMPLE: RESULTS

Step 1A

Separate unconditional single event models were fit for the time to the first, second, and third offenses using the corresponding subset of event indicators. In all cases and for all subsequent models, the baseline hazard probabilities were permitted to vary freely across time periods and event enumerations because misspecification of the structure of the baseline hazard function can unnecessarily bias other parameter estimates, for example, covariate effects (Trussel & Richards, 1985).

Step 1B

For each separate model, event-specific covariates were added, investigating significance of effects and evidence of nonproportionality of effects. For the time to first offense model, no covariates (x⁽¹⁾-variables) were included. For the time to second offense, the age, type, and disposition of first offense were included as covariates (x⁽²⁾-variables). The disposition of first offense was not significantly related to the hazard probabilities of the second offense once accounting for the type of first offense and was not included in later models. There were only negligible differences in fit between the model including age at first offense as a continuous variable and age of first offense as a categorical variable, suggesting that a linear association between age of first of offense and the logit hazard of the second offense was consistent with the data. However, there was a significant improvement in fit when allowing the effect of age of first offense to vary across the second offense gap time event indicators suggesting a nonproportional hazard odds model, that is, time-varying effects of age of first offense, was more consistent with the data.

For the time to second offense, the age, type, and disposition of first offense and the gap time of the second offense were included as covariates (x⁽³⁾-variables), along with a binary indicator of first and second offense occurring in the same time interval as the third (vs. only the second offense) as a covariate affecting only the event indicator corresponding to a gap time of zero. Patterns of association for the time to third offense were similar to those found for the second offence. In no cases for the gap time to second event and the gap time to third event models, were the effects of x-variables on event indicators corresponding to time spans of more than one year constrained to be equal to the effects on event indicators corresponding to time spans of one year.

Step 2A

The final three separate models, with all related x-variables with effects specified as in the separate models, were combined into a single, one-class partial gap time model without the latent factor.

Step 2B

The frailty factor specification was added, and for each model with two or more latent classes the factor mean was fixed at zero in the first latent class. The factor loadings of the first offense event indicators were fixed at unity with the exception of the loading for the event indicator corresponding to the 6- to 9-year age span. The factor loadings of the 1-year interval gap time event indicators for the second offense were constrained to be equal as were the loadings of the 2-year interval gap time indicators. The factor loadings of the gap time event indicators for the third offense were constrained to be equal with the exception of the loading corresponding to the 4- to 5-year gap time span.

Based on the relative fit indices and resultant class sizes and meaning, a two-class model was selected as most appropriate. It offered marked improvements in fit over the one-class model while little was gained with the addition of a third class.

Step 3

The covariates of race and income level were added as latent class predictors in the final model from (2B). Both were significantly associated with class membership. Race and income could have been included as x-variables, predicting directly to the event indicators, rather than z-variables predicting latent class membership. With survival mixture models, it is possible to make a conceptual and analytic distinction between those variable believed to directly influence event risk and those variables believed to influence the underlying individual frailty or susceptibility to a particular event process. In this example, it could be argued that background variables such as race and income represent proxy measures of risk context that would best be modeled as predictors of the shared variance across the event processes. (For more on persons-as-contexts in longitudinal models, see the work of Hoffman and Stawski in this issue). Ultimately, the decision of when and how observed covariates are included in these models (as x- or z-variables) must be an informed choice made by the researcher with full knowledge that different specifications for the paths of influence could yield substantive differences in the number and nature of the resultant latent classes.

Final model results

Tables 3 and 4 display the final model results for the within-class logit hazard regressions and the latent class regression, respectively. (For Table 3, some parameter estimates for the final model are excluded from the table for the sake of space.) Age at first offense was significantly and positively associated with the 0-, 1-, and 2-year gap time hazards for the second offense, with the hazard odds 1.15–1.22 times higher for each 1-year increase in age of first offense. This implies that the risk of early recidivating is higher for older first offenders. However, of those who do not reoffend within 2 years of the first offense, the influence of age of first offense becomes negligible as is evidence by the nonsignificant effect of first offense age on the 3-, 4–5-, and 6–7-year gap time hazards. Of those who offend twice, the gap time hazards for the third offense are not associated with the age of first offense with the exception of the 4- to 5-year gap time hazard. This negative association is likely due in part to the fact that this analysis only deals with juvenile offending before the age of 18. Only those offenders with a second offense by the age of 13 have even the possibility of contributing information to the estimation of this age of first offense effect and their age range of first offense in the sample is limited to 8 to 13 years.

TABLE 3.

Final 2-Class Model Results for Within-Class Logit Hazard Regressions (n = 9681, log-likelihood = –19,452.30, Number of Free Parameters Estimated = 67)

	Factor Loadings (Factor Means: Class 1= 0.00; Class 2= −2.88)			X2, X3			X2, X3			X3
				Age (Years) at 1st Offense			Ist Offense = Non-index, Curfew			Gap Time (Years) From 1st to 2nd Offense
Event Indicator	Est.	SE	hORa	Est.	SE	hORb	Est.	SE	hORb	Est.	SE	hORb
1st offense at 6–9 years	0.85*	0.09	11.40
1st offense at 10 years – 1st offense at 17 years	1.00	fixed	17.76
2nd offense at same age as 1st	0.38*	0.05	2.96	0.20*	0.03	1.22	−2.26*	0.17	0.11
2nd offense at age 1 yr older than 1st	”			0.19*	0.03	1.21	”
2nd offense at age 2 years older than 1st	”			0.14*	0.04	1.15	”
2nd offense at age 3 years older than 1st	”			0.01	0.05	1.01	”
2nd offense at age 4–5 years older than 1st	0.53*	0.15	4.53	−0.07	0.06	0.93	−2.80*	0.58	0.06
2nd offense at age 6–7 years older than 1st	”			−0.09	0.14	0.92	”
3rd offense at same age as 2ndc	0.32*	0.06	2.50	−0.26	0.16	1.06	−2.59*	0.53	0.08	−0.03	0.05	0.98
3rd offense at age 1 yr older than 2nd	”			−0.002	0.04	1.00	”			−0.10**	0.05	0.90
3rd offense at age 2 years older than 2nd	”			0.06	0.07	1.07	”			−0.04	0.09	0.97
3rd offense at age 3 years older than 2nd	”			−0.08	0.11	0.92	”			−0.15	0.15	0.86
3rd offense at age 4–5 years older than 2nd	0.07	0.32	1.21	−0.51**	0.20	0.60	0.00	fixedd		−0.79**	0.28	0.45

hOR = hazard odds ratio.

^”Constrained to be equal to preceding parameter estimate.

^aCorresponding to hazard odds for Class 1 versus Class 2 at respective factor means.

^bCorresponding to a one unit increase in x-variables.

^cLogit hazard for 3rd offense gap time of zero years adjusted for number of previous offense occurring at the same age (both 1^st and 2_nd offense vs. 2nd offense only).

^dPath not estimated due to zero observations with a non-index, curfew offense, and a gap time between the 2nd and 3rd offense of 4–5 years.

^*p < .00l.

^**p < .05.

TABLE 4.

Final Model Results for the Latent Class Regression and Estimated Class Proportions

	Estimated Proportions
	Class 1	Class 2
Overall population	.16	.84
Offender subpopulation	.43	.57
Recidivating subpopulation	.57	.43

	Estimated Proportionsa		Coefficientsb
Subpopulation	Class 1	Class 2	Est.	SE	OR
Black	.24	.76	1.52*	0.14	4.57
White, Caucasian	.05	.95	0.00	fixedc	1.00
≤ $4,500	.21	.79	2.16*	0.42	8.67
$4,501 – $5,783	.19	.81	2.02*	0.42	7.53
$5,784 –$6,779	.08	.92	1.08*	0.39	2.94
≥ $6,780	.03	.97	0.00	fixedc	1.00

^aEstimated at average of other variable.

^bCorresponding to multinomial logistic regression with Class 2 as the outcome reference category.

^cReference category for categorical class membership predictor.

^*p < .01.

Boys whose first offenses fall in the category of nonindex, curfew offenses have significantly lower hazard odds (2.26–2.80 times lower) for second and third offenses, meaning that their overall likelihood of recidivating prior to age 18 is lower and that their average time between offenses, if they do recidivate, is significantly longer than those boys committing more serious offenses.

The gap time from the first to second offense is somewhat negatively related to the gap time hazard for the third event, suggesting those with longer gap times between the first and second offense are also likely to have longer average gap times between the second and third offense. Conversely, this implies that those with shorter gap times between the first and second offense are likely to continue with shorter recidivism times.

In terms of the latent classes, the fact that a two-class model offered a significant improvement in fit over the one-class model indicates that there was shared variance across the event time processes not explained by the explicit associations included in the model between each event process and the observed event time of the preceding offense(s). This source of shared variance could be attributed to unobserved heterogeneity between individuals related to an underlying diathesis, frailty, or susceptibility to offending or delinquent behavior. The factor mean of Class 1 was fixed at zero for identification and the factor mean of Class 2 was negative and significantly different from zero (Est. = -2.88, SE = .14, p < .001). With all the factor loadings greater than zero, this indicates that Class 2 has a significantly lower susceptibility to offending and to recidivating and has an older average age of first offense and longer average gap times between offenses. The factor loadings decrease in magnitude across sets of event indicators suggesting that the underlying frailty has greater influence in the time to first offense process than in the gap time processes among recidivators. Exponentiating the additive inverse of the product of each factor loading with the Class 2 factor means yields the hOR for each time period comparing Class 1 to Class 2. For example. Class 1 has exp (-.38 × -2.88) = 2.96 times the hazard odds of a second offense occurring at the same age (i.e., gap time of zero) as the first offense. Class 1 might be labeled a "high-risk" class of boys with elevated risks of offending and reoffending as juveniles at younger ages. Figure 3 displays the model-based, class-specific hazard probabilities for the time to first offense (Panel A) and the gap time from first to second and second to third offense (Panel B).

FIGURE 3.

Model-estimated, class-specific average hazard probabilities (located at sample mean values of all x-variables) for (A) time to first offense and (B) gap time from first to second offense and from second to third offense.

Table 4 displays the model results related to the latent class regression and also model-based estimates of the latent class distributions across the different offender subpopulations. Race and income were significantly associated with class membership. Boys in the Black or African American group had 4.57 times the odds of being in the high-risk Class 1. Lower income levels corresponded to significantly elevated odds of being in the high-risk Class 1 with boys in the lowest income category having 8.67 times the odds of being in Class 1 compared to boys in the highest income category. Table 4 also gives the estimated class proportions within each race and income group based on the regression estimates. The skew toward Class 2 is particularly pronounced in the White race category and the highest income category. It is worth noting here that with income as the only other latent class covariate, race in this case likely acts as a crude proxy for exposure to a host of risk factors at the individual, family, and neighborhood levels. Furthermore, with only two racial groups, the race variable for this sample does not reflect the full range of diversity possible and is certainly not representative of the racial and ethnic diversity of present-day Philadelphia.

The top part of Table 4 presents the model-estimated class proportions in the overall population, including offenders and nonoffenders. These are followed by the model-estimated class proportions among offenders (those with one or more offense prior to age 18), and the model estimated class proportions among recidi-vators (those with two or more offenses prior to age 18). Because Class 1 represents a subgroup of individuals at elevated risk for offending and recidivating across time, it is not surprising that members of Class 1 constitute an increasingly larger portion of the population among those at risk for a repeat offense. (Full details of the calculations for these class proportions using Equation (7) and the parameter estimates from the final model are available in a technical appendix available upon request from the author.)

DISCUSSION

Although there is some literature about recurrent event models in discrete time, there is no thorough treatment of the different approaches in modeling recurrent event processes. Furthermore, some of the more common recurrent event models in use lack one or more of these critical features: event-specific baseline hazard probabilities and covariate effects; multiple event occurrences in a single time period for a single individual; within- as well as between-individual correlations of event times; distribution-free unobserved heterogeneity; and event-specific influences of unobserved heterogeneity. This article presents the partial gap time formulation of time scale and risk for recurrent events, with a focus on processes with low frequencies of recurrences. It was demonstrated how the partial gap time model could be specified as a restricted factor mixture model in a manner flexible enough to accommodate all of the features listed above but more parsimonious than a fully unrestricted latent class model.

This approach for modeling low-frequency recurrent event histories should hold great appeal for the applied developmental researcher. A researcher could investigate questions related to the differences in duration dependence and covariate effects for different event enumerations. For example, are the significant risk factors for time to first occurrence also significant risk factors for the time between recurrences? Are those individuals who have already experienced one event at increased risk of experiencing a (second) event? Is there evidence of an unobserved, underlying frailty for individuals to the event process and does it influence the risk and timing of all event occurrences in the same way?

The limitations of the current article point to some of the many directions in which future research in the area of discrete-time survival using latent variables may lead. For instance, though this article only carefully considers predictors of latent class membership, there is an opportunity for a full treatment of extensions that allow actual event times as well as individual frailty class membership to predict to distal outcomes of the event history process. As another extension, mediation of risk factor effects on the event history process could be modeled applying the principles of longitudinal mediation as described by Selig and Preacher (this issue). Additionally, although this article focuses on recurrent event history processes with low event enumerations, the approach presented can be modified to accommodate high-frequency recurrent event histories.

Moving beyond the scope of this article are the challenges of and exciting possibilities for adapting the general latent variable modeling framework to accommodate other multivariate survival processes; for example, competing risk processes for which there is more than one possible event that could terminate a subject’s risk. Another example of a multivariate survival process would be a situation in which two or more single event processes are running concurrently but, unlike competing risks, the occurrence of one event doesn’t preclude the occurrence of the other events for a given individual. In addition, modeling event histories within a latent variable framework allows for the interesting prospect of jointly modeling survival times with other longitudinal outcomes, such as joint survival and latent growth curve processes. This article establishes a strong foundation that will allow future exploration into the many methodology extensions that will provide researchers with full and flexible models that best represent the complexity of behavioral event history processes, specifically, the interplay between developmental longitudinal processes, more generally, and individual differences in those processes over the human life span.