Critical assessment of automated flow cytometry data analysis techniques

In this analysis, the authors directly compared the performance of flow cytometry data processing algorithms to manual gating approaches. The results offer information of practical utility about the performance of the algorithms as applied to different data sets and challenges.

Supplementary information

The online version of this article (doi:10.1038/nmeth.2365) contains supplementary material, which is available to authorized users.

Abstract

Traditional methods for flow cytometry (FCM) data processing rely on subjective manual gating. Recently, several groups have developed computational methods for identifying cell populations in multidimensional FCM data. The Flow Cytometry: Critical Assessment of Population Identification Methods (FlowCAP) challenges were established to compare the performance of these methods on two tasks: (i) mammalian cell population identification, to determine whether automated algorithms can reproduce expert manual gating and (ii) sample classification, to determine whether analysis pipelines can identify characteristics that correlate with external variables (such as clinical outcome). This analysis presents the results of the first FlowCAP challenges. Several methods performed well as compared to manual gating or external variables using statistical performance measures, which suggests that automated methods have reached a sufficient level of maturity and accuracy for reliable use in FCM data analysis.

Supplementary information

The online version of this article (doi:10.1038/nmeth.2365) contains supplementary material, which is available to authorized users.

Main

Flow cytometers provide high-dimensional quantitative measurement of light scatter and fluorescence emission properties of hundreds of thousands of individual cells in each analyzed sample. FCM is used routinely both in research labs to study normal and abnormal cell structure and function and in clinical labs to diagnose and monitor human disease as well as response to therapy and vaccination. In a typical FCM analysis, cells are stained with fluorochrome-conjugated antibodies that bind to the cell surface and intracellular molecules. Within the flow cytometer, cells are passed sequentially through laser beams that excite the fluorochromes. The emitted light, which is proportional to the antigen density, is then measured. The latest flow cytometers can analyze 20 different characteristics for individual cells in complex mixtures¹, and recently developed mass spectrophotometry–based cytometers could dramatically increase this number^2,3,4.

A key step in the analysis of FCM data is the grouping of individual cell data records (that is, events) into discrete populations on the basis of similarities in light scattering and fluorescence. This analysis is usually accomplished by sequential manual partitioning ('gating') of cell events into populations through visual inspection of plots in one or two dimensions at a time. Yet many problems have been noted with this approach to FCM data analysis, including its subjective, time-consuming nature and the difficulty in effectively analyzing high-dimensional data⁵.

Since 2007, there has been a surge in the development and application of computational methods to FCM data in an effort to overcome these serious limitations in manual gating–based analysis, with successful results reported in each case^{6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28}. However, it has been unclear how the results from these approaches compared with each other and with traditional manual gating results because every new algorithm was assessed using distinct data sets and evaluation methods. To address these shortcomings, members of the algorithm development, FCM user, and software and instrument vendor communities initiated the FlowCAP project (http://flowcap.flowsite.org/). The goals of FlowCAP are to advance the development of computational methods for the identification of cell populations of interest in FCM data by providing the means to objectively test and compare these methods, and to provide guidance to the end user about how best to use these algorithms. Here we report the results from the first two FlowCAP-sponsored competitions, which evaluated the ability of automated approaches to address two important use cases: cell population identification and sample classification.

Results

FlowCAP I: cell population identification challenges

The goal of these challenges was to compare the results of assigning cell events to discrete cell populations using computational tools with the results from manual gates produced by expert analysts. Algorithms competed in the four following challenges. For “Challenge 1: completely automated”, we compared completely automated gating algorithms for exploratory analysis. Software used in this challenge either did not have any tuning parameters (for example, skewing parameters or density thresholds) or had tuning parameters whose values were fixed in advance and used across all data sets. For “Challenge 2: manually tuned,” we compared semiautomated gating algorithms with manually adjusted parameters tuned for individual data sets. For “Challenge 3: assignment of cells to populations with predefined number of populations,” we compared algorithms for cases in which the number of expected populations was known. “Challenge 4: supervised approaches trained using human-provided gates” was similar to Challenge 2, with 25% of the manual gates (that is, population membership labels) for each data set provided to participants for training and tuning their algorithms.

Four human data sets (graft-versus-host disease (GvHD), diffuse large B-cell lymphoma (DLBCL), symptomatic West Nile virus (WNV) and normal donors (ND)) and one mouse data set (hematopoietic stem cell transplant (HSCT)) were used for these challenges (Online Methods).

For these challenges, the current standard practice for FCM data analysis—manual gating performed by expert analysts from the laboratory that generated the data sets—was used for comparison against cell population membership defined by each automated algorithm. The F-measure statistic (the harmonic mean of precision and recall; Online Methods) was used for this comparison. An F-measure of 1.0 indicates perfect reproduction of the manual gating result with no false positive or false negative events.

Algorithm performance.

Fourteen research groups submitted 36 analysis results (Table 1 and Supplementary Note 1). The results of the cell population identification challenges are summarized in Table 2 and Supplementary Figure 1. Not all algorithms were applied in all challenges. For example, supervised classification methods, such as RadialSVM, require training data to establish classification rules and therefore were not appropriate for Challenges 1–3. Algorithms were sorted by their rank performance score for each challenge (Online Methods). Many algorithms performed well in multiple challenges on multiple data sets, with F-measures exceeding 0.85. Some algorithms were always in the top group—that is, F-measures were not significantly different from the top algorithm—such as ADICyt in Challenges 1–3 and SamSPECTRAL in Challenge 3; some were in the top group for some of the data sets (such as flowMeans, FLOCK and FLAME in Challenge 1); and some were never in the top group (such as flowKoh).

Table 1.

Participating algorithms: algorithms that were applied in at least one challenge

Algorithm name	Availabilitya	Brief descriptionb	SN/ref.c
Cell population identification
ADICyt	Commercially available	Hierarchical clustering and entropy-based merging	1.1.1/–
CDP	Python source code	Bayesian nonparametric mixture models, calculated using massively parallel computing on GPUs	1.1.2/ ref. 25
FLAME	R package	Multivariate finite mixtures of skew and heavy-tailed distributions	1.1.3/ref. 9
FLOCK	C source code	Grid-based partitioning and merging	1.1.4/ref. 13
flowClust/Merge	Two R/BioC packages	t mixture modeling and entropy-based merging	1.1.5/refs. 7,8
flowKoh	R source code	Self-organizing maps	1.1.6/–
flowMeans	R/BioC package	k-means clustering and merging using the Mahalanobis distance	1.1.7/ref. 15
FlowVB	Python source code	t mixture models using variational Bayes inference	1.1.8/–
L2kmeans	JAVA source code	Discrepancy learning	1.1.9/ ref. 26
MM, MMPCA	Windows and Linux executable	Density-based Misty Mountain clustering	1.1.10/ref. 14
NMFcurvHDR	R source code	Density-based clustering and non-negative matrix factorization	1.1.11/ref. 10
SamSPECTRAL	R/BioC package	Efficient spectral clustering using density-based downsampling	1.1.12/ref. 12
SWIFT	MATLAB source code	Weighted iterative sampling and mixture modeling	1.1.13/ ref. 27
RadialSVM	MATLAB source code	Supervised training of radial SVMs using example manual gates	1.1.14/ref. 6
Ensemble clustering	R/CRAN package	Combines the results of all participating algorithms	Online Methods/refs. 39,40
Sample classification
2DhistSVM	Pseudocode	2D histograms of all pairs of dimensions and support vector machines	1.2.1/–
admire-lvq	MATLAB source code	1D features and learning vector quantization	1.2.2/–
biolobe	Pseudocode	k-means and correlation matrix mapping	1.2.3/–
daltons	MATLAB source code	Linear discriminant analysis and logistic regression	1.2.4/–
DREAM–A	Pseudocode	2D and 3D histograms and cross-validation of several classifiers	1.2.5/–
DREAM–B	Pseudocode	1D Gaussian mixtures and support vector machines	1.2.6/–
DREAM–C	Pseudocode	1D gating and several different classifiers	1.2.7/–
DREAM–D	Pseudocode	4D clustering and bootstrapped t-tests	1.2.8/–
EMMIXCYTOM, uqs	R source code	Skew-t mixture model and Kullback-Leibler divergence	1.2.9/–
fivebyfive	Pseudocode	1D histograms and support vector machines	1.2.10/–
flowBin	R package	High-dimensional cluster mapping across multiple tubes and support vector machines	1.2.11/–
flowCore-flowStats	R source code	Sequential gating and normalization and a beta-binomial model	1.2.12/ ref. 28
flowPeakssvm, Kmeanssvm	R package	k-means and density-based clustering and support vector machines	1.2.13/ref. 16
flowType, flowType FeaLect	Two R/BioC packages	1D gates extrapolated to multiple dimensions and bootstrapped LASSO classification	1.2.14/refs. 17,18
jkjg	JAVA source code	1D Gaussian and logistic regression	1.2.15/–
PBSC	C source code	Multidimensional clustering and cross-sample population matching using a relative distance order	1.2.16/ ref. 13
PRAMS	R source code	2D clustering and logistic regression	1.2.17/–
Pram Spheres, CIHC	Pseudocode	Genetic algorithm and gradient boosting	1.2.18/–
Random Spheres	Pseudocode	Hypersphere-based Monte Carlo optimization	1.2.18/–
SPADE, BCB	MATLAB, Cytoscape, R/BioC	Density-based sampling, k-means clustering and minimum spanning trees	1.2.19/ref. 23
SPCA+GLM	Pseudocode	1D probability binning and principal-component analysis	1.2.20/–
SWIFT	MATLAB source code	SWIFT clustering and support vector machines	1.2.21/ ref. 27
Team21	Python source code	1D relative entropies	1.2.22/–

^aSee Supplementary Table 3 for algorithm contact information.

^bSee Supplementary Note 1 for more details about each program.

^cSupplementary Note 1 section (SN) and reference citation.

Table 2.

Summary of results for the cell identification challenges

F-measurea
	GvHD	DLBCL	HSCT	WNV	ND	Mean	Runtime h:mm:ssb	Rank scorec
Challenge 1: completely automated
ADICyt	0.81 (0.72, 0.88)	0.93 (0.91, 0.95)	0.93 (0.90, 0.96)	0.86 (0.84, 0.87)	0.92 (0.92, 0.93)	0.89	4:50:37	52
flowMeans	0.88 (0.82, 0.93)	0.92 (0.89, 0.95)	0.92 (0.90, 0.94)	0.88 (0.86, 0.90)	0.85 (0.76, 0.92)	0.89	0:02:18	49
FLOCK	0.84 (0.76, 0.90)	0.88 (0.85, 0.91)	0.86 (0.83, 0.89)	0.83 (0.80, 0.86)	0.91 (0.89, 0.92)	0.86	0:00:20	45
FLAME	0.85 (0.77, 0.91)	0.91 (0.88, 0.93)	0.94 (0.92, 0.95)	0.80 (0.76, 0.84)	0.90 (0.89, 0.90)	0.88	0:04:20	44
SamSPECTRAL	0.87 (0.81, 0.93)	0.86 (0.82, 0.90)	0.85 (0.82, 0.88)	0.75 (0.60, 0.85)	0.92 (0.92, 0.93)	0.85	0:03:51	39
MMPCA	0.84 (0.74, 0.93)	0.85 (0.82, 0.88)	0.91 (0.88, 0.94)	0.64 (0.51, 0.71)	0.76 (0.75, 0.77)	0.80	0:00:03	29
FlowVB	0.85 (0.79, 0.91)	0.87 (0.85, 0.90)	0.75 (0.70, 0.79)	0.81 (0.78, 0.83)	0.85 (0.84, 0.86)	0.82	0:38:49	28
MM	0.83 (0.74, 0.91)	0.90 (0.87, 0.92)	0.73 (0.66, 0.80)	0.69 (0.60, 0.75)	0.75 (0.74, 0.76)	0.78	0:00:10	28
flowClust/Merge	0.69 (0.55, 0.79)	0.84 (0.81, 0.86)	0.81 (0.77, 0.85)	0.77 (0.74, 0.79)	0.73 (0.58, 0.85)	0.77	2:12:00	24
L2kmeans	0.64 (0.57, 0.72)	0.79 (0.74, 0.83)	0.70 (0.65, 0.75)	0.78 (0.75, 0.81)	0.81 (0.80, 0.82)	0.74	0:08:03	20
CDP	0.52 (0.46, 0.58)	0.87 (0.85, 0.90)	0.50 (0.48, 0.52)	0.71 (0.68, 0.75)	0.88 (0.86, 0.90)	0.70	0:00:57	19
SWIFT	0.63 (0.56, 0.70)	0.67 (0.62, 0.71)	0.59 (0.55, 0.62)	0.69 (0.64, 0.74)	0.87 (0.86, 0.88)	0.69	1:14:50	15
Ensemble clustering	0.88	0.94	0.97	0.88	0.94	0.92	–	64
Challenge 2: manually tuned
ADICyt	0.81 (0.71, 0.89)	0.93 (0.91, 0.95)	0.93 (0.90, 0.96)	0.86 (0.84, 0.87)	0.92 (0.92, 0.93)	0.89	4:50:37	34
SamSPECTRAL	0.87 (0.79, 0.94)	0.92 (0.89, 0.94)	0.90 (0.86, 0.93)	0.85 (0.83, 0.88)	0.91 (0.91, 0.92)	0.89	0:06:47	31
FLOCK	0.84 (0.76, 0.90)	0.88 (0.85, 0.91)	0.86 (0.83, 0.89)	0.84 (0.82, 0.86)	0.89 (0.87, 0.91)	0.86	0:00:15	23
FLAME	0.81 (0.75, 0.87)	0.87 (0.84, 0.90)	0.87 (0.82, 0.90)	0.84 (0.83, 0.85)	0.87 (0.86, 0.87)	0.85	0:04:20	23
SamSPECTRAL-FK	0.87 (0.80, 0.94)	0.85 (0.81, 0.89)	0.90 (0.86, 0.92)	0.76 (0.71, 0.81)	0.92 (0.91, 0.93)	0.86	0:04:25	23
CDP	0.74 (0.67, 0.80)	0.89 (0.86, 0.91)	0.90 (0.88, 0.92)	0.75 (0.71, 0.78)	0.86 (0.85, 0.88)	0.83	0:00:18	19
flowClust/Merge	0.69 (0.53, 0.78)	0.87 (0.85, 0.90)	0.96 (0.94, 0.97)	0.77 (0.75, 0.79)	0.88 (0.81, 0.91)	0.83	2:12:00	18
NMFcurvHDR	0.76 (0.69, 0.82)	0.84 (0.83, 0.86)	0.70 (0.67, 0.74)	0.81 (0.77, 0.84)	0.83 (0.83, 0.84)	0.79	1:39:42	13
Ensemble clustering	0.87	0.94	0.98	0.87	0.92	0.91	–	41
Challenge 3: assignment of cells to populations with predefined number of populations
ADICyt	0.91 (0.84, 0.96)	0.96 (0.94, 0.97)	0.98 (0.97, 0.99)			0.95	0:10:49	26.2
SamSPECTRAL	0.85 (0.75, 0.93)	0.93 (0.91, 0.95)	0.97 (0.95, 0.98)			0.92	0:02:30	26.2
flowMeans	0.91 (0.84, 0.96)	0.94 (0.91, 0.96)	0.95 (0.93, 0.96)			0.93	0:00:01	23.4
TCLUST	0.93 (0.91, 0.96)	0.93 (0.91, 0.95)	0.93 (0.90, 0.95)			0.93	0:00:40	23.4
FLOCK	0.86 (0.79, 0.93)	0.92 (0.89, 0.94)	0.97 (0.95, 0.98)			0.92	0:00:02	22.2
CDP	0.85 (0.77, 0.92)	0.92 (0.89, 0.94)	0.76 (0.72, 0.81)			0.84	0:00:21	16.9
flowClust/Merge	0.88 (0.82, 0.93)	0.90 (0.86, 0.94)	0.83 (0.79, 0.88)			0.87	0:49:24	15.9
FLAME	0.85 (0.79, 0.91)	0.90 (0.86, 0.93)	0.86 (0.82, 0.91)			0.87	0:03:20	15.9
SWIFT	0.90 (0.84, 0.95)	0.00 (0.00, 0.00)	0.88 (0.84, 0.92)			0.59	0:01:37	11.9
flowKoh	0.85 (0.80, 0.90)	0.85 (0.82, 0.88)	0.87 (0.84, 0.91)			0.86	0:00:42	9.5
NMF	0.74 (0.69, 0.78)	0.84 (0.80, 0.88)	0.80 (0.76, 0.84)			0.79	0:01:00	7.5
Ensemble clustering	0.95	0.97	0.98			0.97	–	35
Challenge 4: supervised approaches trained using human-provided gates
RadialSVM	0.89 (0.83, 0.95)	0.84 (0.80, 0.87)	0.98 (0.96, 0.99)	0.96 (0.94, 0.97)	0.93 (0.92, 0.94)	0.92	0:00:18	21
flowClust/Merge	0.92 (0.88, 0.95)	0.92 (0.89, 0.94)	0.95 (0.92, 0.97)	0.84 (0.82, 0.86)	0.89 (0.88, 0.90)	0.90	5:31:50	19
randomForests	0.85 (0.78, 0.91)	0.78 (0.74, 0.83)	0.81 (0.79, 0.83)	0.87 (0.84, 0.90)	0.94 (0.92, 0.95)	0.85	0:02:06	15
FLOCK	0.82 (0.77, 0.87)	0.91 (0.89, 0.93)	0.86 (0.76, 0.93)	0.86 (0.82, 0.89)	0.86 (0.77, 0.92)	0.86	0:00:05	13
CDP	0.78 (0.68, 0.87)	0.95 (0.93, 0.97)	0.75 (0.71, 0.78)	0.86 (0.84, 0.88)	0.83 (0.80, 0.86)	0.83	0:00:15	11
Ensemble clustering	0.91	0.94	0.95	0.92	0.94	0.93	–	26

^aIn each data set/challenge, the top algorithm (highest mean F-measure) and the algorithms with overlapping confidence intervals with the top algorithm are boldface (see Online Methods for F-measure calculations).

^bRun time was calculated as time per CPU per sample.

^cAlgorithms are sorted by rank score within each challenge (see Online Methods for rank score calculations). Data sets: GvHD, graft-versus-host disease; DLBCL, diffuse large B-cell lymphoma; WNV, symptomatic West Nile virus; ND, normal donors; HSCT, hematopoietic stem cell transplant.

Allowing participants to tune algorithmic parameters did not result in much improvement, as the highest overall F-measure did not increase (0.89 for both completely automated and manually tuned algorithms); only three of the six algorithms that participated in both Challenge 1 and Challenge 2 (SamSPECTRAL, CDP and flowClust/Merge) demonstrated a modest improvement in overall F-measure, and in some cases the F-measures actually decreased after human intervention (for example, with FLAME). In contrast, providing the number of cell populations sought in Challenge 3 made predictions more accurate for seven of the eight algorithms that participated in both Challenge 1 and Challenge 3, with five algorithms achieving overall F-measures greater than 0.9 (ADICyt, SamSPECTRAL, flowMeans, TCLUST and FLOCK). In addition, providing a set of example results for algorithm training and parameter tuning in Challenge 4 improved the results of flowClust/Merge by 0.13 and allowed the Radial SVM approach to outperform the fully automated algorithms used in Challenge 1 for four of the five data sets. Taken together, these results suggest that estimating the correct number of cell populations (as defined by manual gates) remains a challenge for most automated approaches, and providing training data improves performance.

Table 2 and Supplementary Figure 2 show the estimated run times of the algorithms on single-core CPUs or GPUs (for CDP only). Run times ranged from 1 s to >4 h per sample. ADICyt, which had the highest rank score in the first three challenges, also required the longest run times. flowMeans, FLOCK, FLAME, SamSPECTRAL and MM&PCA needed substantially shorter run times and still performed reasonably well in comparison with ADICyt. Note that, owing to hardware and software differences, these numbers may not be precisely comparable; the information is provided to give some sense of the differences in time requirements for these specific implementations.

Improving algorithmic performance by combining predictions.

Much as in other data analysis settings (see ref. 29 for a review), combining results from different cell population identification methods provides improved accuracy over any individual method. For all four cell population identification challenges, ensemble clustering, which combines the results of all the submitted algorithms (Online Methods), resulted in a higher overall F-measure and rank score than any individual algorithm (Table 2 and Supplementary Figs. 3 and 4). In addition, ensemble clustering gave a higher F-measure for each of the individual data sets in each challenge, with only four exceptions in Challenge 4.

In addition to identifying cell populations more accurately, ensemble clustering can provide an alternative approach for evaluating algorithms by using ablation analysis to measure their contribution to the combined predictions. For example, in Challenge 3, when only four algorithms were included in the ensemble (TCLUST, ADICyt, FLAME and SWIFT), the F-measure was still close to 0.95 (Supplementary Fig. 5). Adding two more algorithms to the set resulted in only a minor improvement. Similar patterns were observed in the other challenges. Although the absolute order differed in the ablation analysis, algorithms with higher F-measures tended to be removed later (that is, they had a larger contribution to the ensemble). We also performed the ablation analysis in the reversed order (meaning that the algorithm with maximum contribution was removed first). As expected, the algorithms with a higher F-measure tend to be excluded earlier (Supplementary Fig. 6).

Algorithm performance with refined manual gates.

In the population identification challenges, predefined populations identified by human experts corresponded to a single set of manual gates prepared by the original data providers for comparison. However, manual gating is known to be subjective and potentially error prone even in the hands of domain experts³⁰. Without detailed guidance on the goals of FlowCAP, the data providers tended to focus gating only on cells considered relevant to the goals of their studies and therefore provided incomplete population delineation in some cases. In addition, relying on a single set of gates meant that inconsistencies in manual gating between different analysts were not taken into account. To address these deficiencies, we instructed eight individuals from five different institutions to identify all cell populations (exhaustive gating) discernible in the HSCT and GvHD data sets (Supplementary Note 2). These data sets were selected because they had the highest and lowest overall F-measures, representing the best and worst cases for the automated methods, respectively.

A consensus of the eight manual gates was first constructed as a reference (Online Methods). Algorithm comparison against this reference started with cell populations in the entire data set that demonstrated the best match across all eight manual gates and then gradually proceeded to include more cell populations with weaker matches between the human analysts (Fig. 1). The inclusion of cell populations with less agreement between the human experts resulted in a gradual reduction in F-measures for both individual manual gates and algorithms, suggesting that certain populations were more difficult to resolve for both manual and automated analysis, especially for the GvHD data set. However, the overall relative performance of algorithms for both data sets using these multiple sets of exhaustive gates was generally consistent with the initial results. For example, the top four algorithms for the HSCT data set were FLAME, ADICyt, flowMeans and MM&PCA for both the initial and the consensus manual gates (Supplementary Table 1). In addition, ensemble clustering performed well within the range of manual results, especially for the most consistent populations.

Figure 1. F-measure results of cell population identification challenges.

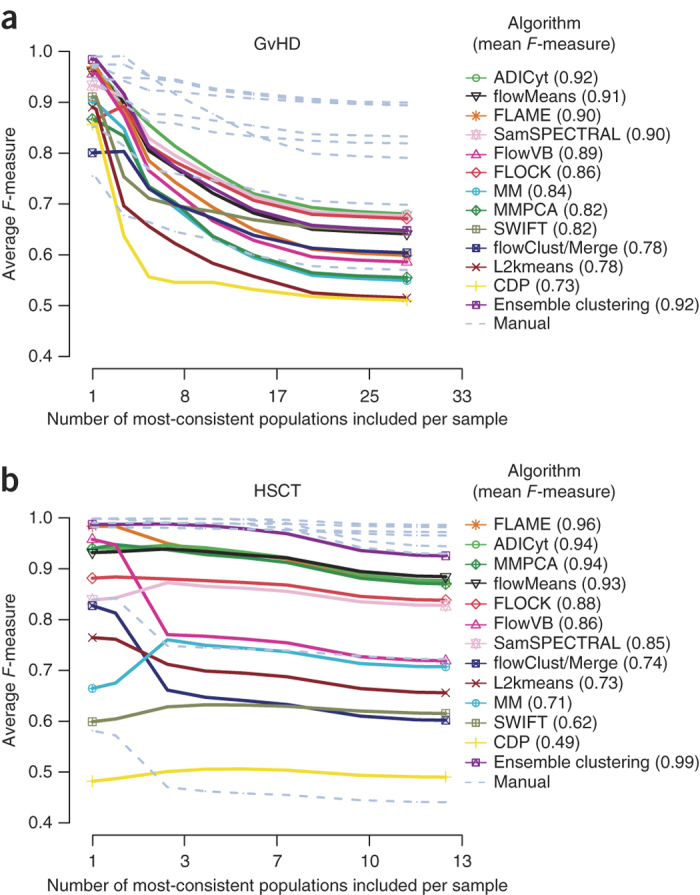
Average manual and algorithm F-measures are represented against the manual consensus cluster as a function of the number of populations included, ranked from most consistent to least consistent. For a given population, consistency was defined as the agreement among manual gates, calculated as the average manual F-measures against the manual consensus cluster for that population. All populations across all samples were included in this calculation, and, as such, the numbers on the x axis should be multiplied by 12 and 30 (for GvHD and HSCT, respectively) to reflect the total number of populations in all samples in the reference. Individual manual gating results are plotted as gray lines. (a) Graft-versus-host disease (GvHD) data set. (b) Hematopoietic stem cell transplant (HSCT) data set.

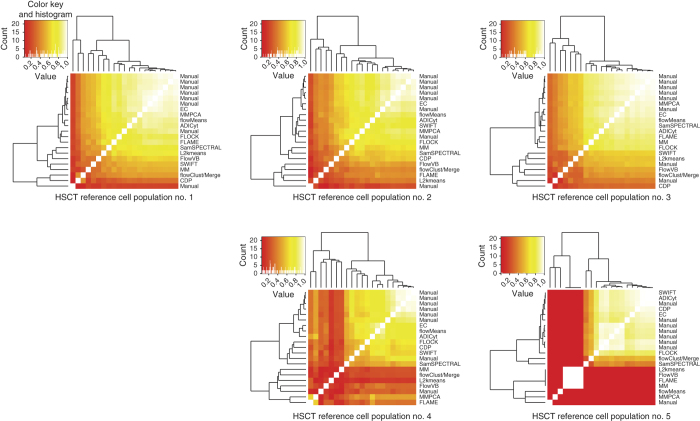
As an alternative to the overall F-measures, we used consensus manual clusters as a reference in a per-population analysis (Online Methods) to determine whether certain cell populations were responsible for high or low algorithm performance by determining F-measures for each cell population separately (Fig. 2 and Supplementary Figs. 7 and 8). For most populations in both samples, the high F-measure values highlighted the close agreement between manual and automated results. For example, cell population no. 3 in the HSCT data set demonstrated high pairwise F-measures between all of the algorithms and manual gates, which indicated that this cell population was easily identified manually and algorithmically. In contrast, cell population no. 5 was effectively identified by only the manual gates and a few of the algorithms: SWIFT, ADICyt, CDP and FLOCK. Similar conclusions were reached for the GvHD data set (Supplementary Figs. 9 and 10).

Figure 2. Per-population pairwise comparisons of the cell population identification challenges.

Average F-measures of all pairs of results for the five cell populations across all samples in the hematopoietic stem cell transplant (HSCT) data set are represented as heat maps. The heat-map color in individual squares reflects the pairwise agreement between each method for each cell population independently, and the position in the matrix reflects the pattern of agreement across all methods on the basis of hierarchical clustering. The manual-gate consensus cluster for each sample was used as a reference for matching of the automated results of that sample. Pairwise F-measures between all algorithms and manual gates for the HSCT data set are shown. The dendrogram groups the algorithms and manual gates on the basis of the similarities between their pairwise F-measures. EC, ensemble clustering.

Practical considerations.

The F-measure analysis provides a rigorous quantitative measure of algorithm performance for population identification. On the basis of this analysis, although several algorithms performed well on individual data sets, combining the results of a subset of the algorithms produced better results than did individual algorithms in almost every case. The per-population analysis showed that the best-matching algorithms were not always the same for each population, suggesting that different algorithms may have different abilities to resolve populations, depending on the exact structure of the data. This result was not surprising given the wide range of strategies used by the different algorithms, and it motivates the recommendation for using an ensemble approach over any single algorithm for optimal performance.

Further demonstration of the practical utility of ensemble clustering of automated algorithm results is provided through a visual example using the HSCT data set (Fig. 3). Cell population classification by ensemble clustering was compared against consensus manual gating in two- and three-dimensional dot plots. One sample was selected as an example of strong agreement and one sample was selected as an example of weak agreement between the computational and manual results. For both samples shown, cell events determined to be members of the same cell population by ensemble clustering were nearly always located within a single polygon from manual gating. CD45.1 and CD45.2 are allotype markers of murine hematopoietic cells that are frequently used to distinguish between donor and recipient cells after transplantation, with CD45.1 marking recipient cells and CD45.2 marking donor cells in this case. In one sample (Fig. 3a,b), ensemble clustering identified some CD45.2⁺ cells that were either Ly65⁺ or Mac1⁺ (indicating that they are either granulocytes or monocytes from the myeloid lineage) and others that were both Ly65⁻ and Mac1⁻ (indicating that they are lymphocytes), thus indicating repopulation of both major hematopoietic lineages and successful hematopoietic stem cell engraftment. In contrast, although the other sample (Fig. 3c,d) was found to contain CD45.2⁺, Ly65/Mac1⁻ lymphocytes, no CD45.2⁺, Ly65/Mac1⁺ granulocytes/monocytes were observed, which indicated unsuccessful stem cell engraftment. Thus, ensemble clustering was found to be an excellent method for automated assessment of hematopoietic stem cell engraftment using CD45 allotype markers in mouse models.

Figure 3. Comparison of manual-gate consensus and ensemble clustering results.

Dots are color-coded by population membership as determined by ensemble clustering, with donor-derived (CD45.2⁺) granulocytes/monocytes in green and donor-derived lymphocytes in red. Colored polygons enclose regions corresponding to the consensus clustering of manual gates. Fluorochromes used: FITC, fluorescein isothiocyanate; PE, phycoerythrin; APC, allophycocyanin. (a,b) Sample for which all of the cell populations have been accurately identified. (c,d) Sample in which the tail of the blue population has been misclassified as orange by the algorithms, resulting in a lower F-measure for the blue population. The red, blue, green, purple and orange cell populations match cell population 1–5 of Figure 2, respectively.

FlowCAP II: sample-classification challenges

Another important application for FCM analysis is the use of biomarker patterns in FCM data for the purpose of sample classification. We assembled a benchmark of three data sets in which the subjects/samples were associated with an external variable that could be used as an independent measure of truth for sample classification. The benchmark consisted of three data sets for (i) studying the effect of human immunodeficiency virus (HIV) exposure on African infants who were either exposed to HIV in utero but uninfected (HEU) or unexposed (UE), (ii) diagnosis of acute myeloid leukemia (AML) using AML and non-AML samples from a reference diagnostic laboratory and (iii) discriminating between two antigen stimulation groups of post-HIV vaccination T cells (Gag versus Env stimulated) from the HIV Vaccine Trials Network (HVTN) (Online Methods). For each data set, half of the correct sample classifications were provided to participants for training purposes; the other half were used for independent testing and validation. For the AML challenge, additional results were submitted through the DREAM (Dialogue for Reverse Engineering Assessment and Methods)^31,32,33,34 initiative.

Algorithm performance.

We received a total of 43 submissions (Table 1 and Supplementary Note 1), including 14 through the DREAM project (Supplementary Note 3). The results of this challenge are summarized in Table 3, Supplementary Figure 11 and Supplementary Tables 2 and 3. The precision, recall, accuracy and F-measure values on the test set show that for two of the data sets (AML and HVTN), many algorithms were able to perfectly predict the external variables. For example, flowCore-flowStats, flowType-FeaLect, Kmeanssvm, PRAMS, SPADE and SWIFT all gave perfect classification accuracy (that is, F-measure = 1.0) on the HVTN data set. For the third data set (HEUvsUE), despite mostly accurate predictions on the training data, none of the algorithms performed well on the test data. The lack of good performance of any algorithm on this data set combined with a theoretical consideration of the underlying biology (nonproductive HIV exposure several months before sampling may not lead to long-term changes in peripheral blood cell populations) suggests that these samples may be unclassifiable on the basis of the FCM markers used.

Table 3.

Performance of algorithms in the sample-classification challenges on the validation cohort^a

	Recall	Precision	Accuracy	F-measure	Recall	Precision	Accuracy	F-measure	Recall	Precision	Accuracy	F-measure
	Challenge 1: HEUvsUE				Challenge 2: AML				Challenge 3: HVTN
FlowCAP
2DhistsSVMb	0.50	0.091	0.50	0.15	0.00	0.95	0.99	0.97
EMMIXCYTOM					0.95	0.95	0.99	0.95
flowBin	0.012	0.00	0.45	0.00	0.10	0.30	0.92	0.46
flowCore-flowStats	0.56	0.455	0.55	0.50					1.00	1.00	1.00	1.00
flowPeakssvm					1.00	1.00	1.00	1.00
flowType	0.58	0.636	0.59	0.61	0.95	0.95	0.99	0.95	0.88	0.71	0.81	0.79
flowType-FeaLect	0.55	0.545	0.55	0.55	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Kmeanssvm									1.00	1.00	1.00	1.00
PBSC	0.33	0.273	0.36	0.30	0.75	0.75	0.94	0.75	0.95	0.95	0.95	0.95
PRAMS									1.00	1.00	1.00	1.00
Pram Spheres	0.36	0.364	0.36	0.36					0.90	0.90	0.90	0.90
Random Spheres					0.95	0.95	0.99	0.95
SPADE					1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
SWIFT	0.67	0.545	0.64	0.60					1.00	1.00	1.00	1.00
DREAM
admire-lvq					1.00	1.00	1.00	1.00
bcb					1.00	1.00	1.00	1.00
biolobe					1.00	1.00	1.00	1.00
cihc					1.00	0.95	0.99	0.97
daltons					1.00	1.00	1.00	1.00
DREAM–A					0.95	0.95	0.99	0.95
DREAM–B					1.00	0.85	0.98	0.92
DREAM–C					1.00	0.85	0.98	0.92
DREAM–D					0.95	0.95	0.99	0.95
fivebyfive					0.95	1.00	0.99	0.98
jkjg					1.00	1.00	1.00	1.00
SPCA+GLM					0.89	0.85	0.97	0.87
team21					1.00	1.00	1.00	1.00
uqs					1.00	0.95	0.99	0.97

^aNot all algorithms were applied in all challenges. Particularly, a large number of algorithms participated through the DREAM project that included only the AML data set. Data sets: HEUvsUE, HIV-exposed–uninfected versus unexposed; AML, acute myeloid leukemia; HVTN, identification of antigen stimulation groups of post–HIV vaccine T cells.

^bContact information of the participating teams can be found in Supplementary Table 3.

Outlier analysis.

In all data sets, the misclassifications were uniformly distributed across the test sets (Fig. 4a and Supplementary Figs. 12 and 13), with only a single exception (sample no. 340 of the AML data set), suggesting that no systematic problems were causing misclassifications. Visualization of FCM data from the sample no. 340 outlier in comparison with those of typical AML and non-AML subjects suggested that the outlier, like typical AML cases, had a sizable CD34⁺ population; however, the forward-scatter values overlapped with those of normal lymphocytes (Fig. 4b–g). Obtaining additional information on this patient was not possible. However, an independent evaluation of the FCM results by a hematopathologist suggested alternative explanations for why this sample was an outlier. For one, the forward scatter (roughly proportional to the diameter of the cell) of the blasts was lower than that found in other AML patients. Leukemic blast size shows wide variation from patient to patient, and even within a given patient, being medium to large in size in most³⁵ and very small ('microblastic') in rare patients (as in refs. 36,37). The other possibility is that given the lower blast frequency (16.7%), this patient may have been diagnosed with high-grade myelodysplasia (blasts 10%–19%)—a preleukemic condition—rather than AML, which requires a blast count of >20% for diagnosis. Alternatively, the patient may have AML by morphological blast count, but FCM may be underestimating the blast frequency because of hemodilution of the bone marrow specimen or presence of cell debris or unlysed red blood cells³⁸.

Figure 4. Acute myeloid leukemia (AML) subject detected as an outlier by the algorithms.

(a) Total number of misclassifications for each sample in the test set (sample nos. 180–359) of the AML data set. (b–g) Forward scatter (FSC)/side scatter (b–d) and FSC/CD34 (e–g) plots of representative normal (b,e) and AML (c,f) samples and the outlier sample no. 340 (d,g), with the CD34⁺ cells highlighted in red. Cell proportions of the CD34⁺ population are reported as blast frequency (freq.) percentages.

Predictive cell populations identified.

Previous manual gating–based analysis of the HVTN data identified the CD4⁺ interleukin-2 (IL-2)⁺ T-cell subpopulation as discriminative between Env- and Gag-stimulated samples, with the proportion of CD4⁺ IL-2⁺ cells in the Env-stimulated samples being systematically higher than in the Gag-stimulated samples (data not shown). This effect was not observed in manually gated placebo data, which indicates that it is vaccine specific and consistent with the Env glycoprotein 120 boost given to study participants. Notably, examination of the features selected by automated methods for classification between Env- and Gag-stimulated samples revealed that, of the eight methods that directly identified predictive features, four selected features containing the CD4⁺ IL-2⁺ phenotype. The sample classifications using the CD4⁺ IL-2⁺ population gated manually were slightly less accurate than the automatic results obtained from the same population. Post hoc examination of the data revealed that several of the control and stimulated samples in the data set were matched from different experimental runs, suggesting a possible run-specific effect. When these samples were filtered out of the analysis, manual gating was able to perform as accurately as the algorithms, which suggests that the algorithmic approaches were actually more robust with respect to the technical variation than the manual analysis. For more details, see Supplementary Note 4.

Practical considerations.

Of the three data sets assembled to test algorithms in the sample-classification challenge, the AML data set represents an important real-world patient-classification use case. FCM is the laboratory method of choice for the diagnosis of acute leukemia because it not only allows for the identification of abnormal cell populations via comparison with normal blood or bone marrow but also allows for the classification of the disease into different subtypes with different prognoses and treatment options. Of the 25 algorithms that participated in the AML sample-classification challenge, 12 provided perfect classification of all 359 patient samples (F-measure = 1.00) into the AML versus non-AML categories using data from 2,872 separate FCM staining samples. An additional eight algorithms were discrepant on only sample no. 340 classification, which, although labeled as a non-AML sample, appears to be a borderline case. This impressive result, in which 80% of the automated methods performed near perfectly in the classification of acute leukemia, indicates that these methods can now be incorporated into diagnostics pathology laboratory workflows for the diagnosis of AML, and possibly other neoplastic diseases, thereby eliminating the labor-intensive, subjective and error-prone features of manual analysis.

The HVTN challenge represented a relatively difficult problem of distinguishing between T-cell responses to two viral antigens present in the same HIV vaccine. Considering the modest results of previous manual analysis (data not shown), we were surprised by the high performance of classification algorithms in the HVTN challenge. This was an important conclusion of this part of FlowCAP: that several sample-classification algorithms performed much better than expected. Notably, two of the four algorithms that provided results for both of the data sets (flowType-FeaLect and SPADE) gave perfect classifications for both, thereby suggesting that automated methods perform very well in sample classification, even for data sets that were challenging for manual analysis.

Discussion

The FlowCAP project represents a community effort to develop and implement evaluation strategies to judge the performance of computational methods developed for FCM data analysis. Two sets of benchmark FCM data were assembled to evaluate automated gating methods on the basis of their ability to either reproduce cell populations defined through expert manual gating or classify samples according to external variables. Seventy-seven different computational pipeline/challenge combinations were evaluated through these efforts. Every approach to automated FCM analysis published in the last 5 years, as well as several unpublished methods, participated in at least one of the challenges. Participation by the flow informatics community was not only widespread but also collaborative, including the sharing of ideas and the distribution of work to avoid duplication of efforts. The recent establishment of the flow informatics discipline has also coincided with the growth of the open-source software philosophy, which has been widely adopted by the flow informatics community. This open-access philosophy has most certainly contributed to the rapid maturation of these novel methods. One of the sample classification challenges was organized in collaboration with the DREAM initiative^31,32,33,34, which aims at nucleating the systems biology community around important computational biology problems. Given the growing use of FCM data in systems biology research, the collaboration between DREAM and FlowCAP was natural and fruitful.

One of the major goals of the FlowCAP project was to determine whether automated algorithms had reached a level of maturity such that they could be considered practically useful for routine FCM data analysis. Although none of the individual methods provided perfect results for all use cases and sample sets, the results clearly show that automated methods are now practical for many FCM use cases. From the cell population identification challenges, it is now clear that many of the individual algorithmic techniques provide excellent delineation of many different cell populations in diverse data sets. Because users are often focused on the analysis of well-defined subsets of cell populations in a given experiment, many high-ranking techniques (especially those that can learn from manual gating examples) appear to be well suited for this purpose.

In addition, ensemble clustering provides further improvement by combining the best results from multiple methods, giving excellent performance across all of the cell population identification data sets. The mean F-measure values and rank scores showed that the combined predictions obtained by ensemble clustering were more accurate than the results from individual algorithms and individual manual gates. This is important because in practice it may not be feasible to solicit multiple experts for manual gating; however, it is realistic to run multiple automated methods at minimal cost. The ablation analysis (Supplementary Note 3) confirmed that increasing the number of algorithms in the ensemble resulted in improved predictions up to a certain point. In cases in which algorithms with high scores were more frequent, the ensemble clustering performed better and was less sensitive to the exclusion of several of the algorithms (Challenges 1 and 3). This suggests that having several good algorithms is necessary to obtain good ensemble results, but there might be a point after which adding more algorithms does not significantly improve the results. Particularly, when a large number of algorithms with high F-measures were available (the entire HSCT data set and the top 50 most consistently identified populations in the GvHD data set), the ensemble clustering outperformed the individual algorithms. When the individual algorithms were performing poorly (the remaining cell populations in the GvHD data set), the ensemble clustering's performance decreased as well. However, it remains to be determined whether this reflects a poor performance of the automated methods or poor performance of manual gating.

In the sample-classification challenges, many individual methods provided perfect sample-classification accuracy for two different representative data sets, with the leukemia classification use case being an important practical example. The excellent performance of automated methods, even with the relatively challenging HVTN data set, was somewhat surprising but indicates that automated methods can perform well on sample classification use cases, detecting useful biomarkers in FCM data. Although this result is promising, it will be important to obtain additional sample classification data sets for future FlowCAP challenges to determine whether they have reached a level of maturity sufficient for broad routine use, especially for clinical diagnosis applications. The third data set (HEUvsUE), on which none of the algorithms performed well, revealed an additional interesting outcome from the sample classification challenges: situations in which algorithms consistently perform well on training data but poorly on test data may indicate sample sets that are not classifiable given the data provided.

In conclusion, the FlowCAP project has provided a valuable venue for comparison of computational methods for FCM data analysis. Though there is still much to be done to make these methods optimally useful and broadly adopted (Supplementary Note 5), the results presented here are promising and suggest that automated methods will soon supplement manual FCM data analysis methods. The ability to rapidly, objective and collaboratively compare these methods through FlowCAP should catalyze rapid progress in the flow informatics field.

Methods

Availability.

To promote reproducible research⁴¹, the detailed methodologies for all approaches participating in FlowCAP are included by reference to free, open-source software packages or algorithms, or through detailed descriptions (as pseudocode) as described in Supplementary Note 1. The display items presented in this manuscript can be fully reproduced using the scripts provided on the FlowCAP website (http://flowcap.flowsite.org/codeanddata/). Raw data annotated with MIFlowCyt descriptions⁴² are available through FlowRepository (http://flowrepository.org/) via the following experiment IDs: FR-FCM-ZZY2 (GvHD), FR-FCM-ZZYY (DLBCL), FR-FCM-ZZY3 (WNV), FR-FCM-ZZY6 (HSCT), FR-FCM-ZZYZ (ND), FR-FCM-ZZZU (HEUvsUE), FR-FCM-ZZYA (AML), and FR-FCM-ZZZV (HVTN).

Cell population identification.

Data sets. The following data sets were used in the Cell Population Identification challenges:

Diffuse large B-cell lymphoma (DLBCL). The DLBCL data set consists of data from 30 randomly selected lymph node biopsies from patients treated at the British Columbia Cancer Agency between 2003 and 2008. Cell suspensions were produced from freshly disaggregated lymph node biopsies. Patients were histologically confirmed to have DLBCL. This data set was provided by A. Weng at the BCCRC.

Symptomatic West Nile virus (WNV). Samples are human peripheral blood mononuclear cells (PBMCs) from patients with symptomatic WNV infection stimulated in vitro with peptide pools representing different regions of the WNV polyprotein. This data set was provided by J. Bramson at McMaster University.

Normal donors (ND). For this data set, the investigators examined differences in the response of a variety of cell types to various stimuli for a set of healthy donors. For the samples used here, the time periods were relatively short, such that the surface markers would not be expected to change. The staining panel contains antibodies to surface markers and intracellular proteins. Note that these experiments were done with phosflow-fixed cells, and thus some of the populations are not as distinct or clean as would be seen with other processing methods. This data set was provided by H. Rand at Amgen, Inc.

Hematopoietic stem cell transplant (HSCT). This set contains data from 30 randomly selected samples derived from HSCT experiments done in the Terry Fox Laboratory. Suspensions were produced from bone marrow cells. The suspensions were depleted of erythroid precursors by immunomagnetic removal of biotin-conjugated anti-Ter119–labeled cells using EasySep reagents (STEMCELL Technologies). This data set was provided by the C. Eaves at the BCCRC.

Graft-versus-host disease (GvHD). Data were derived from 12 FCM samples designed to identify cellular signatures that predict or correlate with early detection of GvHD. PBMCs were collected from patients pre– and post–allogeneic blood and marrow transplantation. Cells were isolated using Ficoll-Hypaque and then were cryopreserved for subsequent batch analysis. The data set was publicly available as part of previous research⁴³, with additional analysis provided by J. Schoenfeld at Treestar, Inc.

The protein markers evaluated are listed in Supplementary Table 4.

Data preprocessing. The following preprocessing steps were applied to these data sets before they were provided to the participants: (i) compensation (to account for the overlap of emission spectra from fluorochrome labels); (ii) transformation to linear space (to scale data appropriately for visualization); (iii) pre-gating for removal of irrelevant cells (for example, dead cells, as routinely performed by human analysts).

Clustering F-measure. The F-measure is the harmonic mean of the precision and recall according to the equation F = (2 × Pr × Re)/(Pr + Re). Precision (Pr) and recall (Re) can be described in terms of a 2 × 2 contingency table comparing results for a test method—in this case, the results of a cell population identification algorithm—with some reference method—in this case, the results of manual gating by the subject matter expert as the current standard practice—with true positive (TP) defined as the situation in which the positive assignment of the prediction algorithm matches a positive assignment of manual gating, false positive (FP) when the positive assignment of the prediction algorithm matches a negative assignment of manual gating, and false negative (FN) when the negative assignment of the prediction algorithm matches a positive assignment of manual gating. Recall is calculated as TP/(TP + FN); precision is calculated as TP/(TP + FP). F-measure values are always in the interval [0,1], with 1 indicating a perfect prediction.

In this analysis, Pr corresponds to the number of cells correctly assigned to a cluster divided by the total cells assigned to that cluster, and Re corresponds to the number of cells correctly assigned to a cluster divided by all the cells that should have been assigned to that cluster. Given a correct set of reference clusters C = {c₁, c₂, ..., c_n}, and a clustering result K = {k₁, k₂, ..., k_m}, the number of matches between combinations of C and K is a matrix, M = [a_ij], where i ∈ [1,n] and j ∈ [1,m]. Then Pr(c_i,k_j) = a_ij/|k_j| and Re(c_i,k_j) = a_ij/|c_i|, where |c_i| denotes the number of elements in c_i. The F-measure to compare one cluster to another is then F(c_i,k_j) = (2 × Pr(c_i,k_j) × Re(c_i,k_j))/(Pr(c_i,k_j) + Re(c_i,k_j)). To calculate the F-measure of an entire clustering result, for each cluster c_i in the reference, a set of F-measures against every predicted cluster k_j is calculated, and the largest F-measure (best match), normalized by the size of k_j is reported. The sum of these scores produces a total F-measure, defined as

To show the relationship between F-measure and recall and precision, we plotted recall, precision and F-measure values for flowMeans when the number of clusters was iterated from 2 to 10 (Supplementary Fig. 14), using the same HSCT sample plotted in the main manuscript. For this sample, four populations were identified by manual gating, whereas ensemble clustering suggested that there are five populations. This figure provides some intuition about F-measure behavior. For example, missing one cluster (total of three clusters) results in a drop of less than 0.05 in F-measure, but missing two clusters (total of two clusters) results in a drop of 0.3. However, identifying an additional cluster (remember that the ensemble clustering suggested that there are actually five real populations) doesn't decrease the F-measure. The figure also shows the trade-off between recall and precision. From 2 to 5 populations, recall and F-measure increase, and precision decreases slightly. After that, precision decreases quickly, whereas recall remains constant, resulting in a decrease in F-measure. F-measure is relatively low when either recall or precision is low.

See ref. 44 for a comparison of F-measure versus other metrics in the evaluation of clustering algorithms.

Though mean F-measures can be used to assess the performance of each of the algorithms on each data set, the significance of the difference in the F-measure values must be accounted for to truly rank the algorithms. Therefore, to measure how significant these differences were (i.e., how sensitive they were to this specific set of samples), bootstrapping was used to compute 95% confidence intervals (CIs). Bootstrapping is a nonparametric, resampling-based method for measuring the accuracy of a sample estimate⁴⁵. For a vector F of F-measure values produced by a given algorithm on a given data set, we produced the 95% bootstrap percentile CI for the mean as follows: (i) repeat 10,000 times: sample from F with replacement (sample size = size of F) and calculate the mean F-measure of the sample; (ii) report the 2.5th and 97.5th percentiles of the average F-measures as the CI; (iii) end. The results are presented in Supplementary Figure 1. Algorithms with overlapping CIs were subsequently considered tied (bold in Table 2).

Rank score. To derive an overall ranking of the algorithms, we used their rank score, calculated as the sum of fractional rankings of each algorithm across different data sets. Fractional ranking is based on the Borda count strategy⁴⁶: for N algorithms, the top algorithm scored N points, the second one scored N − 1 points, and so on. The last algorithm scored 1 point. The average number of points was used in case of ties (i.e., overlapping CIs). For D data sets, rank score values are in the [D, N × D] interval; an algorithm that scored first in every data set would have a rank equal to N × D.

Ensemble clustering. To evaluate the hypothesis that a consensus of all methods would provide a result better than any individual method, we combined populations that were identified by all methods using ensemble clustering. The consensus clustering problem is defined as follows: given a set of partitions (the ensemble), find a new partition P that minimizes the dissimilarity between P and the partitions in the ensemble. A partition M is defined as a binary matrix with each column corresponding to a class label. The dissimilarity (d) between a partition P and a partition element of the ensemble Q is defined as

where || · ||_p is the entry-wise p-norm. The permutation matrix provides a mapping between corresponding classes. For example, given three observations x, y, z, one partition may label the observations as x ∈ A, y ∈ B, z ∈ C, and another may label the observations (with independent labels) as y ∈ α, x ∈ γ, z ∈ γ. The partitions in fact are the same if we consider the classes as A = γ, B = α, C = γ. The permutation matrix Π determines how the classes in P correspond with the classes in Q. When P = 1, the measure is known as the Manhattan distance. This distance can be calculated efficiently using linear programming methods. Once a dissimilarity measure is defined—in our case, the Manhattan distance with P = 1—we must solve the harder problem of finding the partition P* that minimizes the distance for all of the partitions Q in the ensemble E.

This is an NP-hard problem (multidimensional assignment), so we used a heuristic method³⁹ that provides approximate solutions for the consensus partition problem, as implemented in the CLUE package⁴⁰.

Ablation analysis was performed as follows. For a set of N algorithms A = {a₁, a₂, ..., a_N} and an ensemble clustering result EC, the following steps were performed to measure the contribution of each individual algorithm to the EC: (i) find the algorithm a_i that results in the smallest reduction in F-measure when excluded from the EC; (ii) remove a_i from EC; (iii) record the F-measure of EC; (iv) if A is not empty, go to (i); (v) end.

Consensus of manual gates. As discussed in the main text, consensus clustering of manual gates was used to rank the algorithms in the refined manual gate analysis. For each population in the consensus clusters, the mean F-measure to the matching population in all other manual gates was calculated. A comparison of the relationship between the score assigned to each cell population in the consensus was compared with the absolute or relative cell frequency in linear or log space (Supplementary Figs. 15–17). This showed that there was usually considerable agreement between human experts and their consensus for large cell populations. However, for small populations, there was often (although not always) considerable disagreement across the experts. For this reason, we focused our ranking on cell populations with an F-measure of higher than 0.8. For evaluation of the algorithms, we started by limiting the comparison to only those cell populations that matched strongly across all manual gates (F-measure cutoff = 1) and relaxed this condition gradually (Fig. 1).

After we completed the comparison between these independent manual gates and the automated results, it became apparent that one and perhaps two sets of manual gates were somewhat different from the others. We considered whether it might be appropriate to remove these from the ensemble of manual gates that was used in the F-measure comparison because they might be statistical outliers. However, the differences between the individual gates represent an expert's valid interpretation of the data rather than statistical noise or outliers, a conclusion supported by the observation that the outlier effect is observable in only a subset of the cell populations. That two of the gating results diverge from the others is not a sufficient justification for calling them outliers or discarding them. Removing these two sets of manual gates would, in fact, bias the results of our study because the decision would have been made after observing the results. For this reason, we would argue that removal of an outlier set of manual gates from this analysis is not scientifically or statistically justified. Indeed, this wide variation in manual gating analysis reflects the current state of flow cytometry analysis^47,48 and provides additional support for the importance of adopting objective automated approaches.

Per-population analysis. Human consensus clustering results were matched across samples to the sample with the maximum number of populations. Then the human consensus for each sample was used as a reference for matching of the automated results of that sample. Pairwise F-measures between all algorithms and manual gates for the HSCT and GvHD data sets are shown in Figure 2 and Supplementary Figure 9, respectively. We calculated the dendrograms using the complete-linkage hierarchical clustering and Euclidean distance between the F-measures as the metric.

These results can be used to identify cell populations that are responsible for high (or low) F-measures for further visual investigation. For example, cell population no. 3 in the HSCT data set demonstrates a high overall pairwise F-measure between all of the algorithms and manual gates (Fig. 2), which suggests that this cell population has been relatively easy to identify. This was visually confirmed in Supplementary Figures 7 and 8. In contrast, cell population no. 2 in the GvHD data set represents a cell population that was identified only by manual gating (Supplementary Fig. 9). Further evaluation shows that this population (colored in red) is generally identical to the cyan population in every channel but has a lower FSC (Supplementary Fig. 10). This emphasizes the importance of designing methodologies that can use background biological knowledge in the clustering process. In this case, the humans used their knowledge about the scatter channels to partition these cells into two different populations on the basis of cell size despite their similarity in every other channel (see Supplementary Fig. 18 for a density plot of the sample).

Sample classification.

FlowCAP-II included three data sets for sample classification (markers are listed in Supplementary Table 5).

Challenge 1: HIV-exposed–uninfected versus unexposed (HEUvsUE). The goal of this challenge was to find cell populations that can be used to discriminate between HEU (n = 20) and UE (n = 24) infants. Blood samples were taken at 6 months after birth and were left unstimulated (for control) or stimulated with six Toll-like–receptor ligands. In addition to raw FCS files, half of the subject labels were provided for training purposes. Algorithms were to use these data to label the rest of the samples. These labels were used to evaluate algorithm performance.

Challenge 2: acute myeloid leukemia (AML). The goal of this challenge was to find cell populations that can discriminate between AML positive (n = 43) and healthy donor (n = 316) patients. Peripheral blood or bone marrow aspirate samples were collected over a 1-year period using eight tubes (tube #1 is an isotype control, and #8 is unstained) with different marker combinations. In addition to raw FCS files, half of the subject labels were provided for training purposes. Algorithms were to use these data to label the rest of the samples. These labels were be used to evaluate algorithm performance.

Challenge 3: identification of antigen stimulation group of intracellular-cytokine staining of post–HIV vaccine antigen-stimulated T cells (HVTN). The goal of this challenge was to correctly label the antigen stimulation group of post–HIV vaccine T-cells. The data set contains samples from 48 individuals from the HIV Vaccine Trials Network. Each individual received an experimental HIV vaccine. Samples were collected approximately 10 months later and T cells were challenged with two antigens: ENV-1-PTEG and GAG-1-PTEG. The response of CD4⁺ and CD8⁺ T cells was measured by FCM for each group. Cells were found to respond differently to the two antigen stimulations. This is essentially a classification challenge (see Supplementary Fig. 19 for an example). For training purposes, we provided data from 24 individuals in each group. The antigen-stimulation label was provided. Participants were to correctly identify the antigen stimulation group of the test data (n = 24). The complete data set consisted of 240 FCS files. The data were compensated, transformed and partially gated (gated for singlets, live cells and lymphocytes).

Classification F-measure. The F-measure for classification is defined as the harmonic mean of precision and recall (the additional 'matching' step for clustering F-measure is not required). Precision is defined as TP/(TP + FP), and recall is defined as TP/(TP + FN), where TP, TN, FP and FN are true positives (e.g., AML predicted as AML), true negatives, false positives and false negatives, respectively.

Participants in the DREAM6/FlowCAP II challenge were required to submit a list of subjects ordered according to the confidence assigned to the subject being affected with AML. That allowed us to compute more metrics than the ones used in the other FlowCAP challenges (Supplementary Note 3).

Features used for classification. A post hoc analysis of the HVTN Challenge 3 results was performed to determine whether the features used by automated algorithms for sample classification were similar to the features selected during manual gating. A detailed description of this analysis is presented in Supplementary Note 4 and Supplementary Figure 20.

Author Contributions

N.A., G.F., H. Hoos, T.R.M., R.G., R. Brinkman and R.H.S. were responsible for the formation of the FlowCAP consortium, the development of all FlowCAP challenges, results evaluation and manuscript preparation. Members of the FlowCAP consortium contributed as follows. Population identification challenge data analysis team: D. Dougall, A.H.K., P. Mah, G.O., J.S., I.T. and S.A.W. Population identification challenge data providers: J.B., C.E., A.P.W., E.S.F., K.H., T.R.K., W. Rogers and S.D.R. Clinical and hematopathological consultation: B.D. Population identification challenge algorithm developers and challenge participants: A.A., A.P., A.B., H.B., R. Bruggner, R.F., R.J., N.Z., M.L., D. Dill, G.N., C.C., F.E.K., K.O., M.C., Y.G., S.S., I.S., A.G., P. Shooshtari, H.Z., P.L.D.J., M.J., J.K., J.M.M., G.L., A.A.B., P. Májek, J.V., T.M., H. Huttunen, P.R., M.N., G.J.M., K.W., I.N., G. Sharma, R. Nikolic, S. Pyne, Y.Q., P.Q., J.Q. and A.R. Members of the DREAM consortium contributed as follows. Sample classification challenge designers: P. Meyer, G. Stolovitzky and J.S.-R. Sample classification challenge data analysis team: R. Norel. Sample classification challenge algorithm developers and challenge participants: M. Bhattacharjee, M. Biehl, P.B., K.B., B.D.C., F.S., T.S., E.T., G.T., S.D., R.D., G.A., J.G., I.G., S. Posch, N.G., J.K., M.K., W. Rudnicki, B.L., M.M.-C., T.M., H. Huttunen, P.R., M.N., P. Schneider, M. Seifert, M. Strickert and J.M.G.V.

Competing interests

At the time of this study, J.Q. was an employee of Tree Star Inc., and P. Májek and J.V. were employees of ADINIS s.r.o. and consultants for Cytobank Inc., which make commercial FCM analysis software. G.N. is a consultant, equity holder and member of a scientific advisory board and/or board of directors at Nodality, DVS Sciences, Beckton Dickinson, Cell Signaling Technologies, BINA Technologies, and 5AM Ventures.