The Effects of the Previous Outcome on Probabilistic Choice in Rats

Abstract

This study examined the effects of previous outcomes on subsequent choices in a probabilistic-choice task. Twenty-four rats were trained to choose between a certain outcome (1 or 3 pellets) versus an uncertain outcome (3 or 9 pellets), delivered with a probability of .1, .33, .67, and .9 in different phases. Uncertain outcome choices increased with the probability of uncertain food. Additionally, uncertain choices increased with the probability of uncertain food following both certain-choice outcomes and unrewarded uncertain choices. However, following uncertain-choice food outcomes, there was a tendency to choose the uncertain outcome in all cases, indicating that the rats continued to “gamble” after successful uncertain choices, regardless of the overall probability or magnitude of food. A subsequent manipulation, in which the probability of uncertain food varied within each session as a function of the previous uncertain outcome, examined how the previous outcome and probability of uncertain food affected choice in a dynamic environment. Uncertain-choice behavior increased with the probability of uncertain food. The rats exhibited increased sensitivity to probability changes and a greater degree of win–stay/lose–shift behavior than in the static phase. Simulations of two sequential choice models were performed to explore the possible mechanisms of reward value computations. The simulation results supported an exponentially decaying value function that updated as a function of trial (rather than time). These results emphasize the importance of analyzing global and local factors in choice behavior and suggest avenues for the future development of sequential-choice models.

The outcome of a choice is often unpredictable. For instance, the choice between not gambling and gambling is essentially the choice between an outcome that is certain (i.e., not losing money) and an outcome that is uncertain (i.e., winning or losing money). The choice to gamble can be affected by both the probability of winning and the amount that could potentially be won (Rachlin & Frankel, 1969). The product of the probability and magnitude of reward is the expected value of that outcome. Decreases in the probability of reward (i.e., decreases in the expected value of the choice) result in decreases in the subjective value of a choice. This phenomenon, referred to as probability discounting, has been documented in both humans (e.g., Myerson, Green, Hanson, Holt, & Estle, 2003; Rachlin, Raineri, & Cross, 1991) and nonhuman animals (e.g., Cardinal & Howes, 2005; Mazur, 1988; Mobini et al., 2002; Stopper & Floresco, 2011).

Probability-discounting procedures with humans have typically involved the choice between one hypothetical monetary amount that will certainly be delivered (i.e., the certain outcome) and a second hypothetical monetary amount that will probabilistically be delivered (i.e., the uncertain outcome). The magnitude of the certain outcome is sometimes adjusted to converge on an equivalent subjective value between the certain and uncertain outcomes (e.g., Myerson et al., 2003). Therefore, the potential outcomes of each choice may be different from many, if not all, other previous choices. Additionally, some probabilistic-choice studies in animals involve the choice between an uncertain outcome after a fixed delay and a certain outcome after a varying delay (e.g., Mazur, 1989), such that the time until receiving the certain reward may differ across all trials. Most gambling devices (e.g., slot machines) do not operate in this fashion, as the probability of winning for each response remains constant (see Crossman, 1983; Madden, Ewan, & Lagorio, 2007). Thus, a more stable choice situation may prove useful in studying animal choice behavior to more closely mimic gambling situations in humans (Madden et al., 2007; Weatherly & Derenne, 2007; Winstanley, 2011).

A second characteristic of many probabilistic-choice studies is that choice behavior tends to be reported from a global, or molar, perspective, such that average or overall values are presented in place of values that reflect choice behavior at an individual-trial, or molecular, level (e.g., Bateson & Kacelnik, 1995; Green, Myerson, & Calvert, 2010). An analysis of choice behavior at a molar level does not necessarily provide information about individual choices, but molecular analyses of choice behavior can predict overall choice patterns (Kacelnik, Vasconcelos, Monteiro, & Aw, 2011). Furthermore, given the differences in choice behavior when individuals face isolated versus sequential gambles (Keren & Wagenaar, 1987), molecular analyses of sequential choices may provide insight into the cognitive processes of choice behavior that have yet to be elucidated by molar analyses of choice behavior.

One factor that can be addressed by a molecular analysis of choice behavior is the effect of the previous outcome on subsequent choice behavior. McCoy and Platt (2005) showed that rhesus macaques were more likely to choose an uncertain outcome (i.e., an outcome that rewarded variable amounts) over a certain outcome (i.e., an outcome that rewarded a constant amount) as the previous outcome deviated more from the expected value of the certain outcome (for a similar result in humans, see Hayden & Platt, 2009). In a probabilistic-choice task, Stopper and Floresco (2011) found that rats were more likely to choose an uncertain outcome after receiving an uncertain reward (i.e., four pellets) than after receiving no reward for an uncertain choice (i.e., zero pellets). Because these results were collapsed across probability of food, it is difficult to determine whether the probability of food interacted with the previous-outcome effects on subsequent choice behavior. Greggers and Menzel (1993) examined several postoutcome behaviors in a bee that was given the choice between four feeders that offered different reward amounts; the amount of reward at each feeder affected the rate of staying at that feeder versus switching to another feeder. Therefore, in conjunction with other reports demonstrating previous-outcome effects in humans (e.g., Demaree, Burns, DeDonno, Agarwala, & Everhart, 2012; Dixon, Hayes, Rehfeldt, & Ebbs, 1998; Leopard, 1978; McGlothlin, 1956; Myers & Fort, 1963), these results indicate the potential importance of previous outcomes on subsequent choices, but the possible mechanisms underlying such effects are still poorly understood.

One possible factor that may prove important in contributing to the previous-outcome effects on subsequent choices is the framing of an outcome. For instance, humans will choose a certain gain over an uncertain gain, but an uncertain loss over a certain loss (e.g., Kahneman & Tversky, 1979). Choice behavior is affected by whether or not the choice was framed as a gain or a loss. Interestingly, previous outcomes may also serve to frame choices. Marsh and Kacelnik (2002) showed, in starlings, that the probability of choosing a variable amount over a constant amount of food depended on the relationship between the variable amount and the amount of food received on forced-choice trials (e.g., some starlings were risk prone to minimize relative losses). Therefore, choice was affected by the relative amount of reinforcement that could be earned (or lost). Humans have also been shown to be affected by whether or not they were informed of a previous gain or loss before making a choice between a certain and an uncertain outcome (Thaler & Johnson, 1990; also see Hollenbeck, Ilgen, Phillips, & Hedlund, 1994; Slattery & Ganster, 2002). These results suggest that previous outcomes in a sequential-choice paradigm may very well produce a dynamic framing effect from trial to trial. For instance, the reception of a large probabilistic outcome may allow an individual to be riskier in the subsequent choice, but the reception of no reward or small outcome may force the individual to be more conservative in his or her subsequent choice such that these losses can be reduced (see Thaler & Johnson, 1990). Thus, a critical factor in analyses of probabilistic-choice behavior would be the magnitude of the previous outcome.

The goal of the present experiment was to further investigate the effects of both global (i.e., the overall probability of an uncertain outcome) and local (i.e., the outcome of the previous choice) factors on the subsequent choice in a probability-discounting task. The current task involved aspects of probability-discounting procedures, but differed from the adjusting procedures described here. Cardinal, Daw, Robbins, and Everitt (2002) showed that performance criteria in adjusting-delay tasks can be achieved in the same time frame by computer simulations programmed to make choices randomly from trial to trial. Thus, to discourage the possibility of pseudorandom behavior, a more stable choice paradigm was employed. However, in the final phase of the experiment, the probability of uncertain food depended on the most recent uncertain outcome to explore the impact of dynamic changes in reward probability in comparison with the previous static conditions. Furthermore, many probabilistic-choice paradigms confound variability with risk (see Searcy & Pietras, 2011), thereby clouding the ability to determine risk sensitivity as an independent factor; the certainty or constancy of an outcome can have a considerable influence on choice (see Battalio, Kagel, & MacDonald, 1985; Kahneman & Tversky, 1979). Accordingly, the food rewards associated with both of the choice options were variable in the present study. Analyses of choice behavior were conducted at both molar and molecular levels to determine how both global and local factors collectively affect sequential choice behavior.

Method

Animals

Twenty-four male Sprague–Dawley rats (Rattus norvegicus; Charles River, Portage, Michigan) were used in the experiment. They arrived at the facility (Kansas State University, Manhattan, Kansas) at approximately 60 days of age. The rats were pair-housed in a dimly lit (red light) colony room that was set to a reverse 12-hr light– dark schedule (lights off at approximately 8:00 a.m.). The rats were tested during the dark phase. There was ad libitum access to water in the home cages and in the experimental chambers. The rats were maintained at approximately 85% of their projected ad libitum weight during the experiment, based on growth-curve charts obtained from the supplier. When supplementary feeding was required following an experimental session (see Procedure), the rats were fed in their home cages approximately 1 hr after being returned to the colony room (see Bacotti, 1976; Smethells, Fox, Andrews, & Reilly, 2012).

Apparatus

The experiment was conducted in 24 operant chambers (Med-Associates; St. Albans, Vermont), each housed within sound-attenuating ventilated boxes (74 × 38 × 60 cm). Each chamber (25 × 30 × 30 cm) was equipped with a stainless steel grid floor, two stainless steel walls (front and back), and a transparent polycarbonate sidewall, ceiling, and door. Two pellet dispensers (ENV-203), mounted on the outside of the operant chamber, delivered 45-mg food pellets (Bio-Serv; Frenchtown, New Jersey) to a food cup (ENV-200R7) centered on the lower section of the front wall. Head entries into the food magazine were transduced by an infrared photobeam (ENV-254). Two retractable levers (ENV-112CM) were located on opposite sides of the food cup. An audio generator (ANL-926) delivered white noise through a speaker mounted on the rear wall of the chamber. Water was always available from a sipper tube that protruded through the back wall of the chamber. Experimental events were controlled and recorded with 2-ms resolution by the software program MED-PC IV (Tatham & Zurn, 1989).

Procedure

Pretraining

The rats were trained to eat from the food magazine and press both the left and right levers. The first two sessions involved magazine training. Food pellets were delivered to the food magazine on a random-time 60-s schedule of reinforcement. The rats earned approximately 120 food rewards during the 2-hr sessions. The final two sessions of pretraining involved lever-press training. Each session began with a fixed-ratio (FR) 1 schedule of reinforcement and lasted until 20 pellets were delivered on each lever. The FR 1 was followed by a random-ratio (RR) 3 schedule of reinforcement, which lasted until five pellets had been delivered for lever pressing on both sides. The RR 3 was followed by an RR 5, which lasted until the rats earned five pellets from each lever.

Static probability training

Each session began with the onset of the 70-dB white noise, which remained on for the entire session; this served as a masking noise in addition to the ventilating fan. The session involved eight forced-choice trials followed by a maximum of 160 free-choice trials. In forced-choice trials, one lever was inserted into the chamber. Each lever corresponded to one of two choices—a choice with a certain outcome and a choice with an uncertain outcome; lever assignment was counter-balanced across rats. When the lever was pressed, a fixed-interval (FI) 20-s schedule began; the first lever press after 20 s resulted in lever retraction and food delivery. On certain-outcome trials, either one or three pellets were delivered; the probability of delivery of each magnitude was .5. On uncertain trials, either three or nine pellets were delivered; the probability of delivery of each magnitude was .5. In the eight forced-choice trials, food was always delivered following forced choices for the uncertain outcome. Each of the food amounts for the certain choice (one and three pellets) and uncertain choice (three and nine pellets) was presented twice in the eight forced-choice trials; the order of presentation was random. A 10-s intertrial interval (ITI) was initiated following food delivery.

On free-choice trials, both levers were inserted into the chamber. A choice was made by pressing one of the levers, causing the other lever to retract. Following completion of the FI 20-s schedule, a certain choice terminated with the equally probable delivery of one or three food pellets, and an uncertain choice probabilistically terminated in the delivery of three or nine pellets. In different phases, the probability of uncertain food delivery of either three or nine pellets was .1, .33, .67, or .9. The probability of each magnitude was .5. At the end of each trial, the chosen lever was retracted and a 10-s ITI began.

There were three orders of presentation of uncertain food probabilities (see Table 1). All rats were first exposed to the .33 probability (20 sessions), as this probability resulted in equal expected values for the certain and uncertain outcomes, E(food) = 2.0. In Phase 2, the lever assignments of certain and uncertain outcomes were reversed (30 sessions) to reduce side biases. The 24 rats were then partitioned into three groups (n = 8) determined by the percent choice of the uncertain outcome in Phase 2, with each group receiving a different order of uncertain food probability. The rats with the highest baseline uncertain-choice values were assigned to Order 1 and experienced the .1 probability in Phase 3, the eight rats with the lowest percent uncertain-choice values were assigned to Order 2 and received the .67 probability in Phase 3, and the eight rats with intermediate percent uncertain-choice values were assigned to Order 3 and received the .9 probability in Phase 3 (see Table 1). Given the baseline percentages in Phase 2, this assignment was designed to promote a clear shift in the proportion of choices of the uncertain outcome in Phase 3 relative to that of Phase 2. Following delivery of the .1, .67, and .9 probabilities in Phases 3 through 5, all rats were returned to the .33 probability in Phase 6. Phases 3 through 6 lasted for 10 sessions each.

Table 1.

Probability of Food (P[Food]) and the Corresponding Expected Value of Food (E[Food]) on the Uncertain Side in Each Phase for the Subgroups of Rats That Experienced Different Orders of Exposure to the Probabilities of Food Delivery

	Order 1		Order 2		Order 3
	P(food)	E(food)	P(food)	E(food)	P(food)	E(food)
Static Probability of Food
Phases 1 and 2	.33	2.0	.33	2.0	.33	2.0
Phase 3	.1	0.6	.67	4.0	.9	5.4
Phase 4	.9	5.4	.1	0.6	.67	4.0
Phase 5	.67	4.0	.9	5.4	.1	0.6
Phase 6	.33	2.0	.33	2.0	.33	2.0
Dynamic Probability of Food
Phase 7	.17	1.0
	.33	2.0
	.67	4.0

Note. The expected value of the certain choice was always 2.0. The three probabilities of food during the dynamic probability-of-food phase were experienced by all rats.

Dynamic probability training

Prior to the onset of the dynamic probability phase, all rats experienced five sessions in which the probability of uncertain food was .33, due to a brief gap between the end of Phase 6 and the beginning of the dynamic probability phase. In the dynamic phase, the rats were exposed to an overall probability of uncertain food of .33, but the local probability of food delivery for the uncertain choice was adjusted depending on whether food was delivered following the previous uncertain choice. Each session began with a probability of .33. The local probability of food delivery for the uncertain choice was .17 when the most recent uncertain choice was unrewarded and .67 when the most recent uncertain choice was rewarded. The dynamic probability training phase lasted for 20 sessions.

Data Analysis

The final five sessions of each phase were used for data analyses. The analyses conducted on the static probability manipulation focused on Phases 3 through 6, following the lever reversal. Phase 6 was used for the analysis of the .33 probability condition to account for carryover effects that may have emerged over the course of the study. Two rats with health issues did not complete one of the phases of the experiment. One rat did not complete Phase 6, so Phase 2 was used for analysis of his .33 condition instead. A second rat did not complete the dynamic probability training phase but did complete all other phases; this rat was not included in the analysis of the dynamic phase. In the molar analyses, all rats that completed the task were included in all analyses of the static and the dynamic phases. In the molecular analysis, some rats had missing data due to the failure to make enough choices at the extreme probabilities and thus were not included in the analysis. The number of rats omitted from the molecular analyses ranged from zero to five. Statistical analyses of both the static and dynamic probability manipulations were collapsed across different orders of exposure to probabilities in the static phase, as there were no major differences among the rats in these subgroups.

Results

Static Probability Training

Molar analyses

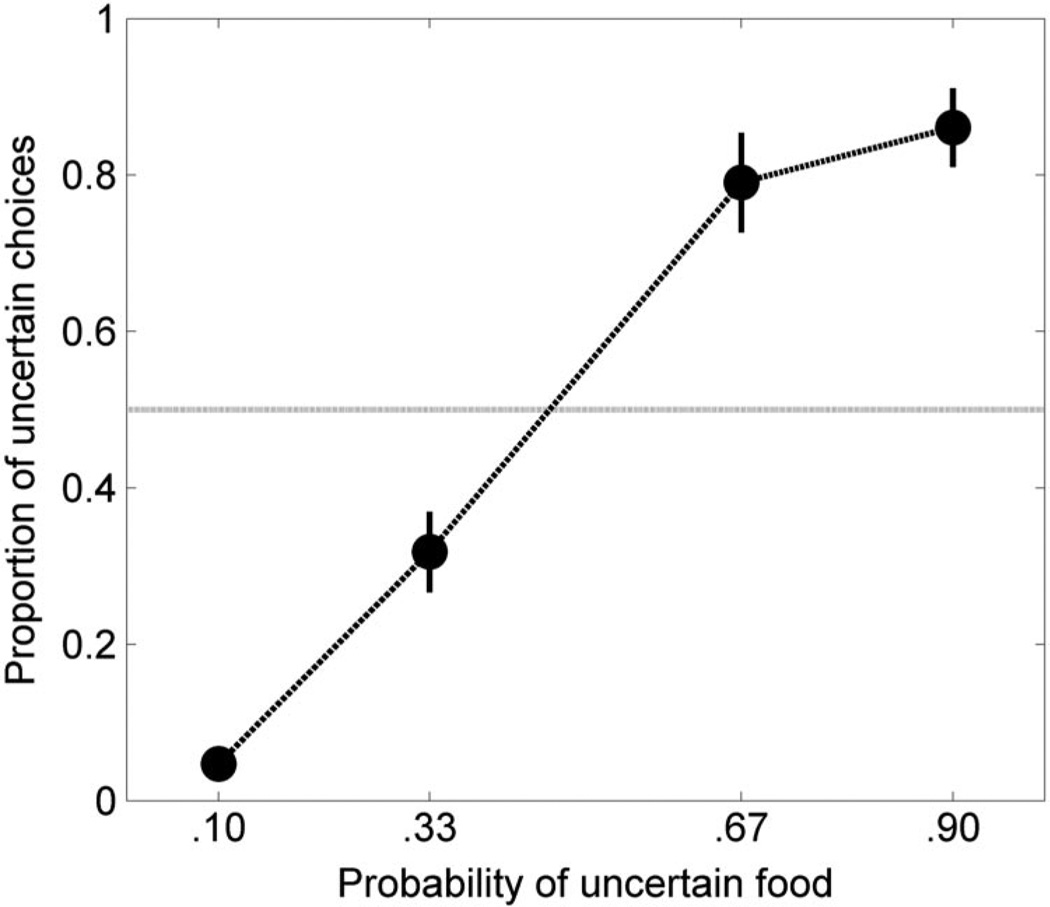
Figure 1 shows the mean (± SE of the mean) proportion of choices for the uncertain outcome (the total number of choices for the uncertain outcome divided by the total number of free choices) as a function of the probability of food on the uncertain side. The horizontal line indicates the point of risk neutrality (choice behavior = .5). The proportion of choices for the uncertain outcome increased systematically as the probability of uncertain food increased. Moreover, when the probability of uncertain food was less than .5, the probability of uncertain choice was also less than .5 (risk aversion), and when the probability of uncertain food was greater than .5, choices were also greater than .5 (risk proneness). An ANOVA revealed a main effect of probability on the proportion of choices for the uncertain outcome, F(3, 69) = 90.29, p < .001. Post hoc Tukey’s Honestly Significant Difference (HSD) comparisons revealed significant differences between all probabilities of food delivery, p < .05, except for the comparison between probabilities of .67 and .9.

Figure 1.

Mean (± SEM) proportion of choices for the uncertain side as a function of the probability of uncertain food during the static probability-of-food training phase.

Molecular analyses

Figure 2 shows the proportion of choices for the uncertain outcome as a function of the probability of food on the uncertain side following each of the five possible outcomes of the previous trial. Following previous outcomes certain-small (C-S), certain-large (C-L), and uncertain-zero (U-Z), the rats generally increased their uncertain choices as the probability of uncertain food increased. There was a smaller effect of probability of uncertain food on choices following the uncertain-small (U-S) and uncertain-large (U-L) outcomes. In addition, there was a general tendency to choose the certain outcome more following reward on the certain side and to choose the uncertain outcome more following reward on the uncertain side. There were no considerable differences in choice behavior following the small- and large-magnitude rewards of both choices. Following U-Z outcomes, the rats were more likely to make a certain choice at the lowest probability of food delivery on the uncertain side (i.e., when the expected value of the certain choice was greater than that of the uncertain choice), but to make an uncertain choice at probabilities of food delivery .33, .67, and .9 (i.e., when the expected value of the uncertain choice was greater than or equal to that of the certain choice).

Figure 2.

Mean (± SEM) proportion of choices for the uncertain outcome, as a function of the probability of uncertain food, following each of the five possible previous outcomes in the static probability-of-food phase. C-L = certain-large; C-S = certain-small; U-L = uncertain-large; U-S = uncertain-small; U-Z = uncertain-zero.

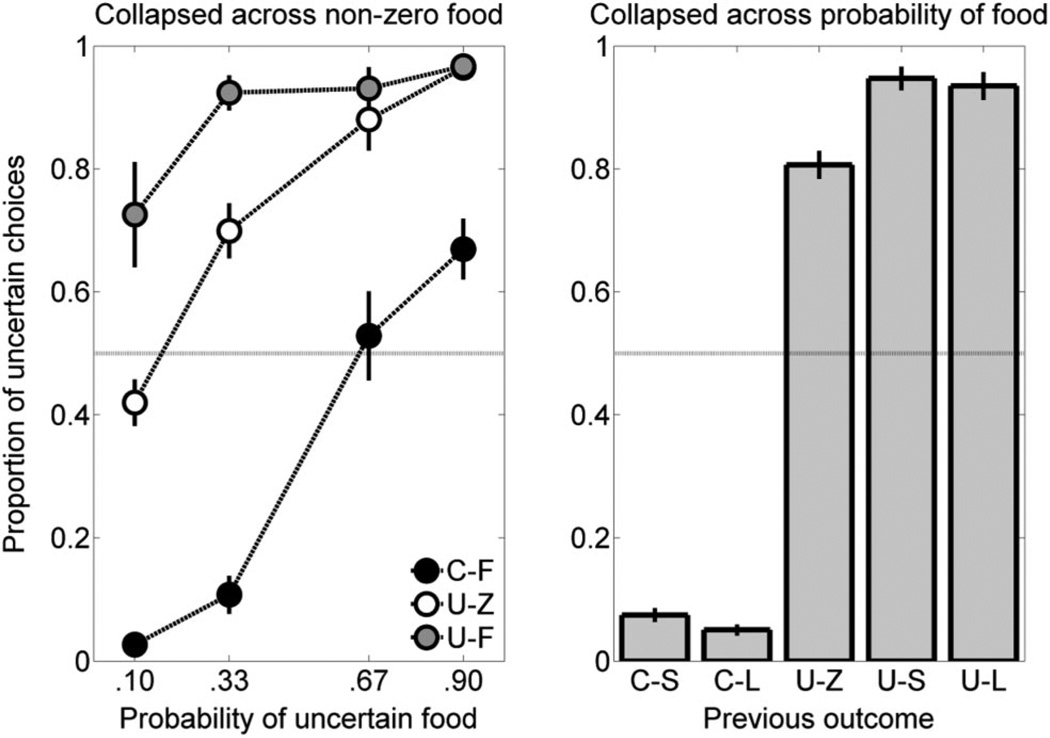
Given the conditional nature of the molecular analysis (that is, P[uncertain choice | previous outcome]), there were missing data in some conditions for a subset of the rats. If a given outcome was never received, then there were no data for the proportion of uncertain choices following that outcome. To reduce the impact of missing data on the analysis, the data were collapsed in two different ways. The first analysis involved collapsing across the food outcomes on both the certain and uncertain sides to assess the effect of probability on certain and uncertain choices regardless of the food amount delivered. The sum of the choices for the uncertain side following the C-S and C-L outcomes was divided by the sum of the total number of choices following C-S and C-L outcomes. Similarly, the sum of the choices for the uncertain side following the U-S and U-L outcomes was divided by the sum of the total number of choices following the U-S and U-L outcomes. The U-Z outcome was treated separately in this analysis. These collapsed results are shown in the left panel of Figure 3. There was a general increase in the proportion of choices for the uncertain side as the probability of uncertain food increased; additionally, the rats were most likely to choose the uncertain side following reward on the uncertain side, then followed by no reward on the uncertain side, and then followed by reward on the certain side. An ANOVA revealed main effects of probability, F(3, 54) = 53.60, p < .001, and previous outcome, F(2, 36) = 155.46, p < .001, and a significant Probability × Previous Outcome interaction, F(6, 108) = 11.89, p < .001.

Figure 3.

Mean (± SEM) proportion of choices for the uncertain outcome as a function of the probability of uncertain food, collapsed across food amounts of both outcomes (left panel), and the mean (± SEM) proportion of choices for the uncertain outcome following each outcome in the previous trial collapsed across the probability of uncertain food (right panel). These data are from the static probability-of-food phase. C-F = certain-food; C-L = certain-large; C-S = certain-small; U-F = uncertain-food; U-L = uncertain-large; U-S = uncertain-small; U-Z = uncertain-zero.

Simple effects analyses (i.e., repeated-measures ANOVA) were conducted for each probability of food delivery with previous outcome as the within-subjects factor. For each probability of food delivery on the uncertain side, there was a main effect of previous outcome, all Fs(2, 36) ≥ 29.61, all ps < .001. For probabilities of food .1 and .33, post hoc Tukey’s HSD comparisons indicated that the proportion of choices for the uncertain outcome following a certain-food (C-F) outcome was significantly less than that following a U-Z outcome, which was significantly less than that following an uncertain-food (U-F) outcome, ps < .05. For probabilities of food .67 and .9, post hoc Tukey’s HSD comparisons indicated that the proportion of choices for the uncertain outcome following a C-F outcome was significantly less than that following both a U-Z and a U-F outcome, p < .05, but the proportion of choices for the uncertain outcome following a U-Z or U-F outcome did not differ.

A second analysis was conducted by collapsing across the probability of uncertain food to assess differences in performance as a function of food amount on the certain and uncertain sides. The number of the choices for the uncertain side following each outcome across the probabilities of food delivery was divided by the total number of choices following each outcome. These collapsed results are shown in the right panel of Figure 3. There was a general tendency to choose the uncertain side more following all uncertain outcomes than following certain outcomes. (Note that the low levels in uncertain choices following C-S and C-L outcomes when collapsing across the probabilities of uncertain food delivery, in the right panel of Figure 3, is due to the predominance of observations at the lower probabilities.) An ANOVA revealed a main effect of previous outcome on the proportion of choices for the uncertain outcome, F(4, 92) = 1100.06, p < .001. Post hoc Tukey’s HSD comparisons indicated that the proportion of choices for the uncertain side following the C-S and C-L outcomes was significantly less than that of the U-Z, U-S, and U-L outcomes, and that the proportion of choices for the uncertain side following the U-Z outcome was significantly less than that of the U-S and U-L outcomes, p < .05. There were no significant differences in choice behavior for the uncertain outcome following the C-S and C-L outcomes and following the U-S and U-L outcomes.

Dynamic Probability Training

Molar analysis

Figure 4 shows the proportion of choices for the uncertain outcome as a function of the dynamic (open circles) and static (filled circles) probability of food on the uncertain side; the static function is the same as Figure 1, apart from the removal of two rats that had incomplete data in the dynamic phase. The rats were more likely to choose the uncertain outcome as the local probability of uncertain food increased in the dynamic training phase. The dynamic probability function was steeper than the static function. The rats displayed risk proneness for probabilities .33 and .67, and risk aversion for the probability of .17.

Figure 4.

Mean (± SEM) proportion of choices for the uncertain side as a function of the probability of uncertain food during the dynamic probability-of-food phase. The results from the static probability-of-food phase are included for comparison purposes.

An ANOVA revealed a main effect of probability on the proportion of choices for the uncertain outcome, F(2, 42) = 39.56, p < .001. Post hoc Tukey’s HSD comparisons indicated that the uncertain outcome was chosen significantly less when the probability of food was .17 than when it was .33 or .67, p < .05, and that there was no significant difference in the proportion of choices for the uncertain outcome when the probability of food was .33 and .67.

A comparison of the common probability values delivered in the dynamic and static probability phases indicated a significantly greater proportion of choices for the uncertain outcome in the dynamic phase when the probability of food was .33 compared with the static phase, F(1, 21) = 14.02, p < .01. When the probability of food was .67, there was no significant difference in proportion of choices for the uncertain side between the static and dynamic phases, F(1, 21) = .79, p = .383.

Molecular analysis

Figure 5 shows the proportion of choices for the uncertain side following each outcome in the static and dynamic probability phases. Because the probability of food was dependent on the most recent outcome of an uncertain choice, it was not possible to conduct molecular analyses as a function of probability of food on the uncertain side (e.g., following food rewards on the uncertain side, the probability of food became .67 and was never .33 or .17 following these outcomes). The certain outcome was chosen more following certain rewards, and the uncertain outcome was chosen more after uncertain food rewards. There was a main effect of previous outcome on the proportion of choices for the uncertain outcome, F(4, 80) = 381.58, p < .001. Post hoc Tukey’s HSD comparisons revealed that uncertain choices were significantly lower following the certain outcomes (C-S, C-L) than following the uncertain food outcomes (U-S, U-L) and the U-Z outcome, and were significantly lower following the U-Z outcome than following both the U-S and U-L outcomes. There were no significant differences in the proportion of choices for the uncertain side following C-S and C-L outcomes and following U-S and U-L outcomes.

Figure 5.

Mean (± SEM) proportion of choices for the uncertain outcome following each of the five possible outcomes in the previous trial, collapsed across probability of uncertain food, in the dynamic probability-of-food phase. The results from the static probability-of-food phase are included for comparison purposes. C-L = certain-large; C-S = certain-small; U-L = uncertain-large; U-S = uncertain-small; U-Z = uncertain-zero.

The effect of the previous outcome on choice behavior was also compared across the static and dynamic probability-of-food phases (see Figure 5). There were main effects of phase, F(1, 20) = 13.36, p < .01, and previous outcome, F(4, 80) = 885.84, p < .001, and a significant Phase × Previous Outcome interaction, F(4, 80) = 34.24, p < .001. Simple effects analyses (i.e., paired-sample t tests) revealed that the rats were significantly more risk averse following C-S, C-L, and U-Z outcomes in the dynamic than in the static probability-of-food phase, all ts(20) > 3.58, all ps < .01. Additionally, the rats were significantly more risk prone following U-S outcomes in the dynamic than in the static probability-of-food phase, t(20)= −2.79, p < .05. There was a trend toward more risk proneness following U-L outcomes in the dynamic phase, but this was not significant, t(20) = −1.47, p = .158.

Discussion

The present experiment was designed to determine the effects of both the overall probability of food and the previous outcome of a choice on the subsequent choice in static- and dynamic-choice situations. Regarding the first goal, the rats showed an increased proportion of choices for the uncertain outcome as the probability of uncertain food delivery increased in both the static (see Figure 1) and dynamic (see Figure 4) probability manipulations. Therefore, similar to previous results (e.g., Cardinal & Howes, 2005; Green et al., 2010; Mazur, 1988; Mobini et al., 2002; Stopper & Floresco, 2011), the probability of food did have an impact on choice behavior in the current probabilistic-choice task. Furthermore, the increased steepness of the choice-behavior gradient in the dynamic probability phase (relative to the static probability phase; Figure 4) suggests that the more dynamic choice environment may have encouraged increased attention to probability information; such a result is similar to results found in the foraging literature regarding faster learning in more dynamic environments (e.g., Dunlap & Stephens, 2012).

Although previous studies have analyzed the effect of transitions of the probability of food delivery on subsequent choices (e.g., Mazur, 1995), the current dynamic probability training, to our knowledge, has not been employed previously, nor have there been any direct comparisons of static and dynamic probability adjustments like those used in the present experiment (but see Dunlap & Stephens, 2012, for related work). The typical adjusting procedures described here have involved an adjustment of the amount of or the delay until reward, and the corresponding analyses are commonly derived from a molar perspective (but see Cardinal et al., 2002). The results suggest the interesting possibility that weighting of local versus global information may be flexible depending on the stability of the choice environment (see Lea & Dow, 1984).

The second goal of the experiment was to determine the effect of the previous outcome on choice behavior. The previous outcome (C-F, U-F, or U-Z) strongly affected the probability of making a subsequent uncertain choice, and this interacted with the probability of food on the uncertain side in the static phase (see Figure 3). Interestingly, when the probability was high (.67 or .9), there was no difference in the effect of U-Z versus U-F, indicating that the high probability of uncertain food attracted subsequent uncertain choices, regardless of the previous outcome (see Figure 3). This, however, was not due to the overall bias for the uncertain side, because uncertain choices following C-F outcomes were lower than choices following uncertain outcomes. This suggests that there may have been a bias to stay on the same side (win–stay), but that this bias was modulated by the overall probability of food. In support of this idea, when the probability of uncertain food was low (.1), the rats were more likely to shift to the certain side following U-Z outcomes (lose–shift). Stopper and Floresco (2011) similarly showed a win–stay/lose–shift behavior in rats performing a probabilistic-choice task, but the choice behavior in their study was collapsed across different probabilities of food delivery. Additionally, the rats exhibited a greater degree of win–stay/lose–shift behavior in the dynamic phase than they did in the static phase (see Figure 5), indicating that the dynamicity of the environment may modulate how the previous outcome affects subsequent choice behavior. Therefore, the current results offer insight into the effects of the previous outcome on choice behavior and how these effects are moderated by the probability of the available outcomes.

An additional question of interest was whether or not a gain or loss in terms of the magnitude of the previous outcome relative to the expected value of that choice (i.e., the prediction error) would differentially affect subsequent choices. Individuals tend to be risk-averse when choosing between a certain and uncertain gain, and risk-prone when choosing between a certain and uncertain loss (e.g., Kahneman & Tversky, 1979); this behavior may be affected by previous outcomes (see Hollenbeck et al., 1994; Marsh & Kacelnik, 2002; Slattery & Ganster, 2002; Thaler & Johnson, 1990), such that small versus large outcomes may differentially affect subsequent choices. In the present study, there were no differences following either C-S and C-L outcomes or U-S and U-L outcomes across different probabilities of food in the static (Figures 2 and 3) and dynamic phases (see Figure 5). This indicates that local framing effects due to the most recent outcome were most likely not playing a considerable role in sequential choice behavior.

The combined results of the present experiment suggest that the mechanisms involved in sequential choice behavior take into account more than the most immediately recent outcome due to the modulation of behavior by overall probability. Accordingly, previous research has also considered the impact of the previous series of outcomes on choice behavior. The common finding across these studies has been a general decay of the weight of a previous reward as that reward recedes farther into the past (Kennerley, Walton, Behrens, Buckley, & Rushworth, 2006; Lau & Glimcher, 2005; McCoy & Platt, 2005). One way to examine this issue within the current study is through the use of quantitative models of sequential choice to determine the weighting rule that best explains the current pattern of results.

Simulations of Two Models of Sequential Choice Behavior

The impact of a previous reward has been suggested to decay either exponentially (e.g., Glimcher, 2011) or hyperbolically (e.g., Devenport, Hill, Wilson, & Ogden, 1997) in models of sequential choice behavior. The exponential model (EXP) is based on the linear operator model initially developed by Bush and Mosteller (1951) and extended by Rescorla and Wagner (1972). Here, the value of an outcome is updated with each new reward; the contribution of a previous reward decreases exponentially as a function of the number of rewards, or trials (Glimcher, 2011). The hyperbolic model is formally known as the temporal weighting rule (TWR; Devenport, Patterson, & Devenport, 2005; Devenport et al., 1997; Devenport & Devenport, 1994; Winterrowd & Devenport, 2004). In the TWR model, the impact of previous rewards decreases hyperbolically as a function of time since that reward was delivered. The TWR is a more parsimonious valuation mechanism compared with the EXP model, as there are no free parameters in the TWR compared with the single free parameter (i.e., the decay rate, α) in the EXP model (Devenport et al., 1997; Glimcher, 2011). These models were simulated to determine whether either of the valuation rules could account for the general pattern of the molar and molecular results under static- and dynamic probability conditions. To disentangle the effect of decay function (exponential vs. hyperbolic) from the effect of trial-versus time-based decay, modified versions of both models were employed. Specifically, the TWR was implemented both in its original form and as a trial-based model and the EXP model was implemented in its original form and as a time-based model.

Method

Procedure

Valuation rules

Both the EXP and the TWR models have been suggested to serve as mechanisms for determining the overall value of an outcome in sequential choice situations (see Bayer & Glimcher, 2005; Devenport et al., 1997). As the present experiment was designed to determine the effect of previous outcomes on subsequent choices, both models were simulated to determine whether valuation of outcomes in the present study may have occurred as a function of trials or time, and whether the weight of previous outcomes decayed exponentially or hyperbolically. Thus, both the TWR and the EXP rules were simulated so that the weight of previous outcomes decayed either as a function of trials (for that choice) or time since the reception of each outcome.

The valuation computation in the TWR takes the following form:

$$V_{N,t}=\sum _{i=t-1}^{t-(n-1)}(R_{N,i}/T_{N,i})/\sum _{i=t-1}^{t-(n-1)}(1/T_{N,i}),$$ (1)

where V_N,t is the value of choice N on trial t, and R_N,i is the quality of individual reward i of choice outcome N that occurred T_N,i seconds prior (e.g., Devenport et al., 1997). For the trial-based rule, the number of trials since an outcome refers to the number of trials for the corresponding choice; this value was substituted in place of T_N,i such that this value now referred to trials rather than time. To conserve computing power and memory, the present simulations considered a maximum of the previous 30 rewards for each valued outcome (i.e., maximum n = 30). Thus, i reflects a maximum of the 30 most recent rewards received for choosing choice N. For example, on trial t, the value of the certain outcome would be a function of the 30 most recent certain rewards, even if these did not reflect the 30 most recently immediate trials (i.e., certain and uncertain rewards). In relation to the experiment above, V_N,t was the overall subjective value of the certain (V_C) or uncertain (V_U) choice on trial t; R_N,i was the reward magnitude received for a particular choice N (certain or uncertain) on the ith previous choice of N; and T_N,i was the amount of time (or number of trials) since previous outcomes for choice N (including ITI and trial duration for time-based model).

The EXP valuation rule takes the following form for the trial-based and time-based rules, respectively:

$$V_{N,t}=\sum _{i=1}^n\alpha R_{N,i}{(1-\alpha )}^{i_{N^{-1}}},$$ (2)

$$V_{N,t}=\sum _{i=1}^n\alpha R_{N,i}{(1-\alpha )}^{T_{N,i}},$$ (3)

where V_N,t was the value of choice N on trial t; R_N,i was the quality of individual reward i of choice outcome N; and α was a free parameter that influenced how rapidly the weights of previous outcomes decayed over trials or over time (see Bayer & Glimcher, 2005; Bush & Mosteller, 1951; Greggers & Menzel, 1993; Lea & Dow, 1984; Rescorla & Wagner, 1972). For the trial-based rule (Equation 2), the exponent was i_N−1, so that a choice’s value following the first outcome of that choice would be αR_N,i, but subsequent valuation determinations would be affected by the outcomes of the previous choices of N. However, in the time-based rule (Equation 3), the exponent was T_N,i, reflecting the time since receiving R_N,i (similar to the time-based TWR model). Again, to conserve computing power and memory, the present simulations considered a maximum of the previous 30 rewards for each valued outcome. For both the trial- and time-based simulations, three values of α were used; these were .2, .5, and .8. Because α can range from 0 (the previous reward contributes no weight to an outcome’s value) to 1 (the previous reward contributes all the weight to an outcome’s value), the chosen values of α served as a reasonable range of values for which to test the effect of this parameter on choice behavior.

Decision rules

In addition to the different valuation rules, two different decision rules were used in order to determine the method by which the rats may be choosing between outcomes. Both decision rules were based on the value of the certain outcome relative to the uncertain outcome’s value. In both decision rules, the relative value of the certain outcome was computed according to Equation 4:

$${\widehat{V}}_C=\frac{V_C}{V_C+V_U},$$ (4)

where V̂_C is the relative value of the certain outcome, V_C is the value of the certain outcome, and V_U is the value of the uncertain outcome (computed from Equations 1, 2, or 3).

One set of simulations used a continuous decision rule in which the relative value of the certain outcome was compared with a uniformly distributed random threshold, b, which could range from 0 to 1. The second set of simulations used a categorical rule in which V̂_C was compared with a random threshold b when V̂_C was between .4 and .6. The range of values between .4 and .6 was considered the “zone of indifference” (Devenport et al., 2005, p. 358). If the relative value was smaller than .4 or greater than .6, then the uncertain outcome or certain outcome was chosen, respectively. Boundary values of .4 and .6 have been proposed previously (Devenport et al., 2005), so these values were used in all simulations so as to provide a constant decision rule in comparing the simulation results from the different valuation mechanisms.

Model simulations

The simulations examined two different valuation rules (TWR and EXP), two units of the decaying valuation weights (trial-based and time-based), and two decision rules (continuous and categorical) to determine the possible valuation mechanisms that affected choice behavior in the first experiment presented. Each simulation was designed to mirror the procedure experienced by the rats in the experiment. The simulations were performed using MATLAB (MathWorks; Natick, Massachusetts). The sets of simulations were partitioned into three groups that were exposed to the probabilities of food in each of the three different orders (see Table 1). Phase 1 of the simulations lasted for 20 sessions, Phase 2 lasted 30 sessions, and Phases 3 through 6 were each 10 sessions, to mimic the conditions received by the rats (see the section “Static probability training” in the Method section of the experiment). Furthermore, there were 20 sessions that followed the static probability training that mimicked the dynamic probability training phase (see the section “Dynamic probability training” in the Method section of the experiment). Each session included eight forced trials followed by 160 free-choice trials. To account for the time between sessions for the time-based rules, 79,200 s separated the last trial in session n and the first trial in session n + 1, the average interval between successive sessions (22 hr). The output of the simulations was similar to the time-event format provided by the MED-PC software. Analysis of the simulated data was conducted as described for the molar and molecular analyses. The primary differences between the experiment proper and the model simulations were that all 160 free-choice trials were included in the model simulations, whereas the rats did not always complete all 160 free-choice trials in every session of the experiment proper. In addition, the 24 simulations were not partitioned into groups based on performance in Phase 2, as the individual differences in the model simulations were much smaller than the individual differences among the rats.

Results

Static probability training

Molar analyses

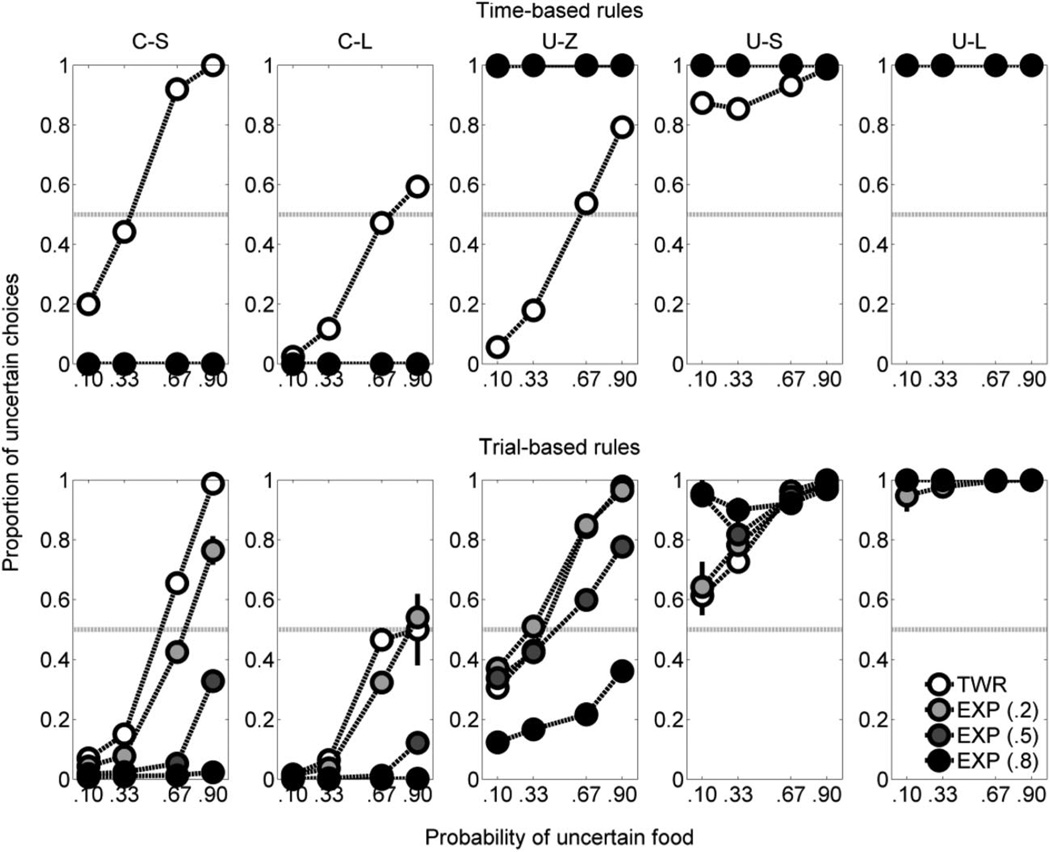
The top row of Figure 6 shows the simulations with the categorical decision rule. The left column shows the simulations with time-based valuation rules; the right column of Figure 6 includes the simulations with the trial-based valuation rules. The time-based TWR and all of the trial-based simulations with a categorical decision rule showed an increase in proportion of choices for the uncertain outcome as the probability of uncertain food increased, similar to the rats’ behavior (see Figure 1). The time-based EXP model showed little or no increase in uncertain-choice behavior as the probability of uncertain food increased (Figure 6, top left panel). Furthermore, at probabilities of uncertain food .10 and .33, the time-based models with a categorical decision rule showed greater uncertain-choice behavior than the corresponding trial-based models; additionally, at probabilities of uncertain food .67 and .90, the trial-based TWR and EXP (.2) models with a categorical decision rule showed a higher proportion of uncertain choices than the corresponding time-based models. Overall, the trial-based TWR with a categorical decision rule performed similarly to the trial-based EXP (.2) with a categorical decision rule, and both of these more closely approximated the rat data (see Figure 1) than the corresponding EXP models with higher α values.

Figure 6.

Mean (± SEM) proportion of choices for the uncertain side for the static probability-of-food phase for each of the simulations. The top row shows the simulated data from simulations that used a categorical decision rule; the bottom row shows a continuous decision rule. The left column shows the simulated data when the weights of the previous outcomes decayed as a function of time since the reception of the outcome; the right column, as a function of trials since the outcome. The α parameter for the exponential (EXP) valuation rules is indicated in parentheses. TWR = temporal weighting rule.

The bottom row of Figure 6 shows the simulations with the continuous decision rule. Apart from the time-based EXP models with the continuous decision rule, all of the other time- and trial-based TWR and EXP models with the continuous decision rule showed an increase in the proportion of choices for the uncertain outcome as the probability of uncertain food increased, similar to the rats’ behavior (see Figure 1). In comparison with the time- and trial-based models with a categorical decision rule, the time- and trial-based TWR and the trial-based EXP (.2) and EXP (.5) models with a continuous decision rule showed flatter choice-behavior functions, indicating systematic deviations from the rats’ data (see Figure 1). The pattern of systematic deviation was due to the models underpredicting uncertain choices at higher probabilities and/or overpredicting at lower probabilities. With the continuous rule, there will be a general convergence of the computed values of each outcome to the expected values of each outcome, with some exception depending on the value of the α parameter. As such, the certain outcome will be estimated to have an approximate value of 2.0, and the uncertain outcome will have approximate values of 0.6, 2.0, 4.0, and 5.4 when the probability of uncertain food is .1, .33, .67, and .9, respectively (see Table 1). Therefore, the approximate relative value of the uncertain outcome (V̂_U) across these conditions will be .23, .5, .67, and .73, respectively. These values are similar to the proportion of choices for the uncertain outcome in some simulations with a continuous decision rule. This reflects a form of matching behavior (e.g., Herrnstein, 1961), such that the uncertain outcome is chosen over the certain outcome proportionately to the ratio of the value of the uncertain outcome to the value of the certain outcome. In this situation, the uncertain outcome will rarely be chosen more than 73% of the time (see Figure 6, bottom row). This was not the case in the data (see Figure 1), suggesting that the rats were not matching their choices based on relative value, as the continuous decision rule would suggest should happen. The strong preference for one outcome over another at the extremes does not reflect the matching of relative value but rather a preference for the better alternative. Therefore, a categorical decision rule is a more plausible cognitive mechanism by which the rats’ choices were made. Accordingly, the simulations discussed next will focus on the categorical decision rule.

Molecular analyses

Figure 7 (top row) shows the proportion of choices for the uncertain side following each of the five possible outcomes in the previous trial for the time-based valuation rules. Following the C-S, C-L, U-Z, and U-S outcomes, the TWR simulations showed a general tendency for the proportion of choices for the uncertain outcome to increase as the probability of uncertain food increased; following the U-L outcome, the TWR simulation resulted in exclusive preference for the uncertain side, regardless of probability. The time-based EXP models did not demonstrate such sensitivity to the probability of uncertain food delivery, showing exclusive preference for the certain outcome following C-S and C-L outcomes across all probabilities of uncertain food and exclusive preference for the uncertain outcome following U-Z, U-S, and U-L outcomes across all probabilities of uncertain food. Such exclusive preference did not depend on the probability of uncertain food, as there are data at all probabilities following each outcome. Thus, in some sessions, some of the 24 iterations of the time-based EXP models always chose the certain outcome, whereas the others always chose the uncertain outcome (see the Discussion section for further details).

Figure 7.

Mean (± SEM) proportion of choices for the uncertain side in the simulated static probability-of-food phase as a function of the most recent outcome and the probability of uncertain food. The simulations using a time-based rule are shown in the top row; those with a trial-based rule, in the bottom row. The α parameter for the exponential (EXP) valuation rules is indicated in parentheses. C-L = certain-large; C-S = certain-small; TWR = temporal weighting rule; U-L = uncertain-large; U-S = uncertain-small; U-Z = uncertain-zero.

The trial-based valuation rules (Figure 7, bottom row) showed a general tendency for the proportion of choices for the uncertain outcome to increase with the probability of uncertain food delivery following all outcomes. Additionally, the trial-based TWR and EXP models, as well as the time-based TWR model, showed a greater tendency of choosing the uncertain side following the C-S outcome than following the C-L outcome, suggesting that the smaller certain outcome decreased the certain choice’s value, such that the uncertain outcome was more likely to be subsequently chosen. This was unlike the mean rat data shown in Figure 2, as the rats showed similar behavior following C-S and C-L outcomes. These models, however, did show a greater tendency to choose the uncertain side following the U-S and U-L outcomes than following the U-Z outcome (similar to the rats’ behavior; Figure 2).

Dynamic probability training

Molar analysis

Figure 8 shows the simulated data from the dynamic probability training phase for both the time-based TWR and EXP models (left panel) and the trial-based TWR and EXP models (right panel). The time-based TWR model and the trial-based TWR and EXP models all showed an increasing proportion of choices for the uncertain outcome as the probability of uncertain food delivery increased, similar to that shown by the rats (see Figure 4). Furthermore, these models showed a greater likelihood of choosing the uncertain outcome when the probability of food was .67 than when it was .17, similar to the rats’ behavior. However, the time-based EXP models did not show such a monotonic function, choosing the uncertain outcome exclusively when the probability of food was .17 and .67, and rarely choosing the uncertain outcome when the probability of food was .33.

Figure 8.

Mean (± SEM) proportion of choices for the uncertain side as a function of the probability of uncertain food in the simulated dynamic probability-of-food phase. The simulations using a time-based rule are in the left panel; those using a trial-based rule are in the right panel. The α parameter for the exponential (EXP) valuation rules is indicated in parentheses. TWR = temporal weighting rule.

Molecular analyses

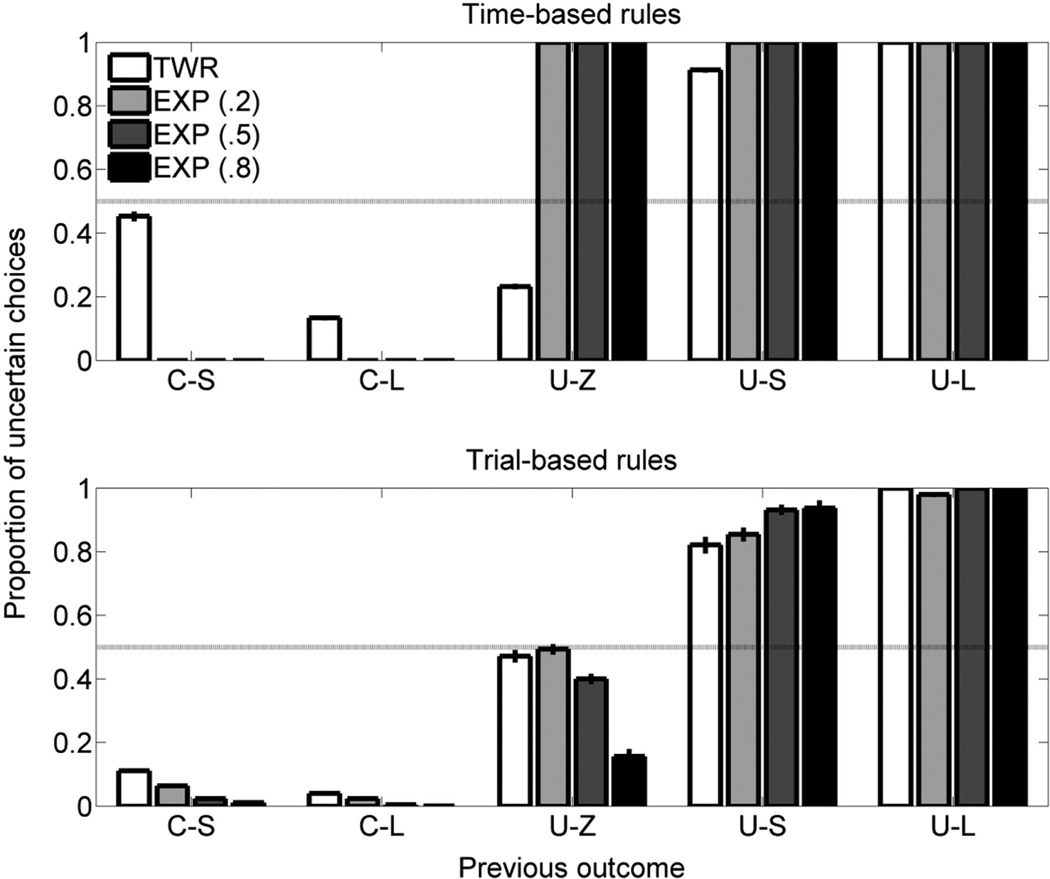
Figure 9 shows the simulated postoutcome choice data in the dynamic probability training phase. The simulations using time-based rules are shown in the top panel and the simulations using trial-based rules are shown in the bottom panel. Again, the time-based EXP models produced very different behavior than the other models did (i.e., staying on the same side regardless of the previous outcome). However, following C-S and C-L outcomes, all of the other models showed a tendency to make another certain choice, comparable with the rats’ behavior above (see Figure 5), and following U-S and U-L outcomes, the models were likely to stay on the respective side and make another uncertain choice. Furthermore, all of the trial-based models showed a stronger tendency to make an uncertain choice following U-Z outcomes than following both C-S and C-L outcomes, similar to the rats’ behavior (see Figure 5). Finally, both of the TWR models and the trial-based EXP models were more likely to make an uncertain choice following C-S than following C-L outcomes, similar to the rats’ data (see Figure 5), although this effect was somewhat overinflated in the time-based TWR model.

Figure 9.

Mean (± SEM) proportion of choices for the uncertain side in the simulated dynamic probability-of-food phase as a function of the most recent outcome and the probability of uncertain food. The simulations using a time-based rule are in the top panel; those using a trial-based rule are in the bottom panel. The α parameter for the exponential (EXP) valuation rules is indicated in parentheses. C-L = certain-large; C-S = certain-small; TWR = temporal weighting rule; U-L = uncertain-large; U-S = uncertain-small; U-Z = uncertain-zero.

Discussion

Despite the extensive literature on choice procedures involving differently valued options (e.g., Battalio et al., 1985; Rachlin, Logue, Gibbon, & Frankel, 1986; Rachlin et al., 1991), computational mechanisms of value (e.g., Devenport et al., 1997; Glimcher, 2011; March, 1996), and regions of the brain associated with the processing of value (e.g., Peters & Büchel, 2010), it seems that no consensus has been reached concerning the method by which value is ultimately determined. Simulations of two simple valuation models have provided several clues concerning the features of the mechanisms that compute value in the context of a sequential choice environment. Analyses of the simulations supported the time-based and trial-based models as well as TWR and EXP valuation rules in different contexts (Figures 6 through 9). Each of the models and the support (or lack of) for these models will be considered in turn. It is important to consider that only existing models of sequential choice behavior were tested here, rather than attempting to create a new model of sequential choice. In order to reconcile such discrepancies in the possibilities for valuation mechanisms (e.g., Devenport et al., 1997; Glimcher, 2011; Lau & Glimcher, 2005), the critical initial step in model development is to fully comprehend the extant models of choice behavior. Accordingly, two computationally simple established models were tested here to provide a potential basis for future theoretical accounts of sequential choice.

As described, the weight of a previous outcome on the value of a choice has been suggested to decay either exponentially (see Glimcher, 2011) or hyperbolically (e.g., Devenport et al., 1997) as the outcome recedes farther into the past. Previous experiences that decay exponentially have been encompassed in general theories of learning (Bush & Mosteller, 1951), theories of association formation in classical conditioning (Rescorla & Wagner, 1972), and timing theories (Guilhardi, Yi, & Church, 2007; Kirkpatrick, 2002). Furthermore, Bayer and Glimcher (2005) showed that the activity of midbrain dopamine neurons was related to an exponentially decaying average of previous rewards. Given such long-standing support for exponentially decaying functions, it would seem reasonable to assume that value is computed in a similar way. In fact, some of the EXP-based simulations did show behavior similar to that exhibited by the rats (Figures 6 through 9). However, the TWR-based simulations also showed some behavior similar to that of the rats’ (Figures 6 through 9). Previous research has indeed supported hyperbolic decay rates (Devenport et al., 1997; Rachlin, 1990; Vasconcelos, Monteiro, Aw, & Kacelnik, 2010). Vasconcelos et al. (2010) described how the weight assigned to forced-choice-trial-initiation latencies, which has been suggested to predict subsequent choices (Shapiro, Siller, & Kacelnik, 2008), decays hyperbolically as these latencies recede farther into the past. Furthermore, temporal discounting, which is the reduction in a reward’s value as the time until that reward’s reception increases, has been proposed to take a hyperbolic form similar to the TWR valuation rule. This decay in value as a function of time has been shown to be better fit by a hyperbolic, rather than an exponential, function (e.g., Myerson & Green, 1995). Therefore, strict comparisons purely based on the form of the decay of previous outcomes’ weights may not be feasible. Accordingly, the unit of decay (i.e., time-based or trial-based) is considered next.

Traditionally, exponential models have employed a trial-based rule, such that value is updated with each outcome (i.e., trial) received following a choice (Glimcher, 2011). As the name implies, the TWR has employed a time-based rule, such that value is continuously updated as a function of time since receiving each outcome (e.g., Devenport et al., 1997). However, both the EXP and TWR models were employed in a trial-based and time-based format to determine whether the strength (or lack of) of these models was due to the unit of the decay function rather than the form of the decay function. Evaluating both rules without considering any interaction with the valuation computation (EXP or TWR), it is apparent that both time- and trial-based models are capable of producing behavior similar to that of the rats (Figures 1 through 5 vs. Figures 6 through 9); the time- and trial-based rules exhibited sensitivity to the probability of uncertain food delivery and differences in choice behavior following different outcomes. Therefore, given the performances of the TWR and EXP models, as well as those of the time- and trial-based models, it is apparent that superiority of one model over another cannot be determined along a single dimension. Thus, it is necessary to examine the models beyond their established settings (i.e., time-based TWR and trial-based EXP). Whether the TWR or EXP models are time- or trial-based may be critical to how these models perform under the present conditions.

In examining the overall pattern of the simulation results, it is clear that the form of decay (exponential vs. hyperbolic) and the unit of decay (trials or time) interacted. For the static probability training phase, the time- and trial-based TWR models and the trial-based EXP (.2) model exhibited sensitivity to the probability of uncertain food delivery similar to that shown by the rats (see Figure 1). Following each outcome in the static probability phase, the time- and trial-based TWR and the trial-based EXP models showed sensitivity to the probability of uncertain food delivery as the rats did (see Figure 2); however, these models showed more choices for the uncertain outcome following C-S than following C-L outcomes, unlike the rats’ behavior in the static probability phase (see Figure 2). For the dynamic probability training phase, the time- and trial-based TWR models and trial-based EXP models, especially EXP (.5), produced choice behavior similar to the rats (Figures 4 and 5). Across such analyses of the two phases, it was clear that the time-based EXP models showed many severe and systematic discrepancies from the rats’ data, suggesting that the rats’ valuation mechanism is not characterized by such a mechanism under any of the circumstances tested here.

An additional analysis of the time-based EXP models’ data was conducted to determine the source of these discrepancies. A correlational analysis revealed that the time-based EXP models’ behaviors were significantly influenced by the last forced-choice trial (certain [0] or uncertain [1]) experienced prior to the series of free-choice trials in both the static probability, rs > .96, ps < .001, and the dynamic probability phases, rs > .99, ps < .001. In other words, if the last forced-choice trial was a certain or uncertain forced-choice trial, then the time-based EXP models chose the certain and uncertain outcome, respectively, throughout the entire session. Such exclusive choice behavior is unlike the behavior shown by the rats in the present experiment and by animals in previous experiments (e.g., Battalio et al., 1985; Shapiro et al., 2008). Neither the time-based TWR model nor any of the trial-based models exhibited such dependence on the final forced-choice trial in the static probability, −.07 < rs < .03, ps > .15, or dynamic probability phases, −.08 < rs < .11, ps > .27. The rats’ choice behavior was also not influenced by the last forced-choice trial in the static probability, r = .024, p = .597, or dynamic probability phases, r = .011, p = .908. This analysis lends further support to the notion that the rats’ valuation processing system is not characterized by a mechanism in which the weights of previous outcomes decay exponentially as a function of time. To confirm whether the time-based EXP model results were due to the nature of the model or possibly the assigned parameter values, a set of simulations (not included here) was performed in which the decay-rate parameter values were .001, .00001, and .0000001, such that the most recent outcome would have minimal weight on the value of a choice and the weights of previous outcomes would decay less quickly. The time-based EXP model that exhibited choice behavior most similar to that of the rats was the simulation with the .0000001 decay rate, a parameter value that is substantially smaller than the typical rate parameters assumed in the exponential learning or valuation models (see Bayer & Glimcher, 2005; Greggers & Menzel, 1993; Montague, Dayan, Person, & Sejnowski, 1995; Rescorla & Wagner, 1972). Therefore, the TWR models as well as the trial-based EXP models with rate parameters in a more suitable range seem to be more viable candidates for a valuation mechanism under the present conditions.

Although the time-based EXP models displayed the largest differences in choice behavior compared with that of the rats, the other three models (time-based TWR, trial-based TWR, and trial-based EXP) are not without differences, which may very well guide our understanding of the basis of the rats’ valuation mechanisms. As described here, the trial-based TWR and EXP (.2) models chose the uncertain outcome less than the time-based TWR model did at probabilities of uncertain food .1 and .33, and more than the time-based TWR model did at probabilities of uncertain food .67 and .9 (Figures 6 and 8). Thus, the trial-based models may be more equipped to account for more extreme choice behavior, which is shown in the rat data in Figure 4. As the most recent outcome occurred only a single trial ago in the trial-based models, but 30 s ago in the time-based models, the most recent outcomes are given more weight in the trial-based models. In the time-based models, the weights of the most recent outcomes are more similar to each other than they are in the trial-based models, which is comparable with the similarities in weights of past outcomes that occurred many trials ago in EXP models. Given the more extreme choice behavior shown by the rats at the anchor probabilities (e.g., Figure 4), it is likely that recent outcomes are influencing the value of a choice more than what would be assumed in the time-based TWR rule.

It is also worth noting the differences in behavior exhibited by the trial-based EXP functions due to different decay-rate parameter values (Figures 6 through 9) compared with the trial-based TWR model. As there are no free parameters in the TWR model, the free parameter in the EXP models may serve to reflect individual differences in choice behavior, assuming that individuals weight previous outcomes differently. The TWR does not permit this in its current form, but a free parameter could presumably be added to a hyperbolic model to allow for fitting of a broader range of data. In a set of simulations not shown here, the denominators of the fractions in both the numerator and denominator of Equation 1 were changed to 1+k(T_N,i) to mimic previously proposed hyperbolic discounting equations (Mazur, 1987). The parameter k, which reflects the rate of discounting, was given values .2, .5, and .8 (i.e., the parameters used above for the EXP models). There were no considerable differences between the behaviors produced by each of these parametric TWR models. Therefore, the current form of the TWR may be unable to accurately account for individual differences in choice behavior, suggesting that such individual differences may be best accounted for by the trial-based EXP model, which is parametric by default.

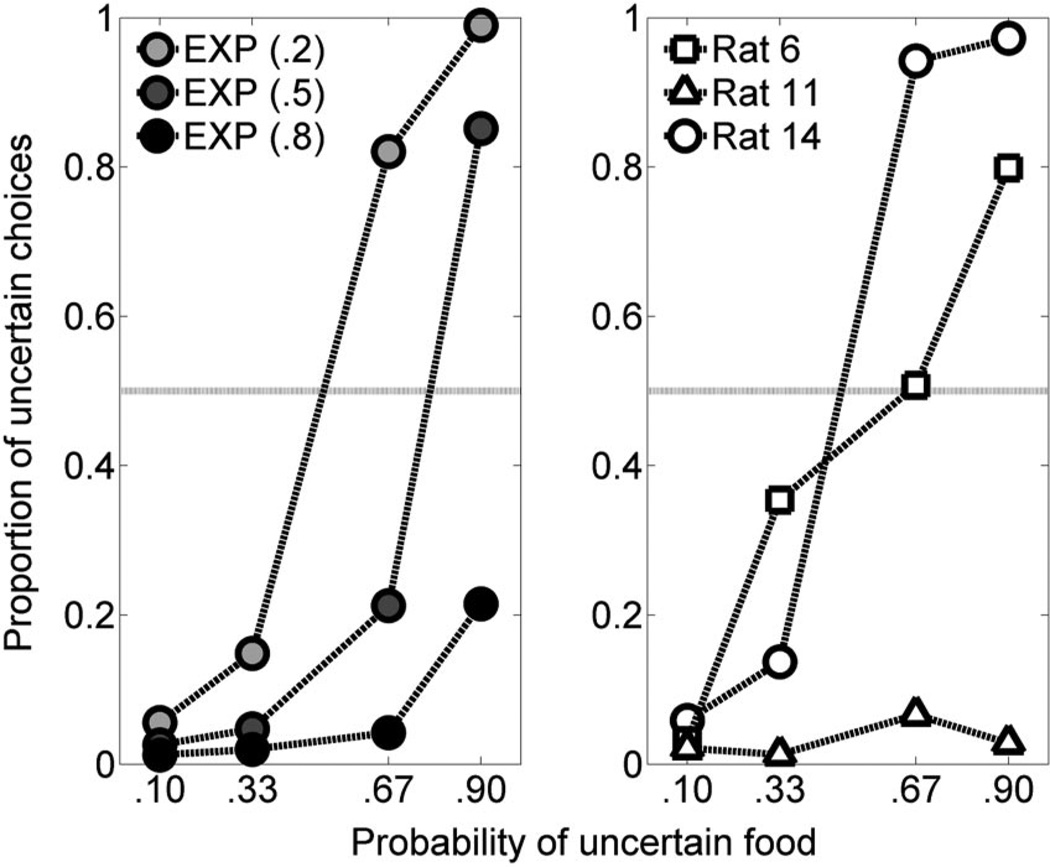
Variations in α have been suggested to reflect variations in risk-seeking behavior (March, 1996), one characteristic of behavior that is likely to differ among individuals. Figure 10 shows simulated data by the trial-based EXP rules in the left panel (taken from the top right panel of Figure 6); in the right panel are data from three individual rats from the present experiment. A striking aspect of the choice data from individual rats is the large variation in sensitivity to the probability of uncertain food, a factor that could be accounted for by different values of the α parameter. Therefore, the trial-based EXP models ultimately appear to be best equipped to account for choice behavior under the present conditions in their current form, which is reasonable to assume given the features of the experimental environment. This model provides a reasonably accurate account of the mean choice data across rats as well as supplying a mechanism for modeling individual differences in choice behavior.

Figure 10.

Mean (± SEM) proportion of choices for the uncertain side as a function of the probability of uncertain food in the simulated static probability-of-food phase for the trial-based EXP models with a categorical decision rule (left panel) and three rats’ individual data from the current experiment (right panel). The α parameter for the exponential (EXP) valuation rules is indicated in parentheses.

One noteworthy factor that may have skewed the present results toward the trial-based EXP model is the nature of the choice environment. The environment was relatively stable under some conditions (static probability training), depended on the outcome of the previous trial under other conditions (dynamic probability training), and was set to have constant FI and ITI durations (i.e., a relatively consistent duration of time between choices and outcome delivery). Devenport and Devenport (1994) did indeed suggest that the TWR as a valuation mechanism may be suboptimal in situations in which “regularity” exists; as described, several features of the environment may be described as “regular.” Therefore, although the time since an outcome has been previously suggested to contribute to computations of value and future choices (e.g., Devenport et al., 1997; Devenport & Devenport, 1994; Mazur, 1996), it may not have been as critical to the animal’s choice as the trial in which the outcome occurred. This suggests that a time-based valuation rule may play a role in more changeable environments, especially if time is a relevant feature of the change in the environment. Further research will be required to determine the conditions that may promote the reliance on trial-versus time-based information. It does, however, appear that the present conditions were more amenable to the use of a trial-based EXP valuation rule.

General Discussion

Previous research has described several factors that govern choice behavior. One factor that has been relatively less studied is the effect of the previous outcome on subsequent choice behavior. The present experiment showed that both the previous outcome and probability of food delivery affect the subsequent choice. The uncertainty of an outcome is prevalent in several contexts that individuals frequently experience. Due to the variability of the outcomes, and thus an implied uncertainty in the outcomes of both choices in the present procedure, the “uncertain” outcome was the outcome in which no reward was possible following such a choice. Behaviors such as foraging, gambling, investing, and buying and selling stocks all involve situations in which the outcome of a choice may not be followed by a positive reward. Given that positive outcomes are critical for quality of life and survival, it is important to consider the effects of outcomes within contexts in which choices may go unrewarded (see Dixon et al., 1998).

The data from the static probability training condition suggest that individuals were likely to gamble again following a successful gamble (i.e., delivery of three or nine pellets following an uncertain choice), regardless of the expected value of the gamble (i.e., the uncertain outcome; Figure 2). However, following unsuccessful gambles (i.e., U-Z outcomes), the probability of making a subsequent gamble was dependent on the expected value/probability of food for uncertain choices. The modulation by the probability of food delivery on the effect of the previous outcome on the subsequent choice strongly suggests that choice behavior is a function of both global and local factors. The data from the dynamic probability training phase also reflect the impact of the previous outcome on subsequent gambling behavior; the rats were more likely to make a certain choice following a certain reward and an uncertain choice following an uncertain reward. One noteworthy feature of the dynamic phase is that the probability of winning a subsequent gamble increased following successful gambles and decreased following unsuccessful gambles. Therefore, the increased rate of gambling behavior following successes may have been due to either the previous outcome or the increased probability of reward. One way of disentangling such an effect would be to implement a procedure in which the probability of food decreases following a successful gamble and increases following an unsuccessful gamble.

The empirical results were complemented by the evaluation of mathematical models of sequential choice behavior. Under the present set of conditions, the trial-based EXP model appeared to be the superior model, given the similarity between its behavior and that of the rats (Figures 1 through 9), as well as its ability to potentially account for individual differences (see Figure 10). However, a time-based TWR model has fared better when the time since an outcome’s receipt was a critical determinant of a choice’s value (e.g., Devenport et al., 1997); furthermore, although Greggers and Menzel (1993) reported differential decay-rate parameters for gains and losses in an exponential linear-operator equation, they also found a temporal dependence to the choices that the bee made. Therefore, future work should continue to elucidate the computational mechanisms of valuation; upon the future development of a model that can account for sequential choice behavior under several different conditions, differing viewpoints about valuation and decision-making processes may be reconciled (e.g., Devenport et al., 1997; Lau & Glimcher, 2005; Mazur, 1995, 1996).

In conclusion, the present experiment and series of simulations have advanced our understanding of sequential choice behavior.Outcome variability is a defining feature of foraging, gambling, and other risky-choice behaviors that are prevalent in the daily lives of human and nonhuman animals. Future research should further identify the cognitive and neurobiological mechanisms that govern choice behavior as a function of the magnitude of the previous reward and of the probability of that reward in subsequent choices. Greater understanding of the psychological phenomena that define sequential choice behavior should guide the development of computational models that will represent the next generation of the theoretical accounts of choice behavior.