Revisiting the Fundamentals in the Design and Control of Nanoparticulate Colloids in the Frame of Soft Chemistry

Abstract

This review presents thoughts on some of the fundamental features of conceptual models applied in the design of fine particles in the frames of colloid and soft chemistry. A special emphasis is placed on the limitations of these models, an acknowledgment of which is vital in improving their intricacy and effectiveness in predicting the outcomes of the corresponding experimental settings. Thermodynamics of self-assembly phenomena illustrated on the examples of protein assembly and micellization is analyzed in relation to the previously elaborated thesis that each self-assembly in reality presents a co-assembly, since it implies a mutual reorganization of the assembling system and its immediate environment. Parameters used in the design of fine particles by precipitation are discussed while referring to solubility product, various measures of supersaturation levels, induction time, nucleation and crystal growth rates, interfacial energies, and the Ostwald–Lussac law of phases. Again, the main drawbacks and inadequacies of using the aforementioned parameters in tailoring the materials properties in a soft and colloidal chemical setting were particularly emphasized. The basic and practical limitations of zeta-potential analyses, routinely used to stabilize colloidal dispersions and initiate specific interactions between soft chemical entities, were also outlined. The final section of the paper reiterates the unavoidable presence of practical qualitative models in the design and control of nanoparticulate colloids, which is supported by the overwhelming complexity of quantitative relationships that govern the processes of their formation and assembly.

1. INTRODUCTION

With a little bit of imagination, the world of chemistry, as of today, could be visualized as standing at a crossroad. Behind us, the old world marked with the traditional reliance on ionic and covalent bonds rests, whereby in front of us lie the horizons of unlimited potentials of the new world of chemistry wherein chemists have mastered dealing with weak bonds and interactions that the biological world has taken advantage of in creating the fascinating phenomenon called life [1, 2]. “We are at a wonderful time for chemistry. It is, I believe, in the position of physics in the 1910s, just before quantum mechanics made the world impossibly strange, or biology in the 1950s, just before the double helix obliterated the old biology” [3], George M. Whitesides uttered, while having exactly the ideals of soft chemistry in mind.

Soft chemistry as a concept can be seen as opposing the robust and manipulative molecular machining approach to design of fine structures with its flexibility, softness, elegance and, implicitly, a respect of Nature, as we shall realize close to the end of this summery review [4]. Hierarchical self-assembly defined as programmed non-covalent organization of individual building blocks over distinct multiple levels calls for sophisticated fundamental models in their design [5]. Understanding multiple subjects is a must for grasping the essence of soft chemistry, and some of those discoursed about in this work will be colloids, chemistry of precipitation, nanostructured materials, proteins and self-assembly. This review will, however, be mostly focused on covering the elementary physicochemical aspects of formation of finely dispersed matter. The materials that this work will refer to more than any others will by hydroxyapatite (HAP) and proteins in general. The former is the mineral constituent of our very selves and certainly one of the most complex materials in the Universe [6]. Since it is ingrained in us and is extensively exploited in the very biological realm more than any other material it secured a special place in this review. As for proteins, they can be considered as lying at the very boundary between the biological and inanimate entities, and as such present the prototypes of complex systems that rely on weak chemical interactions as they undergo self-assembly and other soft chemical transformations [7].

The core of the author’s work in philosophy of science has been done in support of the so-called co-creational thesis [8], which, to put it simply, claims that all physical or cognitive qualities are always the product of creation of two sides. From the epistemological viewpoint, e.g., the entire experience could be seen as an intersection of biological predispositions and the physical structure of the cognitive subject on one side and the reality as-it-is on the other. The idea that the evolution of physicochemical systems, such as during structural transformations, is determined by both the structure of the system in question and its environment presents a natural consequence of this concept of co-creation. Also, by substituting the ideal of perfect control of chemical systems by leaving some room for their spontaneous transformations, as is intrinsic to self-assembly processes, the evolutionary trajectories outlined by Nature and those outlined by the scientist are let intersect and produce exciting outcomes. Some parts of this work will more than others appear as if revolving around this fundamental thesis, which provides a chemical point of view in favor of the much broader aforementioned co-creational thesis.

Finally, as each successful chemical endeavor should be flavored with intuitive and aesthetic insights that pertain more to the artistic rather than to the rational and analytical in us [9–11], the final section of this work will take us to a seashore where we will play with a pebble and realize the immense aesthetic potential of science as well as the crucial importance of these artistic insights in driving the wheels of scientific explorations. In such a way, we will touch the great complementariness between chemistry and alchemy in the world of soft chemistry, which will be the final touch of this discourse.

2. THERMODYNAMICS OF SELF-ASSEMBLY PHENOMENA

Colloid systems, which have been tackled by the author in numerous previous discourses [12, 13], are those in which one or more phases are dispersed in a continuous phase of different composition or state. Colloids, in particular sols, gels and latexes, share numerous features with other soft, self-assembled chemical systems. For example, in contrast with ordinary solutions, both of these systems are thermodynamically unstable and only due to the existence of large interfacial energies that are higher than thermal energy, kT, is their order preserved.

Earlier, I have proposed the thesis that self-assembly as a term is a misnomer. This insight was supported by arguments in favor of every self-assembly being, strictly speaking, a co-assembly since it should imply a mutual ordering of the assembling system and its immediate environment. Thermodynamics per se demonstrates that the properties of every physical system depend on the context of its interaction with the environment besides its intrinsic properties. For example, the overall heat content of the system, which is represented as enthalpy (H), is composed of 2 terms: one corresponding to the internal energy of the system (U) and the other in which the system’s pressure (P) and volume (V) contribute.

$$H=U+PV.$$

Hence, to define the heat content of the system, one has to look at the inner properties of the system as well as at the context of its relationship with the environment. By compressing or expanding a system, an effect on its pressure and/or volume is exerted, which affects its enthalpy. Chemical bonds themselves, as contributing to the internal energy of the system, also tend be modified in strength, that is, the bond energy, depending on their close surrounding even under non-extreme conditions. This is, ultimately, the effect of electron “clouds” of atomic and molecular species being non-localized and sensitive to physicochemical forces dominant in their physical surrounding. On a similar note, interface chemistry can remind us that solid particles suspended in a liquid medium carry a “cloud” of charged species glued to them, which affects not only their hydrodynamic diameters, but also the resulting surface charge, an important determinant of the inter-particle forces and the stability of the given sols. That properties of nanoparticles applied as intracellular carriers of plasmids and drugs are determined not only by their size, shape and elasticity, but also by the properties of biochemical species bound on their surface, deriving from either cell culture media, blood plasma or the cytoplasm, has also been recently confirmed [14]. The fact that modifications of the mechanical properties of the surfaces onto which the cells adhere lead to changes in the mechanical features of the cytoskeleton, so that stronger materials induce stronger cells, also suggests inescapable mutuality between the biological systems and their environment [15]. In addition, internal energy of a crystalline body, which equals the sum of its bond energies, depends on the temperature owing to the effect of thermal expansion, which is, on the other hand, a consequence of the anharmonic vibration modes of units of the crystal lattice. Consequently, depending on where we place the boundary between the system and its environment, we may need to account for various environmental effects on the internal energy of the system. Ultimately, the experimentalist manipulating the given chemical system belongs to this environment and referring to the laws of thermodynamics may be on one hand essential in improving his ability to manipulate these systems and produce more efficient and designable outcomes than what is attainable today. On the other hand, the co-assembling nature of one such chemical treatment demands that the system itself exerts an influence on the experimentalist, implying his/her own cognitive and physical change during this process.

Thermodynamic quantities can be, just like about anything else, measured only through their change, which explains why one always uses infinitesimal changes of these quantities in describing them. In equilibrium, internal energy is never constant, but always fluctuates with some energy added to the system (dQ) and some work done on the surrounding (dW). Hence, the following applies:

$$dU=dQ-dW=dQ-pdVdH=dU+pdV+vdP=dQ+VdP=TdS+VdP.$$

Enthalpy can be represented as composed of free energy and entropy (H = G + TS and dH = dG + TdS for constant temperature). The Gibbs free energy, G, is equal to chemical potential (μ) per unit of change in composition (∂μ_i = ∂G/∂N)_{p, v, Ni ≠ Nj}, and is also the energy of the system that can be converted to work at constant temperature and pressure, whereby Helmholtz free energy, H, is that which can be converted to work at constant temperature and volume. Hence, G stands for the free energy for non-volume work, and it is in the nature of physical systems to tend to achieve a minimum of free energy. As both free energies are related to H and S, the energetic favorableness of a thermodynamic process, which in the absence of kinetic factors determines how spontaneously it will proceed, is defined by the relation between dH and dS for the given process; thus, even endothermic processes can be spontaneous if the corresponding increasing in G is offset by increased S of the system, or, as is the case with most crystallization reactions, a lower S that entails the process is often coupled to an exothermic reaction (dH < 0) which leads to lower G. Be that as it may, from the definitions of G and H, we can conclude that both forms of free energy can be defined only in relation of the system with its environment. Just as the kinetic energy of an electron in its flight through a medium can be described only as proportional to its relative velocity with respect to the given environment and just as an activity of protons can be defined only with respect to the rheological, dielectric and finer molecular properties of the solvent, the same environment-dependent character can be ascribed to all thermodynamic properties of a system and all measurable physical qualities too.

In contrast to free energy, entropy (S) is energy that is irreversibly transferred to the system, and thus can only be dissipated. As dS = dQ/T, heat transferred to a system at low temperature will contribute to a larger increase in entropy than the heat transferred at high temperature. Statistical definition of S, however, tells us that it is the measure of disorder within the system. As such, S = klnw, where k is the Boltzmann constant and w is the number of ways by which the system can adopt certain energetic state. Entropy is thus directly proportional to the freedom of movement. There is only one way to adopt the ground state, the state of the lowest entropy. In order to leave enough room for the system to explore all the possible states and correspondingly evolve by assembling into more intricate states than originally adopted, the level of entropy has to be optimal. Apparently, it has to have a higher value than in the ground state, which is the most stable one and also the one in which the system is essentially locked and unable to internally change or evolve. However, if the number of possible states is too high, the system may be overwhelmed by their number, which decreases the probability that it will settle down in a range of those that promote its evolution in the direction of decreasing entropy.

This all shows us that the concept of entropy lying at the heart of thermodynamics ultimately pertains to the interplay between order and freedom [16]. In order for a system to properly evolve, a balance between order and well-imposed boundaries on one side and freedom to transform between different states on another has to be optimized and finely tuned. This observation is relevant to self-assembly processes in soft chemical settings too. Namely, in order to enable the spontaneous transitions among multiple metastable states that typify the system in question, the system has to be brought close to a range of states of optimal entropy and relatively far from equilibrium which would correspond to the state of the lowest entropy for the given conditions.

Referring to thermodynamically stable states is correct only insofar as one means that the system is in a state of equilibrium corresponding to a local minimum of a thermodynamic potential chosen for the specified constraints on the system, since thermodynamic stability cannot be defined in an absolute sense. This explains why some colloid systems, such as microemulsions, are oftentimes called thermodynamically stable [17], although colloid systems in general are by definition thermodynamically unstable since it only depends on how slow the phase segregation process which leads to a greater thermodynamic equilibrium is. Sometimes this phase segregation proceeds on the geological time scale and sometimes it is in the order of milliseconds as in the case of rapid precipitation. Attaching the attribute of stability to a colloidal system is thus merely another way of saying that its particles do not aggregate at a significant rate. Hence, a soft chemical system has to be in a far-from-equilibrium, metastable state in order to undergo self-assembly, and as the rules of thermodynamics dictate and as the living systems serve as an evidence of, such a transition is preconditioned by the relative openness of the system to its environment.

3. THE SELF-ASSEMBLY EXAMPLE OF PROTEINS

Proteins that are naturally prone to exhibit incessant conformational fluctuations among a wide range of metastable states, known as “protein breathing”, preconditioning a single protein molecule, strictly speaking, never to exist in the same conformation twice, may serve as an illustration of this flexible nature essential for their bio-functional engagement in self-assembly and molecular recognition interactions. Unlike DNA which is known for its exceptional stability (it remains intact in centuries old fossils and requires bringing its solution almost to boiling point to merely separate its two strands, as during a PCR analysis), proteins are only marginally stable under physiological conditions since the free energy required to denature them is only about 0.4 kJ/mol per amino acid residue (for comparison, a typical hydrogen bond has the energy of circa 20 kJ/mol). Since various non-covalent influences that define the native conformation of the protein combined reach thousands of kJ per mole over the entire protein molecule, a protein structure may be said to be a result of a delicate balance among powerful countervailing forces [18].

Now, the main effect involved in defining the native conformation of the protein is the hydrophobic effect, which tends to position hydrophobic residues in the interior of the molecule and hydrophilic ones on the surface, in contact with water. Hence, one can immediately conclude that the medium in which the protein is dissolved or suspended directly defines the conformation of the protein. Water as a polar solvent and oil as a non-polar one would tend to induce thoroughly different residues and side chains to be exposed on the surface of the molecule. Aside from the fact that changes in the pH of the medium modify the hydrophilicity of titratable residues by affecting their dissociation, shifts in pH of the aqueous environment away from the neutral range also lead to more pronounced hydrophobicity of hydrophobic residues and hydrophilicity of hydrophilic ones, resulting in stretched hydrophobicity plots of protein primary structures following one such shift. That context, in terms of the environmental settings, defines the qualities of the system thus becomes evident. Converting insights obtained from the assembly of polypeptides in dilute and strongly polar aqueous environments to in vivo settings which are typically dominated by more dense and occasionally even more hydrophobic milieu is thus doubtful in its correctness. One example comes from the assembly of amelogenin, the main protein of the developing enamel matrix, into nanosized spherical aggregates due to their comparatively high hydrophobicity [19], and the immediate application of these insights in speculated mechanisms of the interaction of amelogenin and HAP during which elongated HAP crystals of enamel are formed [20–22]. Since the enamel matrix is a dense environment composed of multiple polypeptide species, many of which are different amelogenins and their proteolytic fragments, the chances for their existence in form of nanospheres can be seriously questioned, especially since it is known that in dense and less polar environments amelogenin can assemble into ribbon- and rod-shaped morphologies [23].

The other effect involved in stabilizing the protein structure and defining its conformation are electrostatic forces, including van der Waals forces between electric dipoles. The association of two ionic protein groups of opposite charge is known as an ion pair or salt bridge, and these form mainly on the protein surface. However, unlike van der Waals forces which exert an important stabilizing influence, this cannot be said for those between charged residues. This is explained by the fact that the free energy of an ion pair interaction usually fails to compensate for the loss of entropy of the side chains and the loss of solvation free energy following the formation of one such pair. In any case, as the medium mediates these electrostatic interactions via its relative permittivity, it can also be said that it exerts a decisive influence on this aspect of the assembly of polypeptide chains too. Changes in the dipole moments of the molecular constituents, affecting the vibration modes of the molecules can be thereby detected following modifications of the medium in which these species are dispersed. Molecular and nuclear spectroscopies offer numerous examples of how the physical context is able to change the qualities of the investigated atomic and molecular species [24–26]. These electrostatic interactions take place between dissociated acid/base pairs of the titratable side chains of amino acid residues, including the carboxyl and amino groups at the C- and N-terminals, respectively. The extent of this dissociation that preconditions the formation of salt bridges and thus the proper assembly of the protein largely depends on the pH and the ionic content of the aqueous medium in which the protein is dissolved or dispersed. Additionally, values for the dissociation constants of the titratable side chains in the protein structure were empirically determined for individual amino acids alone and not as parts of a peptide chain, let alone folded into specific 3D confirmation where they may be forming weak bonds with other residues. Just as increasing the length of an aliphatic chain decreases the frequency of C–C vibrations, a similar synergetic effect occurs herein as well. Amine groups in a chain would not possess the same pKa values as in isolation; surrounding cationic amine groups will, for example, electrostatically suppress the protonation of the neighboring amines [27]. Increasing the length of a polyamine chain will thus decrease the protonated fraction of its amine group constituents. pKvalues of given acid-base pairs of titratable side chains of amino acid residues can vary by as much as several pH units depending on the microenvironment. For example, Asp residue in nonpolar environment or in close proximity to another Asp would attract protons more strongly than otherwise and hence have a higher pK [18]. pKa values of amino acids also change depending on the ionic strength of the solution. pI values of proteins vary from one type to the other and are intrinsically determined by the content of the titratable residues and extrinsically by the adsorption of ionic species and the effect of the diffuse double layer of charges. Finally, binding of ionic species is sufficient to markedly modify the structure of the entire protein. Fluorescence measurements relying on the intrinsic fluorescent activity of three aromatic residues in proteins–tryptophan, tyrosine and phenylalanine—are based on the shifts in fluorescence peaks depending on whether the fluorescent groups are exposed on the surface of buried in the interior of the protein. However, binding of a single element on any segment of the protein structure is known to affect its overall conformation thoroughly so that a shift in this fluorescent peak, even though it may come from a single residue distant from the binding site, can be resolved [28].

The thermodynamic point of view suggests that hydrogen bonds, which are the central features of protein structures, make only minor contribution to protein stability since hydrogen bonding groups in a folded protein are assumed to form energetically equivalent bonds with water molecules as in unfolded state. On the other hand, hydrogen bonding is the main force behind the hydrophobic effect, and water molecules tightly bound in the interior of the protein or serving as bridges to hydrogen bonds between adjacent side chains are an important factor in ensuring the stability of the protein. Numerous cases wherein settling into a proper conformation has been dependent on the optimal water content have been documented in literature, and proteins, once drawn against a black background, are now increasingly depicted together with their water contents at the molecular scale [29]. Even in the case of fibrous proteins, such as collagen, in which backbone hydrogen bonding between polypeptide chains in its triple-stranded structure does not present the major stabilizing force, as opposed to the case of α-helices and β-sheets, additional enthalpic contributions come from water molecules that form a “scaffold” around the surface of the collagen triple helix, implying that water nonetheless serves an intimate role in stabilizing this protein [7]. Mechanical testing of individual collagen fibers has thus demonstrated a 10-fold drop in the tensile strength following dehydration of the fibers [30, 31]. Diminished mechanical performance of collagen-comprising hard tissues has been verified for biological samples too [32–34]. The entropic contribution of trapping or release of water can be the determinant of the free energy change for crystallization, and an example comes from human hemoglobin C, which has a comparatively large positive enthalpy of crystallization of 160 kJ/mol, signifying the energetically unfavorable nature of this process [35]. However, since the entropic contribution to free energy of crystallization due to release of about 10 water molecules is—180 kJ/mol, the net gain of free energy turns out to be—20 kJ mol, making the overall process favorable in the end [36]. Such a sensitivity of protein stability to the water content and the crucial role of water in preserving the native conformation of the proteins explain why slow thawing of the frozen protein solutions is important in preserving their native conformation, as well as why proteins on average live up to five cycles of freezing/thawing.

In addition, collisions of solvent molecules with residues exposed on the surface of the protein are known to result in continuous “breathing” of the protein conformation in space. In the absence of the surrounding molecules of solvent, this thermal movement would be drastically lessened, and in certain cases it would disable the protein from adopting the biologically active range of “flow” of its tertiary structure. Such a situation may occur with enzymes and antibodies, which need to be able to exhibit a wide range of conformational movements in order to be prone to recognize and properly react with the given substrates and antigens, and are therefore particularly sensitive to the effect of collisions with solvent molecules. Owing to their ridged energy landscapes rather than ones composed of well defined energy levels and a single stable energy minimum, a single protein molecule, strictly speaking, never exists in the same conformation twice during its existence [7]. In fact, owing to the tightly coupled dynamics of a protein and a solvent, they are often conceived as a single entity with a unique energy landscape [37]. Proteins are thus often seen as engaged in continuous feedback interaction during which they influence their solvation environment, but are in turn “finely tuned” and modified by the latter [29]. As the structure of protein molecules can be no longer thought of as being static in space, but rather dynamic and constantly changing, the image of unchangeable stick-and-ball models of these molecules could be substituted with the one depicting their incessant structural dancing in togetherness with their immediate physical surrounding. Such conformational dancing, during which the integrity of their structural elements is still maintained, is essential for the preservation of their biological activity.

4. MICELLIZATION AS A SIMPLEST SELF-ASSEMBLY PROCESS

To design structure and properties of a material, one has to precisely set the boundary conditions under which the reactions of their formation will proceed. And yet, these limiting conditions per se will be subject to change during the process. A recent near-edge X-ray absorption fine structure (NEXAFS) spectroscopic study, for example, indicated a shift from a well-oriented structure of the soft film before the deposition of gold onto it to a disoriented structure during the assembly process of gold nanoparticles [38]. During biomineralization, proteins bind onto growing crystals, directing their growth, and yet they typically undergo changes in their tertiary and secondary structures following the binding [39,40], suggesting that biomolecules and organic matrices act as templates for the crystal growth, whereas the latter also serves as a template for structural rearrangement of the former molecules and assembly of their aggregates. This has also been supported by studies on reverse micelles [17] where it was noticed that these molecular aggregates do not act as passive templates for the formation of nanocrystals within their cores [41], but undergo mutual transformations with the nucleating phase [42]. They also play an active role in catalyzing the transformations between intermediaries which may have crucial effect on the final products of precipitation reactions and other phase transitions that take place in their presence [43, 44]. The thermodynamics of the co-assembling nature of the transition from a solution to a suspension can be illustrated on the example of formation of micelles, one of the simplest imaginable self-assembly processes in Nature.

First of all, the rules of thermodynamics can be used to predict molecular behavior during a specific process. For example, during a gas adsorption, a layer of molecules with a lesser number of degrees of freedom compared to the gaseous state forms on a surface, implying a local decrease in entropy. Since adsorption proceeds spontaneously, that is, with a decrease in free energy, dG, by knowing that dG = dH – TdS, one can conclude that dH < 0 and that adsorption is an exothermic process. The extent of gas adsorption will, thus, increase with an increase in temperature [45]. As for the micellization, dissolution of a hydrophobic molecule in water has similarly been shown to lead to decreased entropy because of the formation of rigid “cages” of water molecules around the hydrophobic groups, resulting in limited freedom of movement of both. Since non-polar groups can neither accept nor donate hydrogen bonds, this leads to disruption of the H-bonding network of liquid water. Since the number of possible ways in which water molecules can form this network is lesser around the surface of a non-polar group than in bulk water, to recover their lost hydrogen bonding energy, water molecules reorient themselves to form a more rigid hydrogen bonded network. This unfavorable free energy of hydration of non-polar substances has the net result that a hydrophobic substance tends to be excluded from water [18].

It is interesting that formation of micelles of an amphiphilic compound is followed not by an increased order, as one may have intuitively inferred, but with an increase in the entropy of the system, which is the major contributor to dG < 0 that follows this self-assembly process. As already stated, below the critical micelle concentration (CMC), water molecules surrounding the hydrophobic tails of surfactant molecules become more structured compared to the bulk water. With the formation of micelles, the bulk structure of water is mostly restored and the entropy of the water correspondingly increases. The same, seemingly counterintuitive effect of increased entropy, explainable by referring to diminished hydration of reactive species, is observable upon binding of biological macromolecules to each other, be it enzymes and substrates or transcription factors and nucleic acids [46]. Furthermore, the freedom of movements of hydrocarbon tails occupying the hydrophobic core of a micelle increases compared to their solvated state. Although the head-groups do not affect the entropy of micellization because they are surrounded by water molecules at all stages of the process, electrostatic, van der Waals and steric interactions between the head-groups within the same micelle will determine its size and shape. Also, the micelle components are subject to incessant thermal motion of Brownian nature, which inherently opposes the second law of thermodynamic on the small time scale at which it appears. These factors combined imply that in a regular micelle, e.g., a portion of the hydrocarbon tails is exposed to water because a close-packed arrangement of polar head groups cannot be achieved. Micelles also incessantly exchange molecules with the bulk phase and fluctuate in size and concentration of cargo molecules. These processes are particularly intensive at and around the CMC [47]. Consequently, micelles in reality do not look as perfectly spherical and symmetrical as when they are schematized, and the simulations of their structure have confirmed this (Fig. 1) [48].

Fig. 1.

Reverse micelles drawn (a) and as outcomes of simulations (b) look different. Unlike in the idealized drawing, the surfactant head groups do not completely shield aqueous interior of the modelled reverse micelle. Blue spheres represent the surfactant head-groups, whereby smaller yellow spheres denote counterions. Reprinted with permission from [49, 50].

Intricate ordering of water molecules associated with various types of amphiphilic assemblies in microemulsions has been verified using multiple spectroscopic experimental techniques, ranging from infrared spectroscopy [51] and its ultrafast relaxation [52, 53] and pump-probe and vibrational echo modes [54, 55] to nuclear magnetic resonance [56] to small angle X-ray and neutron scattering [57]. Reverse micelles have been particulary interesting subject of these studies because of their ability to confine nanosized water droplets. All these studies, althogether with molecular dynamics simulations [58], have indicated that water approaching an interface undergoes drastic changes in structure, molecular mobility, hydrogen bonding properties, relaxation processes and the overall solvent characteristics [59, 60]. What all of this indicates is that a mutual ordering of the amphiphilic molecules is followed by the ordering of molecules that comprise the medium in which they are dispersed and on the properties of which their self-assembly crucially depends. The ordering of the assembling system and its immediate environment closely mirrors each other as it proceeds at the same spatial and time scales.

Since micellization can be seen as a thermodynamic phenomenon, it is worth mentioning that temperature has a drastic effect on micelle properties [61]. Thus, for ionic surfactants below a certain temperature, known as the Krafft point, the surfactant comes out of solution and there are no micelles present. In case of non-ionic surfactants, increasing the temperature reduces hydrogen-bonding solvation of the head-groups and initiates phase segregation at the so-called cloud point. Surface tension, conductivity, turbidity and osmotic pressure are all subject to change at following an increase in the concentration of a surfactant and crossing the CMC at which micelles form. All of these qualities could be measured, alone or in parallel, to detect the onset of micellization. What this implies is that during the transition between metastable states that typify a self-assembly process abrupt changes in multiple physical qualities may be detected. These, in turn, could be used to control the very self-assembly processes in question. Such a mutuality of parameters indicative of a self-assembly process and parameters usable in directing it is a natural implication of the co-assembling nature of the former.

5. INTRINSIC PROPENSITIES STILL MATTER

It is, however, still correct to state that intrinsic structural propensities of self-assembling systems predispose them to adopt certain morphologies and structures. Eventually, it is through the conjunction between the intrinsic propensities of the system and the conditions set by the environment that the evolution of any system in Nature proceeds. As far as the soft matter is concerned, this can be illustrated by the example of diblock copolymers oftentimes used for producing mesostructured self-assembling templates [62]. They have been considered as attractive because changes in the length of the two covalently linked chains are reflected in the structures obtainable. For example, if the chains are equal in length, bilayer structures are typically obtained, whereas if one of them is longer than the other, the curvature appears and micelle-like forms result. Lamellae to gyroids to cylinders to spheres thus appear as one cuts the length of one of the chains, as the consequence of the direct dependence of the interfacial curvature of packed block polymer chains and their chain conformation within the assemblies on a simple structural parameter, such as the length ratio [63].

As far as the hard materials are concerned, the example of ceramics can be used to illustrate this point. First of all, with nanoparticles in general, the competition between high interfacial energy and the quantum nature of many physical properties at the small scale produces drastic changes in materials properties following negligible modifications of the particle size, polydispersity inter-particle interaction or morphology. However, with ceramic materials which are inherently more complex at the structural level compared to metals, the situation gets even more complicated. Most of the primary chemical bonds found in ceramic materials are a mixture of ionic and covalent types. In general, electronic configuration, the bond type and dimensions of crystal units determine the type of crystal structure/symmetry. Whereas ionic bonds involve a transfer of bonding electrons from electropositive atoms to electronegative ones, covalent bonds involve orbital sharing of electrons between the constituent atoms or ions. Due to electron sharing, covalent bonds are highly directional in nature (somewhat similar to hydrogen bonds), often dictating the types of crystal structure possible, whereas ionic bonds are non-directional. However, even NaCl, which is referred to as a prototype of an ionic compound, is not perfectly ionic in nature because Na atom has still retained a certain control over the donated, that is, less shared electron. The implication of all this is not only that there is no clear-cut division between covalent and ionic bonds, but that combinations of their different directional characters and packing constraints, including the coordination defined by the size of the elementary crystal units and secondary bonds, calls for great complexity and versatility of potential properties among ceramic materials in general.

Simple changes in stoichiometry and/or the crystalline configuration may thus result in drastic modifications of already pronounced materials properties or arising of new and unexpected ones. Rare-earth doped manganites in which a complex competition between ferromagnetic metallic and antiferromagnetic insulating phases outlines the resulting electrical and magnetic properties may present a neat example at this point [64–67]. Even though double exchange interaction between Mn³⁺ and Mn⁴⁺ ions had been for a long time assumed to solely define the physical properties of perovskite manganites, it eventually became obvious that double-exchange models cannot be sufficient to explain the whole range of behavior of these materials. It is nowadays clear that in addition to including superexchange interaction in the Mn³⁺–O–Mn⁴⁺ ionic system and the corresponding Jahn–Teller effect, spin lattice or charge lattice interactions, i.e., polaron effects need to be taken into account when explaining the physical characteristics of these compounds [68]. This means that small variations in stoichiometry or Mn³⁺/Mn⁴⁺ ratio, as well as in microstructural properties, and that particularly at the nano scale, including the thin films (which may exhibit colossal magnetoresistance effect), may lead to unexpected and attractive resulting properties of the material. Only lanthanum-strontium manganites may thus exhibit colossal, giant or low-field magnetoresistance (due to unusual magnetotransport properties), high electrical conductivity, electrical field polarizability, half-metallicity of electron bands, anisotropic superexchange interaction due to Jahn–Teller effect, exceptional magnetoelastic properties, large sensitivity of interaction between the conductive and insulating phases to temperature (with the typical transition at Curie point), etc. This versatility in terms of structure and properties of materials in question also results in a similar versatility of their performance and application potential [69]. Lanthanum-strontium manganites have therefore been used in magnetic refrigerators, as cathode materials for solid oxide fuel cells, as magnetic sensors, as read heads in magnetic storage media, as segments of magnetic tunnel junctions, as catalysts in waste gas purification and catalytic combustion processes, and have recently been proposed by the author [70, 71] as a convenient self-regulating material for the hyperthermic treatment of cancer due to their tunable, stoichiometry-dependent Curie point. Unlike doped manganites which exhibit a broad set of potential electric and magnetic characteristics depending on the structural arrangement of the constitutive ions, in the case of HAP the main emphasis has been on the breadth of possible mechanical properties depending on different phase arrangements and the structure and morphology of the compound [6]. Among many mysterious features of this material, which one may reasonably connect to the Greek roots of its name— απαταο, which means “to deceive”—belong to (a) a considerably low crystal growth rate even under relatively high supersaturations, (b) low crystallinity of particles precipitated under physiological conditions, (c) complex formation pathways in accordance with the Ostwald–Lussac’s rule involving numerous transient phases, and (d) stoichiometric sensitivity to the mildest changes in synthesis conditions.

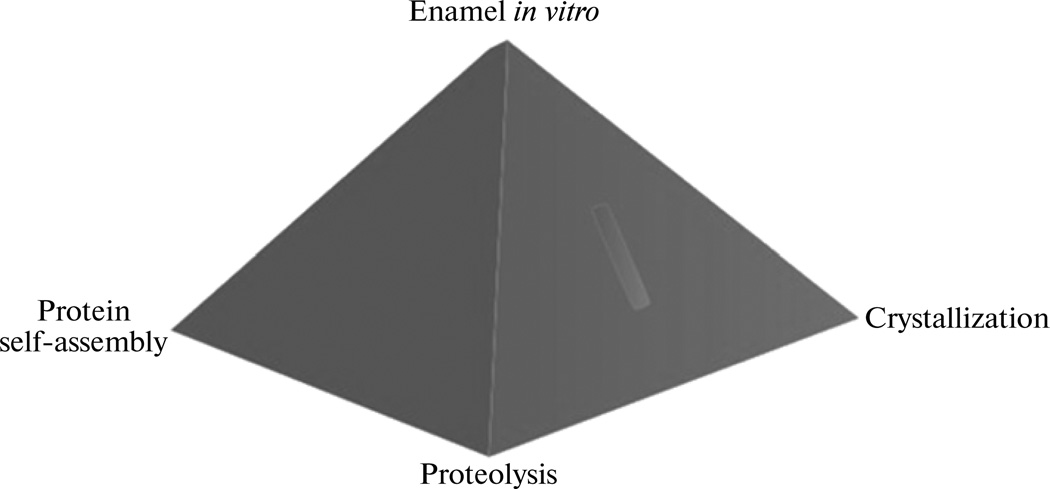
A particular case that pertains to formation of elongated HAP crystals during mineralization of the tooth enamel has led to a model according to which the self-assembly of the protein matrix, its proteolysis and the crystallization process are all intertwined. A large body of evidence is acquired in support of not only the fact that the protein matrix guides the crystal growth, but that the proper crystal growth may be essential for the self-assembly of the protein matrix into physiologically relevant morphologies, which might also expose the right active groups on the protein surface for the timely digestive action of the protease (Fig. 2). The notion of co-assembly is consequently increasingly finding usage in explaining the mutual fibrilization of the protein and mineral phases during amelogenesis [72, 73]. The cooperative and simultaneous assembly of the macromolecular and the mineral phases may thus be applicable for a wide range of biomineralization processes in general [74].

Fig. 2.

A pyramid depicting the intertwined nature of crystallization, protein assembly and proteolysis during the process of amelogenesis.

6. CONTROL OF SYNTHESIS OF FINE PARTICLES BY PRECIPITATION

Colloids and fine particles in general can be prepared by two means: top-down and bottom-up. The former deal with dividing the size of macroscopic and microscopic aggregates down to dimensions that allow for their facile dispersion, whereas the latter are based on precipitation and present the main fabrication route utilized in modern soft chemistry. Precipitation presents the basic method for preparation of materials in the world of soft chemistry, and this section will look at some of the basic parameters useful in controlling.

Manipulating thermodynamic concepts to control the chemistry of formation and stability of nanoparticulate systems is difficult. This is why for the sake of conducting the formation of particles by precipitation these are converted to solubility product and various measures of supersaturation levels, which pertain to more easily measurable activities and concentrations of reacting species [75]. Solubility product can be defined as the product of the activities of dissolved ions of a solid substance in the equilibrium between the dissolved ions precipitating and the precipitated ions dissolving. The lower the value of the solubility product, the less soluble the salt is. In the reaction ${\text{CaSO}}_{4(\mathrm{s})}={\text{Ca}}_{(\text{aq})}^{2+}+{\text{SO}}_{4(\text{aq})}^{2-}$, the equilibrium constant (K) equals:

$$\mathrm{K}=\{{\text{Ca}}_{(\text{aq})}^{2+}\}\{{\text{SO}}_{4(\text{aq})}^{2-}\}/\{{\text{CaSO}}_{4(\mathrm{s})}\}.$$

Solubility product (K_sp) equals:

$$K_{\text{sp}}=[{\text{Ca}}_{(\text{aq})}^{2+}][{\text{SO}}_{4(\text{aq})}^{2-}].$$

Often K = K_sp because the activity of a solid compound is by convention taken as equal to 1. K_sp is derived from solubility, as its name itself suggests, and can be therefore estimated by measuring solubility (s) of the compound:

$$A_n{B}_{m(\text{solid})}\leftrightarrow n{A}_{(\text{aq})}^{+}+m{B}_{(\text{aq})}^{-}$$

[A] = ns, [B] = ms, provided s is given in [mol dm^–3] units.

However, this is where the main limitations to using the concept of K_sp in describing phase transitions that occur during precipitation become obvious. Namely, in case of precipitation of ionic compounds, the dissolved ions are subject to interaction with each other, and these association effects account for the fact that K_sp is not applicable for very soluble salts. Solubility products are thus usually listed for insoluble and sparingly soluble salts, but not for soluble salts too [76]. However, ionic species interact with one another at all ionic concentrations and behavior of ionic solutions, even at high dilutions, is always in some extent far from the ideal. Consequently, ionic activities are usually smaller than ionic concentrations.

To partially correct for these shortcomings of the concept of K_sp, instead of using molar concentrations in the equations for K and K_sp, one uses ionic activities. Activity α = γc, where γ is known as activity coefficient, calculable through $\text{log}\mathrm{\gamma }=-A{z}_i^2{I}^{1/2}$ (Debye–Hückel equation), where z_i is the charge number of the ion species i, I is the ionic strength of the solution, and A is the constant depending on the dielectric constant of the solution, temperature and Debye screening length. Debye screening length is a length scale for the electric field generated at the charged surface. At a distance greater than the Debye length, the electric field is effectively shielded and therefore does not affect other charged species. In most biological systems the ionic strength is near 0.15 M, corresponding to a Debye length of approximately 1 nm. Increasing the ionic strength leads to compression of the Debye distance surrounding the charged entity. This effect in colloidal systems leads to a higher aggregation propensity of charged colloidal particles induced by high ionic strengths, which is known as the “salting out” effect. Multivalent ions are especially prone to exhibit this effect, as described by the Schulze–Hardy rule [77].

In order to overcome the inaccuracy involved in estimating the activity coefficients of the dissolved ionic species from the known concentrations, Victor La Mer suggested that an aqueous solution of 0.165M NaCl, a solvent of biological importance, may be considered as a standard solvent of reference in which all the activity coefficients may be assigned a value of unity [78]. Both theory and experiments indicate that it is more correct to use ionic strength than ionic concentrations when it comes to evaluating the effects of ionic species on other components of a solution. Ionic strength is calculated according to the following equation. The 1/2 coefficient is used irrespective of the number of salts dissolved, and because the ionic charge is squared it becomes clear why multivalent ions contribute to ionic strength significantly.

$$I_c=\frac{1}{2}\sum _{B=1}^n{c}_B{z}_B^2.$$

The effect of multivalent ions on the ionic strength of the solution becomes apparent by realizing that for 150 mM KCl I = 150 mM, whereas for 150 CaCl₂, I = 450 mM. Thus, for 1 : 1 salts (such as KCl), I/c = 1, for 2 : 1 salts (such as CaCl₂), I/c = 3, and for 3 : 1 salts (such as KH₂PO₄), I/c = 6, where c is the concentration of the electrolyte. The constant A that figures in the Debye–Hückel equation can be represented as:

$$A=q^3/(2^{1/2}(4\pi {({\mathrm{\epsilon }}_r{\mathrm{\epsilon }}_0{k}_{b}T)}^{3/2})).$$

Here q is the elementary charge, ε_r is the relative permittivity of the solvent, and ε₀ is the relative per mittivity of the free space. An extended Debye–Hückel law suggests that $\text{log}\mathrm{\gamma }=-A{z}_i^2/(I^{1/2}+B{a}_i)$, where A is a temperature dependent constant equal to 0.5115 at 25°C. B and a_i are, like A, constants depending on temperature and dielectric constant of the solution; a_i = 6 × 10^–8 for Ca²⁺; 9 × 10^–8 for H⁺; and 4 × 10^–8 for ${\text{PO}}_4^{3-}$ ions. Another way to put Debye–Hückel equation is the following:

$$\text{log}\mathrm{\gamma }=-A{z}_i^2/(I^{1/2}/(1+I^{1/2})-0.3I).$$

However, this particular equation gives satisfactory values only at I < 0.1 M.

Related to free energy of the dissolution reaction (ΔG_s = – RTlnK_sp), K_sp is a thermodynamic property. ΔG of the precipitation reaction is equal to: ΔG = –RTlnS, which implies that the larger the S, the greater the driving force for precipitation. When S > 1, ΔG < 0 and the precipitation reaction is favored, but when S < 1, ΔG > 0 and the dissolution reaction is favored. This implies that solution speciation in general is a thermodynamic consideration. Consequently, whenever kinetic effects take place, solubility product fails to provide a good basis for describing the precipitation process. The effects of the interaction of ions and small particles with organic molecules present such cases. As the result, the effects of ion association and complexation in the solution may significantly lower the free ion concentrations compared to the calculated values.

Calculating ionic activities that figure in equations for S and K_sp is always an approximation owing to the following effects. Firstly, all the additional species (ions, aliphatic additives and macromolecules, etc.) can influence the solubility of the given compound, even though they may not participate in the reactions. Common ion effect is the consequence of Le Châtelier’s principle, and according to it, a salt will be less soluble if one of its constituent ions is already present in the solution (Fig. 3). Uncommon ions tend to increase solubility by increasing the ionic strength of the solution and lowering the ionic activities, which is usually referred to as the salt effect or the diverse ion effect. Namely, as the ionic activities become lower than the measured concentrations, an effective increase in ionic concentrations is detected in the solution at the point where the threshold for precipitation is reached. Unlike the common ion effect which can decrease the molar solubility by several orders of magnitude, the diverse ion effect is much less potent (Fig. 3). Complexation can also modify the amount of free ions in the solution (that is, their activities). This is particularly the case for biological fluids where complexation reactions involving many organic species in the solution may make ionic concentrations markedly deviate from the resulting ionic activities. Also, in case of purely inorganic systems, such as iron oxides, the substantial complex formation equally prevents a meaningful application of the concept of solubility product. In addition, whenever covalent solids are precipitated from neutral species, the solubility product criterion could not be applied. Such is the case of polycondensation of silicic acid (Si(OH)₄) from which silica biominerals are formed [79]. Also, according to Le Châtelier’s principle, an increase in temperature entails a rise in solubility in case of endothermic dissolution processes and a drop in solubility in case of exothermic ones.

Fig. 3.

Solubility of silver chromate heavily depending on the presence of other salts in the solution (left) and a table displaying formation constants for some complex ions (right). Reprinted with permission from [80].

Furthermore, the assumption that all the oppositely charged ions in solution are thoroughly hydrated and separate is not valid. The effects of ion association and complexation in the solution may significantly lower the free ion concentrations compared to calculated values. When other equilibriums are present in the solution, they too need to be taken into account too if they affect the equilibrium in question, and dissociation of water represented by K_w presents one such example. Also, the equilibrium described by K_sp refers not to all chemical compositions of the solid phase, but to a specific phase. Hence, calcite, aragonite and vaterite are all described with the same chemical formula (CaCO₃) and yet have different K_sp. Even so, it is only one phase that in most cases enters the equilibrium. Then, K_sp is defined for large monocrystals for which surface area effects are negligible. However, solubility increases with decreasing the particle size and once particles become <1 µm in diameter, this effect has to be accounted for. Specific structuring of water molecules around solutes and colloidal species also affects the thermodynamics of phase transitions in solution. For example, the release or trapping of water following the formation of a solid has been shown to modify the energy landscape of initial and final free energy states of most precipitation reactions [81]. Consequently, each crystallization event can be seen as a process of a simultaneous rearrangement and restructuring of the interfacial water molecules, which speaks in favor of each self-assembly event entailing a co-assembly of the immediate environment surrounding the assembling system. Similarly, although diffusion phenomena have been paradigmatically treated by assuming the movement of solutes through the solution, it is impossible to discern whether diffusion is caused by solutes diffusing from the area of their higher concentration to the area of their lower concentration or by molecules of the solvent moving driven by a similar concentration gradient, because, as we see, the ordering of a system and its environment during a physicochemical transformation is inextricably mutual. From one such point of view, the kinetic attributes of the water rearrangement process with its significant enthalpic and entropic contributions can be considered as a crucial factor in determining the crystal formation rate. This is certainly evidenced by the fact that out of multiple steps that follow a crystallization event, from diffusion of ions to nucleation to surface bonding, dehydration is the one that is associated with the highest energy barrier.

Ionic activity product (Q) is the product of activities of ions in the solution that participate in a given reaction. Hence, K_sp can be considered as Q in the equilibrium state. In relation to K_sp, Q defines whether the solution is undersaturated (Q < K_sp), saturated (Q = K_sp), or supersaturated (Q > K_sp). The degree of saturation (DS) is, thereupon, calculated as:

$$\text{DS}=p{K}_{\text{sp}}-pQ.$$

In addition to DS, there are 3 quantities that can also be used to represent the saturation limit: super-saturation ratio (S), supersaturation (σ), and relative supersaturation (σ_rel).

Supersaturation ratio: S = Q/K_sp

Supersaturation ratio normalized per growth unit would be equal to S = (Q/K_sp)^1/n, where n is the number of ions in the formula unit, also known as “the number of growth units”.

Supersaturation per molecule σ = Δμ/kT = ln S (where Δμ is normalized per molecule)

Supersaturation per growth unit σ = Δμ/kT = ln S^1/n (where Δμ is normalized per growth unit)

For S ~ 1 (i.e., near saturation) the natural logarithm can be expanded (ln x ~ 1 – x for x ~ 1), leading to what is commonly termed the relative supersaturation:

$${\sigma }_{\text{rel}}=S^{1/n}-1=({(Q)}^{1/n}-K_{\text{sp}}^{1/n})K_{\text{sp}}^{-1/n}.$$

Supersaturation range can be divided to three parts: undersaturation (S < 1), metasaturation (0 < S < S_m) and supersaturation (S > S_m). The line dividing the latter two is not strictly defined and is subject to shift depending on the foreign surfaces in the system that may favor heterogeneous nucleation. In the metastable range, which is of particular interest to self-assembly and soft chemical reactions, unstable solid aggregates called embryos continuously form and disintegrate, but the resulting nucleation rate is zero since the system does not appear to be able to overcome the energy barrier that leads to formation of stable nuclei. Solution under these conditions may be stable for long periods of time without precipitating the solid phase. In the metastable region, heterogeneous crystal growth is favored over homogeneous nucleation in the solution [82]. The foreign substrate lessens both the size of a critical nucleus and the nucleation work, and it is known that in some cases it can even induce two-dimensional nucleation in an undersaturated range [83]. Surface defects of the nucleation substrate additionally decrease the critical nucleus size and nucleation work and rate [84], and the activation barrier for nucleation on a surface step can be so small that a nucleus composed of only two growth units might be supercritical under those circumstances [85], as compared to 10–100 growth units in the critical nucleus for a typical solidification process in homogeneous conditions or on flat surface. On the other hand, considering crystal lattice parameters, the greater the difference thereof between the foreign substrate upon which heterogeneous nucleation or an epitaxial growth is initiated and the crystallizing compound, the greater degree of S or supercooling is required [86].

The critical conditions for the growth of a nucleating cluster of atoms or molecules is dependent on its size and since the radius of a semi-sphere spread on a surface is much larger than a sphere composed of the same number of atoms and dispersed in the medium [87], heterogeneous nucleation is favored over homogeneous one when foreign surfaces are present in the supersaturated system, particularly at low and intermediate values of S. Thereupon, the contact angle between the nucleating island and the surface on which it is adsorbed, θ, presents one of the key parameters in estimating the nucleation propensities of the nucleant/nucleus system. The greater the affinity of the nucleation surface for ions comprising the nucleus, the greater the degree of wetting will be, resulting in more oblate nucleus shapes and higher radii for an equivalent number of comprising growth species, which leads to faster attainment of critical nucleus sizes. The lower interfacial energy during nucleation on a foreign surface leads to lower energy barrier for integration of ions from the solution onto the growing nucleus; however, the lesser total nucleus surface implies the opposite effect, which typically leads to lower heterogeneous nucleation rate compared to homogeneous one [88]. Heterogeneous nucleation also more often takes place on small particles, such as dust particles or gas bubbles in solution, rather than on large surfaces, such as vessel walls [87]. As impurities act as potential heterogeneous nucleation agents, the purer the solution, the higher is the S required for the system to undergo precipitation, which is an observation valid for phase transitions in general. Hence, pure liquid water at atmospheric pressure is known to freeze at –42°C rather than at 0°C; the greater the concentration of impurities, the closer the freezing point is to 0°C. Hence, the ordinary tap water freezes at circa –5°C [87]. Note also that the termination of growth in case of complex mixtures does not normally occur exactly at the supersaturation limit (S = 1), but somewhere in the metastable zone, which may be caused by various effects, including, for example, accumulation of surface defects, overgrowth of a more soluble phase or the effect of additives, such as macromolecules, which may block the growing faces (at both high and low concentrations) or hinder the diffusion of ions (at higher concentrations only). Also, even when agitation is intensive and the rate of addition of reactants extremely slow, locally inhomogeneous distribution of reactants will exist, frequently favoring precipitation of compounds even below their solubility limit, which is the effect routinely employed in co-precipitation syntheses of nanosized magnetic ceramic particles [89]. This implies that the sequence and rate of addition of reactants may affect the precipitation conditions due to producing local concentration inhomogenities. These factors significantly limit the range of applicability of the concept of solubility product in the design of fine particles.

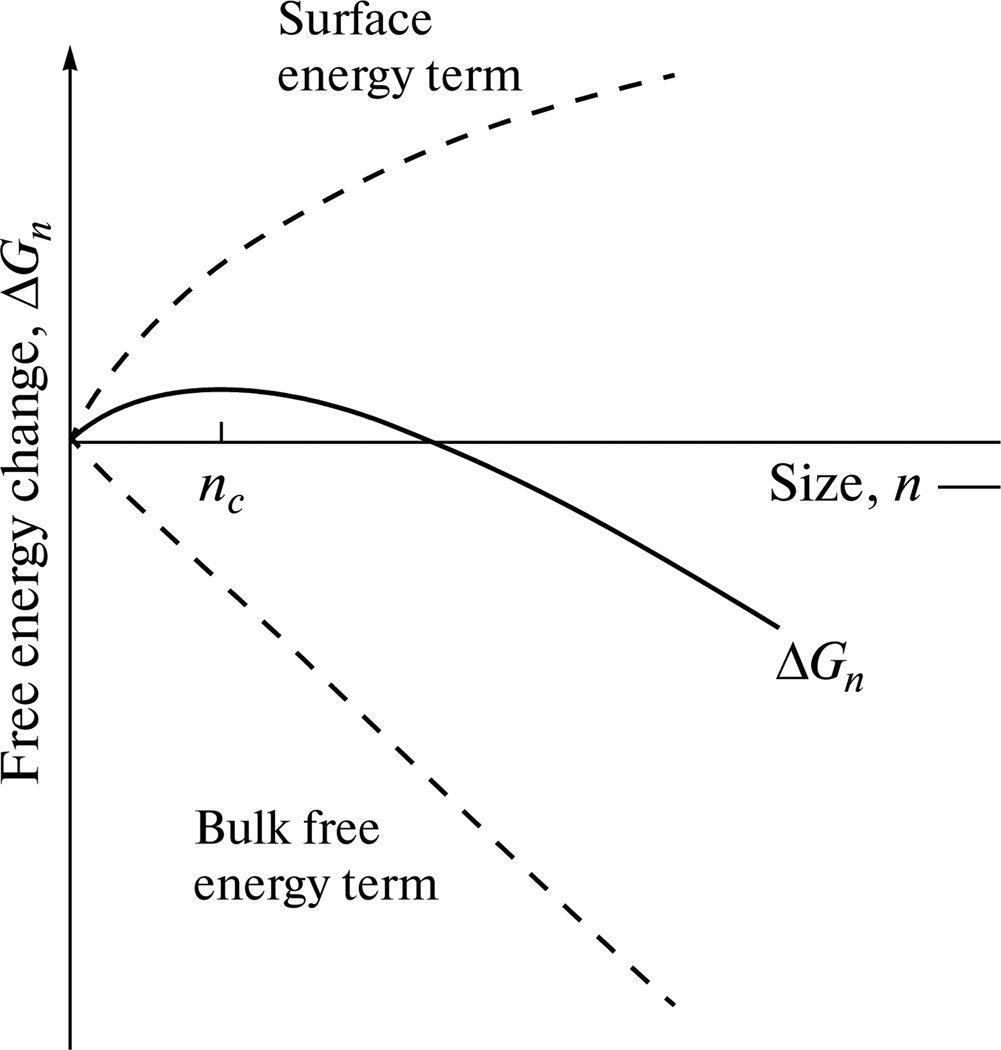
In the first stages of nucleation, phase fluctuations in terms of nuclei forming and dissolving occur, and if a given fluctuation results in the reduction of the system’s free energy, an embryonic atomic cluster might survive and grow. Whether this will happen depends on the sum of two energy terms: surface free energy (ΔG_s) and bulk free energy (ΔG_v). The former energy term, proportional to the squared nucleus radius, unfavorably increases with an increase in the nucleus size, whereas the latter, proportional to cubed radius, favorably decreases. Initially, this model predicts that the former initially grows faster than the latter, but the trend is reversed once nucleus radius crosses a critical point. Hence with a³ being the volume of each growth unit, r being the nucleus radius, and σ being the surface energy:

$$\mathrm{\Delta }G=\mathrm{\Delta }{G}_v+\mathrm{\Delta }{G}_s=-(4/3)\pi r^{3}kT\text{ln}S/a^3+4\pi r^2\sigma .$$

The sum of the two free energy terms has a maximum at the point at which dΔG/dr = 0 (Fig. 4). With ΔG_vol being the free energy per volume unit, the solution of this differential equation gives value for the critical radius of the nucleus (r_c), the crossing of which during its growth marks the point when the further growth becomes energetically favorable:

$$r_c=\sigma /\mathrm{\Delta }{G}_{\text{vol}}.$$

Fig. 4.

Free energy change during the nucleation of a new phase, with ΔG_n denoting the net free energy and n_c being the critical nucleus size.

Crystal growth rate (J) is equal to kS^x, where k is the rate constant and x is the reaction order. By plotting ln J vs. ln k + x ln S, tg of the slope would correspond to the reaction order, which is indicative of the mechanism of crystal growth. Thus, there are four main scenarios: (1) mass transport and diffusion-limited growth at very high levels of S (x = 1); (2) polynucleation of surface growth islands at high S (x > 2); (3) layer-by-layer growth at moderate S (x = 1); and (4) screw dislocation growth at low S (x = 2). Except for the case of x > 2, these mechanisms are valid for both growth and dissolution. Multiple factors affect the rate of crystal growth, including:

1. The amount of the material available. As already noted, higher S correspond to higher rates of crystal growth;

2. Viscosity of the medium, which affects the rate of diffusion of ions onto the growing particles. Diffusion dictates that as ions in the vicinity of the crystal surface are depleted from the solution, those from far away come to cede their place owing to diffusion and eventually become attached to the growing crystals. Since viscosity in the immediate vicinity of a growing particle (~1 nm away from it) is typically million times larger than that in the bulk solution (>10 nm away from the particle), the diffusion through this dense medium and replacement of the solvent that entails this movement provides the greatest energy barrier for the particle growth, regardless of whether it occurs by attachment of individual growth units or by particle coalescence;

3. Adsorption of impurities or additives, which typically act as growth inhibitors;

4. The morphology and surface irregularities of the growing phase, as the probability of successful attachment of a growth unit to a growing interface is directly proportional to the interfacial roughness [90];

5. The interplay between the three interfacial energies upon growth on a substrate: liquid-crystal, substrate-crystal and substrate-liquid. For example, the greater the substrate-liquid interfacial energy in comparison with the substrate-crystal and liquid-crystal ones, the more favorable and faster does the heterogeneous crystal growth proceed.

The time required for the system to transverse the energy barrier that separates the initial, supersaturated state and the final, precipitated state, depends on the height of this barrier (inversely proportional to S) and multiple kinetic factors that may modify it, is called the nucleation lag time or the induction time, τ. Expressions for the inverse of the induction time for nucleation, τ, and for the nucleation density, N, are given by classical nucleation theory as:

$$\frac{1}{\tau }=\mathrm{\Omega }\text{exp}(-\frac{\mathrm{\Delta }{G}^{*}}{kT})=A\text{exp}(-\frac{\mathrm{\beta }{v}^2{\mathrm{\gamma }}^3}{{(kT)}^3{(\text{ln}S)}^3})N=B\text{exp}(-\frac{\mathrm{\beta }{v}^2{\mathrm{\gamma }}^3}{{(kT)}^3{(\text{ln}S)}^3}).$$

ΔG* is the activation energy for nucleation, Ω is a pre-exponential factor, γ is the interfacial tension for the formation of the critical nucleus (circa 1.2 nm in size; prior to the onset of the induction time, the nucleus size is typically smaller than 1.2 nm and such an unstable aggregate of atomic/molecular entities is called crystallization embryo), β is a shape factor, v is the molecular volume, and A and B are constants. Induction time is, therefore, related to the activation energy required for nucleation, ΔG*, which depends upon the interfacial tension for formation of the critical nucleus, γ, and the solution supersaturation, S. From the equations above, we could see that the induction time is reduced and the nucleation density is increased by lowering the solution interfacial tension, γ.

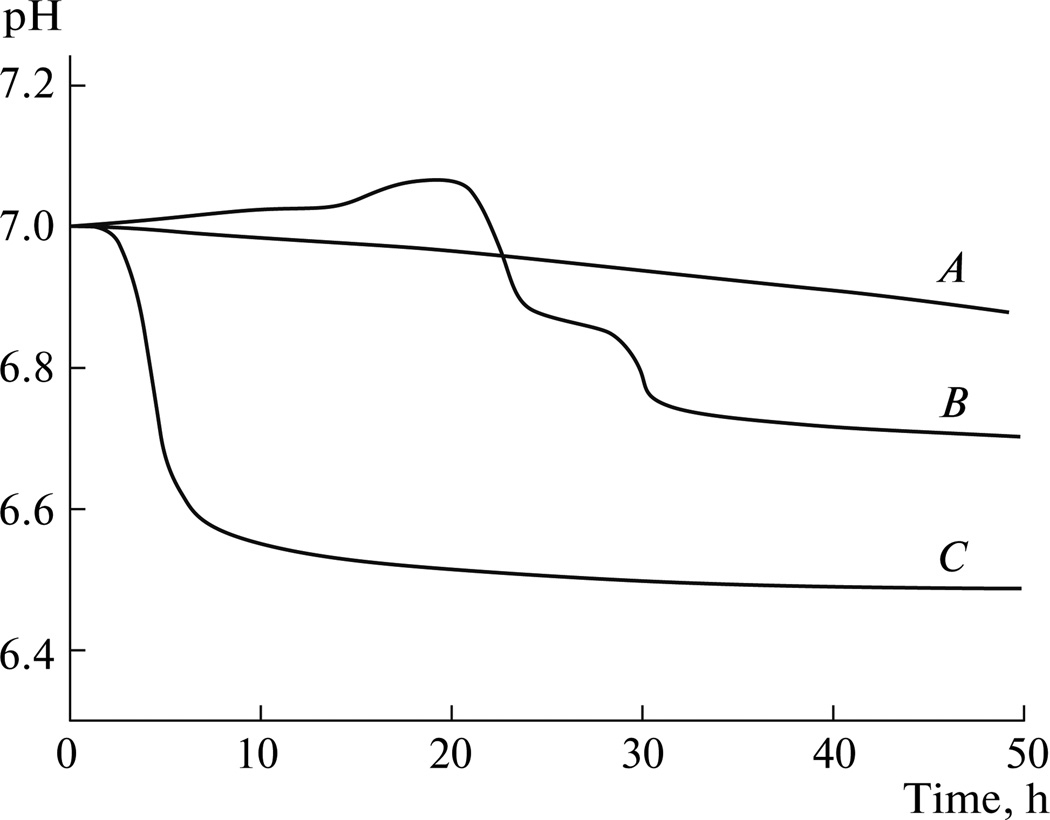
In the case of experimental systems for which a pH change is associated with the phase transition, pH vs. time curves can be conveniently analyzed to yield information about the nucleation lag time and therefore the levels of metastability of the system. Figure 5 demonstrates a case of three identically prepared metastable solutions which, however, yielded widely different nucleation lag times; as such, this figure neatly illustrates inherent difficulties in ensuring repeatable nucleation lag time measurements. The problem of unreliable estimations of the metastability levels of supersaturated solutions is closely tied to the co-assembly principle; namely, not a single physical system could be perfectly isolated from its environment. Not only does measuring nucleation lag time with respect to homogeneous nucleation require perfectly pure solutions, free from all the contaminants, but it also depends on the structure and chemical identity of the container. Aside from the fact that all reaction vessels leak their atomic constituents in finite amounts into the solution, their surface texture also markedly influences the activation energy for nucleation [91]. This is why Tadashi Kokubo, the inventor of the method for assessing the bioactivity of materials based on immersing them in stimulated body fluid (SBF), which is metastable with respect to precipitation of calcium phosphates, and monitoring the extent of precipitation of HAP on the materials surface, claims that a polyethylene vessel in which a precipitate formed once or a scratch is visible has to be discarded and not used for any future storage of SBF [92]. That the smooth surfaces can promote significant superheating or supercooling of solutions has been documented in the popular case of microwave ovens. Namely, producers of the early microwave ovens have regularly placed ultraclean and smooth cups for boiling water as parts of their shipments. However, it would often occur that the water would not start boiling inside of these cups even though the temperature had significantly exceeded 373 K. Instead, this process would be explosively initiated once a teaspoon of coffee is added to the superheated water, which posed risk to the consumers and caused substitution of such ultraclean cups with those with rougher and “crumblier” walls. Still, although plastic materials are usually considered more inert than glass, it has been documented that rubber, polyethylene and Teflon all undergo chemical degradation over time and may significantly disrupt the experimental reproducibility [93]. As for metallic and ceramic containers, culinary chefs have known for a long time that cooking acidic sauces in iron pots mildly corrodes the pot and increases the amount of iron in the sauce, while whipping eggs in a copper-based bowl makes protein molecules in the egg form complexes with copper, stabilizing the protein suspension and modifying its color. Proteins deposited on vessel walls have been shown to occasionally exert a thoroughly different effect on nucleation and crystal growth compared to the same molecules dissolved or suspended in the solution; oftentimes, whereas the latter may prevent nucleation, the former may promote it. Then, not only does every pH electrode applied for the measurement of the induction time leak some of its electrolyte content, but similar to the container walls, the stir bar or gaseous cavities, it also presents a foreign surface which may cause premature, heterogeneous “crashing” of the solution. Finally, even though a condenser system is applied, evaporation effects in small systems can never be overcome, because even a tiny condensation of the solvent on the vessel walls will produce changes in concentration of the dissolved or dispersed entities. Strictly speaking, vacuum would present the only correct environment for estimating homogeneous nucleation of solutions (and that in a perfectly pure state of the latter), and yet under such a low pressure liquid state could not be sustained. In view of this argument, it can be concluded that there could no experimental conditions for the perfectly reliable measurements of the metastability of supersaturated solutions. As a matter of fact, the induction time for homogeneous nucleation should reach a practical infinity more often than it does in reality, which would be in agreement with the original proposition of the Gibbs– Fowler theory of nucleation. Nevertheless, as of today, our ability to experimentally estimate the metastability of supersaturated solutions could be seriously questioned. The scope of this problem becomes obvious once we realize that both artificial and natural self-assembly processes, including biomineralization, occur exactly under conditions of low supersaturation when phase transformations are governed by subtle interactions conveyed by weak chemical forces.

Fig. 5.

Different pH vs. time curves (A, B, C) for three identically prepared metastable solutions (4 mM CaCl₂, 2.5 mM KH₂PO₄, 150 mM KCl, 1 mM Bis-Tris/HCl at room temperature), which precipitate calcium phosphate phases via different phase transition pathways.

Promotion of heterogeneous nucleation indicates that another phase in the system reduces the solution interfacial tension compared to homogeneous nucleation in the absence of the additive. Since the nucleus of a new phase is typically adsorbed on the foreign surface that promotes nucleation by means of physical bonds, it implies that although the new solid phase may remain on the substrate and thus block the inflow of other growing units, it is most often not the case as a constant overturn of the nucleating material occurs due to thermal motion, liquid flow due to agitation or local turbulences, the density gradient (nucleated gas bubbles thus tend to segregate by creaming, strictly speaking, while compounds denser than their medium will be affected by gravity and will tend to phase segregate by precipitation), temperature gradient, electromagnetic fields, interaction with the moving steps of the substrate, the strained structure of the nucleus owing to irregular or curved seed surface or complex molecular dynamics of the environment, as in the case of osteocalcin and other proteins that initiate mineralization on their surface, but do not form lasting complexes with the apatite nuclei and nanocrystals. Even during the formation of thin films, when the attractive force between the nucleant and the nuclei is quite high, the islands of the freshly nucleated phase are known to intensively migrate across the substrate surface due to the aforementioned effects [85]. In general, small and intermediate sized seeds tend to continuously produce nuclei that detach from their surface once they reach a certain size, while bigger and flatter seeds tend to yield a single crystal that grows to macroscopic size [94].

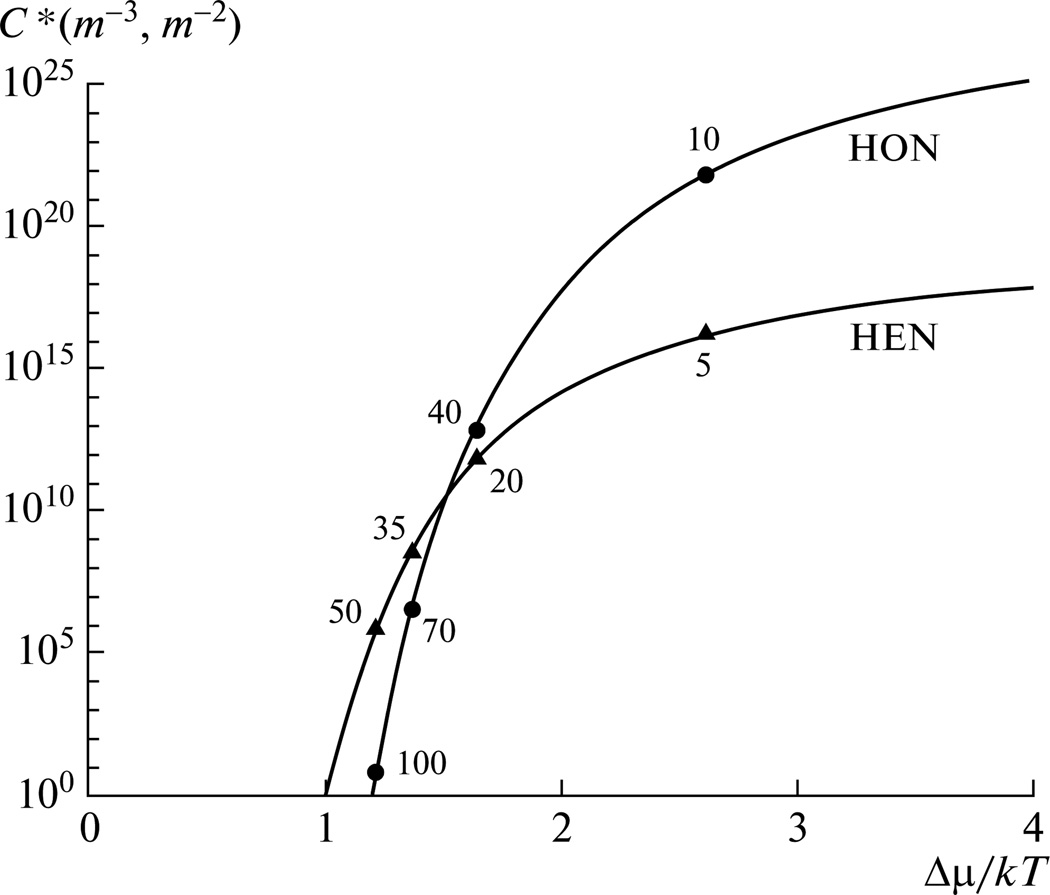
Another criterion that determines how facilely the nuclei will detach from the seed surface is the chemical identity of the adjacent phases, as some compounds due to lattice matching or other physicochemical affinities tend to adhere better than others, and the chemically closer the two compounds are, the greater the chance that the nuclei will be more intensively adsorbed on the seed surface, blocking it from catalyzing the formation of any additional nuclei. Hence, when a material is attempted to be nucleated on chemically identical seeds, the surface growth of the seeds is naturally to be expected. When the removal of the nucleated material from the seeds is retarded, it can be the rate-limiting step for crystallizations that occur strictly owing to heterogeneous nucleation and at finite seed sizes. In those cases, the seeds are prevented from acting as true crystallization catalysts or “assembly lines” for the production of nuclei [94], and the crystallization rate will be determined to a great extent by the concentration of heterogeneous nucleants [90]. Still, as the nucleation surface merely assists in controlling the density fluctuation and clustering of adsorbed growing units of the nucleating phase without forming chemical bonds with it, the phenomenon of heterogeneous nucleation is significantly different from the mere growth of the given surface. Also, as in any system that exhibits spontaneous, homogeneous nucleation in its bulk content heterogeneous nucleation occurs too in some extent owing to an unavoidable contact of the system with foreign surfaces, such as container walls, it is worth knowing the ranges in S where these two forms of nucleation are dominant, and one such relationship is shown in Fig.6. The equations given earlier have predicted that nucleation will be promoted by increasing S. However, at low S in the supersaturated range the heterogeneous nucleation dominates over the homogeneous one, whereas this trend is reversed at comparatively higher S, as shown in Fig. 6. The given equations have also indicated that systems that have higher nucleation densities should exhibit shorter induction times. For solutions with low nucleation densities, larger particles naturally result.

Fig. 6.

Concentration of the nuclei formed by homogeneous (HON) and heterogeneous (HEN) nucleation as a function of the supersaturation, Δμ/kT. Reprinted with permission from [83].

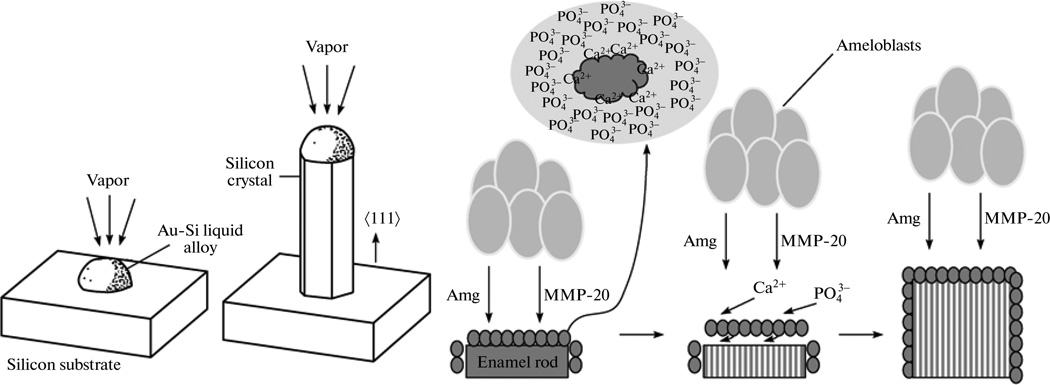
The amount of the material precipitated also varies with the concentration of the additive. Larger amounts of the additive may result in higher degrees of binding of the precipitating ions, causing depletion of species from the solution, lowering S and reducing the driving force for nucleation, provided this sequestration does not lead to nucleation. It has often been found that the same additive may have different, nucleation-promoting or nucleation-inhibiting effects, depending on its concentration [95]. In those cases, one would typically observe nucleation-promoting effects at low surface coverage, whereas at higher concentrations the additive would exhibit a nucleation-retarding effect. At very low concentrations, additive molecules are assumed not to be able to influence the volume transport processes and their effect, therefore, should be due to their participation in the surface reactions in the adsorption layer. It was, for example noticed that at low concentrations of a particular protein, an increase in its concentration leads to increased amounts of the material precipitated, whereas this trend becomes reversed at higher concentration of the protein [96]. This nucleation-promoting effect has been explained by invoking lowering of the surface energy due to adsorption, but as pointed out by Zhang and Nancollas, “Since the surface underneath covered by additive molecules can no longer participate in the formation of surface nuclei, this explanation for rate promotion is merely phenomenological” [97]. However, the role of the additive anchored to the surface in channeling the ions onto the growing crystal surfaces or even delivering the ions thereto by diffusion through the solution has recently been invoked [95, 98]. On these occasions, additive molecules may be adsorbed specifically on certain sites of the crystal surface (in general, their binding will be strongest at kinks, moderate at steps, and weakest on crystal terraces), so that bridges are formed, wherein the additive molecules may transport the growth units more efficiently to the crystal surface. This mechanism bears resemblance to the one describing the formation of silicon nanowires in the vapor-liquid-solid (VLS) process, during which nanodroplets of gold deposited on top of silicon wafers attract silicon atoms from the vapor, and after becoming supersaturated with respect to silicon begin to precipitate it, building well-aligned nanowires oriented perpendicular to the underlying surface (Fig. 7a) [99–101]. A similar model based on protein molecules adsorbing onto the growing crystal faces was recently proposed to explain the formation of the extremely elongated apatite crystals in the tooth enamel [98], contrasting the paradigmatic explanation according to which the macromolecules align along the crystal sides where the growth is blocked and negligible (Fig. 7b) (102). The nucleation promoting influence can also be explained by remembering that many foreign agents, such as organic matrices, may serve as sites for nucleation, often remaining as interstitial layers in the grown crystals [103, 104].

Fig. 7.

Schematic illustration of the model for the protein-controlled crystal growth of tooth enamel apatite based on the adsorbed amelogenin assemblies (blue spheres), channeling calcium and phosphate ions from the solution onto the growing crystal surface (left), and the mechanism of growth of silicon nanowires in the vapor-liquid-solid (VLS) process. Reprinted with permission from [99].

The Ostwald–Lussac law of phases dictates that if the solution is supersaturated with respect to multiple phases, the least stable ones would be the first the form, which would be followed by their transformation to more stable phases or might even result in sequential precipitation. A strict application of Ostwald– Lussac’s rule implies the formation of a structured liquid phase prior to the formation of an amorphous solid, which is reflected in the thought offered by D’Arcy Thompson in his book On Growth and Form: “In accordance with a rule first recognized by Ostwald, when a substance begins to separate from a solution, so making its first appearance as a new phase, it always makes its appearance first as a liquid” [105]. Spherical nuclei correspond to lower edge free energies, whereas polygonized nuclei correspond to higher edge free energies, implying gradual morphological refinements of the nuclei considering this empirical rule. To minimize the edge free energy, a step in equilibrium with the solution always has a certain number of kinks at T > 0. Also, as pointed out by Frenkel in 1945, steps in equilibrium above T = 0 will necessarily contain kinks due to thermal fluctuations, which implies that from a purely thermodynamic point of view, kinks are part of the step structure [106]. Sites on solid surface can be divided to terraces, steps and kinks, the latter of which present the most favorable sites for the attachment of nucleating growth units, since the adsorbed ions will be attached by three bonds (assuming Koesler’s depiction of the crystallization process). For surface-controlled processes, the growth rate is indirectly proportional to the edge free energy. In fact, the entire Ostwald–Lussac rule could be seen as a consequence of the fact that nucleation rate depends on S and the interfacial free energy (σ) as proportional to σ³/ln S². A difference in supersaturation levels between multiple phases could thus be compensated by the lower interfacial energy of the less ordered and less stable phases compared to more ordered and stable ones. In any case, since nucleation events are exceptionally hard to study because of the small size of nuclei (1–100 nm) and rapidly proceeding events in their evolution, the Ostwald–Lussac law of phases is suggested to be viewed as a guiding principle only rather than a statement of fact [81].

The dependence of the induction time on S can be used to determine the interfacial energy (σ) between the nucleated phase and the solution in case of homogeneous nucleation or between the nucleated phase and the substrate in case of heterogeneous nucleation. As described by the classical nucleation theory [107], it can be calculated as follows:

$$\sigma =2.303kT{((5\mathrm{\alpha }/2\mathrm{\beta }{v}^2))}^{1/3}$$

k is the Boltzmann constant (1.38 × 10¹⁶ erg°K^–1), T is the absolute temperature (K), β is a dimensionless geometric factor (167π/3 for spherical particles), v is the molecular volume of the precipitated compound (for HAP, equal to 5.287 × 10⁻²⁸ m³), and α is the slope of a plot of log τ vs. 30 ogs⁻² curve. In case of the classical heterogeneous nucleation, the nucleation rate is equal to:

$$J=A\text{exp}(-\mathrm{\Delta }G/kT)=A\text{exp}(-16\pi v^2{\mathrm{\gamma }}^{3}f(\mathrm{\theta })/3k^3{T}^3{(\text{ln}S)}^2)$$

where v (molecular volume defined by the crystal structure) values for HAP, OCP and DCP are 263.24, 310.59 and 126.53 A³, respectively, f(θ) is the contact angle function for a nucleus on a substrate, (16π/3) is the geometric factor, corresponding to spherical nucleus, and should be changed for other nucleus shapes (32 for cubic, for example). To relate S to J, one can also use the following equation:

$$J=A\text{exp}(-4{\mathrm{\gamma }}^2{a}^4/3k^2{T}^2\text{ln}S).$$

The slope of ln J vs. (ln S)⁻¹ curve can thus yield the interfacial tension (γ).

For polynucleation model, which HAP dissolution is assumed to follow, the following equation can be used as well:

$$\mathrm{\tau }=C\text{exp}(\mathrm{\beta }{\mathrm{\gamma }}^2{\mathrm{\nu }}^{4/3}/3k^2{T}^2\text{ln}S)$$

ν is the mean molecular volume of the crystallizing phase, β is a geometrical factor, involving the perimeter to surface (for cubic shaped nuclei equal to 4). In case of homogeneous precipitation, these values correspond to particle/solution interface, but when heterogeneous precipitation is induced on a foreign substrate (Fig. 8), these values correspond to the interfacial energy between the forming solids and the substrate [108].

Fig. 8.

Nucleation rate as a function of supersaturation (a); different nucleation rates depending on whether nucleation proceeds homogeneously (C), heterogeneously on a foreign phase with variable nucleation efficiency (B), or heterogeneously on a foreign phase with uniform nucleation efficiency (A) (b); nucleation rate as a function of the interfacial tension between the crystal and the fluid (c); and the size of a critical nucleus as a function of supersaturation estimated for a hypothetic system by means of vibrational frequency calculations (d).

Since the direct measurement of the nucleation rate is difficult, to characterize the kinetics of nucleation, one of the most common ways is to measure the nucleation induction time (τ) at different S. The following equation then applies:

$$\text{ln}\mathrm{\tau }=\mathrm{\kappa }f(m)/{(\text{ln}(1+\sigma ))}^2-\text{ln}(V{(R^s)}^2{N}^{0}f"(m)(f{(m)}^{1/2}B)$$

$\mathrm{\kappa }=16\mathrm{\pi }{\mathrm{\gamma }}_{cf}^3{\mathrm{\Omega }}^2/3{(kT)}^3$, which remains constant under given conditions. R^s and N⁰ are radius and density of the substrates, respectively, B is the kinetic constant, γ_cf is the specific interfacial free energy between the crystals and the mother phase, Ω is the volume of the growth units, and m is a function of the interfacial free energy difference between the phases of crystal, fluid, and substrate, and it depends on the interaction and interfacial structural match between the crystalline phase and the substrate.

Hence, a plot of ln τ versus (ln(1 + σ))² will give rise to a straight line for a given f(m). If the slope of this line decreases upon the addition of an additive, it signifies a promotion of nucleation. If it increases, it means that the additive suppresses nucleation. This is because changing the additive concentration is equivalent to a change in N⁰. This method is, however, applicable only when the amounts of the additive are minor. The induction time is also often represented as a simple inverse of the nucleation rate: τ ≈ 1/J. This simple equation is useful when estimating the induction time and therefore the time span of metastability for a given value of S. Hence, for J = 0, the time required for the formation of stable nuclei reaches infinity; for J = 10⁻⁷ nuclei m⁻³ s^–1, τ ≈ 115 days, and for J = 1 nuclei m⁻³ s^–1, τ ≈ 1 s.

So we see that since exp(−1/lnS²) = S², both the nucleation density and the nucleation rate are proportional to S², whereas the crystal growth rate is proportional to S^x. x is equal to 1 for diffusion-limited growth, typically taking place at high S. This implies that in a relatively high S range, with an increase in S the nucleation rate will increase more than the crystal growth rate. At the same time, the corresponding increase in nucleation density dictates the formation of a greater number of smaller nuclei as the value of S goes up, and as shown in Fig. 8d. This explains why the smaller the particles one intends to obtain, the higher the S one should use. More nuclei are then produced, and consequently the final particles will be smaller in size. Also, the fast nucleation rate means that the material is used up rapidly, so that the concentration of growing units in solution quickly drops. No nuclei can be then produced after the initial burst because S is too low, and the nuclei subsequently grow all at the same rate, leading to small and monodisperse particles, provided aggregation and ripening effects do not take place in parallel. In contrast, when one wants to obtain a monocrystal, a single nucleation event has to be produced followed by the crystal growth by diffusion, and for it a low S has to be maintained. Should we accelerate the process or induce competition for solute species by producing a large number of nuclei, the monocrystal formation process would be disrupted.

Also, anyone familiar with the physical phenomena of crystal growth can confirm that growing fast does not really pay off in the world of crystals. Namely, crystal faces that grow rapidly get to slowly disappear from the final crystal surface. Such is the case of the growth of a hexagonal unit cell, where a faster growing plane, clinched between a pair of slower growing ones eventually turns into an edge of a cubic crystalline particle [79]. HAP can also offer an instructive example in this case. Although about 6 hexagonal unit cells of pure HAP (Ca₁₀(PO₄)₆(OH)₂) fit inside of a round-shaped 1 nm sized crystalline particle thereof [109], the subsequent growth often occurs relatively fast along the direction of [hk0] axes, while it is negligible in the direction perpendicular thereto, that is, along [001] axis, which results in plate-shaped particles with mostly (001) faces exposed on the surface [110]. In other cases, as during the formation of enamel-like, needle-shaped HAP crystals, the growth may be high along [001] axis, while (hk0) faces in the hexagonal plane are prevented from growing, which eventually results in only a minor presence of (001) faces on the crystal surface. In case of a cubic unit cell, the situation is somewhat milder. Any faster growth along a single axis of growth would yield elongated, rod-shaped particles, in which the fastest growing face would still be present, although in a diminished proportion comparing to the crystal planes growing slow. The aesthetic meaning of this observation suggests us that slowness and patience are the ones that yield long-lasting products of knowledge, whereas whatever grows fast vanishes fast as well.

To sum up, how the system sets itself for the phase transition defines the state in which it will emerge on the other side. The phase transition itself is spontaneous. This brings in mind that the word “nucle-ation” has originally referred to the concept of the progenitor, or the mother and the father of a family [111]. Yet, according to Gibbs–Fowler theory, every metastable phase should be absolutely stable without an additional energy introduced into the system. The argument used to support this states that a free energy expense is required to overcome the energy barrier posed by high surface energy of the nuclei of the new phase. The subsequent theory of fluctuations developed by Volmer edified the original Gibbs’ approach by observing that entropy of a system is not uniformly distributed, but is subject to random fluctuations, which enable the formation of stable nuclei with probability equal to dW = Ce^−E_a/kTdl₁dl₂, where E_a is the activation energy for the given phase transition and dl₁ and dl₂ are the phase space elements. It can also be shown that dW = C exp(–4r²πσ/3kT), as the maximal work for the formation of a nucleus is equal to one-third of the interfacial energy of the nucleus. This essentially points at the antagonistic nature of phase transitions in general. Namely, the higher the temperature, the lower the S and the thermodynamic drive for nucleation associated with S. On the other hand, an increase in temperature corresponds to increased thermal motion and a higher probability of forming low entropy islands for which the critical nucleus size will be reached and from where on the crystal growth will proceed spontaneously. In addition, all cooperative phenomena of ordering and disordering in solid state can be seen as caused by different interaction energies of the adjacent atomic or molecular elementary constituents of the system. This also reinforces the view of energy gradients in the surrounding of the self-organizing system as those that are crucially involved in defining the trajectory of the assembly process along its energy landscape.

Every crystallization process is, kinetically speaking, a multistep process composed of: (a) nucleation; (b) diffusion in solution; (c) adsorption; (d) surface diffusion; (e) surface attachment; (f) dehydration; and (e) incorporation into the crystal lattice [112]. Nucleation itself is composed of two main kinetic events: (a) the transfer of ions to the nucleation island, determined by diffusion properties; and (b) the passage of ions from the old to the new phase, determined by the interfacial properties. Free energy of the crystal growth, excluding the nucleation events, may be divided to free energies of the following stages of the process: bulk diffusion, surface attachment, dehydration, surface diffusion, and incorporation to the crystal lattice. As already mentioned, out of all of these processes, dehydration poses the highest energy barrier [79], and it may take place during adsorption, surface diffusion or bonding to a surface site. The rate of the overall process is determined by the slowest or the so-called rate-limiting step. When the rates of these processes are comparable, each may have a significant influence on the crystal growth. For example, in diffusion-controlled reactions the formation of products from the activated complex is faster than the diffusion of reactants; hence, the rate is governed by diffusion. Reactions where the activated complex forms easily and the products form rapidly, such as catalytic and enzymatic reactions, are most likely to be limited by diffusion control. Heterogeneous reactions where reactants are in different phases are also candidates for diffusion control. To find out whether bulk diffusion presents a crucial step, crystallization may be performed at various stirring rates or at various viscosities of the medium. If an effect on the crystal growth rate is observed, it may signify bulk diffusion-controlled process. This method is, however, not applicable in case of nanoparticles due to the high nucleation densities. Also, if one detects a linear dependence by measuring concentration of the adsorbed layer vs. time, one can conclude that the process is diffusion-controlled. Activation energies, obtained by running experiments at different temperatures, may also help in differentiating between volume diffusion (16–20 kJ/mol) and surface-controlled process (35 kJ/mol or higher). Typically, at high S, precipitation is diffusion-controlled because the energy barrier for nucleation is low after the point at which atoms reach the right place in the vicinity of the nucleation surface. Also, just as it takes more time for a person to move from one side of a dance floor to another when the floor is crowded than when it is empty, the same principle of retarded diffusion at higher concentrations applies in the crystallization world and for phase transitions in general. Namely, more frequent collisions hold back hydrated growing units from promptly reaching the nucleation surface. At high S, therefore, the crystal growth typically tends to be diffusion-controlled. In contrast, at low S, the process is usually surface-controlled. At medium values of S, both adsorption and volume diffusion mechanisms may participate for a first order reaction.

In addition to the aforementioned sequential kinetic steps of crystallization, there are competing processes that interfere with and complicate the former. Some of these processes are aggregation and ripening, as well as morphological and structural refinements that take place during the aging time either through the dissolution/re-crystallization mechanism or through the bulk rearrangement of the crystal lattice units. A change in a single parameter that defines the experimental conditions of precipitation typically affects all of these competing processes, and their synergetic effect on the process defines the final phase compositions, crystal structures and particle morphologies.

Some materials are particularly intricate with respect to the complexity of competing stages of crystallization process, and HAP can be one of the examples. Namely, crystallization of HAP typically proceeds by following the Ostwald–Lussac rule, which dictates that the most soluble calcium phosphate phase will be the first to form, followed by formation of less soluble phases. Amorphous calcium phosphate transforming to OCP and then to HAP thus presents the typical route during precipitation of HAP. According to Ehrenfest, solid state phase transitions may be divided to first-order transitions, during which the system passes through a state of inhomogeneity, and second-order ones which proceed through a state of continuity with respect to a given thermodynamic potential. The former apply for transitions between two phases of different symmetries, such as crystallization from solution and condensation, whereas the latter apply for those between phases of similar symmetries, such as polymorphic phase transitions in solid state, magnetic ordering, liquid/gas phase transitions, etc. However, in complex multiphase systems, such as calcium phosphates, the Ostwald–Lussac rule implies that these two transitions take place almost simultaneously, as precipitation of ions is complemented by the bulk and surface rearrangements of ions that involve phase transitions, thus introducing additional complexities to their thermodynamic considerations. The free energies of nucleation and diffusion for HAP are also comparable, which implies that there is no definite time period that separates these two processes. And such an overlap of nucleation and crystal growth stages is responsible for the lack of monodispersity of synthesized particles. High nucleation rates taking place at high S are responsible for small particles, and apatite is known to have a considerably low crystal growth rate even under relatively high S. A simple calculation can show that unrealistic energy barriers, requiring unrealistic time scales to be transcended, are related to formation of nanosized apatite crystals directly from the solution; however, the assumption of crystal formation by aggregation of either 1-nm-sized Posner units or preformed unstable clusters with respect to whom the solution is undersaturated [113], though just slightly below S = 1, has been shown to provide a much lower and realistic barrier pathway to crystallization in such cases that include biomineralization of apatite. Ostwald ripening that calcium carbonate and calcium phosphates undergo, coupled with their sparingly soluble nature, implies an extensive amount of aggregation, which results in ridged and irregularly shaped particles with a wide distribution of sizes. Typically, microsized particles present aggregates composed of smaller subunits [114–117]. Even monocrystalline systems, such as the basic crystalline units of enamel, micro-sized apatite fibers, are accepted to be, are assumed to form through aggregation of subunits [118]. It has also been documented that long and defect-free filaments with the aspect ratios of up to 10⁴ can be obtained by the aggregation mechanism [119], overthrowing the idea that so grown apatite fibers would be prone to fracture due to many defects. This all implies that in the case of HAP and many other structurally complex fine particles, there is a significant overlap of all the sub-processes that define crystallization process, from nucleation to growth to ripening. Already now the paradigm shift from the old model that considered crystal growth to occur strictly through diffusion to the new model that adds the growth via aggregation of pre-nucleated subunits to the equation can provide an excellent example from the domain of materials science that confirms Kuhn’s views on mechanism of the (r)evolution of cientific thought [120]. For, this paradigm shift has not occurred abruptly, by means of a single finding and immediate dispelling of the old model. Rather, it has proceeded gradually, over the last couple of decades, including along the way (a) the gradual collection of evidence from many research groups and studies, (b) the slow process of convincing the supporters of the old views in their inexactness and the existence of a better model, and (c) the generational changes at the level of academic authority.

Note that nuclei of the newly formed phase, although typically containing about 100 atoms, do not necessarily need to be associations of atoms or molecules. Sometimes they are individual atoms or molecules in the excited or ionized state, such as in the case of not only the formation of water droplets from supersaturated vapor, but the formation of ferrites when an oxidation event of a single ferrous ion triggers the nucleation event [43]. Note also that all these equations belong to the classical nucleation model, and at high S in particular, when the critical nuclei may contain only a few atoms or molecules (Fig. 8d), the assumptions of classical nucleation theory are not valid. Although the classical nucleation model predicts that the nucleation rate should continuously increase with increasing saturation, in reality every phase transition follows a non-classical model. According to it, there are two antagonistic effects taking place [121]. Namely, the higher the S, the higher the thermodynamic driving force for nucleation, inducing the latter to proceed at a higher rate (although this rate normally decreases as nucleation proceeds due to depletion of growing units from the mother phase). But on the other hand, moving the system state away from equilibrium modifies the transfer of matter between the growing embryos and the mother phase, and since this transfer has to be ensured for the nucleation to proceed, this shift can significantly delay nucleation in some cases. In case of the glass formation, for example, an ultrafast cooling promotes the latter effect, leaving the system in the metastable state with an extremely slow transformation to the stable, crystalline form. If one would make an attempt to condense water vapor at the temperature of liquid nitrogen, at first it may seem that such a transition would proceed momentarily. But it is not so. Namely, at such a low temperature, the equilibrium pressure of water vapor (p₀) is so low that one collision between its molecules (which is the first step to the formation of an embryo that then has to advance forming a stable nucleus or to simply dissipate) occurs every 10¹⁶ years. To induce nucleation, one would have to increase supersaturation ratio (p/p₀) to ~ 10¹², by compressing the system and increasing its concentration, for instance. In contrast, condensation of water vapor at atmospheric conditions occurs in the supersaturation range p/p₀ = 5–8. As we see, this antagonistic effect entailed by the fact that the mother phase has to ensure sufficient supply of matter to the embryo for nucleation to proceed becomes most critical in far-from-equilibrium conditions, although complex kinetic conditions within a system may sometimes predispose it to exhibit such far-from-equilibrium characteristics even thought its state lies close to equilibrium. The fact that the nucleation rate is subject to variations, both before and after the critical point is reached, and depends on the system in question, contributes to difficult predictions of nucleation and crystal growth rates in any real systems.

7. LIMITATIONS OF THE CONCEPT OF ZETA-POTENTIAL

Surface charge of particles in sols has been used for centuries to regulate the stability of colloidal suspensions [122–124]. The ancient Egyptians used to render many colloids, from clays to inks, stable by electrostatic means, without being aware of that [125–128]. In 1857 Michael Faraday described the preparation of colloidal gold sols which are still stable and on display in the British Museum [129]. Although Faraday used different salt contents to control the electrostatic repulsion between the particles and therefore the extent of their aggregation (nowadays known as the “salting out” effect), neither was he aware that he had been indeed manipulating with the surface charge of the particles, although he was on the right track of explaining the cause of the stability of his sols. “There is probably some physical change in the condition of the particles, caused by the presence of the salt and such affecting media, which is not a change of the gold as gold, but rather a change of the relation of the surface of the particles to the surrounding medium” [130], stands written in his extensive treatise. The Gouy–Chapman model of the particle-solution interface then postulated a separation of charges at the interface and the formation of the so-called double layer composed of counter-ions and co-ions, some of which are, as later pointed out by Stern, tightly bound to the surface and some of which are free to diffuse [131]. Built on the basis of this model, DLVO theory developed in 1940s independently by Derjaguin and Landau in Russia and Verwey and Overbeek in the Netherlands explained the stability of colloids by invoking a balance between the repulsive electric double layer forces and the attractive, short-range van der Waals forces [132, 133].

Opposing the exclusively attractive and short-range van der Waals forces, the charged nature of suspended particles is a crucial factor in controlling the stability of colloidal systems. An essential measurable quantity used to control the intensity of the repulsive electrostatic interaction between the charged colloidal particles is zeta-potential (ζ-potential). Zeta-potential of ±15 mV is usually considered as the threshold for agglomeration, whereas ±30 mV is considered as the threshold above which the colloidal system becomes thoroughly stable. In between 15 and 30 mV, the system may be either agglomerated or dispersed. Electrostatic forces tunable by controlling the ζ-potential have regularly been shown as crucial for setting the optimal conditions for the growth of nanocrystals in desirable sizes and morphologies. For example, it was recently shown how elongated HAP particles were obtained in the presence of poly(L-lysine), whereas in the presence of more charged poly(L-glutamic acid), small nanocrystals resulted in otherwise same conditions of precipitation [134]. The reason is that the more charged the heterogeneous nucleation surface, the more cations would be attracted thereto and the more nuclei would be formed. Consequently, the particles will be smaller and there would be no biaxial growth, unlike in the case of the less charged macromolecular surface. Manipulating surface charges of interacting species in order to produce complex soft matter morphologies has also been recently mentioned as a prospective path [135]. For example, it is known that enzyme-ligand binding is favored under conditions of electrostatic attraction [136]. Recently, the same concept was invoked to explain the aggregation of cholesterol particles, pointing out that a control over ζ-potential may be used to prevent the formation of pathological cholesteric deposits, including atherosclerotic plaque and gallstones [77, 137]. However, numerous limitations are associated with this method and will be mentioned in this section.

Prior to determining the ζ-potential for a given system, the particle size is measured using the same dynamic light scattering (DLS) principle that is applied during microelectrophoretic analyses. The main limitation that the DLS faces in analyzing the particle size is the spherical particle shape approximation that it employs. Hence, every elongated particle will not be detected as such, but rather as a spherical one with the diameter averaged over the three axes [138]. The reason is that in addition to Brownian, translational diffusion of suspended particles, they also undergo rotational diffusion around their axes. The latter form of diffusion contributes to randomization of the particle orientation, implying that any particle deviating from spherical shape would be treated as an “ellipsoid of revolution”. For a dispersion of rod-like particles, for example, the translational diffusion coefficient (D₀) of the particle can be represented [139] by a linear combination of the diffusion coefficient parallel and perpendicular to the long axis of the rod, D_II and D_I:

$$D_0=1/3x{D}_{\mathrm{I}\mathrm{I}}+2/3x{D}_{\mathrm{I}}.$$

For very diluted dispersions, particle interactions become negligible and the overall expression for the diffusion coefficient can be written in the following way [140]:

$$D_0=kT/2\mathrm{\pi }\mathrm{\eta }{l}_{\text{ef}}{l}_{\text{ef}}=l{[\text{ln}(l/d)+0.316+0.5825d/l+0.050{(d/l)}^2]}^{-1}$$

l is the length, d is the diameter of the rod and l_ef represents an effective average particle length. For rod-like particles with large aspect ratio, the last three terms within square brackets can be neglected [139].

When the particles are shape-anisotropic, the electrostatic force exerted during ζ-potential measurements will depend on their orientation. However, an orientationally averaged mobility could be considered by assuming that the electric field is too low to align the rod-like particles. Still, due to high polydispersity it is convenient to treat the particles as spheres, although in this approximation the absolute value of the ζ-potential may change by a factor from 0.8 to 1.5 depending on the particle orientation [141]. Finally, the same Brownian motion on which the DLS device relies in measuring the particle size of a colloid is the source of an intrinsic error during the measurements of ζ-potential. The DLS device, therefore, takes the average mobility of an ensemble of particles into account, which implies that the measurement error becomes more pronounced at high polydispersities. The greater spread is typically found in the vicinity of the isoelectric point because dispersions are inherently unstable in that range. Quite often, ζ-potential values are immensely scattered in this range and interpolation based on arbitrary connecting data points from + and – sides of the ζ-potential vs. pH curve is carried out; depending on the concaveness of the sigmoidal curve drawn, isoelectric point detected may vary significantly.

Impurities in suspension are normally concentrated on the particle surface, and tiny amounts thereof may be enough to drastically interfere with the ζ-potential output [122]. As for impurities, silicate and carbonate ions present the main ones, as they are present in water and other reagents in minute quantities and are also adsorbed from air and leach from parts of the device. Their sorption leads to an increase in the negative charge and thus a shift of the isoelectric point to lower values. Typical distilled water also contains a few solutes at a level higher than 0.01 mM (a few ppm), a few dozens of solutes at a level higher than 1 nM, and hundreds of solutes at a level higher than 10 pM. Then, water under atmospheric conditions contains approximately 5 mM of dissolved gas, which adds up to a single gas molecule per each 3 nm (note that oils contain ten times more than that). The effect of dissolved gas on various chemical transformations in wet conditions is mostly unknown, except for the fact that their presence can be comparable to defects in a solid body [142]. There are many cases in which the gas content significantly influences the reaction taking place in the system. One example comes from a synthesis of vaterite in reverse micelles of SDS/hex-ane/water microemulsion [44]. The formation of calcium carbonate is triggered by a continuous purging of nitrogen gas through the microemulsion. This leads to a gradual removal of carbon dioxide bubbles, which are, however, unable to escape from the dispersed water phase and become trapped at the oil-water interface where they form a gas-water interface. Gas bubbles (strictly speaking, they are cavities, as bubbles are defined as possessing a boundary of a different phase beyond which the same phase as the one comprising the bubble exists) are known for their ability to intensify hydrophobic forces, as shown in the case of a ten-fold decrease in flocculation rates upon the removal of dissolved gas in a colloid system composed of paraffin and stearic acid [143]. After all, the finer and more sensitive interferences with the assembling soft chemical systems become, the more critical the effects of impurities will be.

As for the ζ-potential measurements per se, it is unclear what distance from the particle ζ-potential corresponds to. Namely, ζ-potential is a difference in potential between the potential of the bulk and neutral liquid and the potential at a certain distance from the particle surface, corresponding to the so-called slipping or shear plane, which is actually the boundary of the sphere composed of both firmly adsorbed ions (Stern layer) and some of the diffusing ions surrounding the charged particle. Hence, the distance from the particle surface at which ζ-potential is measured is further away from Stern layer (Fig.9a). However, the exact location of the shear plane is an unknown feature of the electric double layer. Experiments have shown that assuming the identity of these two potentials, especially for lyophobic surfaces, does not produce a significant error. Differences between the two will most likely be pronounced at high surface potentials and at high electrolyte concentrations because of the effect of compression of the diffusion layer of charges that leads to a higher slope of the surface potential vs. distance curve between the Stern layer boundary and the slipping plane.

Fig. 9.

Distribution of counter-ions in the double layer surrounding a negatively charged colloidal particle (left) and an electron micrograph showing negatively charged nanosized gold particles adsorbed on electronegative plate-shaped kaolin crystals (right). Although kaolin platelets are negatively charged as a whole, their edges are electropositive and as such attract the gold particles onto them. Reprinted with permission from [148, 149].

Also, ζ-potential, including the isoelectric potential (IEP), is merely indicative of the surface charge and, especially when polyvalent ions are present in the system or when specific adsorption takes place, it does not faithfully reflect the charge on the particles. Hence, as a consequence of the fact that ζ-potential analysis cannot differentiate between the charge on the surface and the charge contributed by the double layer of ions, a particle with the zero surface charge may have a non-zero value of ζ-potential owing to the adsorbed ions and thus may move in the electric field, whereas the particle at the isoelectric point may not have zero surface charge and still be stationary in the electric field.

The problem with analyzing HAP and other complex ceramics and minerals with respect to ζ-potential is that at the mineral surface pH not only does shift the surface charge by changing the distribution of protons and hydroxyl groups hydrating the interface, but it also influences the selective dissolution of the surface ions, which then induce rearrangement of the surface charge layers, oftentimes shifting the ζ-potential values in unpredictable ways. This selective leaching of ions is the source of great unpredictability and irreproducibility of the electrophoretic analyses. Thus, whereas some studies report negatively charged particles in the entire pH range in which HAP is the stable phase [144], others report IEP values at anywhere between 5 and 7.5, below which the particles become positively charged [145, 146]. There are, however, reports on IEP of HAP suspensions detected at pHs as high as 10 [147]. In addition, HAP, like many other materials, has two types of crystal planes that carry different charges: positive on a-planes and negative on c-planes. Zeta-potential analyses are not able to differ between the two and oftentimes it happens that an electrostatic attraction that leads to specific adsorption is observed between two types of particles carrying the same net charge [148]. In such cases, planes or edges of one of the particles carry the opposite charge compared to the particles as wholes, inducing the electrostatic attraction and aggregation to occur, as shown in Fig. 9b.

To sum up, although long-range and non-directional electrostatic interaction can be useful in providing conditions for soft chemical systems to assemble into attractive morphologies, the crucial steps belong to finer, short-range and highly directional weak force interactions, which microelectrophoretic analyses are insensitive to. Soft chemical systems utilized to yield advanced materials and assemblies are too fine to allow for their control via long-range and non-directional electrostatic forces. Probing static nanostructures at the fine scale is already an enormous challenge [150], and understanding the dynamic evolution of soft matter morphologies at an ultrafine scale and with respect to the short-range and highly directional weak forces stands forth as an even greater one. Combination of modeling and theoretical approaches and versatile characterization techniques that complement each other certainly presents the prospective option for the bright future of soft chemistry.

8. FINAL REMARKS AND A TRIP TO THE BEACH

Up to this point, some fundamentals of the physical chemistry of preparation and control of mesoscopic and nanoscopic self-assembled and colloidal systems that fall in the reign of soft chemistry were revisited. As we could see from the discourse on the thermodynamics of formation of colloids, the use of its conceptual apparatus is qualitative and although the transition to solubility products and parameters that pertain to supersaturation levels and other measures of metastability of the systems introduce more of the quantitative account, the ultrafine nature of phase, structural and morphological transformations in soft chemical systems still predestines these models to possesses numerous exceptions and approximations as well as to be useful only in a broad, qualitative sense. As of today, for example, although quantum dots exhibit size-dependent optoelectronic properties, their Fermi levels cannot be designed prior to depositing them. Only after the material is prepared and characterized for properties of interest, one could repeat the experimental conditions which would correspond to the given properties. Although the term “tunable” has been extensively used to describe size-dependent material properties, this term cannot be linked with “designable” since the connections between the bench blueprints and final experimental outcomes in terms of desirable materials properties are not that easily established. In late 1930s, the chemical industry financed theoretical projects aimed at deriving such connections, and among other models, they resulted in DLVO theory [151], which is still, 70 years after its conception, used as the basis for quantifying colloidal phenomena and predicting experimental outcomes in this field. Stagnations in successful drawing of these links have led to most modern synthetic soft chemists relying on trial-and-error approaches when designing new materials. To be consoled for their efforts, they can always peer into the field of drug delivery where a similar situation is present. Namely, despite the extensive initial screening steps, the final candidates for drugs undergo randomized, trial-and-error studies in vitro, on animals and then on humans, eventually unexplainably failing or living up to their promises. Although it has been a persistent dream of materials scientists to establish a perfectly precise algorithm that connects synthesis parameters, materials structure and properties, and their function and performance, it is still permeated with numerous missing links. As we try to fill those gaps in our knowledge, we will undoubtedly use qualitative models such as those outlined in this review.

The lack of quantitative models that could be used in the design of fine particles and the control of their stability with the same precision as those that are used at the atomic or macroscopic scales predisposes scientists to rely on these qualitative models as well as to “alchemically” use the powers of intuition and metaphors in conducting experiments. Having been an apprentice of a wizard in the world of colloid chemistry [137], the one standing behind some of the most fascinating particles ever made [152, 153], I have crafted the art of mingling the artistic and the scientific on the lab bench, aside from being inclined to this balance ever since I read the Glass Beads Game and decided to dedicate my life to fully living up to its merits. The first stable dispersions of uniform cholesterol particles stabilized relying merely on their surface charges [154] I thus produced by using the powers of intuition and altruistic aspirations as much as by relying on the qualitative principles mentioned in this work. Likewise, most new materials are synthesized today following trial-and-error approaches within the windows of conditions predicted by the aforementioned models. Whether we will witness times when sophisticated algorithms in which one would input the desired materials properties and composition and as an outcome obtain the right experimental conditions will be made available is a big question. It could be that dreams of one such perfect algorithm are similar to hopes in building a Laplace’s demon, nowadays epitomized by the deterministic theories of everything in fundamental physics. In contrast, the charms of chemistry lie exactly in the lack of perfect precision that typifies physics and reliance on approximate and qualitative approaches. The philosopher of chemistry, Michael Polanyi, would have thus reminded us of the following: “The mere fact that there is no absolute security for the validity of what we consider exact natural laws should lead to the conclusion that these laws are only valuable in combination with the element of uncertainty in them, which is compensated by the supreme sanction of validity, which is faith… It is indeed obvious, that if at any time chemists would have been so ill-advised as to let themselves be frightened by physicists into abandoning all vague methods, and to restrict themselves to the field where exact laws (or what are supposed to be such by the physicists) pertain, the development of chemistry, would, at that moment have stopped dead, and its most valuable parts would have melted away in the rays of such foolish criticism…. Chemistry, indeed, leads us so far away from physics, that the description of chemical substances and the art of dealing with them lies quite near, by comparison, to the types of human behavior and the art of commanding human behavior. The mythological language of the alchemists persists in chemistry and is still characteristic of its most vital element” [155]. Hence, for the sake of advancement of the field, we should not hesitate to continually stick to this balance between conceptual and intuitive in the experimental design.

This is, of course, not the call to give up on improving the quantitative models and return to the approach to chemistry from the times of Renaissance and Dark Ages. It is simply recognizing the basic limitations that chemists face nowadays, an awareness of which is essential in drawing better quantitative models as well as more effective connections between them and the qualitative ones. For, it is by tackling horizons where the unknown and the obscure dwell that we spur the evolution of our knowledge.

What this perspective naturally calls for is an inflow of intuitive insights that would be blended with the rational ones and as such guide us to various problem-solving paths. At the very end of this work, which has contained a plenty of equations and analytic threads of thought, we will balance it with aesthetic parallels and insights. For that purpose, we will set off to a beach and pick a random pebble from the shore.

One of the first things that could be observed now is that the properties of the stone do not lie in it alone, but result from the interaction between it and the measuring device that includes the observer’s senses and mind. If we press the stone, we may notice how ridged or smooth, hard or soft it is, and we would endow it with some qualities. But these qualities are not absolute. They are defined by the nature of the observer and his own notions of hardness and softness. The mechanical characteristics of a solid material are defined with respect to certain units, be it Pascals in physics or the numbers of the Mohs scale in mineralogy. This demonstrates that each of these properties is always denoted as relative to some referential scales, and thus essentially to properties of other stones as well as to properties of the observer. Hence, all qualities need to be defined as relationships between the observer and the observed. If we look more closely, we would realize that it is the intersection of the ontological set of relationships of the observed system with the rest of the physical reality and the epistemological set of relationships of the observed system with the fundamental base of the observer’s characterization approach that defines the qualities of the observed system. Essentially, for every quality that we are aware of can be said that it is experiential and natural at the same time, as it can be represented as arising from the “touch” between mind and Nature.

Thus, by simple, yet profound looking at a pebble, we could arrive at the core of the co-creational thesis proposed by the author earlier [156]. The whole world of one’s conceptions can thus be literally built from a scratch on the stone’s surface. Realizing this, I will draw the final figure of this paper, a simple yellow line (Fig. 10). For, each line on the stone’s surface can inspire us to think of its origins, and sooner or later, we would come to the idea that it has been shaped from within as much as from without. We would, therefore, show that each minute detail of the world around us carries inexhaustible sources of inspiration.

Fig. 10.

Together with the first two images, this yellow line gives rise to a smiling face. An imperfection, a loop and a drive: a key to it all. Hans-Georg Gadamer noticed that the meaning of every letter and symbol, including this simple line, can be seen as an intersection of horizon of potential meanings ascribed to it by the creator and a similar horizon created by the interpreter. A simple line such as this one can thus be seen as arising from the touch between mind and Nature, I and Thou, implicitly telling stories about both.

One can now infer that the qualities of any physical system do not lie in the system alone, but are equally shaped by the context in which it exists, aside from the context of its observation. The history of the interplay between the inner potentials defined by the stone’s composition and crystal structure, and environmental factors, such as temperature, pressure, humidity, pH and friction, defines the actual appearance and properties of the stone. Crystals have a natural tendency to grow such that their visible faces correspond to the most energetically stable atomic planes in the crystal lattice, but at the same time the environmental factors add up their own influence to the physicochemical conditions of the crystal growth. The level of supersaturation in the medium surrounding the growing crystals defines the crystal growth rate and influences the surface topography, but the latter are also dependent on the initial properties of the crystal surface (e.g., whether it can be considered as flat, kinked or stepped) [121]. The origins of shape, symmetry and all the ridges on the pebble surface can be thus traced back to its inside as much as to its outside. Just like sentences co-define the meanings of individual words and letters that they comprise, the same can be said for any natural system. For, the intrinsic structural features of the system in question predispose it for certain types of interaction, whereby these interactions, always involving the attributes of the environment equally, define qualities displayed by the system. As Heisenberg’s uncertainty principle suggests, there is no measurement without an interaction, and whatever we detect in physical systems is always the product of an interaction between the system and the measuring device, where both are involved in shaping what we will come to consider as qualities of the system.

The origin of the way a seashore pebble appears to us can be traced back to the properties and propensities of us as observers, as well as to the inner and outer factors that determined its formation and evolution. The atomic composition and crystal structure thus have to be taken into account in this explanation as much the environmental effects present at the time of its crystallization and interaction with the sea waves and the surrounding rocks, pebbles and organisms.

The same principle of inner and outer factors being together involved in shaping qualities applies for all systems in Nature, from atoms and molecules to cells, organisms, social groups, evolutionary lineages and ecosystems. For example, should we try to find a thorough general explanation of human behavior, we would not be able to refer only to genetic predispositions or inherited mental aptitudes. Beside these inner factors that act as behavioral determinants, environmental and social effects need to be taken into consideration in order for a broader view to be constructed. Only merging of the paradigms of genetics and behaviorism could bring satisfying descriptions of life and humanity.

As we could see, a tiny seashore pebble can spark an exciting stream of thoughts in the mind of an imaginative observer. The butterfly effect of the chaos theory has told us that minor deeds occurring on one side of the planet can produce significant effects on the other side. As pointed out by Nikola Tesla, “There is no thing endowed with life—from man, who is enslaving the elements, to the nimblest creature—in all this world that does not sway in its turn; whenever action is born from force, though it be infinitesimal, the cosmic balance is upset and the universal motion results” [157]. As we see, enormous meanings lying hidden in tiny patches of the reality are also sometimes enough to trigger a phenomenal chain of thought in their observers, producing ideas that may change them and the world. In such a development of the story of life in crucial correspondence with the smallest of its details, science and experience may be seen as reminiscent of fairytales in which plucking a flower or biting an apple may produce tremendous effects on the destiny of the hero [158]. Scientific rigor and the artistic fancy have indeed always presented two sides of the coin of a truly creative human thought [9].

That a single pebble can have significance in drawing original connections in the scientific realm can be demonstrated by the example of Abbe Haüy who dreamed of becoming a botanist about one and a half century ago. One day, he paid a visit to a friend who had a large collection of minerals. Abbe himself had a rather modest collection at the same time, and during the visit he was handed a specimen of calcite, which he accidentally dropped and broke. At that moment, he could not have dreamt that this accident would change the course of his career and the worldwide understanding of the world of minerals and crystals. Namely, Abbe received the broken stone as a gift at the end of the evening and went home with it. Looking at it later, he noticed that the face along which the mineral broke possessed a rather smooth surface. Intrigued by this observation, Abbe decided to break it into even smaller pieces and see if the exposed surfaces would be equally smooth. Interestingly, they were and Abbe came up with an explanation of this rather strange effect, which is today known as the law of rational indices. However, he erroneously believed that he had broken the crystal into its elementary building blocks. Despite the incorrect interpretation, his discovery indicated a correlation between the symmetry of the elementary cell of the crystal and its shape as well as the cleavage planes, which presented a giant step for the understanding of crystal structures. The accidental dropping of a crystal and Abbe’s clumsiness eventually turned out to have had a major significance for solid state science. It also prompted Abbe to change his career path and become a crystallographer instead of a botanist [159].

Just like living creatures renew themselves during each instance of their living, the same goes on with the seashore pebble. It is crushed by waves, clinched against the surrounding pebbles and subject to air streams and temperature changes. The formation of each stone is thus never over. Even while we hold it in our hands, microscopic and atomic species fall off from it, never to be returned again to be the part of the stone. But also, some other atoms from the surrounding get attached onto it and, if driven to the right spots on the diffusion streams, may become a permanent part of it. Such processes are particularly instigated in the seawater that contains numerous ions that readily become parts of the water’s stony surrounding. In fact, an equilibrium involving a crystal immersed in a solution implies not a constant and unchanging existence of the solid material in the medium from which it was precipitated, but the continuous process of dissolution and re-precipitation. The same is with living organisms that constantly dissipate their essence and yet continuously reintegrate and recreate themselves, thus becoming a structurally and cognitively new creature at every moment of their lives.

This can remind us of the effect of the history of the formation of the seashore pebble and any crystal alike on the patterns of their future growth. Namely, the way the seashore pebble has grown so far largely determines the way it will further grow. Thus, for example, if a crystal grew at a relatively high rate for some time in a highly supersaturated environment, the later growth of the crystal under a lower supersaturation will proceed at a different rate compared to a crystal that had been kept in a lower supersaturation environment all of the time [160]. This is normally explained by the different roughness of the crystal surface. First of all, the faster the crystals grow, the more imperfect their surfaces will be. Therefore, crystals grown in highly supersaturated media will tend to have rougher surfaces than those grown in lowly supersaturated solutions. Subsequent growth in the solution of the same supersaturation will proceed faster for the former, topologically rougher crystals than for the latter, smoother ones. Hence, sometimes the same level of supersaturation may induce growth of one form of crystal, whereas the other one with an identical composition will grow slower or may even remain unchanged. Likewise, the same type and amount of external impressions can sometimes leave one person thoroughly untouched and the other one crushed by the waves of emotion. Hence, just like the habit of crystal growth influences its future growth, the habits of our thinking and judging about the world, which remain deeply ingrained in us, outline the way for the future absorption of impressions. Eventually, one may even adopt a belief that patiently and persistently cultivating goodness in our mind and heart pays off, as it would spontaneously predispose us to benefit from the environmental stimuli exerted on us.

If we were to follow how crystal growth proceeds on an atomic scale, we would arrive at yet another remarkable parallel between the world of crystals and that of human thinking. Namely, atoms and molecules from solution or gas have a hard time finding sites to attach onto an ideal, perfectly flat surface, and the same applies during the crystallization of our knowledge. Surface irregularities, such as kinks, steps or terraces, are those where atoms most easily anchor during crystal growth. Likewise, imperfections on the surface of our knowledge—the surface being composed of relationships that are the direct subjects of our reflections—are the starting points for the growth of the crystal of our knowledge. Should we believe that we have reached a sheer perfection while reflecting on the ideas that appear on the surface of the glacier that our mind is, that we have arrived to ideal and immaculate worldviews in our thinking, the further growth of our knowledge would naturally be retarded. Little ideas that would land on us randomly during our daily contemplations, just as atoms and molecules from a supersaturated solution land on crystals in touch with it, would simply diffuse around the crystal faces of our knowledge and eventually bounce back from such an inaccessible surface, which would remain to exist in the pretentious light of seeming perfection. But for as long as our wonder clusters ideas that stick from the surface of our body of knowledge, tickling our curiosity and urging us to rethink them innumerable times, for as long we believe that perfection in our models of reality is far from being reached, and for as long as wonderful questions that are the cause of our amazement with the world we inhabit never cease to appear on the surface of our mind, rearranging the atoms thereon so as to incessantly search for more perfect ordering thereof, the new ideas will easily attach to the body of our knowledge, somewhat like new words and sentences that comprise this and other writings of mine do, contributing to its unlimited growth.

The same principle undoubtedly applies for the refinement and diversification of the inspirational repertoire of our acts in the world. Since Heinz von Foerster mentioned in his aesthetical imperative, “If you desire to see, learn how to act” [161], we should also know that inspirational acting leads to vital shifts in perspectives which help us enrich our knowledge about the world too. Acting is thus intrinsically related to knowing and vice versa. Be that as it may, for as long as we tend to perform only acts for which we think that they satisfy the criterion of sheer perfection, we would remain blocked and frozen, calculating that perfect move which is ultimately unattainable and will never arrive. Any exciting acts will then hardly ever be performed on the substrate of our obsession with perfection, just as atoms difficultly attach onto perfectly smooth and flat crystal surfaces. On the other hand, if we are not pressed with the burden of perfection, but are driven by spontaneity, naturalness, loving acceptance of our human fragileness, holding a pencil of love in one hand and a mop of light forgiveness in another, realizing beauty and perfections in imperfections, we would be able to strew the world around us with endlessly inspiring and versatile acts.

Little by little, it gets clear that all many wonderful ideas can be deduced from one such patient and faithful watching of a stone. Like “the stone cut out of a mountain by no human hand” that destroys a brilliant statue and “becomes a great mountain that fills the earth” in Nebuchadnezzar’s dream (Daniel 2: 31–35), a tiny stone quietly placed besides the main road of human lives may prove to be more important and inspiring than many of the adored manmade products to a beautiful human mind. This is in concert with the verses of the alchemist, Arnaldus de Villa Nova, who died in 1313: “Here is the poor and unsightly, utterly trumpery stone! The more disdained by the fools, the more adored by the sages” [162].

A careful looking at a simple stone can also make us realize that despite its often being used to epitomize dead and inanimate matter, a music fascinating endless generations of scientists and thinkers permeates every tiny segment thereof. Although a stone in our hands may indeed appear as a symbol of inanimateness and inertness, if we were able to penetrate with our attention deep into its atomic structure, we would be able to recognize and listen to a music produced by vibrating and oscillating atoms that the stone is composed of. Moreover, this music could be explained only by invoking the quantum principles of atomic physics, which do not have a consistent explanation, as of today. To understand this music, a more fundamental theory of the Universe would be required. Hence, with plunging deep into the music that a quiet “heart of stone” beats with one travels into the greatest mysteries of time, being and Cosmos. Answering the secrets of this music would mark the steps towards answering the secrets of the entire Universe. Maybe this is what the ancient alchemical quest for the mystical philosopher’s stone is all about? Maybe it is pointing at every little pebble on the side of the road as a base of a pyramid of knowledge that may penetrate the cloud of the most sublime insights. So, instead of looking at distant stars, we could equally start carefully observing the quiet music played in any stone in our vicinity, and yet come to grasp it all.

Any tiny detail of Nature can thus present the starting point for our philosophy to come to the highest peaks of human knowledge. Whatever the starting point of our inquiries, we can always get to these peaks. And using metaphors and other tools of artistic insights as the crucial elements of our perception and reasoning seems to be required for successfully climbing along the pyramid [163].

This train of thought also signifies that although the classical intellectual streams have for a long time maintained that human thinking is limited to the logical patterns of induction and deduction, that is not so. Ever since the dawn of human consciousness, analogies and metaphors have presented an equally important creative drive for human thinking. In fact, the essential messages that Nature communicates to humans are transmitted as metaphoric signs that draw parallels between different perceptual and conceptual levels of the experiential reality. Thus, I claim that it is impossible to find a natural system that could not serve as a metaphor for the order of the Universe as a whole with its own intrinsic order and interaction with the environment. Previously, I have shown how observing a single tree can lead to many metaphors that may enrich one’s ethical and aesthetic understanding of the reality [164]. The same is with any stone. The question Jorge Luis Borges asked, “Does this Aleph exist in the heart of a stone” [165] could be therefore answered with one big Yes. By looking at it alone, we can learn about the endless secrets of nature, our being and life.

Learning how to see “see a world in a grain of sand”, as in the William Blake’s poem [166], may, in fact, put us on the way to become a true systemic thinker. One of the essential aspects of systemic thought is applicability in an endless number of different systems. Moving back and forth between these systemic, all-encompassing thoughts and their reflections on small, directly observable systems, thus dynamically shifting our attention and references from special to general and vice versa, hides the true art of systemic thinking. Another crucial principle that all the systemic approaches are aware of is the contextual co-definition of natural qualities. Namely, the qualities of the systems are not defined by what they carry inside them solely, but by the environment that they exist in as well. Therefore, for a systemic thinker even a small stone may present a source of limitless discoveries and descriptions, knowing that even though this tiny stone may not change, the “realistic” context in which it exists and the “idealistic” context in which it is observed may be subject to modifications, which would bring about seeing always new qualities of the stone in always new lights.

In this section, I have shown that the balance between logical and metaphoric thinking, inherent in systemic reasoning, presents the way to reach the highest summits of human knowledge. Aesthetic insights, such as those outlined in this section, are shown as equally important for sustaining our scientific creativity as those gained by analytical training. They instill passion and sensitivity which are essential for successful scientific practice. On the other hand, scientific inventions themselves could be seen as providing the substrate for expanding the potential for intellectual and emotional growth of human beings, which fall in the domain of arts. Artistic and scientific spirits could thus be merged into one [9].

And so, with this pebble that hides the secrets of the entire Universe in our hands, we gaze at the sea of many unknown opportunities and discoveries stretching in front of our feet. I will lightly try to retain this landscape in the space of my mind for a long time. With it, the game of science and life alike can start. For, science is easy. The beach ball set to fly, the starfish, butterfly. It’s just so beautiful.