Waterborne cues from crabs induce thicker skeletons, smaller gonads and size-specific changes in growth rate in sea urchins

Abstract

Indirect predator-induced effects on growth, morphology and reproduction have been extensively studied in marine invertebrates but usually without consideration of size-specific effects and not at all in post-metamorphic echinoids. Urchins are an unusually good system, in which, to study size effects because individuals of various ages within one species span four orders of magnitude in weight while retaining a nearly isometric morphology. We tracked growth of urchins, Strongylocentrotus droebachiensis (0.013–161.385 g), in the presence or absence of waterborne cues from predatory Jonah crabs, Cancer borealis. We ran experiments at ambient temperatures, once for 4 weeks during summer and again, with a second set of urchins, for 22 weeks over winter. We used a scaled, cube-root transformation of weight for measuring size more precisely and for equalizing variance across sizes. Growth rate of the smallest urchins (summer: <17 mm diameter; winter: <7 mm diameter) decreased by 40–42% in response to crab cues. In contrast, growth rate of larger urchins was unaffected in the summer and increased in response to crab scent by 7% in the winter. At the end of the 22-week experiment, additional gonadal and skeletal variables were measured. Cue-exposed urchins developed heavier, thicker skeletons and smaller gonads, but no differences in spine length or jaw size. The differences depended on urchin size, suggesting that there are size-specific shifts in gonadal and somatic investment in urchins.

Introduction

Predators exert both direct and indirect effects on their prey. Direct consumption alters prey size distribution and density and can even prevent recruitment. For example, predation by Cancer crabs may be preventing recovery of over-harvested populations of the green sea urchin Strongylocentrotus droebachiensis in the Gulf of Maine (Steneck et al. 2004). However, indirect effects of predators can be equally important (Trussell et al. 2003; Trussell et al. 2004). Indirect effects occur when predator cues induce avoidance behaviors such as escape, use of refugia and aggregation, and when they cause changes in normal activity levels, feeding behavior, physiology and life-history (Kats and Dill 1998).

Inducible responses to waterborne, chemical cues from predators have been documented in many invertebrate taxa including: bryozoans (Harvell 1992), barnacles (Lively et al. 2000), cladocerans (Stibor and Lünig 1994), bivalves (Reimer and Tedengren 1996; Leonard et al. 1999; Freeman and Byers 2006) and gastropods (Appleton and Palmer 1988; Crowl and Covich 1990; Palmer 1990; Trussell 1996; Trussell and Smith 2000; Trussell and Nicklin 2002; Trussell et al. 2004; Dalziel and Boulding 2005; Edgell and Neufeld 2008). For example, the marine snails Littorina littorea and Tegula funebralis increased predator-avoidance behavior in response to extracts of seawater conditioned by crabs fed conspecifics (Jacobsen and Stabell 1999; Jacobsen and Stabell 2004).

Waterborne cues from predators can induce changes in life history. For example, the freshwater snail Physella virgata increased growth rate and delayed reproduction when exposed to effluent from crayfish actively feeding on conspecifics (Crowl and Covich 1990). Morphological changes, such as increased shell weight or thickness, have been observed in blue mussels Mytilus edulis (Reimer and Tedengren 1996; Leonard et al. 1999; Freeman and Byers 2006) and in marine snails such as Nucella lapillus (Palmer 1990), L. obtusata (Trussell 1996; Trussell and Smith 2000; Trussell and Nicklin 2002), L. littorea (Trussell et al. 2004), L. subrotundata (Dalziel and Boulding 2005) and N. lamellosa (Edgell and Neufeld 2008).

Inducible defenses require phenotypic plasticity

Inducible defenses, such as shell thickening, are underlain by genotypes that allow individuals to change phenotypes in response to environmental variation. Thus, prey may allocate more energy to life history traits such as growth and reproduction when predators are absent (Crowl and Covich 1990). Such phenotypically flexible defenses are favored in spatially and temporally variable environments for defenses that incur a cost; otherwise, defenses are expected to evolve towards fixed phenotypes (reviewed in Harvell 1990; Tollrian and Harvell 1999; Hollander 2008).

Phenotypic flexibility is widespread among echinoderms. For example, starved urchin larvae respond to food cues by increasing arm length (Strathmann et al. 1992; Miner 2007). Similarly, juvenile and adult sea urchins can reallocate energy among body components including spines (Raymond and Scheibling 1987), body wall and jaws (Ebert 1980; Edwards and Ebert 1991; Levitan 1991), gut (Lawrence et al. 1965; Pearse et al. 1970; Bishop and Watts 1992) and gonad (reviewed in Russell 1998). In adult sea urchins, larger size, longer spines, greater attachment forces or thicker skeletons may protect individual sea urchins from predation (Tegner and Levin 1983; Guidetti and Mori 2005). Recently, it has been found that sand dollar larvae can rapidly clone when exposed to the slime of fish predators (Vaughn and Strathmann 2008), but nothing is known about how post-metamorphic sea urchins change growth, morphology or reproduction in response to cues from predators.

Inducible responses can occur to a variety of predator cues

Howe and Sheikh (1975) identified the alarm pheromone anthopleurine in the sea anemone Anthopleura elegantissima and Howe and Harris (1978) subsequently demonstrated diet-related labeling of nudibranch predators via that alarm pheromone. Subsequent studies have often found that the strongest responses of prey species are elicited by chemical signals from damaged conspecifics (Appleton and Palmer 1988; Palmer 1990; Jacobsen and Stabell 1999; Hagen et al. 2002; but see Griffiths and Richardson 2006) or from predators fed a diet of conspecifics (reviewed in Kats and Dill 1998; Chivers and Smith 1998; see also: Behrens Yamada et al. 1998; Jacobsen and Stabell 1999; Hagen et al. 2002; Trussell and Nicklin 2002; Jacobsen and Stabell 2004; Griffiths and Richardson 2006; Laforsch and Beccara 2006). However, prey also respond to chemical cues from predators that are (1) of unknown feeding history and are not fed during experimental trials (Phillips 1978; Côté 1995; Côté and Jelnikar 1999; Mckay and Heck 2008), (2) starved (Nakaoka 2000; Freeman and Byers 2006) or (3) fed on species other than conspecifics (Appleton and Palmer 1988; Palmer 1990; Leonard et al. 1999; Hagen et al. 2002; Trussell and Nicklin 2002; Griffiths and Richardson 2006; Edgell and Neufeld 2008). For example, Rotjan et al. (2004) found that hermit crabs increased their occupancy of intact shells in the presence of effluent from green crabs, Carcinus maenus, fed on the same fish diet as the hermit crabs and then starved for 48 h prior to collection of the effluent for experiments. Thus, the generality of any specific biochemical cue is unknown.

The green sea urchin S. droebachiensis responds behaviorally to waterborne cues from urchin predators such as lobsters and Cancer crabs (Mann et al. 1984; Scheibling and Hamm 1991; reviewed in Scheibling and Hatcher 2001). These behaviors can be cue-specific: S. droebachiensis respond most strongly to cues from crushed conspecifics or predators fed conspecifics (Hagen et al. 2002). However, urchins also respond to chemical cues from predators that are starved (Freeman 2006; McKay and Heck 2008) or fed non-echinivorous prey (Scheibling and Hamm 1991; Hagen et al. 2002).

Smaller urchins typically respond more strongly to predator cues, exhibiting increased cryptic behavior (S. droebachiensis: 10–15 mm diameter, Scheibling and Hamm 1991; <20 mm diameter, Bernstein et al. 1981) and slowed feeding (S. franciscanus: Freeman 2006), although larger S. droebachiensis (>20 mm diameter) may exhibit increased aggregation (Bernstein et al. 1981). Similarly, the extent to which S. droebachiensis exhibit defensive, cryptic behavior by covering themselves with small rocks, algae and shells decreases with increasing size up to 15–20 mm (Dumont et al. 2007). Possibly, reinforcing the size-specificity of prey behavior is the size-specificity of predator choice; for example, smaller urchins are preferred over the largest urchins by lobsters (Tegner and Levin 1983; Hagen and Mann 1992) and crabs (Himmelman and Steele 1971). However, the size specificity of induced morphological responses to predators is relatively unstudied in general and is unknown in urchins.

We are interested in the size specificity of induced changes in growth, morphology and reproduction of the sea urchin S. droebachiensis in response to waterborne cues from a crab predator, independent of cues from conspecifics in the diet of those crabs. Thus, we test the effect of waterborne cues from C. borealis fed a non-echinivorous diet on growth, morphology and reproduction of juvenile and adult S. droebachiensis that ranged in size over four orders of magnitude.

Precision in measuring growth

The more precise is the measurement of size, the smaller the differences in growth that are detectable in an experiment. In urchins, the most commonly used measure of size is diameter (reviewed for S. droebachiensis in Scheibling and Hatcher 2001; see also: Scheibling and Anthony 2001; Russell and Urbaniak 2004; Brady and Scheibling 2005; Pearce et al. 2005). The measurement of diameter, however, is necessarily imprecise because the surface of an urchin is covered with spines and spine bases and because urchins are pentagonal rather than circular in cross-section. Instead, we use a more precise, weight-based measure of size, called nominal diameter (Ellers and Johnson 2009). Ellers and Johnson (2009) found that nominal diameter, which is derived from the cube root of weight, has a standard deviation 1/6 as large as the standard deviation of measured diameter and is therefore much more precise. An additional advantage of nominal diameter is that it incorporates size changes in all dimensions of the urchin, not just in diameter. Furthermore, using the cube root of weight also solves problems that would otherwise occur in regression analyses using weight because the variance of the dependent variable would be proportional to the magnitude of the independent variable.

For convenience of comparison to measured diameter, we determine nominal diameter by multiplying the cubed root of weight by a scaling constant derived from a linear regression between the cubed root of weight and measured diameter for 281 urchins ranging in weight from 0.065 to 161.385 g, and in diameter from 5.17 to 76.82 mm. Thus, while nominal diameter is an alternate measure of size that is similar in magnitude to measured diameter, nominal diameter is not an estimate of measured diameter.

Methods

Experimental design and source of urchins

To test the effect of upstream, waterborne cues from Cancer borealis crabs on urchin growth, 112 individual urchins, S. droebachiensis, were grown either in the presence or absence of four upstream C. borealis crabs. Urchins were maintained in individual hanging cube-shaped mesh baskets (11.4 × 11.4 × 10.8 cm); square holes in the mesh were 4 mm on the diagonal. Baskets were hung in two Plexiglas™ seawater aquaria (1.0 × 2.0 × 0.1 m, 200 l). The water depth was maintained at 0.1 m with a vertical standpipe and was aerated with bubblers. Crabs were housed behind a plastic grating made of eggcrate light panels (1.3 × 1.3 cm grid squares) located upstream of the experimental urchins; there was an identical uninhabited enclosure upstream of the urchins in the no-crab tank. Each tank was supplied with 10 μm filtered seawater from Harpswell Sound, Maine, through 19 mm diameter tubing. Flow into tanks was maintained at 4–5 L min⁻¹, as in Scheibling and Hamm (1991).

An initial experiment was run for 1 month during 14 June 2005 and 12 July 2005 and, to test the repeatability of those results, a second experiment was run for 5 months during 14 October 2005 to 17 March 2006 with a second set of urchins. Both the experiments were conducted under natural light and at ambient seawater temperatures. Seawater temperature was recorded hourly in each tank with temperature dataloggers. During the 4-week experiment water temperature averaged 14.9°C (range = 13–18°C); during the 22-week experiment water temperature averaged 6.0°C (range = 0–13°C).

For the 4-week experiment, urchins (0.065–161.385 g) were collected by hand from three field sites in Maine: subtidal sites near Mount Desert Island and in Cobscook Bay; and the rocky intertidal at Lands End, Bailey’s Island. Urchins were acclimated to laboratory conditions for at least 1 week prior to beginning the experiment. For the 22-week experiment, urchins (0.013–39.276 g) were obtained from the sea urchin hatchery run by the R. J. Peacock Canning Company in Lubec, Maine. These urchins were acclimated to tank conditions for ten days prior to beginning the experiment. In all experiments, urchins were fed Wenger urchin chow pellets (hereafter, pellets) ad libitum.

Prior to each experiment, each urchin was drip–dried and weighed (to the nearest 0.001 g). Urchins were sorted into size-matched pairs by weight. Within each pair one urchin was assigned at random to a treatment and the second in the pair was placed in the opposite treatment. Positions of the rows of eight baskets within each tank and of the baskets within each row were rotated once per week to minimize effects of basket position.

Cancer borealis crabs were collected in subtidal lobster traps near Harpswell, ME. Mean carapace length was 134.4 ± 2.02 mm (mean ± SE; N = 4) and 132.5 ± 3.0 mm (mean ± SE; N = 4) for the 4-week and for the 22-week experiment, respectively. To eliminate the potential for diet-related predator-labeling of crabs by S. droebachiensis (sensu Hagen et al. 2002), crabs were held in a flow-through seawater aquarium at ambient seawater temperatures and were not fed for 48 h prior to placement in the experiment. Crabs were subsequently fed a non-echinivorous diet of one Wenger urchin pellet per week for the duration of the 4-week experiment and for the first 8 weeks of the 22-week experiment. This protocol was changed as follows after one crab died in the 9th week of the 22-week experiment. Five crabs, of mean carapace length 139.4 ± 2.0 mm (mean ± SE), were added to the experiment. Four non-feeding crabs were always maintained upstream of the urchins by rotating eight crabs once per week between the urchin tank and an external holding tank. In the external holding tank, crabs were maintained at ambient seawater temperatures and fed a non-echinivorous diet of bivalves (mussels, M. edulis; soft-shell clams, Mya arenaria). Feeding was stopped and crabs were not fed for 48 h prior to rotation back into the experimental tank.

Weight and nominal diameter

We quantified size using nominal diameter, d _n, which is a measure of size that is based on weight, instead of measured diameter, d _m, because nominal diameter has a standard deviation 1/6th that of measured diameter and is therefore a more precise measure of size (Ellers and Johnson 2009). Nominal diameter is:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ d_{n} = k{\text{w}}^{0.33} , $$\end{document} 1

where the coefficient, k, is obtained from a linear regression of measured diameter as a function of the cube root of weight, w, with a defined intercept of zero. For 281 urchins ranging in weight from 0.065 to 161.385 g, and in diameter from 5.17 to 76.82 mm, k was 13.3 (r ² = 0.999, P ≪ 0.001). The resulting relationship between nominal and measured diameters is: d _m  = 1.01 d _n  − 0.57 (r ² = 0.996), with an intercept slightly below zero (P < 0.001) and a slope slightly greater than one (t test; P = 0.003).

Gonad and skeletal measurements

At the end of the 22-week experiment, gonads were dissected, blotted and weighed (to the nearest 0.001 g). A common convention in the urchin literature (Guillou and Lumingas 1999; Havardsson and Imsland 1999; Guillou et al. 2000; Chiaverano et al. 2004; Knip and Scheibling 2007) is to represent changes in gonad mass relative to the body mass using the gonad index (GI), which we calculate as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{GI}} = \frac{\text{gonad weight}}{\text{final wet weight}} \times 100\% , $$\end{document} 2

where final wet weight is the urchin’s weight at 22 weeks.

After removing the gonads the coelomic fluid was discarded. Ashed and ash-free dry weights were determined as in Wetzel et al. (2005). The gonads and somatic parts were kept separately, frozen at −80°C until they could be dried and ashed. After drying for 24 h at 85°C in pre-ashed, pre-weighed tin foil packets, samples were moved to a glass dessicant chamber for 4–6 h to cool and then weighed to determine dry weights. After ashing at 550°C for 4 h in an ashing oven and subsequently cooling for 6 h in the glass dessicant chamber, skeletons and gonads were weighed (to the nearest 0.0001 g) to obtain ashed weight. Ash-free dry weight (AFDW) was determined by subtracting ashed weight from dry weight. A gonadal AFDW index (GAI) was calculated as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{GAI}} = \frac{\text{gonadal AFDW}}{\text{total AFDW}} \times 100\% $$\end{document} 3

We calculate the fraction of an urchin’s weight that is due to skeleton by using a skeletal index (SI):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{SI}} = \frac{\text{skeletal ashed weight}}{\text{final wet weight}} \times 100\% $$\end{document} 4

We took additional measurements from 30, randomly selected and ashed skeletons: (1) length and ashed weight of the demipyramids of the Aristotle’s lantern (jaws), (2) the length of the spines and (3) the thickness of the skeletal plates. We measured spine length to the nearest 0.2 mm and demipyramid length to the nearest 0.08 mm using a dissecting microscope. We measured weight to the nearest 0.0001 g on all unbroken demipyramids; if fewer than ten demipyramids were intact, then the average weight of intact pyramids was multiplied by ten to obtain a total weight of demipyramids. We calculated mean spine length from the five longest spines of each urchin; maximum length was the longest spine. Test thickness, measured on a dissecting microscope to the nearest 0.02 mm, was determined from three interambulacral plates near the ambitus and from three interambulacral plates near the aboral end of each urchin.

Data analysis for growth, plate thickness, spine length and demipyramid weight

We use analyses of covariance (ANCOVA; Zar 1996) for the following dependent variables: change in nominal diameter, aboral and ambital plate thickness, maximum spine length, mean spine length, mean demipyramid length and cube root of demipyramid weight. Initial and final nominal diameters are the covariates for growth analyses (change in nominal diameter) and skeletal analyses (all other variables), respectively.

Least-squares linear regression analyses, such as ANCOVA, are appropriate when measurement error in the independent variable is negligible; however, problems arise if variance in measurement of the independent variable is substantial (Warton et al. 2006). Specifically, significant error in the measurement of the independent variable results in the underestimation of the slope for allometric relationships with a low r ² (LaBarbera 1989). Thus, either the absence of significant measurement error needs to be established or measurement error has to be estimated and used to adjust the analysis. Reduced major axis estimates are often used to avoid such underestimation of the slope; however, the use of reduced major axis can yield meaningless results, such as a slope between two uncorrelated variables (Harvey and Pagel 1991). The simplest way to determine whether measurement error creates problems in the analysis is to make multiple measurements of the independent variable. If repeated measurements of the independent variable are highly correlated then the bias in the slope due to measurement error will be small (Warton et al. 2006). The independent variable for all of the analyses above is nominal diameter, which is a size proxy for our measured variable, weight. We use the reliability ratio, κ (where κ = r, and r is the correlation between repeated measurements of a variable; Fuller 1987) to estimate the measurement error in weight. The slope corrected for the measurement error is the slope obtained from the regression divided by the reliability ratio, κ. To determine κ, we made three separate measurements of weight (to the neareast 0.001 g) on 50 S. droebachiensis ranging in size from 0.031 to 88.558 g and converted these weights to nominal diameter. We find that κ = 0.9999 for all pairwise linear regressions between separate measurements of nominal diameter. Thus, slopes of ANCOVA analyses using nominal diameter as the independent variable are not adjusted for error in the independent variable.

ANCOVA first tests for common regression slopes among treatment groups. When slopes do not differ significantly, then ANCOVA tests for differences in elevations. When slopes do differ, a posteriori pairwise comparisons of slopes and intercepts are assessed using Tukey’s q test (Zar 1996, pp. 367–368). When slopes are parallel, the common slope is used to plot the regression lines shown in figures; when there are no differences in slopes or intercepts, the common slope and common intercept are used to plot the regression lines shown in figures.

We separate our analyses of growth into three phases based on the Tanaka function, which is a function that is often used to fit urchin growth (Ebert and Russell 1993; Russell et al. 1998; Ebert et al. 1999; Russell 2001; Ebert 2001; Johnson et al. 2002; Ebert 2008). Based on the Tanaka function, we expected that growth rate would (1) initially be low and increase with increasing size up to a maximum for the smallest urchins (the lag region), (2) subsequently decrease linearly with increasing size for mid-sized urchins (the steadily declining region) and (3) approach a zero growth rate for the largest urchins (the tail region).

ANCOVA analyses were run separately for each of these regions, with the breakpoints decided by eye. The breakpoints between regions (1) and (2) are particularly clear because when a group of urchins is grown together over the size range encompassed by this study there is a visual gap in size created. This gap occurs because urchins experiencing the fastest, peak growth accelerate in size away from those growing more slowly in region (1).

Data analysis for gonads

An ANCOVA of gonad mass as a function of body mass is not appropriate because the relationship is nonlinear both on standard and on logarithmic plots. This is because the smallest urchins have disproportionately smaller gonads. Ebert (1999, p. 197) suggested using the following nonlinear fitting function for fitting gonad development:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ y = \alpha \left( {x - \gamma } \right)^{\beta } $$\end{document} 5

where y is gonad size, x is urchin size and α, β and γ are fitted variables. The specific measure of y and x was not specified in Ebert (1999); however, Ebert (2008) used gonad weight as y and urchin diameter as x. We use the general form from Ebert (1999, 2008):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ g = \alpha_{g} \left( {s - \gamma_{g} } \right)^{{\beta_{g} }} $$\end{document} 6

where g is the cube root of gonad weight and s is nominal diameter (d _n) in cm (d _n/10). This physical representation of mass can be envisioned as the size of the mass if it had the shape of a cube and a density of one (g cm⁻³), which is the density of seawater at 20°C to one significant figure. We call the length (cm) of such a cube the equivalent length. Thus, g is the gonad equivalent length.

We use the cube root transformation because this transformation makes errors in the regression independent of the independent variable (Ellers and Johnson 2009). Many other common representations of the data have error increasing as a function of the independent variable. For example, log–log, inverse and square root transforms all fail to produce regression errors that are independent of the independent variable.

For gonadal AFDW we use:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ g_{\text{afdw}} = \alpha_{\text{ag}} \left( {s_{\text{afdw}} - \gamma_{\text{ag}} } \right)^{{\beta_{\text{ag}} }} $$\end{document} 7

where g _afdw is the gonadal AFDW equivalent length (the cube root of AFDW of the gonads) and s _afdw is the total AFDW equivalent length (the cube root of the total AFDW).

Prior to running the nonlinear regression to solve for the fitted constants in Eqs. 6 and 7 we excluded gonads with g and g _afdw that fell within one standard deviation of zero. The standard deviation in the error of g and g _afdw was calculated as the standard deviation of the repeated measurements of d _n/k (Ellers and Johnson 2009), where k is the coefficient from Eq. 1. This calculation gives a standard deviation of 0.0091 cm. This exclusion is necessary because it is possible to get complex numbers when the measured value of x is less than the fitted x intercept (i.e., when s is less than γ). This criterion resulted in the exclusion from analysis of one individual with zero gonad weight and six individuals with zero gonadal AFDW weight.

We fit pooled data from both treatments with Eqs. 6 and 7 and calculate the mean residuals for each treatment. We compare mean residuals with t tests and Mann–Whitney U tests.

We plot gonad data as GI and GAI, for clarity and for consistency with general usage in the literature (Guillou and Lumingas 1999; Havardsson and Imsland 1999; Guillou et al. 2000; Chiaverano et al. 2004; Knip and Scheibling 2007), by converting the fitted lines to GI by:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{GI}}_{\text{fitted}} = 100 \times \frac{{(\alpha_{g} (s - \gamma_{g} )^{{\beta_{g} }} )^{3} }}{{(10s/k)^{3} }} $$\end{document} 8

and to GAI by:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{GAI}}_{\text{fitted}} = 100 \times \frac{{(\alpha_{\text{ag}} (s_{\text{afdw}} - \gamma_{\text{ag}} )^{{\beta_{\text{ag}} }} )^{3} }}{{(s_{\text{afdw}} )^{3} }} $$\end{document} 9

Data analysis for skeletal ashed weight

We compare skeletal ashed weight between treatments using ANCOVA, with final wet weight as the covariate. We log-transform the variables for this ANCOVA because the relationship between the non-transformed variables is nonlinear.

In addition, we fit SI with the following nonlinear fitting function:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{SI}} = \alpha_{\text{si}} + \beta_{\text{si}} e^{{ - \gamma_{\text{si}} {\text{d}}_{n} }} $$\end{document} 10

where α _si, β _si and γ_si are fitted variables. We chose this function because it results in no systematic residuals (sensu Weisberg 1980). We fit pooled data from both treatments with Eq. 10 and calculate the mean residuals for each treatment. We compare mean residuals with t tests and Mann–Whitney U tests and when treatments are significantly different each treatment is fit separately.

Results

Growth at ambient temperatures for 4 weeks (June–July 2005)

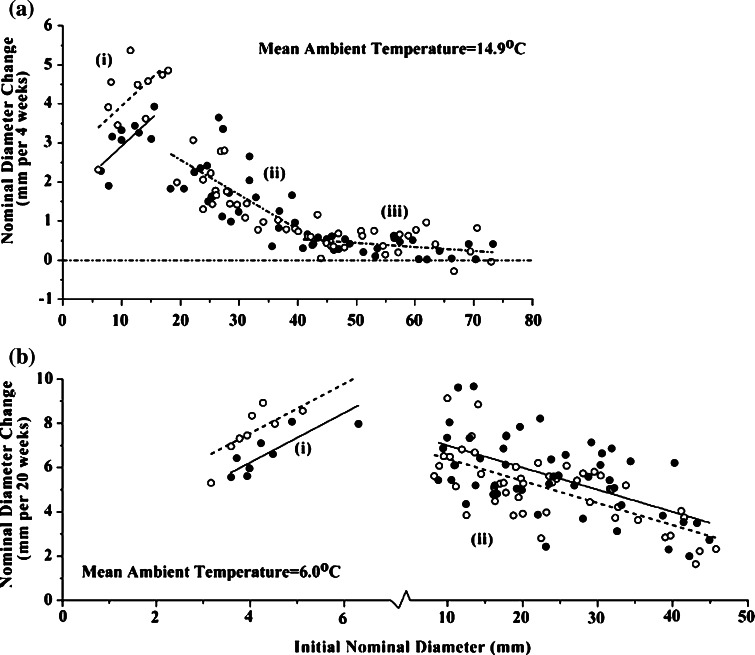
Urchins in the (1) lag region (up to 17 mm nominal diameter) grew 67% faster in the absence of upstream waterborne cues from C. borealis than in the presence of such cues, and this difference is significant (Table 1; Fig. 1a). There are no significant differences in growth rate for urchins in the (2) steadily declining and (3) tail regions of growth.

Table 1.

Strongylocentrotus droebachiensis: comparison of growth in the presence or absence of effluent from crabs (Fig. 1) in the 4- and 22-week experiments

Date	Size class (mm)	df	Common slopea	Slope SE	R2	Crab interceptb	No crab intercept	P value that intercepts are different between crab and no crab
4 week growth
(i)	0–17	2, 15	0.14	0.045	0.60	1.5	2.5	0.003
(ii)	17–40	2, 41	−0.089	0.018	0.37	4.3b		0.86
(iii)	40–80	2, 47	−0.0089	0.0039	0.15	0.90b		0.09
20 week growth
(i)	0–7	2, 13	1.1	0.242	0.69	1.8	3.1	0.002
(ii)	7–50	2, 95	−0.10	0.012	0.41	7.9	7.4	0.044

Results of ANCOVA analyses for: (i) small urchins in the lag region; (ii) middle-sized urchins in the steadily declining region; and (iii) larger urchins in the tail region

^aAll slopes significantly different from zero (all P < 0.05), but not significantly different between treatments (all P > 0.05), so only common slopes are given

^bOne value is given for the intercepts of both treatments when not significantly different from each other

Fig. 1.

Strongylocentrotus droebachiensis. Nominal diameter change (mm) as a function of initial nominal diameter (mm) for urchins grown in the presence (black circles, solid lines) or absence (open circles, dashed lines) of waterborne cues from the crab Cancer borealis. Growth is shown for a four and b 20 weeks. Lines indicate least squares linear regressions for: i small urchins in the lag region, ii middle-sized urchins in the steadily declining region; and iii larger urchins in the tail region. For clarity, the scale is expanded for the lag region in the 20-week period. Separate lines for each treatment indicate that an ANCOVA analysis indicates that a one slope, two intercept model best fit these data; a single dot-dash line for both treatments indicates that a one slope, one intercept model best fit these data. See Table 1 for statistics

Growth at ambient temperatures for 20 weeks (October 2005–March 2006)

There are also significant differences in growth rate in the second experiment (Table 1; Fig. 1b). Urchins in the (1) lag region (up to 7 mm nominal diameter) grew 72% faster in the absence of crab effluent. Conversely, urchins in the (2) steadily declining region grew 7% faster in the presence of crab effluent. There were no urchins large enough to be in the (3) tail region at the ambient temperatures of this experiment (mean = 6.0°C; range = 0–13°C).

Gonads

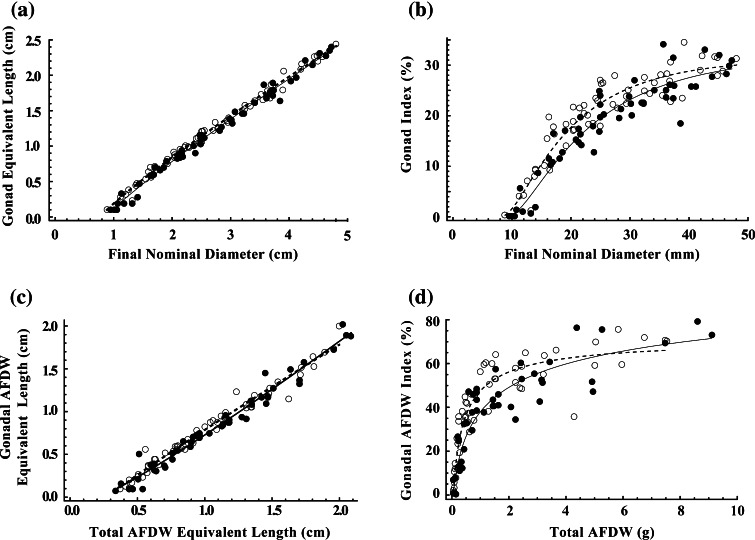
The t tests and Mann–Whitney U tests on residuals from nonlinear fits of pooled data to Eqs. 6 and 7 indicate that between treatment differences in gonads are significant (Table 2; Fig. 2a, c). GI and GAI increase up to a maximum of 30 and 70%, respectively, with increasing size (Fig. 2b, d). Gonad indices are, on an average, 10% (GI) and 16% (GAI) greater for urchins grown in the absence of cues. Between treatment differences in gonad indices are greatest for intermediate-size urchins: the fitted lines converge for urchins larger than 25 mm nominal diameter or three grams total AFDW.

Table 2.

Strongylocentrotus droebachiensis: nonlinear fits of each treatment to Eqs. 6 and 7

Gonad measurement (cm)	N (crab, no crab)	Crab nonlinear fit	No crab nonlinear fit	P values of t test; U test
g	56, 57	0.70 (s–0.86)0.90	0.70 (s–0.77)0.88	Both <0.0001
gafdw	51, 57	0.95 (safdw–0.21)1.12	1.07 (safdw–0.27)0.94	0.03; 0.004

The t tests and Mann–Whitney U tests compare the mean residuals for each treatment from the nonlinear fit to the pooled data for gonad equivalent length (g) as a function of final nominal diameter in cm (s) and gonadal AFDW equivalent length (g _afdw) as a function of total AFDW equivalent length (s _afdw). Fits to each treatment are shown separately in Fig. 2

Fig. 2.

Strongylocentrotus droebachiensis.a Gonad equivalent length (cm) and b gonad index (%) both as a function of final nominal diameter (mm), c gonadal AFDW equivalent length (cm) as a function of total AFDW equivalent length (cm) and d gonadal AFDW index (%) as a function of total AFDW (g) for urchins grown for 22 weeks in the presence (black circles, solid lines) or absence (open circles, dashed lines) of waterborne cues from the crab Cancer borealis. Lines in a, b, c and d indicate the fit of Eqs. 6, 8, 7 and 9, respectively, to each treatment. All lines are significantly different between treatments. See Table 2 for statistics

Skeleton

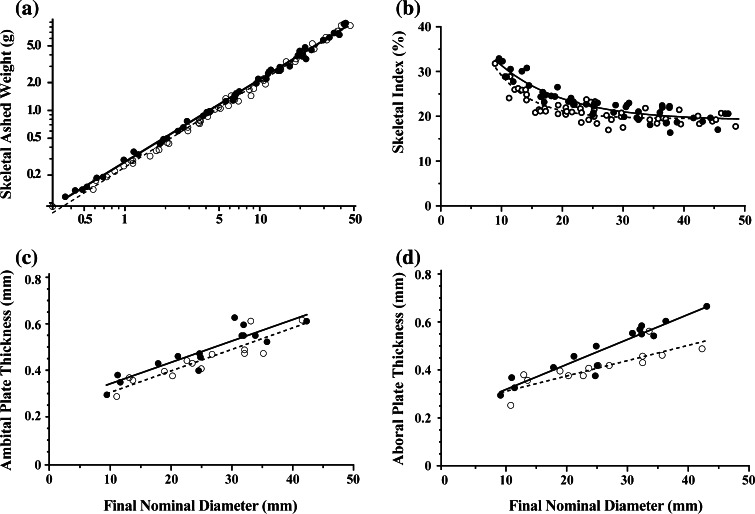
Significant differences in slopes of log-transformed data indicate that differences in skeletal ashed weight are greatest for smaller urchins and converge for larger urchins (Table 3; Fig. 3a); urchins exposed to crab cues tend to have greater skeletal ashed weights. Similarly, t tests and Mann–Whitney U tests on residuals from a fit to Eq. 10 indicate that between treatment differences in skeletal index (SI) are significant (Table 3; Fig. 3b). SI decreases from 30 to 20% with increasing size of urchin, and between treatment differences in SI are greatest for intermediate-sized urchins: the fitted lines converge for urchins greater than about 25 mm nominal diameter. On an average, the proportion of final wet weight that was skeleton increased by 8.2% for urchins grown in the presence of crab cues.

Table 3.

Strongylocentrotus droebachiensis: comparison of skeletal variables from the 22-week experiment (Figs. 3, 4)

(A) Skeletal variables for two slope ANCOVAs	df	Crab				No crab				P value of ANCOVA that slopes differ
		N	Slope	Slope SE	R2	N	Slope	Slope SE	R2
Skeletal ashed weight (g)	2, 104	53	0.893	0.007	0.997	56	0.920	0.008	0.995	0.01
Aboral plate thickness (mm)	2, 26	15	0.010	0.001	0.88	15	0.006	0.001	0.71	0.01

(B) Skeletal variable for nonlinear fits	n	Crab (n = 53)	No crab (n = 56)	P value of t test/U test
Skeletal index	109	19.1 + 30.8\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{e}}^{{ - 0.092 d_{n} }} $$\end{document}	19.4 + 52.1\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{e}}^{{ - 0.17d_{n} }} $$\end{document}	both <10−6

(C) Skeletal variables for one slope ANCOVAsa	df	Common slope	Slope SE	R2	Crab interceptb	No crab interceptb	P value of ANCOVA that intercepts differ
Ambital plate thickness (mm)	2, 26	0.0091	0.0008	0.824	0.251	0.215	0.001
Maximum spine length (mm)	2, 26	0.0309	0.0021	0.888	0.143		0.74
Mean spine length (mm)	2, 26	0.0298	0.0021	0.880	0.127		0.55
Mean demipyramid length (mm)	2, 26	0.0202	0.0008	0.960	0.051		0.86
Demipyramid weight (g)	2, 26	0.0133	0.0005	0.956	0.049		0.94

(A) Results of ANCOVA analyses on skeletal variables for which the slopes were significantly different between treatments; final nominal diameter (mm) is the covariate; regression for skeletal ashed weight was on log-transformed variables

(B) Result of a t test and a Mann–Whitney U test comparing the mean residuals from the nonlinear fit (Eq. 10) of the skeletal index (Eq. 4) as a function of final nominal diameter for all urchins pooled. The nonlinear fits to each treatment are shown separately in Fig. 3

(C) Results of ANCOVA analyses for skeletal variables for which the slopes were not significantly different between treatments; final nominal diameter (mm) is the covariate; regression for demipyramid weight is on the cube root of that variable

^aAll slopes significantly different from zero (all p < 0.05), but not significantly different between treatments (all p > 0.05), so only common slopes are given

^bOne value is given for the intercepts of both treatments when not significantly different from each other

Fig. 3.

Strongylocentrotus droebachiensis.a Skeletal ashed weight (g), b skeletal index (%), c ambital plate thickness (mm) and d aboral plate thickness (mm) each as a function of final nominal diameter (mm) for urchins grown for 22 weeks in the presence (black circles, solid lines) or absence (open circles, dashed lines) of waterborne cues from the crab Cancer borealis. For a the lines indicate least squares linear regressions on the log transformed data; for b the lines indicate fit of Eq. 10; for c and d the lines indicate least squares linear regressions. Separate lines for each treatment indicate significant differences between treatments. See Table 3 for statistics

Skeletal plate thickness differs significantly between treatments: ambital plates of crab-exposed urchins are 15% thicker than those of controls (Table 3; Fig. 3c). Thickening of aboral plates is significantly more sensitive to size of urchins (ANCOVA, Table 3), with as much as 25% greater thickening of aboral plates in the largest cue-exposed urchins (Fig. 3d).

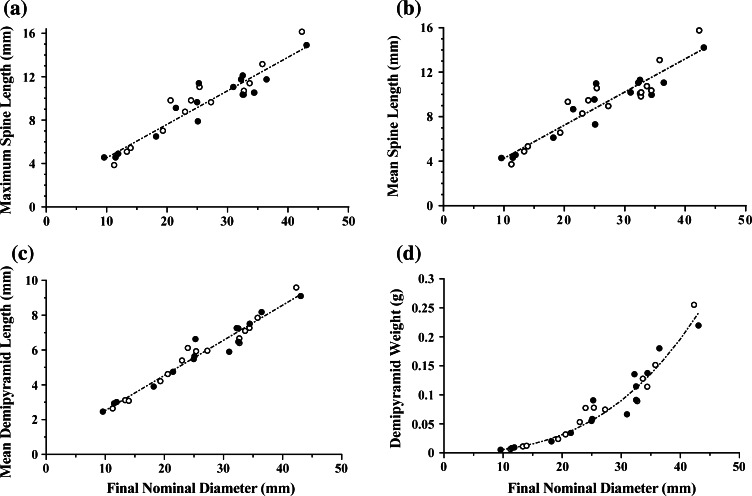
Maximum spine length, mean spine length of the five longest spines, mean demipyramid length and demipyramid mass do not differ between treatments (ANCOVA analyses: Table 3; Fig. 4).

Fig. 4.

Strongylocentrotus droebachiensis. a maximum spine length (mm), b mean spine length (mm), c mean demipyramid length (mm) and d demipyramid weight (g) all as a function of final nominal diameter (mm) for urchins grown for 22 weeks in the presence (black circles, solid lines) or absence (open circles, dashed lines) of waterborne cues from the crab Cancer borealis. For a–c the lines indicate least squares linear regressions on the axes variables shown; for d the line indicates the least squares linear regression fit for the cube root of demipyramid weight as the dependent variable shown transformed back to demipyramid weight. The single dot-dash line indicates no significant difference between treatments. See Table 3 for statistics

Discussion

Strongylocentrotus droebachiensis is known to exhibit defensive behavioral responses to waterborne cues from predators (Hagen et al. 2002) and these behaviors can be size-specific (Bernstein et al. 1981; Scheibling and Hamm 1991; Freeman 2006). However, this is the first study to demonstrate growth, skeletal and reproductive differences in sea urchins in response to such cues. The size-specificity of our results supports the hypothesis that in S. droebachiensis there are predator-induced, size-specific strategic shifts in resource allocation between growth, skeletal thickness and reproduction.

Growth, size and risk of predation

Predation risk can vary with prey size. For example, urchin predators typically prefer smaller urchins (lobsters and crabs: Himmelman and Steele 1971; lobsters: Tegner and Levin 1983; Hagen and Mann 1992; seastars: Freeman 2006). The behavioral avoidance of predators can also depend on size. For example, increased crypticity and immobility of S. droebachiensis smaller than 3–6 mm diameter (Scheibling and Hamm 1991) or smaller than 20 mm in diameter (Dumont et al. 2007) lowered risk of predation. Perhaps, lower energy acquisition due to predator-induced cryptic behaviors explains the slowed growth rate of our smallest urchins (winter: <7 mm; summer: <17 mm).

Field observations support the hypothesis that risk of predation is size-specific in S. droebachiensis. For example, wild S. droebachiensis larger than 6 mm start to outgrow spatial refuges offered by cobble and require larger boulders to achieve the same measure of protection (Scheibling and Hamm 1991). Thus, Scheibling and Raymond (1990) found that the density of juvenile S. droebachiensis living in a cobble area declined, presumably because of this greater vulnerability, once their size exceeded 7 mm. Similarly, urchins 6–10 mm (Hereu et al. 2005) and 25–30 mm (Scheibling and Hamm 1991) in diameter were consumed at higher rates than urchins 2–6 mm in erect algal assemblages or on cobbles, respectively. The largest urchins, however, attain a size refuge from many predators (Himmelman and Steele 1971; Tegner and Levin 1983).

For wild urchins, predation risk is inversely proportional to body size because larger size, thicker skeletons (Guidetti and Mori 2005; this paper, Fig. 3) and longer spines make them harder to grasp (Tegner and Levin 1983), to crack (Ellers et al. 1998; Guidetti and Mori 2005) and to detach (Guidetti and Mori 2005). The exact diameter at which an urchin is safe depends on predator type and size. For example, S. droebachiensis larger than 38 mm diameter are too large to be eaten by the size of C. borealis we used (based on Himmelman and Steele 1971). Thus, perhaps our mid-sized (>7 mm) urchins switched to more rapid growth in the presence of predator scent to reduce the time spent at the most vulnerable sizes.

Skeletal and reproductive changes

The increased investment in calcite indicated by the greater skeletal mass and skeletal index of urchins exposed to crab-effluent could have been due to greater investment in spines, jaws or skeleton, all of which are developmentally plastic (see “Introduction”). For example, both increased spine length (Raymond and Scheibling 1987; Johnson, Ellers and Davies, unpublished data) and increased jaw height (Edwards and Ebert 1991; Levitan 1991) can occur in response to food limitation. However, the increased skeletal weight of our urchins was due only to thickening of skeletal plates. Energy reallocation towards skeletal thickening could have contributed to the decreased growth rates observed in small urchins and to smaller gonads, but was additional to the increased growth rate of the mid-sized urchins. This latter result supports the hypothesis that skeletal thickening was not just due to reduced somatic growth consequent to reduced foraging, but also in part to direct morphogenetic responses to cueing (for snails see: Palmer 1990; Brookes and Rochette 2007; Edgell and Neufeld 2008). For post-metamorphic urchins, this is the first time it has been shown that predator cues can induce changes that impact shell form.

Plate thickening presumably strengthens the skeleton. Urchin skeletons consist of arrays of plates sutured together with a combination of calcitic, stereomic projections and collagenous ligaments. The strength of the skeleton depends on the strength of the individual plates themselves and on the strength of the sutures holding the plates together. Assuming the material strength of the skeletal calcite remains similar, the greater cross-sectional area of thicker skeletal plates provides increased structural strength making individual plates less likely to break. In growing urchins, sutural calcite is replaced by sutural ligaments, which increases the strength of urchin skeletons (Ellers et al. 1998). Increasing the cross-sectional area of skeletal plates also provides more attachment area for the collagenous sutural ligaments, generating greater potential sutural strength. Thus, by thickening skeletal plates, urchins produce stronger, more crush-resistant skeletons.

Some responses to crab effluent diminished with increasing urchin size: (1) there are no significant changes in growth rate for urchins larger than 17 mm nominal diameter in the 4 week study (Fig. 1a), (2) differences in gonad indices diminish for urchins larger than 25 mm nominal diameter or three grams total AFDW (Fig. 2b, d) and (3) differences in skeletal ashed weights and SI diminish for urchins greater than 25 mm nominal diameter (Fig. 3a, b). Not all significant differences decrease with size, however: between treatment difference in skeletal plate thickness is constant over all sizes of urchins for ambital plates and actually increases with size for aboral plates (Fig. 3c, d). Plates are initially produced aborally, and so skeleton in this area represents the most recent growth history. Thus, although there are some indications that there is less selective pressure for larger sea urchins to divert resources in response to crab cues, thickening of aboral plates may be an exception.

Lower gonad indices in mid-sized urchins do not necessarily represent a diversion of resources away from reproduction, because mid-sized urchins also grew more rapidly to a larger size: an equal investment in gonads between treatments would result in a smaller size-specific gonad index in the faster growing urchins. However, if lower gonad indices also represent a delay in immediate reproductive output, this delay can be favored by increased fitness if juvenile mortality is greater than adult mortality (Crowl and Covich 1990; Stibor and Lünig 1994). Mortality in wild urchins probably falls predominantly on mid-sized (10–40 mm diameter) individuals (reviewed in Scheibling 1996; Hunt and Scheibling 1997), which is within the size range where our urchins showed growth acceleration.

Magnitude of the response

The specific kind and intensity of waterborne cues received by our urchins are not known, but they emanated from four, large crabs fed a non-echinivorous diet. Sensitivity to cue type is common (see “Introduction”). For example, it has been well documented in intertidal snails, which increase predator-avoidance behavior (L. littorea: Jacobsen and Stabell 1999; T. funebralis: Jacobsen and Stabell 2004) or shell thickening (L. obtusata: Trussell and Nicklin 2002) in response to cues from predators fed conspecifics relative to other diets. In S. droebachiensis, stronger avoidance responses were elicited by waterborne cues from wolf–fish fed a diet of urchins than from a crab (C. pagurus) fed a diet of urchins; behavioral responses to both predators weakened when the predator’s diet was mussels (Hagen et al. 2002). The intensity of indirect responses to predators can depend not only on cue type, but also on cue intensity. For example, S. droebachiensis responded less strongly to water conditioned with extracts of crushed conspecifics when it was diluted (Hagen et al. 2002). Increased predator density or size could increase the intensity of the cue; conversely, increased density of conspecifics might decrease the intensity of prey response (for a model, see Peacor 2003). For example, N. lamellosa exposed to waterborne cues from big (83–104 mm carapace width) C. productus grew more slowly and had thicker shells than those exposed to cues from small (46–70 mm carapace width) C. productus (Edgell and Neufeld 2008). Based on studies such as these, we expect that induced responses to cues released from crushed conspecifics, from crabs fed conspecifics or from larger predators might be stronger than those we observed.

Shell form and paleontology

Factors that change shells in extant animals can provide clues to paleontological changes in shell form over evolutionary time. Over short periods, existing developmental pathways accelerate evolutionary responses to novel predators (Freeman and Byers 2006; Edgell and Neufeld 2008). Over longer evolutionary time periods, selection for anti-predator traits such as shell form may have led to the divergence of prey populations and the subsequent evolution of new species (Vamosi 2005). Vermeij (2002) postulated that changes in shell form are driven by changes in metabolism and shaped by metabolism-powered mechanical forces, such as those exerted by muscles or by coelomic pressures during the building of echinoid skeletons (Ellers 1993; Ellers and Telford 1997). Vermeij (2002) argued that shell thickness and sculpture are negatively correlated with growth rate and that growth rate in turn is constrained by the availability of energy for metabolism-powered processes. Thus, he hypothesized that early molluscan forms were low energy animals with relatively simple, thin shells and that the subsequent radiation of molluscs involved the evolution of higher metabolic rates; the resultant increase in available metabolic resources made possible the evolution of heavier, thicker shells.

Future directions

Our urchins were fed ad libitum; in the field, resource availability will fluctuate and resource allocation might well be affected. For example, perhaps the gonads of the largest urchins were unaffected because they had reached maximum capacity; a study that included food limitation might reveal differences in allocation to gonads even in the larger urchins. Furthermore, the largest urchins grow, and therefore accumulate differences, very slowly; longer-term studies might also reveal differences even in the largest urchins. Temperature also influenced the results of this study, for example: colder urchins grew more slowly. It would be interesting to explore more deeply the effect of temperature on size-specific growth and resource allocation in sea urchins.

Sea urchin skeletons are strengthened by the collagen in their sutures (Ellers et al. 1998). This collagen is a catch connective tissue (CCT) that can be strengthened or softened under nervous or hormonal control. CCT softens during growth and experimentally softened CCT weakens skeletons (Johnson et al. 2002). Thus, CCT has the potential to control short-term induced changes in skeletal strength. Given the degree of skeletal and growth changes we observed and the strong behavioral responses of urchins to predators observed by other studies, it would also be interesting to test whether urchins can further increase skeletal strength by active, behavioral stiffening of their CCT in response to predator scent.