Statistical Considerations for Analysis of Microarray Experiments

Abstract

Microarray technologies enable the simultaneous interrogation of expressions from thousands of genes from a biospecimen sample taken from a patient. This large set of expressions generates a genetic profile of the patient that may be used to identify potential prognostic or predictive genes or genetic models for clinical outcomes. The aim of this article is to provide a broad overview of some of the major statistical considerations for the design and analysis of microarrays experiments conducted as correlative science studies to clinical trials. An emphasis will be placed on how the lack of understanding and improper use of statistical concepts and methods will lead to noise discovery and misinterpretation of experimental results. Clin Trans Sci 2011; Volume 4: 466–477

Introduction

Microarray technologies were developed in the 1990s in the field of molecular biology as a means of simultaneously measuring the expression of thousands of genes from a single sample. The use of microarrays has extended across the fields of basic science and translational research, and has changed the way investigators approach the scientific goals of discovery and validation. Clinical trials are designed to test hypotheses and rigorously monitor and assess health interventions, whether as observational studies or randomized controlled trials. To investigate correlative science objectives related to the treatment and disease processes, the collection of biospecimens has become increasingly common in treatment trials. Increasing availability and decreasing costs of genomic assays allows for evaluation of gene expression profiles as biomarkers of disease. The hope is to use this genomic information of individual patients to select or optimize their preventative and therapeutic care. The data structures and volume generated by microarrays create many bioinformatic challenges: data warehousing, annotation, and hardware and software requirements. Furthermore, they require proper understanding of the statistical considerations for the design and analysis.

Micorarray studies yield a genomic profile based on thousands of gene expressions for each patient. Heatmaps have been used extensively in the genomics literature to illustrate the presence of clusters among the patients and also among the genes solely based on these genomic profiles. Two sample heatmaps are shown in Figure 1 . In each heatmap, the columns represent gene expression profile for the patients while the rows represent the expression profiles for each gene across all patients. The intensity of the colors is used to illustrate the relative level of expression. Bright red indicates relative overexpression while bright green indicates relative underexpression. These specific examples show gene expression profiles for two sets of patients: responders and nonresponders. The heatmap to the left consists of 20 patients from each group while the heatmap on the right consists of 3 patients from each group. The presence of two clusters across the rows and two clusters across the columns is observed. This may suggest that the gene expression profiles can distinguish a responder from a nonresponder. This also suggests that there may be two main categories of genes driving this pattern of separation among the patient class. These apparent observations are deceiving as both illustrations are produced on the basis of simulated noise. Any observed clustering or pattern among the patients or genes is completely random. In due course, we will carefully examine how improper use and interpretation of statistical tools and methods can lead to this type of noise discovery.

Figure 1.

These heatmaps illustrate noise discovery. Each heatmap is based on gene expression profiles from fictitious n responders and n nonresponders (n= 20 and n= 3 in the left and right panels, respectively). For each example, gene expression profiles consisting of m= 50,000 probes were simulated. For each probe, the Student t‐test was calculated. The heatmaps were constructed based on the probe sets for which the corresponding marginal p‐value for the t‐test were less than 0.05. The colors red and green are used to annotate relative over‐ and underexpression. The responder and nonresponder clusters have been annotated with blue and yellow bars, respectively.

The concepts discussed in this article will be extensively motivated within the context of two public and highly cited cancer microarray data sets. Golub et al. ¹ identified expression profiles in leukemia patients distinguishing acute lymphoblastic leukemia (ALL) and acute myeloid leukemia (AML) subtypes while Beer et al. ² identified and validated a prognostic set of genes for early‐stage lung adenocarcinoma. Both data sets were hybridized to the Affymetrix hu6800 chip (Affymetrix, Santa Clara, CA, USA).

When designing and analyzing a microarray experiment within the context of a clinical trial, it is imperative to clearly identify the experimental units. These will typically be the patients who were registered to the clinical study, and provided consent and usable RNA to be assayed on microarray chips. Note that the RNA from a patient may be assayed on multiple chips as technical or biological replicates, or as repeated measurements taken within the context of a longitudinal study. The number of experimental units equals the number of patients and not the number of chips. It is also important to identify any experimental factors. These may include the study drug the patient was randomized to, or the time points (e.g., baseline or post–drug exposure) at which the samples were obtained. In microarray experiments, the covariables of primary interest are the genes interrogated or probed by the microarray assay. What is measured is not the expression of genes but rather light intensities on probes designed to interrogate the gene. We shall, at a potential risk of abuse of notation, refer to these probes as genetic features or markers. For each patient, the vector of expressions constructed from these genetic features, or a subset thereof, will constitute a gene expression profile.

This article is not meant to provide an exhaustive account of statistical issues related to the analysis of microarrays. Its primary focus will be to illustrate how lack of understanding of statistics invariably leads to misinterpretation of the results and, as we have already illustrated, to noise discovery. The books by Speed, ³ McLachlan et al., ⁴ and Simon et al. ⁵ provide general and accessible accounts on statistical methods for analysis of microarray data.

Preprocessing

A primary objective of most microarray studies is to identify individual features associated with a phenotype or an experimental factor. The phenotype of interest may be binary (e.g., AML vs. ALL), a measurement (e.g., blood pressure or drug clearance), or a censored time to event outcome (e.g., time to death or time to recovery). To this end, an analysis data set consisting of phenotypic and molecular data must be constructed. The molecular data set will typically consist of a gene expression profile for each experimental unit. The genetic feature for an Affymetrix arrays is called a probe set. Each probe set consists of a number of perfect match (PM) probes that are designed to match the target along a 25 mer oligosequence. A mismatch probe is paired as a control to each PM probe. The nucleotide at the 13th position is reverse complemented. For Illumina chips whole‐genome chips, the genetic features are called a probe that consist of microscopic beads. Following the hybridization of the samples to the chips, what is generated is not the gene expression profile but rather a large set of probe intensities. These need to be preprocessed in an attempt to quantify the expression for each genetic marker of interest en route to the construction of an analysis data set to be used in high‐level association analyses. The principal steps of any preprocessing may consist of background correction, normalization, and summarization. It is the last step that produces the expressions.

The purpose of background correction is to reduce, among other things, effects attributed to nonspecific bindings between the probe and target and artifacts not removed during the wash cycle. Variability in the probe intensities attributed to nonbiological technical issues is to be expected. The purpose of normalization is to make the intensities for features that are not differentially expressed similar across the arrays. We illustrate the effect of preprocessing on the lung cancer data using the RMA algorithm. ⁶ , ⁷ The results are shown in Figure 2 by applying the algorithm to 86 tumor and 10 normal samples from this data set. This algorithm summarizes probe set summaries from the PM probes. In the top‐left panel, we present the density estimates based on the raw intensities. We distinguish the tumor versus normal samples using the colors red and blue, respectively. The normal samples are observed to have rather similar distributions while the tumor samples are quite heterogeneous. The first stage of this algorithm is to background correct the probe intensities of each array. The corresponding density estimates of the background‐corrected intensities are shown in the top‐right panel. The resulting estimates suggest that the background‐corrected densities are less skewed. The second stage of this algorithm is to normalize the background intensities. Quintile normalization is used for this purpose. This method effectively forces the empirical densities for the background‐corrected intensities to coincide. The resulting density estimates are shown in the bottom‐left panel. As expected, the density estimates are now mostly superimposed, with some exceptions in the right tails. The last step of this algorithm is to produce expressions for each probe set on the basis of the background‐corrected and normalized probe intensities in that set. This step is carried out within the framework of a linear regression model where the expression for each probe set is a model parameter. These parameters are estimated using a method that is robust to outliers. Once the probe set intensities are estimated, we can construct the gene expression profile for each patient. It is common to investigate similarities among patients on the basis of these gene expression profiles. This often facilitates the identification of batch effects or outliers. An illustration is shown in the bottom‐right panel. Each point corresponds to a patient. The relative distance between two points quantifies the relative similarity between two patients. We note that as in the case of normalized density estimates, a number of points seem to cluster away from the majority of samples. A more thorough analysis and discussion of these outliers is presented in Owzar et al. ⁸

Figure 2.

Illustrating the application of the RMA algorithm to preprocessing the Beer lung cancer data set consisting of 86 tumor and 10 normal samples. These are distinguished by the colors red and blue, respectively. The top‐left panel present estimates of the density function of the probe intensities for each sample. The top‐right panel presents these density estimates following background correction. The bottom‐left panel presents the density estimates following normalization of the background‐corrected intensities. The bottom‐right panel is a scatter plot of the first two principal components of the expression matrix.

The choice of the preprocessing algorithm employed will have an effect on the gene expression estimates and consequently on the resulting statistical association analyses. The importance and implications of preprocessing have not enjoyed the same level of scrutiny afforded to research related to association testing and model building for microarray data. Discussions of background correction and normalization methods are provided in Owzar et al., Cope et al., and Irizarry et al. ⁸ , ⁹ , ¹⁰ for Affymetrix arrays and in Xie et al. and Schmid et al. ¹¹ , ¹² for Illumina bead arrays. We note that normalization is typically carried out by estimating a common reference distribution based on all arrays from an experiment. The existence of this common reference distribution may not be a plausible assumption when dealing with arrays from specimens that are biologically different (e.g., different cell or tumor types). We will address this issue further within the context of the two data sets.

Statistical Inference for Genetic Markers

The primary goal of many microarray studies is to identify individual genetic features associated with a phenotype. We begin this discussion by considering the case of a single gene. Misinterpretation of the statistical results from microarray studies is invariably attributed to lack of understanding of basic key concepts of statistical inference. The basic foundation of statistical inference is to specify a hypothesis addressing the scientific question of interest. For example, based on a series of experiments, one may hypothesize that the expression of a certain gene is higher for patients who respond to a therapy than those who do not. This is known as the working or alternative hypothesis. Benefit of the doubt has to be given to the hypothesis that this is not true. This is known as the null hypothesis. A new experiment is to be carried out to determine there is sufficient evidence for null hypothesis is to be rejected in favor of the alternative hypothesis. A test statistic along with a clear decision rule is to be prespecified to reach this decision. The null hypothesis is either true or false. The rule will lead to a correct or wrong decision. Rejecting a true null hypothesis is called a type I error or a false‐positivity while failing to reject a false null hypothesis is called a type II error or a false‐negativity. Note that failure to reject the null hypothesis does not imply that the null hypothesis is true. This is a common and serious misunderstanding. It simply means that there is not sufficient evidence based on the observed data to conclude that the null hypothesis should be rejected in favor of the alternative.

Choosing a test statistic based on a cookbook recipe cannot be recommended. The choice of the test statistic should, among other things, be based on the type of outcome variable observed and the assumptions one is a priori willing to make regarding the size and distribution of the observed data. For RNA microarrays, the marginal distribution of the expression for each gene is assumed to be continuous. Therefore, methods appropriate for continuous markers should be used. For example, the use of methods for contingency tables would not be recommended as it would require that the expression levels are arbitrarily dichotomized. Usually a choice is made between using parametric or nonparametric tests. No matter what test is used, one has to be able to at least approximate the null distribution. Parametric tests are appropriate when one feels comfortable in making strong assumptions on the size and distribution of the data. These tests may perform miserably if the assumptions are inappropriate. Nonparametric tests are typically more robust than their parametric counterparts as they do not require making strong assumptions on the distribution of the observations. In the case of binary outcomes, the statistical problem can be formulated within the context of a two‐sample problem. Two standard test statistics for this case are the t‐test and the Wilcoxon rank‐sum test. If there are more than two classes, two standard test statistics are the F‐test (parametric) and the Kruskal‐Wallis test (nonparametric). The F‐test is also known as the ANOVA test In the two‐sample case, the F‐test and Kruskal‐Wallis tests reduce to the two‐sample t‐test (with a pooled variance estimator) and Wilcoxon test, respectively. For quantitative traits, tests based on the Pearson, Spearman rank, or Kendall’s rank correlation could be considered. The details for these classical tests are covered in many statistics textbooks (e.g., Bhattacharyya and Johnson ¹³ ). For censored time to event outcomes, the Cox score ¹⁴ or Cox rank score ¹⁵ could be used.

It should be noted that hypothesis testing is carried out to investigate statistical and not biological significance. Statistical significance does not necessarily imply biological significance and vice versa. Consider the case of weight loss pills where the manufacturer claims significant weight loss. While there may indeed be statistical evidence suggesting a significant weight loss attributed to the pill, the clinical efficacy may be irrelevant. It is the responsibility of the investigators to pose a biologically relevant hypothesis. It is also the responsibility of the investigators to ensure that a statistically significant finding is biologically plausible/realistic.

For any testing procedure, one has to consider the trade‐off between type I and II error rates in the sense that reducing one comes at the cost of inflating the other. This is analogous to a smoke detector. If the benefit of the doubt is given that there is no fire, an alarm in the absence of a fire is considered a type I error while the failure of the detector to sound an alarm in the presence of a fire is a type II error. By making the detector more sensitive, one will certainly increase the chance of experiencing false alarms, hence increasing the type I error rate. Conversely, decreasing the sensitivity of the detector may potentially lead to a delay in detecting a real threat with potentially devastating repercussions.

For any testing procedure, ideally one would like to have exact type I error control. The type I error rate prespecified for the decision rule is usually referred to as the nominal level. If the true type I error rate is less than the nominal level, the testing procedure is said to be conservative and anticonservative otherwise. Permutation resampling ¹⁶ has proven to be an effective approach for providing accurate type I error control in the case of high throughput data by accounting for coregulation among genes.

In these discussions, we have assumed that the expression level is actually observable. It is unrealistic to expect that all probes will be sufficiently expressed above background. In this sense, the expression levels are subject to left truncation. The intensity recorded for a probe below background is a random number within the interval between zero and the lower limit of quantification. Furthermore, clinical outcomes are not necessarily observable. For example, if the end point of interest is tumor response induced by aggressive therapy, one may decide to classify each patient as a responder or nonresponder. The response status may not be observed for patients who miss visits for response assessment or die due to disease or treatment before response is achieved. Classifying these patients as nonresponders may not be appropriate. Nonassessment due to death is an example of informative censoring or missingness. Dealing with this issue may not be trivial.

Multiple Testing

Association analysis in the microarray setting is not concerned with testing the association between a single genetic feature and a clinical outcome but rather with the testing for association for tens of thousands of features. Accordingly, one has to account for the impact of testing not one but rather say m hypotheses. Here, each hypothesis asserts that the expression of a feature is not associated with the clinical outcome. According to the decision rule employed, each of these m hypotheses will either be rejected or not. The operating characteristics of the decision rule must be evaluated within a prespecified framework for multiple testing. The operating characteristics may include the expected number of nonprognostic features declared prognostic (i.e., false positives) or the number of prognostic features missed (i.e., false‐negatives) among other things. The various quantities involved in any decision rule are tabulated in Table 1 . When reviewing this table, it is important to understand which quantities are fixed parameters and which are random. Among m features, m ₀ and m ₁= m −m ₀ denote the number of nonprognostic and prognostic features. Note that unlike m, both m ₀ and m ₁ are unknown parameters. Let A and R=m−A denote the number of accepted and rejected hypotheses. It should be noted that A and R are random but observable quantities. Among the R hypotheses rejected and A hypotheses accepted, there will be R ₀ and A ₁ type I and II errors committed, respectively. Note that A ₀, A ₁, R ₀ and R ₁ are random and, unlike A and R, are unobservable quantities. We will limit these discussions to two standard frameworks used to account for multiple testing in the microarray setting: the family‐wise error rate (FWER) and the false discovery rate (FDR).

Table 1.

Tabulating the parameters and random quantities associated with testing m > 1 hypothesis. Here, m ₀ and m ₁=m−m ₀ denote the number of nonprognostic and prognostic genes. A and R=m−A denote the number of accepted and rejected hypotheses. R ₀ and A ₁ denote the number of false‐positive and false‐negative decisions.

	Decision
	Reject	Accept	Total
Truth
Nonprognostic	A 0	R 0	m 0
Prognostic	A 1	R 1	m 1
Total	A	R	m

FWER controls the probability of committing any false‐positive given that none of genes are prognostic. If the desired FWER level is α, FWER control aims to ensure that P[R ₀ > 0 | m=m ₀] is at most α. Note that when applied to the single gene setting of the previous section, where m= 1, the definition of FWER coincides with the definition of type I error rate. In this sense, FWER is the type I error rate for multivariable problems. A very simple method that can be used to control FWER at the nominal level α is to test each hypothesis at the α/m level. This method, known as the Bonferonni test, will ensure FWER control. It could, however, be conservative in the case where there is dependency among the expressions of the genes. Resampling methods could be used to sharpen FWER control. ¹⁶ , ¹⁷

An FDR multiple testing procedure controls the expected false‐discovery rate. Recall that R ₀ denotes the number of false positives. The FDR is given as R ₀/R. As R ₀ is unobservable, so is this ratio. So, rather than controlling the actual false‐discovery, an FDR procedure aims to provide control of the expected value of this ratio 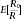. Three methods frequently used for FDR control are Benjamini and Hochberg (BH), ¹⁸ Benjamini‐Yekutieli (BY), ¹⁹ and the Storey q‐value. ²⁰

When considering issues related to multiple testing, it is important to distinguish between the framework or criterion used to account for multiple testing and the specific statistical method used within that framework. FWER and FDR are two frameworks for multiple testing. The Bonferroni and permutation resampling approach are two methods that can be used within the FWER framework while the BH, BY, and q‐value approach are methods that can be used within the FDR framework. In Figure 3 , we illustrate the results from an analysis of the Golub leukemia data set. We use the Student t‐test ¹³ to assess the association between each probe set and disease subtype. We calculate the unadjusted asymptotic and permutation FWER‐adjusted p‐values. Based on the unadjusted asymptotic p‐values, we obtain FDR‐adjusted p‐values using the BH approach. The empirical distribution of the unadjusted p‐values is illustrated by the histogram shown in the top‐left panel. The distribution is greatly skewed to the left. Specifically, a considerable proportion of features, 2,106 out of 7,129 features, are observed to have p‐values less than 0.05. Next, we randomly shuffle the labels (i.e., ALL vs. AML). Note that by shuffling the labels, we have broken the dependence between the disease subtype and the features. The corresponding empirical distribution of the unadjusted p‐values is illustrated by the histogram in the bottom‐left panel. While these p‐values are observed to be uniformly distributed, we still observe a sizeable proportion to be less than 0.1. This is not surprising as we would expect 5% of the features to have an unadjusted p‐value of less than 0.05 even if none of the 7,129 features are prognostic. To study this further, in the right panel, we plot the number of features declared significant, according to the unadjusted, Bonferonni‐adjusted FWER, and BH‐adjusted FDR p‐values. The corresponding three traces based on the observed data are illustrated using solid lines while those based on the permuted data are illustrated using dashed lines. As expected, the unadjusted p‐value approach uniformly declares more significant features than the other two approaches. The FWER approach uniformly declares less features significant than FDR. Looking at the dotted traces, 278 features are incorrectly declared significant based on the unadjusted p‐value. In this case, neither the FWER nor FDR approach declares any features significant at levels of at most 0.1 so that the two corresponding traces overlap. As illustrated in Jung and Jang, ²¹ FDR methods may actually fail to provide FDR control when there is coregulation among the features. What this example illustrates is that it is imperative to consider the issue of multiple testing when analyzing high throughput data. The framework and method to be used is subject of extensive discussion and often subject to disagreement in the research community. However, failure to account for multiple testing will result in high false discovery in microarray studies.

Figure 3.

Analysis of the Golub leukemia data. The empirical distribution of the unadjusted p‐values is illustrated by the histogram in the top‐left panel. The bottom‐left panel illustrates the empirical distribution of the unadjusted p‐values after a random permutation of the labels (AML vs. ALL). The right panel illustrates the number of features declared significant at a given cutoff p‐value based on using unadjusted, BH‐adjusted, and Bonferonni‐adjusted p‐values (red, blue, and green solid lines, respectively). The dashed lines are the corresponding traces based on permuting the label. The FWER and FDR traces for the permuted case overlap over the given interval.

Class Discovery

One of the objectives for microarray studies is to detect patterns or aberrations induced among samples by nonbiological factors, such as batch or plate effects, or by biological or experimental factors based on the genomic profiles. Given the high dimensionality of these expression profiles, direct visualization is not possible. To this end, class discovery methods have been found to be very useful. The algorithms used by these methods solely use the gene expression profiles and are not guided by any outcome data. Therefore, they are often referred to as unsupervised learning methods. Many class discovery methods aim to quantify the similarity or dissimilarity among patients solely based on the gene expression profile. To this end, a distance measure needs to be defined. Suppose that two gene expressions are assayed for three samples: A, B, and C. The corresponding three pairs of expressions are illustrated in the left panel of Figure 4 . A natural measure to quantify the distance between two points on a plane is the Euclidean distance. The three corresponding pairwise distances are drawn in the figure. What is observed is that the distance between samples A and B is shorter than that of between samples A and C. With respect to this distance measure, sample A is more similar to sample B when compared to C. The notion of distance can be extended to arbitrarily high dimensions. For the two data sets, each patient is represented by a genetic profile consisting of expressions from m= 7,129 probes. The distance is computed for each set of pairs. Multidimensional scaling (MDS) ²² is a useful method for visualizing similarities among samples. The basic idea is to project the genomic profiles from m= 7,129 dimensional space into a low dimensional space while preserving the pairwise distances. A related method is called principal components analysis. ²² Both are examples of ordination methods putting similar samples closer while putting dissimilar samples farther from each other. In this context, what is important is not the actual distance among a set of samples but rather the relative distance. We have already applied the MDS method to the lung cancer data (bottom‐right panel of Figure 2 ), to illustrate that the samples from normal tissues are more similar compared to tissues from lung tumors and next apply it to the leukemia data. The resulting figure is shown in the right panel of Figure 4 . What is observed is that the AML samples are more similar to each other than the ALL samples. The samples were provided by five institutions and have been colored accordingly. What is also observed is that with three exceptions all ALL samples were provided by one institution while all AML samples were provided by the other four institutions. The observed separation between the AML and ALL samples may be due to different cell types or due to a potential batch effect among institutions. The observed separation between the AML and ALL samples explains the large number of prognostic genes observed in the previous section. Both data examples suggest that the assumption of a common reference distribution between normal and lung cancer samples or between ALL and AML samples may be inappropriate. This type of analysis is very useful as it helps with better understanding of the microarray data and how they relate to biological or experimental factors. The leukemia data example also stresses the importance of using experimental designs to minimize potential confounding between main and batch effects. Other popular methods include hierarchical agglomerative clustering and k‐means clustering. A monograph by Mardia, Kent, and Bibby ²² is a comprehensive and accessible reference for the technical and applied aspects of class discovery methods.

Figure 4.

The left panel illustrates the relative distances among three points on a plane. Specifically, point A is relatively closer to point B compared to point C. The right panel illustrates an MDS analysis of the leukemia data. The samples have been provided by five institutions. These have been highlighted using colors. The disease subtype (AML vs. ALL) is used as the plotting character.

We now return to our simulated heatmap example illustrated in Figure 1 . These were produced as follows. A random expression matrix consisting of 2n patients and m= 50,000 features was simulated. The first n columns were arbitrarily assigned to class 0 while the remaining n samples were assigned to class 1. By virtue of this arbitrary labeling, none of the 50,000 probes are associated with this artificial labeling. The Student t‐test was used to assess the marginal significance between each probe and the simulated outcome. The heatmaps were constructed based on probes with marginal unadjusted p‐values of less than 0.001. The statistically naïve algorithm used to produce these heatmaps fails to account for several important issues. The feature selection process employed does not properly account for multiple testing as it would expect to yield about 50 noisy features “differentially” expressed with respect to the labeling. The algorithm is not unsupervised as the feature selection step uses the outcome variable. A class discovery method can only be considered to be an unsupervised learning method if none of its components are supervised. Finally, one should keep in mind that clustering algorithms are designed to find clusters. Hence, the discovery of clusters in microarray data using these methods is by no means grounds for celebration for a scientific breakthrough.

Predictive Models

The statistical inference methods for association testing are concerned with finding prognostic or predictive features for a given outcome. Often what is of interest is to use the expression profiles to predict an outcome for a patient or classify a patient with respect to phenotypic class by building a multivariable prediction model whose predictors are the features. For example, for the leukemia data set one may be interested in using the molecular profiles to predict disease subtype, AML versus ALL, while for the lung cancer set one may want to investigate if the expression profiles can be used to classify patients as short versus long survivors. To this end, a predictive or classification model has to be developed. The main idea is to construct a machine that can render an outcome prediction solely based on the gene expression profile of a patient. Unlike the methods considered in the last section, the methods used for the purpose of model building are supervised or guided by the outcomes. The terms machine learning, supervised learning, and pattern recognition are equivalent terms used in the statistical literature for this class of methods.

For simplicity, let us assume that for each patient, we have observed the expressions for two genes, say X ₁ and X ₂, along with the phenotype of interest say Y. Let μ[x ₁, x ₂] denote the expected value of Y given that the genes X ₁ and X ₂ have realized values x ₁ and x ₂, respectively. Needless to say, if the pair (X ₁, X ₂) is not related to Y then E[Y] =μ[x ₁, x ₂]. In other words, the expected outcome does not depend on the two gene expressions. We consider two standard models next. The linear regression models this conditional mean as

For binary outcomes (e.g., Y= 0 or Y= 1), the logistic regression model relates the odds of the event of interest

In both cases, we assume that, with the exception of the parameters β ₀, β ₁, and β ₂, the relationship between the mean value of the outcome and the pair of gene expressions is known. Note that if we knew the actual values of these parameters, we could use these models not only to determine the expected or predicted outcome for each patient but also classify the patient with respect to risk. Suppose that large values of Y are indicative of high risk. In the binary case, a large value for Y is 1. For the continuous outcome, we could classify a patient as high‐risk if the expected conditional outcome for the patient exceeds μ [η ₁, η ₂], where η ₁ and η ₂ are the means for the two gene expressions. For the binary case, we classify the patient as high‐risk if the expected conditional probability exceeds one half. As neither the model parameters, nor the mean gene expressions, are known, in practice, one has to estimate these parameters using the observed data. This is often referred to as training the model. The part of the data that is used to train the model, is generally referred to as the training data set while the part of the data set aside to validate or test the model is called the validation or testing data set.

A fundamental concept in statistical modeling is parsimony, which suggests that a model should be as simple as possible. Inclusion of too many noisy variables into the model may degrade the performance of the prediction but more importantly lead to overfitting. We consider two simple examples to illustrate the concept of overfitting. We simulate gene expression profiles consisting of 45 probes for n= 50 patients. Independent of these gene expression profiles, we simulate a continuous measurement for each patient. All random variates are drawn from a normal distribution. Note that, by design, there is no relationship between the gene expression and outcome. Any predictive model constructed on the basis of these data would be an example of noise discovery. For the sake of illustration, we fit a linear regression model consisting of 45 covariables to these data. The results are summarized in the left panel of Figure 5 . A visual device for assessing the fit of a model is to plot the outcomes as predicted by the model against the observed outcome. These are shown as red dots. We have seemingly succeeded in constructing a predictive model. In due course, we will examine the flaw in evaluating a model using this approach known as error resubstitution (see e.g., Simon et al. ⁵ ).

Figure 5.

Illustrating overfitting in the context of linear regression. In each case, we simulate gene expression profiles, consisting of m probes (m= 45 left panel and m= 50,000 right panel), for n= 50 patients from a standard normal distribution. The outcomes for the n patients are drawn independent of these gene expressions from a standard normal distribution. In the left panel, the red dots illustrate the substitution error predictions while the blue crosses illustrate the LOOCV predictions based on a linear regression model based on all m= 45 probes. In the right panel, the red dots illustrate the naive LOOCV predictions based on using the top m*= 10 features, among the m= 50,000 features, in a linear regression model. These m* features are calculated once from the training data (size n) and subsequently used in the cross‐validations. The blue crosses illustrate the LOOCV predictions when the feature selection process is properly cross‐validated.

Aside from the adhering to parsimony as a matter of principle, it is not practical to build a model based on tens of thousands of features in the genome‐wide setting. To this end, one typically applies a filter to train the model based on a subset of features. This, known as feature selection, variable selection, or feature extraction, is a critical, if not the most important, component of model building. One cannot expect to build a good model based on poorly selected features. We will consider a few approaches that have been used in the literature. The simplest method is to select features based on the magnitude of the marginal association. For example, the absolute value of the Student t‐test statistic could be used to rank the probes sets in the leukemia data set while the marginal Cox score statistic can be used to rank the probes for the lung cancer data set. The model could then be constructed based on the, say, top 10 or 15 probes or based on any probe set for which the corresponding marginal p‐value is less than a given threshold. If one is concerned about outliers, then a more robust statistic such as the Wilcoxon test statistic or Cox rank score test ²⁸ could be used. Another common approach is to use the methods of principal components ²² to find a small set of genetic features that represents maximum variability in the microarray data.

While the model is trained based on the training data, its performance has to be assessed based on an independent data set. There are several strategies available for constructing training and testing data sets. The simplest approach is the holdout method where the data are split into two mutually exclusive parts. The testing set is immediately locked away, preferably by a so‐called honest broker, while the model is trained and refined based on the training set. A standard split is to randomly assign two‐thirds of the cases to the training set and the remaining to the testing set. If there are important clinical or demographic baseline factors for the outcome of interest, it may be prudent to stratify the randomization accordingly. This holdout method is not practical for many microarray experiments where the number of samples is small. Another standard approach to construct training and testing data set is k‐fold cross‐validation. To implement this method, the samples are randomly split into k folds roughly of same size. At each step, one fold is tucked away as the testing set while the model is trained based on the data in the remaining k− 1 folds. A special case of this is n‐fold cross‐validation, also known as leave‐one‐out cross‐validation (LOOCV), which may be a practical approach for very small experiments.

Proper validation of a model is mandatory. We return to the overfitting example discussed in this section, where we were able to come up with a good model based on set of entirely noisy features. This time, we will assess the performance of the model using LOOCV. The results are shown in the left panel of Figure 5 using blue crosses. It is noted that unlike the error resubstitution predictions, the LOOCV predictions do not suggest that the model provides good predictions. Although this example suggests that LOOCV or other cross‐validation schemes could be used as a protection against overfitting, improper use of these validation methods in a high‐dimensional setting may be equally misleading. To illustrate this, we conduct another simulation study where we generate noisy expression profiles based on m= 50,000 probes from n= 50 patients. Next, we select the top m*= 10 probes based on Student t‐test based on the data from these n= 50 patients and use LOOCV to assess the performance of the model. The results are shown in the right panel of Figure 5 using red dots. Again, we have seemingly succeeded in coming up with a decent model from noise despite using cross‐validation. The caveat here is that the feature selection process was not part of the cross‐validation process. Next, we reselect the new top 10 features during each of the 50 cross‐validation steps. The results are shown using blue crosses. There is no evidence, as expected, that these noisy genomic profiles can predict the outcome.

When evaluating the operating characteristic of a statistical model, one has to take into account accuracy and precision. In the statistical literature, these are referred to as bias and variance, respectively. Another fundamental concept in statistics is that of the bias‐variance trade‐off, which implies, similar to the type I and II error trade‐off, one cannot simultaneously minimize bias and variance. This brings us to an important issue that is often overlooked when using statistical software for supervised learning. It is unrealistic to assume that the default parameters chosen by the software developers will be optimal for any given data set. One approach is to define a broad selection of combinations for the tuning parameters and then exhaustively compare the operating characteristics of the model. This is usually called a grid search. It is noted that the grid search should be part of the cross‐validation process. To this end, one may have to split the training set further into a subtraining and validation set. In other words, one may have to conduct two layers of cross‐validation.

The statistical methods used in the microarray setting are typically more flexible than the two standard models we have considered. These include k‐nearest neighborhood, ²³ support vector machines, ²⁴ regression and classification trees, ²⁵ or more generally random forests, ²⁶ neural nets ²⁷ among others. Least absolute shrinkage and selection operator type methods (LASSO) ²⁸ have been widely used in the analysis of high throughput data as they provide the facilities to conduct model estimation and feature selection simultaneously. The monograph by Hastie, Tibshirani, and Friedman ²⁹ provides a modern account on machine learning methods and their applications.

Statistical Inference for Pathways

The inferential methods considered thus far evaluate the significance of individual features. A common approach to summarize the results from this type of analysis is to produce a gene list consisting of the top individual features, selected based on a set of criteria, along with statistical summaries, such as effect size estimates and p‐values, and genomic annotation such as gene symbols and related pathways. Gene category tests are increasingly common way of characterizing patterns of differential expression and associations with outcome across gene sets and pathways of interest in an attempt to move away from ad hoc perusal of gene lists to more systematic approaches. The evaluation of gene sets has two related goals. Gene set analysis can be used to identify enrichment within a set of genes that provides a biological understanding for the observed associations at the individual feature level. It could also identify association across a pathway that may not be strong enough to be detected by individual features. A category is defined a priori as a subset of the genes under investigation. Popular categories include Gene Ontology, KEGG Pathways, and Transcription factors. Gene sets could also be defined through previous experimentation. A complicating factor, both from a statistical point of view but also from the point of view of interpreting the final results, is that gene sets are overlapping. Consequently, one has to account for dependency induced by coregulation among genes within a gene set as well as across gene sets. Most of the methods proposed in the literature compute a gene set‐level statistics by aggregating the test statistics of the corresponding probes within that gene set. Permutation resampling can be used to generate the sampling distribution of the gene set statistics while properly accounting for coregulation among genes and for multiple testing. Methods available for gene set analysis include Gene Set Enrichment Analysis, ³⁰ Gene Set Analysis, ³¹ and Significance Analysis of Function and Expression. ³² , ³³ As these gene set categories are updated on a regular basis, it is very important to archive the version used for a given analysis so that the results can be reproduced in the future.

Power and Sample Size Calculation

As discussed previously, there are two popular frameworks, FWER and FDR, for multiple testing in gene discovery. In this section, we discuss sample size (number of subjects) and power calculation methods for FWER‐ or FDR‐based multiple testing procedures that can be used when designing microarray studies. We consider discovery of genes that are related to a binary outcome, such as case versus control or response versus no response.

There have been several publications on sample size estimation for FWER‐based multiple testing procedures without examining the accuracy of their estimates. They focus on exploratory and approximate relationships among statistical power, sample size, and effect size (often, in terms of fold‐change), and use the conservative Bonferroni adjustment without any attempt to incorporate underlying correlation structure. (e.g., reviewed in Refs. 34, 35, 36, 37, 38, 39). Since an accurate control of the FWER depends on the dependence among genes (see Westfall and Young ¹² ), an accurate sample size formula for the FDR‐based multiple testing requires specification of the correlation structure among genes. Jung, Bang, and Young ⁴⁰ propose a sample size calculation method for the Westfall and Young’s permutation method under a hypothetical correlation structure called block compound symmetry. Because of the high dimensionality and complicated dependency of gene expression data, however, it is almost impossible to model the true correlation structure accurately. To overcome this barrier, Jung and Young ⁴¹ propose a sample size calculation method by approximating the true correlation structure from pilot data. If no pilot data are available, we can adopt a two‐stage design to use the first‐stage data for sample size recalculation. Jung, Bang, and Young ⁴⁰ define the power for a FWER‐based multiple testing as the probability to discover at least one gene. Jung and Young ⁴¹ extend the concept of power to the probability to discover certain number of prespecified prognostic genes.

Contrary to the FWER case, there has been no multiple testing method that controls the FDR exactly in the presence of dependence among genes. So, the popular FDR‐based multiple testing methods, such as Benjamini and Hochberg ¹⁸ and Storey, ²⁰ assume independence or weak dependence among genes. Jung and Jang ²¹ show that the q‐value method proposed by Storey ²⁰ controls the FDR relatively accurately for real microarray data sets. Jung ⁴² proposes a simple sample size method for the q‐value method. This method calculates the sample size for given design parameters: number of candidate genes on each array, number of the prognostic genes and their effect sizes, the FDR level to be controlled at the gene discover, and the probability to discover a specified number of prognostic genes. Pounds and Cheng ⁴³ and Liu and Hwang ⁴⁴ later propose similar sample size calculation methods.

Genomics and Clinical Trials

As described above, microarray technologies have been used extensively to develop classifiers of disease subtypes ¹ , ⁴⁵ , ⁴⁶ and predict clinical outcome, ² , ⁴⁷ and have traditionally been correlative objectives to clinical studies. Ultimately, the genomic profiles of individual patients may be able to select or optimize their preventative and therapeutic care. This goal has been termed personalized medicine. To reach this goal, clinical trials play a pivotal role of taking genomic discoveries and validating their clinical utility as biomarkers of disease. In this context, it is important to distinguish between the types of biomarkers, including surrogate markers for clinical outcomes and biomarkers that provide prognostic or predictive information as illustrated in the left panels of Figure 6 . Therein, survival profiles are stratified by two hypothetical treatment arms (A vs. B) and further by a dichotomous genomic marker classifying patients as positive or negative. It is noted that in both illustrations, patients randomized to arm B have a superior survival profile than those randomized to arm A, and that patients who are classified as positive by the genomic marker have a superior survival profile. However, in the top panel the relative effectiveness from being classified as positive is equal within the two arms. This is an example of a prognostic marker. In the bottom panel, the relative effectiveness from being classified as positive is greater in arm B than arm A. This is an example of a predictive marker. The clinical trial designs for validating genomic model will be determined by their hypothesized clinical utility as a biomarker. The standard framework for evaluating therapies within the context of clinical trials typically consists of four formal and well‐defined phases. A similar framework has not been formally established for evaluating genomic biomarkers; but can be broadly characterized as follows. First, investigations can be delineated as discovery‐based research, or designed to validate an a priori defined genomic model as a biomarker. In the clinical validation of a genomic biomarker, it is important to distinguish between retrospective and prospective studies. For retrospective studies, biospecimen are banked during the course of the trial and only evaluated on completion. This allows for nested trial designs, for example, case‐control, to be embedded into larger randomized or observation studies of treatment interventions. Furthermore, retrospective studies can be more efficient when the clinical outcome is rare, or when resources for conducting the laboratory work are limited. However, only a prospective application of genomic technologies will fully evaluate the clinical utility of a genomic‐based assay in terms of the accessibility of tissue, evaluation of quality control, and the feasibility of making a genomic determination. For prospective trials, the National Cancer Institute has designated two types of essential biomarker trials that are illustrated in the right panels of Figure 6 :

Figure 6.

The figures in the top‐left and bottom‐left panels illustrate a prognostic versus a predictive marker for survival, respectively. In each illustration, the stratifications are with respect to a hypothetical arm (blue vs. red curves) and a hypothetical dichotomous genomic marker (solid vs. dashed curves). In the right panels, examples of an integrated and integral biomarker study are shown. In the first, patients are randomized to two treatments without regard to the genomic marker, although the planned analysis is to test a treatment/biomarker interaction. In the second, a two‐stage randomized clinical design is illustrated for genomic‐guided treatment. A patient is randomized to be on the genome‐guided or unguided arm. Patients randomized to the guided arm, are assigned to arm B if they are positive for the marker or to arm A otherwise. Patients who are randomized to the unguided arm are randomized to arm A or B.

• • Integrated studies: Involve assays that are clearly identified as part of the clinical trial and are intended to identify or validate assays planned for use in future trials. They should be designed as hypothesis‐testing and not hypothesis‐generating. Assays are to be performed in real time and include complete plans for specimen collection, laboratory measurements, and statistical analysis.
• • Integral studies: Designed such that assays must be performed in order for the trial to proceed. Examples include tests to establish eligibility, tests used for patient stratification, and tests that inform treatment assignment.

Thus far we have left out a critical issue when prospectively applying models developed from genome‐wide assays. Gene expression from a new patient has to be compatible with the expressions used to train the prediction model that yielded the genomic biomarker. In experiments with few analytic features, one can incorporate internal controls to ensure that the measurements are properly normalized. This is considerably more complicated when using commercial genome‐wide assays, because microarray assays provide estimates of relative, and not absolute levels of mRNA expression. In this sense, the expression profiles may only be comparable within the batch and not across batches. But, in the prospective setting each patient will constitute a batch of size one. It should also be noted that when the marker is used to determine a treatment strategy in an integral biomarker study, the bar for ensuring compatibility and reproducibility of both the assay and genomic classification is greatly raised due to ethical considerations. These issues have not been adequately addressed in the literature and deserve greater attention.

Software

The analysis of microarray data poses considerable computational challenges. Academic and commercial software environment and applications have been and are being developed to meet these challenges. The commercial applications have primarily focused on user‐friendliness, by providing fancy point and click graphical user interfaces. While this may be a desirable feature for some, it is unlikely to be a useful feature for research. What is important to research is for the software to be flexible and extensible so as to allow the user to determine the analysis method thought to be best suited to address the scientific questions at hand. To this end, we have found the R statistical environment ⁴⁸ to be an ideal match. It should be emphasized that R is not a software application designed to facilitate a certain number of prespecified analyses thought to be useful or important by the software developers, but rather “an environment to conduct statistical analyses and computation.” By providing the requisite building blocks, including an object‐oriented programming language and outstanding facilities to produce graphics, the user is put in charge. These capabilities are complemented by extension packages contributed by other R users. Of special note is the Bioconductor project, ⁴⁹ which provides a comprehensive library of extension packages specifically developed for the preprocessing, analysis, visualization, and annotation of molecular data. In addition to technical documentation, most Bioconductor packages offer vignettes, which serve as tutorials.

As an interpreted language, R may not be as fast as some compiled languages. It is possible to include C/C++ and FORTRAN code in R. It is also possible to call R from these languages to build stand‐alone packages. Another powerful programming language used by the bioinformatics community is Python. R can be interfaced from Python through rpy and rpy2. R can be installed on laptops, desktops, and servers running a variety of operating systems including GNU/Linux, Windows, and MacOS. It is open‐source and distributed under a public license.

Many statistical algorithms and procedures used to analyze microarray data are parallelizable. Packages that allow the user to parallelize code over clusters or multicore servers include snow, multicore, and Rmpi. Graphical Processing Units (GPUs) provide another hardware resource for conducting stream computing. Two extension packages that enable the use of GPUs within R are gputools ⁵⁰ and permGPU. ⁵¹

An important principle in conducting genomic research is reproducibility. This does not only apply to the scientific experiment where the use of technical or biological replicates is used to ascertain the reproducibility of the assay, but also applies to the quantitative component of the research. It should be noted that reproducibility is a necessary but not sufficient component of good research as poor research can be conducted in a reproducible fashion. The R statistical environment greatly facilitates the conduct of reproducible research by providing a framework for literate programming ⁵⁷ through Sweave ⁵⁶ by combining L^AT_EX(http://www.latex‐project.org) as the typesetting engine and R as the computational engine.

Venables and Ripley ⁵⁴ and Dalgaard ⁵⁵ provide extensive and accessible accounts on conducting programming and statistical analyses using R. Gentleman et al. ⁵⁶ and Hahne et al. ⁵⁷ provide accounts on conducting statistical analysis using Bioconductor extension packages. All statistical analyses presented in this paper were conducted using R.

Conflicts of Interest

None.