Population-level effects of suppressing fever

Abstract

Fever is commonly attenuated with antipyretic medication as a means to treat unpleasant symptoms of infectious diseases. We highlight a potentially important negative effect of fever suppression that becomes evident at the population level: reducing fever may increase transmission of associated infections. A higher transmission rate implies that a larger proportion of the population will be infected, so widespread antipyretic drug use is likely to lead to more illness and death than would be expected in a population that was not exposed to antipyretic pharmacotherapies. We assembled the published data available for estimating the magnitudes of these individual effects for seasonal influenza. While the data are incomplete and heterogeneous, they suggest that, overall, fever suppression increases the expected number of influenza cases and deaths in the US: for pandemic influenza with reproduction number 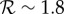, the estimated increase is 1% (95% CI: 0.0–2.7%), whereas for seasonal influenza with 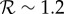, the estimated increase is 5% (95% CI: 0.2–12.1%).

1. Introduction

For millennia, humans have suppressed fevers without understanding the potential effects [1,2] beyond the obvious alleviation of symptoms. Antipyretic drug treatment is extremely prevalent in Western countries—especially by parents [3], and also by healthcare professionals [4–6]. Even when treatment is not aimed at fever specifically, fever is likely to be reduced, because most common drugs that relieve other typical symptoms of infectious diseases also contain an antipyretic component [7].

Previous investigations of the effects of fever suppression have focused on the clinical benefits and costs to the individual [8,9]. The adaptive value of fever [10–13] is well known to immunologists; for example, Janeway's Immunobiology [14, p. 110] notes that ‘At higher temperatures, bacterial and viral replication is less efficient, whereas the adaptive immune response operates more efficiently’. Others argue that the adaptive value of fever arises instead from activation and coordination of the immune response [12]. By contrast, a common view in the medical community, as expressed for example in Harrison's Principles of Internal Medicine, is that the ‘treatment of fever and its symptoms does no harm and does not slow the resolution of common viral and bacterial infections’ [15, p. 107]. Here, we consider some population-level effects of widespread fever suppression, effects that do not appear to have been investigated previously.

An individual whose fever has been reduced is likely to feel better and is therefore more likely to interact with others. In addition, fever suppression may increase both the rate and duration of viral shedding, further increasing the pathogen's transmission rate; this effect has been shown experimentally for influenza in ferrets [16]. A higher transmission rate will in general lead to larger epidemics [17,18] and hence to greater morbidity and mortality. The increase in epidemic size is larger for more weakly transmissible pathogens.

2. Theoretical argument

To make this idea more precise, suppose that (i) a proportion p of infected individuals develop a fever and are treated with antipyretics (the treatment probability) and (ii) on average, antipyretic treatment of febrile individuals increases their probability of infecting others by a factor f_i (the individual transmission enhancement factor). The proportion of infected individuals with enhanced transmission is then p, and the proportion without enhanced transmission (i.e. with transmission enhancement factor 1) is 1 − p. Antipyretics therefore increase the overall transmission rate by the factor

2.1a

2.1b

which we call the population transmission enhancement factor. (Note that f_p > 1 given that f_i > 1 and 0 < p ≤ 1.)

Transmissibility of a pathogen is normally quantified by the basic reproduction number 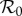, the average number of secondary cases caused by a primary case in a wholly susceptible population [19]. In a population that is not wholly susceptible—which is always the situation for seasonal influenza—the effective reproduction number is reduced by the proportion susceptible at the start of the epidemic 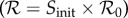. In these terms, antipyretic use has the effect of increasing the reproduction number

2.2

We would like to estimate how many additional infections, and correspondingly how many severe illnesses and deaths, can be expected to result from this increase in 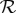during an influenza epidemic or pandemic [20].

For a very large class of epidemic models, the proportion of the population that is expected to be infected during an epidemic (the expected final size Z) is related to the reproduction number by the classical final size relation [17,18],

2.3

which can be solved explicitly (see the electronic supplementary material). Note that Z is the final size as a proportion of those who were initially susceptible; if everyone were susceptible initially (S_init = 1), as is possible in a pandemic, then 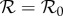and Z is the proportion of the entire population infected.

Figure 1a shows this final size relation, 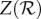, and figure 1b shows the relative incremental change in final size,

2.4

as a function of the population transmission enhancement factor f_p, for three values of 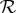in the plausible range for influenza, 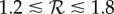( 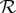is likely near the lower end of this range for seasonal influenza [21,22] and the higher end for pandemic influenza [23–26]). Because the final size Z is a decelerating function of the reproduction number 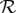(figure 1a), antipyresis always enhances transmission more for less transmissible diseases (which have smaller 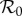: figure 1b). The precise quantitative predictions in figure 1b depend on our use of the standard final size relation; however, the qualitative conclusions are very general because the expected final size always increases (typically in a decelerating fashion) as 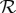increases [27–31].

Figure 1.

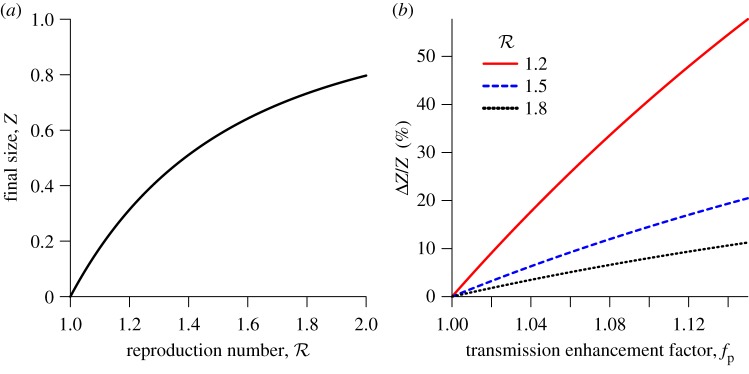
The effects of increases in transmission rate (by the factor f_p) on the expected proportion of the initially susceptible population that will be infected in a single influenza epidemic (the final size Z). (a) The standard final size relation (2.3), for the plausible range of (effective) reproduction number for influenza. (b) The relative increase in final size resulting from increasing the transmission rate by the factor f_p. For example, a 10% increase in the proportion of individuals infected during an epidemic will arise from a 2% transmission enhancement if 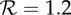, a 6% enhancement if 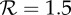or a 12% enhancement if 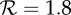. (Online version in colour.)

3. Estimating the effect for influenza

To predict the magnitude of the effect in practice, we need an estimate of the population transmission enhancement factor f_p. We have insufficient data to estimate how all the relevant biological mechanisms contribute to increasing f_p; in particular, we expect the increase in social interaction owing to reduced symptoms to lead to a major increase in the epidemiological contact rate, but are unable to quantify this. Nevertheless, by focusing on how antipyretics affect individual infectivity, we can at least estimate a lower bound on f_p for influenza. Throughout all stages of the calculations described below, we propagate error estimates by randomly sampling 10 000 values from the sampling distribution of each of the estimated parameters (assumed normal unless otherwise specified), computing the relevant metric with each set of parameters in the random sample, and finding the lower 2.5% and upper 97.5% quantiles of the resulting distribution. All computations were done in the R language [32] (see the electronic supplementary material).

The two components of f_p in equation (2.1) (p and f_i) are independent. Limited information is available concerning the treatment probability p: parents treat febrile children with antipyretics in approximately 90% of cases [3], and nurses treat fever with antipyretics in approximately 70% of cases [5,6]. We know that adults frequently take analgesics that are antipyretic, but we have little influenza-specific information. On these grounds, we propose a broad distribution for p (Beta(4,2)), with mean 0.67 (95% CI: 0.28–0.95). (Substituting a uniform [0,1] distribution for p instead to represent complete uncertainty does not change the results qualitatively; see the electronic supplementary material.) We must also adjust our estimate of p to take into account that only 67% (95% CI: 58–75%) of individuals show symptoms and only 35% (95% CI: 27–44%) develop a fever ([33]; see the electronic supplementary material).

To obtain a lower bound on individual transmission enhancement f_i, and hence to complete an estimate of a lower bound on population transmission enhancement f_p from equation (2.1), we consider two aspects of infectivity enhancement for which data exist.

First, antipyretics appear to increase viral shedding. To our knowledge, the only published experiment concerning the effects of antipyretic treatment on influenza viral shedding was conducted in ferrets (considered the best animal model for human influenza [34]). The study, conducted by Husseini et al. [16], considered two strains of influenza A/H3N2 that differed in virulence. For both strains, and regardless of whether fever was suppressed by shaving the ferrets or by administration of an antipyretic drug, the authors found that ‘significantly more virus was shed in the nasal washes of ferrets whose febrile response was suppressed and the viral levels decreased less rapidly than in untreated ferrets or in those in which the treatments were ineffective’ [16, p. 520]. This study was prompted by an earlier study from the same group showing that unmedicated ferrets with higher fevers shed less influenza virus [35]. The results are consistent with other studies showing that antipyretic treatment increases viral shedding in human volunteers infected with rhinovirus [36] and lengthens the infectious period in children with chickenpox [37]. Moreover, in a study of human volunteers infected with influenza A, the number of antipyretic doses received was positively correlated with the duration of illness [38]. Some cytokines reduce viral shedding, so a likely mechanism by which antipyresis increases viral shedding is the suppression of temperature-dependent cytokine responses to influenza infection (see the electronic supplementary material, §3.2). Based on these considerations, we assume that the clinical effects of fever suppression on nasal shedding in humans infected with influenza virus are similar to the effects measured in ferrets. Based on inverse-variance weighted mean values for the difference in the logarithm of viral titres between the antipyretic-treated and untreated ferrets, we estimate that antipyretic treatment increases influenza viral titres in nasal droplets by a factor of order 1.78 (95% CI: 1.35–2.35) (see the electronic supplementary material for further details).

Second, greater viral shedding increases infectivity. This is unsurprising, but estimating the strength of the effect is challenging. A recent review [39] describes 30 studies in which human volunteers were given various doses of a variety of influenza viruses. To analyse these data, we used a binomial generalized linear mixed model incorporating random effects of strain and study [40,41] to estimate the relationship between log₁₀(dose) and probability of infection. We conclude (see the electronic supplementary material) that a dose that is larger by a factor 10 (which we assume would arise from an increase in viral titres in nasal droplets by the same factor) yields an increase of 0.28 (95% CI: 0.01–0.54) in the log-odds of infection. (This effect would correspond to an increase of 0.07 (95% CI: 0.004–0.13) in the proportion infected if we started from a baseline infection probability of 0.5.)

In order to infer the overall transmission implications, we need an estimate of the natural infectivity of influenza, i.e. the probability that a susceptible contacted by an (non-antipyretic-using) infectious individual will become infected. We are not aware of direct measurements of this probability, so we use published estimates [42] of the household secondary attack rate (SAR) as a proxy. We used a linear mixed model incorporating variation among strains and among studies to estimate the log-odds of the SAR, based on measurements of antibody response of individuals between the beginning and end of the influenza season. Based on the coefficients of this model, we estimate the expected SAR to be 0.14 (95% CI: 0.07–0.27). As study participants were not prevented from taking antipyretics, the reported SAR likely represents an overestimate of the natural infectivity (which will make our inferences more conservative; see the electronic supplementary material, §5).

Associating proportional changes in the viral titre of nasal washes in the ferret study [16] with proportional changes in viral titres in nasal sprays in the human challenge studies [39], and taking the household SAR to approximate natural infectivity, we estimated the antipyretic-induced individual transmission enhancement factor f_i using equation S22 in the electronic supplementary material. We infer a conservative lower bound of 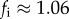(95% CI: 1.002–1.14).

Putting together our estimates of the treatment probability p and the individual transmission enhancement factor f_i using equation (2.1) (details in the electronic supplementary material), we conclude that the current practice of frequently treating fevers with antipyretic medication has the population-level effect of enhancing the transmission of influenza by at least 1% (95% CI: 0.04–3%) (i.e. f_p > 1.01 (95% CI: 1.00–1.03)). This estimate does not take into account the known effect that the infectious period of influenza is also increased by antipyresis [16], nor does it take into account the potentially large effect of increasing the rate of contact among infectious and susceptible individuals because antipyresis makes infectious individuals feel better.

4. Discussion

To put our lower bound for f_p into perspective, consider that approximately 41 400 (95% CI: 27 100–55 700) deaths per year are attributed to seasonal influenza epidemics in the United States [43] (and an order of magnitude more worldwide [44]). Taken at face value, our results indicate, for example, that if 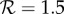then at least 700 deaths per year (95% CI: 30–2100) (and many more serious illnesses) could be prevented in the US alone by avoiding antipyretic medication for the treatment of influenza (see table 1). While subject to large uncertainty, our estimates in table 1 should be considered conservative, as we have ignored concomitant antipyretic-induced increases in infectious periods and contact rates.

Table 1.

Percentage of influenza deaths attributable to common use of antipyretic medication (for the plausible range of reproduction number for influenza). See the electronic supplementary material for details.

	attributable influenza deaths
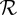	estimate (%)	95% CI
1.2	5	(0.3%, 12.6%)
1.5	2	(0.1%, 4.9%)
1.8	1	(0.1%, 2.8%)

The population-level effects of antipyretic treatment during influenza pandemics could be especially dramatic. It has been suggested that widespread use of aspirin in 1918 may have increased disease severity, and consequently death rates, during the pandemic [45], and experimental research in humans and other animals suggests that antipyretic use may increase the risk of death from serious infections [10,46]. Even without this individual-level effect, the population transmission-enhancing effect that we have highlighted here could have increased the final size of the 1918 pandemic significantly, suggesting that a non-negligible proportion of the 50–100 million [47] pandemic-related deaths could have been attributable to transmission enhancement from widespread use of antipyretic medication.

While our theoretical argument that links antipyretic treatment with an increase in epidemic size is straightforward, estimation of the magnitude of this effect is necessarily indirect, and our attempt here provides only a crude lower bound. We have been conservative in every step of our estimation of this lower bound, but we have not been able to quantify all potentially contributing factors. One further effect that could be important in principle is transmission of influenza by infected individuals before they show symptoms; however, evidence for this effect—and for asymptomatic transmission in general—is weak [48] and seems likely to be balanced in our calculations by ignoring the known lengthening of the infectious period caused by antipyresis [16]. Another potentially important effect that we have not considered is age-dependent mixing. Exceptionally high rates of antipyretic treatment in children [3] might contribute to the disproportionate role that children play in influenza transmission [26,49]; taking this into account would increase our estimated lower bound. Readers who want to consider the impact of including additional factors, or modifying our estimates, can use figure 1 to approximate the effect of changes to the population transmission enhancement factor f_p. Because the estimated absolute magnitude of f_p is fairly small, and because the curves in figure 1(b) are close to linear, most effects will be close to linear as well. For example, if amelioration of symptoms led to a lengthening of the infectious period by 20%, the number of estimated attributable cases would increase by 19.2%.

Experiments and observational studies designed specifically to estimate the magnitude of transmission enhancement by antipyresis could give much more precise constraints on the population-level effects of antipyretic use. In particular, randomized trials assigning individuals to antipyretic or placebo treatment could characterize increases in the infectious period and viral shedding owing to antipyretic drugs, while challenge experiments could better characterize the relationship between dosage and infection probability. Increases in contact rates caused by infectious individuals feeling well enough to go to work, school and other gathering places may be even more important in practice. These effects would best be estimated as part of the randomized trials discussed above, but even observational studies that survey individuals' symptoms and behaviour and correlate them with variation in use of medications could be a useful first step; we are beginning pilot studies of this sort.

We have shown that—as is well understood for antibiotics [50]—the use of antipyretics can have subtle and potentially important negative effects at the population level. Any medical intervention that aims to relieve the symptoms of an infectious disease in an individual should also be evaluated in light of potentially harmful effects at the population level. Practices that prevent infection (e.g. vaccination), or increase individual comfort without increasing transmission, are preferable from a population perspective. We hope that our analysis in this paper will spur further research to determine more precise estimates of the effects that we have discussed. Such estimates should assist in the development of evidence-based guidelines for antipyretic treatment practices.

Funding statement

D.J.D.E. and B.M.B. were supported by NSERC and the M.G. DeGroote Institute for Infectious Disease Research.