Growth and cellular patterns in the petal epidermis of Antirrhinum majus: empirical studies

Abstract

Background and Aims

Analysis of cellular patterns in plant organs provides information about the orientation of cell divisions and predominant growth directions. Such an approach was employed in the present study in order to characterize growth of the asymmetrical wild-type dorsal petal and the symmetrical dorsalized petal of the backpetals mutant in Antirrhinum majus. The aims were to determine how growth in an initially symmetrical petal primordium leads to the development of mature petals differing in their symmetry, and to determine how specific cellular patterns in the petal epidermis are formed.

Methods

Cellular patterns in the epidermis in both petal types over consecutive developmental stages were visualized and characterized quantitatively in terms of cell wall orientation and predominant types of four-cell packets. The data obtained were interpreted in terms of principal directions of growth (PDGs).

Key Results

Both petal types grew predominantly along the proximo-distal axis. Anticlinal cell walls in the epidermis exhibited a characteristic fountain-like pattern that was only slightly modified in time. New cell walls were mostly perpendicular to PDG trajectories, but this alignment could change with wall age.

Conclusions

The results indicate that the predominant orientation of cell division planes and the fountain-like cellular pattern observed in both petal types may be related to PDGs. The difference in symmetry between the two petal types arises because PDG trajectories in the field of growth rates (growth field) controlling petal growth undergo gradual redefinition. This redefinition probably takes place in both petal types but only in the wild-type does it eventually lead to asymmetry in the growth field. Two scenarios of how redefinition of PDGs may contribute to this asymmetry are considered.

INRODUCTION

Flower petals are characterized by an extremely diverse morphology manifested in a variety of shapes and sizes and a whole range of colours. This diversity is thought to have evolved as an adaptation to biotic pollinators, primarily insects (Glover, 2011; Fenster et al., 2004). It is commonly claimed that, among all floral morphological features, zygomorphy (bilateral symmetry) in particular is closely linked to insect pollination (Neal et al., 1998; Kalisz et al., 2006; Zhang et al., 2010). On the one hand this type of symmetry increases flower attractiveness for pollinators (Rodríguez et al., 2004; Gómez et al., 2006), but on the other hand it is associated with a more complex corolla structure (Cubas, 2004). Zygomorphic flowers have only one plane of symmetry and often, though not always, asymmetrical petals occur within their corollas (Preston and Hileman, 2009). The genetic background of zygomorphy and symmetry/asymmetry of individual petals was first studied in Antirrhinum majus – nowadays used as a model in flower symmetry studies (Luo et al., 1996, 1999; Corley et al., 2005; Almeida and Galego, 2005) – but later also in many other plant species (Cubas et al., 1999; Feng et al., 2006; Busch and Zachgo, 2007; Wang et al., 2008; Howarth et al., 2011, etc.; for review see Jabbour et al., 2009). These investigations led to the conclusion that, despite independent evolution, the genes that are engaged in the regulation of zygomorphy in different families are conserved (Hileman and Cubas, 2009; Jabbour et al., 2009; Preston and Hileman, 2009). However, knowledge about these genes is not enough to predict petal shape, because the form of individual petals varies considerably between species. In order to obtain a more comprehensive model of petal development it is essential to find a link between molecular signals, such as genes, and growth, which has a straightforward influence on petal form (Coen et al., 2004).

Petals, like other plant organs, grow in a continuous way (Kennaway et al., 2011), i.e. symplastically (Erickson, 1986). Such continuity implies that growth of all petal cells must be coordinated. Mathematically, such a property of plant growth may be explained by the fact that the field of growth rates in the organ (the growth field) is of the tensor type (Silk and Erickson, 1979; Hejnowicz and Romberger, 1984; Nakielski and Hejnowicz, 2003; Kennaway et al., 2011). At every point in such a field, unless growth is isotropic, there are three mutually orthogonal principal directions of growth (PDGs) along which growth rate attains extreme values: maximal (PDG_max), minimal (PDG_min) and intermediate, of a saddle type (PDG_int). Within an organ, PDGs are arranged into three families of PDG trajectories: maximal, minimal and intermediate. These trajectories, usually curvilinear, intersect at right angles and preserve orthogonal intersections during growth (Hejnowicz and Romberger, 1984; Nakielski and Hejnowicz, 2003). A pattern of PDG trajectories, either fixed or changing in time, is present in the growing organ. Thus, keeping in mind the organismal theory of multicellularity (Fleming, 2006), it is interesting to consider that at the organ level this pattern may work as a source of directional information involved in the control of growth. For example, Hejnowicz (1984, 1989) postulated that information included in PDGs is used by cells to properly orient their division planes, so that the new cell wall is typically formed in the plane specified by two PDGs, i.e. it is perpendicular to the third of these directions. In the case of anisotropic growth, Hejnowicz's postulate can be considered as a generalization of the three classical rules of cell division formulated in the 19th century by Hofmeister, Sachs and Errera (Kwiatkowska, 2004; Alim et al., 2012). Moreover, it does not contradict Lintilhac's hypothesis (Lintilhac, 1974a; Lintilhac and Vesecky, 1980) that the new walls are formed in shear-free planes (Nakielski and Hejnowicz, 2003).

In plants, the history of divisions that the cells have undergone during development can be deduced from the cellular pattern (Barlow, 1987, 1991). Cell wall arrangement and differences in wall thickness allow one to identify cell packets, i.e. groups of cells descended from a single cell, and to determine the sequence of cell divisions within each packet (Barlow, 1987, 1991; Zagórska-Marek and Turzańska, 2000). Qualitative and quantitative features of the cellular pattern, in particular cell packet shape and the relative orientation of walls formed at different times, enable speculation about growth isotropy/anisotropy (Lück et al., 1988; Barlow, 1991) and about the PDG pattern (Hejnowicz, 1984, 1989; Nakielski, 1987; Hejnowicz et al., 1988). For instance, mutually orthogonal lines, known as periclines and anticlines (Sachs, 1887), commonly used to describe the cellular pattern in median sections of shoot or root apices, are postulated to represent PDG trajectories (Hejnowicz, 1984, 1989; Kwiatkowska, 2004; Kwiatkowska and Nakielski, 2011). In the present research the cellular pattern was analysed in the epidermis of A. majus dorsal petals.

The bilaterally symmetrical corolla of wild-type A. majus is composed of five petals that are joined in their proximal portions into a tube, whereas their distal portions form five distinct lobes (Fig. 1A). The two dorsal petals (Fig. 1B) and the two lateral petals are asymmetrical. The fifth (ventral) petal is bilaterally symmetrical (Coen, 1996; Schwarz-Sommer et al., 2003). The development of the A. majus flower from its initiation to opening lasts for 58 successive plastochrons (P0–P57; Vincent and Coen, 2004), which is equivalent to about 24 days if plants grow at 25 °C. Petal primordia become visible at stages P18–P20 and grow continuously until P57 (Vincent and Coen, 2004). Cell divisions in developing petals in later stages are gradually silenced and cease approximately at stage P46. After that time, growth results only from cell expansion (Rolland-Lagan et al., 2003, 2005).

Fig. 1.

Morphology of wild-type A. majus flower and backpetals mutant flower. (A) Wild-type (WT) flower, face view; the symmetry plane is marked by a dashed line. (B) Wild-type dorsal petal. (C) Face view of backpetals mutant flower. (D) Symmetrical petal with dorsal identity (the same as d_S in C) formed in backpetals flower. In (B) and (D) the lobe is dissected from the tube; d, dorsal petal; l, lateral petal; v, ventral petal; d_S, symmetrical petal with dorsal identity. Scale bars = 5 mm.

Dorsal identity in A. majus corolla depends on the activity of two genes: CYCLOIDEA (CYC) and DICHOTOMA (DICH), both encoding TCP transcription factors (Luo et al., 1996, 1999; Almeida and Galego, 2005). In early development CYC and DICH are expressed in the whole dorsal region of the flower primordium. Later, CYC expression is preserved in the entire dorsal petals, whereas DICH expression is restricted to the inner (dorsal) halves. This non-uniform distribution of DICH is supposed to account for the internal asymmetry of the dorsal petal. Such a conclusion is confirmed by the dich mutant phenotype. The mutant produces dorsal petal lobes that are more symmetrical than wild-type lobes. More evidence for DICH involvement in dorsal petal asymmetry comes from the backpetals mutant. In this mutant CYC is expressed ectopically in all petals, whereas DICH expression is unaffected. As a result, all petals have dorsal identity, but only the two with normal expression of DICH are asymmetrical. The remaining three dorsalized petals, formed in place of the ventral petal and two lateral petals, are bilaterally symmetrical (Fig. 1C, D; Luo et al., 1996; 1999).

The complex shapes of plant organs such as the A. majus corolla arise when rates and directions of growth are modified (Coen et al., 2004). The proposed mechanisms capable of such modification are based on mechanical stresses (reviewed in Dumais, 2007; Boudaoud, 2010) and/or molecular signals that propagate and provide local polarities within the tissue (Kennaway et al., 2011). The latter mechanism was successfully adopted during modelling of A. majus corolla development (Green et al., 2010; Cui et al., 2010). These authors assumed that genes, through encoded signalling factors, had an influence on a coordinated field of polarities which in turn was capable of modulating the growth pattern. Data obtained previously on the basis of clonal analysis (Rolland-Lagan et al., 2003, 2005) were extended to all A. majus petals and incorporated in the proposed framework. By combining these data and molecular genetics with 3D computer modelling, various hypotheses on the interactions underlying the formation of diverse shapes were tested and as a result realistic shapes of the wild-type and mutant corolla were generated. This framework, though predictive and offering a wide range of possible interactions and final forms, did not account for cellular patterns in generated tissues, providing an open area for further studies.

The present research was conducted to fill this gap. The cellular pattern was investigated in developing dorsal petals of wild-type A. majus and in bilaterally symmetrical petals with dorsal identity that develop in backpetals mutant. The pattern in different zones of the petals is described qualitatively and analysed quantitatively in terms of cell wall orientation and the predominant types of four-cell packets (tetrads). The data obtained are used as the basis of a discussion of the putative role of PDGs in A. majus corolla development.

MATERIALS AND METHODS

Plant material

Seeds of Antirrhinum majus wild-type (stock JI7) and backpetals mutant (stock JI705) were obtained from the John Innes Centre by courtesy of Professor E. Coen and Dr L. Copsey. Plants were grown in a greenhouse in long days (14 h day/10 h night) and temperature ranging from 20 to 24 °C. When the oldest buds were about 8–9 mm long, the inflorescence was harvested and the calyx was removed from each bud. In the case of older buds, the petals were dissected and cuts were made in order to facilitate flattening. The developmental stage of each bud was identified according to Vincent and Coen (2004) on the basis of bud size (with the calyx), the sequence of buds on the inflorescence axis and morphological features of the growing corolla (presence of trichomes, formation of ventral furrow).

In order to visualize the cellular pattern in the petal epidermis, young buds (without calyx) or dissected petals were stained by the periodic acid–Schiff method (O'Brien and McCully, 1981, modified). Briefly, the material was fixed in FAA (acetic acid:formalin: 50 % ethanol, 1:1:18 by volume) and rinsed in water. The samples were then treated with 0·5 % periodic acid for 1 h and rinsed three times in water (15 min each time). Subsequently, they were stained in Schiff's reagent (Sigma) for 25 min and rinsed three times in a rinsing solution (1 m HCl:10 % Na₂S₂O₅:water, 1:1:18, by volume; each time for 20 min). Stained samples were dehydrated in a graded ethanol series and embedded in Euparal (Roth) between two cover glasses to facilitate analysis of both abaxial and adaxial petal surfaces. Specimens were observed in UV light under an epifluorescence microscope (Olympus BX 41). Images were acquired with a digital CCD camera (Olympus XC50).

Analysis of cellular pattern in petal epidermis

On the basis of the pattern of anticlinal cell walls and differences in wall thickness, cell packets in the epidermis were identified and the sequence of cell wall formation was determined within each packet (Fig. 2). The pattern of longitudinal cell walls was approximated by a family of smooth lines (Fig. 3), subsequently referred to as ‘d-lines’. In order to draw these lines, cell packets in different regions of petals were outlined and the shapes obtained were approximated by ellipses. The orientation of the long axes of these ellipses was used to estimate a direction field (Neuhauser, 2004) consisting of a large number of short segments (white segments in Fig. 3). In the central part of the lobe the orientation of these segments corresponded very well to the longitudinal boundaries of packets. d-Lines were drawn, consistently with the continuity criterion, as curves locally tangential to these segments. Usually several d-lines were drawn to characterize the cellular pattern in general, but for the purpose of quantitative analysis of the pattern in specific zones, they were drawn more densely with a distance of two to three cells between neighbouring lines. To assess whether the d-line pattern was symmetrical or asymmetrical, the lines tangential to d-lines were drawn at approximately one-quarter, one-half and three-quarters of petal length. Subsequently, the tangents from the left half of the petal were reflected (mirror transformation) with respect to the proximo-distal petal axis and after transformation the angle was measured between the pair of tangents drawn for corresponding points (from the left and right halves). If the angle for any of the measured pairs of tangents was greater than 10°, the pattern was classified as asymmetrical; otherwise it was deemed symmetrical.

Fig. 2.

Cell packets in petal epidermis (abaxial surface) visualized by the staining method used in the present investigation. A few cell packets consisting of several cells are outlined. In three of them, cell walls formed during the first, second, third and fourth rounds of cell division are marked in green, brown, yellow and red, respectively. Black arrow points to a trichome primordium. Scale bar = 50 μm.

Fig. 3.

Specification of d-lines characterizing the cellular pattern in A. majus petal epidermis. The lines (black dashed) were drawn manually tangentially to white segments approximating the long axes of cell packets identified in different regions of the petal. Scale bar = 200 μm.

Three groups of petals were chosen for quantitative analysis of the cellular pattern, each consisting of petals in two subsequent developmental stages: group I, P27–P28; group II, P31–P32; and group III, P41–P42. Six square zones with sides 150 μm long were analysed within the dorsal (or dorsalized) petals of each group (Fig. 4). Zones 1 and 2 (Z1 and Z2) were located in the regions of contact between petal lobes (between two dorsal petals and in contact with a lateral petal, respectively), Z3 and Z4 were in the distal part of the lobe and Z5 was in the central part of the lobe, whereas Z6 was in the tube (Fig. 4). In the case of wild-type petals, Z1 and Z2 were located in the dorsal half while Z2 and Z4 were in the lateral half of the lobe. The frequency of different types of tetrads was determined in each zone. Depending on the wall arrangement, tetrads are classified into five basic types: I, T, S, Z and X (Barlow, 1991). In the present study S- and Z-type tetrads were considered together, whereas the X type, known to be very rare in normal somatic tissues and inconsistent with the rule about avoiding four-way junctions (Lloyd, 1991), was excluded from the analysis. The frequency (as a percentage) of the tetrad types was calculated for the zones after quantification of at least ten tetrads (usually over 15) in four petals of each group. Subsequently, the average frequency in each zone was determined, separately for wild-type and mutant petals, and for abaxial and adaxial surfaces.

Fig. 4.

Localization of zones Z1–Z6 in the analysed petals and types of tetrads distinguished within these zones. (A, B) Schematic representation of two joined dorsal petals of wild-type A. majus (A) and three joined dorsalized petals of backpetals mutant (B); the zones are outlined by squares; black arrowheads mark the parts that are joined to other petals. (C) Schematic representation of five basic types of tetrad. X-type tetrads occurred very rarely in the petal epidermis and were excluded from the analysis.

To analyse the orientation of cell walls, the angle between the wall and the neighbouring d-line was determined. This analysis was performed for zones 3–5 on both sides of three or four petals in each group. Within the zones, 20–25 cell packets, each consisting of five to eight cells, were recognized and the sequence of cell wall formation was determined (Fig. 5). In the majority of analysed packets three rounds of cell divisions had taken place, leading to the generation of three types of walls differing in their relative age. One wall was formed during the first round of cell divisions, two walls were generated during the second round, and one to four walls (depending on the number of cells) were formed during the third round. For simplicity, these walls will be referred to as the oldest, intermediate and youngest ones, respectively. For left petals, the angle was measured anticlockwise from the wall to the neighbouring d-line located on the left side of the wall (Fig. 5). For right petals, the angle was measured clockwise from the wall to the neighbouring d-line located on the right side of the wall. In total, about 360 walls for each zone in each group were analysed. The frequencies of measured angles were calculated and the distributions obtained were compared statistically between different zones by means of the Kolmogorov–Smirnov test (Zar, 1999).

Fig. 5.

Angles measured between cell walls and d-lines. Three cell packets are outlined and the cell walls formed within the packets during the first, second and third rounds of cell divisions are marked in brown, yellow and red, respectively. d-Lines are marked in black; three examples of angles located between the oldest (α_I), intermediate (α_II) or youngest wall (α_III) and the neighbouring d-line located on the left side of the wall (left petal) are labelled. Scale bar = 25 μm.

RESULTS

Qualitative features of the cellular pattern in dorsal petals of wild-type and dorsalized petals of backpetals mutant A. majus

Throughout all the investigated developmental stages of wild-type dorsal petals and backpetals dorsalized petals, a characteristic fountain-like cellular pattern was maintained in both the abaxial and the adaxial epidermis (Fig. 6A, B). In the central part of the petals, cell packets were elongated along the proximo-distal axis; thus, the d-lines were nearly parallel and arranged longitudinally. In the distal parts the lines were bent towards the petal margin (Fig. 6A, B). Although the cellular pattern in general preserved the fountain-like character during development, the d-lines appeared not to be fixed, but to be slightly modified in time. For instance, in subsequent stages in the proximal part they tended to lengthen, whereas in the distal parts they became more curved towards the petal margin. In wild-type petals this distinct fountain-like cellular pattern also changed in terms of symmetry: it remained approximately symmetrical until fairly late developmental stages (P35, Fig. 6A), but about stage P37 the transition from a symmetrical to an asymmetrical arrangement of d-lines took place (compare P35, P37 and P41 in Fig. 6A). This transition was also manifested in the overall wild-type petal shape. The main difference between the wild-type and mutant petals was that the mutant petals did not become asymmetrical after stage P37, but instead remained approximately symmetrical till maturity (Figs 1D; 6B). This bilateral symmetry is visible, not only in the overall mutant petal shape but also in the cellular pattern, i.e. d-lines maintained their symmetrical arrangement during development (Fig. 6B).

Fig. 6.

Cellular pattern in the epidermis of A. majus petals in different developmental stages (shown in the lower right corner of each image). (A) Wild-type; two dorsal petals joined together (P26, P30 and P35) or the right dorsal petal (P37 and P41) are shown; P26, P30, adaxial side; P35, P37, P41, abaxial side. (B) backpetals mutant; the abaxial side of the dorsalized petals is shown. d-Lines in (A) and (B) are represented by black curves; the zones marked in (A, P37) and (B) are shown at higher magnification in Fig. 7. Arrows point to the staminode (i.e. rudimentary dorsal stamen); arrowheads point to trichome primordia. Scale bars = 200 μm.

The family of d-lines did not seem to have a single common focal point that would be fixed and localized within the dorsal/dorsalized petal, either in the wild-type or in the backpetals mutant. However, within the whole Antirrhinum corolla there were five local sites where cell packets converged. They were restricted to the contacts between lobes. In the wild-type they were located between the two dorsal lobes (part of it is visible in zone Z1, Fig. 7A), between the dorsal and lateral lobes (Z2, Fig. 7A) and between the lateral and ventral lobes (not shown). In the backpetals mutant they were localized correspondingly, i.e. between the two dorsal lobes (not shown), between each of the two dorsalized lobes (Z1, Fig. 7B) and between the dorsal and dorsalized lobes (Z2, Fig. 7B).

Fig. 7.

Details of cellular pattern in various zones of a wild-type A. majus dorsal petal (A) and a backpetals dorsalized petal (B). Micrographs show abaxial epidermis of petals in stage P37; Z1 and Z2 (A, B) are shown at slightly lower magnification to reveal the converging d-lines; within Z4 and Z5 (A, B) exemplary cell packets are outlined. Scale bar (Z1, Z2) = 75 μm; (Z3–Z6) = 50 μm.

In both wild-type and mutant petals, the shape of cell packets was to some extent different in different petal regions. In the central part of the lobe (Z5, Fig. 7A, B) and in the tube (Z6, Fig. 7A, B) the packets were elongated and arranged into clearly visible files. Often packets with a ladder-like cell wall arrangement occurred (marked in Z5, Fig. 7A, B). In the regions of contact between petals (Z1, Z2) and in distal parts of the lobe (Z3, Z4) packets were less elongated and their shape was more diverse (marked in Z4, Fig. 7A, B). In these regions packets with a ladder-like cell wall arrangement were far less common.

Frequency of different tetrad types in various zones of petals

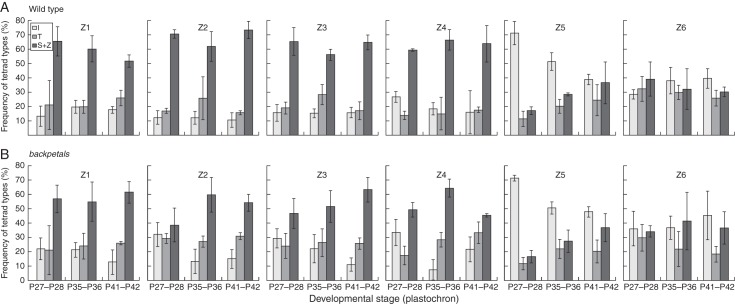
Various petal zones differed in the frequency of different types of tetrads (Fig. 8 and Supplementary Data Fig. S1 for abaxial and adaxial epidermis, respectively). In wild-type the regions of contact between petals (Z1 and Z2), as well as distal parts of the dorsal lobe (Z3 and Z4), were characterized by an abundance of S- and Z-type tetrads (taken together) with their frequency usually greater than 50 % in different developmental stages in both abaxial and adaxial epidermis (Z1–Z4 in Fig. 8A and Supplementary Data Fig. S1A). The frequency of I-type tetrads in these zones was relatively low. An opposite tendency was seen in the central part of the lobe (Z5), where I-type tetrads prevailed over the other types, especially in the abaxial epidermis of the earlier stages (Z5 in Fig. 8A). However, the frequency of I-type tetrads in Z5 decreased with petal age (Z5 in Fig. 8A and Supplementary Data Fig. S1A). In the tube (Z6), frequencies of all types were similar in all stages examined, with the frequency of I-type tetrads increasing slightly with petal age (Z6 in Fig. 8A and Supplementary Data Fig. S1A).

Fig. 8.

Frequency of different tetrad types (I, T, S + Z) in various zones (Z1–Z6) of abaxial epidermis in A. majus wild-type dorsal petals (A) and backpetals dorsalized petals (B) in different developmental stages. S- and Z-type tetrads were considered together; the graphs show the mean frequency ± standard deviation in three developmental groups.

There were no obvious differences between wild-type dorsal petals and mutant dorsalized petals, but generally it seemed that I-type tetrads occurred more frequently and S + Z type tetrads less frequently in the mutant than in the wild-type (compare Fig. 8A with 8B and Supplementary Data Fig. S1A with S1B). This tendency was more apparent on the abaxial side.

Orientation of cell walls with respect to d-lines

Distributions of angles between cell walls and d-lines in wild-type dorsal petals and backpetals dorsalized petals indicated that walls perpendicular to the d-lines were most common in both the abaxial (Fig. 9A, B) and the adaxial epidermis (Supplementary Data Fig. S2A, B). The peak obtained for 90° was usually distinct and high. Often a second, much lower peak for 180° (0°) was also distinguishable (Fig. 9A, B and Supplementary Data Fig. S2A, B). This suggests that the cells tend to orient their walls either perpendicularly or parallel to the d-lines. The graphs also demonstrate the differences between the analysed petal zones. The maxima for 90° were usually the highest in the centre of the lobe (Z5), reaching a frequency of 30–50 % in the wild-type and 40–65 % in the backpetals mutant. In the distal part of the lobe (Z3, Z4), especially in the abaxial epidermis, the maxima were mostly lower (Fig. 9A, B). The differences between petal zones were especially apparent in earlier developmental stages, whereas in later stages the zones become more similar (compare stages P27–P28 with P41–42 in Fig. 9A, B). Statistical analysis (P = 0·05, Kolmogorov–Smirnov test) indicated that in wild-type the distributions obtained differed significantly between Z3 and Z5 as well as between Z4 and Z5, in particular on the abaxial surface, whereas the dorsal and lateral parts (Z3 and Z4, respectively) were not significantly different. In the backpetals mutant the differences between the central (Z5) and distal (Z3, Z4) petal zones were statistically significant only in the earliest examined stage. Neither in the wild-type nor in the mutant was the abaxial side significantly different from the adaxial side. The distributions obtained for the same zone but in different developmental stages (e.g. compare Z5 in all stages shown in Fig. 9A, B) also did not differ significantly, suggesting that the tendency of cell walls to orient perpendicularly or parallel to the d-lines is sustained during growth.

Fig. 9.

Orientation of cell walls with respect to d-lines in abaxial epidermis of A. majus wild-type dorsal petals (A) and backpetals dorsalized petals (B) in different developmental stages. The graphs show the mean distributions of wall orientation (obtained by measurements in three or four lobes in each developmental group) in three zones: Z3, Z4 and Z5. Cell walls of different relative age were considered together.

Statistical comparison of cell wall orientation between wild-type and mutant petals did not reveal significant differences in the distributions of the measured angles. However, the graphs show that the frequency of cell walls perpendicular to the d-lines was slightly higher in the mutant (Fig. 9B and Supplementary Data Fig. S2B) than in the wild-type (Fig. 9A and S2A).

The relative age of cell walls had an influence on their orientation with respect to d-lines in both the wild-type and the backpetals mutant (see example graphs in Fig. 10A, Supplementary Data Fig. S3A and Fig. 10B, Supplementary Data Fig. S3B, respectively). The maxima for the youngest walls were always at 90° and were higher than the maxima for older walls (Fig. 10 and Supplementary Data Fig. S3). Lower and less apparent maxima occurred for the intermediate cell walls, whereas the lowest ones occurred for the oldest cell walls. This tendency was observed regardless of the petal zone (e.g. Z3, Z4 and Z5 in Fig. 10A, B) or developmental stage (not shown). Interestingly, lower maxima were sometimes shifted to the left or right from the angle of 90° (e.g. Z3 and Z5 in Fig. 10A, and Z3 and Z4 in Fig. 10B). Such shifts were usually larger for the oldest walls than for the intermediate ones (e.g. Z3 in Fig. 10A).

Fig. 10.

Orientation of cell walls of different relative age with respect to d-lines in three zones: Z3, Z4 and Z5 in the abaxial epidermis of A. majus wild-type dorsal petals (A) and backpetals dorsalized petals (B). Representative graphs for individual petals in stage P35–P36 are shown.

DISCUSSION

During petal growth in A. majus the epidermal cellular pattern is continuously modified, but despite these modifications it remains fountain-like in general. This fountain-like pattern is the most characteristic feature of the petal epidermis, manifested in both the wild-type dorsal petal and the dorsalized petal of the backpetals mutant. Similarities between the two analysed petals, observed especially in early developmental stages, suggest that the ‘programmes’ of young petal growth are the same. The differences arise later and seem to lie mainly in progressive changes in growth field symmetry, leading eventually to the formation of either asymmetrical or symmetrical mature petals. The present analysis also showed that the orientation of cell division planes is not random, but clearly reveals some supra-cellular organization, which is, in our opinion, related to the PDGs.

Cellular pattern and principal directions of growth

The present investigations showed that the fountain-like cellular pattern was manifested in all the examined A. majus petals, independently of their side (abaxial, adaxial), developmental stage (P23–P42) or genotype (wild-type, backpetals). Although small, gradual modifications of this pattern were observed, no transformation into another pattern was noted. A similar fountain-like pattern was also visible in the arrangement of pigmented clones (Green et al., 2010), formed after induced excision of unstable transposons.

The d-lines describing the system of longitudinal anticlinal walls in the petal epidermis in the present study were drawn in a similar way to the displacement lines (periclines) in the classical studies of apical meristems (Schüepp 1926, 1966). In terms of the tensor approach (Hejnowicz and Romberger, 1984), periclines and anticlines represent PDG trajectories (Hejnowicz 1984, 1989). We assume that in petals a similar correspondence takes place, i.e. d-lines represent one family of PDG trajectories. This assumption is confirmed by the numerically determined main orientations of growth, also arranged in a fountain-like pattern (Green et al., 2010). Support for our assumption also comes from arabidopsis petals, in which there is a concurrence between the recently proposed divergent polarity field (Sauret-Güeto et al., 2013), d-lines recognized in the epidermal cellular pattern and the directions of maximal growth rate (PDG_max) determined for individual cells (M. Raczyńska-Szajgin, unpubl. res.) by means of sequential replica method (Williams and Green, 1988). The modifications in the d-line pattern described for A. majus petals suggest that PDG trajectories, although preserving the general fountain-like pattern, undergo continuous redefinition. This redefinition is in agreement with the postulate that growth of petals is controlled by a dynamic polarity field (Green et al., 2010; Kennaway et al., 2011).

The local foci in the d-lines observed at the contact sites between two lobes are interesting from a mechanical point of view. We hypothesize that these foci result from stresses generated in the course of corolla development, since PDGs are postulated to resemble principal directions of stress (Kwiatkowska, 2004; Potocka et al., 2011). In a model of A. majus corolla development (Green et al., 2010) these regions, located between ventral and lateral petals, were suggested to play a role as organizers of tissue polarity.

Growth anisotropy and orientation of cell division planes

Green and collaborators (2010) demonstrated that initially circular virtual sectors on the surface of the A. majus petal changed into ellipses during development. This indicates that petal growth is anisotropic, with the maximal growth in the proximo-distal direction. To qualitatively assess the growth anisotropy in different petal parts, we analysed the frequency of various types of tetrads in the epidermis. According to Barlow (1991), if I-type tetrads predominate, growth anisotropy is high, while if S- and Z-type tetrads are abundant the organ is growing isotropically or almost isotropically. The predominant tetrad types indicate that the central part of the lobe and the tube grow in a highly anisotropic way in both wild-type and mutant petals. In other zones, including distal parts of the petal lobe, anisotropy is lower. These spatial differences are maintained in successive developmental stages.

Several hypotheses have been proposed to explain the orientations of cell division planes in growing plant organs (reviewed by Smith, 2001; Müller, 2012; Roeder, 2012). The classical rules assume that cells divide perpendicularly to the main growth axis (Hofmeister, 1863), almost perpendicularly to the existing walls (Sachs, 1878) and/or along the shortest path dividing the cell into two daughters of equal size (Errera, 1888). These rules and their modifications (compare Besson and Dumais, 2011) emphasize the role of the geometry of the individual cell. They seem especially important when cells lack internal or external cues regulating the plane of cell division (Besson and Dumais, 2011; Alim et al., 2012), and are therefore particularly useful in isotropic growth modelling (Sahlin and Jönsson, 2010). On the other hand, empirical studies (Lynch and Lintilhac, 1997; Hamant et al., 2008; Potocka et al., 2011) revealed that mechanical stresses within organs are also capable of regulating the orientation of cell divisions, and such results are consistent with organismal theory (Green, 1980; Kaplan, 1992).

The present analysis of the orientation of the newly formed cell walls in A. majus petals, in particular the prevalence of walls perpendicular and parallel to d-lines, supports Hejnowicz's postulate (1984, 1989) that cells typically divide perpendicularly to PDGs. This postulate can be regarded as a combination of the previously mentioned concepts. In the case of anisotropic growth it is a generalization of the cell geometry-based rules (Hejnowicz and Hejnowicz, 1991; Kwiatkowska, 2004; Alim et al., 2012). On the other hand, it also takes into account mechanical aspects of tissue growth, since growth is an irreversible deformation resulting from stresses in cell walls and it is reasonable to expect a relationship between PDGs and principal directions of stress (Kwiatkowska, 2004; Potocka et al., 2011). Although this relationship needs further investigation, we postulate that PDG-oriented cell divisions may emerge as a result of mechanical cues ‘sensed and interpreted by the highly dynamic and regulated microtubule cytoskeleton’ (Alim et al., 2012; see also Mirabet et al., 2011).

In A. majus petals, comparison of cell walls differing in age showed that, among older walls, the percentage of walls that were oblique with respect to d-lines was higher than among newly formed walls. This phenomenon can be explained by the continuous redefinition of PDG trajectories postulated above. The older cell walls perpendicular to the PDGs at the time of their formation are no longer perpendicular to the redefined PDGs represented by slightly modified d-lines. This effect deepens with time. A similar tendency of successive cellular pattern modification was also visible in computer simulations of lateral root formation when PDG trajectories were changed (Szymanowska-Pułka and Nakielski, 2010).

The dynamic growth field and its role in the emergence of petal asymmetry

The wild-type dorsal petal and the dorsalized petal of the backpetals mutant differ in DICH expression (Luo et al., 1999) and symmetry at maturity. However, these petals are of the same identity and, according to our observations, their early development proceeds similarly. Both are initiated as bilaterally symmetrical primordia and this bilateral symmetry is maintained not only in the mutant, but also, approximately until stage P35, in the wild-type. Moreover, they both exhibit a fountain-like cellular pattern in the epidermis; in both, the orientation of new cell walls is consistent with Hejnowicz's postulate, and redefinition of PDG trajectories presumably take place. This suggests that in early developmental stages the growth fields and the ‘programmes’ of modification of these growth fields are very similar in the two petals. The differences in the fields arise later and are manifested in progressive changes of wild-type petal symmetry.

In the model of A. majus corolla development (Green et al., 2010; Kennaway et al., 2011) a dynamic growth field and a network of gene interactions determining growth rates and polarity within the tissue are used. Polarity organizers, which are influenced by genes, specify a polarity field and this field can modulate growth, in particular the direction of maximal growth. Incorporation of mechanical constraints leads to the resulting growth, which can feed back to modify tissue polarity. According to this polarity-based approach, wild-type petal asymmetry results from interactions between growth and the polarity field. We relate this asymmetry to the gradual redefinition of PDG trajectories, assuming that the petal growth field is characterized by a fountain-like PDG arrangement manifested in the cellular pattern (Fig. 11). The young petal of both the wild-type and the mutant is located in the symmetry plane of this field. In the mutant (Fig. 11A), the field maintains its bilateral symmetry throughout development and the petal remains in the field symmetry plane. As a result, it preserves its symmetrical shape. In the case of wild-type petals, in later developmental stages the redefinition of PDG trajectories leads to the asymmetrical PDG pattern (Fig. 11B). The proposed PDG redefinition explains why the adjustment of older cell walls to the d-lines is better in the mutant than in wild-type. Specifically, in the wild-type the modifications of PDG trajectories are likely more pronounced due to the transition to asymmetry versus the maintenance of bilateral symmetry in the mutant. The restriction of DICH expression in the dorsal part of the wild-type dorsal petal takes place about stages P25–P28 (Luo et al., 1999) but it does not result immediately in petal asymmetry. This delay suggests that the gradual redefinition of PDGs in response to genetic signals proceeds slowly rather than abruptly.

Fig. 11.

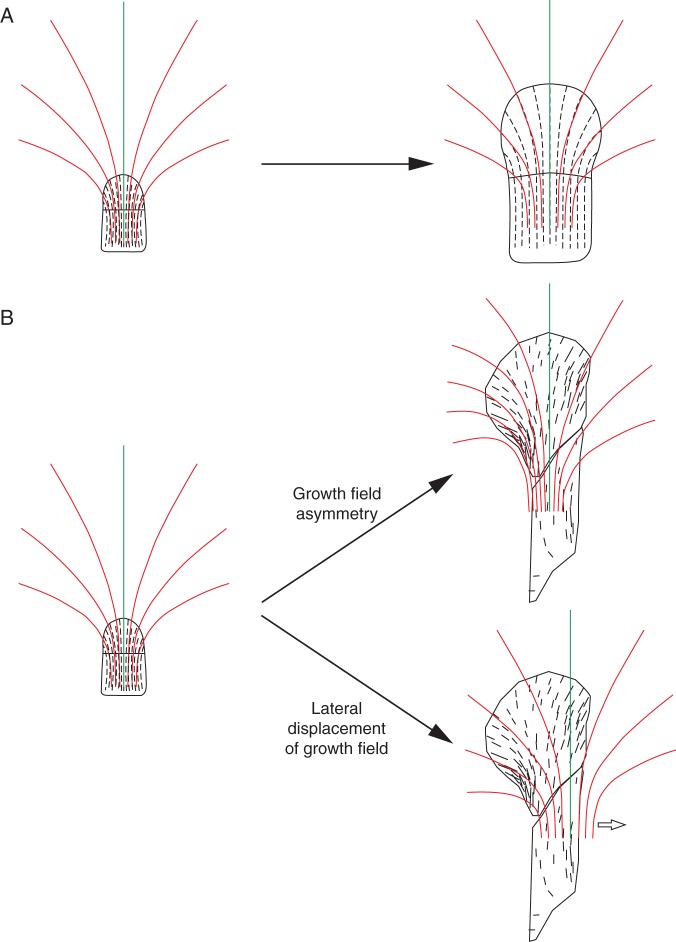
Model of symmetry maintenance in the mutant petal (A) and transition from symmetry to asymmetry caused by PDG trajectories redefinition in the wild-type petal (B). Red lines represent PDG trajectories in the adopted growth field, and the central trajectory is marked in green; petal outlines and patterns of d-lines (except for the later stage in B) are drawn on the basis of the specimens obtained; the petal with marked orientations of growth, representing a later stage in (B), is drawn on the basis of Green et al. (2010).

Theoretically, the asymmetrical pattern of PDG trajectories observed in wild-type petals can be achieved via two different scenarios (Fig. 11B). In the first scenario, the PDG trajectories in the two halves of the initial field change in different ways, so the field gradually loses its internal symmetry. In the second scenario the field remains symmetrical, but it is progressively displaced with respect to the petal. The horizontal component of this progressive displacement results in the petal no longer being located in the field symmetry plane. The modifications observed in the cellular pattern of the wild-type petal lobe support the second scenario rather than the first; in our future studies we will therefore investigate petal development further by means of a simulation model that would include growth field modifications and an appropriate cell division algorithm.

The progressive displacement of the growth field with respect to the petal can be interpreted in terms of a putative link between PDGs and the principal directions of stress (Kwiatkowska, 2004; Potocka et al., 2011). We hypothesize that the PDG trajectories manifested in the cellular pattern of petal epidermis are in fact related to a specific and complex pattern of tension and compression stresses in the growing Antirrhinum bud (such a pattern of stresses has been proposed for other plant organs on the basis of photoelastic or mathematical modelling; e.g. Lintilhac, 1974b; Lintilhac and Vesecky, 1980; Hamant et al., 2008). Genetic signals are likely to change this pattern of stresses by modifying the mechanical properties of plant cell walls (e.g. Cosgrove, 2005). When the Antirrhinum corolla is growing, the positions of all petals, including the dorsal one, within such a genetically regulated ‘stress field’ is changing, and this process may be described by progressive displacement of the field with respect to the petal. So far there are no available techniques to show or measure stresses within the Antirrhinum corolla, but, as already mentioned, plant cells are probably capable of detecting them (the cytoskeleton is postulated to be involved in this process) and use the cues as directional cues (Lynch and Lintilhac, 1997; Hamant et al., 2008; Mirabet et al., 2011; Uyttewaal et al., 2012).

The polarity-based system used for modelling Antirrhinum petal growth (Green et al., 2010; Kennaway et al., 2011) was based on data on the size and arrangement of pigmented sectors initiated at different stages. The present results are based directly on the analysis of the cellular pattern in the epidermis. These two approaches complement each other and lead to the general conclusion that the pattern of main growth direction within the petal is dynamic and changes during development, but preserves a general fountain-like nature. Our results imply in addition that the dynamic pattern of PDGs operates not only at the organ level but also at the cellular level, affecting the orientation of cell divisions. In this sense this approach leads to coherence between the growth of the whole petal and particular cell packets within the petal.

The present results may serve as a basis for simulations of cell divisions and cellular pattern development in growing petals. We posit that such simulations should implement the redefinition of PDG trajectories, which probably takes place in both petals, but only in wild-type results in the final asymmetrical PDG arrangement. The nature of the link between asymmetrical DICH expression, asymmetrical PDG arrangement and the asymmetrical cellular pattern still needs investigation. However, one may assume that the mechanism generating an accurate petal shape may involve not only proper gene expression and a dynamic growth field but also some mechanical constraints capable of remodelling the coordinated field of polarities within the tissue and directional cues enabling cells to divide in appropriate directions.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Figure S1: frequency of different tetrad types (I, T, S + Z) in distinct zones of adaxial epidermis in the examined petals. Figure S2: orientation of cell walls with respect to d-lines in the adaxial epidermis of the examined petals. Figure S3: orientation of cell walls of different relative age with respect to d-lines in three zones (Z3, Z4 and Z5) in the adaxial epidermis of the examined petals.