Do root hydraulic properties change during the early vegetative stage of plant development in barley (Hordeum vulgare)?

Abstract

Background and Aims

As annual crops develop, transpirational water loss increases substantially. This increase has to be matched by an increase in water uptake through the root system. The aim of this study was to assess the contributions of changes in intrinsic root hydraulic conductivity (Lp, water uptake per unit root surface area, driving force and time), driving force and root surface area to developmental increases in root water uptake.

Methods

Hydroponically grown barley plants were analysed during four windows of their vegetative stage of development, when they were 9–13, 14–18, 19–23 and 24–28 d old. Hydraulic conductivity was determined for individual roots (Lp) and for entire root systems (Lp_r). Osmotic Lp of individual seminal and adventitious roots and osmotic Lp_r of the root system were determined in exudation experiments. Hydrostatic Lp of individual roots was determined by root pressure probe analyses, and hydrostatic Lp_r of the root system was derived from analyses of transpiring plants.

Key Results

Although osmotic and hydrostatic Lp and Lp_r values increased initially during development and were correlated positively with plant transpiration rate, their overall developmental increases (about 2-fold) were small compared with increases in transpirational water loss and root surface area (about 10- to 40-fold). The water potential gradient driving water uptake in transpiring plants more than doubled during development, and potentially contributed to the increases in plant water flow. Osmotic Lp_r of entire root systems and hydrostatic Lp_r of transpiring plants were similar, suggesting that the main radial transport path in roots was the cell-to-cell path at all developmental stages.

Conclusions

Increase in the surface area of root system, and not changes in intrinsic root hydraulic properties, is the main means through which barley plants grown hydroponically sustain an increase in transpirational water loss during their vegetative development.

INTRODUCTION

Annual crop plants such as barley and wheat lose the equivalent of their shoot water content by transpiration within hours under hydroponic growth conditions. For example, 2-week-old barley plants grown at 70–80 % relative humidity, 300–400 μmol photons m⁻² s⁻¹ photosynthetically active radiation and 21 °C have a shoot water content of approximately 1 g and daytime transpiration rates of 10⁻¹⁰ m³ s⁻¹ (Knipfer and Fricke, 2010, 2011). These plants lose the equivalent of their shoot water content every 2–3 h by transpiration. Under field conditions, transpirational water loss rates are even higher (Nobel, 1991). This water loss has to be matched by an equivalent rate of root water uptake.

Although the above figures apply to plants when grown under water-sufficient conditions, they highlight the need to have evolved mechanisms to rapidly (minutes to hours) adjust the rate of water loss to changes in the availability of water in the root environment or vapour pressure deficit between leaf internal air spaces and ambient air. The main means by which this is achieved is the reversible opening and closing of stomata, and this includes hormonal control (Raschke, 1970; Jackson, 1993; Davies et al., 2002). Similarly, roots must be able to adjust water uptake. The discovery of aquaporins, membrane-intrinsic proteins that facilitate the movement of water and some neutral, small-molecular-weight solutes across the (plasma) membrane of cells, has provided molecular entities with which short-term regulation of root water uptake can be accomplished (for reviews see Tyerman et al., 1999; Javot and Maurel, 2003; Maurel 2007; Maurel et al., 2008, 2010). For example, aquaporin activity has been shown to change in response to changes in soil water potential (Ψ), salinity, oxygen levels and the day/night cycle (Clarkson et al., 2000; Gerbeau et al., 2002; Tournaire-Roux et al., 2003; Boursiac et al., 2005, 2008; Hachez et al., 2006, 2012; Aroca et al., 2012; Gambetta et al., 2012). Plants also experience longer-term changes in transpirational water loss as part of their ontogenetic development, but it is not clear how root water uptake is adjusted accordingly. The aim of the present study was to obtain information on the relationship of increases in transpirational water loss and root hydraulic properties for the barley crop during its first 4 weeks of vegetative development.

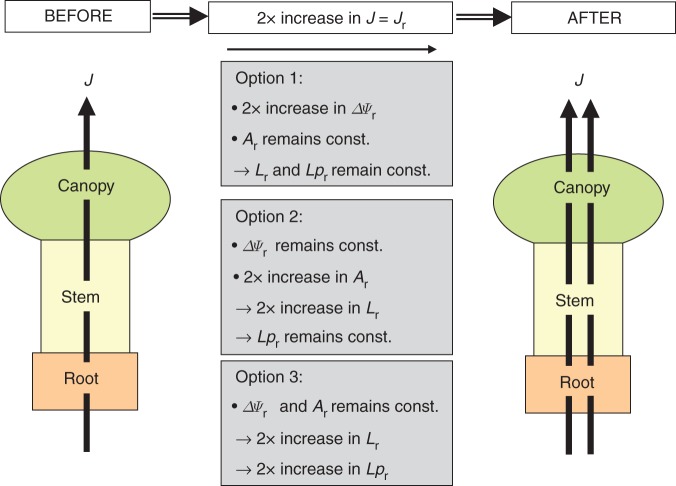
Water uptake through the root system can be increased by three basic means: (i) increase in the absorbing surface area (A_r, m²); (ii) increase in intrinsic water-uptake properties (hydraulic conductivity, Lp_r, m s⁻¹ MPa⁻¹) per unit surface and driving force (water potential gradient, ΔΨ, MPa); and (iii) increase in the biophysical force that drives water uptake between the root medium and the xylem (ΔΨ_r, MPa). By analogy to an electric circuit and Ohm's law (van den Honert, 1948; Landsberg and Fowkes, 1978), the flux of water (J, m³ s⁻¹) through a system (here, the plant) equals the product of conductance for water (hydraulic conductance, L, m³ s⁻¹ MPa⁻¹, which is the inverse of resistance, L = 1/R) of that system, and ΔΨ, which acts between the starting point (here, the external solution and soil) and the end point (here, ambient air) of the flow path (J = L × ΔΨ); in an electric circuit, the equivalent quantities are I (current), G (conductance) and V (voltage), with I = G × V (Fig. 1A). In the root medium–plant–air continuum, the overall driving force for the flux of water through the plant is the difference in Ψ between soil and air. As these are two external quantities, which cannot easily be controlled by the plant, plants have to adjust J mainly through changes in L. No matter how big or small J is, it has to be the same through each component of the plant's hydraulic circuit, yet ΔΨ, which operates across each component, is inversely related to L. The conductance of a plant consists of several components (Fig. 1: root system, subscript ‘r’; stem, subscript ‘s’; canopy, subscript ‘c’), which are arranged in series (1/L_plant = (1/L₁) + (1/L₂) + …+ (1/L_n); or R_plant = R₁ + R₂ + … R_n), similar to the way in which electrical conductances are arranged in series in an electric circuit (1/G_total = (1/G₁) + (1/G₂) + … (1/G_n)) (Fig. 1A). When considering only water flow through the root system, individual roots can be treated as being arranged in parallel. As in an electric circuit, the fluxes, and conductances, through individual component roots add up to the total flux, and conductance, of water through the root system (L_r = L₁ + L₂ + …+ L_n) (Fig. 1B). It is important to note here that conductance L (units, m³ s⁻¹ MPa⁻¹) is a surface-dependent size and does not provide information about the intrinsic hydraulic properties of, for example, a root per unit root surface (A). Rather, these hydraulic properties are expressed as conductivity (Lp, with Lp = L/A, m s⁻¹ MPa⁻¹). The difference between L_r and Lp_r is highlighted in Fig. 1C.

Fig. 1.

(A, B) Water flow through a plant in analogy to flow of a current through an electric circuit, and (C) highlighting the difference between root hydraulic conductance and conductivity. (A) Arrangement of conducting elements in series. (B) Arrangement of conducting elements in parallel, with the focus on the root system. (C) Changes in root hydraulic conductance and conductivity for the scenario in which water flows through a root system (blue, flat squares) double. Left-hand panels in (A) and (B) show the electric circuit. R, overall resistance; R_1–3, resistances of conducting elements 1–3; V, overall voltage applied; V_1–3, voltages that operate across conducting elements 1–3; I, current; G, electric conductance, with individual-component conductance G_1–3. Right-hand panels in (A) and (B) show the plant. L, overall hydraulic conductance of plant, with component conductance through root system (L_r), stem (L_s) and canopy (L_c) and individual roots 1–3 (L_1–3); ΔΨ, overall water potential gradient between soil and air, with component water potential gradients across the root system (ΔΨ_r), stem (ΔΨ_s) and canopy (ΔΨ_c); J, overall water flow through the plant, with component flows through individual roots 1–3 (J_1–3). Abbreviations in (C): A_r, root surface area; J_r, water flow through the root system; L_r, hydraulic conductance; Lp_r, hydraulic conductivity; ΔΨ_r, water potential gradient across the root system, here fixed at 0·1 MPa. The figures provided for A_r and J_r (= J_c, water flow at the leaf level by transpiration) represent typical data for 2- to 3-week-old barley plants (e.g. compare Knipfer and Fricke, 2011).

Figure 2 summarizes the basic options by which, for example, a 2-fold increase in root water uptake could be achieved during plant development. In option 1, ΔΨ_r doubles while the conductance of each component (root) remains unchanged. In option 2 the root surface area doubles, as the second root, of identical conductance and with dimensions and conducting properties identical to those of the original root, is arranged in parallel. This effectively doubles the overall conductance, L_r, while ΔΨ_r and hydraulic conductivity, Lp_r, remain unchanged. Finally, in option 3 L_r and Lp_r double while ΔΨ_r does not change. The original root is replaced with a root that has identical dimensions but has twice the surface-area-specific conductance of the original component root. For the reasons outlined above, option 1 is of limited value in adjusting root water uptake as ΔΨ_r is under limited control. In comparison, options 2 (increase in root surface area) and 3 (increase in root Lp_r) are better suited to the adjustment of root water uptake. However, options 2 and 3 differ fundamentally from each other in terms of underlying regulatory mechanisms. They can be summarized as ‘more of the same’ (option 2) and ‘something new or different’ (option 3) (Fig. 2). For example, a developing plant adopting option 2 may double water uptake through the root system either by doubling the number of roots, such that these roots have identical water uptake (hydraulic) properties compared with the previous roots, or by simply doubling the surface area of the existing roots in the root system [the main hydraulic resistance in these roots is the radial uptake path across the root cylinders, which are arranged parallel to each other (Steudle, 2000)]. In both cases, root water uptake has been increased by providing more root surface with the same hydraulic properties. The Lp_r of the root system has not changed. In contrast, Lp_r changes in a plant adopting option 3 (Figs 1C and 2). How can Lp and Lp_r change in an individual root and in a plant root system, respectively?

Fig. 2.

Three basic options for plants to increase root water uptake during development. Here, an increase in whole-plant water flow by transpiration (J) by a factor of 2 is considered. According to Fig. 1, J is considered to be equivalent to flow of water through the root system (J_r). In option 1 the water potential gradient (ΔΨ_r) across the root doubles but there are no changes in root surface area (A_r), root system hydraulic conductance (L_r) or root system hydraulic conductivity (Lp_r). In option 2 root surface area doubles, as does L_r; neither ΔΨ_r nor Lp_r changes. In option 3 Lp_r and L_r double; neither ΔΨ_r nor root surface area changes.

The Lp of an individual root depends on the hydraulic properties of the axial flow path along (predominantly) mature metaxylem vessels and a radial flow path between the root epidermis and stele. It is generally accepted that the radial flow path constitutes the hydraulic bottleneck within roots and is the limiting hydraulic conductance (Frensch and Steudle, 1998; Steudle and Peterson, 1998; Steudle, 2000; Knipfer and Fricke, 2010, 2011). For this reason, the radial flow path is particularly suited to adjust water uptake. The radial flow path consists of two transport routes of water arranged in parallel: the apoplastic and cell-to-cell paths. The apoplastic path provides free diffusional space outside the plasma membrane and consists mainly of the wall space. The cell-to-cell path involves symplastic flow through plasmodesmata and transmembrane flow across cellular membranes. It is currently not possible to distinguish experimentally between the symplastic and transmembrane paths.

Water flow along the apoplast and cell-to-cell paths is driven by a gradient in Ψ between the root medium and xylem. This Ψ gradient has an osmotic and a hydrostatic pressure component. The osmotic component drives water uptake only in the presence of a semipermeable barrier, and since such a barrier is provided by cellular membranes but not by the apoplast, the currently accepted idea (e.g. Steudle, 2000) is that osmotic gradients drive water uptake only along the cell-to-cell path. In contrast, a gradient in hydrostatic pressure between the root medium and xylem can drive radial water uptake in two ways. Along the cell-to-cell path, a hydrostatic pressure gradient drives water uptake by lowering xylem Ψ. For example, an increase of 0·1 MPa in xylem tension lowers xylem Ψ by 0·1 MPa. This drives as much additional water flow along the cell-to-cell path as is driven by an increase in xylem osmotic pressure of 0·1 MPa. In addition, hydrostatic pressure gradients can drive water flow along the apoplast path by bulk flow. The apoplast provides less resistance to water movement compared with the membranous cell-to-cell path, provided that the apoplast is not blocked by depositions of suberin, such as Casparian bands or suberin lamellae (e.g. Schreiber et al., 1999; Enstone et al., 2003). Also, bulk flow provides a much faster mode of transport compared with diffusion over longer distances. Together, these findings have led to the concept that the apoplastic and cell-to-cell routes provide a low-resistance (high-conductance) and high-resistance (low-conductance) path, respectively, for radial water movement across roots (Steudle, 2000; Steudle and Peterson, 1998). To make it easier to distinguish between water flow driven radially through osmotic and hydrostatic gradients, we refer in the following to ‘osmotic Lp’ and ‘hydrostatic Lp’, respectively. The relative sizes of osmotic and hydrostatic Lp indicate which path contributes most to radial water uptake. If osmotic and hydrostatic root Lp values are of similar magnitude, most water flows along the cell-to-cell path; if hydrostatic Lp exceeds osmotic Lp several-fold, most water flows along the apoplast path (Steudle and Peterson, 1998). The contributions of the apoplast and cell-to-cell pathways to root water uptake can vary among plant species, most likely due to species-specific root morphological and anatomical features (e.g. Bramley et al., 2009; for reviews see Steudle and Peterson, 1998; Steudle, 2000; Maurel et al., 2008). For example, in barley, recent evidence suggests that radial water uptake occurs mainly along the cell-to-cell path, involving aquaporin (Knipfer and Fricke, 2010, 2011).

Many studies have shown that resistance to water flow decreases with increasing flux through the root system (for reviews see Steudle and Peterson, 1998; Steudle, 2000). The composite model of water transport provides an explanation for this observation in that it proposes that at times of high transpirational water loss (during the day) xylem tensions cause water to move predominantly across the (low-resistance) apoplastic route, while in the absence of transpiration tension, such as during the night, osmotic gradients drive radial water uptake along the (higher-resistance) cell-to-cell path (Kramer, 1932; Steudle and Peterson, 1998; Steudle, 2000). Furthermore, recent studies on rice and poplar suggest that the rate of transpirational water flow directly impacts root Lp (Sakurai-Ishikawa et al., 2011; Kuwagata et al., 2012; Laur and Hacke, 2013). Since both the type of pathway (cell-to-cell, apoplast) and the Lp of the pathway seem to depend on the water flow rate through the root and the prevailing type of driving force (osmotic, hydrostatic), it is important to analyse root hydraulic properties under conditions where the type of driving force and the water flow rate are similar to those in the intact, transpiring plant. This applies not only to daytime transpiration, but also to night-time transpiration, which are 10–15 % of daytime water loss rates in many plant species, including barley (Caird et al., 2007; Knipfer and Fricke, 2011). Therefore, to relate root Lp to daytime transpirational water loss, Lp should be determined in the presence of xylem tensions and rates of root water uptake approximating daytime transpirational flow in intact plants. To relate root Lp to night-time transpirational water flow, Lp should be determined in the presence of osmotic gradients and rates of root water uptake approximating night-time water flow.

Aquaporins are water-conducting channels that are gated, i.e. they exist in an open, conducting, or a closed, non-conducting conformation (Törnroth-Horsefield et al., 2006; for review see Maurel et al., 2008). The amount of water flowing through aquaporins per unit root plasma membrane surface and time (‘aquaporin activity’) can be increased in several ways (Maurel et al., 2008). The number of aquaporin molecules in the membrane can be increased by increased synthesis or altered trafficking; the number of aquaporins that are in an open state at any one time can be increased by post-translational modification, including phosphorylation, methylation and local pH changes; and some aquaporins conduct water faster than others, and conductance can be increased by interaction of different aquaporin isoforms. In a plant, where most water is taken up through root aquaporins along the cell-to-cell path, any significant increase in aquaporin activity will lead to an increase in root Lp (compare option 3 outlined above). Such an increase, which is aimed specifically at aquaporins, should be metabolically cheaper than a general increase in the conducting root surface (compare option 2 outlined above). From this point of view, one would expect that root Lp increases substantially during plant development. The study in which this question has been addressed in most detail (Fiscus and Markhart, 1979) was carried out on bean (Phaseolus vulgaris), and the authors observed an initial overshoot in Lp, with Lp subsequently stabilizing at a lower value. However, that study was carried out in the pre-aquaporin era and did not consider different flow paths (apoplast, cell-to-cell) or the contributions of different types of root to water uptake by the root system. Also, water flow through the root system was induced by sealing an excised root system in a pressure chamber and applying significant hydrostatic pressure to the root system. Under these conditions, and unlike the situation in a transpiring plant, the hydrostatic pressure of the root medium can force water along the apoplast and into any intercellular air spaces. This can lead to axial water flow along the root cortex, effectively short-cutting any endodermal or stelar resistance to water flow. Also, any feedback from the shoot to control root water uptake, which can occur in intact, transpiring plants, is not possible in excised root systems. This is particularly important as recent studies suggest that transpiration and shoot excision directly impact root water uptake by affecting aquaporin activity (Sakurai-Ishikawa et al., 2011; Kuwagata et al., 2012; Laur and Hacke, 2013; Vandeleur et al., 2013), and therefore the Lp of the cell-to-cell path. The aim of the present study was to overcome these potential shortcomings by studying different types of root and applying techniques that can measure water flow driven by hydrostatic and osmotic gradients without applying hydrostatic pressure to the root medium. Also, hydrostatic Lp_r was determined for intact, transpiring plants. Barley plants were studied in four windows of their vegetative development between 9 and 28 d after germination.

MATERIALS AND METHODS

Outline of experimental procedure

Hydroponically grown barley (Hordeum vulgare ‘Jersey’) plants were analysed when they were 9–13, 14–18, 19–23 and 24–28 d old. These ages are referred to as developmental windows I, II, III and IV, respectively. At the two younger developmental windows, the root system consisted entirely or almost entirely of seminal roots; at the older developmental windows, adventitious roots contributed increasingly to the surface area of the root system. Four sets of experiments were carried out, each involving plants derived from several independent batches. (i) In one set of experiments, individual seminal and adventitious roots were analysed for osmotic Lp and hydrostatic Lp using exudation and root pressure probe analyses, respectively. This made it possible to compare osmotic and hydrostatic Lp both within and between the two types of roots. (ii) In another set of experiments, plants were first analysed for transpiration rates in the growth chamber and subsequently used for analyses of the osmotic Lp_r of entire root systems. This approach made it possible to obtain osmotic Lp_r values for the entire root system and to relate osmotic Lp_r to exudation rates. By using information from a previous study (Knipfer and Fricke, 2011) on the relation between day- and night-time transpiration rates in barley, it was possible to conclude whether exudation rates observed here for isolated root systems were in the range of night-time transpiration rates of intact plants, and whether any developmental increase in the latter is accompanied by changes in root system osmotic Lp_r. (iii) In a third set of experiments, hydrostatic Lp_r was determined by analyses of intact, transpiring plants. In these plants, xylem Ψ, which was required for the calculation of root system Lp_r, together with values of transpirational water loss and A_r, was derived from analyses of Ψ of leaf epidermal cells. The hydrostatic Lp_r obtained in this way could be related to the transpiration rates of plants, and this made it possible to conclude whether developmental increases in plant transpirational water loss were due mainly to increases in A_r, ΔΨ_r or hydrostatic Lp_r (Figs 1 and 2). This experiment also made it possible to compare hydrostatic Lp_r obtained in intact plants with osmotic Lp_r obtained in isolated root systems, a comparison that provides information on the main path of radial root water uptake during vegetative development in barley [compare with experiment (i)]. (iv) Data obtained through experiments on osmotic Lp of individual roots and Lp_r of entire root systems showed that osmotic Lp was consistently higher than Lp_r. To follow up this observation, a fourth set of experiments was carried out in which osmotic Lp_r (exudation analyses) was determined in succession for the entire root system and its individual component roots. This experiment was carried out only for younger plants, in which one type of root (seminal root) made up the bulk of root surface area.

Plant material and growth conditions

Hordeum vulgare ‘Jersey’ plants were grown in modified half-strength Hoagland solution in a growth chamber (Microclima, MC1000HE, CEC Technology, Glasgow, UK) as described previously (Fricke and Peters, 2002; Knipfer and Fricke, 2011). The root medium was aerated throughout development, and plants grew under a day/night cycle of 16/8 h at temperatures of 21/15 °C. Relative humidity was 70 % and photosynthetically active radiation at plant level was 300–350 μmol m⁻² s⁻¹. Plants were analysed when they were 9–13 d old (the first leaf becoming fully expanded and the second leaf gaining half to almost full size), 14–18 d old (leaf 3 developing and gaining full size), 19–23 d old (leaf 4 developing and gaining full size; first tiller developing) and 24–28 d old (leaf 5 and further tillers developing). Barley plants had between five and seven seminal roots. Adventitious roots started to emerge when plants were 11–13 d old. Plants at more advanced developmental stages had between 3–5 adventitious roots.

All root hydraulic analyses were carried out in a normal laboratory environment, with or without supplementary lighting to keep plant transpiration rates comparable with those in the growth chamber. Ambient air temperature and temperature of root media was between 17 and 23 °C. This rather small variation in temperature was not taken into consideration when calculating root Lp and Lp_r. Recent analyses of roots of maize showed that the Q₁₀ of water diffusion transfer in the range 10–30 °C is between 1·3 and 1·4 (Ionenko et al., 2010). The variation in temperature during the present experiment did not extend into a temperature range (∼0–15 °C; cold stress) that would be considered to change Lp and Lp_r substantially (for review see Aroca et al., 2012).

Transpiration measurements and leaf area

Transpirational water loss of plants growing in the growth chamber (relative humidity 80 %, daytime temperature 21 °C) was determined gravimetrically. Individual barley plants were transferred at least 2 d prior to analysis into 100- or 250-ml Erlenmeyer flasks that had been wrapped in aluminium foil. Plants were supported by foam pieces, and flasks were filled with nutrient solution and aerated. For measurements, each flask was placed on a balance and changes in weight were recorded after 2 or 4 h, 5–9 h into the photoperiod. Water loss was corrected for any weight decrease that resulted from evaporative loss of water from the flask by the use of flasks that contained nutrient solution and a foam piece but no plants. Water loss was minimized by not aerating (bubbling) the solution (flasks with or without plants) during measurements; the background water loss accounted for less than 10 % of transpirational water loss. Bubbling or not bubbling solutions during a 2- or 4-h measurement period of transpiration did not affect the value of transpiration, but bubbling increased the error significantly (not shown), probably due to variable amounts of water vapour escaping between the foam and the Erlenmeyer flask.

Leaf area was determined for the same plants as those used for transpiration and exudation experiments of entire root systems. Leaf blades were taped onto paper, photocopied and cut out from photocopies. The cut-out leaf pieces were weighed on an analytical balance, as was a piece of paper of known area (4 × 5 cm, upper surface 20 cm², lower surface 20 cm², total surface 40 cm²). The weight of paper of known area was used to convert weight readings of leaf pieces into areas.

Root surface area

Two approaches were used to determine the surface area of roots. In exudation and root pressure probe experiments on individual roots, the surface area was determined after each hydraulic experiment by measuring the length of the main axis of roots and the number and length of lateral roots using a ruler. Details and examples of calculations are provided in the Supplementary Data. Surface area was calculated by treating the roots as a cylinder (surface = π× length × diameter). The average diameter of the main axis of seminal roots and their lateral roots during these experiments was 0·5 and 0·25 mm, respectively, as determined with a stereomicroscope (Nikon UK, Kingston upon Thames, UK) fitted with a calibrated graticule. The corresponding figures for adventitious roots were 0·75 and 0·25 mm, respectively; lateral roots emerging from adventitious roots were only visible at the latest developmental stage analysed and were then often few in number or completely absent. In exudation experiments in which the entire root system of a plant was studied, the root system was scanned and images were analysed for root length and diameter (seminal roots: main axis and lateral roots; adventitious roots: main axis) using ImageJ software (http://imagej.nih.gov/ij/). These data were then used to calculate root surface area as detailed above and in the Supplementary Data Figs S1 and S2.

Hydraulic analyses

Root hydraulics were determined 5–9 h into the photoperiod.

Osmotic and hydrostatic Lp of seminal and adventitious roots

Roots were analysed in exudation (osmotic Lp) and root pressure probe (hydrostatic Lp) experiments. Details and examples of calculations are provided in the Supplementary Data. Root pressure probe and exudation experiments were performed as detailed previously (Knipfer and Fricke, 2010, 2011). In short, during root pressure probe experiments, individual roots were fixed to the probe and bathed in the same medium in which the plant had been grown. The medium was circulated to minimize external unstirred layer effects (Knipfer and Fricke, 2010). When a stable root pressure was reached (0·5–2 h), pressure relaxations were induced by imposing a hydrostatic pressure pulse (±0·05 MPa). Half-times of pressure relaxations (T_1/2) were used to calculate root hydrostatic hydraulic conductivity (Knipfer and Fricke, 2010, 2011).

During root exudation, an individual excised root was attached at its cut end to a glass capillary (Harvard Apparatus, Edenbridge, UK) using superglue of gel-like consistency (Gel Control, Loctite); leaks of liquid at the root–capillary junction were easy to detect within minutes of application of glue, and only roots without leaks were considered for further analyses. The root was bathed in the same medium in which the plant had grown. The inner diameter of the glass capillary was 0·58 mm for analyses of seminal roots and 0·86 mm for analyses of adventitious roots. The rise of xylem sap in the capillary was measured at intervals of 10 min over a period of up to 80 min by marking the position of the exudate with a permanent fine marker on the capillary. Plots of exudate volume versus time confirmed that the rise of fluid increased linearly with time and that, by implication, root hydraulic properties remained constant during the experimental period (Supplementary Data). At the end of the experiment, the entire exudate was ejected from the capillary with the aid of a syringe and collected in a 0·25-ml microcentrifuge tube. An aliquot of root medium was also sampled. Tubes were stored at –20 °C for up to 2 weeks prior to analysis, or samples were analysed on the same day for osmotic pressure using a Vapro osmometer (Wescor, South Logan, UT, USA). Osmotic hydraulic conductivity (m s⁻¹ MPa⁻¹) was calculated by relating exudate flow rate (m³ s⁻¹) to root surface area (m²) and the osmotic driving force for water uptake (difference in osmotic pressure between exudate and root medium, MPa; for calculations see Knipfer and Fricke, 2010, 2011).

Root surface area was determined as part of the exudation and root pressure probe experiments since this variable was required to calculate root Lp. A total of 25 seminal and 18 adventitious roots were analysed during root exudation measurements, and 11 seminal and 8 adventitious roots were analysed with the more laborious root pressure probe technique. Between 4 and 13 seminal and between 5 and 9 adventitious roots were analysed in total for each developmental interval (except for 9- to 13-d-old plants, where no adventitious roots were analysed since they had just started to emerge).

Osmotic Lp_r of entire root system

Exudation analyses were also carried out for the entire root system of plants. The shoot of a plant was cut ∼1 cm above the root–shoot junction. This location contains the basal portion of leaf elongation zone(s), where leaves and sheaths are wrapped tightly round each other. Although this arrangement does not provide a solid stem as provided, for example, by a hypocotyl or mesocotyl, it is sufficiently stable to be fixed into a glass capillary; also, it is sufficiently tight to prevent leakage of exudate through the rolled-up leaves and sheaths, most likely because the hydrostatic pressures that develop during exudation in xylem are minute (0·0001 MPa; Knipfer and Fricke, 2010). The shoot base with the root system was inserted carefully into a glass capillary (inner diameter 1·59 mm) or silicon tubing of appropriate inner diameter (∼1·8–4 mm). The silicon tubing was connected either directly or through tubing of smaller diameter to a glass capillary of 0·58 or 1·16 mm inner diameter. The connection between shoot and tubing or capillary was sealed with high-viscosity superglue (Power Easy, Loctite). For plants that had tillers, the severed (see above) root–shoot junction of the main shoot and each tiller was fixed separately into tubing or glass capillaries. The root system was placed horizontally into a large (28 × 28 cm) Petri dish, which was filled with dilute nutrient solution (between one-third and half of normal strength of the medium used for plant growth). The nutrient solution was ∼2 cm deep, and the presence or absence of aeration did not affect exudation rates (not shown). The shoots with capillary and tubing were placed horizontally ∼1 cm above the level of nutrient solution and supported through 3-cm thick sheets of polystyrene. Exudate flow was determined typically over a period of 20–60 min, depending on the developmental stage of the plant and the size of the main shoot or tiller. The meniscus of the exudate was marked on capillaries at 5- to 10-min intervals using a permanent marker. Exudate was collected and analysed for osmotic pressure and the exudation rate calculated as detailed above for analyses of individual roots. Following exudation analyses, the root system was scanned and analysed for root surface area using ImageJ. Thirteen or 14 plants were analysed for each developmental period. Plants were derived from five independently grown batches and values were pooled for each developmental period.

Hydrostatic Lp_r of intact, transpiring plants

Hydrostatic Lp_r was analysed under transpiring conditions, at root water flow rates more similar to those encountered during growth. This was particularly important with respect to recent studies on rice and poplar, which suggest that the rate of transpirational water flow directly impacts root hydraulics (Sakurai-Ishikawa et al., 2011; Kuwagata et al., 2012; Laur and Hacke, 2013). Root water uptake was set equal to plant transpirational water loss (i.e. J_r = J_c = J; Fig. 1A), which was measured gravimetrically. Xylem Ψ was derived by determination of Ψ in leaf epidermal cells. Leaf Ψ was determined in epidermal cells by measuring turgor with a cell pressure probe and cell osmotic pressure by analysing extracted cell sap with picolitre osmometry. Water potential was calculated as the difference between turgor and osmotic pressure. Details of single-cell methods can be found in Tomos and Leigh (1999), Fricke and Peters (2002), Fricke (2012) and Tomos et al. (1994). The experimental setup was as follows. Barley plants to be analysed were transferred at least 1 h prior to analysis into a 100-ml Erlenmeyer flask containing the same nutrient solution as that in which the plant had grown previously. The solution was not aerated (see above, section Transpiration measurements and leaf area). The plant was supported with a piece of foam that fitted tightly into the flask to minimize background evaporative loss of water. This loss accounted for less than 5 % of plant transpirational water loss (not shown). The plant was then transferred onto a three-digit balance (CP323P, Sartorius, Göppingen, Germany), on an analysing stage, which was in a normal laboratory environment (ambient temperature 17–23 °C) and had supplementary lighting (250–300 μmol photons m⁻² s⁻¹) to increase transpirational water loss. There was a constant, low flow of air (windows and door open) through the laboratory to avoid any build-up of temperature beneath the supplementary lighting. Relative humidity was ambient and ranged between 58 and 75 %. Transpirational water loss had stabilized within 1 h, after which time cell turgor analyses commenced. These typically took 20–30 min for each plant. A balance reading was taken just prior to and following completion of cell turgor analyses, and the difference in readings was taken as transpirational water loss. Cell turgor was determined half-way along the blade of the youngest fully or almost fully expanded leaf using a cell pressure probe. Cells overlying large lateral veins on the adaxial surface were analysed. Between five and eight of these ‘ridge’ cells (Fricke, 1997) were analysed for each leaf, and the average was taken as epidermal cell turgor for that particular leaf. The variation in turgor between replicate cells was within 5–15 % of the average (not shown). A 2-cm portion of the leaf region that had been analysed was then sampled, transferred into a 1·5-ml microcentrifuge tube containing a mesh insert, and then kept for at least 30 min at –20 °C before bulk leaf sap was extracted by centrifugation (5 min at 10 000 r.p.m.) in a table centrifuge (Fricke and Peters, 2002). The osmolality of bulk leaf sap was determined using a Vapro osmometer. The surface area of the root system was determined with a scanner and ImageJ software as described above.

To derive cell osmotic pressure from values for bulk leaf sap, a separate series of experiments was carried out in which the osmotic pressure of ridge epidermal cells was determined by picolitre osmometry. Plants and leaves were of the same developmental stage as those analysed with the cell pressure probe, and analysis conditions in the laboratory were also comparable to those during turgor analyses. Three or four ridge cells were sampled in quick succession using a liquid paraffin-filled glass microcapillary, and this pooled sample was transferred beneath a 10–20 μl droplet of liquid paraffin on a cover slip on the picolitre osmometry stage. Four pooled samples were harvested from each leaf before osmotic pressure was determined within a freezing cycle of the picolitre osmometer. The average value of these four samples was taken as representative of the osmotic pressure of ridge cells of that leaf. The leaf section analysed was then processed for analysis of bulk leaf osmotic pressure, as detailed above, to directly relate bulk leaf to ridge cell osmotic pressure for each leaf. This relationship was then used to convert values of bulk leaf osmotic pressure of leaves analysed for cell turgor into the respective value of cell osmotic pressure. The resulting values of cell osmotic pressure were subtracted from the previously determined values of cell turgor to calculate Ψ of ridge cells in leaves analysed for turgor and transpiration rate. This cellular Ψ value was taken as representative of Ψ of the leaf analysed. An alternative approach could have been to determine cell turgor and osmotic pressure successively in the identical epidermal cell (Fricke, 1997). However, this approach requires a cell pressure probe with an instant cell-sap sampling device to avoid dilution of cell contents through rapid (seconds) water inflow (Malone et al., 1989). Such a device was not available for the present study.

Calculation of xylem solute loading net rate

Exudation analyses of entire root systems provided pairs of values of exudation rate and exudate osmolality for a particular root system. This information was used to calculate the net rate of xylem solute loading as exudation rate × exudate osmolality.

Statistical analyses

Data were subjected to ANOVA using the general linear model and Tukey analysis in Minitab.

RESULTS

Root surface area and transpiration

The surface area of the entire root system of plants increased 13-fold during development, from 4·96 × 10⁻⁴ m² in 9- to 13-d-old to 6·39 × 10⁻³ m² in 24- to 28-d-old barley plants (Fig. 3A). At the youngest developmental stage, the main axis of five to seven seminal roots accounted for almost the entire surface of root system (Fig. 3B). As plants grew older, lateral roots, which developed along seminal roots, contributed increasingly to root surface area and accounted for 60 % of the area in 24- to 28-d-old plants (Fig. 3B). Adventitious roots, which started to emerge when plants were 11–13 d old, contributed between 17 and 18 % of surface area in 19- to 23- and 24- to 28-d-old plants (Fig. 3B). The surface area of leaves increased 15-fold during plant development (Fig. 3C), and the ratio of leaf to root surface area was 1·9–2·7 (Fig. 3D). The rate of transpirational water loss increased almost 10-fold, from 2·32 × 10⁻¹¹ m³ s⁻¹ in 9- to 13-d-old plants to 2·18 × 10⁻¹⁰ m³ s⁻¹ in 24- to 28-d-old plants (Fig. 3E). Water loss per unit leaf area was significantly higher in the first leaf (9- to 13-d-old plants) compared with leaves of older plants (Fig. 3F).

Fig. 3.

Root and leaf surface area and plant transpiration rate in barley plants at different times during development. Plants were analysed during four developmental windows, when they were 9–13, 14–18, 19–23 and 24–28 d old (developmental windows I, II, III and IV, respectively). During development in the growth chamber, plants grew at a day/night temperature of 21/15 °C. (A) Surface area of the entire root system. (B) Contribution of the main axis of seminal roots (SR), their lateral roots (LR) and adventitious roots (AR) to root system surface area. (C) Total leaf area per plant. (D) Ratio of leaf to root surface area. (E) Transpiration rate per plant. (F) Water loss rate per unit leaf area. Thirteen or 14 plants were analysed for each developmental window and used to derive all the variables shown (i.e. transpiration was measured on the same plants as those used for determination of root and leaf surface areas). The same plants were used for determination of root system osmotic Lp_r (see Fig. 4). Data are means ± s.e. (error bars). Data were subjected to one-way (A, C–F; developmental window) or two-way (B, developmental window × type of root or root portion) ANOVA followed by Tukey's test; different letters denote statistically significant differences (P < 0·05).

Osmotic Lp_r of exuding root systems

Osmotic Lp_r was determined for the entire root system of plants by removing the shoot (main shoot axis and any tillers) about 1 cm above its base and measuring exudate flow of the decapitated root system. Care was taken at older developmental stages that all shoots (main shoot and up to three tillers) gave exudate flow; if there was no exudate flow the plant was discarded. The total exudation rate per root system increased 18-fold during development, from 2·89 × 10⁻¹² m³ s⁻¹ in 9- to 13-d-old plants to 5·2 × 10⁻¹¹ m³ s⁻¹ in 24- to 28-d-old plants (Fig. 4A). The driving force for exudation is effectively a difference in osmotic pressure (and Ψ) between exudate and root medium. Exudate osmotic pressure decreased significantly with development, from 72 to 44 mosmol kg⁻¹ (Fig. 4B). Since the osmotic pressure of root medium was similar between experiments and averaged 0·016 MPa (not shown), the exudation driving force decreased during plant development significantly too, from 0·171 MPa in 9- to 13-d-old to 0·106 MPa in 24–28-d-old plants (Fig. 4C). The net rate of xylem solute loading for a particular root system was calculated as the arithmetic product of exudation rate (m³ s⁻¹) and exudate osmotic pressure, and mosmol kg⁻¹ approximated mm. The net rate of xylem solute loading increased 10-fold during development, from 2·12 × 10⁻⁷ mm in the youngest to 2·25 × 10⁻⁶ mm in the oldest plants analysed (Fig. 4D). The osmotic Lp_r of the entire root system averaged 4·2 × 10⁻⁸ m s⁻¹ MPa in 9- to 13-d-old plants. In older plants, osmotic Lp_r was almost twice as large and did not change with development (Fig. 4E). The plants analysed for root system exudation had previously been analysed for plant transpirational water loss in the growth chamber. This made it possible to compare, for each plant, exudation rate with transpiration rate (Fig. 4F). In 9- to 13-d-old plants, the root system exudation rate approached 15 % of the rate of daytime transpiration. In older plants, exudation rate was between 24 and 34 % of the rate of transpiration.

Fig. 4.

Root system exudation in barley plants at different times during development. Plants were analysed during four developmental windows, when they were 9–13, 14–18, 19–23 and 24–28 d old (developmental windows I, II, III and IV, respectively). During development in the growth chamber, plants grew at a day/night temperature of 21/15 °C. During analyses of root hydraulics in the laboratory, ambient air and root medium temperatures were between 17 and 23 °C. (A) Exudation rate of the entire root system. (B) Exudate osmolality and (C) driving force for exudation; the latter was calculated as the difference in osmolality between root medium and exudate; 40 mosmol kg⁻¹ approximates 0·1 MPa of osmotic pressure. A positive value represents a higher osmotic pressure in exudate compared with root medium; root medium osmotic pressure varied little between experiments, averaging 0·016 MPa. (D) Net rate of xylem solute loading, calculated as the product of exudation rate and exudate osmolality (for details see Materials and methods section) of each root system analysed. (E) Osmotic hydraulic conductivity (Lp_r) of the root system. Lp_r was calculated by dividing the exudation rate of the root system (panel A) by the driving force for exudation (panel C) and the surface area of that root system (Fig. 3A). (F) Exudation rate of the root system expressed as percentage of daytime transpiration rate in the growth chamber of the same plant as that used for exudation analyses. Thirteen or 14 plants were analysed for each developmental window, and data are means ± s.e. (error bars). Data were subjected to one-way ANOVA (developmental window) followed by Tukey's test. Different letters denote statistically significant differences (P < 0·05).

Osmotic and hydrostatic Lp of individual seminal and adventitious roots

Hydraulic conductivity was also determined for individual, detached roots. Seminal and adventitious roots were analysed using the exudation (osmotic Lp) and root pressure probe (hydrostatic Lp) methods. The osmotic and hydrostatic Lp values obtained for a certain type of root and plant developmental stage were similar, in particular for seminal roots (not shown; compare Knipfer and Fricke, 2011). Therefore, values from exudation and root pressure probe experiments were pooled for each root type to increase the sample number, aiding statistical analysis. The resulting Lp is referred to as ‘osmotic/hydrostatic Lp’. The average osmotic/hydrostatic Lp of seminal roots ranged from 2·0 to 3·0 × 10⁻⁷ m s⁻¹ MPa⁻¹ during plant development; Lp of adventitious roots ranged from 2·3 to 2·5 × 10⁻⁷ m s⁻¹ MPa⁻¹. There was no significant difference in osmotic/hydrostatic Lp between developmental windows and types of root (Fig. 5).

Fig. 5.

Hydraulic conductivity (Lp) of individual seminal and adventitious roots of barley. Plants were analysed during four developmental windows, when they were 9–13, 14–18, 19–23 and 24–28 d old (developmental windows I, II, III and IV, respectively). During development in the growth chamber, plants grew at a day/night temperature of 21/15 °C. During analyses of root hydraulics in the laboratory, ambient air and root medium temperatures were between 17 and 23 °C. Hydraulic conductivity of individual roots was determined in exudation (osmotic Lp) and root pressure probe (hydrostatic Lp) experiments. Since the two types of approach gave similar values, the values were pooled and are referred to as ‘osmotic/hydrostatic Lp’ in the text and as ‘Lp’ in the figure labels. Between 4 and 13 seminal roots and 5 and 9 adventitious roots were analysed for each developmental period. Data are means ± s.e. (error bars). Data were subjected to two-way nested ANOVA (developmental window × type of root) followed by Tukey's test. Values did not differ statistically significant from each other. Also, there was no significant effect of developmental window or type of root on Lp.

Leaf (cell) water potential and hydrostatic root Lp_r in transpiring plants

Those leaves that were analysed for cell turgor were also analysed for bulk osmotic pressure of the respective leaf region. However, to calculate cell (and leaf) Ψ, values of cell osmotic pressure were required. Therefore, a series of experiments was carried out in which cell and bulk leaf osmotic pressure were determined in succession for a particular leaf and leaf region, and this relationship was then used to convert bulk into cell osmotic pressure for leaves analysed for turgor. The relationship between cell and bulk osmotic pressure was analysed in plants of the youngest (9–13 d) and oldest (24–28 d) developmental windows. The ratio of cell to bulk osmotic pressure averaged (± s.e.) 1·30 ± 0·09 in 9- to 13-d-old and 1·34 ± 0·09 in 24- to 28-d-old plants (n = 5 plants analysed each; not shown). These two values did not differ statistically significantly from each other, and an overall average ratio of 1·32 was taken as being representative of all four developmental windows.

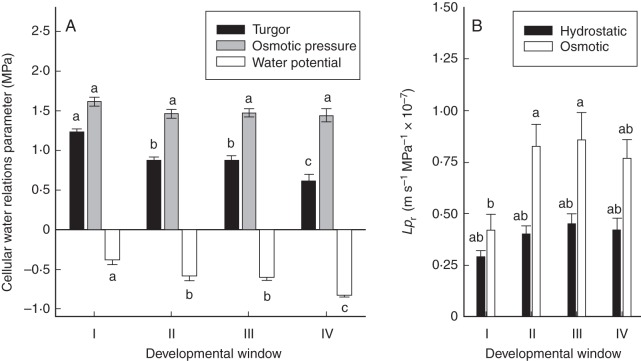
Epidermal ridge cell turgor of plants analysed under transpiring conditions averaged 1·23 MPa in 9- to 13-d-old barley plants (Fig. 6A). In older plants, cell turgor was significantly lower, and lowest (0·61 MPa) in 24- to 28-d-old plants. In comparison, cell osmotic pressure decreased little during plant development, and was almost identical in developmental windows II–IV (Fig. 6A). As a result, cell (and leaf) Ψ, calculated as the difference between turgor and osmotic pressure, became increasingly negative during plant development (Fig. 6A). While Ψ of 9- to 13-d-old plants averaged –0·38 MPa, Ψ of 24- to 28-d-old plants averaged –0·83 MPa. Since root medium Ψ was close to zero (∼ –0·02 to –0·04 MPa) for all developmental windows, the difference in Ψ between root medium and leaf cell, which drives water movement between these two locations, very much approximated leaf Ψ and became larger (more negative) with increasing plant age. In 24- to 28-d-old plants, the force driving water movement was 2·3-fold that in 9- to 13-d-old plants.

Fig. 6.

Water relation parameters used for determination of hydrostatic Lp_r in transpiring barley plants. Plants were analysed during four developmental windows, when they were 9–13, 14–18, 19–23 and 24–28 d old (developmental windows I, II, III and IV, respectively). During development in the growth chamber, plants grew at a day/night temperature of 21/15 °C. During analyses of root hydraulics in the laboratory, ambient air and root medium temperatures were between 17 and 23 °C. Analyses were carried out under supplementary lighting to increase transpiration to rates that were similar to those in the growth chamber where plants had been growing prior to analyses. (A) Cellular water relations parameters. Cell turgor was analysed in the youngest fully or almost fully expanded leaf, at the lower epidermis, half-way along the blade. Cells overlying large lateral veins (‘ridge’ cells) were probed with the cell pressure probe. The same leaves and leaf regions used for determination of cell turgor were then used to extract bulk leaf sap for determination of bulk leaf osmotic pressure. Using the relation between bulk-leaf and cell osmotic pressure determined in a different set of experiments, using picolitre osmometry, cell osmotic pressure could be determined. Values of cell turgor and osmotic pressure were used to calculate cell water potentials (= turgor – osmotic pressure). Data are means ± s.e. (error bar) of four (window I) and six or seven (windows II–IV) leaf analyses. Data were subjected to one-way ANOVA analysis (developmental window) followed by Tukey's test. (B) Hydrostatic Lp_r calculated from leaf water potentials (which approximated the water potential gradient between root medium and leaf) and root surface area and transpiration rate of plants during analyses. For comparison, osmotic Lp_r of entire root systems is also shown (see Fig. 4E). Root surface areas of plants of developmental windows I–IV averaged 0·717, 1·60, 3·50 and 8·63 × 10⁻³ m², respectively, and transpiration rates averaged 0·0763, 0·356, 0·961 and 3·09 × 10⁻¹⁰ m³ s⁻¹. Values of Lp_r were subjected to two-way ANOVA (developmental window × type of Lp_r) followed by Tukey's test. There was no significant effect of developmental window on Lp_r (P = 0·09), but a significant effect of the type of Lp_r (hydrostatic versus osmotic; P < 0·001). Different letters denote statistically significant differences.

The calculated Ψ gradients were used, together with data on the root surface area and transpirational water loss (see legend of Fig. 6) of the respective plants, to calculate hydraulic conductivity. This conductivity includes a series of paths (root medium to root xylem; root xylem to leaf xylem; leaf xylem to leaf epidermal cell). Despite this, it is referred to here as ‘root hydrostatic Lp_r’, since the radial path in the root most likely presented the major hydraulic barrier along this series of paths (see also Discussion). This root system hydrostatic Lp_r averaged 2·92 × 10⁻⁸ m s⁻¹ MPa⁻¹ in 9- to 13-d-old control plants (Fig. 6B). In older plants, hydrostatic Lp_r was up to 50 % higher and averaged 4·02 to 4·52 × 10⁻⁸ m s⁻¹ MPa⁻¹. The difference in hydrostatic Lp_r between developmental windows was not statistically significant (Fig. 6B). Osmotic Lp_r of entire root systems, which is shown for comparison in Fig. 6B, was up to twice as high as hydrostatic Lp_r, though the two types of Lp_r did not differ statistically from each other in a developmental window. The surface area of the root system of plants analysed for hydrostatic Lp_r averaged 7·17 × 10⁻⁴ m² in 9- to 13-d-old plants and was 12-fold larger in 24- to 28-d-old plants (8·68 × 10⁻³ m²; see legend to Fig. 6). In comparison, the rate of transpirational water loss, which was determined during cell pressure probe analyses, averaged 7·63 × 10⁻¹² m³ s⁻¹ in 9- to 13-d-old plants and was 40-fold larger in 24- to 28-d-old plants (3·09 × 10⁻¹⁰ m³ s⁻¹; see legend to Fig. 6).

Relationships of root surface area, hydraulic conductivity and water potential gradient with water flow through the root system

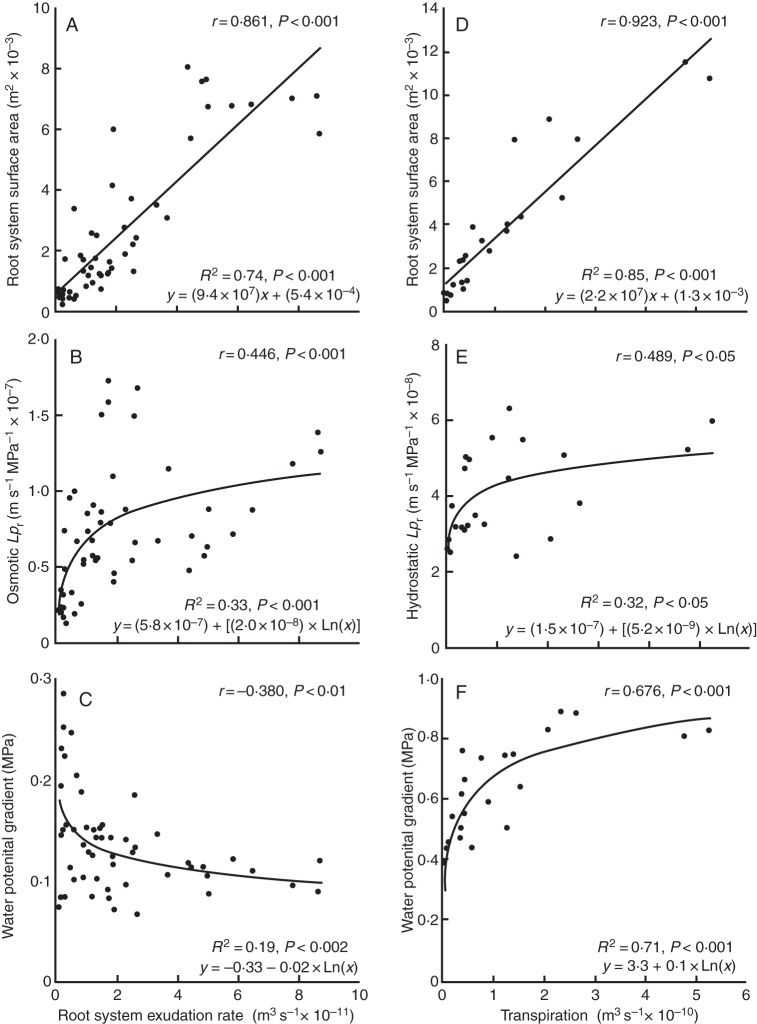
The experiments in which osmotic Lp_r had been determined for entire root systems and hydrostatic Lp_r had been determined for intact, transpiring plants provided pairs of data for individual plants. A Pearson correlation analysis was performed on these individual plant data to test whether changes in A_r, Lp_r and Ψ gradient between root medium and exudate (root system) or leaf (intact plant) are related to the developmental increases in flow rate of water through the root system (exudation rate, Fig. 7A–C) and intact plant (transpiration rate, Fig. 7D–F). In addition, regression analysis was performed to predict the best fit of relationships, by comparing values of R² of fitted linear and non-linear equations. In both the root system and the intact plant, A_r, Lp_r and ΔΨ were correlated significantly (P < 0·05) with increasing rates of whole plant water flow (Fig. 7A–F). Root surface area and rate of water flow showed by far the closest correlation (Pearson correlation coefficient r = 0·861 in Fig. 7A; r = 0·923 in Fig. 7D). The correlation of osmotic Lp_r with root system exudation rate was almost identical to that of hydrostatic Lp_r with plant transpiration rate (r = 0·446 and 0·489, respectively). The driving force for water movement correlated positively with plant transpiration rate, and aided the developmental increase in transpiration. In other words, the difference in Ψ between leaf and root medium (ΔΨ = ψ_leaf – Ψ_medium) became more negative with increasing transpiration rate (Fig. 7F). In contrast, the driving force for root exudation (ΔΨ_r = Ψ_exudate – ψ_medium) correlated negatively with the rate of exudation and rather counteracted the developmental increase in root system exudation rate (Fig. 7C). The regression analysis predicted that a linear equation best described (highest R²) the relationship between the developmental increase in the rate of water flow and root surface area (R² = 0·74, Fig. 7A; R² = 0·85, Fig. 7D). In contrast, the relationship between developmental changes in Lp_r or ΔΨ and the rate of water flow was best described by a non-linear equation of the type y = y_o + a(ln(x)) (Fig. 7B, C, E, F). Osmotic and hydrostatic Lp_r increased disproportionally during the very early stages of plant development (Fig. 7B, E).

Fig. 7.

Relationships of (A, D) root surface area, (B, E) root hydraulic conductivity, Lp_r, and (C, F) driving force (Ψ gradient) with developmental increases in rate of water flow through the isolated root system (A–C) and intact plant (D–F). In (C) and (F), a more positive driving force represents a more negative Ψ in exudate and leaf compared with root medium. Each point represents a pair of values obtained for an individual plant. Data were derived from two large experiments, one in which exudation rate and osmotic Lp_r were determined for entire root systems of plants (see data in Figs 3 and 4) and one in which hydrostatic Lp_r was obtained for intact, transpiring plants (see data in Fig. 6 and legend to Fig. 6). Data were subjected to Pearson correlation analysis (r, Pearson correlation coefficient) and linear and non-linear regression analysis. Each regression line represents the best fit (highest R², as shown together with equation of fit) of data; the highest R² was significant (P < 0·05).

Comparing entire root system with individual root hydraulic conductivity

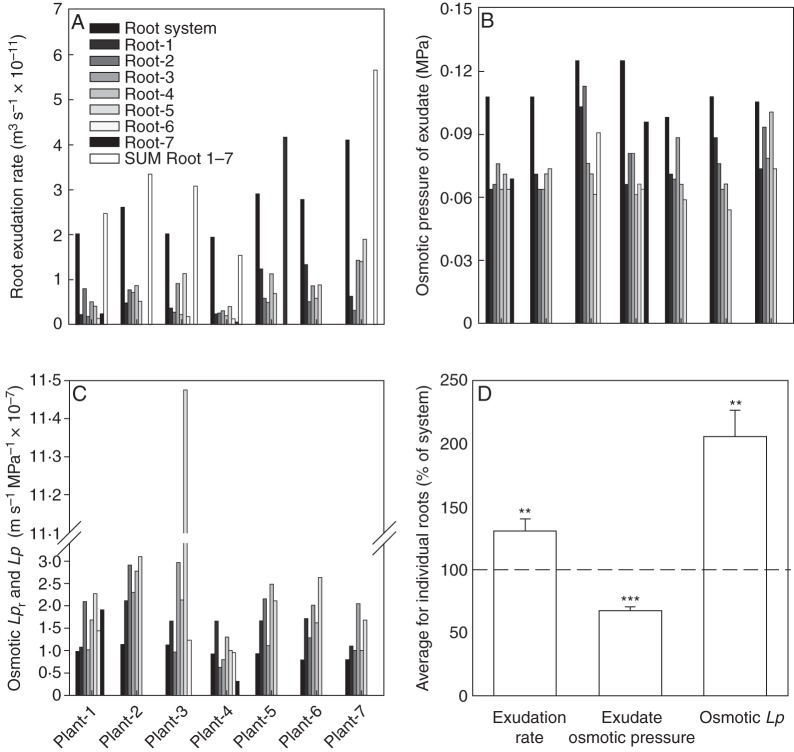
The Lp values obtained on individual roots in exudation and root pressure probe experiments (Fig. 5) were on average 2- to 3-fold larger than the Lp_r values obtained in exudation experiments on entire root systems of plants (Fig. 4). To test whether this difference was indeed due to the use of individual roots compared with entire root systems, a series of exudation experiments was carried out in which Lp_r was determined for the entire root system and then Lp was determined for all the component roots of that root system. Seven plants were analysed. These plants were 17–18 d old and had between five and seven seminal roots each. Adventitious roots, which contributed negligibly to root surface area at this developmental stage (compare Fig. 3B), were not included in analyses. The rate of exudation varied between individual seminal roots of a plant (Fig. 8A), unlike exudate osmotic pressure, which was within a narrow range (Fig. 8B). The variation in exudation rate observed among roots of a plant mainly reflected differences in their surface area (not shown). As a result, Lp varied comparatively little between roots (Fig. 8C); plant 3 had one root (root 5) with an exceptionally high Lp value, the reason for which is not known.

Fig. 8.

Exudation experiments carried out on entire root systems and their component roots. During development in the growth chamber, plants grew at a day/night temperature of 21/15 °C. During analyses of root hydraulics in the laboratory, ambient air and root medium temperatures were between 17 and 23 °C. The entire root system of a plant was first analysed in an exudation experiment, and then all the individual component (seminal) roots of that root system were analysed. Seven plants in total were analysed (plants 1–7). These plants were between 17 and 18 d old and each had up to seven seminal roots (roots 1–7); adventitious roots contributed negligibly to the surface area of root system. The numbering of seminal roots was randomly chosen for each root system. (A) Exudation rate for entire root systems (‘Root system’), individual component roots (‘Roots 1–7’) and the sum of individual values (‘SUM Root 1–7’). (B) Osmotic pressure of exudate collected from the entire root system of a plant or individual component roots. (C) Osmotic hydraulic conductivity determined for the entire root system of a plant (Lp_r) or individual component roots (Lp). (D) Comparison between values obtained for entire root systems and for component roots. For each plant, the exudation rate, exudate osmotic pressure or osmotic Lp_r obtained for the entire root system was set to 100 % and the sum of exudation rate, average exudate osmotic pressure and average Lp obtained for the component roots of that plant was expressed as a percentage of this 100 % value (dashed line). Data are means ± s.e. (n = 7). Values for individual roots differed significantly from the 100 % value of the entire root system (**P < 0·01; ***P < 0·001).

In theory, the sum of exudation rates of all component (seminal) roots of a plant should equal the exudation rate of the entire root system of that plant. This was not the case, as the sum of exudation rates was higher by 33 % (Fig. 8D; see also Fig. 8A for individual plants). The average osmotic pressure of exudate of all component roots of a plant was 33 % lower than the exudate osmotic pressure of the entire root system of that plant (Fig. 8D). Since root surface area was, by definition, identical between the entire root system and the sum of component roots, Lp was on average twice as large when derived from individual-root analysis (average 1·95 × 10⁻⁷ m s⁻¹ MPa⁻¹) compared with Lp_r derived from entire-plant root system analysis (average 9·16 × 10⁻⁸ m s⁻¹ MPa⁻¹; Fig. 8D).

DISCUSSION

Pathway of radial water movement in roots during barley plant development

Osmotic and hydrostatic Lp were in the same range, irrespective of whether individual seminal and adventitious roots were analysed (see also Knipfer and Fricke, 2011) or whether osmotic Lp_r obtained for entire root systems was compared with hydrostatic Lp_r obtained for intact, transpiring plants. If anything, the osmotic Lp_r of root systems was higher than the hydrostatic Lp_r of intact plants. As discussed further below (see section Method of determining root system Lp_r in intact plants), a lower hydrostatic Lp_r could result in part from consistent overestimation (more negative) of xylem Ψ when deriving this value from leaf Ψ. Such overestimation would lead to a Ψ gradient being used for calculation of Lp_r that is larger than the true Ψ gradient and consequently underestimation of the true Lp_r value. Even if this possible source of error is taken into consideration, the present data provide strong experimental evidence that the cell-to-cell path facilitates most of the radial root water uptake in 9- to 28-d-old barley plants. This is further supported by the present finding that osmotic and hydrostatic Lp values were was comparable for individual seminal and individual adventitious roots. The data extend the results of a related study on 14- to 17-d-old barley plants in which a radial root reflection coefficient close to 1·0 was observed, which indicates near-perfect osmotic behaviour of barley roots (Knipfer and Fricke, 2010; compare also Steudle and Jeschke, 1983). Similarly, Bramley et al. (2009, 2010) concluded on the basis of experimental and modelling approaches that, in the closely related wheat, a significant if not major portion of radial water flow occurs along the cell-to-cell path.

Developmental changes in root Lp_r

The primary aim of the present study was to analyse barley plants over a considerable period of their vegetative development and test whether increases in transpirational water loss and associated root water uptake are accompanied by significant increases in osmotic or hydrostatic root Lp_r – increases that could be mediated through aquaporin activity in barley (Knipfer et al., 2011). There was an increase in average root system osmotic Lp_r and in hydrostatic Lp_r between the youngest and second-youngest developmental stages, and in individual root Lp in seminal roots between younger and older developmental windows. This increase was up to 2-fold, and over the four developmental windows analysed only the osmotic Lp_r of entire root systems differed significantly between 9- to 13-d-old plants and older plants. Similarly, when Lp_r data of entire root systems and of transpiring plants were plotted against the water flow rate through the system (Fig. 7B, E), the best curve fits were rather asymptotic, with Lp_r of increasing comparatively steeply at first and then approaching a plateau. In transpiring plants, the initial increase in Lp_r was accompanied by an increase in the Ψ gradient driving water uptake (Fig. 7F), while root surface area increased less than predicted from the linear regression fit (Fig. 7D). Therefore, at the earliest growth stage analysed, increases in Lp_r and ΔΨ made significant contributions to sustaining increased transpirational water loss rates and compensated for a comparatively small increase in root surface area [compare also the initial overshoot in Lp_r observed by Fiscus and Markhart (1979) in developing bean (Phaseolus vulgaris) plants]. However, when considering the entire developmental period analysed here (9–28 d), root surface area was clearly the main means through which increased transpiration rates were sustained.

Root surface area correlated highly and increased linearly with both root system exudation and plant transpiration rate (Pearson correlation coefficient 0·861 and 0·923, respectively). It can be concluded from these data that barley plants applied option 2 rather than option 3 (see Introduction), by producing ‘more of the same’ in terms of root hydraulics to accommodate large (10- to 40-fold) developmental increases in water flow rates.

Rather minor changes in Lp_r during plant development have also been reported for the root system of developing bean (P. vulgaris) plants (Fiscus and Markhart, 1979), except that Lp_r showed an initial overshoot. Modelling of root water uptake in maize resulted in a continuous decrease in root Lp_r during plant development (Doussan et al., 1998); this decrease was due mainly to a decrease in the portion of the root system that was active in water uptake, an assumption that, as the authors pointed out, was not supported by experimental data. Martre et al. (2001) observed parallel increases in root hydraulic conductance (L_r) and leaf area during development of Festuca arundinacea plants. Root surface area will also have increased in that study, and it can only be speculated that Lp_r will have increased less, or not at all, during development compared with increases in hydraulic conductance. Rodriguez et al. (1997) observed no differences in root Lp_r between 3- and 9-d-old tomato plants. Saliendra and Meinzer (1992) expressed root hydraulic conductance per unit leaf area and observed 0·5- to 3-fold changes, with an early peak during sugarcane plant development.

Root system of barley plants during development

The root system of the barley plants analysed underwent major changes in morphology during development. At the youngest stage, the main axis of seminal roots accounted for almost the entire root surface area. As plants grew older, lateral roots emerging from the main axis of seminal roots contributed increasingly to the surface area of the root system and accounted for 60 % of the root surface in 24- to 28-d-old plants. Despite these changes, Lp of individual seminal roots and Lp_r of entire root systems hardly changed. One could conclude from these data that water uptake rates per unit root surface and ΔΨ were uniform along the main axis of roots and between the main axis of seminal roots and their emerging lateral roots. We think that this conclusion is valid and justifies the current (and generally adopted) approach of relating water flow rates to total root surface area for the calculation of Lp_r. Roots can be treated as porous pipes (for review see Zwieniecki et al., 2003) in which the ratio of axial to radial conductance affects water uptake along roots. As the basal portion (the region closer to the point of shoot insertion) of a seminal root of barley matures, the axial conductance increases (Knipfer and Fricke, 2011). Maturation of endodermal walls (Knipfer and Fricke, 2011) can be expected to decrease the radial conductance. This will shift the zone of rapid water uptake to more distal (tip) regions of the root. Such a shift is supported by the study of Sanderson (1983) on barley, where the zone of the highest rate of water uptake was found at a distance 4–5 cm from the tip. However, the study by Sanderson (1983) also showed that the bulk of water (75 %) taken up by the entire root system of barley plants was provided through the suberized portion of the main root axis further than 10 cm from the tip and its associated lateral roots (Sanderson, 1983). The present data show that this root region, in particular the lateral roots, contributed increasingly to the surface area of the root system as the plants developed. The modular design of this region, with existing lateral roots maturing and new ones developing, should have averaged out any local differences in Lp between older and younger root regions and justify the use of total root surface area for the calculation of root Lp_r. Also, it could be argued that total root surface area represents an integrative investment of plants over developmental time. This investment can be related to plant water flow rates to distinguish between strategies involving the production of more root surface and the production of a surface area of different (hydraulic) quality. The observation that water uptake is not confined to the tip region of fine roots but also involves mature, suberized regions, has also been reported for woody plants (e.g. Queen, 1967; Kramer and Bullock, 1966) and the tap root of lupin (Zarebanadkouki et al., 2013).

Driving forces sustaining day- and night-time transpirational water loss

Daytime transpirational water loss. The gradient in Ψ between root medium and leaf increased almost 3-fold during barley plant development, making some contribution to facilitating increased root water uptake. Leaf Ψ decreased to –0·83 MPa in 24- to 28-d-old plants, and this decrease was largely due to a decrease in turgor to 0·61 MPa. A leaf Ψ of –0·83 MPa is far from the permanent wilting point of –1·5 MPa of crop plants such as barley. If hydrostatic Lp_r had not increased by ∼50 % over the developmental period studied, and if plants had shown the same increases in transpirational water loss rates and root surface area as observed here, the Ψ gradient would have been 50 % larger, lowering leaf Ψ to –1·2 MPa and turgor to 0·2 MPa (ΔΨ = transpiration rate/root hydraulic conductivity × root surface area). Leaf Ψ would still not have approached the permanent wilting point, yet cell turgor would have been in a region where the need to accommodate daily fluctuations in evaporative demand could pose the risk of transient plasmolysis. The developmental increase in hydrostatic root Lp_r may have been small compared with that of root surface area, but it might have safeguarded the water relations of barley leaf cells.

Night-time transpirational water loss

A previous study on 14- to 17-d-old barley plants showed that rates of night-time transpirational water loss amounted to 11 % of day-time rates (Knipfer and Fricke, 2011). If we apply this figure to all developmental windows in the present study, then exudation rates obtained for root systems, which amounted to 15–34 % of daytime transpiration rates, were in excess of what was required to sustain night-transpiration rates of intact plants. Also, exudation experiments were carried out during the day period, and a previous study on 14- to 17-d-old barley plants showed that exudation experiments carried out during the day and night periods give similar exudation rates for seminal roots, which make up most of root system surface (Knipfer and Fricke, 2011). Exudation experiments on entire root systems lasted less than 1 h, and it could be argued that the xylem solute loading rates involved are not sustainable over a full 8-h night cycle. This is unlikely since exudation rates in 14- to 28-d-old plants were actually 2- to 3-fold larger than required to sustain night-time transpiration rates. Furthermore, the net rate of xylem solute loading increased 10-fold between developmental windows I and IV. This increase cannot be explained by changes in the volume proportion of xylem parenchyma (loading solutes) and xylem vessels (receiving solutes) during the same period. The most likely explanation is that other factors, which are under developmental control, caused xylem solute loading rates to increase that much. We do not know what these factors could be.

Osmotic Lp in individual roots compared with osmotic Lp_r of entire root systems

When Lp_r was determined on entire root systems and Lp was then measured for the individual component roots, average osmotic Lp was twice as large as osmotic Lp_r. In theory, both Lp and Lp_r values should have been the same, and the reason for the discrepancy between the two is not known. Individual roots were excised close (<1 cm) to their base, and the very small portion of (possibly low-conducting) root base lost in this process cannot explain differences in Lp and Lp_r, which still contained this centimetre portion. Similarly, the root–shoot junction does not hydraulically limit water flow in barley (Knipfer and Fricke, 2011) and this cannot explain the lower Lp_r in entire root systems. Rather, to calculate Lp and Lp_r, the difference in osmotic pressure between exudate and root medium was taken as the driving force for exudation, and osmotic pressure was significantly higher in exudate collected from entire root systems than in exudate collected from individual roots. This difference in exudate osmotic pressure could have resulted from solute loading of xylem through the remaining shoot or through seed endosperm, particularly in 9- to 13-d-old but also in 14- to 18-d-old plants, as these tissues were present only during root system analyses. This would have resulted in the lower calculated Lp_r values obtained for entire root systems.

Method of determining root system Lp_r in intact plants

There is accumulating evidence which suggests that excision of shoots causes rapid changes in the Lp_r of the root system (Sakurai-Ishikawa et al., 2011; Vandeleur et al., 2013). Therefore, methods that are routinely used to determine the hydrostatic Lp_r of the excised root system, such as use of the pressure chamber or high-pressure flow meter (e.g. Passioura and Munns, 1984; Tsuda and Tyree, 2000), may yield a root system Lp_r that is not representative of the value in intact plants. In the present study we used an alternative approach in which use of the cell pressure probe was combined with a picolitre osmometry technique to determine the Ψ of leaf cells of intact, transpiring plants to derive the Ψ gradient driving root water uptake. While this approach overcomes the problem associated with shoot excision, it has the potential disadvantage that the Ψ gradient driving root water uptake is overestimated, and the resulting calculated root system Lp_r is underestimated. This is because leaf Ψ may differ from root xylem Ψ. The difference between the two will increase as any hydraulic resistance between root xylem and leaf epidermal cells increases (which were analysed here for Ψ). Similar problems are encountered when determining leaf Ψ in intact plants with Wescor-type psychrometer sampling chambers, which can be clamped directly onto the leaf surface to measure leaf Ψ in situ, and with which small (<1 °C) variations in ambient temperature can lead to large errors in the range of slightly negative Ψ values, as encountered here (e.g. Shackel, 1984; Bennett and Cortes, 1985). In the present study, mature or almost fully mature leaves were analysed for leaf cell Ψ. This minimized the contribution of any axial resistance in basal leaf meristems (Martre et al., 2001) to the establishment of Ψ gradients between root xylem and leaf epidermal cells. The only other resistance that could have contributed to such gradients is the radial resistance between leaf xylem and peripheral epidermal cells. This radial resistance is particularly pronounced in growing tissue (Tang and Boyer, 2008) and increases with transpirational flow (Shackel and Brinkmann, 1988; Melcher et al., 1998; Ehlert et al., 2009; Martre et al., 2001). Transpiration rates encountered here during hydrostatic Lp_r analyses (about 1–2 × 10⁻⁸ m³ m⁻² leaf surface s⁻¹) are within the range of transpiration rates specified as low-transpiring conditions in Ehlert et al. (2009) and Martre et al. (2001), where radial gradients in Ψ were about 0·1 MPa. For the present approach, this would mean that xylem Ψ may have been overestimated (more negative) by as much as 0·1 MPa and that the true hydrostatic Lp_r may have been up to 50 % higher than the calculated one, particularly in younger plants; in older plants the overestimation of Lp_r would have been much smaller (about 10–20 %).

Probably the best way to determine xylem Ψ in transpiring plants would have been direct measurement with a xylem pressure probe (e.g. Melcher et al., 1998; Schneider et al., 1997). This technique is difficult to apply at tensions exceeding –0·3 to –0·5 MPa (e.g. Melcher et al., 1998; Schneider et al., 1997), and leaf epidermal cell Ψ obtained here for transpiring 14- to 28-d-old barley plants was almost twice as negative.

In conclusion, the present study shows that most of the developmental increase in the rate of transpirational water loss and associated root water uptake in 9- to 28-d-old barley plants is facilitated primarily through a (similar-fold) increase in root system surface area. Changes in individual root Lp and root system Lp_r are comparatively minor and are restricted to an early stage during this developmental period. Although leaf Ψ decreases significantly during development, it does not reach values at which it may threaten the functioning of leaves, possibly also because of the early increase in root hydraulic conductivity. It would be interesting to examine more advanced stages of vegetative development, when transpirational water loss rates can be expected to increase even further and when plants experience substantial changes in their morphology, such as stem elongation and increased tillering.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of details of the calculations associated with exudation (Figs S1, S2), root pressure probe and root surface area analyses.