Pulsed IR Heating Studies of Single-Molecule DNA Duplex Dissociation Kinetics and Thermodynamics

Abstract

Single-molecule fluorescence spectroscopy is a powerful technique that makes it possible to observe the conformational dynamics associated with biomolecular processes. The addition of precise temperature control to these experiments can yield valuable thermodynamic information about equilibrium and kinetic rate constants. To accomplish this, we have developed a microscopy technique based on infrared laser overtone/combination band absorption to heat small (≈10⁻¹¹ liter) volumes of water. Detailed experimental characterization of this technique reveals three major advantages over conventional stage heating methods: 1), a larger range of steady-state temperatures (20–100°C); 2), substantially superior spatial (≤20 μm) control; and 3), substantially superior temporal (≈1 ms) control. The flexibility and breadth of this spatial and temporally resolved laser-heating approach is demonstrated in single-molecule fluorescence assays designed to probe the dissociation of a 21 bp DNA duplex. These studies are used to support a kinetic model based on nucleic acid end fraying that describes dissociation for both short (<10 bp) and long (>10 bp) DNA duplexes. These measurements have been extended to explore temperature-dependent kinetics for the 21 bp construct, which permit determination of single-molecule activation enthalpies and entropies for DNA duplex dissociation.

Introduction

Over the years, single-molecule fluorescence techniques have proven to be quite powerful in allowing researchers to monitor the kinetics and dynamics of individual biomolecules in real time. These techniques have resulted in a number of important scientific advances regarding a wide variety of biological systems (1). One of the most common applications of single-molecule fluorescence, Förster resonance energy transfer (FRET), has been particularly advantageous for the observation of distinct conformational transitions (2,3). Although direct observation of biomolecular dynamics provides valuable kinetic and mechanistic insight into the particular conformational transitions, even more information can be obtained by combining such single-molecule FRET (smFRET) experiments with control of other biophysically relevant variables such as applied force and temperature (4–11). For example, the addition of explicit temperature control to smFRET experiments can provide thermodynamic information not only on the free-energy change, but also on the enthalpy and entropy changes associated with the observed processes (4,9). In particular, efficient integration of high-resolution spatial and temporal control of temperature with existing single-molecule fluorescence technology represents a significant advance and offers quantitative thermodynamic details about biomolecular dynamics (12).

The most widely used method for controlling the temperature of an aqueous sample on a single-molecule fluorescence microscope is using an objective-stage heating system (4,7,9). However, there are three major problems associated with such a heating technique: 1), a limited range of accessible temperatures (<45°C) resulting from temperature restrictions on high-numerical-aperture objectives; 2), large heated volume, determined by the size of the sample; and 3), long equilibration times limited by thermal conduction. Recently, a number of techniques have been developed that use focused near-infrared (IR) light to directly (10,12–16) or indirectly (17,18) modulate the temperature of aqueous samples. The indirect heating methods are based on IR absorption by thin metal films on glass substrates, which then transfer heat to the aqueous solutions. The direct heating techniques all rely on the modest ability of water molecules to absorb near-IR light (19), exciting various vibrational modes of the liquid water and effectively increasing the local temperature. Of specific interest in this work is the absorption band near 1440 nm corresponding to the (ν₁ν₂ν₃) = (1,0,1) combination state for one quantum of both symmetric and asymmetric OH stretching excitation. These IR heating techniques can alleviate many of the limitations associated with the objective-stage heating systems, specifically by providing a broader range of available temperatures and vastly superior spatiotemporal control of temperature (10,12,18,20). Though indirect IR heating techniques have been well described (17), none of the direct techniques have been quantitatively characterized, which represents the first major aim of this work.

As a second target, we focus on specific applications in single-molecule biophysics. Although the emergence of IR-based heating methods has alleviated many deficiencies of conventional stage heating techniques, it also has revealed experimental restrictions associated with continuous observation of single molecules at elevated temperatures (e.g., >45°C). Two particularly important restrictions arise from 1), the temperature-dependent dissociation of the noncovalent bond between biotin and streptavidin (21), and 2), the temperature-dependent quantum yields of common single-molecule organic fluorophores (22,23). Due to the unusually high binding affinity of biotin for streptavidin (K_d ≈ 5 × 10⁻¹⁴ mol/L) and the extremely slow dissociation rate (k_diss ≈ 3.8 × 10⁻⁶ s⁻¹ at 37°C), this ligand-binding interaction has been widely used in single-molecule experiments for surface immobilization to microscope coverslips (24–27). However, as is necessarily the case with all activated rate processes, the rate constant for dissociation of the biotin-streptavidin interaction increases exponentially with temperature, which can therefore result in rapid depletion of surface-immobilized molecules. Key advances in this area of specialized surface-immobilization techniques have been fueled by powerful click chemistry, which can be used to covalently attach single molecules to sample substrates in situations that require stable surface immobilization (28,29).

However, there is one universal difficulty associated with performing smFRET studies at elevated temperatures that represents a more serious experimental problem. In particular, all conventional organic dyes have fluorescence quantum yields that are dramatically reduced at high temperatures. This is predominantly due to rapid growth in the nonradiative decay rate constant, which competes efficiently with the radiative pathway, making observation of single fluorophores challenging at temperatures >45°C. Recently, there have been a variety of attempts to address this problem, including 1), the use of semiconductor nanoparticles (e.g., quantum dots) with much-higher-absorption cross sections; 2), more efficient collection of fluorophore emission by immobilizing individual molecules on colloidal spheres (30); and 3), development of intrinsically brighter fluorophores by conjugation with photophysical stabilizing agents (31). However, these techniques also add significantly to experimental complexity, particularly for single-molecule studies of biophysical interest, and there remains a considerable need for alternative microscopy methods that can offer access to biomolecular dynamics at temperatures where visualization of common organic fluorophores is challenging. The second aim of this study is to describe ongoing efforts to address this issue.

This article is organized into two major sections corresponding to the two parallel aims described above. The first gives a detailed characterization of an all-optical IR-laser-based heating technique (12) for single-molecule microscopy, including quantitative analysis of the thermal, spatial, and temporal characteristics. When compared with conventional microscope-stage heating methods, three advantages of optical temperature control are apparent: 1), the larger range of accessible temperatures; 2), extreme localization of thermal load to picoliter volumes; and 3), orders-of-magnitude faster heating rates. As a complementary thrust, the second section addresses exploitation of the high spatial/temporal control of IR heating for high-temperature smFRET kinetic measurements. In particular, we present results from a proof-of-principle demonstration, wherein rapid heating/cooling cycles are used to obtain detailed kinetic/thermodynamic information on the dissociation of a 21 bp DNA duplex. Interestingly, the results clearly reveal nonmonoexponential temporal behavior in the dissociation kinetics that is used to develop a simple kinetic model based on simultaneous fraying at each end of the DNA duplex. In addition, such a model is capable of describing duplex dissociation for both long (>10 bp) and short (<10 bp) DNA sequences.

Experimental Methods

Fluorescent oligonucleotides

A synthetically modified, double-stranded DNA construct was purchased from a commercial supplier. The construct consists of two oligonucleotides. The first oligonucleotide (reporter strand) sequence is 5′-|Cy3| CCC TTG |(PEG)₁₈| CAA GGG CTC AGA CGA GTG |internal Cy5| AAA AAA AAA AAA |Biotin|-3′. The second oligonucleotide (splint-strand) sequence is: 5′-CAC TCG TCT GAG CCC TTG CAA-3′. The 36 nt reporter strand was annealed to the 21 nt splint strand that is complementary with nucleotides 4–24 of the reporter strand, forming a continuous 21 bp DNA duplex (see Fig. 5 a).

Figure 5.

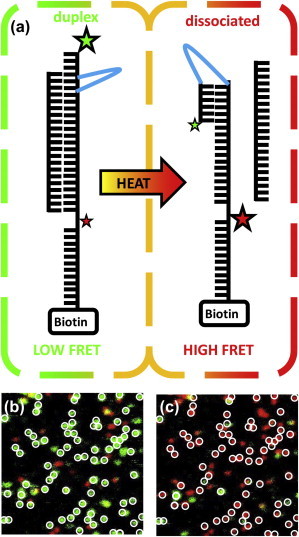
(a) Diagram of the duplex DNA fluorescent construct used for the dissociation experiments. Green and red stars represent the Cy3 and Cy5 FRET pair used in the experiments. The solid cyan line corresponds to the PEG₁₈ internal linker within the construct to easily allow the construct to form the closed conformation (see Experimental Methods for details). (b and c) ALEX surface image (10 μm × 10 μm) before (b) and after (c) exposure to a pulse of IR light. White circles represent the mask used to measure survival probability (see text for details). To see this figure in color, go online.

Sample preparation

All experiments were performed in 1- to 2-mm-wide channels created by two pieces of 85-μm-thick double-sided sticky tape between a 170-μm-thick glass coverslip and a 1-mm-thick glass microscope slide. Samples containing 575 nM Rhodamine B in water were used to measure the temperature in all experiments designed to characterize the IR heating system.

Fluorescence microscope

All fluorescence data were acquired on a previously described inverted confocal microscope (32). Briefly, a pulsed (10 ps, 20 MHz) excitation source (532 nm) was directed into the back aperture of a 1.2 NA water-immersion objective via a dichroic mirror, with the resulting fluorescence emission collected from the diffraction-limited excitation volume by the same objective. The fluorescence photons were then spatially separated by dichroics and polarization beam splitters onto four single-photon avalanche photodiodes, where a time-correlated single-photon counting (TCSPC) module recorded the arrival time of each photon with respect to both the most recent laser pulse (microtime) and the start of the experiment (macrotime). The microtime data were used for fluorescence lifetime measurements, and the macrotime data permitted reconstruction of time trajectories of fluorescence intensity, E_FRET, lifetime, and temperature with arbitrary choice of temporal binning.

Duplex dissociation experiments

For all duplex dissociation experiments the preannealed reporter-splint DNA duplex is immobilized to the glass surfaces using previously established biotin-streptavidin surface-immobilization techniques. The protocatechuate dioxygenase/protocatechuate acid oxygen-scavenging system is used to increase the photophysical stability of the Cy3/Cy5 FRET pair (33). All experiments were performed at room temperature (≈23.2°C) in a buffer containing 50 mM hemisodium HEPES, 100 mM NaCl, 100 μM EDTA, 2.0 mM TROLOX, 5.0 mM protocatechuate acid, 100 nM protocatechuate dioxygenase, and 10 mM KOH, pH 7.5. Duplex dissociation data were collected using a second excitation source to perform alternating laser excitation (ALEX) imaging (34,35). Briefly, a red (636 nm) pulsed excitation source triggers the green (532 nm) 20 MHz primary excitation source. A 25 ns delay places the red laser pulses exactly halfway between the green laser pulses. ALEX provides the ability to filter molecules by fluorescence to ensure that only data obtained from dually labeled fluorescent DNAs are considered in the analysis.

Overtone IR-Laser-Based Heating Technique

Details of the IR heating system used throughout this study can be found in previously published material (12) and can be quickly summarized here. Specifically, the TEM₀₀ Gaussian beam profile from a continuous-wave laser diode with peak wavelength of 1443 nm was fiber-coupled into an optical cage system containing a beam collimator (output spot size, ω = 4.5 ± 0.3 mm) and focusing lens (ƒ = 100 mm) to form a suitably small waist (ω₀ = 10.0 ± 0.4 μm, FWHM ≈ 17 μm) for local heating near the focal plane. A precision three-axis translation stage then translates the optical cage with respect to the diffraction-limited focus of a 532 nm excitation laser beam, which illuminates the sample in the opposite direction through the objective of an inverted fluorescence microscope (Fig. 1). Beers law absorption (α₁₄₄₃= 30.3 cm⁻¹) of IR radiation induces vibrational OH stretch combination band excitation (ν₁,ν₂,ν₃) = (1,0,1) of the solvent water molecules, which relax on the subnanosecond timescale and thus yield a rapid increase in solution temperature in the laser focal region. The following experiments were performed with such an apparatus to experimentally quantify each of the three major proclaimed advantages associated with IR heating: 1), larger range of temperatures; 2), smaller heated volumes; and 3), faster heating.

Figure 1.

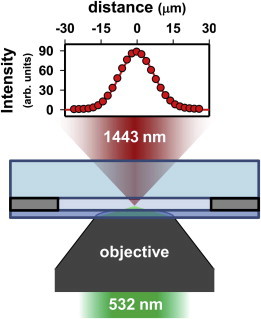
Schematic representation of the IR heating apparatus illustrating the coaxially aligned foci of the IR (red) and excitation (green) lasers within a standard sample holder (not to scale). The intensity plot depicts the experimentally measured radial intensity profile at the focus of the IR laser (ω₀ = 10.0(4) μm). To see this figure in color, go online.

In situ measurement and dynamic range of accessible temperatures

One crucial aspect of the IR heating apparatus is clearly the magnitude of the induced temperature change. As described previously (12), these temperatures can be accurately obtained by measuring the temperature-dependent fluorescent lifetime [τ_fluor(T)] of Rhodamine B (36,37) when the heating and excitation foci are spatially overlapped. The essence of the method relies on the fact that k_fluor(T) is simply the sum of a temperature-independent radiative process, k_rad, and a temperature-dependent nonradiative relaxation, k_nrad(T) (38). Furthermore, k_nrad(T) can be accurately modeled using Eyring transition state theory (Fig. 2, inset), reflecting that nonradiative relaxation is enhanced by tilting the peripheral tertiary amino groups away from the plane of conjugation (38). If we invert this procedure, experimental extraction of k_nrad(T) for Rhodamine B provides an in situ thermometer for the local temperature in the sample region.

Figure 2.

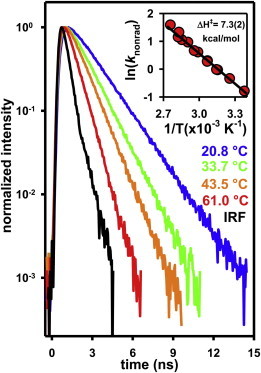
Fluorescence decay profile for Rhodamine B as a function of temperature. The linearity of the fluorescence decay over three orders of magnitude attests to the single-exponential behavior of Rhodamine B. (Inset) Representation of the Eyring analysis of the temperature-dependent nonradiative rate constant for Rhodamine B (see text for details), which is used to determine the temperature rise in the diffraction-limited confocal volume of the sample. To see this figure in color, go online.

Specifically, TCSPC methods are used to acquire the fluorescence decay curve of Rhodamine B in the confocal detection volume of the 532 nm excitation laser. The k_fluor(T) is then determined by single-exponential fits convoluted over the instrument response function of the excitation source, with k_nrad(T) obtained by subtracting the known k_rad value from k_fluor(T). The resulting k_nrad(T) can be used to predict confocal temperatures to within ≈0.5°C, based on the previously determined Eyring transition state parameters for Rhodamine B in water (Fig. 2, inset) (12). Over the range of incident IR laser powers (P_laser = 0–135 mW) focused to a waist of ω₀ = 10.0 ± 0.4 μm at a distance 15 μm above the glass coverslip, the experimental apparatus presented here allows for rapid, systematically controlled temperature increases in the range ΔT = 0–80°C, as illustrated in Fig. 3 a. These results unambiguously demonstrate a range of experimental temperatures significantly larger than that accessible by conventional stage-objective heating systems.

Figure 3.

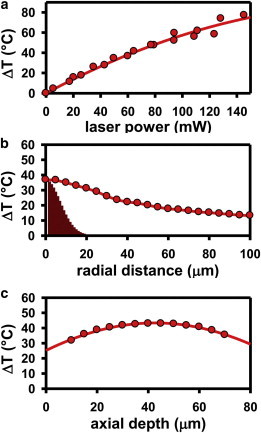
Experimentally measured steady-state temperature rise (ΔT) as a function of incident laser power (a), as well as radial (b) and axial (c) distances from the laser focal point. The solid red region in b represents the radial intensity profile of the IR laser beam scaled to the maximum ΔT. Note the clear broadening of the temperature profile beyond the laser excitation region, which arises largely from thermal diffusion away from the heating axis. To see this figure in color, go online.

High-resolution spatial control of temperature

The second major advantage associated with IR heating methods is the high degree of spatial localization for the induced temperature changes. To quantify this, we first characterized the intensity distribution of the IR heating laser at the beam waist. This can be accomplished by measuring the IR laser light transmitted though a 5 μm circular pinhole translated on a piezoelectric stage. The resulting plot of measured intensity versus lateral displacement (Fig. 1 a) clearly depicts a TEM₀₀ beam, which can be nicely fitted with a Gaussian beam waist of ω₀ = 10.0 ± 0.4 μm. This is also in very good agreement with expectations of ω₀ = 10.3 μm, based on the propagation of a Gaussian beam at the fiber collimator output (ω₀ = 4.5 ± 0.3 mm) that is focused to a waist by a 100-mm-focal-length lens.

To experimentally determine the steady-state radial temperature profile, the optical cage system, and thus the IR laser light, is translated horizontally away from the coaxial position established by the excitation beam. Rhodamine B fluorescence lifetimes are then monitored by TCSPC as a function of distance on the translation stage micrometer. The measured values of k_fluor(T) are then used to calculate ΔT as a function of the radial separation between the heating and excitation sources, as summarized in Fig. 3 b. The data clearly demonstrate that under steady-state heating conditions, the temperature increase is localized in the radial dimension (FWHM ≈55 μm). In addition, the data establish that the radial temperature profile is significantly broader than the incident laser beam. At distances near (i.e., <5 μm from) the axis of heating, the temperature gradient (≈0.1°C/μm) is much smaller than the experimental uncertainty associated with temperature determination (≈0.5°C), which conveniently results in an essentially uniform temperature profile near the heating axis. It is important to note that the temperature begins to gradually decrease at distances farther from the heating axis. This slow radial decay of temperature is consistent with the inverse logarithmic dependence of the radial temperature profile associated with a one-dimensional temperature source and is a result of the elongated column of heat provided by attenuation of the focus IR beam as it propagates through the sample.

By way of further characterization of the spatial temperature profile, ΔT has been measured along the vertical axis of the IR laser, as summarized in Fig. 3 c. It is interesting to note that the measured temperature profiles are relatively flat, with a gradual maximum near the midpoint, and therefore, only a small vertical gradient exists between the two glass boundary surfaces. The reason for this is that overtone absorption strengths for water lie in an ideal intermediate regime, whereby the 85 μm sample thickness is appreciably smaller than the 1/e optical penetration depth (330 μm) and yet not so small as to nonlinearly attenuate laser propagation through the sample. As a result, the on-axis thermal heat deposition is nearly linear with distance, which implies nearly uniform heat load in each axial volume element. Most important, the spatial characterization of heated volume demonstrates that this apparatus confines the temperature rise to extremely small volumes (≈10⁻¹¹ L). This represents a significant improvement relative to conventional bulk heating methods, and furthermore, with sufficiently dilute sample conditions, is extendable down to the heating of a single-molecule construct.

Rapid temperature modulation

The last major advantage offered by IR overtone laser heating is the control of sample temperature in the time domain, which is only limited by diffusion of heat. To provide expectations for the magnitude(s) of such heating and cooling times, we consider the following elementary physical model. The rate of deposition of thermal energy into a laser-illuminated water cylinder of height Δl and cross-sectional area A bounded by an ambient-temperature heat bath (T₀) is

$$\partial Q/\partial \mathrm{t}=\alpha \Delta l{I}_{\mathrm{laser}},$$ (1a)

where α is the normal base e absorption coefficient. By conservation of energy, this thermal deposition must equal the time-dependent change in temperature (∂(T − T₀)/∂t = ∂ΔT/∂t) divided by the heat capacity (C_pAΔl) of the sample volume V = AΔl. This immediately yields the simple equation

$${\left(\partial \Delta T/\partial t\right)}_0=\mathrm{\alpha }{I}_{\mathrm{laser}}/\left[C_{\mathrm{p}}A\right]$$ (1b)

for the instantaneous rate of heating at t = 0. Furthermore, Newton’s law of cooling implies that this initial rate of temperature increase (°C/s) must be linearly proportional to the asymptotic temperature differential (ΔT_∞) when steady-state conditions are achieved, with the coefficient of proportionality given by the exponential rise time. The combination of these relations predicts a characteristic 1/e time for cooling (or heating) given by

$${\tau }_{\mathrm{heat}}=\Delta T_{\infty }/{\left(\partial \Delta T/\partial t\right)}_0.$$ (1c)

One simple qualitative prediction from Eq. 1c is that since both (ΔT/∂t)₀ and ΔT_∞ scale approximately linearly with laser power, the time constant for heating (or cooling) of a localized sample surrounded by material at T₀ should be insensitive to incident laser power and depend only on the sample heat capacity undergoing this ΔT_∞. A second, more quantitative prediction is that for typical conditions of laser power (I_laser ≈ 135 mW), absorption cross section (a = 30.3 cm⁻¹), and beam area (A ∼ ω₀² ≈ 10⁻⁶ cm²), the initial heating rates for the sample volume are remarkably swift, on the order of 1 × 10⁶ degrees/s! Finally, for a typical asymptotic temperature gain under such conditions of ΔT = 80°C, Eq. 1c suggests a 1/e time constant for heating on the submillisecond timescale.

To determine the experimental timescales associated with heating and cooling aqueous solutions using focused IR light, time-dependent trajectories of freely diffusing Rhodamine B (575 nM) were collected as a function of heating duration (Δt). For a given Δt, each trajectory exhibits a rapid rise to steady-state temperature, ΔT_∞, at which point the deposition of thermal energy into the system is perfectly balanced by loss of heat to the surroundings (e.g., objective, stage, and air). At the end of the heating duration, the heat source is turned off and the sample rapidly cools back to T₀ to complete a single heating/cooling cycle (Fig. 4 a). Since the data are collected by TCSPC, the trajectories can be sorted into bins of 100 consecutive photons, with each bin converted into an exponential fluorescence decay rate, k_fluor(T), by maximum-likelihood estimation (39). As described in the section titled In situ measurement and dynamic range of accessible temperatures, these k_fluor(T) values can be corrected for the purely radiative contribution and converted into temperature trajectories ΔT(t) from the k_nrad(T) Arrhenius expression for Rhodamine B (Fig. 2). The heating/cooling behavior of such a temperature trajectory is shown in Fig. 4 a for a heating duration of 500 ms and P_laser = 60 mW, which clearly reveals an extremely sharp increase in the sample temperature. Though too rapid to resolve with 100 photon time bin steps, the time to half-maximal temperature increase (τ_1/2heat) suggests a heating time constant of ≤1 ms, in good qualitative agreement with the above predictions.

Figure 4.

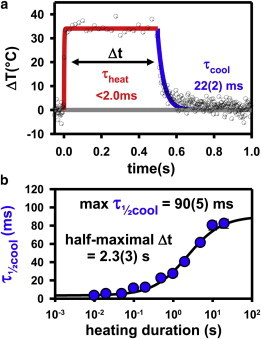
Real-time observation of the IR-heating and cooling behavior, as obtained by time-correlated single-photon fluorescence measurements of Rhodamine B in the confocal excitation region. (a) Sample temperature trajectory (black circles) resulting from a 50 mW heating pulse with a duration of 500 ms. The solid lines represent multiexponential fits used to calculate the half-maximal times for heating (red line) and cooling (blue line). (b) A linear-log plot demonstrating the dependence of cooling time constant on the heating duration, which suggests that the system achieves a steady-state thermal distribution on the few-second timescale. To see this figure in color, go online.

Closer inspection of Fig. 4 a reveals that the cooling profile after the laser is switched off is noticeably broadened with respect to the rise. Specifically, for a laser heating duration of Δt = 500 ms, τ_1/2cool ≈ 22 ± 2 ms, whereas τ_1/2heat ≈ 1 ms. It is worth stressing that this is not inconsistent with the equal times predicted above from Newton’s law of cooling (Eq. 1c). The reason is clearly evident from Fig. 3 b. Lateral thermal conduction away from the laser illumination region during the approach to steady state necessarily increases the surrounding temperature to well above T₀. It is then the presence of this additional heat reservoir adjacent to the laser-heated region that slows the eventual diffusive cooling process back to ambient values. As expected from such a bulk diffusion process, these decays also deviate considerably from single-exponential, making characterization by τ_1/2 values a more useful concept.

One clear prediction from this model is that the cooling times should be strongly dependent on the heating duration. Such a compilation of data is presented in Fig. 4 b, which displays the cooling time (τ_1/2cool) versus duration of the heating laser (Δt). The results (in log time units) are consistent with an approximately proportional growth in τ_1/2cool with Δt, which eventually saturates at some steady-state value for the cooling process. The intercept of this initial linear region is 3 ± 1 ms, which is qualitatively consistent with Newton’s law of cooling expectations that τ_1/2heat ≈ τ_1/2cool for sufficiently short heating durations. Of most importance, such exceptionally short values for τ_1/2heat (and, at sufficiently small Δt, also for τ_1/2cool) represent an enormous improvement (>10⁴-fold) over the typical timescales of minutes associated with conventional stage-objective heating methods. As will become clear in the next section, this offers several critical advantages for single-molecule studies of biophysical kinetics, in particular making it possible to perform high-temperature single-molecule kinetic measurements without temperature-stable fluorescent dyes.

A Test Application: Single-Molecule Kinetics of DNA Duplex Dissociation

As clearly outlined in the introductory sections, the use of IR overtone laser based methods for controlled heating of picoliter volumes within an aqueous sample has considerable potential for applications in a confocal single-molecule microscopy. In particular, the above discussion reveals at least two fundamental complications associated with continuous observation of individual, fluorescently labeled molecules at elevated temperatures: 1), the temperature-dependent rate of dissociation for the biotin-streptavidin surface-immobilization technique (21,40); and 2), the temperature-dependent fluorescent lifetime of commonly used single-molecule fluorophores (22,23). Because of the novel ability to rapidly modulate the local temperature of aqueous solutions, pulsed-heating experiments can in fact be used to circumvent both of these difficulties. On the one hand, rapid T modulation achieves an enormously reduced duty cycle for surface-heating compared to bulk-heating techniques, which dramatically reduces parallel loss of the single molecule biotin–strepavidin attachment. On the other hand, the rapid heating and cooling also greatly limits kinetic effects due to time spent in transition, which permits subsequent FRET dye interrogation under cool, high-quantum-yield conditions. The following pulsed-heating experiments, based on a similar proof-of-principle demonstration for laser-assisted single-molecule refolding (LASR) (10), are used to demonstrate the ability to make high-temperature kinetics measurements of DNA duplex dissociation, tethered to a coverslip with biotin-streptavidin interactions, without the need for thermally stable fluorophores.

Laser-heating-induced duplex DNA dissociation kinetics

To exploit these IR-laser heating methods to investigate the temperature-dependent dissociation kinetics of duplex DNA, a synthetically modified DNA construct was designed with two highly stable conformations—duplex or closed—that can be easily distinguished via FRET (Fig. 5 a). The duplex is formed by hybridization of two oligonucleotides—reporter and splint. The reporter oligo has 1), a 6 bp self-complementary sequence separated by a (PEG)₁₈ linker; 2), Cy3 and Cy5 fluorescent dyes; and 3), a 3′ biotin to permit tethering to the surface via biotin-streptavidin interactions. The splint oligo simply contains 21 nt that are complementary to the reporter oligo. Formation of the duplex conformation is accomplished by hybridization of the reporter and splint oligos, which spatially separates the Cy3 and Cy5 dyes, resulting in low FRET efficiency (E_FRET ≈ 0.1, green). Upon dissociation of the splint, the reporter oligo is able to rapidly form the closed conformation, whereby the first six nucleotides at the 5′ end quickly basepair with nucleotides 7–12 at the 3′ end of the PEG linker (Fig. 5 a). The transition from duplex to closed conformations greatly reduces the radial distance between the Cy3-Cy5 FRET pair, resulting in more efficient FRET (E_FRET ≈ 1.0, red). The basic experimental technique is therefore to use a raster-scanning confocal microscope to image the FRET states under room-temperature conditions before and after the IR laser has induced transient heating of the sample up to a tunable but well characterized temperature for a given time duration.

Before an IR-laser-induced heating episode, ALEX methods (Materials and Methods) are used to scan images (10 μm × 10 μm) of the sample surface, which reveal that nearly all of the dually labeled surface-immobilized molecules are in the low-FRET-state duplex conformation (Fig. 5 b, green). Upon exposure to the IR laser heating pulse (Δt =10 s, T = 72.3 ± 0.5°C) centered on the image, the same surface shows that nearly every duplex has undergone dissociation, as indicated by the abundance (>90%) of molecules in the closed (high-E_FRET) conformation (Fig. 5 c, red). As mentioned previously, the nearly uniform temperature profile near the heating axis conveniently results in all of the molecules in the 10 μm × 10 μm images experiencing the same temperature. Additional evidence for the spatially localized heating and duplex dissociation is demonstrated more dramatically in FRET images of larger 80 μm × 80 μm scans (as shown in Fig. 6) where the temperature gradient is no longer negligible. These larger images reveal a clear dividing line between the inner circular region with dissociated duplexes (high FRET; Fig. 6, red) and the surrounding area with fully intact duplexes (low FRET; Fig. 6, green). The reason is that duplex constructs in the inner circular region have been heated to temperatures with sufficiently large rate constants to have significant dissociation probability during the 10 s heating duration. As a result, most molecules heated by the IR laser reside in the closed conformation (high FRET; Fig. 6, red), whereas those around the periphery remain in the duplex conformation (low E_FRET, Fig. 6, green). Long-term exposure to elevated temperatures is capable of inducing duplex dissociation in a 21 bp DNA double helix, with the same duplexes more or less indefinitely stable at room temperature. Therefore, we exploit the excellent spatial, temporal, and thermal control of the IR overtone heating laser to systematically tune 1), the temperature change and 2), the heating duration (Δt) to extract the temperature dependence of the DNA duplex dissociation rate constant.

Figure 6.

ALEX scanned image (80 μm × 80 μm) of the fluorescent DNA duplex constructs after heating the center of the image to 72.3(5)°C for 10 s. Note the clear circular region of high-FRET molecules (red), corresponding to duplex constructs that have undergone dissociation, surrounded by low-FRET species (green) in the duplex conformation. To see this figure in color, go online.

The degree of duplex dissociation for a given heating duration (Δt) and steady-state temperature (T) can be quantified via the single-molecule survival probability, S(Δt,T), corrected for loss of construct from view caused by, for example, photobleaching and disruption of the biotin-streptavidin linkage. To extract S(Δt,T), one generates a mask (Fig. 5 b) that identifies the number of individually immobilized molecules before the heating pulse with both Cy3/Cy5 dyes and in the duplex conformation (N_duplex(0)). After exposure to the heating cycle, the sample area is overlaid with the same mask (Fig. 5 c) to determine the number of remaining molecules in the duplex conformation (N_duplex(Δt,T)) as well as the very small number N′ (where N′ ≪ N_duplex(0)) removed via parallel pathways such as photobleaching or irreversible dissociation of the biotin-strepavidin linkage. Corrected for these loss channels (e.g., N′_duplex(0) = N_duplex(0) – N′), the survival probability S(Δt,T) can simply be calculated via

$$S\left(\Delta t,T\right)=N_{\mathrm{duplex}}\left[\Delta t,T\right]/N_{\mathrm{duplex}}^{\text{'}}\left(0\right).$$ (2)

The survival probability is monitored as a function of heating duration (Δt) and temperature (T) to probe the underlying kinetics mechanism of temperature-induced dissociation of a 21 bp DNA duplex.

To correctly analyze these heating-pulse experiments, one must make two kinetic assumptions. The first is that the duplex dissociation kinetics are negligible at room temperature and only contribute during the heating episode. This is readily confirmed by the fact that surface-immobilized constructs do not change FRET states over many hours in the absence of the heating laser. The second assumption is that the dissociation event is irreversible, with the liberated splint strand unable to re-form the duplex conformation. Since duplex association is a bimolecular process, this assumption is clearly valid, as the dissociated splint strand quickly diffuses into the bulk to form a solution of vanishingly low concentration.

Pulsed-heating experiments are performed to measure the survival probability as a function of the heating-pulse steady-state temperature (T = 55.2 ± 0.5 to 64.9 ± 0.5°C) and duration (Δt = 50–1000 ms). The results of these experiments clearly demonstrate that measured values of the S(Δt,T) remain near unity for sufficiently short heating durations (<100 ms) regardless of pulse temperature. As the heating duration increases, S(Δt,T) decreases with a distinctly sigmoidal shape, i.e., with the initial ∂²S/∂²t < 0 and a clear inflection point uncharacteristic of purely single-exponential decay kinetics. The impact of heating duration on the kinetics is quite clear from Fig. 7 a, with the timescale for achieving half-maximal survival probabilities decreasing rapidly with increasing temperature. It is worth stressing that such a heating protocol makes it possible to obtain kinetic information at elevated temperatures using standard fluorescent dyes, since the fluorescence photons are harvested only under room-temperature conditions where high quantum yields have been reestablished.

Figure 7.

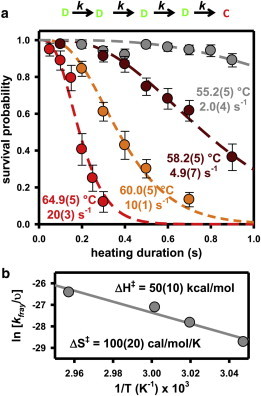
(a) DNA duplex survival probability data, S(Δt,T), as a function of heating duration, Δt, at four steady-state heating-pulse temperatures. Dashed lines represent least-squares fit to a consecutive first-order reaction model, which yields n = 4.1(3) sequential reaction steps with an assumed identical rate constant. Notice the rapid increase in this rate constant with increasing temperature, implying a large endothermic component in the transition-state barrier. (b) Eyring transition-state analysis of the temperature-dependent rate constant, suggesting a highly endothermic (ΔH^‡ = 50(10) kcal/mol) and entropically rewarding (ΔS^‡ = 100(20) cal/mol/K) component of the free-energy barrier for each of the fraying events. To see this figure in color, go online.

We next consider the simple kinetic models necessary to describe these observed S(Δt,T) plots for each of the four heating series. First of all, it is important to note that for any dissociation process over a single rate-limiting barrier (e.g., duplex → hairpin). For such a process, the survival probability would be described by a simple single-exponential decay (Eq. 3) with a rate constant, k_diss(T), that depends on the steady-state temperature of the heating pulse.

$$S\left(\Delta t,T\right)=e^{-\Delta t{k}_{\text{diss}}\left(T\right)}.$$ (3)

However, this model would predict a conventional convex shape (i.e., with initial ∂²S/∂²t > 0) lacking an inflection point and inconsistent with the data. Instead, the experimental survival probabilities clearly reveal an anomalous lag time at short heating durations (Fig. 7 a), which necessarily requires description by a higher-than-first-order kinetic model. The simplest such model is that of consecutive first-order reactions (e.g., D₀ → D₁ → C) where D₀ and D₁ represent some partially dissociated duplex conformation (i.e., still low-FRET), whereas C corresponds to the spectroscopically distinguishable closed (high-FRET) conformation accessible only by dissociation of the full duplex. In such a kinetic model, the lag time arises from the first-order kinetics of D₀ needing to form D₁ before forming the detected species C. Even more likely, there could be a series of n such intermediate species (e.g., D₀ → D₁ ⋅⋅⋅ → D_n → C), which impact both the lag time as well as the cooperative sharpness of the sigmoidal behavior. If all n of the rate constants associated with the steady-state temperature of the heating pulse, k(T), are nearly identical, the solution to this n-step first-order consecutive kinetic model can be solved exactly to yield

$$S\left(\Delta t,T\right)=\frac{\Gamma \left(n,k\left(T\right)\Delta t\right)}{\Gamma \left(n\right)},$$ (4)

where Γ(n) and Γ(n,k(T)Δt) are the gamma function and incomplete gamma function, respectively. Successful examples of the application of sequential chemical reaction models to biological systems include both DNA helicases (41,42) and strand exchange induced by RecA (43). Application of this model to the experiments presented here involves fitting the data in Fig. 7 a to extract the two fitted parameters, 1), the rate constant for each of the steady-state temperatures associated with the IR heating pulse, k(T), and 2), the number of consecutive steps, n. The results of a least-squares analysis of the data yield n = 4.1 ± 0.33, which in the context of such a model would suggest that there may be four consecutive steps before complete duplex dissociation. Furthermore, the values of k(T) increase dramatically with relatively small increases in temperature, which would be consistent with the four sequential steps having to surmount strongly endothermic free-energy barriers. Other, more complex kinetic models can of course fit the data. However, the success of this simple consecutive first-order reaction picture with n ≈ 4 proves a useful starting point from which insights into the duplex dissociation event may be developed further below.

Duplex Dissociation Model

Since the discovery of the double-stranded DNA structure (44), considerable effort has been directed toward understanding the fundamental kinetics and thermodynamics for duplex dissociation and association events (45). A significant amount of work has been directed at characterizing the forward association process, in particular highlighting the importance of prehelical structures for oligonucleotide strands forming the duplex (46–48). For corresponding studies of the duplex dissociation process, however, there has been much less consensus regarding the explicit dissociation mechanism, with conflicting reports of single-exponential (49–51), stretched-exponential (52), and biexponential kinetic behavior (53,54) for different-oligo-length systems and experimental conditions. The single-molecule heating results presented here confirm that the DNA duplex dissociation kinetics are distinctly non-single-exponential for a 21 bp DNA duplex. Specifically, the lag-time dissociation behavior observed in these studies is fundamentally inconsistent with that of an isolated rate process over a single transition-state barrier. Instead, the dissociation kinetics are more correctly described by a first-order consecutive model with n ≈ 4 matching rate constants that increase rapidly with temperature.

This suggests a simple, physically motivated mechanism for duplex dissociation; specifically, fraying of the 21 bp DNA duplex can occur from either of the two ends of the helix. Before developing this model further, it is important to note that the pitch of the DNA double helix is ∼10 bp/360° (55) and largely restricted by base-stacking interactions (56). Thus, for a DNA duplex >10 bp, simple structural constraints make it physically difficult to dissociate without major disruption of the helical pitch. This alone would suggest that duplexes >9 bp must initially peel apart (i.e., fray) at one or both ends to generate a duplex that is sufficiently short to then undergo rapid dissociation in a single step. For the 21 bp DNA duplexes in this study, this would require fraying of at least 12 bp. Although fraying can occur entirely from one end, dissociation preceded by symmetrical fraying of at least 6 bp from each end would be much more highly favored by simple Poisson considerations. Specifically, the statistical ratio between N bp fraying from two ends versus 2N bp fraying from one end is readily shown to be (2N)!/(N!)², which for N = 6 is already 924:1.

Similar ideas have been generated in the literature to help interpret dissociation (49) and end-fraying (57–59) dynamics of DNA duplexes. These studies of end-fraying dynamics at temperatures well below the melting point of the DNA duplex have made it possible to measure small changes in the terminal basepairs that occur on the 10⁻⁷ s timescale. Of course, the analysis presented here, associated with the n-step consecutive first-order kinetic model, is clearly not sensitive to individual-basepair fraying steps, but instead appears to be consistent with approximately four fraying steps with 3- to 5-bp disruptions in each (see Fig. 8). For the four consecutive fraying events, Poisson considerations suggest that fraying from both ends would be sixfold more likely than fraying entirely from one end. In addition, with >3 bp disruptions in each of the observed fraying events, it is not surprising that the timescale for this process is orders of magnitude slower than what has been measured for single-basepair fraying dynamics (57,58). Therefore, it is reasonable to suggest that the 21 bp DNA duplex used in these pulsed heating experiments dissociates via the following pathway: two fraying events, of 3–5 bp each, must occur at the two ends of the DNA duplex, giving rise to a highly frayed intermediate with only a small number (1–9) of remaining basepairing interactions. This intermediate is then able to dissociate in a rapid (i.e., non-rate-limiting) step into the two individual oligonucleotides, as schematically depicted in Fig. 8.

Figure 8.

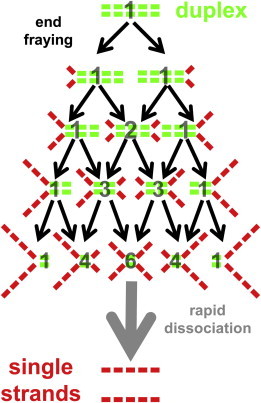
Model depicting the consecutive-fraying-at-both-ends mechanism for duplex dissociation. The colored bars represent short segments of the 21 bp DNA duplex that are either associated (green) or dissociated (red). The transparent black numbers correspond to the relative abundance of each partially dissociated species as predicted by a binomial distribution. After four consecutive fraying events, the single remaining associated (green) segment of the duplex is sufficiently frayed to undergo a final rapid dissociation step. See discussion for details. To see this figure in color, go online.

We note that this highly simplified analysis of the duplex dissociation kinetics is based on a series of rate-limiting steps due to fraying from both ends of the helix to <10 remaining basepairs, followed by rapid dissociation of the remaining duplex. Recently published single-molecule experiments have investigated the association/dissociation kinetics of smaller DNA duplexes (6–9 bp) as a function of temperature (60). The results of these experiments strongly support the assumption of rapid single-exponential survival probabilities for the short DNA duplex at elevated temperatures. Specifically, if one extrapolates to the higher temperatures (65°C) in this study, the temperature-dependent single-exponential rate constants for duplex dissociation would be >10⁴ s⁻¹. This is already considerably faster than the range of rate constants obtained in Fig. 7 and thus consistent with the notion of rate-limiting symmetrical fraying toward the center from both ends, before a rapid (non-rate-limiting) dissociation step.

Finally, the measured temperature dependence of the n ≈ 4 sequential fraying rate constants can be used to extract thermodynamic information about the fraying process itself. Specifically, from Eyring transition state theory, the experimentally measured duplex dissociation rate constant is given by

$$k\left(T\right)=\upsilon e^{\left(-\Delta G^{‡}/kT\right)}=\upsilon e^{\left(-\Delta H^{‡}/kT\right)}{e}^{\left(-\Delta S^{‡}/k\right)},$$ (5)

where υ is some characteristic vibrational-attempt frequency for the fraying event. We can therefore formulate an Eyring transition-state plot of ln(k/υ) vs. 1/T to provide key additional information on the enthalpy (slope) and entropy (intercept) components of the free-energy barrier. Such an analysis is shown in Fig. 7 b, which predicts a large enthalpic transition-state barrier of ΔH^‡ = 50 ± 10 kcal/mol and is consistent with breaking several basepair interactions in each of the four fraying events for the DNA duplex. Indeed, for a mean dissociation enthalpy of ≈8.4 kcal/mol/bp obtained from nearest-neighbor modeling (61), this would be consistent with an average of ≈6 ± 1 basepair disruptions in each of the four consecutive fraying processes. In a similar way, the corresponding entropy change from such an Eyring plot is found to be large and positive, ΔS^‡ = 100 ± 20 cal/mol/K, which from a nearest-neighbor modeling of the average entropy (22.4 cal/mol/K/bp) would suggest disruption of ≈4.5 ± 0.9 bp in each of the four fraying events. Although such an analysis is clearly not intended to be quantitative, these values are at least consistent with end fraying of the DNA duplex down to a small number of basepairs before a final (non-rate-limiting) dissociation event. Clearly, an interesting next step would be to further explore such dissociation kinetics as a function of sequence and length of the DNA duplexes, which would be necessary to further refine such a multistep consecutive-fraying mechanism for duplex oligonucleotide dissociation.

Conclusions

This work provides a detailed description and quantitative characterization of the overtone laser IR-absorption heating method for applications in single-molecule fluorescence studies, highlighting several key advantages of this technique over conventional bulk-heating microscopy methods. First of all, it provides controlled and highly reproducible experimental access to sample temperatures from 20°C up to the boiling point (ΔT ≈ 80°C), greatly exceeding the operating temperature ranges accessible by conventional stage-objective heating. Second, use of high-quality TEM₀₀-mode laser sources permits exceptionally high spatial control and confinement of the heated volume, with typical sample regions on the order of 10⁻¹¹ liters or less. Finally, this optical-laser-based infrared heating system is able to achieve controlled rises in sample temperatures with a half-maximal heating time of ∼1 ms, which is many tens of thousands times faster than the minute to hour timescales of conventional stage-based methods.

In addition, this work demonstrates the greater utility of this optical-laser heating technique by performing pulsed heating experiments. Specifically, single-molecule dissociation kinetics of single DNA duplexes was studied by elevating the sample temperature by a well-characterized amount for a well-characterized duration. Most important, the rapid heating and cooling properties of the system offer the ability to access kinetics at high sample temperatures without the need for temperature-stable fluorescent dyes. These temperature-cycling dissociation studies provide useful kinetic insight into the mechanism by which a 21 bp DNA duplex undergoes dissociation. In particular, the kinetic data reveal a clear sigmoidal time lag in the appearance of the dissociated duplex. This is qualitatively inconsistent with any single-exponential rate process and indeed is more consistent with n ≈ 4 sequential first-order pathways. The working hypothesis for this behavior is that DNA dissociation over this range of duplex lengths is constrained by the helical twist, which makes dissociation occur from a short interior region resulting from rapid fraying from both ends toward the middle. Specifically, fraying inward from each end with two separate rate processes is shown to be sixfold more probable than all four processes occurring from a single end, with rapid dissociation occurring when the duplex is sufficiently frayed from both ends. In summary, the results of this study provide a proof-of-principle demonstration of the efficacy of pulsed-laser-heating studies of single-molecule kinetics with high spatial (<10⁻¹⁰ liter) and temporal (≈1 ms) control of sample temperatures, and they help elucidate the role of sequential, first-order kinetic pathways in the dissociation of DNA duplexes.