Discriminating between Anomalous Diffusion and Transient Behavior in Microheterogeneous Environments

Abstract

Diffusion in macrohomogeneous and microheterogeneous media can be described as effective free diffusion only at sufficiently long times. At intermediate times, the mean-square displacement of a diffusing object shows a transient behavior that can be misinterpreted as anomalous subdiffusion. We discuss how to discriminate between the two.

Free diffusion is a universal description of unbiased motion in a macrohomogeneous media, which is widely used in the analysis of various problems in physics, chemistry, and biology. This is a coarse-grained description that is applicable at sufficiently long times when a typical displacement of the diffusing object exceeds a characteristic length scale associated with the heterogeneity of the medium. For example, treatment of molecular motion in water in terms of self-diffusion is applicable at times larger than 100 ps when the mean displacement exceeds the mean distance between water molecules (1). Another example provides diffusion in crystalline solids, where the displacement should exceed the lattice period (2). It is well known that diffusion in biological systems frequently occurs in microheterogeneous environments (for instance, diffusion in the crowded cytoplasm). In such systems, description in terms of effective free diffusion may become applicable only for times that are comparable or even longer than the duration of the experiment. Therefore, it is not surprising that the data on the mean-square displacements, 〈Δr²(t)〉, are frequently described by the dependences 〈Δr²(t)〉 ∝ t^α with α < 1 (see recent review articles (3,4) and references therein), whereas for free diffusion the exponent α is unity. Because the dependence 〈Δr²(t)〉 ∝ t^α with α < 1 is a fingerprint of anomalous subdiffusion (5), the question naturally arises how to discriminate between anomalous subdiffusion and transient behavior to effective free diffusion regime. The present Letter focuses on this question.

The fundamental difference between anomalous subdiffusion and the transient behavior is that the exponent α is a constant in the former case, whereas it is a function of time in the case of transient behavior. Therefore, in the case of anomalous diffusion, α obtained from the experimental data is independent of the method used to determine the exponent. However, as we show below, different methods lead to different functions α(t) in the case of transient behavior.

Consider three different methods of determining the exponent α from experimental data:

• 1.Fitting the time dependence of the mean-square displacement to the exponential function 〈Δr²(t)〉 ∝ t^α, one can find the exponent that we denote by α_fit.
• 2.
  Assuming that α is independent of time and integrating the dependence 〈Δr²(t)〉 ∝ t^α over time, one can find that the area under the curve 〈Δr²(t)〉 is

  $${\int }_0^t\langle \Delta r^2\left(t^{\prime }\right)\rangle d{t}^{\prime }=t\langle \Delta r^2\left(t\right)\rangle /\left(\alpha +1\right).$$ (1)

  We use this relation to define the exponent, which we denote by α_int:

  $${\alpha }_{\mathrm{int}}=\left(t\langle \Delta r^2\left(t\right)\rangle /{\int }_0^t\langle \Delta r^2\left(t^{\prime }\right)\rangle d{t}^{\prime }\right)-1.$$ (2)
• 3.
  Differentiating 〈Δr²(t)〉 ∝ t^α with respect to time, assuming that α is a constant, we obtain

  $$d\langle \Delta r^2\left(t\right)\rangle /dt=\alpha \langle \Delta r^2\left(t\right)\rangle /t.$$ (3)

Using this, we determine the exponent denoted by α_dif:

$${\alpha }_{\text{dif}}=\frac{t}{\langle \Delta r^2\left(t\right)\rangle }\frac{d\langle \Delta r^2\left(t\right)\rangle }{dt}=\frac{d\ln \langle \Delta r^2\left(t\right)\rangle }{d\ln t}.$$ (4)

When diffusion is anomalous, and α is a constant, all three methods lead to the same value of the exponent: α_fit(t) = α_int(t) = α_dif(t) = α. However, in the case of transient behavior where the exponent is not a constant, the three methods lead to the time-dependent α_fit(t), α_int(t), and α_dif(t), which, importantly, are different functions of time.

As an illustration, consider diffusion in the presence of periodically spaced permeable membranes modeled as infinitely thin planar partitions (see the inset in Fig. 1 A). The effective diffusion coefficient D_eff of a particle in the direction normal to the membranes is given by (6)

$$D_0/D_{\text{eff}}=1+D_0/\left(Pl\right),$$ (5)

where D₀ is the particle diffusion coefficient in the absence of the membranes, P is the membrane permeability, and l is the intermembrane distance. As follows from Eq. 5, the presence of low permeability membranes leads to a significant slowdown of the diffusion. This model of a microheterogeneous system allows for exact solutions for the mean-square displacement 〈Δx²(t)〉 in the direction normal to the membranes, and for the exponents α_int(t) and α_dif(t). To be more specific, one can find an exact analytical solution for the Laplace transform of 〈Δx²(t)〉 (7,8) and then to find 〈Δx²(t)〉 by numerically inverting the transform. Knowing the Laplace transform of 〈Δx²(t)〉, one can find the Laplace transforms of

$${\int }_0^t\langle \Delta x^2\left(t^{\prime }\right)\rangle d{t}^{\prime }\text{and}d\langle \Delta x^2\left(t\right)\rangle /dt.$$

Inverting these transforms one can obtain α_int(t) and α_dif(t) using the definitions of these exponents in Eqs. 2 and 4, respectively (see the Supporting Material for details). In Fig. 1, we show 〈Δx²(t)〉 for D₀ = 1, P = 0.01, and l = 10. The slowdown of diffusion does not manifest itself at short times, where 〈Δx²(t)〉 = 2D₀t and hence α = 1. As time increases, the rate of diffusion slows down, and the mean-square displacement approaches its long-time behavior, 〈Δx²(t)〉 = 2D_efft, which describes effective free diffusion with D_eff given in Eq. 5 and $\alpha =1$. Functions α_fit(t), α_int(t), and α_dif(t) obtained by fitting the dependence 〈Δx²(t)〉, and using the definitions in Eqs. 2 and 4, respectively, are shown in Fig. 1 B.

Figure 1.

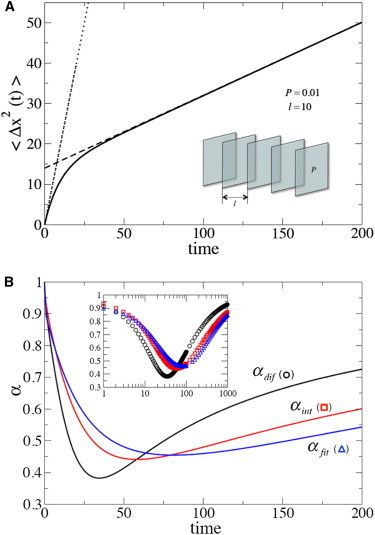
(A) The mean-square displacement 〈Δx²(t)〉 of a particle in the presence of periodically spaced permeable membranes in the direction normal to the membranes. (Inset) System geometry. The parameters in dimensionless units: membrane permeability is 0.01; intermembrane distance is 10; and particle diffusion coefficient in free space is 1. (Dotted and dashed straight lines) Short- and long-time asymptotic behaviors of 〈Δx²(t)〉, respectively. (B) The three exponents α_fit(t), α_int(t), and α_dif(t) obtained by interpreting the transient behavior of 〈Δx²(t)〉 as anomalous subdiffusion. (Inset) The exponents as functions of log t. To see this figure in color, go online.

As another example, consider the tube with periodic dead ends shown in the inset in Fig. 2 A, which is a caricature of a spiny dendrite (9,10). Each dead end is formed by a spherical cavity of volume V_cav connected to the cylindrical part of the tube by a narrow bottleneck of radius a. Particles, from time to time, interrupt their motion along the tube by entering the dead ends that leads to the slowdown of their diffusion along the tube axis. The particle effective free diffusion coefficient, D_eff, is related to its diffusion coefficient D₀ in the absence of dead ends by the relation (11)

$$D_0/D_{\text{eff}}=1+V_{\text{cav}}/V_{\text{tube}},$$ (6)

where V_tube is the tube volume per one dead end. As follows from Eq. 6, D_eff is well below D₀ when V_cav >> V_tube. For such a system, an analytical solution for the Laplace transform of the mean-square displacement 〈Δx²(t)〉 along the tube axis is also available (11). This Laplace transform was used to draw the dependence 〈Δx²(t)〉 shown in Fig. 2 A and the exponents α_fit(t), α_int(t), and α_dif(t) shown in Fig. 2 B (see the Supporting Material for details).

Figure 2.

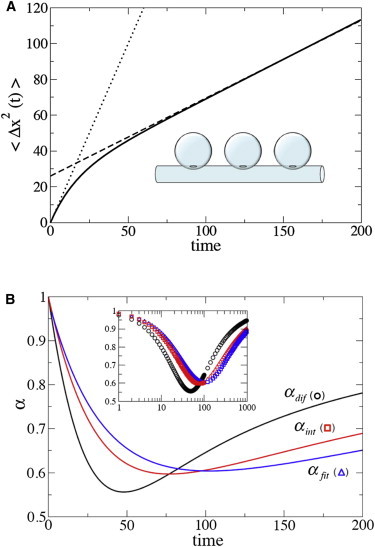
(A) The mean-square displacement 〈Δx²(t)〉 of a particle along the axis of a tube with periodic spherical dead ends (inset). The system parameters in dimensionless units: tube and cavity radii are 0.8 and 1.5, respectively; intercavity distance is 2; radius of the apertures connecting the tube with the cavities is 0.1; and particle diffusion coefficient in free space is 1. (Dotted and dashed straight lines) Short- and long-time asymptotic behaviors of 〈Δx²(t)〉, respectively. (B) The three exponents α_fit(t), α_int(t), and α_dif(t) obtained by interpreting the transient behavior of 〈Δx²(t)〉 as anomalous subdiffusion. (Inset) The exponents as functions of log t. To see this figure in color, go online.

In both examples, the three exponents first decrease rapidly from unity at t = 0 to their minima and then increase slowly approaching unity at sufficiently long times. Although α_dif(t) approaches unity faster than the two other exponents, differentiation of noisy experimental data on 〈Δx²(t)〉 may be difficult. In view of this circumstance, fitting the data on 〈Δx²(t)〉 and determining the area

$${\int }_0^t\langle \Delta x^2\left(t^{\prime }\right)\rangle d{t}^{\prime }$$

seem more reliable procedures for analyzing data on the time dependence of the mean-square displacement. One can see that both α_fit(t) and α_int(t) approach unity rather slowly. It may happen that, on experimentally available times, both exponents are smaller than unity and almost do not change. As a result, this may lead to an incorrect interpretation of the transient behavior as anomalous subdiffusion. As shown in Figs. 1 B and 2 B, most of the time the two exponents are not equal to each other. Therefore, one can discriminate between anomalous subdiffusion and transient behavior by comparing α_fit(t) and α_int(t). In the case of anomalous subdiffusion, the two exponents must be identical and independent of time. If not, the observed deviation of the exponent α from unity can be related to the transient behavior to effective free diffusion regime.