Differentiation of Col I and Col III Isoforms in Stromal Models of Ovarian Cancer by Analysis of Second Harmonic Generation Polarization and Emission Directionality

Abstract

A profound remodeling of the extracellular matrix occurs in many epithelial cancers. In ovarian cancer, the minor collagen isoform of Col III becomes upregulated in invasive disease. Here we use second harmonic generation (SHG) imaging microscopy to probe structural differences in fibrillar models of the ovarian stroma comprised of mixtures of Col I and III. The SHG intensity and forward-backward ratios decrease with increasing Col III content, consistent with decreased phasematching due to more randomized structures. We further probe the net collagen α-helix pitch angle within the gel mixtures using what is believed to be a new pixel-based polarization-resolved approach that combines and extends previous analyses. The extracted pitch angles are consistent with those of peptide models and the method has sufficient sensitivity to differentiate Col I from the Col I/Col III mixtures. We further developed the pixel-based approach to extract the SHG signal polarization anisotropy from the same polarization-resolved image matrix. Using this approach, we found that increased Col III results in decreased alignment of the dipole moments within the focal volume. Collectively, the SHG measurements and analysis all indicate that incorporation of Col III results in decreased organization across several levels of collagen organization. Furthermore, the findings suggest that the collagen isoforms comingle within the same fibrils, in good agreement with ultrastructural data. The pixel-based polarization analyses (both excitation and emission) afford determination of structural properties without the previous requirement of having well-aligned fibers, and the approaches should be generally applicable in tissue.

Introduction

The extracellular matrix (ECM) in tissues provides structural support for adhesion/migration of epithelial cells as well as providing an array of signaling cues that determine cell function. It has been increasingly documented that alterations in the ECM occur in most cancers (e.g., breast, colon, ovary, etc.), although the mechanisms are currently poorly understood. Desmoplasia, or upregulation of collagen, is a hallmark of many cancers, where this can be exemplified by an increase in total collagen, increase in alignment, or both. For example, Provenzano et al. (1) and Conklin et al. (2) found all these behaviors in breast carcinoma, depending on disease stage. We have previously found an increase in organization of collagen in human ovarian cancer across different size scales (3). These findings suggest that quantitative structural analysis of collagen assembly in the tumor microenvironment will improve the understanding of the etiology and classification of cancer. Additionally, this may lead to enhanced diagnostic and prognostic capabilities, and the development of more efficacious treatments.

Remodeling of the ECM in cancer involves alterations in morphology as well as changes in the composition of the collagen isoforms comprising the ECM. For example, collagen V (Col V or type V) is upregulated in breast cancer from negligible levels in normal tissue to ∼20% in invasive carcinoma (4), whereas collagen types III and VI are upregulated in ovarian cancer (5). These isoforms differ in composition of individual α-chains into the collagen triple helix, suggesting their incorporation into the fibrillar network might also be distinguishable with structural-based probes. For both Col V and III, it has been suggested that these minor components comingle with Col I molecules within the same fibrils (6–9). Many reports on upregulation of different isoforms have been based on immunofluorescence microscopic imaging and Western blots (10,11); however, such staining is most often not quantitative and can lack specificity between isoforms.

In general, providing label-free, highly specific discrimination between differing collagen isoforms could be a powerful means to study the underlying biological changes in the ECM in cancer as well as provide a new diagnostic tool. In previous work, we posed this question using second harmonic generation (SHG) microscopy to interrogate the structure of mixed Col I/Col V fibrillar gels, which are models for invasive breast carcinoma. We showed that fibrillar collagen gels comprised of different fractions of Col I and V could be differentiated by morphology, where increasing Col V led to shorter, more randomly distributed fibers (12). Additionally the gels at higher Col V concentration yielded fibers with both lower SHG intensity and lower forward-backward (F/B) ratios, where this metric is related to the size and packing of fibrils in the axial direction (13). Both of these effects arise from less efficient phase matching arising from increased randomness (13).

The fibrillar structures of collagen I, III, and V in tissue are all potentially distinguishable from each other given their different α-chain incorporations, resulting triple helical structure, and concomitant fibrillar structure. For example, Col I and III have 2α₁α₂ and 3α₁ triple helical structures, respectively (14), where the different α-chains are characterized by different charge distributions and also pitch angle (angle of the coil relative to the linear axis of the protein). In principle, changes in isoform distribution should be distinguishable by SHG polarization analyses, which are sensitive to both pitch angle and alignment of molecule dipoles within collagen fibrils/fibers (15–19).

In this article, we extend our previous efforts and describe a series of SHG microscopy metrics to differentiate gels comprised of different Col I/III mixtures (0–40% Col III) that serve as models for stromal changes in ovarian cancer. In addition to the SHG intensity and metrics of emission directionality (i.e., F/B ratios) used previously, we now use two different polarization methods that probe macro/supramolecular structure over different size scales. We interrogate the net α-helical pitch angle using our previous polarization analysis based on a tensor approach (16) combined with a recent pixel-based analysis presented by Duboisset et al. (20) and Aït-Belkacem et al. (21). We found the extracted trends are in agreement with the pitch angles of peptide models in the Protein Data Bank. Lastly, a believed-new pixel-based SHG signal anisotropy measurement (obtained simultaneously with the pitch angle data) is used to measure the extent of dipole alignment within fibers and we found decreased order with increasing Col III concentration. All the metrics indicated decreased organization upon Col III incorporation, and is consistent with previous suggestions that the Col I and III molecules comingle within the same fibrils.

Material and Methods

Preparation of self-assembled collagen gels

Self-assembled collagen gels were polymerized as previously described in Keely et al. (22). Briefly, type-I rat-tail collagen (BD Biosciences, Franklin Lakes, NJ) and recombinant human collagen III (Cell Sciences, Canton, MA) were neutralized with an equal volume of 100 mM HEPES in 5× phosphate-buffered saline to obtain 2 mg/mL collagen gels comprised of a mixture of Col I/III collagen at mixtures of 100:0, 95:5, 90:10, 85:15, 80:20, or 60:40%. A total gel volume of 1 mL was achieved by the addition of phosphate-buffered saline. The collagen gel solution was polymerized in a six-well tissue culture dish overnight at 37°C, the gels were released from the bottoms of the sides of the dish, and fixed in 4% paraformaldehyde. Each series of comparisons of the SHG signatures from the different compositions were carried out with gels polymerized at the same time and the results for each concentration are thus internally self-consistent.

Experimental microscope setup

The details of the SHG imaging system has been described previously in Chen et al. (17) and is only briefly described here. The imaging system consists of a laser scanning unit (FluoView 300; Olympus, Melville, NY) mounted on an upright microscope (model No. BX61; Olympus), where the excitation source is a mode-locked Titanium Sapphire laser (Mira; Coherent, Santa Clara, CA). The laser power is controlled using an Electro-Optic Modulator (ConOptics, Danbury, CT). All imaging was performed with a fundamental laser wavelength of 890 nm with an average power of 5–40 mW at the focal plane using a 40 × 0.8 NA water immersion lens (LUMPlanFL; Olympus) and a 0.9 NA condenser. The resulting lateral and axial resolutions were ∼0.7 and 2.5 microns respectively. The microscope simultaneously collects both the forward (F) and backward (B) components of the SHG intensity using identical detectors (7421 GaAsP photon-counting modules; Hamamatsu, Hamamatsu City, Japan). The two collection pathways (including photomultiplier-tube quantum yields) are calibrated using isotropically emitting fluorescent beads (17). The SHG wavelength (445 nm) was isolated with a 10-nm wide bandpass filter (Semrock, Rochester, NY). The SHG wavelength was confirmed with a fiber-optic spectrometer (Ocean Optics, Dunedin, FL). The field of view size was 170 μm for images used for morphological and F/B analyses and 85 μm for polarization analysis, all with fields of 512 × 512 pixels. The scanning speed was a 2.71 s/frame with three-frame Kalman averaging. For fiber length, intensity, and F/B measurements, circular polarization was used such that all fiber orientations were excited equally. Circular polarization is obtained at the focus by using a half-wave and quarter-wave plate on the optical table, where the former acts as a variable retarder. The final polarization state was verified by imaging lipid vesicles stained with the membrane staining dye Di-8-ANEPPS, where a uniform ring stain was achieved (17).

Additional components/modifications are required for the polarization SHG microscopy experiments. High-purity, rotatable linear polarization was generated using a liquid-crystal rotator (Meadowlark Optics, Frederick, CO) mounted in the infinity space of the microscope. This configuration provides a faster and more precise way to achieve any desired linear polarization than would be possible through polarization control outside the microscope. This is because the optical path can introduce ellipticity into the linear polarization state in a nonlinear manner. Moreover, it eliminates motion artifacts and other inaccuracies introduced by mechanical stage rotation (either outside or inside the microscope) because there are no moving parts. The module (created by three-dimensional printing) containing the liquid-crystal rotator replaced the dichroic in the backward channel, therefore only forward SHG was collected for all polarization-resolved imaging. For forward SHG signal anisotropy measurements, a removable Glan-Laser Polarizer (analyzer) is mounted on a precisely controlled motorized mount (both from ThorLabs, Newton, NJ) before the photomultiplier tube. The polarization direction is calibrated relative to the excitation from the liquid-crystal rotator. A custom LABVIEW program (National Instruments, Austin, TX) controlled the Electro-Optic Modulator (power), liquid-crystal rotator, and Glan-Laser Polarizer (ThorLabs) and was interfaced with the FluoView scanning system (Olympus) using a data acquisition card (model No. PCI-6024E; National Instruments).

Acquisition and analysis of the polarization images

For the polarization-resolved experiments, 361 images were collected at each imaging area, where 19 excitation angles with 19 emission angles at 10° intervals were acquired over 0–180° of each combination. We confirmed that the same locations in the optical sections were used by inspection of the degenerate 0 and 180° points. Three areas of each gel were imaged and used for the analysis. All analysis of the SHG images was performed using the software FIJI (Just ImageJ, http://fiji.sc/Fiji; an open source software based on ImageJ, National Institutes of Health, Bethesda, MD) (23) or the software MATLAB (The MathWorks, Natick, MA). For forward/backward analysis, the same threshold was applied to both channels before averaging the total SHG intensity in each optical section.

Statistical analysis

All the statistical analyses were done using the software SAS (SAS Institute, Cary, NC). To achieve the appropriate sample size, three experimental replicates were performed. All the collagen gels, 0–40% in each replicate, were self-assembled at the same time to allow comparison across them. The individual replicates were self-assembled at separate time points in which slight variations of temperature and pH may have large effects on the fiber length, F/B, and SHG intensity of the self-assembled gel, but does not affect the polarization analyses. For all measurements, each gel was imaged in three separate locations to provide the average and standard deviation of each parameter. To account for the differences in absolute values between runs, these comparisons were performed with nonparametric Friedman’s two-way analysis in which the individual collagen gels were ranked, to allow comparison. Ranks are statistically significant (p < 0.05) when there are no overlapping letters in the rank assignment. Repeated measure analyses of variance followed by least-sum difference (LSD) mean separation tests with an α = 0.05 level were used to investigate the significance of the anisotropy and peptide pitch angle. All of the analysis employed a randomized complete block statistical design to account for the variability between different experimental runs.

Theoretical Models of SHG Polarization

To analyze the SHG polarization intensity response, i.e., the intensity as a function of polarization angle, a combination of the single-axis molecular model (16,18) and a pixel-based generic model developed by Duboisset et al. (20) were used. The former analysis relies on aligning the polarization with respect to a physical fiber axis, and can be used to extract the dipole moment with respect to the physical molecular axis, which physically corresponds to the α-pitch angle. Su et al. (18) recently revised the model to include the second-order susceptibility contribution from the methylene groups such as C-H groups in the side chain of the collagen molecule in addition to peptide groups (single axis) such as C=O and N-H groups in the backbone. The latter model is a pixel-based approach analyzing the contribution of the dipole moments within the focal volume, and does not assume aligned fibers a priori.

Single-axis molecular model

The salient features of the single-axis molecular model are reproduced here and the definition of the coordinates is shown in Fig. S1 a in the Supporting Material. We previously derived the contributing matrix elements of the molecular hyperpolarizability and related these to the corresponding elements of bulk second-order nonlinear susceptibility χ⁽²⁾ and showed how the polarization dependence can be used to extract the α-helical pitch angle (16). The SHG intensity arises from the second-order polarization P⁽²⁾,

$${\mathbf{P}}^{\left(2\right)}={\chi }^{\left(2\right)}\ast \mathbf{E}\ast \mathbf{E},$$ (1)

where P⁽²⁾ is the second-order polarization, E is the electric field vector, and χ⁽²⁾ is the nonlinear susceptibility tensor. The relationship between the bulk susceptibility in the macroscopic coordinates (X, Y, and Z axes) and molecular hyperpolarizability β_ijk in the distribution of molecular axes x, y, and z axes is given by

$${\chi }_{IJK}^{\left(2\right)}=\sum _{ijk}\cos {\theta }_{Ii}\cos {\theta }_{Jj}\cos {\theta }_{Kk}{\beta }_{ijk},$$ (2)

where the angle brackets signify angular averaging over a molecule. Using the simplifying assumptions of the single molecular axis model (i.e., a single axis of hyperpolarizability, β_zzz = β) as the only nonvanishing component, and employing negligible nonlinear coupling in the laser propagation direction with cylindrical, symmetrical, and Kleinman symmetry, we can represent the second-order polarization as

$${\mathbf{P}}^{\left(2\right)}=\left({\chi }_{ZZZ}^{\left(2\right)}-3{\chi }_{ZXX}^{\left(2\right)}\right)\mathit{z}{\left(\mathit{z}\cdot \mathbf{E}\right)}^2+{\chi }_{ZXX}^{\left(2\right)}\mathit{z}\left(\mathbf{E}\cdot \mathbf{E}\right)+2{\chi }_{ZXX}^{\left(2\right)}\mathbf{E}\left(\mathit{z}\cdot \mathbf{E}\right),$$ (3)

where z is the unit vector of Z axis and E is the electric field vector of the incident laser.

Herein, we assume the molecules are well aligned within the point-spread function (PSF) and that the SHG intensity is proportional to the square of the second-order polarization expressed by

$$I_{\text{SHG}}\left(\text{Θ}\right)={\left|N{\mathbf{P}}^{\left(2\right)}\right|}^2=a\left\{{\left({\sin }^2\text{Θ}+b{\cos }^2\text{Θ}\right)}^2+c^2{\sin }^2\text{Θ}{\cos }^2\text{Θ}\right\},$$ (4)

where N is the number density of the elemental dipoles and the three parameters a, b, and c are numerical coefficients. For either off-resonant Kleinman symmetry or single-axis molecules arranged with cylindrical symmetry, those parameters have the following relationship:

$$a=N{\chi }_{ZXX}^{\left(2\right)},b={\chi }_{ZZZ}^{\left(2\right)}/{\chi }_{ZXX}^{\left(2\right)},\text{and }c=2.$$ (5)

The triple helical structure of collagen is essentially a cylindrical array of polypeptide coils where each individual α-helix has a peptide pitch angle θ_p that can be obtained by a ratio of the tensor elements. The relationship is expressed as

$${\theta }_p={\tan }^{-1}\sqrt{2/b}={\tan }^{-1}\sqrt{2/\left({\chi }_{ZZZ}^{\left(2\right)}/{\chi }_{ZXX}^{\left(2\right)}\right)}.$$ (6)

We used this analysis previously for tendon and myofibrils and obtained pitch angles in good agreement with the structural biology literature (16). However, the model is limited by its assumptions of the polarization being well aligned with the fibrillar axis. Therefore, a different analysis for the more randomly arranged collagen in self-assembled collagen gels or tissues must be performed that results in the correct pitch angle.

The generic model

Recently, Duboisset et al. (20) developed a generic model to quantify the distribution of the dipoles within the PSF. This model is more appropriate than the molecular model for randomly arranged collagen fibers, most likely due to minimization of the error from molecules that are not well aligned within the PSF. To describe and quantify the second-order polarization in the focal volume, the distribution function f(Ω) of the N number density molecules in the macroscopic coordinates (X, Y, and Z axes) is represented as

$${\mathbf{P}}^{\left(2\right)}=N\int \left[{\chi }^{\left(2\right)}\ast \mathbf{E}\ast \mathbf{E}\right]f\left(\text{Ω}\right)d\text{Ω}\text{.}$$ (7)

Equation 7 indicates that the second-order polarization is possible from all molecules aligned in all directions even with the same molecular hyperpolarizability. To derive the second-order polarization for a single-axis molecule, the same assumptions were made as in the previous section: β_zzz = β, a negligible nonlinear coupling on the laser propagation direction, and cylindrical symmetry. The coordinate system is defined in Fig. S1 b. The Euler angles are set to Ω = (θ,ψ,ϕ) to describe the molecular direction within the distribution function. By assuming a symmetric distribution of dipole moments along the major fibril axis within the PSF as an equivalent fiber axis, the model is reduced from three- to two-dimensional in the XZ plane, only requiring two angles Ω = (θ,ϕ) to define the distribution function f(Ω) orientation.

Describing the generic model in the two-dimensional plane, the distribution function of dipoles projects to the XZ plane, where the electric field vector E from the incident linear polarization is at an angle θ relative with the Z axis and propagates in the Y direction. The equivalent polarization becomes

$${\mathbf{P}}^{\left(2\right)}=\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\pi }{\int }}\left(\left[{\chi }^{\left(2\right)}\ast \mathbf{E}\ast \mathbf{E}\right]\left[f\left(\theta ,\phi \right)\text{sin}\phi \right]\right)d\phi d\theta =N\beta \underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\pi }{\int }}\mathbf{T}\left(\theta \right)\xi \left(\theta ,\phi \right)d\phi d\theta .$$ (8)

The terms in the integration can be expressed by two functions; a vector function T(θ) and a scale function (θ,φ). For simplicity, the equivalent second-order polarization can be rewritten as

$${\mathbf{P}}^{\left(2\right)}=N\beta \underset{0}{\overset{2\pi }{\int }}\mathbf{T}\left(\theta \right)\left(\underset{0}{\overset{\pi }{\int }}\xi \left(\theta ,\phi \right)d\phi \right)d\theta =N\beta \underset{0}{\overset{2\pi }{\int }}\mathbf{T}\left(\theta \right)\rho \left(\theta \right)d\theta =N\beta \underset{0}{\overset{2\pi }{\int }}\mathbf{\Gamma }\left(\theta \right)d\theta ,$$ (9)

where the vector function T(θ) is the partial of coordination transformation terms and only depends on θ and the direction of a vector, V = (χ^{(2) ∗} E ^∗ E); and ρ(θ) is an unknown scale function and involves the distribution function to quantify the alignment of molecules in the PSF. We expand this unknown function into sine and cosine functions:

$$\begin{array}{c}\rho \left(\theta \right)=a_0+a_1\cos \left(\theta -{\theta }_o\right)+\sum _{n=2}^{\infty }\left\{a_n\cos \left[n\left(\theta -{\theta }_o\right)\right]+b_n\sin \left[n\left(\theta -{\theta }_o\right)\right]\right\}\\ \approx a_1\cos \left(\theta -{\theta }_o\right)+a_3\cos \left[3\left(\theta -{\theta }_o\right)\right]+b_3\sin \left[3\left(\theta -{\theta }_o\right)\right].\end{array}$$ (10)

Therefore, substituting ρ(θ) into Eq. 9 (where the SHG intensity is proportional to the square of the second-order polarization) can be expressed as

$$I_{\text{SHG}}\left(\theta ,{\theta }_o,r,p,q\right)={\left|{\mathbf{P}}^{\left(2\right)}\right|}^2=r\left\{\left(5+p^2+q^2\right)+4\left(1+p\right)\cos 2\left(\theta -{\theta }_o\right)+2p\cos 4\left(\theta -{\theta }_o\right)+4q\sin 2\left(\theta -{\theta }_o\right)+2q\sin 4\left(\theta -{\theta }_o\right)\right\},$$ (11)

where θ is the polarization angle of the incident electric field vector E; θ_o is the equivalent orientation angle from the distribution function expansion; and r, p, and q are three numerical coefficients, which depend upon the molecular type and alignment state.

Note that for reconstruction polarization response, we match the coordination of the excitation and collection with an equivalent collagen fiber orientation. We then rewrite Eq. 11 as

$$I_{\text{SHG}}\left(\text{Θ},p,q\right)=r\left\{\left(5+p^2+q^2\right)+4\left(1+p\right)\cos 2\text{Θ}+2p\cos 4\text{Θ}+4q\sin 2\text{Θ}+2q\sin 4\text{Θ}\right\},$$ (12)

where Θ is the excitation angle related to an equivalent collagen fiber and r is a constant. The parameters p and q are experimentally determined from Eq. 11 and the polarization response is obtained by normalization of the SHG intensity. In Polarization-Resolved Analysis, we will use this pixel-based model to reconstruct the single molecular axis model to extract the next helical pitch angle within mixed Col I/III gels.

Results

SHG intensity, morphology, and forward-backward analysis

Fiber morphology

We compared the fiber morphology and SHG intensity across a range of Col I/III incorporations. Absolute values between experiments differ because the degree of collagen polymerization typically differs between syntheses and because fibrillar size and density are known to be highly sensitive to the temperature and reaction (24). All collagen gels within a single experiment were synthesized at the same time in a multiwell plate to minimize these effects and permit self-consistent comparison between gels of differing Col III composition.

Fig. 1 shows single optical sections of forward-detected SHG images over a range of 0–40% Col III, with the balance being Col I. Higher Col III concentrations resulted in unstable gels. Note that the image intensities shown in Fig. 1 are the raw intensities, and the inset in Fig. 1 f (40% Col III) is contrast-stretched for viewing purposes to show the difference in fiber morphology. The images indicate that shorter and more randomly arranged collagen fibers occur as the percentage of Col III increased. The shorter and randomly arranged collagen fiber/fibrils will also result in less efficient SHG conversion efficiency, which depends on the combined effects of the concentration (squared) and organization. For example, in this series, the SHG intensity from the 100% Col I gel was ∼5.5-fold stronger than for 60% Col I/40% Col III gel, indicating that the Col III incorporation into fibrils results in less organized structures. The relative intensities over the range of 0–40% Col III for three runs are delineated in Table 1, where the relative intensities are normalized volumetric determinations (over three-dimensional image stack). Using ranks, the 0% Col III collagen gels are distinguishable from 20 and 40% Col III; however, we are unable to distinguish the intermediate Col III gels from each other by the use of volumetric SHG intensity.

Figure 1.

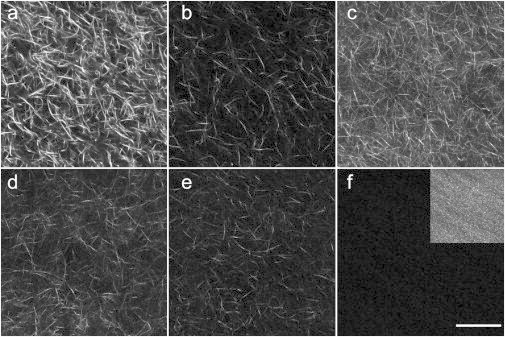
Single SHG optical sections of Col I/Col III gels, increasing from 0, 5, 10, 15, 20, and 40% Col III with the balance of Col I (a–f). The raw intensities are shown, which decrease with increasing Col III content. (Inset, panel f) For viewing purposes, the contrast for 40% Col III was stretched. Scale bar = 50 μm.

Table 1.

Average volumetric SHG intensity, fiber length, and F_SHG/B_SHG values of three experimental gel replicates

Collagen III	0%	5%	10%	15%	20%	40%
Volume intensity	323 (180, 524, 266)	185 (130, 106, 319)	258 (84, 534, 155)	145 (50, 354, 30)	116 (88, 154, 106)	41 (37, 64, 22)
Volume intensity rank	A	AB	AB	AB	BC	C
Fiber length (μm)	22 (26, 20, 20)	20 (23, 16, 21)	18 (19, 15, 19)	18 (19, 16, 19)	17 (15, ND, 18)	ND
Fiber length rank	A	AB	B	BC	C	ND
FSHG/BSHG	6.4 (4.2, 8.5, 6.6)	4.3 (3.6, 3.2, 6)	3.7 (2.5, 3.6, 5.1)	3.5 (2.1, 3.7, 4.6)	3.1 (1.9, 3.4, 3.9)	1.7 (1.8, 1.6, 1.7)
FSHG/BSHG rank	A	B	B	BC	CD	D

Individual replicate values are listed in parentheses. Letter combinations of A, B, C, and D represent the ranks used in the nonparametric Friedman’s two-way analysis, where nonoverlapping letter combinations signify p < 0.05 significance. ND = not determined.

Fiber lengths were next determined in six optical sections taken from the middle region of the three-dimensional image stack using FIRE, a software program that segments individual fibers, affording measurement of their respective lengths (25). It was not possible to uniquely identify individual fibers for all the 20 and 40% Col III gels as they become both too short and weak in intensity. The average fiber length from all the replicates is found in Table 1 where the values in parentheses indicate fiber length from each individual replicate. Overall, the fiber length decreases with increased Col III concentration, where statistically 0% Col III is (p < 0.05) different from 10, 15, and 20% Col III. We are also able to distinguish the difference (p < 0.05) between 10 and 20% Col III by using this metric.

SHG emission directionality

To compare the fibril assembly in these mixtures of Col I/III gels, we next extracted the emission directionality, F_SHG/B_SHG. We have previously shown this parameter arises from the fibril diameter, packing density, and relative regularity on the size scale relative to λ_SHG in the axial direction (13). Large fibrils or fibrils packed on the order of λ_SHG result in primarily forward-directed SHG whereas small fibrils of ∼λ_SHG/10 result in equal forward and backward emission. The measured depth dependence of the measured SHG forward/backward ratio (F/B) is a coupled effect of F_SHG/B_SHG, and subsequent SHG propagation through the tissue based on bulk optical properties at λ_SHG (26). In general, in the presence of multiple scattering, Monte Carlo simulations are needed to decouple these processes because the detected photons are experimentally indistinguishable from each other. The largest increase in F/B from ∼3–5 for Col I in Fig. 2 a would result from approximately one scattering event over this thickness (based on simulations, not shown). In this scenario of weak scattering, we have demonstrated through simulations (not shown) that the 50% point corresponds to the emitted F_SHG/B_SHG. We use that point in this analysis for all the gels. In the limit of no scattering, the measured F/B has little depth dependence and is similar to F_SHG/B_SHG. We note that the relevant parameter is not the physical thickness but the number of scattering lengths contained within the physical thickness. The gels of higher Col III are less scattering, as made evident by the near-zero slopes of their F/B depth-dependent responses. (We note the initial rapid rise at 0-μm depth is an artifact of the PSF of the microscope at the surface, and is always observed in these measurements; therefore this region is not included in the analysis.)

Figure 2.

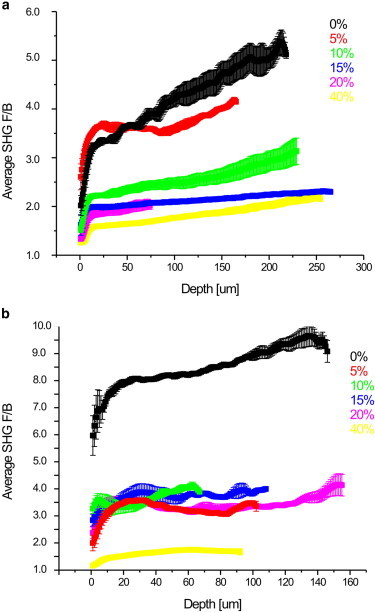
Forward/backward ratios (a and b) as a function of depth for the series of Col I/III gels. After thresholding, the intensities were integrated over the field of view for three series of experiments. The overall trend is that the F/B ratio decreases with increasing Col III content. The statistical analysis is in Table 1. To see this figure in color, go online.

The axially dependent F/B data from three series of gels (same as used for intensity and fiber length measurements) are shown in Fig. 2, a–c. The three runs had different absolute values due to differing extent of polymerization resulting in different thicknesses and resulting different absolute F/B values. Specifically, because the gels were created from the same initial concentrations, the thinner gels are expected to have higher F/B values because the density within each focal volume is higher, leading to more forward-directed emission.

Averaged F_SHG/B_SHG values from the three replicates are in Table 1 where the values in parenthesis are the F_SHG/B_SHG value for each gel within the replicates. Using the Friedman two-way analysis test we are able to statistically (p < 0.05) differentiate 0% Col III from 15, 20, and 40%. Although intermediate Col III percentages (5, 10, 15%) are not distinguishable from each other, we are able to distinguish 5% from 20 and 40% Col III; 10% from 20 and 40% Col III; and 15% from 40% Col III.

We previously developed a heuristic phasematching model to predict trends in the forward and backward propensities and relative SHG intensities as a function of fibril size and packing relative to λ_SHG (13). This built upon a treatment by Mertz and Moreaux (27) showing that axial momentum from a lattice was necessary to produce backward-directed SHG to conserve momentum between the laser and SHG waves Δk = k_2ω – 2k_ω. Thus, nonzero values of the phase mismatch Δk are necessary to satisfy this condition. Moreover, higher values of this mismatch result in decreased SHG intensity, which scales as a sync function of Δk (28). In our treatment, we further suggested that decreased phasematching (and lower F/B) was associated with increased randomness in biological tissues. Thus the small F/B values (∼1) for the more randomly organized 40% Col III gels are consistent with fibrils and their packing being of a size scale much smaller than λ_SHG (in the axial direction). Based on these phasematching considerations, taken together, the values of the SHG intensity and the F/B ratio indicate that increased Col III content results in smaller, more randomly assembled fibrils.

Polarization-resolved analysis

Validation of polarization control

Most polarization-dependent measurements have been performed by either rotating a half-wave plate (mechanically or electrooptically) outside the microscope or mechanically in the infinity space, or alternatively, by fixing the linear polarization and rotating the specimen. To increase the speed and accuracy of the polarization control, we used a liquid-crystal modulator in the infinity space that is under electronic control. Unlike rotation with a half-wave plate, the response of the liquid-crystal modulator is nonlinear and the polarization state needs to be determined. Here we used the Stokes vector formalism to determine the polarization purity at the focus and a lookup table was created for the required voltage to achieve smooth 180° of rotation. Through this approach, we obtained the same polarization-dependent response for rat tail tendon as is achieved with either sample or laser polarization rotation. Moreover, two-photon excited fluorescence of dye-labeled vesicles images displayed the appropriate polarization response for both linear and circularly polarized excitation (17).

The pixel analysis by Duboisset et al. (20), described in The Generic Model, did not use polarization analysis of the signal. Here we probed the SHG intensity dependence on the laser polarization as well as the SHG signal anisotropy by using the same data set of combinations of laser/signal polarizations. To validate our modified treatment, we first verified that the same p and q parameters (Eq. 11) are obtained without polarization analysis, then used analysis when the latter is properly reconstructed to reproduce the former.

The data and analysis flow is shown in Fig. 3. The SHG array, S_A, of each individual pixel is created from raw data from 324 images (M1, 18 excitation × 18 collection angles). We set the threshold to 1000 grayscale units (in 12-bit range of 2048) to distinguish background from true signal intensity, I_sum, summed from the 324 SHG signals in S_A. The Malus law is then used to obtain the total SHG intensity response, I_t(θ_ex) = I_x + I_z, based on the generic model assumption (described in The Generic Model), determined from the measured intensity, S_A, with a Glan-Laser Polarizer (ThorLabs) as an analyzer, as follows:

$$S_A\left({\theta }_{\text{ex}},{\theta }_{\text{co}}\right)=I_x\left({\theta }_{\text{ex}}\right){\cos }^2{\theta }_{\text{co}}+I_z\left({\theta }_{\text{ex}}\right){\cos }^2\left(90-{\theta }_{\text{co}}\right).$$ (13)

For our experiments, the total SHG intensity response can be represented by

$$I_t\left({\theta }_{\text{ex}}\right)=\left(\sum _{{\theta }_{\text{co}}=0}^{{\theta }_{\text{co}}=170}{S}_A\left({\theta }_{\text{ex}},{\theta }_{\text{co}}\right)\right)/\left(\sum _{{\theta }_{\text{co}}=0}^{{\theta }_{\text{co}}=170}{\cos }^2{\theta }_{\text{co}}\right).$$ (14)

The minimum mean-square error was used for fitting the generic model (Eq. 11), with total SHG intensity response used to quantify the dipole distribution of each pixel within the PSF. The parameters r, p, and q and the equivalent fiber orientation, θ_o are recorded on each map from this analysis. The normalized amplitude, r, was set to 1, and the resulting Gaussian distributions of p and q values with and without signal polarization analysis were similar (p = −0.585 vs. −0.590, respectively, and q = 0.01 in both cases).

Figure 3.

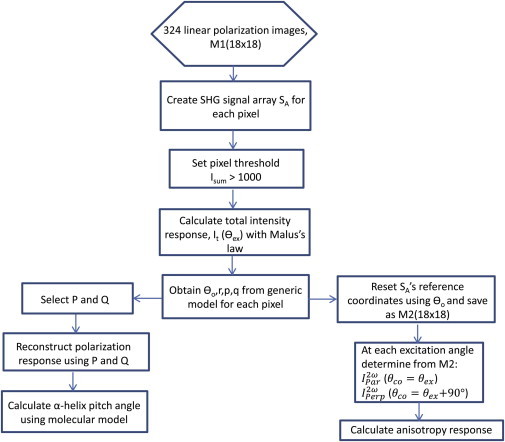
Flowchart of the processes used to extract the α-helix pitch angle and SHG polarization anisotropy, beginning with 324 images of 18 × 18 polarization excitation and collection angles. To see this figure in color, go online.

Polarization analysis of mixed Col I/III gels

Using the same range of Col I/III concentrations as in the morphological and F/B analysis, we used the pixel-based polarization analysis summarized in The Generic Model (20). The p and q parameters were obtained by fitting to Eq. 11 and representative experimental pixel maps, and resulting histograms obtained from 100% Col I and 60/40% Col I/III gels are shown in Fig. 4. The results show the mostly likely values of the respective p coefficients are −0.590 and −0.690. For both gels, the values of q were centered near 0 (0.01 vs. 0.05) and have little influence on the subsequent analysis. Analogous maps were created for the other mixtures.

Figure 4.

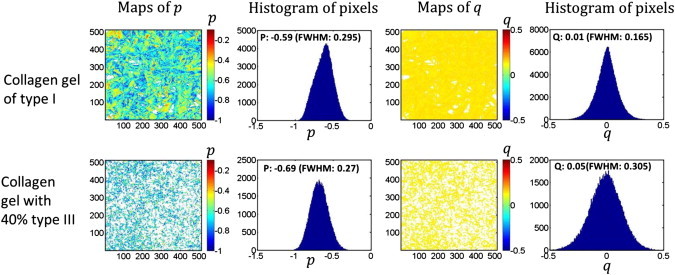
Pixel maps of the p and q parameters (obtained by Eq. 11) for 100% Col I (top panel) and 60% Col I/40% Col III (bottom panel) along with the resulting histograms of the distribution. To see this figure in color, go online.

We can now use the p and q parameters to reconstruct the SHG polarization dependence previously used in the single-axis model, which required a predominant fiber axis (e.g., tendon or muscle) (16). The SHG polarization intensity response is now reconstructed from the generic model (Eq. 12) using the most probable occurring numerical coefficients, P and Q from the p and q histograms (using normalized amplitude r = 1). Fig. 5 shows the normalized SHG polarization response based on experimental P and Q data where there is an 11.7% (0.81–0.69) and 4.0% (0.39–0.43) intensity difference between 0 and 40% Col III at 0 and 90° excitation, respectively. The relative maximum intensity was near 40° for all the gel mixtures. We note that the response for Col I is very similar in terms of the location and relative intensities of the maxima and minima (and extracted pitch angle) to that previously obtained from tendon using the single-axis model (16,19,29).

Figure 5.

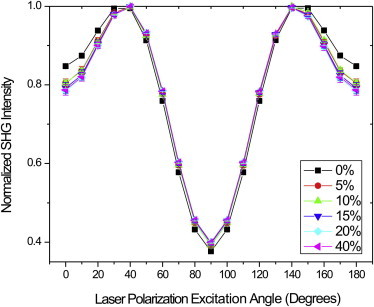
Using the most probable P and Q values, SHG polarization responses are reconstructed by Eq. 12 for mixed different percentage type-III collagen gels. The result for 100% Col I is nearly identical to that previously obtained by the single-axis molecular model. To see this figure in color, go online.

Based on the SHG polarization response in Fig. 5, the effective peptide pitch angle in each mixture was deduced by fitting to the single-axis molecular model (Eq. 4) and the results are presented in Table 2 with standard deviations. The extracted Col I collagen peptide pitch angle is 49.11°, and is similar to our previous result on tendon of 49° (16), which was obtained with fewer data points. There is a 0.95° difference (from 49.11 to 50.06) between 0 and 40% Col III. All the peptide pitch angles for each gel mixture and measurement were combined and analyzed via a repeated measure analysis of variance followed by an LSD test to determine mean separation at the α = 0.05 level. The pure Col I gels were different from gels composed of 15, 20, and 40% Col III with an LSD of 0.52°. All the mixtures of Col III gels were statistically indistinguishable at the α = 0.05 level. The sensitivity of the pitch angle measurement was assessed using the full width at half-maximum (FWHM) values of p and q (P_FWHM, Q_FWHM) to reconstruct the modeled generic polarization response (Eq. 12) that was fitted using the molecular model polarization response. There was no statistical significance at the α = 0.05 level in a randomized complete block statistical design between experimental runs, therefore the LSD angle of 0.52° demonstrates the sensitivity of the peptide pitch angle measurement.

Table 2.

Effective peptide pitch angle of Col I/Col III gels

Collagen III	0%	5%	10%	15%	20%	40%
Pitch angle	49.11(0.15)a	49.77(0.22)	49.82(0.17)a	49.96(0.37)a	50.11(0.15)a	50.06(0.32)a

Standard deviations are in parentheses.

^ap < 0.01 between gels.

Ultrastructural data on the full-length collagen isoforms (including Col I) is limited and pitch angles are largely derived from peptides comprised of similar sequences. Using the Protein Data Bank (PDB) as a reference, the collagen-like peptide pitch angle of Col I (PDB:1ITT, GPPGPPG) and Col III (PDB:1BKV, PPGPPGPPGITGARGLAGPPGPPGPPGPPG) molecules are 46.43 and 48.19°, respectively, as determined from x-ray diffraction data (30). Our results on the limiting cases of 0 and 40% Col III were different by 0.95° and thus lie between the peptide data for the pure Col I and III cases. Note that we do not know the actual incorporation of the two isoforms into fibrils because we have been unable to locate a Col III-specific antibody that has no crosstalk with Col I.

SHG signal anisotropy

We next determined the SHG signal anisotropy within fibers in the Col I/III gels. This anisotropy parameter, β, is reflective of the alignment of dipole moments within the measured area and is expressed as

$$\beta =\frac{I_{\text{Par}}^{2\omega }-I_{\text{Perp}}^{2\omega }}{I_{\text{Par}}^{2\omega }+2I_{\text{Perp}}^{2\omega }}.$$ (15)

The limiting cases are 1 and 0, representing perfectly aligned and totally random structures, respectively. (We note that this use of β is unrelated to that defining the matrix elements of the hyperpolarizability tensor.) This parameter is most often determined relative to a predominant fiber axis and is most easily applied to well-aligned fibrillar specimens such as tendon. However, for the gels used here, especially at higher Col III incorporation, well-aligned, distinct fibers are not present and a pixel-based approach must be used. We again use the SHG single array S_A (see Fiber Morphology and Fig. 3) and shift the reference coordinate of excitation and collection angles to match the equivalent fiber orientation, θ_o, which is recorded into a new reference coordinate image matrix, M2 (18 × 18). Based on this matrix we can plot the parallel $\left(I_{\text{Par}}^{2\omega }\right)$ and perpendicular $\left(I_{\text{Perp}}^{2\omega }\right)$ SHG intensity polarization response, using the average SHG intensity in the M2 matrix at the θ and θ + 90° collection angles where θ is the polarization of the excitation angle, and then repeat the process across the range of 0–180° of excitation.

The resulting anisotropy response for mixed Col I/III gels with Col III content of 0–40% with respect to the excitation angle is shown in Fig. 6. The anisotropy of the pure Col I gel is 0.79 and 0.02 at 0 and 90° excitation, respectively. The former is similar to values we previously reported for collagen in well-aligned specimens, where the analysis was performed on a fiber-by-fiber basis (17), where this process is equivalent to the pixel-based measurement with 0° excitation. Thus, this similarity in β serves to benchmark the method.

Figure 6.

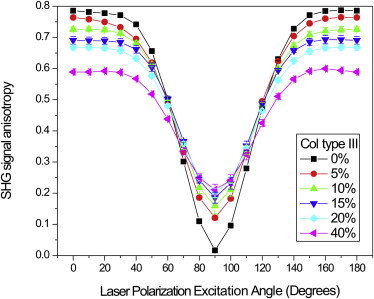
Pixel-based SHG anisotropy responses are determined by using θ_o (Eq. 11) to create a transformed image matrix, M2, of equivalent fiber axes and then calculating β every 10°. The result for 100% Col I is nearly identical to that previously obtained by performing the anisotropy on a fiber-by-fiber basis. To see this figure in color, go online.

The large and small β-values for 0 and 90° excitation, respectively, are consistent with the dipole moments within the Col fibers in the PSF being well aligned. We now compare the results with the mixed gels (Fig. 6). The differences between 0, 15, 20, and 40% Col III gels are significant at p < 0.01 for excitation angles 0–50 and 80–100, and 130–180°. The anisotropy at 0° smoothly decreases with increasing Col III to the limiting case for 40% of β = 0.59. The anisotropy at 90° has the reverse trend where β increases from 0.02 to 0.21 for 0 and 40% Col III gels. This suggests that the dipole moments within the measured volume become less aligned upon incorporation of Col III within Col I fibers.

Discussion

There has been considerable interest in using SHG polarization-resolved techniques to extract details on the molecular organization of protein molecules in connective tissues. This is possible because the second-order tensor contains 27 matrix elements that can be exploited to extract different properties. In 1986, Freund et al. (31) first used this SHG polarization analysis to study connective tissue polarity, and while that work was at lower resolution (∼50 μm), it showed the viability of the approach. Stoller et al. (32) later used polarization modulation in one of the first efforts to characterize the second-order response in tendon at high resolution. Chu et al. (33) further investigated this problem on the related muscle tissue, and showed which approximations (e.g., Kleinman’s symmetry) could be utilized to reduce the number of nonvanishing matrix to four, two of which are degenerate. Based on these efforts combined with the identification of the peptide group being the active harmonophore on peptide surfaces by Mitchell et al. (34), we and others then used this formalism to show that the single-axis model could be used to extract the helical pitch angle in tissues, with consistent results being found between these experiments (16,18,19,35,36) and also in the structural biology literature (37). More recently, Tuer et al. (38) implemented polarization-in/polarization-out, or PIPO, and showed that different matrix elements were associated with different parts of the collagen molecule.

Despite these efforts in understanding the underlying physics, applications using the inherent richness of polarization-resolved SHG have not rapidly emerged. Su et al. (18) demonstrated that the pitch angles of Col I and II could be differentiated by an improved single-axis model in the same and different tissues. However, this analysis still relied on segmentation techniques to spatially delineate regions containing the two isoforms, where this was readily achieved because the respective fibrillar structures are substantially different in appearance. As a step forward, Rouède et al. (39) recently used SHG polarization analysis to differentiate the sarcomere structure in normal mouse tissue and the mdx model of muscular dystrophy.

To the best of our knowledge, this report is the first demonstration of a polarization SHG technique that is able to differentiate collagen isoforms within the same pixel and fibril (see below for further discussion). Most of the previous polarization analysis techniques relied on having a predominant fiber axis; however, that condition does not hold for collagen gels, especially at higher Col III concentrations (see Table 1). In this case a pixel-based approach is necessary, and we implemented a combination of the single-axis molecular model (16,18) and the recent generic model (20) to achieve the extraction of the α-helix pitch angle. For the case of 100% Col I, our reconstruction resulted in the same pitch angle as we obtained in tendon using the single-axis model (16); this method seems robust. Upon extracting the pixel equivalent of a fiber angle and subsequent transformation of coordinates (from the same 361-image data sets), this approach also afforded extracting pixel-based SHG signal anisotropy, to our knowledge, for the first time. We previously needed to perform this analysis on a fiber-by-fiber basis. This analysis is also robust, because the obtained anisotropy for 100% Col I gel was similar to that obtained previously for tendon and fish scales, both of which are comprised of essentially all Col I (15,17).

Although we established the pixel-based method to separate different isoforms in fibrillar gels, the method has potential applications in studying several disease states. This is because minor isoforms that become upregulated in diseased states are not necessarily spatially separated from Col I. For example, Col V is upregulated (up to 20% total collagen content) in invasive breast carcinoma (4), where this normally minor isoform comingles within Col I in fibrils and limits the resulting diameter (6). This analysis has implications with respect to ovarian cancer, because it affords fresh insight into structural changes in the stroma that occur in malignancy. It has been reported that Col III can increase in ovarian cancer but also that it might turn-over faster than in normal tissue (5). The polarization methods (also in conjunction with other SHG metrics) may allow specific probing of this evolution, especially in animal models.

This work is also relevant in terms of structural biology, because although it has been suggested that Col I/III comingle within fibrils, to our knowledge a specific model of the resulting structure has not been presented in the literature. All of the data and analysis presented here indicates that within these fibrillar gels the two isoforms are indeed comingled within the same fibrils. For example, we observed a smooth decrease in fiber length with increasing Col III content, instead of modal distributions. Collectively, the data also shows that Col III incorporation results in decreased fibrillar organization. Specifically, increased Col III content resulted in lower SHG intensity, lower F_SHG/B_SHG ratios (see Table 1), and lower SHG signal anisotropy, all of which are signatures of less-ordered structure. These findings are consistent with Cameron et al. (7), who, based on x-ray data, suggested that the positions of the Col I and III molecules within fibrils could be random. Although we did not use polarization analyses in our previous work on the effect of Col V incorporation into Col I gels, we also observed more disorder with increased concentration of the former. In that system we had the benefit that structural aspects of Col I/V interactions had been documented with a conclusive structural model showing how Col V limited fibril growth (40).

We do not yet know the extent to which different collagen isoforms can be differentiated based on polarization-resolved SHG. For example, our results on Col V have been inconclusive. However, we do have sufficient sensitivity to delineate the relatively small change in pitch angle between Col I and III (∼1.8°). This may have implications beyond ovarian cancer. For example, there is a dynamic change in the Col I and III balance in connective tissue (e.g., skin) during development and also during wound healing (8,41–43). The approaches here would be applicable for such studies. The pixel-based anisotropy may also be useful for probing structure in diseased states such as Osteogenesis imperfecta, which is characterized by misfolded collagen I. We previously showed that SHG-CD could delineate normal and skin with this pathology (44), but existing anisotropy methods provided inconsistent results due to the somewhat random collagen fibrillar structure on skin.

These techniques have yet to be applied to human or animal tissues, but our future plans involve using this technique first in thin histological samples and then in thicker specimens to determine the range over which the methods can be applied. This is an important consideration because multiple scattering events result in a loss of polarization of both the laser and SHG signal. This may not be a strong consideration in ovarian cancer, because the striking changes in morphology occur near the surface of the stroma (3). Still, for ex vivo studies we could use optical clearing to retain the polarization signatures, as we previously demonstrated (45).

Conclusions

Through a combination of metrics we show that SHG microscopy is able to differentiate mixtures of Col I and III within self-assembled gels. This is significant because Col III is upregulated in ovarian cancer and understanding how the Col I/III balance changes in disease may yield insight into carcinogenesis and disease progression. Moreover, the ability to probe the respective content may have eventual diagnostic value. This has been challenging because it is believed that the isoforms comingle in the same fibrils and are not spatially separate. The SHG polarization analyses presented here have sufficient sensitivity to delineate Col I and III based on intrinsic differences in the α-helix pitch angle. The pixel-based analysis further affords extraction of polarization information (input and output) without the previous requirements of predominant fiber alignment, and as a result it should be quite general.

The measurements and analysis here using SHG intensity, emission directionality, and signal anisotropy all suggest that incorporation of Col III results in decreased order of the dipole moments within fibrils and also in terms of fibril size and packing. This conclusion is consistent with a previous x-ray study (7), and suggests this information can be extracted by SHG in tissues. We will use the metrics developed here in the study of ovarian cancer with animal models and ex vivo human tissues to study the compositional changes in the ECM in malignancies. The techniques should also be applicable to other pathologies as well.