Protein Arcs May Form Stable Pores in Lipid Membranes

Abstract

Electron microscopy and atomic force microscopy images of cholesterol-dependent cytolysins and related proteins that form large pores in lipid membranes have revealed the presence of incomplete rings, or arcs. Some evidence indicates that these arcs are inserted into the membrane and induce membrane leakage, but other experiments seem to refute that. Could such pores, only partially lined by protein, be kinetically and thermodynamically stable? How would the lipids be structured in such a pore? Using the antimicrobial peptide protegrin-1 as a model, we test the stability of pores only partially lined by peptide using all-atom molecular dynamics simulations in POPC and POPE/POPG membranes. The data show that, whereas pure lipid pores close rapidly, pores partially lined by protegrin arcs are stable for at least 300 ns. Estimates of the thermodynamic stability of these arcs using line tension data and implicit solvent calculations show that these arcs can be marginally stable in both zwitterionic and anionic membranes. Arcs provide an explanation for the observed ion selectivity in protegrin electrophysiology experiments and could possibly be involved in other membrane permeabilization processes where lipids are thought to participate, such as those induced by antimicrobial peptides and colicins, as well as the Bax apoptotic pore.

Introduction

Toxin pores in lipid membranes are traditionally envisioned as oligomeric barrels in which certain segments from each monomer insert into the membrane and associate with each other to completely line the pore wall. This view has been corroborated by crystal structures of several β-toxins (1,2). However, electron microscopy (3–9) and atomic force microscopy (AFM) (10) images of cholesterol-dependent cytolysins (CDCs) show a large number of incomplete rings, or arcs, sometimes as frequently as complete rings. Similar structures have also been observed for perforin (11,12) and the membrane attack complex of the complement (13,14).

The functional significance of these arcs is a matter of controversy (15). On the one hand, these arcs have been shown to cause ion leakage in membranes (16,17). Based on this, some authors have suggested that pore formation and oligomerization are simultaneous events (16). Other studies, however, support the prepore model, whereby monomers first oligomerize on the membrane surface forming a complete ring before inserting into the membrane (18,19). A conciliating model has been proposed where oligomerization can only take place on the membrane surface before insertion but incomplete rings can also insert into the membrane and form functional pores (20).

If arcs do insert and form pores, this would mean that the part of the pore that is not lined by protein should be a free bilayer edge, most likely bent in a toroidal form (16,21). A free bilayer edge certainly costs free energy, but this cost could in principle be offset by the favorable insertion and oligomerization free energy of the protein arc. Complete rings should have lower free energy, but at low protein concentration formation of a complete ring may not be possible. The question is whether incomplete rings have sufficient thermodynamic and/or kinetic stability inserted into the membrane. The fact that arcs can be observed by electron microscopy and AFM suggests that they are quite stable (22). Alternatively, arcs may only be metastable enough to cause leakage (15,20). This issue could have implications far beyond the field of CDCs. Lipid participation in pores has been invoked in several other cases, such as antimicrobial peptides (23–25), colicins (26), diphtheria toxin (27), and the apoptotic pore of Bax (28) but the precise nature of the pore in these systems is unknown. Phosphatidylserine flip-flop caused by perforin has been suggested as an indication of a toroidal pore (12).

The toxins for which arcs have been identified are large proteins that assemble into pores containing 30–50 subunits (22). Computational studies of arcs made of these toxins would be exceedingly expensive. In addition, their oligomeric structure is unknown, although the pore-forming structure is thought to consist of β-sheets (19). In the course of an implicit-solvent study (29) of β-barrels formed by protegrin-1, an 18-residue β-hairpin antimicrobial peptide stabilized by two disulfide bonds (30,31), we observed self-assembly of the peptides into arcs. We wondered then whether these arcs could be viable and proceeded to test this idea using explicit simulations. Protegrin has been shown to form ion channels in membranes (32,33) and has been the subject of extensive solid-state NMR (34,35) and computational (36) studies. Dozens of analogs have been synthesized and tested for activity (37,38). There is no evidence that protegrin itself forms arcs, but the system is small and simple enough to allow study by molecular dynamics simulations. The simulations show that peptide-arc structures are kinetically stable on a timescale of 300 ns. Further arguments using macroscopic data and implicit solvent calculations suggest marginal thermodynamic stability as well.

Methods

We have run 300-ns explicit simulations of a tetrameric protegrin arc structure obtained from implicit simulations (see the Supporting Material) in a 100% POPC membrane and a 70% POPE: 30% POPG membrane using the program NAMD (39) with the CHARMM36 force field for the peptide (40) and the lipids (41). The equilibrated initial membranes and the membranes with a cylindrical 13 Å pore are the ones used in previous work (29). The 100Å × 100Å × 70Å membrane systems were created and equilibrated using the steps suggested by CHARMM-GUI (42,43). An additional 0.9-ns run was carried out to ensure that equilibration has been achieved. The pore was generated by eliminating the lipids in this region and filling the space with TIP3P water. It was then equilibrated for 1.5 ns in the NPT ensemble while constraining the positions of the lipid headgroups. The temperature of all simulations was 303.15 K, consistent with experimental studies (44–46).

We ran three different simulations for each membrane: a), the pore system in pure membranes with no constraints (the length of these NPT simulations is as long as it takes for the pore to close). These systems consist of 257 lipids, 11,056 water molecules, 28 Cl⁻ ions, and 28 K⁺ ions in the 100% POPC membrane and 191 POPE and 89 POPG lipids, 11,462 water molecules, 24 Cl⁻ ions, and 112 K⁺ ions in the anionic membrane. Although the original membranes were symmetric, the process of creating a pore made the membrane slightly asymmetric. b), 300-ns NPT simulations of the equilibrated cylindrical pores with the protegrin arc inserted into them lining the pore as it does in the implicit simulations. The new systems, with the peptide constrained to its position, are equilibrated for another 2 ns to let the membrane and water molecules adapt to it. The size of these systems is 72 peptide residues, 252 (POPC) or 264 (180 POPE and 84 POPG) lipids, 10,468 or 10,970 water molecules, 52 or 50 Cl⁻ ions, and 28 or 110 K⁺ ions, for the zwitterionic and anionic systems, respectively. c), 300-ns NPT simulations starting from the equilibrated membranes without pores and the protegrin arc structure embedded in them in a transmembrane orientation. The systems are first relaxed using a conjugate gradient minimization and then equilibrated for 4 ns in the NPT ensemble using constraints to fix the position of the peptides so that the membrane can adjust around them. The simulations then continue for 300 ns without any constraints. These systems consist of the peptide arcs (72 residues), 254 (POPC), or 279 (190 POPE and 89 POPG) lipid molecules, 10,372 or 10,698 water molecules, 60 or 47 Cl⁻ ions, and 27 or 112 K⁺ ions, in the zwitterionic and anionic membranes, respectively.

To estimate the size of the pores we calculated the number of water molecules that are close to the membrane center. More precisely, we counted the number of water molecules with a z coordinate ±8.5 Å from the membrane center (the membrane surface being parallel to the xy plane). Because water enters this region only if it is in the pore (the hydrophobic thickness of these membranes is ∼27 Å), this number corresponds to the number of water molecules in the pore. The results obtained for the peptide arc in this work are compared to the 100-ns NCNC parallel β-barrel simulations run in previous work on protegrin (29).

Results

The initial structure of the protegrin arc used in these explicit simulations was obtained by implicit membrane studies of the self-assembly of protegrin monomers in a preformed pore (see the Supporting Material). Most favorable energetically is the tetrameric structure shown in Fig. 1. Unlike the complete β-barrels (29), the peptides exhibit a twist relative to each other. The orientation of each peptide gradually changes from tilting toward the upper leaflet in the leftmost peptide (red in Fig. 1) to tilting toward the lower leaflet in the rightmost peptide (blue). This natural twist cannot be accommodated in a larger arc. Indeed, when six peptides were placed in the same configuration, the final structure was not a continuous arc but a broken one (Fig. S1 B). The structure of Fig. 1 led us to think that closing of the barrel might incur some strain and that protegrin could be an appropriate system to investigate whether pores lined by arcs rather than barrels or unassociated peptides can exist in biological membranes.

Figure 1.

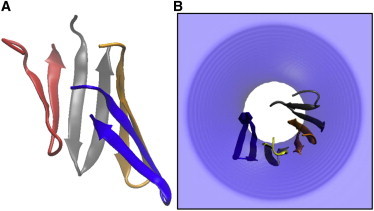
(A) Cartoon representation of the protegrin arc structure obtained in implicit simulations and used as the initial structure in the explicit simulations run in this work. (B) Upper view of the same structure in an implicit pore of R = 13 Å and curvature K = 15 Å. To see this figure in color, go online.

We ran three types of simulations: preformed cylindrical pores in membranes without peptide, the arc structure of Fig. 1 in preformed cylindrical pores, and the same arc structure inserted into membranes without a water pore. Two membrane systems were used, one zwitterionic (100% POPC) and one partially anionic (70% POPE: 30% POPG). To evaluate the size and stability of the pores in these systems, we computed the number of water molecules in the pore as a function of time (Fig. 2). In the absence of peptides the pore closes rapidly: the number of water molecules decreases to zero in ∼30 ns. Very early in the simulations (see 6 ns or 8 ns in Fig. 3 A), the membrane bends and lipid headgroups start to line the pore, which acquires a toroidal shape, as observed previously (47). The headgroup density is lower in the pore than on the membrane surface (48). This pore is smaller than the original cylindrical one and keeps getting narrower with the lipid headgroups gradually returning to the membrane surface (28 or 20 ns snapshots in Fig. 3 A) until the pore closes (30 or 26 ns). In contrast, in the presence of the arcs, regardless of starting conditions, the pores remain open until the end of the simulation.

Figure 2.

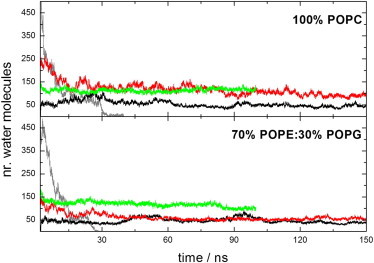
Number of water molecules inside the pore (|z| ≤ 8.5 Å) along the simulation. Green line: octameric protegrin rings inserted into preformed cylindrical pores (29). Red line: tetrameric arc inserted into preformed cylindrical pores. Black line: the same arc inserted into the membrane without a pore. Gray line: preformed pores with no peptide. To see this figure in color, go online.

Figure 3.

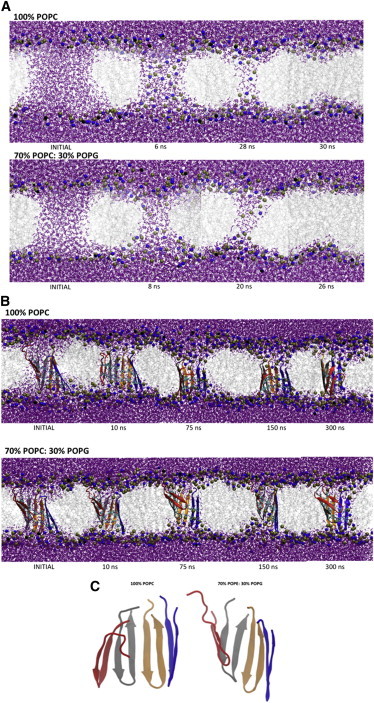
(A) Snapshots along the simulations starting from preformed pores in a zwitterionic and an anionic membrane with no peptide. The INITIAL structures correspond to right before releasing all constraints. Purple balls-and-sticks: water molecules. Silver lines: lipid side chains. Blue and tan spheres: lipid headgroup nitrogen and phosphorus atoms, respectively. (B) Arc pore structures in the membranes starting from a preformed pore. The INITIAL structures correspond to the ones right before releasing all constraints. Purple balls-and-sticks: water molecules. Silver lines: lipid side chains. Blue and tan spheres: lipid headgroup nitrogen and phosphorus atoms, respectively. Cyan licorice: disulphide bridges. Cartoon representations: peptide backbone. (C) Final structure of the peptide in the zwitterionic (left) and anionic (right) membranes (same as in B at 300 ns, eliminating membrane, water, and residue side chains). To see this figure in color, go online.

The complete octameric barrels form very stable pores (29), enclosing 113 ± 8 (zwitterionic membrane) or 119 ± 12 (anionic membrane) water molecules (averages over the entire simulation). The arcs stabilize somewhat smaller pores: 93 ± 15 in the zwitterionic membrane and 58 ± 8 in the anionic membrane (averages over the last 200 ns). This is not surprising: osmotic protection (16) and electrical conductance (22) experiments of CDCs show that the arcs create pores of significantly smaller size than the complete rings. When the arcs are placed in the membranes without preformed pores, we observe rapid insertion of water in the membrane area in the equilibration stage. The resulting pores are smaller than those in the previous simulations, 44 ± 7 water molecules in the zwitterionic membrane and 42 ± 6 in the anionic membrane. The distribution of the number of water molecules inside the pores is shown in Fig. S3. There are also differences in the distribution of water along the pore axis between the two types of simulations (Fig. 3 and Fig. S4 A): it is less evenly distributed in the simulations that start without preformed pores (Fig. S5), presumably due to the limited simulation time. In either case, there is enough water in the pore region to assert that a pore partially lined by a protegrin arc is stable for at least 300 ns.

Fig. 3 B shows snapshots of the simulations of protegrin arcs in preformed cylindrical pores. On the protein side of the pore, the membrane retains a structure similar to that of the complete rings in the same systems (29): the membrane curves slightly to adapt to the size of the arc, but the pore remains essentially cylindrical (or semitoroidal) during the entire simulation. Where there is no peptide the membrane bends and the lipid headgroups line the pore. This is more visible in the POPC membrane. After 10 ns, one or both leaflets of the membranes start to curve. By 75 ns, the lipidic region of the pore has a toroidal structure: the aqueous lumen is lined by lipid headgroups. We observe a similar process in the simulations of the arcs in the membranes with no preformed pores (Fig. S4 A). However, in this case there are fewer headgroups lining the water-lipid interface of the pore and the membrane is less curved. Again, these differences probably reflect a lack of full equilibration. The structure of the pores created by arcs in these simulations (Fig. 3 B) is similar to what has been envisioned by several authors (15,22). The polar surface of the arc is probably what drives water into it, in accord with observations of water defects when arginines are placed in the membrane interior (49,50). The radius along the pore axis is shown in Fig. S6. The average pore radius is equivalent for the zwitterionic and anionic membranes: 6 ± 2 Å and 6 ± 1 Å, respectively. The shape of the pore is irregular, especially in the zwitterionic membrane, but there is enough space for water molecules to circulate through it. The distribution of the center of mass of the arc with respect to the membrane center is shown in Fig. S7.

It is interesting to compare the sequence of events in our simulations of the pores with and without peptide arcs (Fig. 3, A and B). We find that the early events are similar: there is bending of the membrane in both cases. For the arc simulations (Fig. 3 B), this occurs only in the region where there is no peptide. In the simulations with no peptide (Fig. 3 A), this happens all around the pore. With time, this toroidal-like structure of the lipidic part of the pore becomes lined with lipid headgroups. This arrangement is stable for the rest of the simulation when peptides are present. In the absence of peptides, water and lipid headgroups start to retreat toward the membrane surface and the pore closes. It looks like the closing process is the same in both types of simulations, but it is slowed down (and possibly impeded) by the presence of the protein arc. The bending of the membrane is also slowed down by the presence of the arcs: in the pure membrane simulations the pore is completely lined by headgroups at 6–8 ns (Fig. 3 A), whereas it takes longer in the arc simulations (Fig. 3 B).

In all simulations the peptides do not dissociate. We computed the average root mean-square deviation (RMSD) with respect to the starting structure of Fig. 1 over the simulations (excluding the first 50 ns). The values for the arcs in preformed pores were 5.6 ± 0.5 in POPC and 2.8 ± 0.2 in POPE/PG. For the arcs without a preformed pore they were 3.5 ± 0.3 in POPC and 2.6 ± 0.1 in POPE/PG. For the rings they were 2.6 ± 0.1 in POPC and 2.7 ± 0.1 in POPE/PG. The largest RMSD is observed for arcs in the preformed pore in the zwitterionic membrane. Fig. 3 C shows the final structure of the peptide arc in this system, revealing that this high RMSD value is due to the loss of the β-sheet twist. The hairpins orient more perpendicularly to the membrane surface and arrange in a way similar to that in the complete barrel. The same tendency can be observed in the simulations of the arcs in the zwitterionic membrane without the preformed pore (Fig. S4 B). Here, the RMSD value is also slightly higher than the rest, and the final structure is less twisted than the original one. These changes take place in the equilibration phase after releasing the constraints (see snapshots at 2 ns and 10 ns in Fig. 3 B and Fig. S4 A). This rearrangement allows a higher number of water molecules inside the pore than the twisted original structure, which is stable in the anionic membrane. We have not observed any specific interactions of the peptide with the POPC lipids that might explain the different structure obtained with respect to the POPE/POPG membrane. Secondary structure analysis using the COOR SECS command in Charmm revealed a slight reduction in beta content, from 61% initially to ∼50–52% at the end of the simulations.

In a complete β-barrel, all backbone hydrogen bonds are satisfied, providing stability to the structure. In the arc structures, the strands on the edges have backbone polar groups that are not hydrogen bonded to other protein groups. Analysis of the simulations shows that, in most cases, carbonyl and amide groups hydrogen bond to water molecules or, later in the simulation, to ester groups of neighboring lipids. Less frequently, hydrogen bonds are observed between the peptide amides and the oxygen atoms of the phosphate group of the lipids. Thus, the cost of exposing these polar groups is partially alleviated.

As arginines are prominent in the protegrin structure, it is interesting to examine their interactions with lipid headgroups. Looking at the simulation trajectories, we observe that ARG1, ARG4, and ARG10 interact with the pore-lining headgroups. As shown in Fig. S8 C, these residues in the initial structure are either facing toward the pore interior (ARG4) or toward neighboring hairpins (ARG1 and ARG10). The remaining arginines are facing toward the membrane in the initial structure and are located on the arc’s upper and lower boundaries (Fig. S8 D), so that in the pore they interact with the lipid headgroups on the membrane surface. Fig. 4 shows the interactions of these three residues with the lipid headgroups at 300 ns. The interactions with the P atoms lining the pore are highlighted. We observe that these interactions occur mostly with the arginines of the peripheral β-strands (red and blue in the figures). Specifically, ARG4 interacts with the pore-lining P atoms in both the zwitterionic and anionic membrane. Table S3 shows that the Cζ-P distance to the lipid headgroups lining the pore is smaller for the peripheral strands than for the central ones, where ARG4 points toward the pore center (see Fig. 4). Due to the different arc structures in the zwitterionic and anionic membranes, the arginines that interact with the lipid headgroups lining the pore differ. In the POPC membrane, ARG1 of the peripheral hairpins shows a shorter P-Cζ distance with the headgroups in the pore region than the other two monomers (see Table S3). In the POPE/POPG membrane, it is ARG10 that interacts with the lipids lining the pore. Due to the twist of the monomers, in this case it is the leftmost and its neighbor hairpins (red and gray) that produce this interaction. ARG1 and ARG10 in the remaining two monomers mostly interact with the lipid headgroups on the membrane surface (see Fig. 4 and Table S3). It appears that these arginines are contributing to the stabilization of the pore. In addition to the phosphates, arginines were observed to interact strongly with glycerol groups, mostly from the same lipids as the phosphates, but also others.

Figure 4.

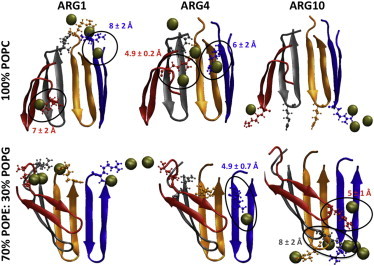
Protegrin arc structures at 300 ns (cartoon representation) of the simulations starting from preformed pores. ARG1, ARG4, and ARG10 are represented by balls-and-sticks. The P atoms of lipid headgroups that are within 7 Å of the arginine side-chain guanidine N atoms are shown using tan-colored spheres. Black circles highlight the interactions between arginines and P headgroup atoms that are lining the pore (|z| ≤ 8.5 Å). In these cases, the average minimum distance between arginine Cζ and pore lining P atoms is indicated (see Table S3). To see this figure in color, go online.

To examine the ability of ions to cross the peptide-stabilized pores, we analyzed the movement of ions across the pore. We first identified the ions that enter the pore region (|z| ≤ 8.5 Å). In Fig. S9 we show several trajectories of Cl⁻ ions in the simulations of the arcs in preformed pores. In the absence of voltage, we do not expect significant ion flow. Indeed, in most cases, they enter the pore region but do not crossover to the other side of the membrane, occasionally spending quite some time in the pore region. The number of ions entering the pore region is higher in the case of POPC membranes, which may be due to the larger pore formed in these membranes. Despite the absence of voltage in our simulations, we observe two events of Cl⁻ ions crossing the zwitterionic membrane (highlighted with a circle in Fig. S9). This further supports the notion that arcs may, indeed, be able to stabilize functional pores. Only one cation was close to the pore center in one simulation and it did not cross to the other side. Detailed analysis of ion conductance will be the subject of future work.

Discussion

The explicit simulation results show that protegrin arcs are kinetically stable. That is, once they are placed in an inserted configuration, they remain there for at least 300 ns. However, starting from free monomers in solution, will they insert? In other words, are the arcs thermodynamically stable? This question cannot be answered with explicit simulations, at least not with our available resources. However, an approximate estimate can be made using macroscopic line tension data and implicit solvent simulations. The free energy of the inserted arc is equal to the free energy of forming the pore in the pure membrane plus the free energy of transfer of the peptides from the flat membrane to the preformed pore. The former is estimated as 2πRγ, where γ is the line tension, and the latter from implicit solvent simulations. The line tension has been measured as 7 pN for PC (51) and 6 pN for PS membranes (52). This gives a free energy of forming an R = 13 Å pore equal to ∼7 to 8 kcal/mol for both membranes. Other measurements of the line tension give higher estimates (53). The effective energy change upon transfer of four associated protegrin monomers from water to the pore estimated using the IMM1 model (see the Supporting Material) is about −13 kcal/mol. For 30% anionic membranes, the effective energy difference for four associated protegrin molecules between the flat membrane and the pore is also about −13 kcal/mol (see the Supporting Material). The entropy cost for localizing the tetramer in the pore should be small in the latter case. In the former case it is more substantial, similar to the entropy of membrane binding and dependent on peptide concentration. At standard state, this entropy cost has been estimated as 1.3 kcal/mol (54). Thus, the favorable transfer energy may be sufficient to overcome the unfavorable free energy of pore formation, especially in anionic membranes.

As mentioned in the Introduction, there is no experimental evidence that protegrin forms arcs. However, to the best of our knowledge, there is no evidence that precludes them either. The oriented circular dichroism data that detected a change in orientation of protegrin as a function of concentration and hydration level (55) and the x-ray diffraction data that detected protegrin-induced membrane thinning (56) and crystallized pores (57), cannot differentiate between complete and incomplete barrels. Furthermore, the reported AFM work (46,58) did not have sufficient resolution to detect barrels or arcs. We hope that in the near future, specifically designed experiments will be able to tell us which of these two possibilities, if any, corresponds to reality.

In this work, we simulated only arcs of NCNC parallel topology based on our previous work that found this topology to be most stable (29), as opposed to the NCCN parallel topology suggested by solid-state NMR experiments (59,60). The data that suggested oligomerization of protegrin into closed β-barrels in anionic lipids were CODEX solid-state NMR experiments with 19F labels at positions 7 and 12 (60). This experiment determines the number of such labels within 15 Å of each other and allows an estimate of the actual distances from the speed of decay of the signal. The 7-7 and 12-12 distances in the NCNC parallel barrel are ∼11 Å and averages of these distances calculated over our arc simulations ranged from 8.6 to 11.6 Å, within the range of detection. In a nitroacetanilide crystal with a 11.5 Å distance between labels, Luo and Hong measured a clear CODEX signal with 52 ms decay constant (61), quite close to the 60 ms decay time measured for Phg7 in protegrin (60). In the barrels each label would have two other labels at those distances, thus, (S/So)eq ∼0.33. In the arcs half the labels would have two and half would have one, thus (S/So)eq should be between 0.33 and 0.5, as was observed for Phg12. The 7-7 and 12-12 distances in the NCCN parallel arrangement are actually longer than 11 Å, because in that arrangement neighboring side chains point to different faces of the β-sheet. In the NCCN antiparallel model the 7-7 distance is 5.3 Å but the 12-12 distance is 14.2 Å. The short distances of 6.5 and 9 Å inferred by Mani et al. for 7-7 and 12-12, respectively, do not seem compatible with any single closed barrel structure. Further discussion of other solid-state NMR results can be found in our previous publication (29).

The ion conductance properties of protegrin channels have been studied by both experimental and theoretical methods. Electrophysiology studies found a weak anion selectivity in azolectin membranes and cation selectivity in lipopolysaccharide membranes (33). A computational study of ion conductance based on the NCCN parallel barrel structure found an anion selectivity that is much stronger than in the experimental studies (62). An arc pore structure provides a possible explanation of this discrepancy. If the conducting ions are exposed to lipid on one side as they cross the channel, they will be quite sensitive to the nature of the lipid and less sensitive to the positive charge of the peptide. Calculations of conductance based on the arc structures would provide a quantitative assessment of this idea.

The standard picture of a peptide-stabilized lipidic pore is a toroidal pore with several peptides dispersed in it with orientation perpendicular to the membrane (23). A different picture came from explicit simulation data, with a pore that is much more disordered and peptides residing mostly on the periphery of the pore (63). Other simulation studies of pores stabilized by antimicrobial peptides produced results intermediate between the above extremes (47,64–67). This work presents yet another paradigm of pore structure: lined by associated protein on one side, and by lipid headgroups in toroidal form on the other. This idea seems to be more in line with findings that aggregation is an essential step in peptide-induced pore formation (68). There are also smaller toxins, such as the colicins (26) and diphtheria toxin (27), which appear to permeabilize membranes as monomers, inserting three or four helices into the membrane. For many of these systems there is not enough protein to completely line a pore (69), which led to the idea that part of the pore is lipidic. Protein arcs offer a new, to our knowledge, intriguing possibility as a solution to this conundrum.