Delays Induce Novel Stochastic Effects in Negative Feedback Gene Circuits

Abstract

Stochastic models of reaction networks are widely used to depict gene expression dynamics. However, stochastic does not necessarily imply accurate, as subtle assumptions can yield erroneous results, masking key discrete effects. For instance, transcription and translation are not instantaneous processes—explicit delays separate their initiation from the appearance of their functional products. However, delays are often ignored in stochastic, single-gene expression models. By consequence, effects such as delay-induced stochastic oscillations at the single-cell level have remained relatively unexplored. Here, we present a systematic study of periodicity and multimodality in a simple gene circuit with negative feedback, analyzing the influence of negative feedback strength and transcriptional/translational delays on expression dynamics. We demonstrate that an oscillatory regime emerges through a Hopf bifurcation in both deterministic and stochastic frameworks. Of importance, a shift in the stochastic Hopf bifurcation evidences inaccuracies of the deterministic bifurcation analysis. Furthermore, noise fluctuations within stochastic oscillations decrease alongside increasing values of transcriptional delays and within a specific range of negative feedback strengths, whereas a strong feedback is associated with oscillations triggered by bursts. Finally, we demonstrate that explicitly accounting for delays increases the number of accessible states in the multimodal regime, and also introduces features typical of excitable systems.

Introduction

Negative feedback loops are ubiquitous features of biological regulatory networks. They are essential ingredients of gene expression and cell signaling, and are largely responsible for generating oscillations (1,2) and modulating noise (3–7), among other functions. Feedback loops are composed of interconnected biochemical reactions, which are discrete and random by nature. Thus, out of all theoretical frameworks, models taking reaction discreteness and randomness into account will always yield more accurate results. Moreover, stochastic discrete models often predict behaviors impossible to obtain with deterministic models. Such stochastic discrete effects include, but are not limited to, noise amplification/attenuation (5–9), bursty expression (7,8,10–12), stochastic resonance (13,14), stochastic focusing (15), stochastic-induced oscillations (14,16,17), and multimodality (7,10,18).

For many years, negative feedback regulation was thought to imply noise reduction (9,19,20). However, recent works (6,7) revealed contrary observations, leaving a question mark over the relationship between gene expression heterogeneity and negative regulation. In (7), a set of simple gene circuits was studied to assess the relationship between noise characteristics and negative feedback strength. There, it was shown that subtle mathematical properties in the modeling framework result in widely distinct expression profiles. In particular, both lumping of transcription-translation reactions and quasi-steady-state assumptions proved to be detrimental for a proper description of noise modulation. Additionally, it was found that bursts and multimodality can be observed in networks with identical architecture that only differ in terms of feedback strength and specific kinetic parameters.

However, a systematic exploration of the roles of transcriptional and translational delays alongside stochastic feedback regulation remained to be seen. Such analysis becomes necessary because explicit delays can reveal dynamics that nondelayed models fail to predict (e.g., oscillations and excitability), independently of whether the modeling approach is deterministic or stochastic (1,21–25). Delays are commonly used to account for the duration of reactions whose kinetic details are often ignored. This strategy significantly reduces the number of equations in the model, although still capturing the essence of the phenomenon by following the dynamics of molecular species of interest (26). Moreover, exact model reduction techniques using distributed delays were recently studied, showing how an exact match between a delayed reaction (with a constant delay) and a nondelayed reaction (with a constant reaction rate) can never be obtained (26). Thus, proposed models exchanging explicit delays with slow rates of reaction may easily yield inaccurate representations of chemical systems of interest.

Thereby, it is natural to ask: how many of the observed properties in gene expression models, such as noise buffering and multimodality would hold if one explicitly accounts for transcriptional and translational delays? And, would introduction of explicit transcriptional and translational delays yield new nonclassic stochastic effects, not yet observed? To answer these questions, we consider a prototypical gene circuit that accounts for transcription, translation, and protein dimerization (Fig. 1). In our system, the dimer acts as a transcription repressor upon binding DNA, resulting in a negative feedback loop at the gene level. Furthermore, we consider explicit delays due to transcription and translation, and identify ranges where sustained oscillations are to be expected.

Figure 1.

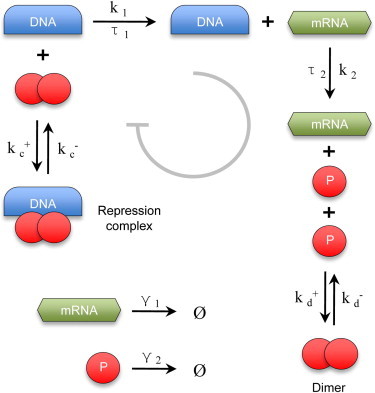
Simple gene regulatory circuit portraying transcription, translation, and dimerization. Transcription and translation are treated as delayed reactions. The dimer binds reversibly to DNA and repress transcription, resulting in a negative feedback loop.

It is worth noting that reaction delays are commonly associated with oscillations in negative self-regulation systems (1,2,27), but the particular way in which oscillations emerge depends on the network architecture as well as the parameter values. In our case, a Hopf bifurcation is the simplest mechanism by which our minimalistic gene circuit could oscillate, but asserting its existence is not straightforward. Separately, stochastic descriptions of gene regulatory networks (GRNs) often exhibit behaviors absent in their deterministic counterparts, such as oscillations, bistability, and bursts (17,21,28–30). Furthermore, noise-induced oscillations without delays have been demonstrated before (14,16,17). Whether this and other behaviors with no deterministic counterpart may be occurring in systems such as Fig. 1 needs to be determined.

After briefly pointing out the differences between deterministic and stochastic descriptions of the circuit, we carry out a systematic study on the role of negative feedback, delays, and kinetic parameters on stochastic gene expression profiles. In agreement with other models (1,21,22,25), oscillations were observed when considering significantly long delays. However, we show the onset of oscillations is quite distinct at low and high feedback strengths, involving a Hopf bifurcation in the former and bursty expression in the latter. Even though the deterministic Hopf bifurcation is mathematically well defined (see the Supporting Material) (31), its stochastic definition is still in development. Here, we used the most recent definition based on the changing shape of the system’s stationary distribution under parameter variations. This definition states that, for a stochastic planar autonomous system, a stochastic Hopf bifurcation appears when the shape of its stationary distribution changes from peak-like to crater-like (32). The latter implies the oscillatory regime has associated marginal stationary distributions that are bimodal functions; a fact that we will show is in full agreement with the shape of distributions in our work.

Finally, when compared to the deterministic analysis, we find the stochastic Hopf bifurcation to be shifted in parameter space (33,34). Furthermore, we demonstrate that this very simple gene circuit can also exhibit multimodality, just as its nondelayed stochastic counterpart (7). However, transcriptional delays play a very interesting role in shaping such multimodal behavior. On the one hand, it increases the number of modes that the system can visit (i.e., states otherwise inaccessible without the use of delays). On the other, it modifies expression dynamics significantly, exhibiting characteristics typical of excitable systems (35).

Materials and Methods

System reactions and model parameters

For this study, we chose a generalized gene expression circuit consisting of transcription, translation, degradation, and dimerization reactions. The circuit architecture in Fig. 1 corresponds to the following set of model reactions

$$\begin{array}{l}DNA\stackrel{k_1,{\tau }_1}{\to }DNA+mRNA\hfill \\ mRNA\stackrel{k_2,{\tau }_2}{\to }mRNA+P\hfill \\ P+P\underset{k_d^{-}}{\overset{k_d^{+}}{\rightleftharpoons }}D\hfill \\ DNA+D\underset{k_c^{-}}{\overset{k_c^{+}}{\rightleftharpoons }}DNA\cdot D\hfill \\ mRNA\stackrel{{\gamma }_1}{\to }\varnothing \hfill \\ P\stackrel{{\gamma }_2}{\to }\varnothing \hfill \end{array}$$ (1)

where k₁ and k₂ represent the transcription and translation rates, respectively. Dimer association/dissociation rates are denoted by k_d⁺ and k_d⁻; a dimer binds and unbinds DNA at rates k_c⁺ and k_c⁻; whereas mRNA and protein turnover are represented by rates γ₁ and γ₂, respectively. For delayed reactions, constant delays τ₁ and τ₂ were chosen to represent transcription and translation processes. A full derivation of the corresponding deterministic and stochastic models can be found in the Supporting Material.

We considered uniform initial conditions of 1, 1, 100, 0, and 0 molecules of DNA, mRNA, protein, dimer, and the repression complex (dimer-bound DNA), respectively. As we focused on the expression of a single gene in one single cell, we used a volume of 1 fL, equivalent to a typical Escherichia coli cell volume (36). To check if our observations hold for volumes as large as those found in unicellular eukaryotes, we also carried out simulations considering a volume of 37 fL, equivalent to a typical Saccharomyces cerevisiae cell volume (37) (see the Supporting Material). Proper conversion to molarity units for the deterministic model was implemented whenever necessary.

Following (7), we used parameter α = k_c⁺/k_c⁻ to account for the negative feedback strength. The latter was varied over eight orders of magnitude and, together with the transcriptional delay, constituted the main parameters under study. Of importance, these parameters were used for both the deterministic and stochastic analyses and tuned within the same ranges, making both cases comparable. Two basic parameter sets were used for all simulations. One set for oscillatory regime simulations and one for multimodal expression profiles (respectively, Table S1 and Table S2). All parameter values were fixed within biologically feasible ranges (7) (Table S3).

The transcriptional delay τ₁ was defined as the elapsed time since transcription initiation up to the appearance of the corresponding mature mRNA. This accounts for intermediate reactions like transcript elongation, editing, and other processes not considered explicitly in our model. In a similar way, the translational delay τ₂ was defined as the time since translation initiation up to the appearance of the corresponding mature protein (but before dimerization). We used the ranges τ₁ ∈ [0, 1200] s and τ₂ ∈ [0, 150] s. To fully assess the effects of introducing delays, we decided to tune them from zero to the upper limits estimated in (22). This choice eases extrapolation of our results to higher delay values, typical of eukaryotic cells where mRNA and protein require further processing and transport between cell compartments.

Bifurcation analysis and numerical solutions

A set of delay differential equations (DDEs) was used to model deterministic dynamics. The bifurcation analysis was performed using DDE-BIFTOOL (38) for continuation and identification of the Hopf bifurcation (Fig. S1). To compute bifurcation diagrams, the numerical step-size and number of branch points were optimized to achieve maximum resolution while completing the calculation in a reasonable amount of time. Given the subtle dependency of DDEs on its history and delay values, we verified our results using XPPAUT (39) and MATLAB dde23 (The MathWorks, Natick, MA) (Fig. S1 F and Fig. S2, A, C, E, and G).

Stochastic simulations and analysis

Biochemical reactions are discrete and random by nature. Thus, systems of delayed chemical reactions are accurately described by the delay chemical master equation (DCME). The validity of the DCME demands a well-stirred system in thermal equilibrium. It ignores spatial information, solely accounting for molecule numbers uniformly distributed throughout a constant volume (40,41). Nevertheless, it is worth noting one may also use delays to account for spatial, nonhomogeneous processes (42), a topic that lies outside the scope of this work. Currently, our system in consideration contains extremely low numbers of molecules. Thus, solving an associated stochastic DDE (e.g., the Langevin approximation) is not an option, as this approach is only valid at high concentrations where no discrete effects are expected. Therefore, we must retort to using the DCME.

Even though the DCME cannot be solved analytically, it is possible to calculate independent exact trajectories belonging to it through an exact delay stochastic simulation algorithm (DSSA). Here, we carry out single cell simulations using an implementation of the DSSA based in the reaction rejection method (21) (Fig. S3). It has been demonstrated in (43), that this method yields exact trajectories according to the DCME, therefore we do not introduce any approximations. In this way, we avoid using perturbed DDEs and unnecessary assumptions about noise that may shadow dynamical subtleties in our system. In our simulations, reactants and products are updated simultaneously only after a delay marks the reaction completion. Nondelayed simulations were verified by means of the stochastic simulation algorithm (SSA) direct method (44).

Within each parameter set describing a dynamical regime (Table S1 and Table S2), parameter sweeps were performed for one parameter at a time, leaving all others fixed. We carried out 100 simulations for each combination of feedback strength and delay values. For each simulation, 10⁶ equally spaced time points were collected. These simulations were used to estimate stationary probability density functions (PDFs) as well as period, amplitude, and time autocorrelation half-life distributions. PDFs were calculated by computing normalized histogram distributions and verified by MATLAB kernel smoothing function estimators. Contoured PDFs were obtained from individual PDFs using MATLAB’s interpolating algorithms.

To calculate amplitude, period, and autocorrelation half-life distributions, the stochastic time course trajectories were smoothed using a moving averages algorithm. The size of the smoothing window was fixed at 9 neighbors for mRNA and 21 for protein and dimer, and these values were kept identical for all trajectories analyzed.

Results and Discussion

Oscillatory gene expression is induced by delays

Several studies of delay-induced oscillations in GRNs exist for both deterministic and stochastic models (17,21,22,28). However, none so far systematically explored the relationship between negative feedback and delays as a means to induce oscillations through a Hopf bifurcation. To fill this gap, we first computed a dynamical portrait of the system by means of a continuous deterministic model. It is worth emphasizing qualitative predictions of the deterministic model were only used as a starting point to a more systematic study using discrete stochastic simulations.

We then performed a bifurcation analysis on the deterministic model of our gene circuit (Eq. S2). To explore the onset of oscillations, we used the parameter values shown in Table S1. Furthermore, we chose three bifurcation parameters: the feedback strength α, and transcriptional and translational delays denoted by τ₁ and τ₂, respectively. Although the feedback strength was varied over a very wide range, a periodic solution was found only within α ∈ [10⁷, 10¹⁵] M⁻¹. The delays were varied within the ranges reported in Table S3.

The result of our analysis is shown in Fig. 2, where a two-parameter (τ₁, α) bifurcation diagram illustrates the boundary between regions where the system exhibits a stable steady-state solution (monostability) versus self-sustained oscillations. Of importance, we found these boundaries correspond to points in parameter space where a single, stable steady-state solution loses its stability and a limit-cycle emerges (Fig. S1), thus defining Hopf bifurcation branches. Therefore, the onset of oscillations in a deterministic model of our gene circuit occurs through a Hopf bifurcation.

Figure 2.

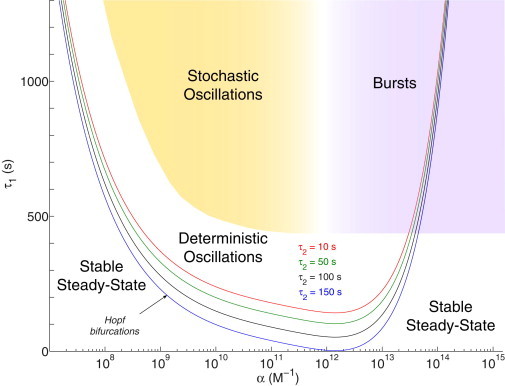
Two-parameter (τ₁, α) bifurcation diagram. A series of Hopf bifurcation branches separate the oscillatory regime (above) from the steady-state solution (below). Color-coded boundaries represent calculated branches corresponding to different values of τ₂. The boundary defined by the Hopf branch at τ₂ = 100 s was used to compare against stochastic predictions (shaded areas).

From Fig. 2, it can be readily observed that oscillations are precluded from regions of very weak and very high feedback strength, whenever both delays are small. Conversely, intermediate feedback strengths (α ∈ [10¹⁰, 10¹³] M⁻¹) allow for periodic solutions whenever the transcriptional delay τ₁ lies above the Hopf branch delineated by the translation delay τ₂. As a general rule, feedback strength intervals allowing for the occurrence of oscillations become wider alongside increasing values of the transcriptional delay τ₁. The same applies for translational delays τ₂, where increasing values of this parameter result in downward displacements of the U-shaped Hopf branch.

Taken together, these results show that high transcription and translation delays and intermediate feedback strengths account for periodic solutions in a deterministic model of the gene circuit.

A stochastic Hopf bifurcation is revealed

We carried out thorough sets of stochastic simulations of the gene circuit by means of the DSSA (21), using the bifurcation diagram in Fig. 2 as a guide for exploring parameter values. A fixed value of τ₂ = 100 s for the translation delay was used for all stochastic simulations. This value is well centered within the biological range (Table S3) and its corresponding Hopf branch does not intersect the τ₁ = 0 s axis, allowing examination of the oscillatory regime at intermediate feedback strengths (Fig. 2). We then selected pairs of values α and τ₁ uniformly distributed over the parameter space. For each pair, we carried out 100 simulations to estimate the corresponding PDF (see Methods and Figs. S4–S10). Single representative samples for each pair (α, τ₁) are shown in Figs. S4–S10. The trajectories portray the time evolution of DNA, mRNA, protein, dimer, and the DNA/dimer repression complex, from where the following qualitative observations can be made:

• 1.Low α and low τ₁: mRNA, protein and dimer trajectories are too noisy to clearly distinguish an oscillatory pattern. However, a clear periodic pattern emerges and stabilizes as τ₁ increases.
• 2.Intermediate α and low τ₁: mRNA, protein and dimer trajectories are spiky and irregular. Once again, a periodic pattern emerges and stabilizes as τ₁ increases.
• 3.High α and low τ₁: mRNA, protein and dimer trajectories are not only spiky but also very sparsely distributed. We refer to these high-level, brief, sudden increments in molecule numbers as expression bursts. In high feedback scenarios, expression bursts increase their lifetime and resemble an oscillation peak with increasing values of τ₁.
• 4.The higher the feedback strength α, the more the mRNA, protein, and dimer oscillation troughs shift closer to zero expression, and the more the oscillation crests become sparsely and irregularly distributed in time. Moreover, the amplitude and period of oscillations seem to increase with α and τ₁.
• 5.From the DNA and repression complex dynamics, one can see that the frequency at which the gene is available to transcribe diminishes alongside increasing values of α. Indeed, this follows from the definition of α, and governs how the oscillation crests are distributed in time. Interestingly, as τ₁ increases, the time the gene remains free for transcription also increases. This effect becomes more critical for the overall dynamics at high feedback strengths.
• 6.For all feedback strengths and all transcription delay values, the time-course evolution of mRNA, protein, and dimer are correlated. This is one significant difference to models that do not consider transcriptional and translational delays explicitly (45,46).

In contrast to the deterministic scenario, where a clear-cut transition from the monostable to the oscillatory regime can be identified, sharp transitions are not obvious in the stochastic setting. Moreover, whereas the Hopf bifurcation in the deterministic framework is well defined (in terms of the loss of stability of a steady-state and simultaneous emergence of a limit-cycle (31,33,47)), the stochastic Hopf bifurcation is not.

However, we can intuitively think of a system that fluctuates close to a stable steady-state and, upon certain parameter variations, decreases its residence time close to that state to instead visit other nearby states. Such a gradual transition seems to contradict the classic deterministic concept of bifurcation, but a stochastic system may well exhibit a superposition of steady-state and limit-cycle solutions close to the putative bifurcation point. Moreover, in discrete stochastic dynamics, states are described by probabilities with no hard definition of an unstable steady-state.

To assess whether transitions from low-amplitude to high-amplitude fluctuations are actually portraying the emergence of an oscillatory pattern, one needs to carefully look at the PDFs. We expect a stochastic transition from monostability to oscillations to be reflected in the PDFs. Namely, through a tendency to change from unimodal to bimodal (32,33,48). Even though a strict mathematical formalism for stochastic Hopf bifurcations is still in development (32,49), some systems have already been described using this approach (e.g., pupil light reflex (33), predator-prey models (32), and neural circuit excitable systems (50)). Thus, we recognize these transitions as stochastic Hopf bifurcations when the PDFs in Figs. S4–S10 change from being unimodal to bimodal. Due to the difficulty of discerning the latter from large sets of data, we summarized our findings as contour plots of the PDFs in two ways. First, as a function of τ₁ with different values of α. Second, as a function of α with different values of τ₁. Results are shown as stacked contoured PDFs in Fig. 3. For the sake of simplicity, we only show mRNA and protein PDFs. The dimer PDFs can be found in Figs. S4–S10.

Figure 3.

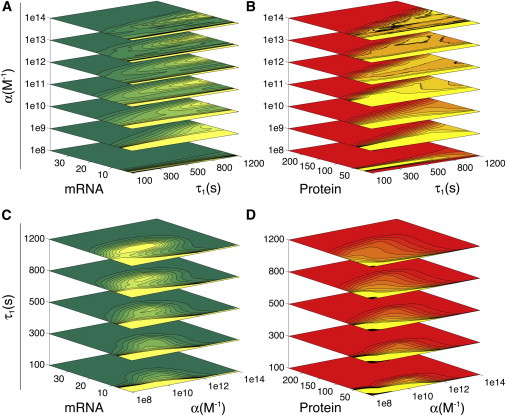
Stacked contoured PDFs reveal a stochastic Hopf bifurcation. Contour slices were calculated for different feedback strengths (A, B), and different transcription delay values (C, D). Stacks for mRNA (A, C) and protein (B, D) are shown. Lighter colors correspond to local maxima in the PDFs. From bottom to top, within each panel, contoured PDFs approach a bimodal shape. The uppermost contours in the top panels (A, B) look less smooth as the burst regime appears beyond α = 10¹² M⁻¹.

In Fig. 3, the successive stacking of contours from bottom to top (either by increasing α or τ₁ values) reveals some interesting changes in the system’s dynamics. For instance, in Fig. 3, A and B, contour PDFs at the bottom (low α-slices) are clearly unimodal and centered at low values of mRNA and protein. This unimodal distribution slightly widens for higher transcriptional delay values. However, for higher values of the feedback strength (upper α-slices), the contour PDFs dramatically widen, although at the same time the former local peak narrows and is displaced to lower molecule numbers. The tendency of each slice’s distribution to become wider at high values of τ₁ is maintained for all α levels. Moreover, a second local peak appears for medium to high values of the transcriptional delay τ₁. This second peak displaces to higher molecule numbers as α and τ₁ increases, hinting at the oscillation amplitude increments already observed in Figs. S4–S10.

On the other hand, from Fig. 3, C and D, and Figs. S4–S10, we observe the PDFs exhibit a tendency to flatten, widen, and become bimodal for higher values of the transcription delay (upper τ₁-slices). In agreement with the top panels (Fig. 3, A and B), they also show how the once unique local peak shrinks and displaces to lower molecule numbers alongside increasing values of α. In contrast to Fig. 3, A and B, the contoured PDFs in Fig. 3, C and D, are bounded. That is, intermediate levels of the feedback strength α concentrate the widest (and bimodal) distributions, whereas the bimodality becomes suddenly extinct at feedback strengths higher than α = 10¹² M⁻¹. This is a very interesting observation when we compare the panels in Fig. 3, C and D, with the two-parameter bifurcation diagram in Fig. 2. It points to a better agreement between deterministic and stochastic predictions at intermediate feedback strengths and high transcription delay (shaded area in Fig. 2).

Overall, the data point to the existence of a stochastic Hopf bifurcation underlying the emergence of oscillations in the gene circuit.

Hopf bifurcation shifting

In the past, bifurcation theory has been extensively used to study gene expression dynamics in connection to network architectures (1,51,52). Nevertheless, with some exceptions (17), it has been largely ignored when stochastic models are employed. One notable exception is the work in (28), where a two-parameter bifurcation diagram exhibiting a Hopf bifurcation was shown for a gene system with negative feedback. The authors subsequently used this bifurcation diagram to compare against stochastic predictions made via a DSSA and, interestingly, found a shift in the bifurcation point when stochastic fluctuations come into play. However, the parameter exploration in (28) is too scarce to assess the influence of feedback and delays within the stochastic bifurcation. Moreover, the generalized SSA they used for simulating stochastic delayed reactions is not exact (43,53).

In this work, we use a different DSSA implementation (21) guaranteeing exact realizations of the DCME, and confirm a shift (postponement) in the stochastic Hopf bifurcation. This is judged by the emergence of bimodal PDFs in Fig. 3 for high τ₁ values and for bounded α intervals. When compared with the clear-cut Hopf branch boundary (τ₂ = 100 s) in the deterministic scenario, one can readily notice that the contoured PDFs from Fig. 3 reveal more than just a fuzzy transition. They also show that the (τ₂, α) parametric domain that sustains stochastic oscillations is smaller than that of its deterministic counterpart. Taking the (τ₂, α) values where bimodal PDFs are clearly noticeable (Fig. 3), we estimate that the leftmost boundary of the oscillatory regime shifts to higher α by approximately one order of magnitude (shaded area in Fig. 2). This implies that the overlapping domain where both the deterministic and stochastic approaches effectively predict oscillations is significantly reduced. Because the stochastic modeling framework is based on assumptions that better account for biological reality, we interpret from the Hopf bifurcation shift that the deterministic approach is systematically misestimating the parametric conditions where periodic gene expression is observable.

The stochastic oscillatory pattern is stabilized from low to intermediate feedback α and high transcriptional delay τ₁

To further understand the behavior of the oscillatory regime, we calculated amplitude distributions for each batch of 100 trajectories at different α and τ₁ values (Fig. S11). For low feedback strength, these distributions show that amplitude increases with the transcription delay already starting from very low molecule numbers. However, for intermediate to high feedback strength, the rise in amplitude as τ₁ increases is not as large as for low α. Interestingly, the amplitude distributions become narrower, showing reduced fluctuations in response to increments in the transcription delay. These observations are summarized in Fig. 4, A–C, where the mean amplitudes for mRNA, protein, and dimer, are shown as functions of τ₁ and α. There, we can see a steady growth in amplitude as the feedback strength and transcription delays increase. For the case of mRNA, this growth dramatically slows down from medium to high values of α, and for all values of τ₁. On the other hand, dimer amplitude distributions always exhibit a maximum at very low molecule numbers and gradually vanish at higher molecule numbers (Fig. S11). This effectively means that, in contrast to mRNA and protein, dimer oscillations do not have any preferential amplitude. Nonetheless, all amplitude distributions for the three aforementioned molecular species are displaced to higher molecule numbers when τ₁ and α values increase (Fig. 4, A–C).

Figure 4.

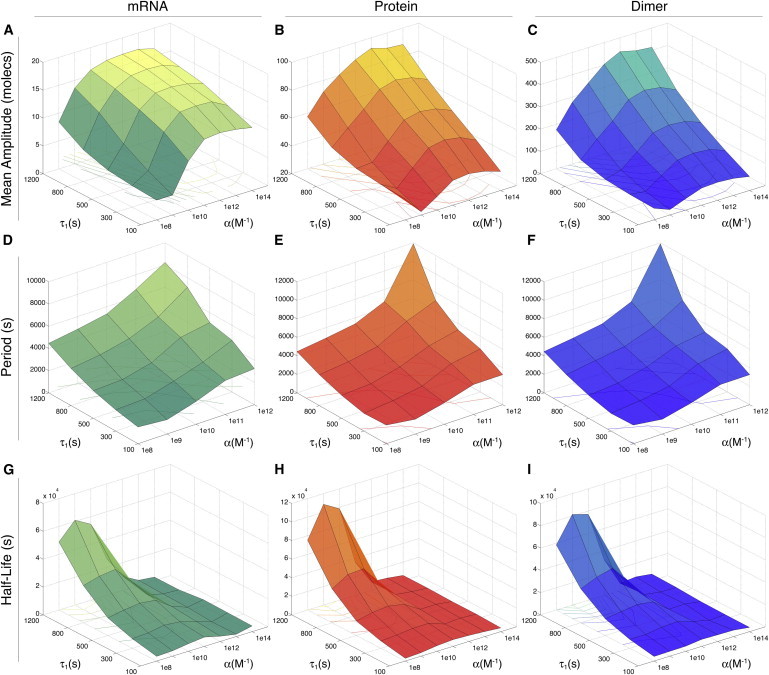
Characterization of stochastic oscillations. From top to bottom: amplitude (A, B, C), period (D, E, F), and autocorrelation half-lives (G, H, I). From left to right: mRNA (A, D, G), protein (B, E, D), and dimer (C, F, I). Period values beyond α = 10¹² M⁻¹ diverge in the burst regime.

To estimate oscillation periods, frequency spectra were calculated for each trajectory by means of a fast Fourier transform algorithm and its inverse (period curve) averaged for each batch of 100 trajectories (see Supporting Text and Fig. S12). In Fig. 4, D–F, the period distributions for mRNA, protein, and dimer are shown as functions of τ₁ and α. There, we can see a steep and steady increment in period as the feedback strength and transcription delay increases. Notably, the very irregular and sparse distribution of peaks in time course trajectories beyond α = 10¹² M⁻¹ precluded a correct period estimation, suggesting that this feedback strength value actually marks the frontier between stochastic oscillations and bursty dynamics.

Finally, we wanted to assess the impact of the negative feedback and transcriptional delay in stabilizing stochastic oscillations. We used a time autocorrelation function C(ω) that measures the correlation of a discrete time series with itself as a function of time shift ω. Although deterministic oscillations have periodic autocorrelations, stochastic time series do not, due to phase memory loss. Typically, stochastic oscillations have autocorrelations that also oscillate, but the envelope of which decreases exponentially. The half-life time of the envelope measures the damping rate of C(ω), and accounts for the impact of noise in the time series.

We calculated time autocorrelation functions for each of the stochastic trajectories and averaged them over each batch of 100 simulations. The damping rate of the averaged functions for each (τ₁, α) pair of values illustrate the phase memory loss (Figs. S13–S19). Half-lives were then obtained from a fitted exponential envelope to the averaged autocorrelation functions. We then used them as indicators of how oscillations are resilient to noise fluctuations when varying the feedback strength and transcriptional delay. The result is shown in Fig. 4, G–I, where autocorrelation function half-lives for mRNA, protein, and dimer, are plotted as functions of τ₁ and α. There, we can see that at low feedback strength, phase memory is better preserved at higher transcriptional delay values. More specifically, there is an optimal interval defined by α ∈[10⁹, 10¹⁰] M⁻¹. This suggests that neither high nor very low feedback strength make gene periodic expression more reliable for the control of downstream processes, but instead there exists an optimal tuning range for α.

In other words, stochastic oscillations are stabilized against random fluctuations for a narrow range of feedback strength. In the context of noise modulation in gene circuits, this result adds to previous counterintuitive stochastic behaviors observed when tuning the negative feedback strength (7). In contrast, phase memory decay rate increases from intermediate to high levels of α, and for all values of τ₁. As was the case with the period distributions (Fig. 4, D–F), this is due to the sparseness and irregularity of expression peaks in time-course trajectories. We argue that this rapid phase memory loss is another indicator that the stochastic oscillatory regime effectively disappears at high feedback strengths, giving rise to a bursty expression domain.

Bursts as precursors to oscillations at high feedback strength

The stacked contour PDFs in Fig. 3, C and D, provide another interesting observation. The PDFs gradually widen as the feedback strength increases (indicating the onset of oscillations), yet they shrink abruptly beyond α = 10¹² M⁻¹. In other words, according to the stochastic model, the probability of observing nonbasal gene expression suddenly becomes negligible for α > 10¹² M⁻¹. This effectively marks the boundary for the oscillatory regime at high α. Nonetheless, stochastic simulations show sudden short-lasting bursts beyond α = 10¹² M⁻¹ (Figs. S9 and S10 and shaded area in Fig. 2).

The precise mechanism by which the system shifts between bursts and oscillations is unknown and requires further investigation. However, a plausible explanation can be formulated by observing the sample trajectories in Figs. S4–S10 and comparing how transcriptional delays affect DNA-repressor complex dynamics at high versus low feedback levels. Even though such trajectories only show 1 out of 100 simulations for each (τ₁, α) pair, they evidence how the state of the mRNA, protein, and dimer are affected by how often the unbinding events occur (opening the gene for transcription each time) and by the elapsed time the gene remains free of the repressor.

As it turns out, the frequency with which the gene is open for transcription is inversely proportional to the feedback strength α. In contrast, the time it remains open correlates with the duration of the transcriptional delay τ₁. Of importance, the latter effect is more noticeable for large α (Figs. S8–S10). Thus, it follows naturally that a bursty pattern emerges whenever the gene sporadically frees from the repressor and remains open long enough for transcription events to trigger the burst. This condition is readily met at high α, where the moment a burst occurs is unpredictable but its size correlates with the elapsed time the gene remained free from the repressor. Conversely, at low α, the elapsed time the gene remains unrepressed varies greatly and with no apparent correlation to τ₁. In this scenario, a high frequency of DNA-repressor binding/unbinding is the chief mechanism governing the occurrence of transcription events. They occur at such a high frequency that a regular oscillatory pattern emerges and is driven by reaction delays. However, at intermediate values of α, the frequency at which the gene is found open for transcription is neither too low nor too high. In this scenario, the gene remains open long enough to beget a few transcription events but, after it’s repressed, it will not be long before it opens again and resumes transcription. This intermediate feedback strength adds enough regularity in the DNA-repressor binding/unbinding dynamics for a clear oscillatory pattern to emerge. We argue that this is the mechanism behind bursts triggering self-sustained stochastic oscillations in our gene system.

Overall, transcriptional and translational delays control the regularity at which the oscillation crests and troughs are observed, whereas the feedback strength α is the driving force behind transitions from bursty to oscillatory gene expression profiles.

Multimodality in the nondelayed and delayed scenario

Multimodal gene expression has been reported in nondelayed negative feedback regulation scenarios (7,10,18). There, multimodality could be easily achieved by tuning the feedback strength and mRNA degradation rate simultaneously. Following this idea, we tuned these parameters together with k_d⁺ and k_d⁻ rates, and concluded that parameters in (7) required only minor variations. The resulting parameter set is shown in Table S2.

We first explored the nondelayed scenario by fixing τ₁ = τ₂ = 0 s in the gene circuit in Fig. 1. To remain consistent with our previous analysis, we explored the effects of delays by increasing τ₁. We fixed the translation delay at τ₂ = 100 s to simplify the analysis of multimodality, because this value is well centered within the biological plausible range (Table S3). As before, we carried out 100 realizations of the DSSA for each parameter combination, and used them to estimate stationary PDFs. Of importance, we calculated PDFs after different simulation times and verified that their shape and statistic measures (such as mode locations, number, and frequencies) remained invariant after 80% of the simulation time reported in here. In other words, the PDFs remain invariant and thus reliably describe the stochastic scenario. In Fig. 5, sample time-course trajectories of mRNA and protein dynamics are shown together with their corresponding protein PDFs. There, it can be observed that each transcription event occurs at a random time and yields an initial amount of mRNA, which is also random. The transcript is then translated to a number of proteins proportional to available mRNA at the time, following a multimodal distribution (see the PDFs in Fig. 5). Interestingly, protein numbers exclusively show small fluctuations around some central values, which we will refer to as modes. We identify these modes in the PDFs, appearing as local maxima, resembling multiple overlapping Gaussian distributions. Moreover, at low τ₁, the system transitions between modes occur rapidly and discretely. On the other hand, at high τ₁, each transcription-translation event drives the system to a very high mode, which gradually decays to lower modes in a discrete fashion. In any case, discrete jumps do not necessarily occur between consecutive modes.

Figure 5.

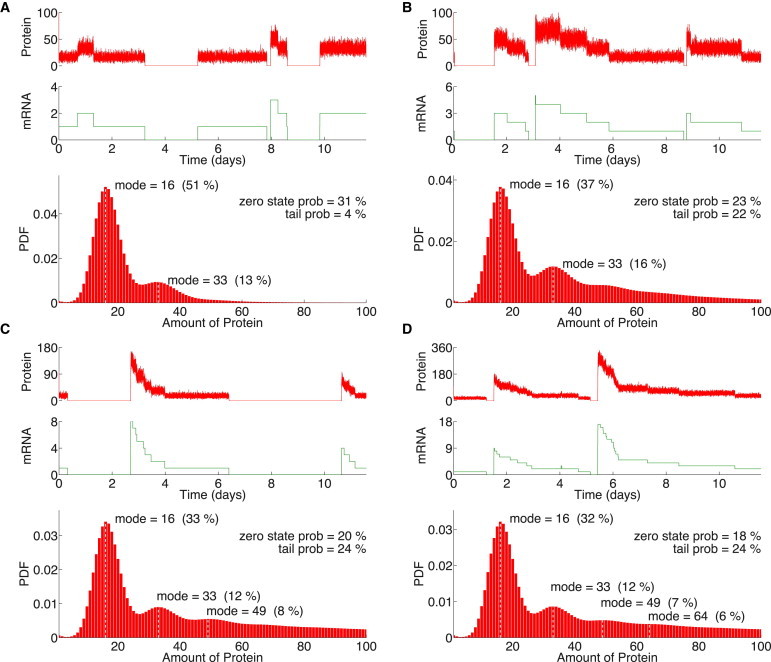
Reaction delays enhance multimodal behavior. Protein and mRNA stochastic trajectories and the corresponding protein stationary PDF are shown for (A) τ₁ = 0 s, τ₂ = 0 s; (B) τ₁ = 100 s, τ₂ = 100 s; (C) τ₁ = 300 s, τ₂ = 100 s, and (D) τ₁ = 500 s, τ₂ = 100 s. The frequency probability of each mode and its position is indicated. Null expression was excluded from PDF calculations.

The PDFs in Fig. 5 account for the time the system spends in a certain state, reflecting the probability of observing each gene expression mode. There, it can be observed that the lowest mode (located at 16 proteins) has the highest probability, and that higher modes are located near integer multiples of such lowest mode, which in turn are observed with decreasing probabilities (see for instance the modes at 33, 49, and 64 proteins). Thus, for all delay values, the modes in the multimodal regime are quantized. Moreover, the number of accessible modes increases with the transcription delay τ₁, albeit always following the quantization rule.

Multimodal regimes reveal an additional interesting effect after introducing delays. Not only does the number of distinguishable modes grow with higher τ₁ values, but also larger excursions of the system are observed after each transcription-translation event. They are characterized by a sudden increase in mRNA and protein numbers, which then gradually decay, visiting lower modes in the process until settling down at zero molecules. During these large excursions, higher modes have shorter residence times, suggesting that lower modes are more stable. Furthermore, the amplitude of these large excursions increases with τ₁. This in turn affects the elapsed time of each excursion as, with higher amplitudes, the system has to visit a greater number of modes before settling in the lowest. Our observations from 100 trajectories point at large excursions exhibiting a refractory phase, in which the system almost never jumps again to a higher mode until it has completely exited from the excursion. In the protein PDFs, excursions of the system are reflected by the appearance of tail distributions: the higher the transcription delay, the wider the tail of the PDF. This follows from the amplitude of the excursion and hence the number of modes visited by the system during the recovery phase. In particular, for the nondelayed system, large excursions were never observed and the width of the PDF tail distribution was negligible (Fig. 5 A). This supports the observation that large excursions are induced by delays.

Taken together, the data suggest that the introduction of delays in the multimodal regime drives the system to an excitable-like behavior. Whether a noisy excitable gene system (35) can originate from coupled delayed reactions remains an open question. Some theoretical studies on excitable neural systems (24,54), stem cell fate decision control (55), and even nonphysiological systems (56) have made some progress in that direction. As was the case when comparing deterministic and stochastic predictions, we observe that multimodality predictions change significantly once explicit delays are accounted for. In particular, the number of modes accessible by the system increases and distinct, transient dynamics emerge.

Conclusions

In this study, we have shown how the modeling of a simple gene circuit with negative feedback at the single-cell level demands a proper handling of reaction delays. In particular, it was demonstrated that the interplay between feedback strength and transcriptional-translational delays shape the dynamical landscape of the system. This landscape was chiefly dominated by the coexistence of two dynamical regimes, monostability and oscillations, which constitute nonoverlapping expression profiles of the gene. Even though both deterministic and stochastic modeling predicts the emergence of oscillations through a Hopf bifurcation, deterministic models mask important dynamical effects. Examples of the latter are discrete stochastic effects, such as bursty expression and multimodality, which we also analyzed in terms of negative feedback strength and delays.

Additional differences between the deterministic and the stochastic models were pointed out. Among them, we found that the buffering of fluctuations varies within the parametric region where stochastic oscillations are predicted. Specifically, there is a small range of negative feedback strength and transcription delays where the impact of fluctuations is diminished and the oscillatory pattern becomes more regular. The parametric boundaries that delimit the oscillatory regime were also different for deterministic and stochastic models. Notably, a shift in the stochastic Hopf bifurcation with respect to its deterministic counterpart was observed. The occurrence of bimodality in the PDFs as a means to report a shift in the Hopf bifurcation is a very stringent criteria. Nonetheless, it safely prevents from false-positive identification of oscillations from mere fluctuations.

Our work also highlights the need for a better understanding of bifurcations in the context of stochastic systems; in particular, when transitions between different dynamical ranges are sensitive to stochastic discrete effects. As the burgeoning field of synthetic biology demands robust control of expression dynamics, we emphasize that choosing a precise and reliable modeling framework is crucial for engineering gene circuits. Important information can be learned from studying bifurcation shifts as well as inspecting the amplitude, period, and phase memory decay inherent to stochastic oscillations.

Of importance, it was shown that the onset of stochastic oscillations from a bursty expression regime depends on a fine balance between the frequency of DNA-repressor binding events and their duration. These properties are in turn modulated by feedback strength and delays, further stressing their importance within the stochastic modeling approach. We are aware that we have not considered a delay between repressor unbinding and transcription initiation. It would be interesting to explore how a delay accounting for processes such as RNA polymerase binding, transcription factor recruitment and chromatin remodeling, affect the dynamics of the gene circuit in Fig. 1.

We also showed how transcription, translation, and dimerization can generate multimodality. The latter was achieved by considering different parameter values while keeping the negative feedback circuit architecture in Fig. 1 identical. We demonstrated that introducing reaction delays not only preserves multimodal behavior, but also, that the number of modes accessible for the system increases alongside the transcriptional delay. Moreover, delays induce a significant change in the transient dynamical behavior of the gene, reminiscent of noisy excitable systems. Accounting for delays on multimodality is of major importance for understanding how genes exert control of downstream effectors. For instance, phenotype heterogeneity is often explained as multiple expression profiles resulting from identical genotypes. Multimodality in turn, is a dynamical emergent property that could readily account for this heterogeneity. In the context of synthetic biology, a deeper understanding into effective construction of tunable gene circuits capable of switching between different expression regimes is highly valuable.

In summary, we have provided deeper insight into the mathematical subtleties that should be considered for proper design of single genes in single cells with oscillatory, multimodal, and bursty expression profiles. Accounting for delays, for instance, allowed us to identify a stochastic Hopf bifurcation and find a gene circuit behaving as a noisy excitable system. This is, to our knowledge, the first time a delay-induced stochastic Hopf bifurcation (and a shift with respect to its deterministic counterpart) is reported for a GRN. Although a thorough analysis of a noisy excitable gene system with delays is beyond the scope of this work, we believe this is the first time such behavior is reported for a GRN with delays.