Enhanced Tethered-Particle Motion Analysis Reveals Viscous Effects

Abstract

Tethered-particle motion experiments do not require expensive or technically complex hardware, and increasing numbers of researchers are adopting this methodology to investigate the topological effects of agents that act on the tethering polymer or the characteristics of the polymer itself. These investigations depend on accurate measurement and interpretation of changes in the effective length of the tethering polymer (often DNA). However, the bead size, tether length, and buffer affect the confined diffusion of the bead in this experimental system. To evaluate the effects of these factors, improved measurements to calibrate the two-dimensional range of motion (excursion) versus DNA length were carried out. Microspheres of 160 or 240 nm in radius were tethered by DNA molecules ranging from 225 to 3477 basepairs in length in aqueous buffers containing 100 mM potassium glutamate and 8 mM MgCl₂ or 10 mM Tris-HCl and 200 mM KCl, with or without 0.5% Tween added to the buffer, and the motion was recorded. Different buffers altered the excursion of beads on identical DNA tethers. Buffer with only 10 mM NaCl and >5 mM magnesium greatly reduced excursion. Glycerol added to increase viscosity slowed confined diffusion of the tethered beads but did not change excursion. The confined-diffusion coefficients for all tethered beads were smaller than those expected for freely diffusing beads and decreased for shorter tethers. Tethered-particle motion is a sensitive framework for diffusion experiments in which small beads on long leashes most closely resemble freely diffusing, untethered beads.

Introduction

In tethered-particle motion (TPM) experiments (1,2), the motion of a microscopic or submicroscopic particle (bead) tethered to a surface by a single polymer, often DNA, is recorded over time. This motion is influenced by the size of the particle, the polymer length, the physical and chemical properties of the polymer, the solution in which the bead and the polymer diffuse, and the nearby surface. Although in experiments all these factors act simultaneously, simulations of beads tethered by DNA molecules have been used to focus on specific factors. For example, the volume-exclusion effect due to the proximity of the bead to the wall can be characterized by an excursion number (N) to indicate whether the motion of the bead is dominated by diffusion of the DNA (N < 1) or diffusion of the bead (N > 1) (3). The impenetrable surfaces restrict the motion of both the DNA and the attached bead to reduce entropy and effectively extend the tether. The tether also restricts the rotational freedom of the bead, and this effect decreases as the tether length increases.

Instead of exploring the DNA and bead diffusion in a TPM experiment, there are models that focus on the bead-DNA and coverslip-DNA interactions (4), which are likely to be significant across a broad range of bead radius and tether length combinations. The Gaussian chain (5) and wormlike chain (6) are the models predominantly used to estimate the average end-to-end distance of the tether, but they do not always accurately describe the motion of tethered particles near broad surfaces or rotationally limited particles. In addition, the bead + DNA assembly is most often assumed to diffuse in a homogeneous medium. However, layers of solution proximal to broad surfaces like the bead or the glass slide can be much more viscous than the more distal layers (7,8).

Among the most challenging aspects to simulate are the exceedingly large numbers of configurations available to DNA tethers of just a few kilobases and the effects of the solvent on the tether. Although statistical mechanical models based on elastic interactions in relatively small DNA fragments can be used to probe the interactions of these fragments with deformable proteins (9), longer DNA with geometrical constraints becomes a computational challenge for Monte Carlo schemes without adjustments to efficiently generate acceptable ensembles (Y.Y.Biton, S. Kumar, D. Dunlap, and D. Swigon, unpublished). In addition, tractable approaches must be further developed to accurately represent the hydrodynamics of diffusing DNA (10) and electrostatic interactions (11). The effects of individual parameters can also be highlighted in experiments. As shown below, a fundamental part of these experiments is the calibration of the excursion, a 2D projection of the end-to-end distance of the DNA tether, as a function of tether length. As in any single-molecule experiment, stringent criteria must be adopted to exclude molecules that are not properly assembled or that interact nonspecifically with the nearby surfaces. Exclusion of any tethered particle that does not exhibit a high degree of symmetry is a powerful screening tool, as shown previously (12). However, the simple requirement that the ellipticity in the scatter of positions observed for a tethered particle be <1.1 fails to exclude some particles with asymmetric motion. Instead, as shown below, the asymmetry becomes apparent in radial histograms of motion by individual particles. Furthermore, it is not sufficient to require uniform behavior throughout the observation of single particles. A significant number of tethered particles appear perfectly symmetric and nevertheless exhibit excursions that differ noticeably from those of most other particles. Criteria based on the average excursion may help identify beads with quite different ranges of motion, but comparing distributions of the excursion using a hierarchical classification scheme identifies similarities and subtle differences in distributions of excursions in an ensemble of tethered particles. As shown below, including these two selection criteria significantly improves the data in a calibration curve.

Another factor that undermines the calibrations based on the average or root mean-square excursion is that the signal becomes relatively insensitive to small changes in the length of the tether of a few kilobases or longer. Instead, plotting mean-square excursion versus DNA length should produce a linear relationship, which should not lose sensitivity at longer tether lengths. Therefore, new calibration experiments were performed to show that this alternative parameter remains sensitive to tether-length changes even for DNA molecules several kilobases in length. Switching calibration parameter for TPM produced remarkably linear calibration curves, which will facilitate the interpretation of topological changes in DNA, such as long-range protein-mediated DNA kinking or looping (13–16). Of course, even with improved calibration methods, subtle modifications of buffer conditions that significantly change excursion must also be taken into account. Therefore, representative calibrations in different buffers were performed to probe the sensitivity of the excursion amplitude to buffer composition. Although excursion amplitude remained constant for tethered beads in a Tris-HCl buffer with KCl concentrations from 10 to 200 mM, even as little as 5 mM MgCl₂ in a buffer of 10 mM KCl greatly reduced excursion. Instead, excursion in a Tris-acetate buffer with 100 mM potassium glutamate and 10 mM magnesium acetate was significantly larger than that observed in a Tris-HCl buffer with 200 mM KCl. Surprisingly, as little as 0.5% Tween added to the buffer containing 200 mM KCl significantly reduced excursions of beads across the entire range of tether lengths tested. These data emphasize the fact that the excursion is sensitive to the composition of the buffer and indicate that careful calibration is necessary for quantitative analysis.

The calibration experiments based on excursion relied heavily on accurately establishing the anchor point of the tether, which is usually achieved through averaging the scatter of positions recorded for a tethered bead. Large numbers of points naturally improve the average at the expense of time resolution, and as shown below, tens of seconds are required to accurately locate the anchor point for a tethered bead in a solution of high viscosity. An alternative method of TPM analysis that dispenses with the need to locate the anchor point is to focus on the dynamics of particle diffusion (8,17). Measuring the mean-square displacements (MSDs) of beads in TPM experiments produces estimates of the confined diffusion coefficients of the beads and the confinement boundary due to the DNA tether, which are more intuitive physical parameters than average excursion. In addition, the effects of viscosity can be directly examined through changes of the confined-diffusion coefficients. Here, MSDs were calculated as a function of time intervals, bead radii, tether lengths, and viscosity, and analyzed with a statistical model of confined motion (18). In these experiments, the excursion number was >1, and tethered beads might have been expected to diffuse with Stokes-Einstein behavior throughout a hemisphere of a size set by the DNA tether length. However, tethered microspheres diffused significantly more slowly than expected for freely diffusing beads, most likely due to increased viscosity of the solution near the bead and anchor surfaces. The confined-diffusion coefficients were found to increase with the DNA tether length, especially for smaller tethered beads.

Methods

DNA preparation

DNA fragments were prepared using the polymerase chain reaction with plasmid DNA as templates, deoxyribonucleotides (Fermentas-Thermo Fisher Scientific Inc., Pittsburgh, PA), and biotin- and digoxigenin-labeled primers (Invitrogen, Life Technologies Corporation, Grand Island, NY, or Integrated DNA Technologies, Coralville, IA) with Taq polymerase (New England BioLabs, Ipswich, MA). All amplicons were purified using silica-membrane-based purification kits (Qiagen, Germantown, MD) and the lengths were checked by gel electrophoresis. The details of the plasmids and primers are available on request.

Chamber preparation

For a detailed description of the chamber preparation protocol, see the Supporting Material.

The flow chambers were prepared using either 240-nm-radius polystyrene beads coated with antidigoxigenin (Indicia Biotechnology, Oullins, France) or 160-nm-radius polystyrene beads coated with streptavidin (Spherotech, Lake Forest, IL).

For 160-nm (radius) beads, TPM chambers were assembled between a coverslip and a microscope slide using a parafilm spacer. Coverslips with dimensions 22 × 22 mm and thickness 0.13–0.17 mm (Gold Seal coverglass, no. 1) and glass microscope slides were cleaned with soapy water, rinsed in deionized water, and then stored in 100% ethanol. Parafilm was cut to make an S-shaped flow channel with a wide entrance and a narrow exit. The parafilm was placed between an air-dried microscope slide and coverslip and heated mildly to seal it to the glass. Such chambers made with parafilm spacers exhibit less drift than those with double-sided tape (19). The chamber volume was ∼30–50 μL. A 150 μL droplet of 0.2 μM filtered phosphate-buffered saline (pH 7.4, 10 mM phosphate, and 150 mM sodium chloride) to the wider opening of the chamber and drawn into the chamber by capillary action. Then 100 μL of 20 μg/mL antidigoxigenin (Roche, Basel, Switzerland) in phosphate-buffered saline was introduced into the chamber and incubated it at high humidity for ∼2 h at room temperature or overnight at 4°C. The chamber was gently flushed with 150 μL of 10 mM Tris-HCl, pH 7.4, 200 mM KCl, and 0.5 mg/mL α-casein and incubated for at least 5 min to passivate the glass. DNA labeled with digoxigenin on one end and biotin on the other end was incubated with streptavidin-coated beads in 10 mM Tris-HCl, pH 7.4, and 200 mM KCl for 10 min at room temperature. The final DNA concentration was ∼100 pM and ∼10 times more beads were used to avoid beads with multiple tethers. To block the unreacted streptavidin 2 μL of 0.1 μM d-biotin (Sigma, St. Louis, MO) in TE buffer (10 mM Tris-HCl, pH 8.0, and 1 mM EDTA) was added to the bead-DNA solution and incubated for 5 min. The chamber was then gently flushed with 250 μL of λ buffer (10 mM Tris-HCl, pH 7.4, 200 mM KCl, 5% dimethylsulfoxide, 0.1 mM EDTA, 0.2 mM dithiothreitol (DTT), and 0.1 mg/mL α-casein). A previously described protocol (16) was used for TPM experiments with 240 nm (radius) beads in λ buffer or 160 nm beads in TR buffer (20 mM Tris-acetate, pH 7.9, 2 mM DTT, 100 mM potassium glutamate, 8 mM magnesium acetate, and 0.5 mg/mL α-casein).

In one series of experiments the viscosity of the λ buffer was changed by increasing the glycerol concentration. The glycerol concentrations used were 0, 20, 30, 50, and 70%, v/v, which corresponds to viscosities of 1.006, 2, 3, 8, and 35.5 in centipoise (20).

Particle tracking, data acquisition, and instrumentation

All TPM was measured at room temperature. A Leica DM LB-100 microscope (Leica Microsystems, Wetzlar, Germany) with oil-immersion objectives (100×, NA 1.2–1.4 or 63×, NA 0.6–1.4) was used to observe tethered beads with differential interference contrast (DIC). DIC has a high signal/noise ratio and allowed short 1 ms exposures with no significant blurring due to motion of the beads (12,21). The user interactively selected single particles (small and symmetric) with circular ranges of motion by circumscribing them in a rectangular region of interest. Standard interlaced video at 50 Hz from a CV-A60 CCD camera (JAI, Copenhagen, Denmark) digitized with an IMAQ PCI-1409 frame grabber (National Instruments, Austin, TX) was analyzed in real time using custom Lab View (National Instruments) routines. The position of each bead was determined in each video frame and the time series of xy coordinates was stored in a text file. In DIC, the bead appears as juxtaposed bright and dark semicircles, and the centroids of both were averaged to establish the bead position. The routine accurately tracks up to 30 beads in real time on a personal computer with 512 MB of 133 MHz RAM and an AMD Sempron 3100+ processor operating at 1.8 GHz. Further details about the instrumentation and the real-time analysis are available (22).

Data preprocessing and drift calculations

Only time series for tethered beads that did not stick directly to the surface during observation were used for the drift calculations. If there were fewer than three beads in a field of view, that field was discarded. A 40 s moving average (center of mass) for the selected beads in a video frame was calculated and subtracted from all the beads to remove the low-frequency drift without reducing the independent Brownian motion of the bead (22). Time series for beads with intervals in which the bead transiently stuck to the surface were edited to eliminate such intervals and use as much of the experimental data as possible. The time series lasting more than a minute were used in the next step of data preprocessing.

Selection of beads

After both symmetry and amplitude selection (see the next section), the total number of beads included in analyses for each experiment ranged from 2 to 63 (see Tables S1–S5). Recordings from an average of 16 beads giving an aggregate observation time of 80 min were used to determine excursions in each condition.

Symmetry

Beads that are attached to the surface by one DNA tether will exhibit symmetrical excursions about the anchor point, whereas those attached to two or more widely separated points will not. Therefore, the symmetry of the drift-corrected beads was checked in two qualitative and one quantitative ways. First, the user judged whether or not the scatter of xy positions of the drift-corrected beads was circular (Fig. S1 A in the Supporting Material). Second, a radial histogram of the angular coordinates was displayed for the user to judge whether or not the bead equally sampled all sectors of the available hemisphere (Fig. S1 B). Third, a covariance matrix of the xy positions was constructed, and the ratio of the longest to the shortest diagonal was determined by calculating the square root of the ratio of the eigen values of the covariance matrix (12,23). Previously, Han et al. (12) accepted beads with a diagonal ratio ≤1.1. In this study, only beads with a diagonal ratio <1.07 were included for further analysis.

Distribution of excursions

To exclude beads attached to two or more DNA tethers that passed the symmetry test and small clusters of beads on a tether, and to assemble a set of beads of the same size attached to single DNA tethers, Nelson et al. (22) rejected beads with distributions of excursions (ρ distributions) that were unlike the majority. Here, the JMP routine from SAS (JMP, Version 9, SAS Institute, Cary, NC) was used to hierarchically cluster ρ distributions using a centroid method to reject outliers and select beads with similar ρ distributions (Fig. S2).

Results and Discussion

Raw traces

To assess excursions on the scale of tens or hundreds of nanometers, false motion due to vibration or thermal expansion/contraction of the microscope must be eliminated. Alternative procedures involve low-pass filtering (12,24) or averaging the motion of a bead over intervals greater than the relaxation time, the time required for the diffusing bead to evenly sample the available hemisphere (8,15). For the experiments described herein, drift was eliminated by subtracting the average position of several tethered beads within the same field of view (22). After drift correction, a bead that satisfied symmetry selection (see Methods) exhibited a circular cloud of xy positions over time, as shown in Fig. 1 a for a 240-nm-radius bead attached to a 2211 basepairs (bp) DNA tether. A further assessment of symmetry was based on a radial distribution function, as shown in Fig. S1, because although some tethered beads exhibited an apparently symmetric cloud of positions, angular histograms of those positions were uneven. In Fig. 1 the x (Fig. 1 c) and y (Fig. 1 b) positions are shown to fluctuate over a constant range as a function of time. Fig. 1 d shows the normalized frequency distribution of excursions, ρ, for the same bead, which was neither a Gaussian nor a Rayleigh function (25) due to the size of the bead.

Figure 1.

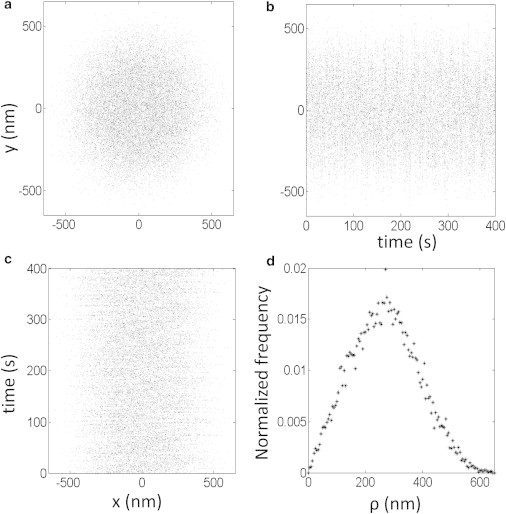
Representative excursion data. A bead with a radius of 240 nm attached to a DNA tether 2211 bp long was tracked for 400 s. (a–c) xy positions (a), x-positions (b), or y-positions (c) are shown as a function of time. (d) Normalized distribution of the projected distances to the anchor point, ρ, are shown for the same time interval.

A second selection was made on the basis of the distribution of ρ values observed for different tethered beads. Many beads exhibited similar ρ distributions, which overlapped to a large degree, as shown in Fig. S2. However, there were a few beads that displayed distinctly different distributions and occupied separate branches of a hierarchical clustering analysis (see Methods). These were discarded, and only distributions in the main cluster were further analyzed.

Mean-square excursion requires averaging

To estimate the excursion amplitude, ${\rho }_t^2={\left({\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2\right)}_t,$ the point of attachment of the tether, $x_t,y_t$ (x and y time averages), must be accurately determined. However, the anchor point cannot be located accurately if the bead does not adequately and evenly explore the available hemisphere. As shown in Fig. 2, positions of a tethered bead in a viscous medium during the first second of observation clustered in the upper right quadrant, and even after 4 s, the xy range had not extended far enough. Anchor points based on these distributions (light blue and red crosses) were clearly quite far from the true anchor (purple cross), an accurate estimation of which required at least 40 s of observation.

Figure 2.

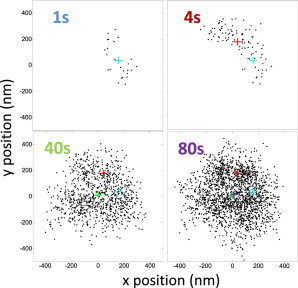
Prediction of anchor points as a function of the averaging time. In λ buffer containing 70% glycerol (v/v), a bead with a radius of 160 nm, attached to a DNA tether 1749 bp in length, was tracked for the time intervals indicated. Black dots are the positions of the bead, and the + symbol indicates the anchor point determined by $x_t,y_t$ (x and y averages). Positions and anchor points are shown for time intervals of 1, 4, 40, or 80 s. An interval of at least 40 s was necessary to accurately predict the anchor point. To see this figure in color, go online.

To further illustrate this time limitation, the excursions of tethered beads in media of differing viscosities were calculated using anchor points determined with a range of observation times. In Fig. 3, plots of ${\rho }_t^{2}vst$ for beads of 160 nm radius tethered by 2103 bp DNA in media of different viscosities show that the averaging time required for maximum excursion increases with viscosity of the medium. This was the case for all DNA tether lengths and also for larger bead radii, although measured excursions were larger for bigger beads than for smaller ones, as previously noted (12). When the glycerol percentage was increased to 50%, slowly diffusing submicron beads required one order of magnitude more time to fully explore the volumes available to them, often referred to as the relaxation time. The confined diffusion of the bead in glycerol was lowered by a factor of 35 compared to the value expected based on the Stokes-Einstein relation,

$$D=\frac{k_{\text{B}}T}{6\pi \eta R},$$ (1)

where D is the Stokes-Einstein diffusion coefficient, $k_{\text{B}}$ is the Boltzmann constant, T is the absolute temperature, η is the viscosity, and R is the radius of the bead. Nevertheless, the maximum excursion was independent of viscosity, indicating that glycerol negligibly altered the flexibility of the DNA.

Figure 3.

Mean-square excursion measured for different observation times and viscosities. The mean-square excursion for a bead with a radius of 160 nm attached to a DNA tether 2103 bp long, in λ buffer containing various percentages of glycerol (0, 20, 30, 50, and 70% (v/v)) was calculated using the formula ${\rho }_t^2={\left({\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2\right)}_t$, for times t = 0.04, 0.08, 0.16, 0.32, 0.64, 1.28, 2.56, 5.12, 10.24, 20.48, 40.96, 81.92 s and plotted against log(t). The points corresponding to the same viscosities (percentage of glycerol) are connected using smooth lines. A tethered bead required a longer time to reach the maximum excursion in a higher-viscosity solution. Error bars indicate standard deviations of the time-averaged excursions measured for an ensemble of symmetrically moving tethered beads with closely clustered values.

Scaling excursion to effective DNA tether length

The excursion of a bead on a DNA tether is much smaller than the contour length of the DNA due to the entropy of the flexible polymer. Without an analytical formula that relates the length of the tether to the excursion of the bead, the excursion must be calibrated for different polymer lengths in the buffer of interest. Different laboratories have used slightly different methods to track microspheres attached to DNA tethers and have also used different parameters for excursion. Some researchers (26–28) have used a moving average of ρ $\left({\rho }_t={\left(\sqrt{{\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2}\right)}_t\right)$, and Vanzi et al. (24) used a Gaussian filtered moving average of ρ to minimize windowing effects. Braslavsky et al. (29) used the radius corresponding to the half-height of the radial distribution function. Manghi et al. (8) used the standard deviation of ρ. Others have used the effective size of beads in averaged images, δ (2,30), and ρ_rms, $\sqrt{{\rho }_t^2}=\sqrt{{\left({\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2\right)}_t}$, has also been used (4,12,16,19,31).

Several of these first-moment-type parameters exhibit curves in which excursion becomes less and less sensitive to tether-length changes as the tether length increases (see Fig. S3). However, an instructive description of the tethered bead system is to consider the DNA as a freely jointed chain and the distance from the point of attachment on the bead to the center as the final (Kuhn) link in the chain (8,32,33). Although the radii of the beads used here are 1.6–2.4 times larger than the Kuhn length of DNA (∼100 nm), this description suggests that the square of the average end-to-end distance (R) will be equal to the contour length (L) scaled by the Kuhn length (l), $R^2=L\ell$. Therefore, the mean-square excursion values for two different bead sizes (radii of 160 and 240 nm) attached to different DNA tethers were determined using the formula ${\rho }_t^2={\left({\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2\right)}_t$, with t = 20.48 s. A long time was chosen to make sure that even the bigger bead attached to the longest DNA reached the maximum excursion (12,31,34). Calibration curves of ${\rho }_{\text{max}}^2\left({\rho }_{20.48s}^2\right)$ as a function of tether length for beads of the same size were linear, which allows a wider range of tether lengths to be estimated from TPM (Fig. 4).

Figure 4.

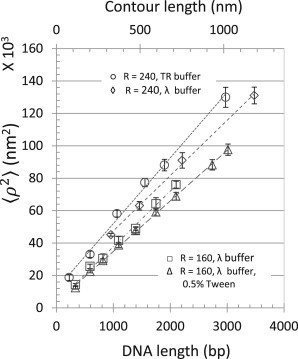
Calibration of mean-square excursion versus DNA contour length. Mean-square excursion values for two sizes of tethered beads (radii of 160 and 240 nm) in different buffers were calculated using the formula ${\rho }_t^2={\left({\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2\right)}_t$, with t = 20.48 s. The data, ${\rho }_{20.48s}^2$, with linear fits are for 240 nm radii beads in λ buffer (<ρ²> = 100.39 × L + 13,383, ⋄), 160-nm-radius beads in λ buffer (<ρ²> = 100.89 × L + 3445, □), 160-nm-radius beads in λ buffer with added Tween (0.5%) (<ρ²> = 91.79 × L + 3594, Δ), and 240-nm-radius beads in TR buffer (<ρ²> = 119.16 × L + 11,475, ○). Error bars indicate standard deviations of the time-averaged excursions measured for an ensemble of symmetrically moving tethered beads with closely clustered values.

Indeed, Nelson et al. compared ${\rho }_{\text{average}}={\sqrt{{\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2}}_t$ and ${\rho }_{\text{rms}}=\sqrt{{\left({\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2\right)}_t}$ for calibrations (22), and Fig. S3 shows a similar calibration based on ρ_rms for two bead sizes. In the case of ρ_rms, the slope of the curve decreases as the DNA contour length increases. In contrast, the mean-square excursion, ${\rho }_t^2={\left({\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2\right)}_t$, is linear across the domain of our experiment. This extends the useful range of TPM experiments and improves the discrimination of small length changes. Yin et al. (2) produced a linear calibration of ρ_rms versus DNA contour length, but suggested that according to the elastic chain model (35), ρ_rms should be proportional to the square root of contour length. They also suggested that the volume exclusion effect of the bead and the glass surface might be the reason for the discrepancy. Brinkers et al. (36) plotted mean-square excursion versus contour length, and although they compared their data to a 2D wormlike chain, a 2D wormlike chain that accounts for volume exclusion in TPM (3), and Monte Carlo simulations, which are all close to linear, the deviations associated with their TPM data undermine conclusions based on curve fitting.

In comparison, the stringent selection of beads described here produced lower deviations and may be used to discriminate models more effectively. For example, the fitted lines for both 160 and 240 nm beads have similar slopes but different y intercepts. The curve does not pass through the origin, as suggested by Yin et al. (2), and perhaps the slope of the line reflects properties of the DNA, e.g., flexibility, whereas the y intercept is most indicative of the bead size. Using the freely jointed chain model, the mean-square end-to-end distance is given by $R^2=R_x^2+R_y^2+R_z^2$. In TPM experiments, the motion of the bead in the z direction is restricted by the coverslip and the DNA tether, whereas that in the xy direction is confined by the tether only. As a simple approximation, $R_x^2=R_y^2=2R_z^2$, and using the fact that we observe the 2D projection of this 3D motion gives $R_{xy}^2=4L\ell /5$. This suggests that the underlying expression for the slope should have the form $8\xi /5$, where ξ is the persistence length in nanometers. Solving for the observed slope for beads with 160 nm radius in λ buffer with 0.5% Tween gives ξ ≈ 57 nm, which corresponds well to what was found in other TPM experiments (22,26,36).

Mean-square excursion versus [KCl]

With a broad selection of DNA sequences, lengths, and ionic conditions available, TPM is one of the best experimental formats for investigating subtle changes in the properties of DNA. This double-stranded polymer has a high negative charge density, and significant rigidity derives from stacking of the basepairs. The stiffness of the DNA depends on both the sequence (free energy) of the base stacking (37) and ionic shielding of the repulsions between negatively charged phosphate groups along the sugar-phosphate backbones (38).

Average DNA extension directly reflects the effects of ions that modify compaction or condensation of the DNA tether. Theoretical studies by Odijk et al. (39) and Skolnick and Fixman et al. (40) have shown the effects of positive ions on the flexibility of DNA. According to their theory, physiological concentrations of cations are sufficient to shield the negative charges of phosphates along the DNA to reduce repulsions, and even higher concentrations do not significantly increase the flexibility of the DNA. On the other hand, lower cation concentrations only partially shield repulsions between the phosphates, leading to stiffer DNA. They also suggest that the charge shielding has a minor effect and that basepair stacking (elasticity) plays a dominant role in the stiffness of the DNA. However, Manning et al. studied the effect of electrostatic repulsion of the phosphate groups on the flexibility of DNA and considered it to be the dominant factor (38). Biton et al. have developed a more complete theoretical model of DNA that considers both the elasticity and the electrostatic interactions and have nicely shown the effect of NaCl concentration on the structure of a 549 bp DNA minicircle (41). In a recent article, Savelyev et al. suggested that both elasticity and electrostatics contribute equally to the flexibility of DNA in the presence of monovalent ions (42).

To investigate the sensitivity of TPM to monovalent salt concentration, the mean excursion was studied as a function of KCl concentration, since potassium is an important intracellular cation (43). In the range 10–200 mM KCl, the mean excursion changed negligibly (Fig. 5). Across this range of monovalent salt concentrations, both Savelyev et al. and Odijk-Skolnick-Fixman theory predict similar DNA flexibility, which suggests that the determining factor in DNA flexibility in these conditions is basepair stacking. Most of the above studies have been done with Na⁺, and different cations do have different effects on DNA conformation. For example, although the contributions of Na⁺ and K⁺ to the stabilization of duplex DNA are very similar (44), it is known that only K⁺ stabilizes certain DNA quadruplexes (45–47). However, it is the duplex form of DNA that is relevant to these TPM experiments, and the persistence length of the DNA tethers does not change across the salt concentrations used in this study.

Figure 5.

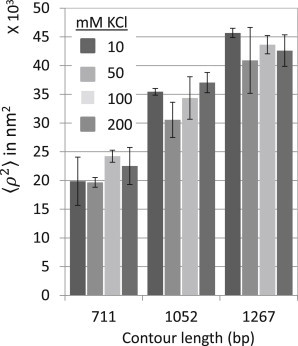
Effect of potassium chloride (KCl) concentration on mean-square excursion. The excursions of beads with 240 nm radius attached to 711-, 1052-, or 1267-bp-long DNA tethers, were measured in buffer (10 mM Tris-HCl, pH 7.4, 5% dimethylsulfoxide, 0.1 mM EDTA, 0.2 mM DTT, and 0.1 mg/ml α-casein) supplemented with 10, 50, 100, or 200 mM KCl. The mean-square excursion of beads attached to DNA tethers changed negligibly within the range of KCl used. Error bars indicate standard deviations of the time-averaged excursions measured for an ensemble of symmetrically moving tethered beads with closely clustered values.

Mean-square excursion versus [Mg²⁺]

Since magnesium is another intracellular cation that is especially important for the stability and proper function of DNA (43), its interactions with DNA have been thoroughly studied and compared to those involving monovalent cations (44). Like potassium, magnesium has unique interactions with DNA that differ significantly from those of other bivalent cations like zinc and calcium. Monovalent cations mainly shield the negative phosphates. Mg²⁺ does this as well, but in addition, through associated waters of hydration, it can establish long-range interactions with sites in the DNA backbone that significantly affect the double helix (43). These interactions can increase the flexibility and compaction of DNA.

Indeed, Dietrich et al. (26) have shown that the end-to-end distance of a DNA molecule decreases with increasing Mg²⁺ concentration. It has also been shown that monovalent and divalent cations compete to shield the negative phosphates (48), and this competition has been quantified (44). To highlight the effects of Mg²⁺, the K⁺ concentration was kept at 10 mM in TPM experiments using beads of 240 nm radius attached to DNA tethers 250 nm long (Fig. S4). For concentrations >3 mM MgCl₂, the motion decreased significantly, as expected, since magnesium is known to shrink the persistence length of DNA and reduce the end-to-end distance (extension) of tethered DNA under tension (49). However, magnesium-induced compaction of DNA tethers depends on buffer conditions. For example, no DNA compaction was observed in TPM experiments with 4 mM MgCl₂ and 130 mM KCl (12) or with 10 mM MgCl₂ and 100 mM KCl (31). In a similar way, in the experiments reported here, no tether compaction was observed in TR buffer with 100 mM KCl (Figs. 4 and S3), and the excursions were even larger than those observed in λ buffer with twice as much KCl.

Calculating the MSD

Mean-square excursion reports on the equilibrium of the bead-DNA-wall system. However, the position of the moving bead as a function of time can be used to study the dynamics of the system. The MSD for different time lags (Δt) can be calculated to determine the confined-diffusion coefficient of a tethered particle. Either all (Eq. 2) or randomly selected (Eq. 3) pairs of positions with identical time lags can be used:

$$\text{MSD}=r^2{\left(n\right)}_A=\frac{1}{N-n}\sum _{i=0}^{N-n-1}{\left[\overrightarrow{r}\left(i+n\right)-\overrightarrow{r}\left(i\right)\right]}^2$$ (2)

$$\text{MSD}=r^2{\left(n\right)}_I=\frac{n}{N-1}\sum _{i=1}^{\left(N-1\right)/n}{\left[\overrightarrow{r}\left(ni\right)-\overrightarrow{r}\left(ni-n\right)\right]}^2$$ (3)

In these equations, a time series of N particle positions, including the position at time 0, is the input. If the time between successive frames, $\delta t$, is constant, the number of frames, n, is proportional to the time lag $\left(\text{Δ}t=n\delta t\right)$ for MSD calculations. The subscripts I and A indicate independent and all pairs, respectively, and although both methods give similar and reliable MSDs, as long as the maximum time lag is less than a quarter of the total observation time, MSD calculations for all pairs is the method of choice in most cases (50). Equation 2 (calculating for all pairs) was used to determine the MSD in the next section.

Calculating the confined-diffusion coefficient (D_c)

One-dimensional MSDs $\left({\text{MSD}}_{\text{Δ}t}\left(x\right)\right)$ were calculated for different time lags (Δt) and plotted (Fig. S5). The calculated MSD asymptotically approached a maximum value, which is characteristic of confined diffusion (18,51), as expected for DNA-tethered beads. If the time lag (Δt) used to calculate the MSD is much smaller than the available area divided by the confined-diffusion coefficient, $\left({\rho }_t^2/4D_c\right)$, the relaxation time (τ) (21), ${\text{MSD}}_{\text{Δ}t}=4D_c\text{Δ}t$ can be used to calculate D_c (51). Otherwise, unexpectedly low values may result. For example, Dietrich et al. have calculated 1D confined-motion coefficients of the beads in TPM experiments using ${\text{MSD}}_{\text{Δ}t}=2D_c\text{Δ}t$, so called because they were much lower than expected from the Stokes-Einstein relation (26). The shortest time lag (Δt) used by Dietrich et al. was 50–80 ms, which was actually at least 10 times larger than ${\rho }_t^2/4D$ (equal to 5 ms in their work), and they reasoned that this long exposure time and increased drag because of the proximity of the bead to the gold support might have been responsible for the low value. Indeed, very short exposures with frame rates of 300–500 Hz allowed accurate calculation of the confined-motion coefficient of small tethered beads (17).

For the experiments reported here, the video frame interval was on the same scale as the relaxation times for 160 nm beads on short DNA tethers in low-viscosity buffer (Tables S8 and S9), and therefore, D_c could not be determined from the displacement versus time modeled as MSD_Δt = 4D_cΔt. However, Kusumi et al. (18) have derived a statistical formula to fit the 1D MSDs for different time lags that uses fitting parameters to calculate the coefficient and confinement of diffusion:

$${\text{MSD}}_{\text{Δ}t}\left(x\right)=\frac{L_x^2}{6}-\frac{16L_x^2}{{\pi }^4}{\sum }_{n=1\left(\text{odd}\right)}^{\infty }\frac{1}{n^4}\text{exp}\left\{-\frac{1}{2}{\left(\frac{n\pi {\sigma }_x}{L_x}\right)}^2\text{Δ}t\right\},$$ (4)

where L_x is a measure of the confinement and the maximum MSD(x) is equal to $L_x^2\text{/}6$ (see below). In contrast, σ_x is related to the confined-diffusion coefficient by the equation $D_c=D_x={\sigma }_x^2/2$. To calculate the confined-diffusion coefficient of beads in TPM experiments, MSD_Δt(x) values were calculated using Eq. 2, and plots of MSD versus Δt were fit using Eq. 4 to estimate L_x and σ_x. Fig. S5 is an example of such a fit. No correction for blur was necessary for the exposure time of 1 ms that was used (21).

${\mathit{L}}_{\mathit{x}}^2$ versus tether length

$L_x^2$ versus tether length exhibits a linear relationship in which the confinement parameter is based only on MSDs (Fig. 6) and constitutes an alternative to the mean-square excursion calibration. This avoids the need to determine the anchor point, which requires careful selection of the averaging time, but the image sequence must still be rapid enough to report diffusion and of sufficient duration to reveal boundaries.

Figure 6.

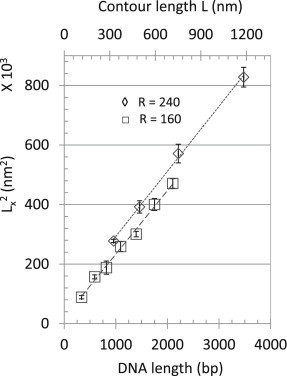
Calibration of DNA contour length versus $L_x^2$. $L_x^2$ was determined from the fit of ${\text{MSD}}_{\text{Δ}t}\left(x\right)$ versus $\text{Δ}t$ for ensembles of tethered beads and plotted as a function of the contour length (L) of the DNA tether. Linear fits to the averaged data were L_x² = 642.87 × L + 74,416 for beads of radius 240 nm (⋄) or L_x² = 627.32 × L + 59,670 for beads of radius 160 nm (□). Error bars indicate standard deviations of $L_x^2$ values determined for an ensemble of identically assembled tethered beads.

Relationship between mean-square excursion and MSD

Qian et al. have shown how the MSD is related to the mean-square excursion through the position correlation function (51):

$$g_r\left(\text{Δ}t\right)=\langle \overrightarrow{r}\left(\text{Δ}t\right)\overrightarrow{r}\left(0\right)\rangle =\langle {\rho }^2\rangle -\frac{{\text{MSD}}_{\text{Δ}t}}{2}$$ (5)

From this equation, ${\text{MSD}}_{\infty }=2\left({\rho }^2-{\overrightarrow{r}}^2\right)$, where ${\rho }^2$ is the maximum mean-square excursion and $\overrightarrow{r}$ is the center of the distribution, which in this case is the anchor point (0,0). From Eqs. 4 and 5,

$${\text{MSD}}_{\infty }\left(x\right)=\frac{L_x^2}{6}=2x^2$$

and

$$x^2=\frac{L_x^2}{12},$$

and by symmetry,

$${\rho }^2=x^2+y^2=\frac{L_x^2}{6}.$$ (6)

Indeed, the slope of the mean-square excursion versus contour length (Fig. 4) is six times smaller than $L_x^2$ versus contour length (Fig. 6). Although these two different statistical methods for calculating the excursion are related, the correct determination of the maximum excursion, ${\rho }_t^2$, was very sensitive to the choice of t (8,21). Once the averaging or relaxation time (t) required to correctly determine the maximum excursion is discovered using MSD measurements, it may be more expedient to rely on ${\rho }^2$ calculated using straightforward moving averages to interpret dynamic changes in tether length. However, the calculation of $L_x^2$ is a more robust choice, since it does not require a priori selection of an averaging time, t, within which to establish the anchor point.

Confined diffusion of beads in TPM experiments

The confined-motion coefficients for beads of 40 nm radius tethered by 4882 bp DNA-tether molecules have been shown by Dietrich et al. (26) to decrease with increasing viscosity (glycerol concentration). In that report, the authors also compared the confined motion to that expected for a freely diffusing bead based on the Stokes-Einstein relation (Eq. 1). To elaborate on this previous work using conditions in which exposure time would not affect the results, TPM experiments were conducted with different DNA tether lengths at different viscosities for two bead sizes. Fig. 3 shows that as viscosity increased, tethered beads required a longer time to explore the available hemisphere and exhibit the maximum excursion. To quantify the effect of bead size and DNA tether length as well, confined-diffusion coefficients based on the data in Fig. 6 were determined using the fitting procedure described above. For all tethered particles, D_c was proportional to 1/η (Tables S6 and S7), and D_cηR versus contour length was plotted to demonstrate the effect of the tether length and the bead size on diffusion. All of the beads diffused more slowly than expected from the Stokes-Einstein relation (Fig. 7, dotted line). Curiously, the confined diffusion of identically sized beads was roughly a linear function of tether length, and relatively smaller beads attached to relatively longer DNA tethers most closely exhibited diffusion characteristic of free particles. This suggests that the confined diffusion of a tethered particle reflects the entropy of the DNA tether. A long tether with many available configurations accommodates effectively free diffusion by the bead, whereas a short tether with lower configurational entropy restricts the bead.

Figure 7.

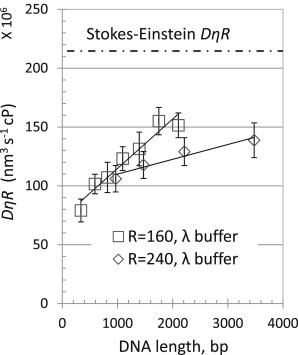
$D_c\eta R$ versus contour length. $D_c\eta R$ for viscosities 1.006, 2, 3, and 8 cP (0, 20, 30, and 50% glycerol) were calculated and the averages were plotted for tethered beads of 160 nm (□) and 240 nm (⋄) radius as a function of the contour length of the DNA tether. D_c is the diffusion coefficient, η is the viscosity, and R is the radius of the bead. Error bars indicate standard deviations of D_c values determined for ensembles of symmetric, tethered beads.

In a theoretical description of TPM, Segall et al. defined an excursion number based on the bead radius, R, the contour length of the tether, L, and the persistence length of the tether, ξ (3): $N_R=R/\sqrt{L\xi /3}$. They suggested that when N_R < 1, the tether dominates TPM such that the hydrodynamics and entropy of the tether will direct the motion of the bead, but when N_R > 1, the Brownian motion of the bead is dominant. For the TPM experiments presented here, the smallest value of N_R is 1.47 (a bead of 160 nm radius attached to DNA of 2103 bp with an assumed persistence length of 50 nm), for which the confined-diffusion coefficient was ∼75% of that corresponding to an untethered particle (Table S6).

If the DNA tether were to act as an ideal spring, on a short timescale a tethered bead would follow the Stokes-Einstein relation (Eq. 1) and D_c would be equal to that of a freely diffusing bead (17). Over longer times, restriction by the tether dominates the apparent motion, reducing D_c. However, particles near a wall experience increased drag forces and diffuse more slowly (52,53). In this case, assuming that the tether only determines the volume accessible to the bead by acting as an ideal spring, the confined-diffusion coefficient of the bead should reflect the weighted average of the diffusion coefficients corresponding to the positions visited by the bead. According to Faxen’s law (7),

$$D_{\text{exp}}=\frac{D_{\text{SE}}}{1-\frac{9R}{16h}+\frac{R^3}{8h^3}-\frac{45R^4}{256h^4}-\frac{R^5}{16h^5}},$$ (7)

where $D_{\text{exp}}$ is the diffusion coefficient determined experimentally, is the Stokes-Einstein diffusion coefficient for a free bead at infinite height relative to the wall, R is the radius of the bead, and h is the apparent or average distance of the bead center from the wall (a glass slide in this case). Using this formula to calculate h for beads in these experiments produced values close to those predicted by Segall et al. (3) (Table 1). The slight discrepancies might be due to the fact that the theoretical formula by Segall et al. is based on a Gaussian random walk. Indeed, it has been reported that using a Gaussian random walk model of the theoretical height $\left(r_z\right)$ distribution did not predict experimental $r_z$ distributions very well (25). One may consider that without the constraints of a TPM experiment, a bead would diffuse according to the Stokes-Einstein relation and a DNA molecule would behave like a freely jointed chain. The confined diffusion of a tethered bead is a combination of both these effects (8). Confined diffusion should reflect the characteristics of the bead when it is relatively large compared to the DNA and vice versa. This might underlie the differences between the average distance of the bead from the surface, h, estimated using these two methods.

Table 1.

Average height of the center of the bead from the coverslip

DNA length (bp)	h from Faxen’s law (nm)	h from Segall et al. (nm)
336	162	179
590	179	217
817	181	224
1093	206	251
1394	209	262
1749	271	291
2103	314	309

The first column shows the different DNA tether lengths attached to beads of 160 nm radii. Fitting excursion data to Faxen’s law (Eq. 7) gives the h values shown in the middle column. Using equations from Segall et al. (3). $\frac{r_z}{\sqrt{L\xi }}=\frac{2\left(1-e^{-N_R^2}\right)}{\sqrt{\text{π}}\text{erf}\left(N_R\right)}+N_R\frac{2-\text{erf}\left(N_R\right)}{\text{erf}\left(N_R\right)}$ and $\frac{r_{xy}^2}{L\xi /3}=2+\frac{4N_R}{\sqrt{\text{π}}\text{erf}\left(N_R\right)}$, where $N_R\equiv R/\sqrt{L\xi }$, the ratio of the average height of the tethered bead center to its root mean-square motion in the plane is given by $\left(r_z/\sqrt{r_{xy}^2}\right)$. The average heights of the tethered beads in the above experiments were predicted using $h=r_z/\sqrt{r_{xy}^2}{\rho }_{rms}$ and are shown in the righthand column.

Conclusions

In TPM experiments, excluded volume effects involving the bead in proximity to the glass, and the DNA in proximity to both the bead and the glass, effectively extend the tether slightly. This loss of entropy also applies to rotation of the bead especially for shorter lengths of DNA. In addition the viscosity of the buffer in proximity to the surfaces slows the diffusion of the tethered beads significantly compared to freely diffusing beads. The complexity of these factors requires that the excursion be calibrated to accurately interpret topological changes in a DNA tether. If data are stringently selected based on symmetry, useful calibrations based on hierarchical clustering of mean square excursion can be assembled for a wide range of tether lengths.

Much TPM analysis relies on determining the boundary of diffusion as an indicator of the tether length. To accurately assess this boundary, the bead must be allowed to adequately explore the entire hemisphere, which requires multiple observations over a time interval dependent on the rate of diffusion and the size of the hemisphere. As an alternative, it is noteworthy that the confined-diffusion coefficient of tethered particles was proportional to the tether length. This relationship suggests that D_c might be used as a calibration parameter for which there would be no need to establish an anchor point. Drift correction based on the motion of reference particles would be essential, and screening of sticking artifacts based on excursions averaged over longer time intervals would be prudent. Nonetheless, using diffusion to indicate tether length should be particularly effective for smaller tethered beads and require only the minimal time necessary to measure the MSD. For example, the first value of MSD in Fig. S5 was measured in only 0.04 s, whereas the boundary was not evident until 0.16 s.