Cellular Sensory Mechanisms for Detecting Specific Fold-Changes in Extracellular Cues

Abstract

Cellular sensory systems often respond not to the absolute levels of inputs but to the fold-changes in inputs. Such a property is called fold-change detection (FCD) and is important for accurately sensing dynamic changes in environmental signals in the presence of fluctuations in their absolute levels. Previous studies defined FCD as input-scale invariance and proposed several biochemical models that achieve such a condition. Here, we prove that the previous FCD models can be approximated by a log-differentiator. Although the log-differentiator satisfies the input-scale invariance requirement, its response amplitude and response duration strongly depend on the input timescale. This creates limitations in the specificity and repeatability of detecting fold-changes in inputs. Nevertheless, FCD with specificity and repeatability by cells has been reported in the context of Drosophila wing development. Motivated by this fact and by extending previous FCD models, we here propose two possible mechanisms to achieve FCD with specificity and repeatability. One is the integrate-and-fire type: a system integrates the rate of temporal change in input and makes a response when the integrated value reaches a constant threshold, and this is followed by the reset of the integrated value. The other is the dynamic threshold type: a system response occurs when the input level reaches a threshold, whose value is multiplied by a certain constant after each response. These two mechanisms can be implemented biochemically by appropriately combining feed-forward and feedback loops. The main difference between the two models is their memory of input history; we discuss possible ways to distinguish between the two models experimentally.

Introduction

Accurately sensing dynamic change in the extracellular environment is essential for proper cellular responses. In some contexts, such as Xenopus dorsal-anterior development and Escherichia coli chemotaxis, it has been reported that cells respond to the fold change in input levels rather than to their absolute levels (1–4); when the input level changes from a certain basal value to its p-fold value in a steplike manner, output level depends not on the basal value but on the value of p (Fig. 1 A). This property is called fold-change detection (FCD), and it enables cells to accurately sense dynamic changes in extracellular signals even though their absolute levels fluctuate (5–7).

Figure 1.

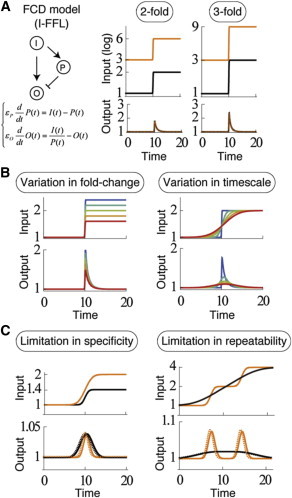
A previous model for fold-change detection (FCD) and the limitation of its function. (A) A typical FCD model (left) and responses to stepwise inputs (right); an incoherent feed-forward loop (I-FFL) works as a module to achieve FCD under appropriate parameter conditions. (B) Output intensity depends not only on the fold-change of inputs (left) but also on the timescale of the input change (right). (C) (Left) Two stepwise inputs that are different in fold-change and timescale and the responses of the I-FFL model to them. The maximum output levels are the same regardless of the differences in input fold-changes. (Right) Two inputs that are different in smoothness and the responses of the I-FFL model to them. The numbers of peaks in outputs are different, although the total fold-changes in inputs are the same. (Dashed curves) Responses of the log-differentiator model. To see this figure in color, go online.

Theoretically, FCD is defined as the invariance of response against input scale transformation (called input-scale invariance) (8,9). Several models of chemical reaction networks that have such a property have been proposed, and their response dynamics have been examined—especially their responses to stepwise or sigmoidal input change.

As discussed in detail below, we have proven that these previous models act approximately as circuits for calculating the time derivative of the logarithm of the input signal, which we call a log-differentiator. Thus, its response amplitude strongly depends on the timescale of input change.

This property creates two limitations in the detection of a specific fold-change in input:

One is the specificity of the fold-change to be detected: the transformation of the timescale of input change with its fold-change remaining constant alters the response amplitude (Fig. 1 B). In other words, two inputs that are different in both fold-change and timescale can produce the same amplitude, making the two inputs indistinct according to the response amplitude (Fig. 1 C, left panel).

The other limitation is the repeatability of detection of specific fold changes: for smoothly changing inputs, multiple peaks of output never appear, regardless of the ratio between input levels at the beginning and end. Hence, it is impossible to repeatedly respond every time the input is amplified by a specific fold (Fig. 1 C, right panel).

Nevertheless, fold-change detection with specificity and repeatability by cells with a continuously changing input is reported in real biological situations; in the context of growth control of the wing imaginal disk during Drosophila development, Wartlick et al. (10) found that the concentration of Dpp (a typical morphogen) that each cell receives changes linearly with time, and cells divide every time they experience a 50% increase (i.e., 1.5-fold) in Dpp signal over the last division (10–12).

In this study, we first prove

• 1.The relationship between the previous models and the log-differentiator model, and
• 2.The limitations of the log-differentiator model in the specificity and repeatability of its response.

After that, by extending the log-differentiator model, we propose two possible mechanisms to achieve fold-change detection with specificity and repeatability (called srFCD) for general input profiles, such as the almost linearly increasing input observed in the wing disk growth process:

One is the integrate-and-fire (IF) model, whereby a system integrates the rate of temporal change of input and makes a response (e.g., cell division) when the integrated value (an intracellular state) reaches a constant threshold and then resets the integrated value to its original value.

The other is the dynamic threshold (DT) model, whereby a system response occurs when the input level reaches a threshold, whose value is multiplied by a certain constant after each response to determine the new threshold, i.e., the threshold value changes with time. We further show examples of how to implement these two models using biochemical reactions and discuss possible ways to distinguish between the two models experimentally.

Our models will also work as possible designs for sensory systems in synthetic biological studies.

Results

A logarithmic differentiator is a minimal model of FCD

In previous studies (8), FCD was defined as response invariance to input scale transformation. For input I(t) and output O(t; I(t)), it is given by

$$O\left(t;pI\left(t\right)\right)=O\left(t;I\left(t\right)\right),$$ (1)

where p is a positive constant. In this article, all system variables are regarded as chemical concentrations and thus they take nonnegative values. Shoval et al. (8) examined sufficient conditions for FCD in detail and proposed three biochemical models satisfying those conditions (see below).

In the following, we show that the previously proposed models for FCD can be approximately regarded as log-differentiators, as

$$O_{LD}\left(t;I\left(t\right)\right)={d\log I\left(s\right)/ds|}_{s=t}.$$

A log-differentiator has an FCD function because, for p-fold multiplied input pI(t), the output is given by

$$O_{LD}\left(t;pI\left(t\right)\right)={\frac{d}{ds}\left(\log p+\log I\left(s\right)\right)|}_{s=t}={\frac{d}{ds}\log I\left(s\right)|}_{s=t}=O_{LD}\left(t;I\left(t\right)\right).$$ (2)

A semilog plot of input function may make this clear; its multiplication by any constant causes nothing but a parallel shift of the graph along the vertical axis, keeping the input time derivative unchanged regardless of the constant (Fig. 1 A).

Three typical models for FCD proposed by Shoval et al. (8) are

• 1.Incoherent feed-forward loop (I-FFL),
• 2.Nonlinear integral feedback, and
• 3.Logarithmic input with linear feedback.

Here we make clear the relationship between each model and a log-differentiator.

Incoherent feed-forward loop (I-FFL)

$${\epsilon }_P\frac{d}{dt}P\left(t\right)=I\left(t\right)-P\left(t\right),$$ (3a)

$${\epsilon }_O\frac{d}{dt}O\left(t\right)=\frac{I\left(t\right)}{P\left(t\right)}-O\left(t\right),$$ (3b)

where I(t) is the variable for input state, O(t) is for output state, and P(t) is the intermediate state (the individual state is called the “Proportioner” (13)). The values ε_p and ε_O represent the time constants for the dynamics of P(t) and O(t), respectively. Integrating Eq. 3a, P(t) is written as

$$P\left(t\right)=I\left(t\right)-{\epsilon }_P{I}^{\text{'}}\left(t\right)+{\epsilon }_P^2{I}^{\text{'}\text{'}}\left(t\right)-{\epsilon }_P^3{I}^{\text{'}\text{'}\text{'}}\left(t\right)+\cdots +c{e}^{-t/{\epsilon }_P},$$ (3a′)

where c is an arbitrary constant. Therefore, when the system dynamics is much faster (i.e., when ε_p and ε_O are much smaller) than the timescale of input change, the output is approximately given by

$$O\left(t\right)\cong \frac{I\left(t\right)}{P\left(t\right)}\cong 1+{\epsilon }_P{\frac{d}{ds}\log I\left(s\right)|}_{s=t}.$$ (3b′)

This indicates that O(t) can be regarded as a log-differentiator.

Nonlinear integral feedback

$${\epsilon }_B\frac{d}{dt}B\left(t\right)=B\left(t\right)\left(O\left(t\right)-O_{st}\right),$$ (4a)

$${\epsilon }_O\frac{d}{dt}O\left(t\right)=\frac{I\left(t\right)}{B\left(t\right)}-O\left(t\right),$$ (4b)

where B(t) is an intermediate variable (called the “Buffer” (13)), the dynamics of which are given the time constant ε_B, and O_st represents the basal level of output O(t). Assuming that the dynamics of O(t) is much faster than the input dynamics (i.e., ε_O << 1), and introducing the new variable P(t) = O_stB(t), we can rewrite the expressions in Eq. 4 as follows:

$$\frac{{\epsilon }_B}{O_{st}}\frac{d}{dt}P\left(t\right)\cong I\left(t\right)-P\left(t\right),$$ (4a′)

$$O\left(t\right)\cong O_{st}\frac{I\left(t\right)}{P\left(t\right)}.$$ (4b′)

This can be solved in the same way as in the I-FFL model. If ε_B/O_st is small enough, the output is approximately given by

$$O\left(t\right)\cong O_{st}+{\epsilon }_B{\frac{d}{ds}\log I\left(s\right)|}_{s=t}.$$ (4b″)

In this manner, the output of this model can also be regarded as a log-differentiator.

Logarithmic input with linear feedback

$${\epsilon }_B\frac{d}{dt}B\left(t\right)=O\left(t\right)-O_{st},$$ (5a)

$${\epsilon }_O\frac{d}{dt}O\left(t\right)=\log I\left(t\right)-B\left(t\right)-O\left(t\right).$$ (5b)

Like the nonlinear integral feedback model, B(t) and O_st represent an intermediate variable and the basal level of output O(t). When O(t) = 0 and ε_O << 1, by applying Laplace transformation and its inverse transformation, we have

$$O\left(t\right)\cong {\int }_0^t{e}^{-\frac{t-s}{{\epsilon }_B}}\left(O_{st}+{\frac{d}{d{s}^{\text{'}}}\log I\left(s^{\text{'}}\right)|}_{s^{\text{'}}=s}\right)ds,$$ (5b′)

meaning that O(t) is equivalent to the series connection of a log-differentiator and a low-pass filter (14).

In this manner, all models can be interpreted as log-differentiators when the timescale of the output is assumed to be smaller than that of the input. This assumption would be reasonable in the case of Drosophila wing disk formation, where the timescale of the cell cycle (∼h) is smaller than that of change in morphogen concentration (∼100 h), whereas it is not appropriate when considering bacterial chemotaxis, where the timescale of transcriptional response (∼h) is larger than that of change in ligand concentration (∼min).

Limitations of the log-differentiator

Although the log-differentiator has input scale invariance, as shown in Eq. 2, its output is susceptible to change in input timescale. Actually, the scale transformations of time from t to t/τ in input I(t) result in different outputs as

$$O_{LD}\left(t;I\left(\frac{t}{\tau }\right)\right)=\frac{d{s}^{\text{'}}}{ds}{\frac{d}{d{s}^{\text{'}}}\log I\left(s^{\text{'}}\right)|}_{s^{\text{'}}=t/\tau }=\frac{1}{\tau }{O}_{LD}\left(\frac{t}{\tau };I\left(t\right)\right),$$ (6)

where s′ = s/τ. Thus, response intensity (i.e., maximum output) is inversely proportional to input timescale τ, and response duration (e.g., time between maximum and half-maximum outputs) is proportional to τ. It should be noted that if O(t;I(t/τ)) = O(t/τ;I(t)) were satisfied, it would mean just transformation of output timescale while keeping output intensity, whereas if O(t;I(t/τ)) = (1/τ) O(t;I(t)) were satisfied, it would mean transformation of output intensity while keeping output timescale. As shown below, this property causes two limitations in detecting input fold-change.

To explain the limitations, we consider the following class of steplike input function (Fig. 2 A):

$$I\left(t;\gamma ,n,\tau ,\Delta T\right)=\exp \left[\log \gamma \sum _{k=1}^n\frac{1}{2}\left(1+\text{erf}\frac{t-k\Delta T}{\tau }\right)\right],$$ (7)

where the error function is defined by

$$\text{erf}\left(x\right)=2/\sqrt{\pi }{\int }_0^x{e}^{-t^2}dt.$$

Parameters γ, n, τ, and ΔT indicate the fold-change in one step, the number of steps, the timescale of input change, and the interval between steps, respectively.

Figure 2.

Response repeatability of log-differentiator type models. (A) Input functions given by Eq. 7. The input shape is determined by parameters for the fold-change in each step γ, the number of steps n, the timescale of input change τ, and the interval between steps ΔT. (B) Responses of the log-differentiator model and the previous FCD models to inputs with different timescales of input change τ; responses of the log-differentiator O(t) ≅ 1 + ε d log I(t)/dt (dashed black curves), incoherent feed-forward loop (red curves), nonlinear integral feedback (green curves), and logarithmic input with linear feedback (blue curves). In this example, when the input timescale is small enough (i.e., much faster input change), all models respond to the two-fold change in input regardless of the system timescale. In contrast, when the input timescale is large (i.e., much smoother input change), none of the models can respond repeatedly to the specific fold-change in input. To see this figure in color, go online.

This input changes smoothly from $1$ to γⁿ in a stepwise manner.

The response of the log-differentiator to this input is given as a linear sum of the normal distribution:

$$O_{LD}\left(t;I\left(t;\gamma ,n,\tau ,\Delta T\right)\right)=\frac{\log \gamma }{\tau \sqrt{\pi }}\sum _{k=1}^n\exp \left(-{\left(\frac{t-k\Delta T}{\tau }\right)}^2\right).$$ (8)

The first limitation is in specificity of fold-change to be detected. According to Eq. 8, in the case of n = 1, i.e., input with a single step, the response always has a single peak at t = ΔT. Moreover, given two inputs, I(t;γ₂,τ₂) and I(t; γ₁,τ₁), which are different in both fold-change and timescale, the ratio of response intensity to these inputs is

$$\frac{O_{LD}\left(\Delta T;I\left(t;{\gamma }_2,{\tau }_2\right)\right)}{O_{LD}\left(\Delta T;I\left(t;{\gamma }_1,{\tau }_1\right)\right)}=\frac{{\tau }_1\log {\gamma }_2}{{\tau }_2\log {\gamma }_1}.$$ (9)

Equation 9 means, for example, a twofold change in input in half an hour and a $1.4$-fold change in an hour (i.e., ${\gamma }_1=2,{\gamma }_2=\sqrt{2},{\tau }_1/{\tau }_2=2$) return the same value for response intensity, i.e., the two inputs cannot be discriminated by intensity alone (Fig. 1 C, left panel).

The second limitation is in the repeatability of detection with continuous input change. For n > 1 in Eq. 7, whether the response of the log-differentiator has n peaks depends on the input timescale τ. As the simplest case, consider the case where n = 2. The top-right panel in Fig. 1 C shows responses to two different inputs with different values for τ (other parameters are fixed). In this case, the response is given as a superposition of two normal distributions:

$$O_{LD}\left(t;I\left(t;n=2\right)\right)=\frac{\log \gamma }{\tau \sqrt{\pi }}\left[\exp \left(-{\left(\frac{t-\Delta T}{\tau }\right)}^2\right)+\exp \left(-{\left(\frac{t-2\Delta T}{\tau }\right)}^2\right)\right].$$ (10)

From the calculation of the first and second derivatives of Eq.10, the response has two peaks when the timescale of input change is small enough ($\tau <\Delta T/\sqrt{2}$), but has a single peak otherwise as a result of the overlap between the two responses (Fig. 1 C, right panel). This means that the log-differentiator has a limitation in repetitive detection of a fold-change in smoothly changing inputs.

In the analysis above, although we showed the limitations of the log-differentiator model, similar limitations hold for the previously-proposed three models for FCD, even when the assumption of timescale is removed (Fig. 2 B).

Fold-change detection with specificity and repeatability)

As stated above, when the input is smoothly changing, the previous log-differentiator type models cannot achieve fold-change detection with specificity and repeatability (srFCD). Nevertheless, as stated before, such detection by cells is reported in real biological situations (10). Motivated by this observation, we here consider systems that can detect only a specific fold-change and respond repetitively even when the input is smoothly changing. An ideal system response is given by

$$O\left(t\right)=\theta \left(\frac{I\left(t\right)}{I\left(T_n\right)}-\gamma \right)\text{for}{T}_n\le t,$$ (11)

where T_n is the time when the last (nth) response occurred (T₀ = 0, I(T₀) = K > 0), and γ is a specific fold-change to be detected. The value θ(x) is a unit step function whose output is 1 if the inequality x ≥ 0 is true, and 0 when it is not. At the moment when

$$\frac{I\left(t\right)}{I\left(T_n\right)}\ge \gamma$$ (12)

is satisfied, this system makes a response, and the dynamics is updated by replacing T_n with T_n+1 in Eq. 11. For an increasing input, responses and updates occur every time the input is increased by γ-fold after the last response. We should note that the requirement for srFCD (Eq. 11) satisfies the condition of the original FCD, i.e., input-scale invariance (Eq. 1), because the output depends only on the ratio of input levels at two different time points.

In the following, by appropriately transforming Eq. 12, we propose two basic models to achieve srFCD. For the purpose of focusing on the logic of the mechanisms, we explain the two models mainly with abstract models, and briefly discuss how to implement them using more concrete biochemical reactions.

Integrate-and-fire model

Equation 12 can be transformed as follows:

$$\frac{I\left(t\right)}{I\left(T_n\right)}\ge \gamma \iff \log \frac{I\left(t\right)}{I\left(T_n\right)}\ge \log \gamma \iff {\int }_{T_n}^t\frac{d\log I\left(s\right)}{ds}ds\ge \log \gamma .$$ (13)

The inequality on the right-hand side of Eq. 13 means that each response occurs when

$${\int }_{T_n}^t\frac{d\log I\left(s\right)}{ds}ds,$$

the accumulation of log-differentiated input from the last response, reaches a constant threshold logγ. By introducing an intermediate variable (L(t), Log-converter) that reflects the accumulation level, the system output given by Eq. 11 is realized by the following dynamics:

$$\frac{d}{dt}L\left(t\right)={\frac{d}{ds}\log I\left(s\right)|}_{s=t},$$ (14a)

$$O\left(t\right)=\theta \left(L\left(t\right)-\log \gamma \right),$$ (14b)

$$L\left(t^{+}\right)=0\text{if}O\left(t\right)>0,$$ (14c)

where t⁺ represents the reset timing immediately after the response. This model is composed of three steps (Fig. 3 A) described in the following:

• 1.Log-conversion of input signal (Eq.14a); because the value of L is reset after every response, its current value is log(I(t)/I(T_n)), i.e., a fold-change of input from the last response. This process can be implemented using a previous FCD model, e.g., the I-FFL (Fig. 3 B).
• 2.When L reaches a certain threshold (log γ), a binary response occurs (Eq. 14b). This thresholding process can be achieved by a bistable system through a positive feedback loop or by a response with a Hill function through multistep phosphorylation and/or a phosphorylation cascade (15–18).
• 3.L is reset to its basal value (Eq. 14c), which is achieved, for instance, by the negative regulation of L by the output O (i.e., O-mediated degradation of L). Fig. 3, B and C, show an example of implementation of the integrate-and-fire (IF) model using biochemical reactions and its response to a linearly increasing input, respectively (see Appendix A for details on this example). Note that to achieve srFCD properly, the system parameters need to satisfy some constraints (see also Appendix A).

Figure 3.

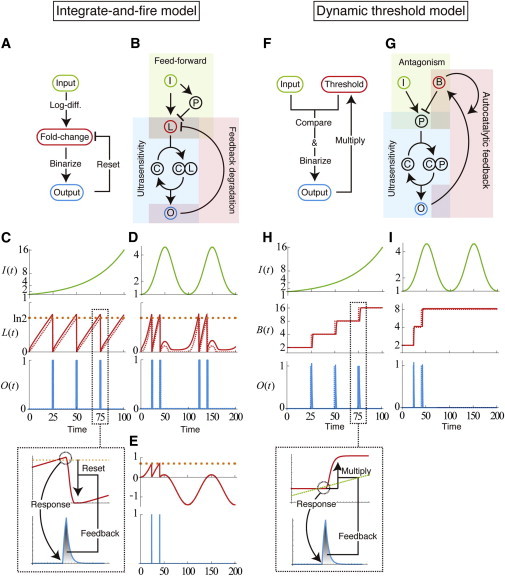
Two possible mechanisms for fold-change detection with specificity and repeatability (srFCD): integrate-and-fire (IF) model and dynamic threshold (DT) model. (A) Logic diagram and (B) biochemical implementation of the IF model. This model consists of three parts: (i) log conversion of input signal I, which is stocked as an internal state L; (ii) binary response O, which depends on the value of L; and (iii) the reset of L after each response through feedback. L is interpreted as the fold-change of input since the last response. After appropriately combining feed-forward and feedback loop motifs, the processes (i–iii) can be biochemically implemented (B). (C and D) Typical responses of the IF model to an exponential input (C) and to a periodic input (D). (Dashed curves) Logic model (see the expressions in Eq. 14); (solid curves) biochemical model (Eq. A1). For a monotonically increasing input, system responses properly occur for every specific-fold change (twofold in this case) in input, but inappropriate responses occur when input includes decreasing phases (D). (E) If L could take negative values, the proper response to a specific-fold change in input would be achieved. (F) Logic diagram and (G) biochemical implementation of the DT model. This model consists of three parts: (i) comparison of the values between input I and an internal state B, which works as a dynamic threshold; (ii) binary response O, which depends on I/B; and (iii) multiplication of the value of B by a constant. The DT model can be biochemically implemented by combining feedback loop motifs (G). (H and I) Typical responses of the DT model to an exponential input (H) and to a periodic input (I); (dashed curves) logic model (see the expressions in Eq. 16); (solid curves) biochemical model (see the expressions in Eq. A2). The DT model can properly detect a specific-fold change in input even with input that includes decreasing phases. The input functions are I(t) = exp(4.0 × 10⁻²t) (C and H) and I(t) = exp(1.1(1 – cos(2π × 10⁻²t))) (D and I). To see this figure in color, go online.

By analogy to a model of spiking neurons, we call this model (Eq. 14) the integrate-and-fire (IF) model (19). The model is also a mathematical formulation of the concept that Wartlick and González-Gaitan presented in a previous article (11). As written in the literature, a variable L is not necessarily a chemical concentration, but can be regarded as a cell volume; if the volume growth rate is proportional to the log-differentiated input and cells divide when their volumes are doubled, and this is followed by the reset of L to a basal volume, then the function of srFCD can be realized by slightly modifying Eq. 14 as

$$\frac{d}{dt}L\left(t\right)={\frac{2}{\log \gamma }\frac{d}{ds}\log I\left(s\right)|}_{s=t},$$ (14a′)

$$O\left(t\right)=\theta \left(L\left(t\right)-2\right),$$ (14b′)

$$L\left(t^{+}\right)=1\text{if}O\left(t\right)>0,$$ (14c′)

where L is the cell volume and the basal volume is set at 1.

Although the IF model fulfills an srFCD function for monotonically increasing inputs, it may not be able to properly detect a specific fold-change in input from the last response if the input includes decreasing phases (Fig. 3 D). To achieve srFCD, L(t) should take the value of log(I(t) / I(T_n)), meaning that L(t) should be negative when I(t) < I(T_n) (i.e., decreasing input). However, this is impossible because L(t) corresponds to chemical concentration or cell volume, which have nonnegative values. Therefore, the IF model cannot deal with the decrement in input, leading to improper responses for nonmonotonic inputs (see Fig. 3, D and E). In contrast, as explained below, the other model properly works as an srFCD module even when the input includes decreasing phases.

Dynamic threshold model

Another possible transformation of the inequality in Eq.12 is

$$\frac{I\left(t\right)}{I\left(T_n\right)}\ge \gamma \iff I\left(t\right)\ge \gamma I\left(T_n\right)={\gamma }^{2}I\left(T_{n-1}\right)=\cdots ={\gamma }^{n+1}K,$$ (15)

where the requirement from Eq. 11 is satisfied if the (n + 1)th response occurs when input I(t) reaches γⁿ⁺¹K, a dynamics threshold that increases by γ-fold after every response. Based on this consideration, and by introducing an intermediate variable (B(t), buffer) that reflects the value of the dynamic threshold, we propose the other basic model of srFCD as follows:

$$\frac{d}{dt}B\left(t\right)=0,$$ (16a)

$$O\left(t\right)=\theta \left(I\left(t\right)-B\left(t\right)\right),$$ (16b)

$$B\left(t^{+}\right)=\gamma B\left(t\right)\text{if}O\left(t\right)>0.$$ (16c)

In this model, the value of B is constant when O = 0 (Eq. 16a). When the current input level is beyond the value of B, a system response occurs (Eq. 16b). After each response, the value of B(t) is updated immediately to the next value by multiplying it by a constant γ (Eq. 16c) (Fig. 3 F). Unlike the intermediate quantity L in the IF model, B continues to increase exponentially instead of being reset (note that, as is true for the Dpp source level, a change in chemical concentration by two orders is plausible in real systems).

How can such a multiplication of variable B by a constant be implemented biochemically? A simple mechanism is an autocatalytic feedback given as (Fig. 3 G)

$$\frac{d}{dt}B\left(t\right)=B\left(t\right)f\left(O\right),$$ (17)

where f(O) is a monotonically increasing function with the constraint f(0) = 0 (Eq.16a). Integrating Eq. 17, we have

$$B\left(t\right)=B_0\exp \int f\left(O\right)dt.$$ (18)

Thus, the ratio of the value of B at the nth and(n+1)th responses is

$$\frac{B\left(T_{n+1}\right)}{B\left(T_n\right)}=\exp {\int }_{T_n}^{T_{n+1}}f\left(O\right)dt.$$ (19)

When the output shape for each response is identical, the right-hand side of Eq. 19 becomes constant, i.e., B is multiplied by a constant after every response. Eq. 17 includes the dynamics given by Eq. 4a in the nonlinear integral feedback model, which is observed in the chemotaxis of E. coli (8,20). By adding a thresholding module, the model can be extended to a dynamic threshold (DT) type of model (see Fig. 3 G for an example of biochemical implementation and Appendix A for details on the model).

Unlike the IF model, the DT model can serve an srFCD function even when the input includes decreasing phases because the value of B is always positive (Fig. 3, H and I).

Discussion

In this study, we proved that previously proposed FCD models can be regarded as log-differentiators and that the log-differentiator-type model has limitations in specificity and repeatability of response in detecting a specific fold-change in input signal. By extending them, we proposed two different mechanisms to achieve such an FCD with specificity and repeatability (srFCD), regardless of the timescales of input signals, i.e., the integrate-and-fire (IF) model and the dynamic threshold (DT) model. We also show that both models can be implemented biochemically by appropriately combining feed-forward and feedback loops.

Major differences between the two models and possible ways of distinguishing between them experimentally

A simple way to distinguish between the IF and DT models is to examine the dynamics of variables for intermediate states. In the IF model, the variable L reflects the log-ratio of input change from the last response (log(I(t)/I(T_n))) and always changes with the change in input. In particular, for exponentially increasing input, L changes periodically (Fig. 3 C). On the other hand, in the DT model, the variable B reflects the threshold for response (γⁿ⁺¹K) and changes only after the response, otherwise remaining constant. Thus, for increasing input, B increases monotonically in a stepwise manner (Fig. 3 H).

Another way is to examine responses to inputs that include decreasing phases. As explained before, the IF model cannot capture the negative rate of input change well, due to the existence of the lower bound of L(t) (i.e., L(t) ≥ 0), leading to incorrect responses. In contrast, in the DT model, the γ-fold level of the input at the last response is memorized as a value of B, and proper fold-change detection can be achieved regardless of the monotonicity of input profiles.

Using this difference, we may be able to determine which model (IF or DT) is represented in real biological systems by observing responses to nonmonotonically changing inputs instead of observing intermediate variables (L or B). For example, as shown in Figs. 3, D and I, when a periodic input is given to the systems represented by Eqs. 14 and 16, the number of responses would be different between the IF and DT models. This difference in the number of responses may be seen more clearly as tissue size in the context of the development of the Drosophila wing disk. Fig. 4 shows results of mechanical simulations of the growth process. The tissue was modeled by the vertex dynamics model, in which each cell is represented as a polygon formed by linking several vertices (Fig. 4 A) (21,22).

Figure 4.

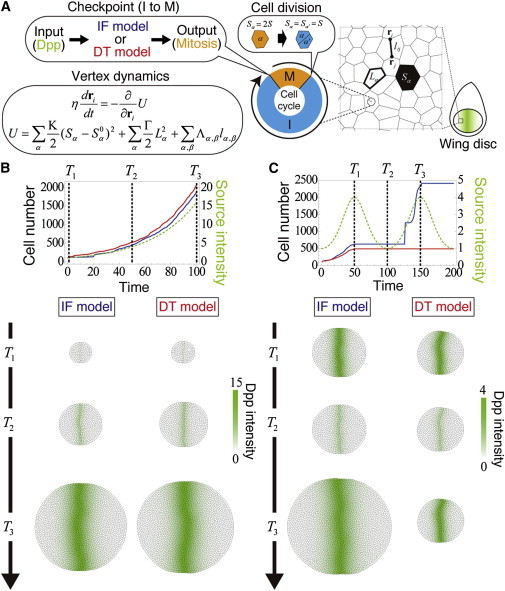
Tissue growth simulation by coupling the vertex dynamics model and srFCD model. (A) Tissue growth simulation during Drosophila wing disk development using the two-dimensional vertex dynamics model in which each cell has a simplified cell cycle regulator whose checkpoint is controlled by the srFCD model, namely the IF or DT model. The Dpp morphogen, the input for the srFCD model, is produced at the source cells adjacent to the anterior-posterior (AP) boundary. (B and C) Simulation results when the Dpp source intensity exponentially increases (B) and periodically changes (C). (Top panels) Temporal profiles of the cell numbers in the IF model (blue curves), in the DT model (red curves), and Dpp source intensity (dashed green curves). (Bottom panels) Representative images at three different time points (corresponding to the dashed lines in the above panels). Color indicates cellular Dpp intensity. Although the IF and DT models gave almost the same results for exponential inputs (B), only the IF model gave biphasic tissue growth for periodic inputs (C). To see this figure in color, go online.

We assumed that every cell cycle length is determined by an srFCD model inside each cell, i.e., the IF or DT model. Dpp morphogen, the input for the srFCD model, is produced at the source cells adjacent to the anterior-posterior (AP) boundary (midline of the tissue) and makes a scaled gradient by diffusion and degradation (see Appendix B). When the Dpp expression at the source was monotonically increasing, as observed in wild-type wing disks, both the IF and DT models gave almost the same results (see Fig. 4 B). However, when Dpp expression was periodic, the growth patterns differed dramatically between the IF and DT models (Fig. 4 C). For the IF model, biphasic tissue growth was observed; the first growth phase corresponded to the first increasing period of input, and the second phase corresponded to the second increasing period of input. On the other hand, for the DT model, only the first growth phase was observed. The resulting difference in tissue size was very clear and may be more useful in distinguishing between the two mechanisms experimentally than by examining differences in intracellular chemical dynamics.

Candidate molecules for implementing srFCD in the growth control of the wing disk

A notable characteristic of the IF model is the dynamics of the intracellular state L(t), whose level periodically changes in synchrony with the cell cycle. Such dynamics, of course, can be seen in cell cycle regulators. Because cell cycle prolongation occurs mainly in the G2 phase during development, regulators of G2/M transition, such as Cyclin B and String, are candidates for L(t) in the IF model (23,24). However, as of this writing, it is unknown whether Dpp regulates these genes. Another interesting possibility for L(t) is not a chemical, but cell volume, as discussed before; Dpp is actually known to regulate the cell growth rate through the Hippo pathway (25). On the other hand, a characteristic of the DT model is its network topology, which consists of a negative feedback loop between the output O(t) and the intracellular state B(t) and a positive feedback loop for B(t). Downstream of Dpp, the growth regulator Yki is part of a negative feedback loop with Myc, and Myc is part of a positive autoregulatory feedback loop (26,27). Therefore, the DT model could be implemented in this network.

Our models are general models to detect relative level changes in focal cues in dynamically changing environments. They provide not only mechanisms that may operate in real biological phenomena, including the growth control of the wing disk, but also can provide basic designs for cellular sensory systems in synthetic biological studies.

Appendix A: Examples of Biochemical Implementation

Integrate-and-fire (IF) model

The following dynamics is an example of biochemical implementation of the IF model (Fig. 3 B):

$$\frac{d}{dt}L\left(t\right)={\alpha }_L\frac{I\left(t\right)}{P\left(t\right)}-\left({\beta }_L+{\gamma }_{L}O\left(t\right)\right)\frac{L{\left(t\right)}^{h_L}}{L{\left(t\right)}^{h_L}+K_L^{h_L}},$$ (A1a)

$$\frac{d}{dt}P\left(t\right)={\alpha }_{P}I\left(t\right)-{\beta }_{P}P\left(t\right),$$ (A1b)

$$\frac{d}{dt}C\left(t\right)={\alpha }_C\frac{K_0+{\left(L\left(t\right)C\left(t\right)\right)}^{h_C}}{{\left(L\left(t\right)C\left(t\right)\right)}^{h_C}+K_C^{h_C}}-{\beta }_{C}C\left(t\right),$$ (A1c)

$$\frac{d}{dt}O\left(t\right)={\alpha }_{O}L\left(t\right)C\left(t\right)-{\beta }_{O}O\left(t\right).$$ (A1d)

In Eq. A1a, the first term indicates that L(t) is regulated by input I(t) through an incoherent type feed-forward loop (IFF-L), and this type of regulation achieves fold-change detection (FCD), i.e., input-scale invariance (5). P(t) is the Proportioner, whose dynamics is given by Eq. A1b. The first term of Eq. A1a can be replaced by other FCD models. When O(t) = 0, α_L = β_L, and L(t) >> K_L, from Eq. 3b′, Eq. A1a can be solved as

$$L\left(t\right)\propto \log \frac{I\left(t\right)}{I\left(T_n\right)}.$$ (A1a′)

This means that L is proportional to the fold-change of input since the last response. The last term in Eq. A1a represents O(t)-promoted degradation. Eq. A1c is the dynamics of intermediate variable C(s), which is introduced to approximate the step function in Eq. 14b. The first term represents a heterodimer-mediated positive feedback regulation called ASSURE, and the second term is the degradation. The ASSURE network motif is known to behave as a robust all-or-none switch (28,29). The first term in Eq. A1c can be replaced by other mechanisms generating all-or-none responses or ultrasensitivity, such as multistep phosphorylation. Because the dissociation constant K_C in Eq. A1c approximately corresponds to the threshold of the response (i.e., logγ in Eq. 14b), its value strongly affects the fold-change to be detected. In Fig. 3, C and D, the values of parameters were chosen as α_L = β_L = 10², γ_L = 1, h_L = 2, K_L = 10⁻³, α_P = β_P = 10², α_C = β_C = 10², K₀ = 10⁻⁶, K_C = 0.32, h_C = 1.1, α_C = 70, and β_O = 10.

Dynamic threshold (DT) model

The following dynamics is an example of biochemical implementation of the DT model (Fig. 3 F):

$$\frac{d}{dt}B\left(t\right)={\alpha }_{B}B\left(t\right)O\left(t\right)-{\beta }_B\frac{B\left(t\right)}{B\left(t\right)+K_B},$$ (A2a)

$$\frac{d}{dt}P\left(t\right)={\alpha }_{P}I\left(t\right)-{\beta }_{P}B\left(t\right)P\left(t\right),$$ (A2b)

$$\frac{d}{dt}C\left(t\right)={\alpha }_C\frac{K_0+{\left(P\left(t\right)C\left(t\right)\right)}^{h_C}}{{\left(P\left(t\right)C\left(t\right)\right)}^{h_C}+K_C^{h_C}}-{\beta }_{C}C\left(t\right),$$ (A2c)

$$\frac{d}{dt}O\left(t\right)={\alpha }_{O}P\left(t\right)C\left(t\right)-{\beta }_{O}O\left(t\right),$$ (A2d)

The first term in Eq. A2a indicates that the activation of B(t) is mediated by O(t) in an autocatalytic manner. Because the level of B(t) needs to continue to increase, its degradation rate is modeled not by a linear function but by a Michaelis-Menten type function with saturation. When B(t) becomes large enough (B(t) >> β_B, i.e., slow degradation), Eq. A2a can be approximated by Eq. 17, i.e., f(O) = α_BO(t), and solved as

$$\frac{B\left(T_{n+1}\right)}{B\left(T_n\right)}=\exp \left[{\alpha }_B{\int }_{T_n}^{T_{n+1}}O\left(t\right)dt\right].$$ (A2a′)

In other words, B(t) increases exponentially with the number of responses. Eq. A2c approximates the step function in Eq. 16b in the same manner as Eq. A1c. When the dynamics of P(t) (Eq. A2b) is much faster, its value is approximately proportional to I(t)/B(t). Eq. A2c can then be rewritten as

$$\frac{d}{dt}C\left(t\right)={\alpha }_C\frac{K_0^{\text{'}}\left(B\right)+{\left(I\left(t\right)C\left(t\right)\right)}^{h_C}}{{\left(I\left(t\right)C\left(t\right)\right)}^{h_C}+{\left(K_C^{\text{'}}\left(B\right)\right)}^{h_C}}-{\gamma }_{C}C\left(t\right),$$ (A2c′)

where K′₀(B) = K₀B(t)^hC and K′_C(B) = K_CB(t). K′_C(B) works as a dynamic threshold that depends on the value of B(t), while the threshold K_C is constant (i.e., static threshold) in Eq. A1c. In contrast to the IF model, the parameter K_C hardly affects the fold-change to be detected. Instead, the parameter α_B, the intensity of feedback regulation of B(t) by the output O(t), does affect the fold-change to be detected. In Fig. 3, G and H, the values of parameters were chosen as α_B = 1, β_B = 10⁻⁴, K_B = 1.0, α_P = 10, β_P = 5, α_C = β_C = 10³, K₀ = 10⁻⁶, K_C = 0.8, h_C = 1.1, and α_O = β_O = 10.

Appendix B: Vertex Dynamics Model

We performed tissue growth simulations with a two-dimensional vertex dynamics model (21,22,30) (Fig. 4 A). In this model, each cell is represented as a polygon formed by linking several vertices. The dynamics of the ith vertex is given as

$$\eta \frac{d{\mathbf{r}}_i}{dt}=-\frac{\partial }{\partial {\mathbf{r}}_i}U,$$ (A3)

where r_i is the positional vector of the ith vertex, η is a coefficient of viscous resistance, and U is the total potential energy of the system, which is given by

$$U=\sum _{\alpha }\frac{K}{2}{\left(S_{\alpha }-S_{\alpha }^0\right)}^2+\sum _{\alpha }\frac{\Gamma }{2}{L}_{\alpha }^2+\sum _{\alpha ,\beta }{\Lambda }_{\alpha ,\beta }{l}_{\alpha ,\beta },$$ (A4)

where the first and the second terms describe the sum of elastic energies for the area S_α and the perimeter L_α of cell α, respectively. S⁰_α is the equilibrium area of cell α. The third term describes the sum of interfacial energies for the boundary l_α,β between cell α and β. The values K, Γ, and Λ_α,β are the parameters representing the weights of those terms. We adopted the parameter values that are given in Wartlick et al. (10).

We also adopted the rules of topological change and cell division given in Wartlick et al. (10), except for the rule of cell cycle progression. In our simulation, cell cycle progression depends on the output chemical level O(t) in the IF or DT model. We assumed that the effect of dilution of intracellular chemicals due to cellular growth is neglected and that their values are copied from a parent cell to daughter cells at each cell division.

The dynamics of the input I_α(t), or the Dpp concentration, is

$$\frac{d}{dt}{I}_{\alpha }\left(t\right)=D_I\left(t\right)\sum _{\beta }{l}_{\alpha ,\beta }\left(I_{\beta }\left(t\right)-I_{\alpha }\left(t\right)\right)-{\gamma }_I{I}_{\alpha }\left(t\right),$$ (A5)

where the first term represents the diffusion process of Dpp, and the second term is the degradation process. The diffusion coefficient is determined so as to achieve a gradient that scales with tissue size (31,32):

$$D_I\left(t\right)=D\sum _{\alpha }{S}_{\alpha }\left(t\right).$$ (A6)

We also assumed that Dpp protein is produced at the source cells, which are adjacent to the midline (AP compartment boundary).

In Fig. 4 B, the source intensity was given by

$$I_{\alpha }\left(t\right)=\exp \left(4.0\times {10}^{-2}t\right)\alpha \in \left(\text{source}\text{cells}\right).$$ (A7)

On the other hand, in Fig. 4 C, the source intensity was given by

$$I_{\alpha }\left(t\right)=\exp \left(1-\cos \left(2\pi \times {10}^{-2}t\right)\right)\alpha \in \left(\text{source}\text{cells}\right).$$ (A8)

In all simulations, the parameter values were chosen as S₀ = 250, K = 0.08, Γ = 0.8, Δ = −38, Λ_midline = 38, Λ_rim = 380, D = 10⁻⁷, and γ_I = 0.7. Each cell cycle length (except for the effect of checkpoints) was randomly determined by a γ-distribution, whose shape parameter was 25 and whose scale parameter was chosen so that the average lengths of M-phase and I-phase are 3 and 20, respectively.