Interactions and Diffusion in Fine-Stranded β-lactoglobulin Gels Determined via FRAP and Binding

Abstract

The effects of electrostatic interactions and obstruction by the microstructure on probe diffusion were determined in positively charged hydrogels. Probe diffusion in fine-stranded gels and solutions of β-lactoglobulin at pH 3.5 was determined using fluorescence recovery after photobleaching (FRAP) and binding, which is widely used in biophysics. The microstructures of the β-lactoglobulin gels were characterized using transmission electron microscopy. The effects of probe size and charge (negatively charged Na₂-fluorescein (376Da) and weakly anionic 70kDa FITC-dextran), probe concentration (50 to 200 ppm), and β-lactoglobulin concentration (9% to 12% w/w) on the diffusion properties and the electrostatic interaction between the negatively charged probes and the positively charged gels or solutions were evaluated. The results show that the diffusion of negatively charged Na₂-fluorescein is strongly influenced by electrostatic interactions in the positively charged β-lactoglobulin systems. A linear relationship between the pseudo-on binding rate constant and the β-lactoglobulin concentration for three different probe concentrations was found. This validates an important assumption of existing biophysical FRAP and binding models, namely that the pseudo-on binding rate constant equals the product of the molecular binding rate constant and the concentration of the free binding sites. Indicators were established to clarify whether FRAP data should be analyzed using a binding-diffusion model or an obstruction-diffusion model.

Introduction

Microstructures in living cells and soft materials are heterogeneous on a wide range of length scales. This is very important for the local diffusion properties, which vary as a function of the spatial position and the degree of heterogeneity (1). Diffusion properties in soft matter strongly depend on obstruction, interactions, and structure dynamics (2). Hydrogels represent an important group of soft materials with many properties that are related to living cells. Local diffusion properties have been determined in various hydrogels such as gelatin, κ-carrageenan, β-lactoglobulin, and phase-separated biopolymer mixtures (3–6). The effect of charge on diffusion in hydrogels has been studied in detail on the partition of (un)charged molecules in agarose gels (7–9), where a hindrance of the diffusion in oppositely charged systems was found. Fatin-Rouge and co-workers (9) also provided a general model to describe partitioning in hydrogels with regard to steric, electrostatic, and chemical interactions. In addition, the effect of electrostatic probe-polymer interactions in polymer solutions was found to influence the diffusion in solutions (10–12).

Determination of solute diffusion and molecular interactions is essential in biophysics (13,14), since protein-protein interactions regulate cellular processes. For instance, the transcription factor mobility in the nucleus (13) and the binding of the protein Ras to membranes (15) have been investigated. Another important field of research concerns the tailoring of solute diffusion in soft materials. This field ranges from pharmaceutical applications (controlling the release of active substances from tablets is important (16)), to water management in food, inhibiting mass-transport through packaging layers, maximizing the liquid uptake in hygiene products (2), and filtering of particles by the extracellular matrix (12).

Solute diffusion is influenced by interactions with a matrix. The solute either diffuses freely or attaches to a binding site. Information about binding and unbinding events and the free diffusion between binding events can be retrieved directly using a confocal microscope at the micrometer level by fluorescence recovery after photobleaching (FRAP) and binding (13). FRAP is a widely established and powerful fluorescence microscopy-based method for obtaining information on the dynamics of mobile fluorescent molecules. In FRAP, the fluorescent molecules are first irreversibly bleached in a limited volume with a short high-intensity pulse of light, which results in a local decrease in the fluorescence intensity. After bleaching, unbleached fluorescent molecules from the surroundings gradually diffuse into the bleached region whereas bleached fluorescent molecules diffuse out. The fluorescence intensity in the bleached region will recover at a rate that depends on the mobility of the molecules. With an appropriate mathematical model, one can then analyze the fluorescence recovery and extract quantitative information on the molecular dynamics. FRAP has been used to measure diffusion of fluorescently tagged microspheres, dendrimers, proteins, and polysaccharides in soft matter systems (3,4,6,7,11,17). By introducing partial differential equations that consider the binding events in the FRAP evaluation model, it is possible to simultaneously estimate the pseudo-on binding rate, the off binding rate, and the diffusion coefficient (13–15,18).

However, the foundation of the FRAP and binding framework still needs to be tested. The vast complexity of processes in the living cell makes it hard to validate the assumptions on which the evaluation models are based. The complexity can be seen in such things as the multitude of different binding sites and the photostability of the green fluorescent protein (14,19). Hydrogels with tailored microstructures present an opportunity to validate some of the fundamental assumptions of the FRAP and binding framework. The gel microstructure is a three-dimensional network of gel strands surrounded by water that percolates through the whole material. The gel strands consist of biopolymer backbones that are single-stranded or aggregated. The biopolymer backbones have repeating units that can have charged groups depending on the pH and the type of biopolymer. Thus the binding sites are approximately evenly distributed over the surface of the gel strands. Given a constant gel strand radius distribution (for example, the degree of aggregation), it is thus possible to control the number of binding sites by altering the biopolymer concentration. It is also possible to evaluate the effect of probe concentration on the diffusion and binding properties in hydrogels. This effect is hard to evaluate in living cells since cells easily become sick when the probe concentrations are too high, and signal-to-noise problems occur at very low probe concentrations. Attempts have been made to cross-validate FRAP and binding using fluorescence correlation spectroscopy (FCS) and single-particle tracking (20,21).

The aim of this work is to validate important model assumptions using a well-controlled model system and to introduce FRAP and binding as a new technique to determine probe diffusion and interaction kinetics in hydrogels. Fine-stranded β-lactoglobulin gels at pH 3.5 were used as a model system to examine diffusion of charged probes in charged hydrogels. β-lactoglobulin (BLG), the major component of whey, is a globular protein with a radius of ∼ 2 nm and a molar weight of 18.2 kDa (22). Long-range electrostatic repulsion causes a stable state for native BLG solutions except close to the isoelectric point (pI) of $\approx 5.1$, where unstable aggregations are observed at room temperature (23). BLG forms a gel upon heat denaturation. Without the addition of salts, BLG forms opaque particulate gels at pH = 4 to 6. Big aggregates with protein-rich domains with diameters in the order of micrometers (24) form close to the pI. pH values above and below this range lead to a transparent fine-stranded structure (25); dextran diffusion in gels at neutral pH has been studied using pulsed field gradient NMR (26). Such a fine-stranded structure is very well characterized for BLG in the absence of salt at pH 3.5 (27,28), where a very brittle gel structure is formed. Overall, the structure of BLG gels depends strongly on the strength of the electrostatic interactions (29), adjusted either by the addition of salt or by pH adjustments. In this study, BLG solutions and gels with different concentrations were used as models system for probe diffusion measurements via FRAP and binding to vary the number of binding sites. Measurements were conducted before and after the heat-induced gelation with probes of different sizes and surface-charge density and with varying probe concentration.

Materials and Methods

Materials

β-lactoglobulin was purchased from Sigma Aldrich, Steinheim, Germany (L0130, lot no. 030M7025V). It contained ≥ 90% β-lactoglobulin A and B from bovine milk determined by polyacrylamide gel electrophoresis (PAGE). With an isoelectric point of pI ∼ 5.1 (22), BLG has an overall positive charge density at lower pH values and a negative charge density at higher values, respectively; the empirical method PROPKA (30) applied to BLG (31) (the crystal structures available in the PDB for bovine-BLG were evaluated, and the results averaged) estimated a single protein to have a net charge of +8 $\left|e\right|$ at pH 3.5. The probes used were Na₂-fluorescein (Fluka, St. Louis, MO) with a molecular weight (MW) of 376 Da and FITC-dextran 70 kDa MW (Invitrogen Molecular Probes, Eugene, OR). The secure-seal spacers used were 120 μm thick and 9 mm in diam. (Invitrogen Molecular Probes, Eugene, OR). The secure-seal spacers are absorbed onto two cover-glass slides in a sandwich manner and contain 7 μl aliquots of the sample. All probes are tagged with fluorescein, which exhibits multiple pH dependent ionic equilibria and a reduced quantum yield at acidic pH (32). Only the monoanion and dianion of fluorescein are fluorescent; upon excitation the neutral and cationic species are converted into the anion and fluoresce (33). The number of fluorescein dyes per probe is given by the manufacturer; therefore, the number of dyes per surface area can be estimated, as is proportional to the overall anionicity of the probes (Table 1).

Table 1.

Characterization of the FRAP probes

Probe	pH	D0	SD	rH	dye
Na2-fluorescein (NaF)	3.5	380	35	0.6	0.2
FITC-dextran 70kDa (FD70)	3.5	29.9	3.1	8.0	0.007

The table shows the free diffusion coefficient D₀ at 298 K (μm²/s); the standard deviation (SD); the associated hydrodynamic radius r_H (nm) calculated using the Stokes-Einstein equation; and the number of dye molecules per surface area (1/nm²), considering a sphere defined by the hydrodynamic radius. SD was determined by averaging over 10 measurements. The D₀ measurements for Na₂-fluorescein at concentrations of 50, 100, and 200 ppm did not differ significantly.

Sample preparation

The β-lactoglobulin was dissolved carefully without stirring—to prevent any structural artifacts (28)—in 1 mL of 50 to 200 ppm solution of the probe in distilled water to yield polymer solutions in the range of 9% to 12% w/w. The probe concentrations were all chosen to be in the regime where the fluorescence depends linearly on the concentration (34). The pH was further adjusted with 1 M HCl to pH 3.5. 7 μl of the polymer solution was placed into secure-seal spacer grids between two cover glass slides and the gelation of the prepared samples was induced on a temperature stage. The samples were heated at a rate of 10 K/min and kept at 358 K for 30 min before cooling in cold water at a cooling rate of ∼ 20 K/min (27).

Methods

Electron microscopy

BLG gels were plastic embedded. Small cubes (1.5 × 1.5 × 1.5 mm) were cut from gels prepared following a slightly modified protocol, excluding the fluorescent probes and heating the BLG solution in aluminum tubes in a water bath instead. The preparation procedure followed the procedure described by Langton and Hermansson (27). It started with a fixation with 2 vol% glutaraldehyde and 0.1% (w/v) ruthenium red in 0.1 M Na₂HPO₄-citric acid buffer of pH 3.5 for 3 h and then washing twice for 10 min. The gel cubes were then fixed a second time, with 1% (w/v) OsO₄ for 2 h, followed by rinsing in 0.1 M Na₂HPO₄-citric acid buffer, before being dehydrated in a graded ethanol series of 50, 70, 90, 99, and 99.5 vol%. The gels were then embedded in polybed (TAAB 812). Thin sections of ∼ 70 nm were cut with a diamond knife and double stained with 5% uranyl acetate and 0.3% lead citrate to visualize the protein phase. The thin sections were examined in a TEM, LEO 906e, (LEO Electron Microscopy, Oberkochen, Germany) at an accelerating voltage of 100 kV.

To correlate the diffusion measurements in the gels with the network microstructure, BLG gels of 9%, 10.5%, and 12% w/w were prepared for plastic-embedding and further TEM visualization. Although rheological studies have shown that all the concentrations in our study are above the gelation threshold (35), the 9% w/w gel was too weak and could not successfully be plastic embedded. The expectation that the concentrations are above the gelation threshold is also supported by the significant decrease in D after the heat ramp treatment (see Figs. 6 a and b).

Figure 6.

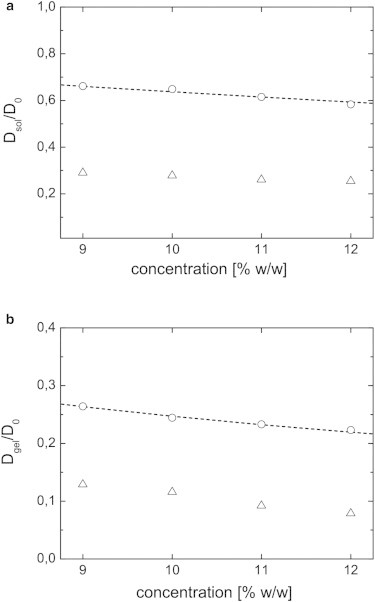
(a) Plot of the normalized diffusion coefficients vs. the polymer concentration of BLG solutions before the onset of the heat-induced gelation. Probes: NaFL (triangles) and FD70 (circles)—both at a concentration of 100 ppm. The dashed line depicts the prediction of the model of Mackie and Meares. (b) Plot of the normalized diffusion coefficients vs. the polymer concentration of BLG gels after the heat induced gelation. Probes: NaFL (triangles) and FD70 (circles)—both at a concentration of 100 ppm. The dashed line depicts the fit within the Ogston model.

CLSM-FRAP protocol

The confocal laser scanning microscope (CLSM) system used consists of a Leica SP2 AOBS (Heidelberg, Germany) utilizing a 20×, 0.5 NA water objective, with the following settings: 256 × 256 pixels, zoom factor 4 (with a zoom-in during bleaching), and 800 Hz, yielding a pixel size of 0.73 μm and an image acquisition rate of two images per second. The FRAP images were stored as 12-bit TIFF-images. The 488 nm line of an argon laser was used to excite the fluorescent probes. The beam expander was set to 1, which lowered the effective NA to ∼ 0.35 and yielded slightly better bleaching and a more cylindrical bleaching profile. The bleached areas will be called regions of interest (ROI) in this study and were 30 μm large discs (nominal radius $r_n=15$ μm) at 50 μm into the sample. The measurement routine consisted of 20 prebleach images. To obtain an initial bleaching depth of $\approx 30\text{\%}$ of the prebleach intensity in the ROI, one to four bleach images were taken depending on the sample. For every recovery, at least 100 frames were recorded. The FRAP data were normalized by the prebleach fluorescence intensity. It is known that fluorescein does not follow first-order bleaching kinetics and would need to be compensated by an actual apparent bleaching intensity distribution. However, it has been shown that for low enough spatial resolution and large enough ROI (> 5 μm with the objective used) those effects are negligible (34,36).

After adjusting the pH and locking the polymer solution between two cover glass slides, FRAP measurements were performed on every sample at 298 K to characterize the mobility of the probes in the polymer solution before the onset of gelation. Thereafter, the previously described heat ramp protocol was run to gel the sample. The measurements on the gel systems were undertaken immediately after cooling the sample and were performed at a constant 298 K. At least six FRAP measurements were performed at different spatial coordinates per sample. Diffusion coefficients and binding rate constants reported in this study represent an average over this spatial sampling. To test reproducibility, every sample was remade at least once. The appearance of all heat-set gels was first checked optically and confirmed to have formed a transparent gel structure. All probes were freshly dissolved on the day of the experiment.

The free diffusion coefficients $D_0$ of the probes were determined at 298 K. To do this the pH values were adjusted and FRAP measurements performed on the probe dissolved in water without the polymer. Probe solutions prepared in this way were also placed in secure-seal spacers between two cover glass slides to avoid convection.

Models

To evaluate the FRAP data, two different FRAP models will be applied to process the sequence of recorded recovery images, to extract the diffusion coefficients of the probes, and to investigate further whether any probe-network interactions influenced the recovery.

Diffusion without binding

A pixel-based framework for analysis of FRAP data was developed by Jonasson and co-workers (34). It starts from the following diffusion equation:

$$\frac{\partial C}{\partial t}=D{\text{▽}}^{2}C$$ (1)

for the concentration of unbleached fluorochromes C and the diffusion coefficient D. Assuming a cylindrical bleached region, which is accomplished by choosing a low numerical aperture objective, one can neglect net-diffusion in the z-direction so that the diffusion equation needs to be solved for a two-dimensional case only. This model uses a pixel-based statistical methodology of minimizing the likelihood function to solve Eq. 1 and therefore efficiently utilizes all recorded pixels—all the information about the diffusion process—in the available set of image data. It will be referred to as the maximum likelihood FRAP (MLH) model. The evaluation of the model was carried out in Matlab (MathWorks, Natick, MA). Previous studies have shown that this model is robust and reliable (4,37), as long as the initial bleaching profile can be assumed to be approximately Gaussian. Twenty postbleach images, corresponding to a recorded recovery time of 10 s, were found to be sufficient for accurate application of the model. A further increase in the number of analyzed postbleach images did not significantly influence the accuracy of the estimated parameters and took a longer to compute (4,34). The model’s limitations are only reached for slow processes, where a hat-shaped intensity profile (only poorly approximated via a Gaussian) dominates the first seconds of the recovery, and when probe-network interactions are not negligible and Eq. 1 not longer captures the physics of the system accurately.

Diffusion with binding

A quantitative approach to analyze binding-diffusion kinetics by confocal FRAP was developed by Kang and co-workers (15).

The binding component of a binding-diffusion process can be described by the following chemical equation:

$$U+S\underset{k_{off}}{\overset{k_{on}}{\rightleftharpoons }}B$$ (2)

where U and S denote unbound molecules and specific binding sites respectively, and B the bound complexes (US). Assuming a high enough density of binding sites, this model considers a system to be at equilibrium before the bleaching. The bleaching perturbs the equilibrium concentrations of the fluorescent free molecules (concentration of free molecules denoted as u) and bound probes (concentration of bound molecules denoted as b) at the binding sites. The equilibrium concentration of free binding sites $s_{eq}$ does not change during the bleaching process and is therefore a constant. After bleaching, the return to equilibrium can be described using the following first-order reaction-diffusion equations:

$$\begin{array}{l}\frac{\partial u}{\partial t}=D_1{\mathrm{▽}}^{2}u-{\overline{k}}_{on}u+k_{off}b\\ \frac{\partial b}{\partial t}=D_2{\mathrm{▽}}^{2}b+{\overline{k}}_{on}u-k_{off}b\end{array}$$ (3)

with $D_1$ and $D_2$ being the diffusion coefficients of U and B respectively; ${\overline{k}}_{on}=k_{on}{s}_{eq}$ and $k_{off}$ are pseudo-on and off binding rate constants ($k_{on}$ is the on binding rate constant). The experimentally accessible total fluorescent intensity equals the sum F = u +b. Fitting the first postbleach image to an exponential of a Gaussian (15) yields an effective bleaching radius $r_e$. Using an effective bleaching radius, $r_e\ge r_n$, enables the model to take diffusion during the bleaching phase into account.

This FRAP and binding (FRAPb) model is solved numerically by the Matlab script BDfrap.m provided by Kang and co-workers (15) for FRAP in a circular bleach region of radius $r_n$. This approach calculates the time evolution of the averaged fluorescent intensity within the ROI. We used this script when analyzing experimental data within the FRAPb framework and employed the following steps and assumptions to determine the diffusion coefficient of the probes $D=D_1$ and the parameters ${\overline{k}}_{on}$ and $k_{off}$:

• •D₂ was set to 0. This implies that the binding sites on the percolated network structure were assumed to be immobile.
• •The intensity curves from six FRAP measurements—on six spatially well separated spots within the sample—were averaged to one curve, which was subsequently fitted.
• •The effective radius $r_e$ of the bleached disc of the first postbleach frame was estimated (38).
• •The Matlab function FMINSEARCH, was utilized during the fitting routine.
• •Two types of minimization were checked. The first was a weighted residual (38), so that differences in the early time period contribute more to the residual. The second minimized the sum of squared residuals.

The starting value of the diffusion coefficient D for FMINSEARCH routine was chosen by analyzing only the first 2.5 s of the postbleach series within the MLH framework. We checked that the shape of the recovery curve depends on the size of the ROI (13,15) and therefore the diffusion is not “reaction dominant” (13). Thus the recovery at short times is a good approximation of the free diffusion of the probes. Thereafter, a careful scan of the parameter-space over five orders of magnitude for the initial values of ${\overline{k}}_{on}$ and $k_{off}$ during the optimization routine was undertaken. Both residual routines were tested and were found not to differ significantly. To save computational time, only the weighted residual fitting routine was employed for the whole study. This procedure of fitting the data using a three-parameter fit yields D, ${\overline{k}}_{on}$, and $k_{off}$. If the diffusion coefficients D obtained by this three-parameter fit were found not to diverge from the diffusion coefficients gained by the MLH model in the limit # postbleach images → 0, D was fixed and a two-parameter fit was employed to determine the final values of ${\overline{k}}_{on}$ and $k_{off}$.

The parameters obtained allow an estimate of the ratio of bound $b_{eq}$ and free probes $u_{eq}$ (13)

$$b_{eq}=\frac{{\overline{k}}_{on}}{{\overline{k}}_{on}+k_{off}},u_{eq}=\frac{k_{off}}{{\overline{k}}_{on}+k_{off}}$$ (4)

An estimate of the average time of free diffusion between binding events is given by $1/{\overline{k}}_{on}$; an estimate of the average time of a probe being “bound” to the polymer matrix is given by $1/k_{off}$.

Physical models of diffusion

Most theoretical models for diffusion in gels and solutions are based on one of three different physical concepts: obstruction effects, free volume effects, or hydrodynamic interactions (39–41). These models try to explain the slower diffusion of the solute through a polymer matrix—compared with their diffusivity in pure solvent—in terms of a few critical parameters such as the volume fraction of the polymer, size of the probes, network strand size or the cross-link density. In this study we apply two of these models.

The model of Mackie and Meares (42) deals with obstruction effects in heterogeneous media. Polymer chains are regarded as motionless relative to the diffusing molecule, and thus the presence of the motionless polymer chains leads to an increase in the mean path length of the diffusing molecules between two points in the system. This model describes a very general approach for small probes in polymer solutions—as it takes only the volume fraction of the polymer into account:

$$\frac{D}{D_0}={\left[\frac{1-\phi }{1+\phi }\right]}^2$$ (5)

with diffusion coefficient D, diffusion coefficient in pure solvent $D_0$, and volume fraction of the polymer φ.

The Ogston model (43) utilizes obstruction theory as well. It considers the volume fraction as well as the polymer probe sizes ($r_d$) and polymer strand radii ($r_p$). The Ogston model implements obstruction effects using a stochastic jump approach. The polymer strands are assumed to be randomly distributed static obstacles that change the diffusive path of a probe molecule. This model, based on the probability that a probe molecule of a certain radius would fit into openings larger than its own size, leads to the following expression for the diffusivity:

$$\frac{D}{D_0}=exp\left[-{\phi }^{0.5}\frac{\left(r_d+r_p\right)}{r_p}\right]$$ (6)

Results and Discussion

We performed a series of FRAP measurements to study the diffusivity of different probes labeled with the anionic fluorescent tracer fluorescein in positively charged BLG systems. This tested the validity of the established MLH FRAP model in charged systems. Analysis within the FRAP and binding framework (FRAPb) was also used. The following probes were investigated: 70 kDa FITC-dextran and Na₂-fluorescein.

Probe diffusion in water

A characterization of the probes in distilled water using the MLH model (34) yielded the free diffusion coefficient $D_0$. $D_0$ and the associated hydrodynamic probe radii, found by applying the Stokes-Einstein equation, are reported in Table 1. We confirmed the FRAP setup by reproducing the measurement by Hagman and co-workers (6) on 10 kDa FITC-dextran at neutral pH and 298 K (data not shown), and further by the observation that the diffusion coefficient of the larger 70 kDa FITC-dextran obeys the power law $D^{-1}\approx M{W}^{0.57}$ (44). The quantum yield of the probes decreased slightly with decreasing pH (32,33). This required a 1.5-fold increase in the scanning beam intensity compared with neutral pH to obtain a good signal-to-noise ratio. The signal was nonetheless found to be stable—without any bleaching effects during the scanning.

Diffusion of probes with different surface-charge densities

A typical FRAP recovery, showing the prebleach and postbleach images as described in the methods section, is shown in Fig. 1.

Figure 1.

CLSM images of a typical FRAP measurement on a BLG gel. The first image (a) depicts the prebleach phase; the second image (b) is recorded directly after bleaching; the following images are recorded (c) 5 s, (d) 20 s, (e) 50 s, and (f) 100 s after bleaching. The circular ROI has a diameter of 30 μm; the image size is 187 × 187 μm.

FRAP analysis considering diffusion without binding

As discussed above, the surface density of fluorescein dyes (see Table 1) gives rise to different anionic surface-charge densities for the probes used. Fig. 2 depicts the measured FRAP recovery curves for the probes 70 kDa FITC-dextran (FD70) and Na₂-fluorescein (NaFL) in positively charged 12% w/w BLG gels at pH 3.5. NaFL has the highest surface-charge density. The recovery curve for FD70 could be fitted by the MLH model and yielded a diffusion coefficient of $D=6.7\pm 0.5\mu m^2/s$. Fig. 2 additionally shows the dependence of the diffusion coefficient gained by the MLH model on the number of recorded postbleach frames. The values for D show no significant deviations, indicating that the MLH model is valid for the FITC-dextran. This is in agreement with Jonasson and co-workers (34) who found that 20 evaluated frames yield a robust estimate of the diffusion coefficient.

Figure 2.

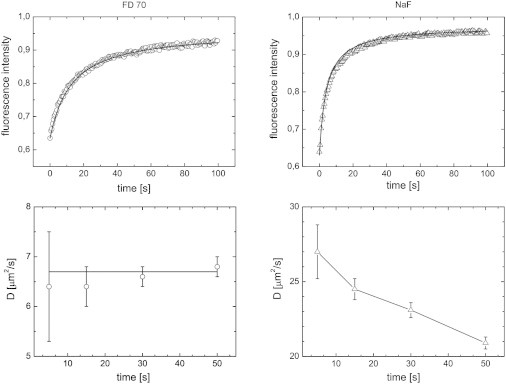
FRAP measurements on a 12% w/w pH 3.5 BLG gel, depicted in two columns for FD70 and NaFL respectively. All depicted measurements are performed with 100 ppm probe concentration. (Top) Recovery curves; the fits to the recovery curves are gained in the no-binding limit with D = 6.7 μm²/s and R² = 0.9996; and D = 24.0 μm²/s and R² = 0.9941, for FD70 and NaFL, respectively. (Bottom) Diffusion coefficients, obtained using the MLH script, as a function of the number of analyzed postbleach images (two frames per second).

The recovery curve for NaFL could not be fitted accurately within the framework of the MLH model (see the fit for NaFL in Fig. 2). Further analysis within the MLH model resulted in a diffusion coefficient that decreases as the number of evaluated postbleach frames increases. It yielded values for D ranging between 27 and 21 $\mu m^2/s$. This raises doubts regarding the applicability of a framework that only solves the diffusion equation Eq. 1 for NaFL in this system. A comparison with the diffusion coefficients of NaFL in the 12% w/w BLG gel with its free diffusion coefficient $D_0$ (see Table 1) shows a decrease of more than 90%. This decrease is significantly more than can be expected from any physical model of diffusion (39,40).

FRAP analysis considering diffusion with binding

As demonstrated above, discrepancies in the analysis using the MLH model—for the probe NaFL—require an extended evaluation model of the FRAP data. Therefore, the coupled reaction-diffusion equations (Eq. 3) for “bound” and “unbound” probes were solved following the FRAPb approach of Kang and co-workers (15). The recovery of the averaged fluorescent intensity within the ROI, as depicted, for example in Fig. 2, was analyzed using this approach.

Analysis of FD70 diffusion in 12% w/w BLG gels within the FRAPb framework yielded diffusion coefficients of $7.1\pm 0.7\mu m^2/s$, with ${\overline{k}}_{on}\le {10}^{-4}{s}^{-1}$ and $k_{off}\ge {10}^4{s}^{-1}$. Thus, the diffusion coefficients obtained using the binding framework do not differ significantly from the results of the MLH model ($D_{MLH}=6.7\pm 0.5\mu m^2/s$) found in the previous section. The extreme values of ${\overline{k}}_{on}$ and $k_{off}$ suggest that binding events do not influence probe diffusion. 70 kDa FITC-dextran, therefore, could be treated successfully in the no-binding limit of the FRAPb model. The standard deviation of the diffusion coefficients obtained by the FRAPb approach (over the ROI averaged time evolution) was found to be higher than those found by the pixel-based MLH model, where the consideration of every recorded pixel improves the accuracy.

The analysis of the NaFL diffusion in 12% w/w BLG gels within the FRAPb framework yielded $D=31.4\pm 2.9\mu m^2/s$; with ${\overline{k}}_{on}=0.16\pm 0.01s^{-1}$ and $k_{off}=4.8\pm 0.4s^{-1}$. The model was found to fit the data in Fig. 3 a accurately with $R^2=0.9990$. As described in the Methods section, compensation for the diffusion during bleaching is an additional step in the evaluation of the FRAPb framework. This is done by estimating the effective bleaching radius $r_e$ (with $r_e>r_n$) of the first postbleach image (15). Fig. 3 c depicts such a radial intensity profile. A value of $D=31.4\mu m^2/s$ is found by FRAPb, whereas the mean value of the MLH model (without binding) is $D_{MLH}=24.0\mu m^2/s$; lower than the value obtained from FRAPb. Further, the fits of the recovery curve in Fig. 3 a show that the no-binding limit clearly deviates from the observed recovery data. Fig. 3 b consistently shows that the values for D do not significantly depend on the number of evaluated postbleach frames.

Figure 3.

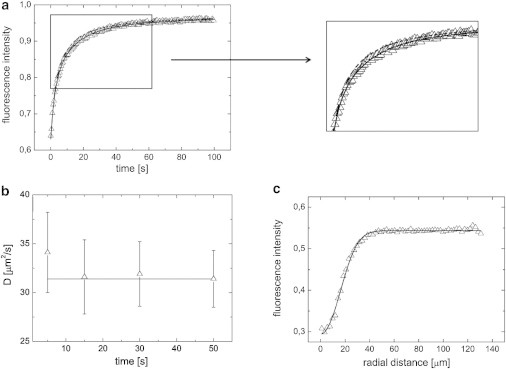
FRAP measurements on a 12% w/w pH 3.5 BLG gel with 100 ppm NaFL. (a) Recovery curve. full line: FRAPb fit: ${\overline{k}}_{on}=0.16s^{-1}$, $k_{off}=4.8s^{-1}$ and D = 31.4 μm²/s with R² = 0.9990; dashed line: no-binding fit for NaFL as in Fig. 2. (b) Diffusion coefficient, obtained using the FRAPb script, as a function of the number of analyzed postbleach images (two frames per second); (c) Radial Intensity profile of the first postbleach image, with an effective radius of $r_e=28\mu m$.

These observations and the fact that within the MLH model the effective diffusion coefficient depends on the number of analyzed postbleach frames confirms the hypothesis that probe diffusion of NaFL is strongly influenced by interaction dynamics, and that the solution of the full reaction-diffusion equations is necessary. Tests containing a larger ROI of 40 $\mu m$ diameter and the evaluation of the time of diffusion across the ROI $\left(t\sim r_n^2/D\sim 1/{\overline{k}}_{on}\right)$—as proposed in other studies (13,15)—also underline the necessity of using a binding and diffusion model. The range of values found for ${\overline{k}}_{on}$ and $k_{off}$ implies that the probes’ time of free diffusion (between interactions) and residency time range between ${10}^{-1}$ and 10 s and are thus detectable within the experimentally accessible time-window. Finally, the rates could also be related using Eq. 4 to the ratio of bound probes $b_{eq}$. This estimate shows that 2% of the probes are on average “bound”—trapped—by interactions with the network strands.

Note that the occurrence of a binding-diffusion mechanism is one subclass of anomalous subdiffusion (45,46), where the probes’ diffusion coefficient is found to be time-dependent and following a power law $D\left(t\right)\approx t^{1-\alpha }$, $0<\alpha <1$. Fitting the data of time-dependent diffusion coefficients in Fig. 2 for NaFL to such a power law yields a subdiffusive exponent $\alpha =0.90\pm 0.02$.

Effect of free binding sites and microstructure on interaction kinetics

To test underlying assumptions of the FRAPb model in more detail, the pseudo-on and off rates in fine-stranded BLG gels with different biopolymer and diffusion probe (NaFL) concentrations were investigated. In the FRAPb model the assumption of equilibrium before bleaching includes a constant concentration of free binding sites $s_{eq}$, which leads to a linear dependence of $s_{eq}$ on the pseudo-on rate ${\overline{k}}_{on}=k_{on}{s}_{eq}$. The binding-diffusion kinetics, quantified in the on and off rate, depend only on the specific polymer-probe interactions. Thus the kinetics are constant at constant external parameters such as pH, temperature, and ionic strength; as a result those rates are independent of a change in the polymer concentration. Assuming, therefore, that each formed network strand in the gel structure gives rise to a certain number of binding sites, an increase in the polymer concentration increases the number of network strands, and thus increases the number of free binding sites.

Fig. 4 shows TEM (transmission electron microscopy) micrographs recorded for 10.5 and 12% w/w BLG gels at pH 3.5. The structures observed in Fig. 4 are fine-stranded (25,27,28), in contrast to the fact that BLG forms close to its pI micron-sized protein-rich aggregates (24). Visual inspection of the micrographs shows a more open structure with some aggregation for the 10.5% w/w gel, compared with the denser structure of the 12% w/w gel. This supports the assumption that the number of free binding sites increases with increasing polymer concentration in BLG gels at pH 3.5. FRAP measurements at a number of concentrations were therefore conducted to test whether an increase in the polymer concentration relates to a linear increase in the pseudo-on rate, as predicted by theory. The data for the pseudo-on and off rate measured for 50, 100, and 200 ppm NaFL and 9%, 10.5%, and 12% w/w BLG are shown in Fig. 5. A linear increase of the pseudo-on rate with increasing BLG concentration and a constant off rate were found. This strongly supports the assumption in the FRAP and binding framework: ${\overline{k}}_{on}=k_{on}{s}_{eq}$.

Figure 4.

TEM micrographs of BLG gels at pH 3.5 (left) 10.5% w/w; (right) 12% w/w.

Figure 5.

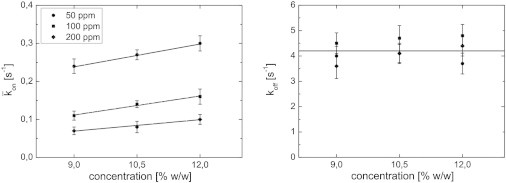
The FRAP and binding framework applied to probe-diffusion measurements in pH 3.5 BLG gels using 50, 100, and 200 ppm NaFL. (Left) The pseudo-on binding rate vs. the polymer concentration; linear fits are employed to the data sets. (Right) The off binding rate vs. the polymer concentration; the horizontal line shows the average over all nine data points. Error bars depict the standard deviation of a series of six measurements.

A second approach to test the implications inherent in the FRAPb model assumption (an increase in the polymer concentration causes an increase in free binding sites) is to study the effect of probe concentration on the equilibrium concentration of free binding sites $s_{eq}$ while keeping all other environmental parameters constant. Increasing the probe concentration should lead to a larger occupation of binding sites and reduce the number of free binding sites, resulting in a decreasing pseudo-on rate. Measurements on NaFL at concentrations between 50 and 200 ppm (Fig. 5) support this hypothesis as well. The highest pseudo-on rates were found for the lowest probe concentration of 50 ppm NaFL, and the lowest pseudo-on rates for the highest probe concentration of 200 ppm NaFL. Further, the linear fits in Fig. 5 were checked upon its intercept of the point of origin, which should be the case following the proposed linear model. For the different concentrations, intercepts in the range between $-0.04$ to $0.06\pm 0.02s^{-1}$ were found. Additionally, the off rate constant is independent of concentration, remaining constant around a mean value of $k_{off}=4.2s^{-1}$. This corresponds to an average residency time of 0.2 s. Depending on the polymer concentration, this represents an average time of free diffusion between binding events of 3 to 4 s for 50 ppm NaFL, 6 to 9 s for 100 ppm NaFL, and 10 to 14 s for 200 ppm NaFL, with 6% to 8%, 2% to 3%, and 1.9% to 2.2% of the probes being “bound” for the respective probe concentrations. These results indicate that the diffusion mechanism of NaFL through fine-stranded network structures of low pH BLG gels is strongly influenced by electrostatic interactions. In the future, a more elaborate TEM study could yield quantitative values of the network-strand surface areas and consequently estimate the number of binding sites per network strand. This would make available not yet exploited input for materials science and mass transport design.

Comparison with physical models of diffusion

To obtain further insight into the binding-diffusion kinetics observed for FD70 and NaFL, we analyzed FRAP measurements in a series of concentrations of BLG systems in the context of two simple physical models for diffusion, as described in the Methods section.

Fig. 6 a displays the normalized diffusion coefficients in BLG solutions at pH 3.5 before the onset of heat-induced gelation. The data show a decrease in diffusivity with increasing polymer concentration for each probe caused by stronger physical obstruction effects, as expected. Furthermore, the FRAP measurements on NaFL yielded a significantly slower normalized diffusion compared with the 70 kDa FITC-dextran. The model of Mackie and Meares (42) is applied to shed light on the differences in diffusion in BLG solutions. The diffusion of FD70 was found to match the prediction of the obstruction model. The diffusion of NaFL, as discussed above, is influenced by probe-polymer interactions and was not found to be described by this pure obstruction model. It is important to note that no fitting parameter exists in this model as the polymer concentration of BLG, $c_{BLG}$, is directly related to the volume fraction of the polymer φ via the density ρ of BLG and H₂O: $\phi =c_{BLG}/{\rho }_{BLG}\text{∗}1/\left(c_{BLG}/{\rho }_{BLG}+\left(1-c_{BLG}\right)/{\rho }_{H_{2}O}\right)$. Thus FD70 does show the typical diffusivity of small probes in a polymer solution—as generically described by the model of Mackie and Meares.

The probe diffusion measured directly after the heat-induced gelation was analyzed similarly. Fig. 6 b displays normalized diffusion coefficients of NaFL and FD70 in the different gels. We again observed a slower diffusivity of NaFL compared with FD70, and a reduction of ∼ 50% of the normalized diffusivity compared with the ungelled system, caused by the formation of fine-stranded network structures. We utilized a more detailed model, the Ogston model (43), to treat the gelled systems. Taking the hydrodynamic radii of the probes (given in Table 1) as input to the Ogston model, the FRAP measurements over a concentrations series were fitted. Using this approach we could estimate the averaged network strand radii. A fit of the FD70 data yielded a polymer strand radius of $r_p=2.4$ nm (Fig. 6 b). The radii clearly agree with the dimensions expected of thin-stranded structures (27,28) formed by dimeric association of a globular protein of radius ∼ 2 nm (22). In this discussion we only argue qualitatively when comparing the microstructures, as the main focus is the consequences of those findings on the diffusion/binding-diffusion kinetics for the different probes. Analyzing the NaFL data using the same approach yielded an unrealistic polymer strand size (< 0.1 nm), which indicates that the Ogston model cannot be applied in this case.

Comparisons with simple physical models show that the diffusion of FD70 through the microstructure is hindered by obstruction only, for the surface-charge density is too low to cause detectable electrostatic interactions. This means that solving the diffusion equation (Eq. 1) is sufficient to describe the FRAP recovery, and that binding kinetics are negligible. By contrast, the diffusion of NaFL is strongly influenced by electrostatic interactions because of its higher surface-charge density. For this reason NaFL could not be analyzed by pure obstruction models. Additionally, the dynamics of NaFL could not be fitted by the MLH model; a FRAPb framework must be applied to gain an appropriate estimate of the diffusion coefficient. These findings strengthen the hypothesis that probe-network interactions are important for the diffusion of charged molecules in charged BLG systems.

Conclusions

Probe diffusion measurements by FRAP and binding combined with probes of different sizes and surface-charge densities, and TEM were found to offer a powerful combination of methods to determine local diffusion and electrostatic interaction properties in charged hydrogels. We were able to validate important assumptions of the FRAP and binding framework, outside its original biophysical context, using a believed new approach with positively charged fine-stranded BLG hydrogels with well-controlled microstructures. By varying the number of binding sites or the probe concentration, a linear relation between the pseudo-on binding rate constant and the concentration of free binding sites was established. This strongly supports an important assumption of the FRAP and binding framework, that ${\overline{k}}_{on}=k_{on}{s}_{eq}$. Further, our probe diffusion experiments in β-lactoglobulin solutions and gels of positive charge revealed that the probe with the highest negative charge, Na₂- fluorescein, exhibits a diffusivity that cannot be described by the well-established MLH FRAP model considering only pure diffusion. A FRAP and binding framework needs to be employed to describe the slowed down diffusion dynamics of Na₂-fluorescein, which consequently treats the FRAP data in terms of probe-network interactions. In our case the probes’ time of free diffusion between interactions and residency time are found to be within 10⁻¹ to 10 s. Thus BLG hydrogels can serve as an important model system for diffusion-binding kinetics where ${\overline{k}}_{on}$ and $k_{off}$ is in a range that requires the full binding diffusion model for FRAP data fitting. An indicator within the MLH model was introduced: the dependence of the diffusion coefficients upon the number of evaluated postbleach frames allowed us to clarify whether FRAP data require analysis using a binding-diffusion model. Our measurements support that the FRAP and binding framework is built on solid foundations, and that FRAP and binding offers important insights for materials scientists when designing hydrogels with tailored mass-transport and release properties.