Analysis of Spatial Correlations Between Patterns of DNA Damage Response and DNA Replication in Nuclei of Cells Subjected to Replication Stress or Oxidative Damage

Abstract

Sites of DNA replication (EdU incorporation) and DNA damage signaling (γH2AX) induced by camptothecin (Cpt) or hydrogen peroxide (H₂O₂) form characteristic patterns of foci in cell nuclei. The overlap between these patterns is a function of the number of DNA double strand breaks (DSBs) formed in replication sites. The goal of this study was to optimize a method of quantitative assessment of a degree of correlation between these two patterns. Such a correlation can be used to estimate a probability of inducing damage in sections of replicating DNA. The damage and replication foci are imaged in 3D with confocal microscopy and their respective positions within nuclei are determined with adaptive image segmentation. Using correlation functions spatial proximity of the resultant point patterns is quantified over the range of distances in cells in early-, mid- and late S-phase. As the numbers (and nuclear densities) of γH2AX and replication foci differ significantly in the subsequent substages of S phase, the detected association values were corrected for the expected random overlap between both classes of foci. Thus, the probability of their nonrandom association was estimated. Moreover, self association (clustering) of DNA replication sites in different stages of S-phase of the cell cycle was detected and accounted for. While the analysis revealed a strong correlation between the γH2AX foci and the sites of DNA replication in cells treated with Cpt, only a low correlation was apparent in cells exposed to H₂O₂. © 2013 International Society for Advancement of Cytometry

In the parallel paper (1), we describe analysis of the pattern of interdependence between the barycenters of histone γH2AX foci (markers of DNA damage signaling, likely representing sites of DNA double-strand breaks; DSBs) and the nearest DNA replication sites (marked by pulse-labeling with EdU). The analysis, based on measurement of the nearest-neighbor distances was carried out on A549 cells treated with hydrogen peroxide (H₂O₂) or DNA topoisomerase I inhibitor camptothecin (Cpt) to induce DNA damage and pulse-labeling them with the DNA precursor EdU to label nascent DNA (2–5). The analysis of these distances gave the expected results particularly in late S-phase, where the replicating regions are well separated from each other, confirming that Cpt preferentially damages replicating DNA. The analysis of distances in early S, where replication occurs in many small areas separated by short distances, was more complex. This was due to the fact that there was a high proportion of accidental overlap between the pattern of γH2AX and the numerous replication foci. Thus, quantitative analysis of any preference toward damage in replicating DNA, which may be a feature of agents damaging DNA in early S phase, requires taking into an account a specific contribution of the random overlap between the two patterns in early, mid and late S-phase, as well as possible nonrandom distributions of each of the foci patterns themselves.

To refine the analysis of interdependencies between the two patterns and take into account a different contribution of a random overlap between foci of both types, we propose to use a correlation analysis. This technique, based on a set of cross-and auto-correlation functions (6–9) was applied to confirm that Cpt causes damage in replication foci, and to quantify the damage inflicted by H₂O₂ in replicating and nonreplicating DNA regions. The probability of spatial association between γH2AX and replication was compared with the respective value expected for random distribution of these objects. The results of this analysis were supplemented with quantification of self association (clustering) of replication and γH2AX foci. These data were used to correct for the change of replication patterns between different substages of S-phase of the cell cycle.

Materials and Methods

Cell Cultures

In vitro cultures of human lung adenocarcinoma A549 intended for imaging experiments were grown on round coverslips submerged in Petri dishes, as described previously (1).

Inducing DNA Damage by Cpt or H₂O₂ and Labeling Nascent DNA

DNA precursor analogue, EdU (10 μM, Click-iT^® EdU AlexaFluor^® 488 Imaging Kit cat. # C10337; Invitrogen/ Molecular Probes) was added to cell cultures 30 min prior to adding camptothecin or hydrogen peroxide. Cpt or H₂O₂ were added to culture medium at a final concentration of 0.2 μM or 0.2 mM, respectively. After 30 min of exposure to a drug (i.e., 60 min of exposure to EdU) cells were fixed. Untreated cells were incubated with EdU for 60 min. Detection of EdU was performed according to manufacturer’s instructions.

Detection of γH2AX

Cells were fixed with methanol-free formaldehyde (4%) and treated with Triton X-100 (0.1%). Blocking was done overnight in 3% (w/v) BSA. Phospho-specific (Ser139) γH2AX mAb (Upstate Biotechnology, Lake Placid, NY) was used, followed by a secondary antibody AlexaFluor 568 goat anti-mouse IgG (H1L), cat. # A11004 (Invitrogen/Molecular Probes).

Confocal Microscopy

Images of cell nuclei fluorescently labeled for EdU and γH2AX were recorded using Leica LSC SP5 confocal microscope (Leica Microsystems GmbH, Mannheim, Germany). The following instrumental parameters were used: 63× HCX PL APO CS NA 1.4 oil immersion lens, excitation 488 (Ar) and 561 nm (HeNe), emission detection bands 500–550 nm for AlexaFluor488 (Click-iT EdU) and 600–660 nm for AlexaFluor568 (immunofluorescence, γH2A.X), registration in sequential mode, scanning 8,000 Hz (resonant scanner), with 8–16 averaged frames.

Image Preprocessing and Segmentation

The 3D images were preprocessed using iterative blind deconvolution, initialized with nominal point spread function (PSF) of the objective, calculated for the centres of the two fluorescence emission bands (525 and 630 nm). The number of iterations was set to 25 and the SNR to 50 (medium). The deconvolved data were subjected to median filtering (3 × 3 × 3 voxel size) to suppress the noise. The gray-scale erosion with structuring elements set (lateral and axial direction, respectively) to 5 × 2 voxels (the green channel, replication) and 9 × 4 (the red channel, damage) was used to estimate the local background, which was then subtracted from the filtered images. The kernel size was chosen empirically (taking into account different diameters of the foci) so as to enhance separation of the close maxima while avoiding their elimination due to low-pass filtering. Image intensity maxima were determined from the background corrected images, after smoothing with Gaussian filter (uniform standard deviation of 0.25). Candidate intensity thresholds were calculated with an isodata algorithm. These thresholds were compared to the respective image maxima (multiplied by 0.3) and low threshold bounds (set to 15 for the green and 25 for the red channel) to chose the highest of these values, used then as final (static) thresholds. It should be noted that the background intensities for these two channels were not the same (thus requiring different low threshold limits). The merged signals in the thresholded images were separated using watersheding, performed on the filtered images. The maximum size of the merged volume was set to 85 voxels, whereas the minimum intensity depth to 10 for both channels. Objects (foci) in the resultant binary images were labeled with 4-connectivity where the minimum volume of the object was set to 15 in the first and 40 in the second channel, respectively. Foci with the maximum intensity lower than 0.5 of the respective image maximum, were regarded as background noise and thus rejected from further analysis. It should be noted that these spots constituted less than 2% of the population. Performance of the described routine was validated with manual segmentation (produced by a human expert), taking into account differences between the two color channels in the signal to noise ratio and the sizes of the foci. The filtered sets of foci were used to estimate the envelope of nuclear volume. First, the foci whose x or y coordinates were outside the range of 1 and 99 percentiles of the whole set were removed. The convex hull of the remaining set of foci was calculated and the hole filing was performed. The nuclear masks were generated with binary dilation (structuring element of 5 × 2 voxels) followed by erosion (structuring element of 1 × 1 voxels). The foci outside the nuclear masks (i.e., in the cytoplasm) were removed from the final set. Centers of mass of the foci were calculated taking the respective masks and the filtered images as the second input.

Calculation of Correlation Functions

Relationship of positions of replication and histone H2AX phosphorylation (DNA damage signaling) was characterized over a range of distances using normalized Ripley’s K function (5,6) and pair correlation functions (9). The estimator of the former, including the correction for border effects (8) is defined as:

$$K\left(d\right)=\frac{V\left(N\right)}{nm}\sum _{i=1}^n\sum _{j=1}^{m}R(i,j)$$ (1)

where: V(N) is the volume of the nucleus; n and m the numbers of foci constituting pairs (phosphorylation and replication, respectively); R(i,j) is the indicator function equal to 1 if the foci i and j are within the distance d and 0 otherwise. To correct for the border effect a modified indicator function R (corresponding to the number of spot pairs) was used:

$$R^{\prime }(i,j)=R(i,j)\ast \frac{V\left(D\right)}{V(D\cap N)}$$ (2)

where: V(D) is the volume of sphere of the radius d, V(D∩N) is the volume of the intersection between the sphere D (centered at the ith focus) and the nucleus. The sphere was approximated with d rounds of subsequent binary dilations starting from the central pixel of the spot. The K function was normalized so that correlation of foci corresponds to its positive and anti-correlation to negative values:

$$L^{\prime }\left(d\right)=\sqrt[3]{\frac{3\ast K^{\prime }\left(d\right)}{4\pi }}-1$$ (3)

where: K′(d) is the Ripley’s function corrected for border effects.

It should be noted that the L′ functions [Eq. (3)] reflect the ratio of the observed probability of association and the probability expected for the random distribution. Where indicated, the number of the phosphorylation foci was further corrected using the data obtained from control nuclei (i.e., from cells not treated with Cpt or H₂O₂). These provided information on the density and distribution of endogenous damage foci (imaged in the red channel). The respective Ripley’s K function was calculated using the formula:

$${K^{\prime }}_m\left(d\right)=\frac{V\left(N\right)}{(n-u)m}\left[\sum _{i=1}^n\sum _{j=1}^m{R}^{\prime }(i,j)-\frac{uw\ast V\left(D\right)}{V\left(C\right)}(L_c^{\prime }+1)\right]$$ (4)

where: u and w are the numbers of foci in the control nuclei (phosphorylation and replication, respectively); V(C) is the volume of control nuclei, L′_c is the corrected and normalized Ripley’s K function for the control nuclei.

The corrected Ripley’s function (K′_m) was normalized using the above formula (3) to yield L′_m. The L-functions corresponding to cross-correlation of H2AX phosphorylation (damage) and replication foci were further normalized to the values of corresponding autocorrelation functions of the latter. At the distances where replication foci were not resolvable (<0.4 μm) their autocorrelation functions were approximated with a phenomenological function:

$$L_a^{\prime }\left(d\right)=A+\frac{B}{d}+\frac{C}{d^2}$$ (5)

where: A, B, C are function coefficients determined with least-square fitting to the autocorrelation function (L′_m, replication foci), at the distances smaller that 0.4 μm.

The Ripley’s K function was finally normalized using the formula:

$$L_f^{\prime }\left(d\right)=\frac{L_m^{\prime }\left(d\right)+1}{L_a^{\prime }\left(d\right)+1}-1$$ (6)

The normalized (corrected) Ripley’s K function (L′_f(d)) was used to represent the spatial relationship of phosphorylation and replication patterns.

The pair correlation functions C(r̄) were implemented as in Ref. 9 in frequency domain:

$$C\left(\overrightarrow{r}\right)=\frac{FF{T}^{-1}(FFT\left(l_1\right)\times FFT\left(l_1\right))\times V\left(N\right)}{\mathrm{nm}\times N\left(\stackrel{‒}{r}\right)}$$ (7)

where: FFT is the Fourier transform, I₁ and I₂ are images corresponding to the first and second channels (the same in case of autocorrelation). To correct for the fact that only a part of the image volume (inside nucleus) might contain foci the normalization factor N(r̄r) was used:

$$N\left(\overrightarrow{r}\right)=FF{T}^{-1}\left({\mid FFT\left(N\right)\mid }^2\right)$$ (8)

where: N is the binary image of the nuclear mask.

Correlation functions were angularly averaged by transformation to polar coordinates and then binning by radius, with the bin width of 0.1 μm. The averaged cross-correlation functions were corrected (similarly to the Ripley’s K) using the data obtained from control nuclei, not treated with Cpt or H₂O₂. The respective C(r̄) function was calculated using the formula:

$$C\left(\overrightarrow{r}\right)=\frac{nC\left(r\right)-u{C}_c\left(r\right)}{(n-u)}-1$$ (9)

where: n and u are numbers of damage foci in treated and control nuclei, C_c(r) nuclei is the cross-correlation function of the control nuclei.

Results

Statistical Analysis of Correlation Between H2AX Phosphorylation and Replication

As discussed in extent elsewhere (1,5), an analysis of 3D images of the foci of replication and histone H2AX phosphorylation can provide information as to their spatial relationship in nuclei of cells subjected to DNA-damaging agents. Calculating the histograms of the nearest-neighbor (nn) distance between replication and histone H2AX phosphorylation foci is the most intuitive way to approach the problem. We present the details of such analysis in the first paper (1) and give an example here (Fig. 1). One can envisage situations, however, when genotoxic agent causes damage in and outside replicating regions, and does so in a concentration-dependent manner, or in certain specific areas of the nucleus. In this case, an analysis of correlation between damage and replication, rather than histograms of damage signaling-to-replication areas could be particularly useful. Moreover, the spatial relationship resulting from stochastic distribution of foci may be accounted for in an explicit manner. We have performed such an analysis of correlations between damage signaling and replication in Cpt- or H₂O₂ treated cells, using modified Ripley’s functions (6,7) and cross-correlation functions (9).

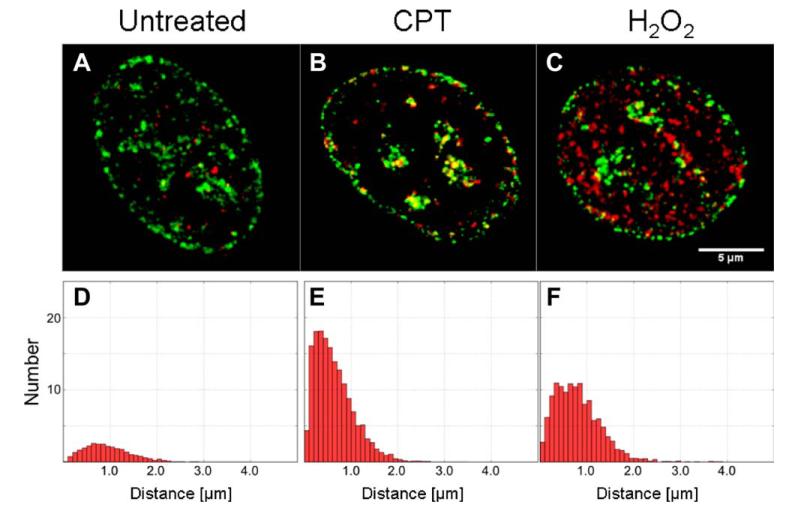
Figure 1.

Images of replication (green) and DNA damage signaling foci (red) in the nuclei of: control (A), and cells treated with Cpt (B), and H₂O₂ (C). Histograms of nn distances corresponding to populations of these nuclei are shown in the panels D, E, and F, respectively. [Color figure can be viewed in the online issue which is available at wileyonlinelibrary.com.]

The L-functions were first normalized to their respective theoretical values calculated under the assumption of random distributions of the same number of foci in both channels. A constant value of 1, which was predicted for a random distribution, was then subtracted. Hence, negative values of the L-functions correspond to anti-correlation of the foci distributions; the mutual exclusion of the foci in space (at a given distance) yields the value of −1 (minimum). Positive values correspond to the probability of association, as compared to a random distribution, and thus indicate spatial correlation (at a given distance) of foci patterns (a maximum at infinity). For instance, the value of 0.5 indicates that the association occurs (at a given distance) with probability by 0.5 (50%) greater than in the case of the random distribution. Conversely, zero values are obtained when the positions of foci of both types are independent (i.e., have random distributions). The same notion applies to C-functions, which do not require normalization. Moreover, to mitigate the effects of self-clustering of the replication foci (particularly in the late S-phase) the L-functions corresponding to cross-correlation of phosphorylation and replication foci were divided by their (auto-correlation) counterparts, calculated for the replication spots (Fig. 2).

Figure 2.

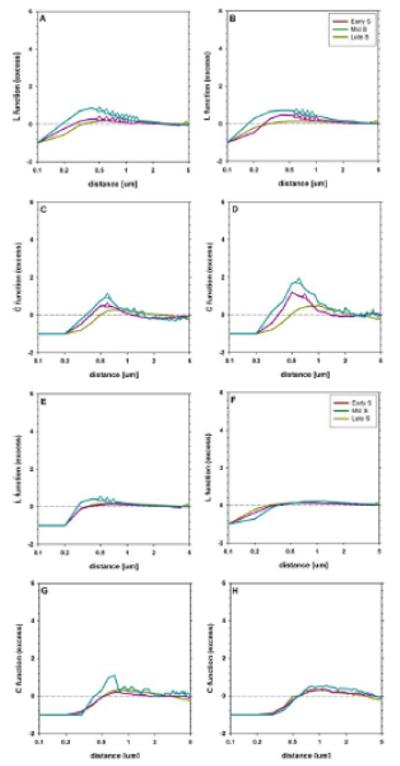
Patterns of spatial distribution of replication (ABCD) and γH2AX (EFGH) foci in the nuclei of cells treated with Cpt (ACEG) or H₂O₂ (BDFH). The pattern of autocorrelation was analyzed with L-functions (L′_m(d), ABEF) and C-functions (CDGH). The early S-phase is represented with yellow lines, the middle S-phase with magenta and the late S-phase with cyan. The distances corresponding to significant (P < 0.01) difference from 0 (no correlation) are marked with triangles. [Color figure can be viewed in the online issue which is available at wileyonlinelibrary.com.]

Analysis of nn Distances Between Replication and γH2AX foci

Fluorescent labeling of the replication (EdU) and DNA damage signaling (γH2AX phosphorylation) in the cell nuclei (mid-S phase) reveals the presence of numerous foci representing both processes (Fig. 1B–1F). In contrast to the cells treated with Cpt (Fig. 1B,E) or H₂O₂ (Fig. 1C,F) only a very low number of histone phosphorylation foci was detectable in the control (Fig. 1A,D). A similar effect was observed in the early and late S phase, although the replication and the damage signaling patters were different (as described in Ref. 1), this issue). The histograms of nn distances indicate that, when the damage signaling was induced by Cpt, more γH2AX foci were found in close proximity to DNA replication foci than in the case of the damage signaling produced by H₂O₂ (Figs. 1E and 1F, respectively). This type of analysis provides intuitive biological interpretation and validation. However, it does not take into account the proximity induced by a large number of foci being present in the same nuclear volume (in early S vs. late S phase). Moreover, possible effects of self-association of replication foci (mid S, late S) are not accounted for. Therefore, to account for these phenomena we applied the pattern correlation functions.

Autocorrelation of Replication Foci

The shape of L-functions corresponding to the replication foci reveals a deficit of point density (anti-correlation) at small distances (<0.4 μm), as the function values are smaller than 0, both in cells treated with Cpt (Fig. 2A) and H2₂O2₂ (Fig. 2B). This observation is compatible with the fact that the finite resolution of microscopy images imposes a limit on the possibility of measuring small distances between signals. For instance, no two foci in the studied population were separated by the distance of 0.1 μm or smaller (the L function value of −1). One may note the fact that, at the large distances (>2 μm) comparable with a nuclear radius, the foci distribution (i.e., the value of L function) approaches the value characteristic for the random distribution (L-function close to 0). However, at intermediate distances grouping (clustering) of the replication signals is observed (L-function greater than 0). The clustering is virtually undetectable in the early S-phase, but clearly visible in the middle and late S-phase at the distances between 0.5 μm and 1.0 νm (P < 0.01), as expected (clusters near nucleoli, and at the nuclear envelope). The maximum of 0.8 μm is obtained at the distance 0.4 μm in the late S-phase, indicating the association occurring with the probability greater by 0.8 than the value corresponding to the random distribution. No difference between autocorrelation patterns in the nuclei treated with Cpt (Fig. 2A) and H₂O₂ is found using L-functions (P > 0.1). Hence, no relationship between DNA damage signaling and replication is detectable in this system. A similar situation is observed using the C-functions (correlation, Fig. 1CD), although these functions are shifted to higher distance values, in comparison with the L-functions. Moreover, a significant clustering (P < 0.01) is detectable at the narrower range of distances. Likewise, the difference in values of C-functions corresponding to Cpt and H₂O₂ treatment was not significant (P > 0.1).

Autocorrelation of γH2AX Foci

Distribution of H2AX phosphorylation (DNA damage signaling) foci exhibits a deficit of density at small distances (Fig. 2EF), similarly to their replication counterparts. Comparison of L-functions corresponding to Cpt and H₂O₂ treatments shows that no neighbors of the foci are detected at (and below) the distance of 0.1 μm in the case of Cpt and 0.2 μm in the case of H₂O₂. This indicates that the foci of H₂O₂ may be slightly smaller (<0.1 μm in diameter) than the replication regions. Furthermore, a slight spot clustering (L-function greater than 0) is detectable (P < 0.01, the probability greater by 0.3 than the random value) only in the case of nuclei treated with Cpt in the late S-phase (Fig. 2E). Moreover, the values of L-function corresponding to nuclei treated with Cpt are significantly higher (with P < 0.01) than in the nuclei treated with H₂O₂, in the late S-phase.

The deficit of density at small distances is also detectable with C-functions (Fig. 2GH). Here, too, these functions are shifted to the higher distances, compared to their L counterparts. However, the clustering of foci in the late S-phase, although compatible with the shape of C-function, has no statistical significance (P > 0.1).

Correlation of γH2AX Foci with Replication Regions

The shape of the normalized L-functions reveals a clear positive correlation between histone H2AX phosphorylation and replication patterns in cells treated with Cpt (Fig. 3A). The correlation is more pronounced in the late S-phase than in early or mid S, that are similar with respect to this parameter. Nonetheless, in all substages of S-phase the highest correlation values are observed at the minimum distance, reaching 2.6 ± 0.3 for the early/middle S phase and 5.3 ± 0.9 for the late S phase. These values correspond to spatial association between foci occurring, respectively, 3.6 and 6.3 times more frequently than expected in the case of a random distribution. The correlation decreases with increasing distance and reaches the value of 0.2, being significantly different (P < 0.01) from 0 (no correlation) up to 1.0 μm (early and middle S-phase) or 1.3 μm (late S-phase).

Figure 3.

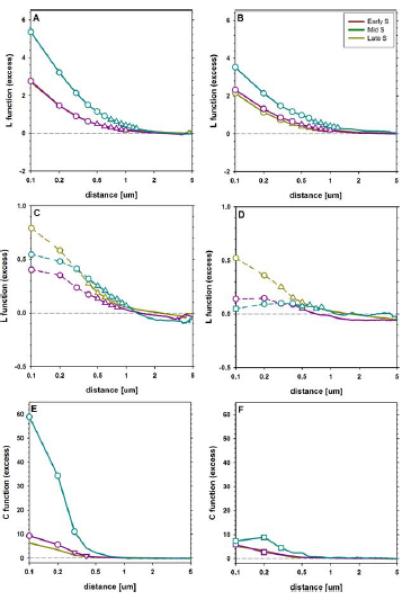
Relationship of spatial distributions of γH2AX and replication foci in nuclei of cells treated with Cpt (ACE) or H₂O₂ (BDF). The pattern of cross-correlation was analyzed with L-functions (L′_m(d), AB), normalized L-functions (L′_f(d), CD) and C-functions (EF). The early S-phase is represented with yellow lines, the middle S-phase with magenta and the late S-phase with cyan. The distances corresponding to significant difference from 0 (no correlation) are marked with triangles, those corresponding to a difference (P< 0.01) between Cpt and H₂O₂ with circles, whereas those at which the latter but not the former is detectable with squares, respectively. Dashed lines (CD) indicate the range where the extrapolated values of the replication autocorrelation were used to calculate the normalized cross-correlation L′_f(d) function. [Color figure can be viewed in the online issue which is available at wileyonlinelibrary.com.]

In the nuclei treated with H₂O₂ a correlation between replication and phosphorylation foci is weaker than in cells treated with Cpt (Fig. 3B). This difference between corresponding phases in H₂O₂ and Cpt is significant (P < 0.01) for the distances from 0.1 μm to 0.6 μm (late S-phase) or to 0.3 μm (early S-phase). The respective correlation magnitudes at 0.1 distance are 2.0 ± 0.6 (early S phase) and 3.5 ± 0.8 (late S phase). Hence, the spatial association between foci occurs, respectively, 3.0 and 4.5 times more frequently than expected in the case of random distribution of the foci. The correlation decreases with distance reaching 0 at 1.3 μm (late S phase), similarly to the data obtained for Cpt treatment.

Normalized L functions also revealed a significant difference between the results of both treatments (Fig. 3CD), in all the stages of S-phase. Positive correlation between damage and replication is observed in the nuclei treated with Cpt. The extrapolated magnitude of this effect is in the range of 0.4 ± 0.1 to 0.8 ± 0.2, at the smallest distance (0.1 μm). Thus, one may estimate that biological correlation between DNA damage signaling and replication resulted in the association between the respective foci occurring from 1.4 to 1.8 times more frequently than in the case of random distribution. These values are smaller than their non-normalized counterparts (Fig. 3AB), indicating that a significant part of correlation between the damage and replication foci may be attributed to autocorrelation (nonrandom distribution) of the replicating regions. Nonetheless, similarly to the previous case, the normalized correlation decreases to 0 at 1 μm in all the substages of S phase. Moreover, the corresponding values are observed in the middle-and late S-phase nuclei treated with H₂O₂ and do not exceed 0.2 ± 0.1. The value extrapolated to 0.1 μm distance in the early S-phase approached 0.5. One should note that the density of the replication foci was the highest in this phase—this affected the accuracy of the calculations described here (as discussed further). Nonetheless, also in this case the DNA damage-to-replication correlation in the nuclei treated with H₂O₂ is lower (P < 0.01) than in the nuclei treated with Cpt.

The difference between the consequences of exposure to Cpt and H₂O₂ is readily observable with C-functions when late S-phase nuclei are studied and becomes detectable (albeit at a smaller magnitude) in the middle S-phase (Fig. 3EF). However, in the early S-phase no significant difference could be detected between both treatments. Similarly to the results obtained with L-functions, the correlation measured with C-functions decreased from the maximum at the smallest distances to 0 (random association), but at a smaller distance of approximately 0.5 μm.

Discussion

It has been shown recently (using laser scanning cytometry) that in the case of certain genotoxic agents induction of γH2AX correlates in time with DNA replication (1,2). To study this and similar phenomena in a quantitative manner and correlate them with each other spatially within the nuclear chromatin, an appropriately tailored data collection and image analysis approach is required. Quantitative assessment of interdependencies between DNA damage and replication cannot be performed accurately using standard colocalization routines. Thus, we approached the problem using nearest neighbor (nn) analysis, described in (1). This method provides a reasonable measure of a tendency to induce DNA damage signaling (γH2AX) in or outside replication foci. However it is error-prone when encountering nuclei with foci of high density. Moreover, this approach cannot account for a stochastic overlap between foci of both types—a phenomenon which is particularly important in the analysis of replication in early S-phase, and is bound to occur when the damage occurs in numerous sites at close proximity to each other. Furthermore, the nn approach is unable to detect and quantitatively analyze the problem of mutual exclusion of events of both types, or the opposite—the clustering of foci, should any of these phenomena occur. The correlation analysis described in this report is intended to extend the nn quantitative analysis so as to embrace the abovementioned problems. The advantages and limitations of the correlation analysis approach proposed here are discussed further.

Replication and phosphorylation foci were isolated using a thresholding algorithm, complemented with watersheding. One should note that the nonspecific (background) fluorescence was more prominent in the images of histone H2AX phosphorylation (labeled with immunostaining) than in the images of replication (labeled using “click” chemistry). Furthermore, signal-to-noise ratios in these two data sets were not identical owing to the different detectable fluorescence intensities of the respective labels (AlexaFluor488 and AlexaFluor568). The algorithm accounted for the former by exclusion of foci with the brightness similar to those present outside nuclei (i.e., in the cytoplasm). The latter was dealt with by using of the isodata thresholding (based on intensity histogram). Therefore, execution of this first segmentation step in an automated way (applied here) and manual thresholding by a human expert yielded similar (within 3%) total volumes occupied by phosphorylation and replication signals. However, when watersheding was applied the numbers of foci increased (by approximately 20–30%), as some of the clustered signals were split. Consequently, the numbers of foci were sufficient in every case to compute robustly the corrected L [Eq. (6)] and C [Eq. (7)] functions, which was not possible without the watersheding. Furthermore, the raw Ripley’s functions [Eq. (1)] were similar in both cases, indicating that better statistics off-sets the position measurement noise, which might be generated by artificial splitting of single foci.

Sets of segmented foci were treated as point patterns and their spatial relationship studied using correlation functions (L and C). Both methods demonstrate preferential damage signalling in replicated chromatin regions under the treatment with Cpt, while such strong preference is not detectable in the nuclei treated with H₂O₂. This conclusion is in agreement with the analysis based on nearest-neighbor (nn) histograms (presented in Ref. 5). One should note that the correlation functions used here were normalized to their counterparts calculated for random spot distributions. Therefore, the influence of foci density is accounted for and the probability of nonrandom association is quantified. The correlation between damage and replication is stronger in the late S phase, as compared to the early and middle stages of this phase. A similar pattern was detectable using the nn histograms. However, in the late S phase self association (clustering) of replication foci was more pronounced than in the other two stages. Normalization of the L- and C-functions describing cross correlation of the damage and replication foci with respect to the autocorrelation functions indicates that this difference between stages of S-phase may be explained by clustering of replication foci. No such correction could be applied for nn analysis [parallel paper (1)]. It should be stressed that there is a clear association between these two classes of objects in nuclei treated with Cpt, which does not result from the clustering of replication foci. The magnitude of this normalized association was slight (but detectable) in nuclei treated with H₂O₂. This may suggest that replicating chromatin is more susceptible to this agent, albeit to a much smaller degree, in comparison with Cpt. However, a purely random distribution of the replication and histone H2AX phosphorylation foci in the nucleus may not be achieved in practice, as the chromatin density in nuclear volume is not uniform. Thus, the nonrandom correlation of these two labeling patterns in the nuclei treated with H₂O₂ may reflect nonuniformity of chromatin distribution.

One should note that accuracy of detection of γH2AX with immunofluorescence is limited by high, nonuniform background, common in this type of experiments as discussed in (1). Moreover, the existence of low level histone H2AX phosphorylation throughout the nucleus cannot be excluded (10,11). The presented method of analysis would certainly benefit from better characterization of biological and instrumental contributions to this background. Reduction of the background combined with a higher sensitivity of detection (using avalanche photodiodes or EMCCD cameras) might also help in detecting early, small replication foci, which incorporate only a low number of DNA precursors. Hence, fewer histone phosphorylation events would fall into a category of false negative counts, that is, damage foci wrongly classified as unrelated to replication. A shorter postdamage lead time which will allow for phosphorylation of a lesser number of histones might also result in smaller foci and a better separation of adjacent independent damage events. Nonetheless, the method presented here is ultimately limited by resolution of optical microscopy images. The inability to detect distances smaller than the size of spot image is reflected in the auto-correlation functions which reach negative values at small distances (mutual exclusion of foci). Consequently, at small distances direct correction of cross-correlation function for self-association of signals is not possible and extrapolation must be used. It may be envisaged that an increase of microscopy resolution, possible with super-resolution techniques, like PALM or STED, would result in a better approximation of an image comprising point-like signals. Finally, improvements of imaging and labeling protocols might be combined with a distance metric, which is optimized for a particular shape and size of the analyzed signals (foci).

In conclusion, the image analysis approach which we describe above constitutes the next step in refining the ability to investigate and quatitate relationships between various sub-cellular phenomena represented by small foci in multicolor 3D confocal images. The information provided in our companion report (1) and in this article demonstrate complementarity between laser scanning cytometry (or flow cytometry) and high resultion 3D confocal imaging, and the potential strength of combining these approaches. The advantages and benefits of combining various cytometry methods, including flow cytometry, image stream, laser scanning cytometry, wide field and confocal microscopy has also been described in two recent reports (12,13).