Magnified Effects of Changes in NIH Research Funding Levels

Abstract

What happens within the university-based research enterprise when a federal funding agency abruptly changes research grant funding levels, up or down? We use simple difference equation models to show that an apparently modest increase or decrease in funding levels can have dramatic effects on researchers, graduate students, postdocs, and the overall research enterprise. The amplified effect is due to grants lasting for an extended period, thereby requiring the majority of funds available in one year to pay for grants awarded in previous years. We demonstrate the effect in various ways, using National Institutes of Health data for two situations: the historical doubling of research funding from 1998 to 2003 and the possible effects of “sequestration” in January 2013. We posit human responses to such sharp movements in funding levels and offer suggestions for amelioration.

1. Introduction

The research enterprise comprises universities, research laboratories, and similar organizations that seek to foster economic growth and well-being for the country by advancing scientific knowledge. In the field of biomedicine, the research enterprise’s performance is critical in discovering new treatment methods and drugs that enhance health and reduce the burden of illness and disabilities in the country. Through recruiting highly knowledgeable individuals in the field of biomedicine, and using well-equipped facilities and laboratories, the enterprise can offer valuable services to other organizations including the pharmaceutical industry. Because of that crucial role, the well-being of the research enterprise has always been a priority with policy makers and the general public.

As most research centers operate on external funds, including taxpayer dollars, we intuitively expect government funding policies to have substantial impacts on the performance of the enterprise. Looking back at the historical trend of funding research institutions, many instances of abrupt changes in funding policies are observable. For example, over the five-year period 1998–2003, the budget of the National Institutes of Health (NIH) doubled from $13.6 billion (1998) to $27.1 billion (2003) (Pear 1998, Smith 2006). Another important example is the current discussion among policy makers about “sequestration,” which would abruptly decrease NIH, National Science Foundation (NSF), and Centers for Disease Control (CDC) funding by about 7.8% starting in January of 2013. From an organizational point of view, the question is what happens within the research enterprise when a federal funding agency abruptly changes research grant funding levels, up or down.

The literature on the performance of research funding institutions such as the NIH is mostly focused on the resource allocation problem across diseases (e.g., Bisias et al. 2012) or the effects of funding on developing a new research workforce and on grant success rates (Teitelbaum 2008, Gomez et al. 2012). Despite the importance of these questions, what remains unanswered is the basic “temporal physics” of grant-making abilities as overall funding levels move up and down. Interestingly, most studies including Bisias et al. (2012) ignore this temporal physics. In this paper, we demonstrate how ups and downs in funding levels can have dramatic and amplified effects on new funding available for grant applicants.

We first develop a simple model of government funding when grants are provided for a four-year period, and then we offer a generalized theory of amplified effects of change in funding (§2). Then we apply the model to the case of NIH during the doubling period in 1998–2003 (§3). We then take a normative approach and analyze alternative policies that could have resulted in better outcomes (§4). Finally, we discuss the results and their implications to the sequestration period, and we highlight other implications of the study (§5).

2. Modeling

We utilize a bottom-up structural modeling approach to develop a theory of the effects of changes in overall funding on yearly new grant awards. Although different modeling approaches could be taken, we deliberately try to make the model as simple as possible in order to develop first-order intuition and insights.

2.1. The Awarding of Four-Year Research Grants

Consider a federal agency that supports fundamental biomedical research. It awards highly competitive research grants each year, with each grant flat-funded for four continuous years; i.e., 25% of the total grant amount is obligated and available to spend during each of the four years of the grant. The agency’s funds for each year are drawn from the congressionally approved budget for the agency for the given fiscal year. For simplicity, let us drop the term “fiscal year” and just use “year” as in a calendar year. Suppose that $10 billion are available for research grants in a given year—say, year Y. Those funds must first be used to provide continuing support for grants awarded in the three previous years, years Y – 1, Y – 2, and Y – 3. Then, after those flat-funded earlier obligations are fulfilled, any funds left over from the $10 billion are available for new grants in year Y. As an example, if the agency’s total yearly funding had been traditionally flat at $10 billion, each year, three quarters of the money is spent fulfilling obligations from the past three years, and one quarter ($2.5 billion) would be available to fund new grants in year Y. Such a situation represents “steady-state” operation. But annual funding changes up or down can dramatically alter steady state. This is a very simplistic first-order depiction of how the NIH works for its major research funding programs—four-year R01 grants. We use this base model to explore the consequences of changes in total year-to-year NIH funding.

We can express some basic quantities mathematically. Suppose we define

$$B(Y)=\text{Budget for research in year }Y,Y=1990,1991,1992,\dots ,$$

,

$$F(Y)=\text{Funding available in year }Y\text{ for new research grants}.$$

The annual research budgets B (Y) are given as input data, where we have started the process at some distant year in the past, 1990 in this case. Now let us consider some year Y = y later than 1993, to avoid start-up modeling effects. In year y, the total research budget is B (y). The amount available for funding of new research grants in year y, F (y), is equal to B (y) minus the sum of obligations stemming from the previous three years’ commitments. In equation form, we have

$$F(y)=B(y)-[F(y-1)+F(y-2)+F(y-3)]\ge 0.$$ (1)

We include the inequality on the right in Equation (1) to require that year y funding is at least sufficient to cover the previous three years’ obligations. Anything left over is then available for new funding in year y. Notice that in steady state, when funding levels and new commitments are constants, i.e., B (y) = C and F (y) = F₀, Equation (1) becomes

$$\begin{array}{c}{F}_0=C-3F_0,\text{or equivalently},\\ F_0=C/4.\end{array}$$ (2)

Equation (2) simply confirms our intuition that in steady state, the funds available for new grants each year are equal to one quarter of the total research funds for that year. Three quarters are used to fund previously awarded grants.

To gain some additional insight into Equation (1), suppose that years are traditionally flat-funded at $10 billion but that year 2000 has a one-time increase to $12.5 billion, a 25% increase in total yearly funding. After that, funding drops back to $10 billion/year. What happens then? Let us work through the equations:

$$\begin{array}{l}\text{F}(2000)=\text{B}(2000)-[\text{F}(1999)+\text{F}(1998)+\text{F}(1997)]=12.5-[2.5+2.5+2.5]=5.0,\hfill \\ \text{F}(2001)=\text{B}(2001)-[\text{F}(2000)+\text{F}(1999)+\text{F}(1998)]=10-[5+2.5+2.5]=0.0,\hfill \\ \text{F}(2002)=\text{B}(2002)-[\text{F}(2001)+\text{F}(2000)+\text{F }(1999)]=10-[0+5+2.5]=2.5,\hfill \\ \text{F}(2003)=\text{B}(2003)-[\text{F}(2002)+\text{F}(2001)+\text{F}(2000)]=10-[2.5+0+5]=2.5,\hfill \\ \text{F}(2004)=\text{B}(2004)-[\text{F}(2003)+\text{F}(2002)+\text{F }(2001)]=10-[2.5+2.5+0]=5.0,\hfill \\ \text{F}(2005)=\text{B}(2005)-[\text{F}(2004)+\text{F}(2003)+\text{F}(2002)]=10-[5+2.5+2.5]=0.0,\hfill \end{array}$$

and so on.

We see that a step increase in total grant funding of 25% in one year has two interesting effects on new grant funding. First, it results in a doubling of new grant funding in that year (2000) and a zeroing out of new funding the following year (2001). Second, the funding of new grants returns to normal levels for the next two years (2002 and 2003), but the entire sequence repeats four years after the one-time 25% increase: in 2004, the system devotes $5 billion to new grants followed in year 2005 with zero new grant funding. In theory, this four-year oscillatory cycle continues ad infinitum. Of course, we are dealing with a simplistic first-order model, and real life is more complicated. But the point remains: An apparently modest one-time step increase in total funding can have dramatic effects on current-year new funding and on new funding in all subsequent years.

The reverse is also true. An apparently modest decrease in total funding can have dramatic effects in new funding for the current year and in subsequent years. For instance, if the 25% increase in new funding for 2000 had instead been a 25% decrease to $7.5 billion, there would be no new funding available in 2000. And the consequences of this occurrence would propagate though the system in subsequent years.

All of the complications that we have seen embodied in Equation (1) stem from the fact that all research grants are given for four years, with equal funding for each of the four years. The weight of the previous three years of funding commitments looms large in new funding available for the year. This new funding is the mathematical “remainder,” after past obligations are paid for. Any changes in total funding for the current year affect this remainder only, not the three years’ prior commitments. Thus there is a huge “round-off magnification effect” in the current year resulting from any change in total research funding, up or down. We theorize the effect as follows.

The Rule of Four

Starting from steady state, an X percent change in this year’s funding results in a 4X% change in new funding for this year.¹

If we are not starting from steady state, the Rule of Four does not apply, but the funding obligations from the previous three years will usually dramatically affect the research funding available for the current year.

2.2. The Awarding of Different Period Research Grants

The Rule of Four, of course, generalizes. For instance, the CDC often awards five-year research grants. For that portion of the national research enterprise that depends on five-year grants, there is the Rule of Five: Starting from steady state, an X percent change in this year’s funding results in a 5X% change in new funding for this year.² In general, there is a “Rule of N,” associated with N-year grants, and as the CDC example illustrates, the amplified impact on current-year new funding becomes even more severe as the parameter N increases in value.

We can extend the argument to the general case with mixed grant durations. Suppose that grants are awarded for any integer number of years i, i = 1, 2, …, M. Suppose that in any year, assuming steady-state operation, there is a total research budget, B. Also, we assume that the yearly flow of dollars awarded to new grants is A, in dollars per year, A < B. We assume that grants can have different durations. We do this by assuming that a fraction p_i of the total new-award amount A is directed to awards of i years’ duration, where we assume ${\displaystyle {\sum }_{i=1}^N{p}_i=1}$. Then in steady state, in any given year, we have obligations OB from previous grants totaling

$$OB=A{\displaystyle \sum _{i=1}^N}(i-1)p_i.$$ (3)

We can see this by picking any given value of i, say, i = 4. For i = 4, in each of the previous (4 − 1) = 3 years, there has been a funding commitment of Ap₄ dollars to grants of four years’ duration. These obligations carry over into the current year. Thus, current-year obligations for previous four-year grants is A (3p₄). This logic applies to each of the terms in Equation (3).

Now for the current year, we observe that the apportioning of research funds B must go first toward commitments from previous years and then toward new awards,

$$B=A{\displaystyle \sum _{i=1}^N}(i-1)p_i+A=A({\displaystyle \sum _{i=1}^N}(i-1)p_i+1)=A{\displaystyle \sum _{i=1}^N}i{p}_i=A\tau ,$$ (4)

where

$$\tau \equiv \text{mean duration of a new research grant}.$$

In other words, τ is the weighted average of grant durations. To solve for A, the dollar flow amount that can be awarded to new grants in any given year, again assuming steady state, we obtain

$$A=B/\tau .$$ (5)

A simple check verifies the Rule of Four (when p₄ = 1.0) and the Rule of Five (when p₅ = 1.0). But the derivation generalizes our results to include mixtures of grant durations. For instance, The Rule of Four is seen to apply to any situation in which the average grant length is four years; there is no need for all of them to be four years. Also, there is no need for the average grant duration to be an integer quantity.

We see that the parameter τ, the mean duration of a new grant, is the single most important factor influencing possibly unstable fluctuations in current year funding once the system is deliberately moved out of steady state. We could say that that the ultimate generalization is

The Rule of τ. Starting from steady state, an X percent change in this year’s funding results in a τ X% change in new funding for this year.³

3. The Case Study

3.1. Application to the Case of NIH

We now apply our simple difference equation model to a key historical case of the NIH. We consider the period 1998–2003, a five-year time frame during which the NIH gradually doubled its annual funding of research grants. To make the numbers simple to remember, say that the 1998 funding level was $10 billion⁴ and the 2003 level was doubled to $20 billion. We assume that all grants are flat-funded for four years.⁵

Table 1 contains a simple spreadsheet showing such a doubling of funding over five years, the doubling occurring with three alternative increment scenarios:

1. Constant, linear increments (a constant 20% of base added to total budget per year).

2. Fixed percentage increments (a constant 14.9% increase in total budget per year).

3. Manually adjusted increments (the authors’ manually adjusted increases with an attempt to minimize disruption).

Table 1.

Spreadsheet Analysis of Three Alternative Methods of Doubling of Funding

	Year
Scenario	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007
1 Constant linear increments
Input:
B	10	12	14	16	18	20	20	20	20	20
Outputs:
C	7.5	7.5	9.5	11.5	13.5	13.5	15.5	15.5	15.5	13.5
F	2.5	4.5	4.5	4.5	4.5	6.5	4.5	4.5	4.5	6.5
%ΔF	0	80	0	0	0	44	−31	0	0	44
2 Fixed percentage increments
Input:
B	10	11.5	13.2	15.2	17.4	20	20	20	20	20
Outputs:
C	7.5	7.5	8.99	10.7	12.7	13.4	15.8	15.5	15.2	13.4
F	2.5	4.0	4.2	4.5	4.7	6.6	4.2	4.5	4.7	6.6
%ΔF	0	59	6	6	7	38	−36	6	7	38
3 Manually adjusted increments
Input:
B	10	11	12.6	15	18	20	20	20	20	20
Outputs:
C	7.5	7.5	8.5	10.1	12.5	14.5	15.9	15.1	14.5	14.5
F	2.5	3.5	4.1	4.9	5.5	5.5	4.1	4.9	5.5	5.5
%ΔF	0	40	17	20	12	0	−25	20	12	0

Notes. In each scenario, total budget (B) in each time period of t enters as input, and commitments (C), new funding (F), and change in new funding (%ΔF) are outputs. The bold numbers depict the input differences across the scenarios. The underlined numbers represent year-over-year percent increases and decreases, respectively, in new funding for two years, 1999 and 2004.

The years range from 1998 to 2007. As shown in Table 1, for each scenario we have a row for total budget (B). These numbers represent the successive values of B (y) in Equation (1). In all scenarios, total budget (B) starts with a base annual funding of $10 billion and ends at $20 billion. The three scenarios differ only in the way the transitions are made from $10 to $20 billion over the five-year period. These figures can, of course, be adjusted to the true historical NIH funding amounts. In these scenarios, funding begins increasing in 1999 and reaches its new steady state in 2003. Actual NIH funding increases over this period resembled a hybrid combination of scenarios 1 and 2.

In each scenario, the spreadsheet uses B as input and calculates three outputs. The first output is labeled commitments (C). This represents the total funding during that year that is already obligated as a result of funding commitments made during the previous three years. This quantity is represented by the term C (y) in Equation (1) and is equal to the sum of the past three years’ new funding (F (y − 1) + F (y − 2) + F (y − 3)).

The second output is the available new funding (F), i.e., the “remainder” after the previous three years of funding obligations are satisfied (F (y) = B (y) − C (y)). Recall that when a new year starts, the funding available for new grants in that year is the total available for that year, minus the funding devoted to old grants from each of the past three years.

Finally, a key performance output is labeled change in new funding (ΔF), defined as the fractional yearover-year increase or decrease in the funding of new grants. We saw in our examples in §1 that modest changes in total funding could increase or decrease current-year new funding by 100%.

Although the details of the three scenarios in the accompanying spreadsheets may be interesting, we draw your attention to two quantities: the underlined values of %ΔF in 1999 (just after the total budget increases start) and in 2004 (just after total budget reaches $20 billion). Under scenario 1’s constant increments, the increase in new funding in 1999 is a whopping 80%. Under scenario 2’s fixed percentage increments, the increase in new funding in 1999 is 59%. Only in the manually adjusted scenario 3 is the increase a more modest 40%, still quite large. Now examine through 2004, the first year of flat funding under the new constant support level of $20 billion per year. The decreases in new funding for 2004 stand at 31%, 36%, and 25%, respectively, for the three successive scenarios.

Imagine the response of the biomedical research communities to these research funding-level percentage changes, first up and then down. One can reasonably imagine that a 59%-to-80% increase in new funding in 1999 caused a very positive set of reactions in the university-based research communities. University department heads could be seen going to deans and provosts, asking for more faculty slots, higher caps on admissions, more space, and perhaps even new buildings. To represent these first reactions, we use the term early euphoria. We define euphoria as the biggest percent increase in year-over-year funding over the five-year doubling period (most likely to happen in 1999).

Now consider the year 2004, the first year of flat funding at the higher total funding level. Under scenarios 1 and 2—the scenarios that most closely resemble NIH’s actual history—new funding for 2004 was 31%–36% lower than that of 2003. Imagine the response of the biomedical university-based research community: they have probably overcommitted to support for doctoral research assistants, new faculty slots, research space, and related investments. They might have imagined that “the sky had fallen.” We label these types of reactions as severe hangovers. We define a hangover as the largest percent decrease in year-over-year funding over the five-year doubling period plus the four years following (most likely to happen in 2004, the first year of flat funding at the new doubled level).

Under scenario 1, with a linear 20% add-on each year, euphoria is 80% followed by a hangover of 31%. Under scenario 2, with a 14.9% research funding increase each year, euphoria is 59% followed by a more severe hangover of 36%. The authors’ manual creation of scenario 3 reduced euphoria to 40% but kept it high for four years, followed by a 25% hangover.

Early euphoria most likely also generated many additional grant proposal submissions by established, respected researchers. In 1999, there were no immediately available additional new researchers who would be competitive in the grant submission process. Thus it is likely that the established researchers garnered the lion’s share of the newly available funds, above the usual annual amount. Those funds would “belong” to that established researcher for four years, with reasonable likelihood of continuation after that time. This process of granting more awards to established researchers likely continued throughout the five-year growth phase, leaving little new funds available for the now larger army of newly minted Ph.D.’s by the early 2000s. Such a lack of funds for new Ph.D.’s would lead to larger pools of postdocs as well as increased age at first grant award for those for tunate enough to become new assistant professors. We explore some of these issues in the next section.

This analysis is not meant to argue against research funding increases; within given fixed grant award structures, it is meant only to demonstrate the underlying physics of the system. Here, “physics” means both the hard mathematical consequences and the softer emotional human responses. We will later discuss how a formal optimization of budget increments and/or grant durations can help to reduce early euphoria and severe hangover.

3.2. Details of the NIH Doubling of Research Funding

We now discuss in some detail what actually happened with NIH funding during 1998–2003. Please keep in mind that the opening two sections of the paper dealt with a simplistic linear difference equation model to depict the first-order physics of the system. The real system is more complex.⁶

In 1997, the U.S. Senate voted unanimously in support of doubling the NIH’s budget in five years to foster research discoveries in the field and research workforce development (Pear 1998). As result, NIH appropriations were increased from $13.6 billion in 1998 to $27.1 billion in 2003 (Smith 2006). The budget doubling flooded academia in a relatively short period of time, having a significant effect on expansion of biomedical research. Approximately half of the money was spent on research grants. Whereas in 1998 NIH funding for research project grants was $7.7 billion, in the next five years it increased to $8.6, $10, $11.3, $12.6, and $13.8 billion, showing annual increases of 13%, 15%, 15%, 12%, and 10%, respectively. The funding supported new grants and fulfilled grant commitments from past years, as the usual duration of an NIH grant is four years. Additional details are provided in Gomez (2012) and Gomez et al. (2012).

The increase in funding influenced many institutions that wanted to expand their research capacities and activities. Several even started spending their own money—as an investment—to build more research laboratories (Brainard 2004) and admitted more graduate students in anticipation of winning NIH grants to support them (Monastersky 2007). The rise in funding also increased the expectations of university researchers and tenure track professors to bring funding to their schools. However, the five-step smooth increase in total research funding was not reflected in the same way in new grant funding, which instead showed periodic unexpected oscillations. As Figure 1 shows, in 1999, new grant funding increased by 31%, creating an exciting early euphoria and sending a signal to researchers on the availability of competing grants. In the next few years, new research funding increased continuously, but at a declining pace: a 16% increase in 2000, a 4% increase in 2001, and a 5% increase in 2002. In 2003 (exactly four years after the first huge increase in new research funding), new grant funding again increased by 10%, sending a mixed signal about the possibilities of winning a grant proposal. But in the next two years, the change in new research funding dropped to 2% and −5%, causing hangover. Interestingly, for several years after the implementation of the doubling policy, new research funding still showed an oscillatory behavior with a four-year time period.

Figure 1.

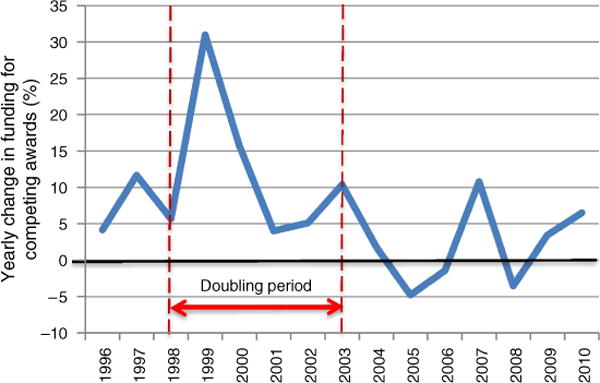
Yearly Percent Change in New NIH Research Funding as Affected by the Doubling Policy

These significant fluctuations resulted in a wide array of consequences in the field. First, the number of competing grants was affected. As shown in Figure 2(a), the number of competing R01 grants increased in the doubling period (+15%), which then was followed by a marked drop at the end of the doubling period (−20% in three years). The effect on the number of grants could have been much worse if NIH had not reacted by changing the size of grants. As depicted in Figure 2(b), during the early euphoria period, grant size was increased, although it was decreased after a few years.

Figure 2.

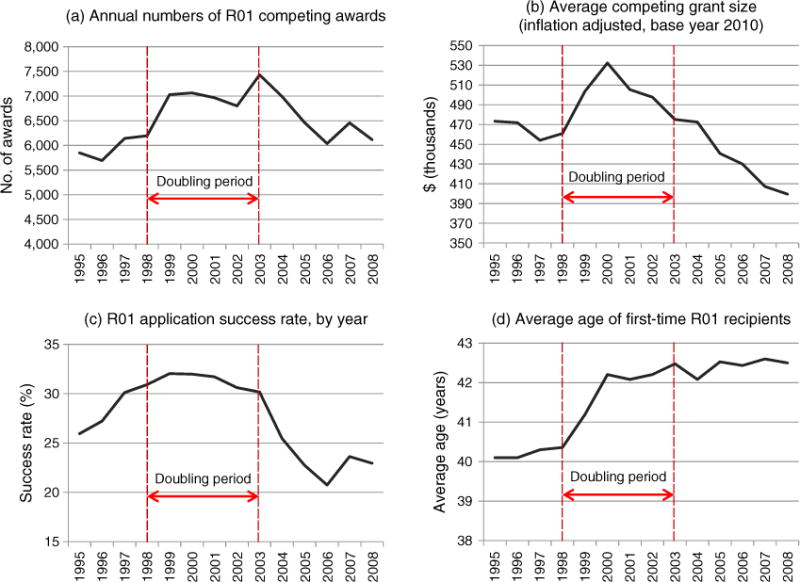
Effects of Change in NIH Research Funding

The rise and fall in competing grants were reflected in the grant application success rate (see Figure 2(c)). After an early euphoria sends a positive signal encouraging researchers to submit grant applications, the latter hangover negatively affects the success rate of already increased grant applications. The combination of more applications and less money worsens the magnitude of the effect at the end of the doubling period.

Finally, effects were also reflected in the average age of first-time R01 recipients. More and larger grants encouraged more established researchers to submit grant proposals, and in the competitive environment, established scholars benefited from their experience and won more grants, leaving fewer opportunities for young scholars. The result was a two-year jump in the average age of first-time R01 recipients (see Figure 2(d)). Interestingly, after the doubling period, the effect remained in the system.

Other effects of the doubling included increasing numbers of graduate students, researchers, and postdocs who later become grant applicants, further lowering the grant application success rate. In 2007, Science magazine concluded that conditions worsened after the NIH’s budget doubled, as the infusion of money was far too rapid and not tied to structural reforms in the field (Benderly 2007).

The Rule of Four is shown statistically in Figure 3, depicting the percentage of NIH grant funding that is committed to prior years’ awards. In steady state, the Rule of Four would show this chart at a constant 75% level. Yet we see that in the early years of the five-year doubling period, the percentage of R01 funding obligated to previous awards drops significantly below 75%. Then, as hangover sets in after 2003, the percent obligated to earlier awards rises above 75%.

Figure 3.

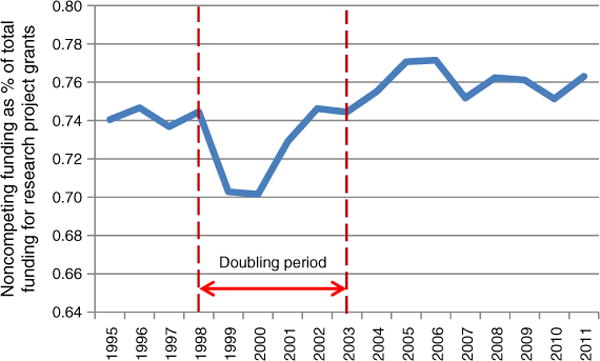
Percentage of Funding for Research Project Grants Obligated to Awards from Prior Years

4. Alternative Policies: Changing Funding Step Sizes and Grant Durations

Given that the federal government plans to double NIH funding in five years, the question is this: “Are there any corrective steps that can be taken to reduce early euphoria and severe hangover?” The answer is, yes. There are two types of policy decisions that can reduce but not eliminate these detrimental outcomes: (1) “optimizing” the step increments of funding in each of the five years and (2) allowing the durations of some of the grants to be different from the usual fixed four-year period. In this section, through an optimization exercise, we offer policy insights to help reduce the effects of early euphoria and severe hangover in the system. The idea is to seek smooth rather than abrupt transitions in new grant funding.

In any optimization, we need to agree on an objective to optimize—that is, a function to maximize or minimize. Here, we wish to reduce (minimize) both euphoria and hangover. So we create reasonable equations for each and then sum the two, giving a weight to each. We define the cost function as a weighted sum of the largest rise (euphoria) and largest fall (hangover) in a 10-year time period, from 1999 until 2008:

$$y=w\left[\text{euphoria}\right]+(1-w)\left|\text{hangover}\right|,0\le w\le 1,$$ (6)

where w is the relative cost weight of euphoria to hangover. We will value equally euphoria and hangover and set w = 0.5. The optimization goal is to minimize y. As a comparison baseline, y in the base case with linear budget increments is equal to 0.55. Our goal is to find “optimum” solutions that are meaningfully (level of precision is 0.01) better than the base case.⁷

Equations (7a) and (7b) define euphoria and hangover:

$$\text{euphoria}=\text{Max}\left\{0,\frac{F_{1999}-F_{1998}}{F_{1998}},\dots ,\frac{F_i-F_{i-1}}{F_{i-1}},\dots ,\frac{F_{2008}-F_{2007}}{F_{2007}}\right\},$$ (7a)

$$\text{hangover}=\text{Min}\left\{0,\frac{F_{1999}-F_{1998}}{F_{1998}},\dots ,\frac{F_i-F_{i-1}}{F_{i-1}},\dots ,\frac{F_{2008}-F_{2007}}{F_{2007}}\right\}.$$ (7b)

There are different decision variables that the government and NIH can partially control. As discussed above, we focus on two sets of decision variables: the NIH annual budget increments and grant award periods.

4.1. Optimal Budget Increments

Assuming that the NIH budget in 1998 is equal to $10 billion and in 2003 is equal to $20 billion, we can find the optimal total budgets for each year from 1999 until 2002: (B₁₉₉₉, B₂₀₀₀, B₂₀₀₁, B₂₀₀₂). Here, “optimal” means minimizing the weighted sum of euphoria and hangover, as depicted in Equations (6) and (7). We use Microsoft Excel 2010 (Solver Add-in) to perform the optimization. Table 2 summarizes the optimal values and shows the outcome results in comparison to the base run with linear growth (fixed increments) in the NIH budget.

Table 2.

Comparison of the Base Run (Fixed Increments) with the Optimized Increments Run

	Activity variable: Annual budget						Outcome variables
	B1998	B1999	B2000	B2001	B2002	B2003	y	Euphoria (%)	Hangover (%)
Base run (linear)	10	12	14	16	18	20	0.55	80	−31
Optimized increments	10	11.03	13.53	16.03	18.54	20	0.21	42	0

Note. The bold values are estimated through optimization.

The optimization suggests an S-shape growth in budget with a small increase in the first year (1999) and larger increments in subsequent years until a final smaller increment in 2003. This S-shaped pattern is similar to the one that the authors discovered by hand, as shown as scenario 3 in Table 1. Compared with the base run with linear growth, early euphoria decreases to +42% (in the base run, +80%) and hangover disappears (in base run, −31%). Figure 4 depicts the trend of new grant funding in comparison to the base run.

Figure 4.

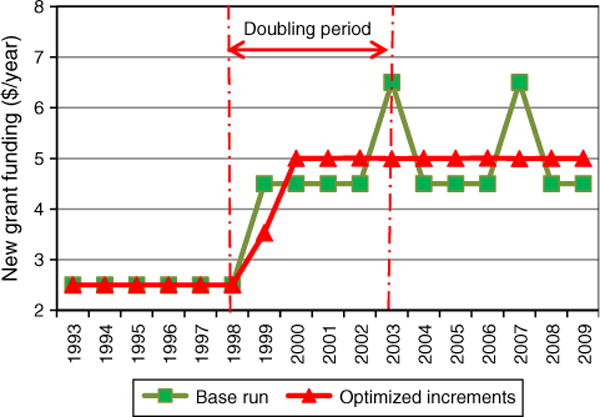
Trend of New Grant Funding Under the Base Run and the Optimized Increments Run

4.2. Optimal Award Periods

Currently, most NIH R01 grants last for four years. But varying the lengths of grants during times of transition can reduce euphoria and hangover. We can find the “optimal mixture” of funding durations that minimizes our cost function. To keep it simple, we limit the optimization to three types of grants: three-year, four-year, and five-year grants. In each year (from year X until 2004), we look for the percentage of the new grant funding that should be awarded as three-year, four-year, and five-year grants. Here, the “base run” is one where all awarded grants are four years in duration and the funding increments during 1998–2003 are kept constant at $2 billion/year.

Let us define F as a 3 × n matrix with arrays of 0% ≤ f_{i, j} ≤ 100%, with f_{i, j} representing the percentage of j-year funding that will be given in the form of i-year duration grants for i = 3 years, 4 years, and 5 years. The grant-awarding years j that we consider range from j = X to j = 2004. The matrix can be presented as follows:

$$\left|\begin{array}{lllll}{f}_{3y,X}\hfill & f_{3y,2001}\hfill & f_{3y,2002}\hfill & f_{3y,2003}\hfill & f_{3y,2004}\hfill \\ f_{4y,X}\hfill & f_{4y,2001}\hfill & f_{4y,2002}\hfill & f_{4y,2003}\hfill & f_{4y,2004}\hfill \\ f_{5y,X}\hfill & f_{5y,2001}\hfill & f_{5y,2002}\hfill & f_{5y,2003}\hfill & f_{5y,2004}\hfill \end{array}\right|$$

where for any j,

$$f_{3y,j}+f_{4y,j}+f_{5y,j}=100\%$$ (8)

X is the year from which the NIH starts changing the mix of grant periods to improved, or what we call optimal values. For example, if we set X = 2003, the optimization will represent a late reaction by the NIH in the years 2003 and 2004 only, to decrease the impending hangover. For earlier years, say, X = 1999, the optimization will represent a proactive approach, where the NIH wants to take the best action at the same time that they observe early euphoria. Starting even earlier, say, X = 1995, represents a much more proactive policy that initiates change several years before implementing the doubling policy.

We conducted several optimizations for different values of starting year X from 1995 to 2000. Figure 5 compares the cost function values. Recall that the cost is the sum of euphoria and hangover divided by 2. The figure shows that all optimizations improve the result when compared to the base run. As we take a more proactive approach (smaller Xs), the results get better. We think X = 1999 represents a more realistic situation, reacting immediately after the approved rise in research funding. As shown, the marginal effect of smaller Xs (X = 1998X = 1997, and 1996) is very small. However, for X = 1995, which represents very “prescient” policy making, we see a huge impact from optimization. The reason is connected to the Rule of Four. When funding is awarded for four years, mitigating the early euphoria is not possible without changing grant periods at least four years prior to doubling. The limitation with the prescient optimum is that decision makers are not likely to foresee the situation four years into the future, before the first increment in the budget. Thus the prescient policy is interesting but most likely infeasible.

Figure 5.

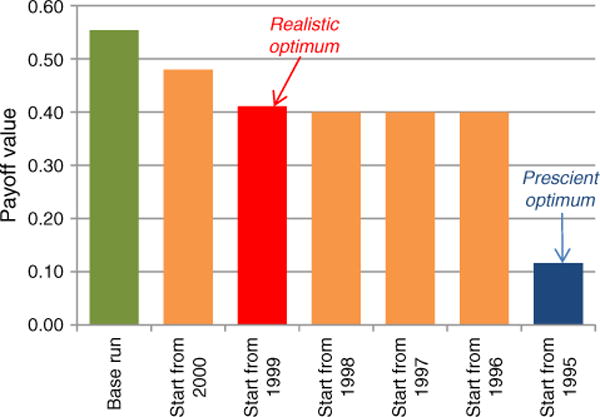
Minimized Costs for Different Starting-Year Scenarios, Optimally Mixing Grant Durations

Figure 6 shows the trend of new grant funding for two of the optimizations (X = 1999, the realistic scenario, and X = 1995, the prescient scenario) in comparison to the base run. Optimized runs make the transitions smoother as new research funding approaches its final equilibrium. The prescient optimization run is the only run that avoids early euphoria.

Figure 6.

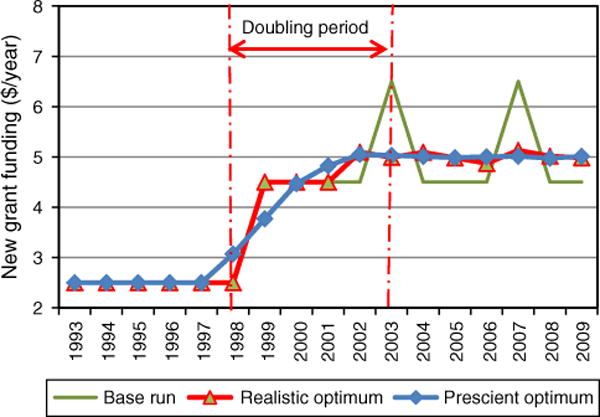
Year-to-Year New Grant Funding Under Three Scenarios

The detailed results of the optimizations are presented in Table 3 and are compared with the base run, where grant duration was fixed at four years and funding increments were kept constant at $2 billion/year. In the realistic optimum scenario, grant durations are changed after 1999. As the table shows, in 1999, 13% of funding is awarded in the form of three-year grants. Immediately after 1999, the balance is shifted toward five-year grants. After 2000, funding is predominantly allocated to four-year grants.

Table 3.

Comparison of the Base Run (100% Four-Year Grants) with the Optimized Grant Durations Under Two Scenarios of Realistic and Prescient Optimal Solutions

	Year										Outcome variables
Cases	1995	1996	1997	1998	1999	2000	2001	2002	2003	2004	y	Euphoria (%)	Hangover (%)
1 Base run											0.55	80	−31
3-year (%)	0	0	0	0	0	0	0	0	0	0
4-year (%)	100	100	100	100	100	100	100	100	100	100
5-year (%)	0	0	0	0	0	0	0	0	0	0
2 Realistic optimum											0.41	80	−2
3-year (%)	0	0	0	0	13	0	2	4	0	3
4-year (%)	100	100	100	100	66	91	97	95	99	97
5-year (%)	0	0	0	0	20	9	1	1	1	0
3 Prescient optimum											0.12	23	−1
3-year (%)	23	0	0	9	10	1	0	2	1	0
4-year (%)	71	92	94	82	72	97	99	98	99	99
5-year (%)	6	8	6	9	18	2	1	0	0	1

Note. The bold values are estimated through optimization.

We now consider the prescient scenario, where a similar pattern of decisions emerges. In 1995, 23% of funding is awarded in the form of three-year grants. In the following year, the balance is shifted to longerduration grants, where 8% of funding goes to five-year awards. The reason for giving three-year funding instead of four-year funding is to decrease ongoing grant commitments three years later. If more three-year grants are awarded now, they will end two years from now, and there will be less prior commitment the year after (three years from now) and thus more funding for new grants. Therefore, more three-year grants awarded in 1995 and 1999 result in more new research funding in 1998 and 2002, exactly one year before the years in which euphoria and hangover, respectively, are most likely to occur.

4.3. Increments and Award Period Optimization

We now optimize for both budget increments and mix of grant periods from 1999 (the realistic case). The optimization is conducted iteratively. First, we optimize the increments, and then with the optimum increments held fixed, we optimize award periods. We then fix the award periods and reoptimize the increments, etc. We continue this iterative process until no significant change is observed in the results, which are shown in Table 4. Overall, the results are improved. As shown in the table, the optimized solution totally removes hangover and decreases euphoria to 36%.

Table 4.

Results from the Optimization of Both Increments and Award Durations

	Year						Outcome variables
	1999	2000	2001	2002	2003	2004	y	Euphoria (%)	Hangover (%)
Optimization							0.18	36	0
Budget	10.9	13.01	15.12	17.31	20	20
3-year (%)	11	1	2	4	3	2
4-year (%)	68	91	97	95	96	98
5-year (%)	21	8	1	1	1	0

5. Discussion

We have constructed our presentation around a simple mathematical model of government research funding. Our analysis shows that an apparently modest net increase or decrease in annual government research spending can have significant magnifying effects on new grant funding, and these effects can reverberate for a long time. We framed this effect as the Rule of Four, generalized it to the Rule of τ, and discussed possible early euphoria and severe hangover as results of change in funding.

The structural reason for the amplified fluctuations in new grant funding is linked to the relation between grant commitments and new grant funding, as depicted in Figure 7. Research grants are planned for a period of time (at the NIH, usually four years). Every year, the government must fulfill commitments made in past years. The remaining research funding is allocated as “new research funding” to provide opportunities for grant applicants. And the story continues through the years: new grants, in turn, lead to future commitments, affecting funding availability for new grants in the upcoming three years. The system has memory, a type of momentum or inertia, that yields a system having rather unstable year-to-year new funding prospects.

Figure 7.

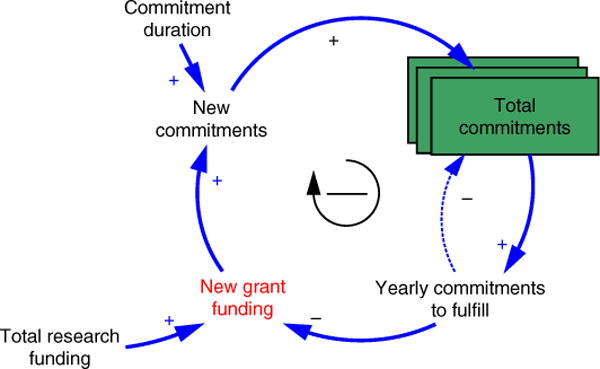
Structural Relation Between New Grant Funding and Commitments

The theory has several policy implications. We discuss these in turn below.

5.1. Applicability to Sequestration

Whereas the case history discussed in this paper has focused on the NIH during a research doubling growth phase (1998–2003), the issues and concerns are equally relevant today. An immediate example is “sequestration,” a term being applied to across-the-board research funding cuts, starting in January of 2013;⁸ these cuts will apply to the NIH, NSF, CDC, and other federal agencies supporting research. The across-the-board cut is estimated to be 7.8%, representing about $2.4 billion for the NIH.⁹ As our analysis has shown, this entire reduction for the NIH would come from new grants, not previously funded and continuously supported grants. Suppose we consider of presequestration budget of a $100. Assuming that four-year grants are being awarded, in steady state, $75 is reserved for the continuous support of previously funded grants; that only leaves $25 for new grants. A 7.8% budget reduction implies that only $92.20 is available for all research, new and previously funded. And the amount available for new research, under sequestration, is $92.20 – $75.00 = $17.20, representing a 31.2% reduction in new research. Based on the Rule of Four, this is four times the 7.8% overall reduction. Again, we magnify by a factor of four because all of the reduction must be absorbed by new grants, as the funds for previously funded grants are already obligated. The estimated 31.2% reduction in new NIH research for 2013 approximates the severe hangover we found for the year 2004. Invoking the Rule of Four, one could argue that a true discretionary reduction of NIH research outlays for 2013 would correspond to a net reduction of 7.8/4 = 1.925%. Such a reduction would require a 7.8% reduction in new research commitments.

We have not attempted to apply any of our model-based optimization tools to sequestration. If sequestration becomes a reality, it seems that the only ameliorative policy change for the NIH would be to create a mixture of grant durations.¹⁰

The issues raised here also apply to the other federal research granting agencies, including the NSF and as we mentioned previously, the CDC, with its five-year grants. But with more varied grant durations, the agencies require a separate detailed analysis, where undoubtedly, the Rule of τ would play a significant role.

5.2. Applicability to Other Cases

Our intuition is that the “euphorias” and “hangovers” occur more frequently than one might think. Recent U.S. “stimulus money,” made possible by the American Recovery and Reinvestment Act of 2009,¹¹ directed billons of dollars to medical schools and biomedical university research labs. The NIH received approximately $9 billion in stimulus funds during fiscal years 2009 and 2010. In full, 2,059 new competing grants were awarded, totaling $2.71 billion—over two-thirds of that in fiscal year 2009.¹² Another 4,497 awards totaling $1.73 billion were given to existing competing proposals that had not been funded under previous constraints; over 80% of these funds were from fiscal year 2009. Assuming flat funding for four years, the majority of these funds are now spent, end-of-grant planning is underway, and resource commitments made two or three years ago are being painfully revisited. It is our belief that even without sequestration, severe hangover is being experienced in many research universities and medical schools today.

Furthermore, it is commonly argued that the NIH should change it resource allocation from one center to another. For example, some studies that argue that NIH funding is not sufficiently based on disease burden or the potential effects on years of life lost (Rangel et al. 2002, Johnston and Hauser 2006, Bisias et al. 2012). An implication of our study to the resource allocation arguments is that the process of change might be more complex than what is usually assumed. If the NIH decides to reallocate its resources (e.g., to reallocate center A’s funding to center B), we will likely see early euphoria, severe hangover, and the Rule of Four within those centers. The need to manage the transition in resource allocation is an inherent lesson of our theory.

5.3. Limitations

We recognize that our models are simplistic and stylized. Actual NIH operations are more complex. But, as statistician George Box once said, “Essentially, all models are wrong, but some are useful” (Box and Draper 1987, p. 424). In a related philosophy of modeling, Albert Einstein said,¹³ “Everything should be made as simple as possible, but not simpler.” We hope that our analyses showing the effects of the Rule of Four have provided useful insights. A more comprehensive systems analysis of the effects of the doubling period 1998–2003 is presented in Gomez (2012) and Gomez et al. (2012).

5.4. Conclusion

Changes in federal research funding can have amplified effects on new funding available for researchers. When grants are awarded for a four-year time period (and in a generic case, for an average of a τ-year time period), a X% change in total funding results in a 4X% change in new funding (in a generic case, τX%). We offered the Rule of Four and the Rule of τ to describe this phenomenon.

Furthermore, a positive step change in total funding results in a situation that might be observed as an early euphoria for grant applicants but is later accompanied by a severe hangover, a situation where grant funding declines, with dramatic effects on researchers.

The amplified effect is mainly due to grants lasting for an extended period, thereby requiring the majority of funds available in one year to pay for grants awarded in previous years. Policies to dampen the amplified effects when total funding is changing include careful changes in grant periods during total budget changes, as well as close-to-optimal increments in the total budget, as discussed throughout this paper.

Biographies

Richard C. Larson is the Mitsui Professor in the Engineering Systems Division at the Massachusetts Institute of Technology (MIT). He has focused on operations research as applied to service industries, primarily in the fields of technology-enabled education, urban service systems, queueing, logistics, and workforce planning. He is founding director of the Learning International Networks Consortium (LINC; http://linc.mit.edu), an MIT-based international project that has held five international symposia and sponsored numerous initiatives in Africa, China, and the Middle East. With Elizabeth Murray, he leads LINC’s newest and largest initiative, Blended Learning Open Source Science or Math Studies (BLOSSOMS;http://blossoms.mit.edu), sponsored by the Hewlett Foundation and other foundations and companies. His current research projects focus on education as a complex system. He is past president of INFORMS, a member of the National Academy of Engineering, an INFORMS Founding Fellow, and a recipient of the INFORMS President’s Award, Lanchester Prize, and Kimball Medal.

Navid Ghaffarzadegan is a postdoctoral researcher in the Engineering Systems Division of the Massachusetts Institute of Technology and the John Glenn School of Public Affairs at the Ohio State University. His studies include applications of system dynamics modeling and other simulation techniques in a wide range of management and public policy contexts, including education and healthcare systems. Navid received his Ph.D. in public administration and policy from the State University of New York (SUNY) at Albany in 2011.

Mauricio Gomez Diaz is a graduate of the master’s program at the Massachusetts Institute of Technology’s Engineering Systems Division. He holds undergraduate degrees in computer science and Japanese, with a minor in political science. His research at MIT was sponsored by the National Institutes of Health and focused on the dynamics of the biological and medical sciences workforce in the United States. Mauricio currently works for the Boston Consulting Group and is interested in modeling and simulation, particularly using system dynamics, as tools for decision makers to understand the impacts and unforeseen effects of particular policies.