Improving Glaucoma Detection Using Spatially Correspondent Clusters of Damage and by Combining Standard Automated Perimetry and Optical Coherence Tomography

Abstract

Purpose.

To improve the detection of glaucoma, techniques for assessing local patterns of damage and for combining structure and function were developed.

Methods.

Standard automated perimetry (SAP) and frequency-domain optical coherence tomography (fdOCT) data, consisting of macular retinal ganglion cell plus inner plexiform layer (mRGCPL) as well as macular and optic disc retinal nerve fiber layer (mRNFL and dRNFL) thicknesses, were collected from 52 eyes of 52 healthy controls and 156 eyes of 96 glaucoma suspects and patients. In addition to generating simple global metrics, SAP and fdOCT data were searched for contiguous clusters of abnormal points and converted to a continuous metric (p_cc). The p_cc metric, along with simpler methods, was used to combine the information from the SAP and fdOCT. The performance of different methods was assessed using the area under receiver operator characteristic curves (AROC scores).

Results.

The p_cc metric performed better than simple global measures for both the fdOCT and SAP. The best combined structure-function metric (mRGCPL&SAP p_cc, AROC = 0.868 ± 0.032) was better (statistically significant) than the best metrics for independent measures of structure and function. When SAP was used as part of the inclusion and exclusion criteria, AROC scores increased for all metrics, including the best combined structure-function metric (AROC = 0.975 ± 0.014).

Conclusions.

A combined structure-function metric improved the detection of glaucomatous eyes. Overall, the primary sources of value-added for glaucoma detection stem from the continuous cluster search (the p_cc), the mRGCPL data, and the combination of structure and function.

SAP and fdOCT data were searched for contiguous clusters of abnormal points, converted to a continuous metric. This combined structure-function metric improved the detection of glaucomatous eyes.

Introduction

Because of the progressive nature of the disease, early detection of glaucomatous damage is one of the key objectives of the glaucoma specialist. However, despite the availability of tests that yield quantitative structural and functional measures relevant to glaucoma, there is currently no “gold standard” for diagnosis. In fact, even for a particular diagnostic test, there is usually no universal consensus on what constitutes an abnormal result. For example, a wide variety of criteria are used when interpreting the results from visual field data obtained from standard automated perimetry (SAP), ranging from simple global metrics, such as mean deviation (MD), to more local analyses, such as the glaucoma hemifield test.¹

Along with other technologies, such as confocal scanning laser ophthalmoscopy and scanning laser polarimetry, the introduction of time-domain optical coherence tomography (tdOCT)² more than 2 decades ago has allowed clinicians access to noninvasive in vivo imagining of optic nerve tissue, yielding a quantitative measure of structure in addition to the functional data already provided by the SAP. The tdOCT measures typically used for glaucoma detection are based on the circumpapillary retinal nerve fiber layer (cpRNFL) thickness, which has performed reasonably well in separating groups of healthy controls from glaucoma suspects and patients (see Refs. 3 and 4 for reviews).

The subsequent development of frequency-domain OCT (fdOCT; also referred to as Fourier- or spectral-domain OCT)⁵ has allowed for faster, higher-resolution imaging, but has further increased the complexity of the data available. A fundamental question is how to make better use of this data. Although fdOCT has the potential to significantly increase the performance of glaucoma detection as compared with tdOCT, current studies have been underwhelming, suggesting performance similar to, or only incrementally better than, tdOCT (see Refs. 6–8 for reviews). A contributing factor for the apparent similarity of fdOCT and tdOCT performance is that many of these studies, to establish agreement with the tdOCT, limit their analyses of fdOCT data to cpRNFL thickness measures (i.e., 1-dimensional circular scans rather than 2-dimensional optic disc RNFL [dRNFL] thickness measures), which can be derived from volumetric scans.

One approach to make better use of the more complex fdOCT information is machine learning, which has been fairly effective in separating healthy controls from glaucoma suspects and patients using both SAP and tdOCT (see Ref. 9 for a review). For example, a recent study reported an improvement in early glaucoma detection by using fdOCT dRNFL thickness combined with machine learning as compared with using thickness alone.¹⁰ An alternative approach for dealing with the complexity of fdOCT data is to try simpler, more intuitive strategies, such as a topographic pointwise probability map, as used in SAP analysis.¹¹ A prior study has suggested that measures derived from such a probability map of the dRNFL may outperform the traditional cpRNFL measures.¹²

Another approach is to use the 2-dimensional topographic information from the fdOCT macular scan protocols. In fairness, reports of quantitative structural damage from macular noninvasive imaging have predated the fdOCT (see Ref. 13 for references), although most of these reports, with a few notable exceptions,^14,15 have relied on macular total retinal (mTR) thickness measures. Nonetheless, perhaps surprisingly, even using fdOCT data and increasingly sophisticated segmentation algorithms to better distinguish the macular RNFL (mRNFL) and macular retinal ganglion cell plus inner plexiform layer (mRGCPL) from the combined macular ganglion cell complex (mGCC; defined as mRNFL+mRGCPL) has yielded diagnostic performance that is, at best, equal or marginally better than cpRNFL (see Refs. 13,16, and 17 for reviews; for use of mRGCPL separate from mGCC, see in particular Refs. 18–20). A more sophisticated approach, similar to the pattern deviation (PD) of SAP, also failed to perform better than average cpRNFL thickness.²¹

Yet another technique employed is hemiretina asymmetry (HA),²² which is similar to the glaucoma hemifield test used in SAP analysis. HA analyses using tdOCT²³ and fdOCT^24,25 did not show a marked improvement over cpRNFL measures. One fdOCT study²⁶ argued for an improvement over cpRNFL measures, but the glaucoma patient population included only localized RNFL defects based on red-free fundus photos, so these results may not generalize to other populations. Notably, all of these fdOCT HA analyses used mTR measurements instead of a subset of inner retinal layers.

Along with the need to better understand how to use the richer fdOCT dataset, another fundamental question is the potential advantage of combining structural and functional measures for the purpose of glaucoma detection. Previous studies have used various strategies (e.g., simple logical rules,^27–29 machine-learning classifiers,^30–39 or a priori models^40,41) to combine measures of visual function (e.g., SAP, short-wavelength automated perimetry, and frequency-doubling technology perimetry) with measures of structure (e.g., fundus photos, confocal scanning laser ophthalmoscopy, scanning laser polarimetry, and OCT). These methods have yielded performance equal to or better than methods using structural or functional measures alone.

In this study, we use fdOCT and SAP data to assess various methods, including a novel continuous cluster criterion, in an attempt to better classify individuals as either healthy or glaucomatous. In particular, we combine the information from the SAP and fdOCT data, using both simple logical rules as well as a relatively simple a priori model that tests for spatially correspondent patterns of damage. In addition, the aspects of these analyses that yield the most value-added are discussed.

Methods

Subjects

The glaucomatous group (156 eyes of 96 patients, aged 55.7 ± 11.9 [mean ± SD] years) consisted of patients in whom at least one eye exhibited glaucomatous optic neuropathy, defined based on stereophotography evaluation by glaucoma specialists using the following criteria: focal or diffuse neuroretinal rim thinning, focal or diffuse RNFL loss, or an intereye vertical cup-to-disc ratio asymmetry greater than 0.2 not explained by differences in disc size. All eyes had open angles as viewed during gonioscopic examination. When the fellow eye had reliable test results, it was included, even if all the test results were normal. Therefore, the glaucomatous group included eyes that were glaucoma “suspects” (based on the fellow eye) without any other indication of glaucomatous damage. Moreover, to avoid bias in evaluation of the classification ability of the SAP data and to increase the number of subtle cases included in the study, abnormal SAP results were not part of the inclusion criteria for the glaucoma group. Consecutive patients were enrolled retrospectively based on availability of test data. Patients with cataracts, a history of ocular surgery, or a history of any other ocular or neurological diseases that could affect structural or functional measures were excluded.

The control subjects (52 eyes of 52 individuals, aged 52.7 ± 7.6 years) were included based on the following criteria: spherical refraction between −6.0 diopters (D) and +3.0 D, IOP ≤ 21 mmHg, axial length between 22 mm and 26 mm, and a normal clinical examination. Subjects were excluded if they had a history of ocular disease or a family history of glaucoma. Controls were part of a previous study.⁴² Normal SAP results were not required for the control group. The characteristics of both groups are summarized in Table 1.

Table 1.

Population Characteristics

	Controls	Glaucoma	Significance, P*
Eyes	52	156
Individuals	52	96
Age, y	52.7 ± 7.6	55.7 ± 11.9	0.208
MD, dB	−0.4 ± 1.2	−3.1 ± 3.7	0.012
PSD, dB	1.5 ± 0.4	3.2 ± 3.0	0.760

^* Significance based on a GEE, accounting for intereye correlations.

Written, informed consent was obtained from all of the participants. Procedures followed the tenets of the Declaration of Helsinki, and the protocol was approved by the institutional review boards of Columbia University and the New York Eye and Ear Infirmary.

Standard Automated Perimetry

All subjects were tested with SAP (24-2 SITA Standard⁴³ protocol, Humphrey 750i Visual Field Analyzer; Carl Zeiss Meditec, Inc., Dublin, CA). Subjects were required to have fixation losses less than or equal to 33%, false-negatives less than or equal to 33%, and false-positives less than or equal to 15%. Other than reliability of the test, the SAP was not used as an inclusion or exclusion criteria. The MD of the control group was −0.4 ± 1.2 dB and of the glaucoma group was −3.1 ± 3.7 dB. The pattern standard deviation (PSD) of the control group was 1.5 ± 0.4 dB and of the glaucoma group was 3.2 ± 3.0 dB. The Advanced Data Export module (Carl Zeiss Meditec, Inc.) was used to obtain the raw data in XML format. To classify the subjects as either normal or glaucomatous, the significance level of the MD of the 24-2 was used as a baseline metric (p_MD). The total deviation (TD) SAP data, converted to probability values based on the internal normative database of the machine, also were analyzed for clusters of abnormal points (see Cluster Analysis, below).

Optical Coherence Tomography

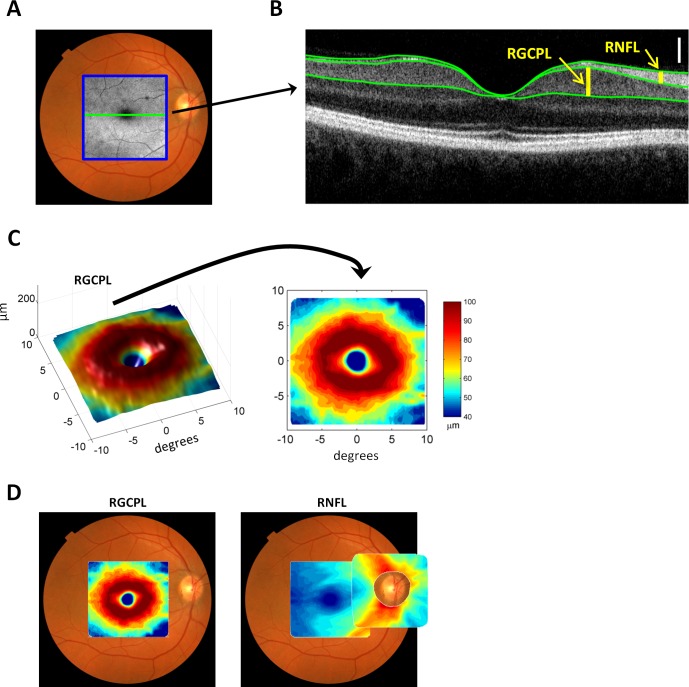
All subjects were also tested using fdOCT (3D-OCT 1000/2000; Topcon Medical Systems, Inc., Oakland, NJ) with the volume (cube) scan protocol (6 × 6 mm, 128 horizontal B-scans with 512 A-scans each, see Fig. 1A) with both macular and optic disc fixation targets. Scans with poor fixation (as indicated by poor B-scan alignment or by grossly off-center scans) and blink artifacts (as indicated by missing B-scans) were rejected. The thickness of retinal layers was determined using a previously validated segmentation algorithm,⁴⁴ which was manually corrected as necessary⁴⁵ (see Fig. 1B). In particular, the thickness of the retinal nerve fiber layer (RNFL) and the combined retinal ganglion cell plus inner plexiform layer (RGCPL) was determined for the macular and disc scans (see Figs. 1B–D). Because the RGCPL is quite thin near the disc, only the mRGCPL, mRNFL, and dRNFL were analyzed (Fig. 1D).

Figure 1.

Measurements from fdOCT. (A) Fundus photo with an en face fdOCT (C-face) intensity image superimposed within a blue square. (B) The central slice through the macula of the fdOCT image (B-scan) corresponding to the horizontal green line in (A). Superimposed green lines mark the boundary between anatomical layers. The thicknesses of the RNFL and RGCPL are shown with yellow vertical bars. The white vertical calibration bar represents 100 μm. (C) The 3-dimensional macular RGCPL thickness (left) and a top-down view (right) with thickness represented in pseudo-color. (D) The macular RGCPL superimposed on a fundus photo (left) and the macular and disc RNFL superimposed on a fundus photo (right).

The mean thickness of the cpRNFL, converted to probability (p_MT), was used as a baseline metric for classifying the subjects as either normal or glaucomatous. (The cpRNFL, extracted from the volume scan, was based on a circle, centered at the optic nerve head, with a diameter of 3.4 mm and was therefore analogous to the 1-dimensional RNFL circle scan obtained from a tdOCT machine.) The mean thickness of a layer over the entire 2-dimensional cube scan, converted to p_MT, was also used as a baseline metric. The thickness data were also converted to point-by-point probability values as previously described¹¹ (see Figs. 2A, 2B for a control and Fig. 2C for a patient) and clusters of abnormal data points were determined (see Cluster Analysis, below). For ease of comparison, the fdOCT data are presented in field view from Figure 2 onward. In addition, the layer thicknesses were normalized in a manner similar to the PD analysis of SAP (by dividing the thickness values based on the 85th percentile of thickness within a scan), and the HA across the horizontal midline was assessed by taking the difference between the superior and inferior retinal thicknesses. Both PD and HA values were also converted to probability values based on controls and were analyzed for clusters of abnormal points. Note that, unlike the thickness probability values, the probability values for the PD and HA were two-tailed because both low and high values suggested abnormalities.

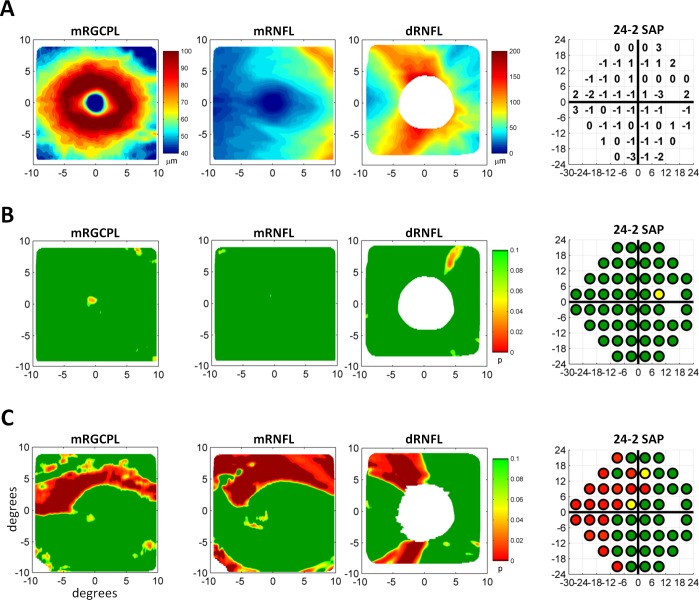
Figure 2.

Measurements from fdOCT and SAP converted to probability values. (A) The mRGCPL as well as the mRNFL and dRNFL thicknesses for a healthy control eye (left three panels). The 24-2 SAP total deviation values for the same eye (right). (B) The data in (A) converted to probability values. (C) Data from a glaucomatous eye in the same format as (B).

Cluster Analysis

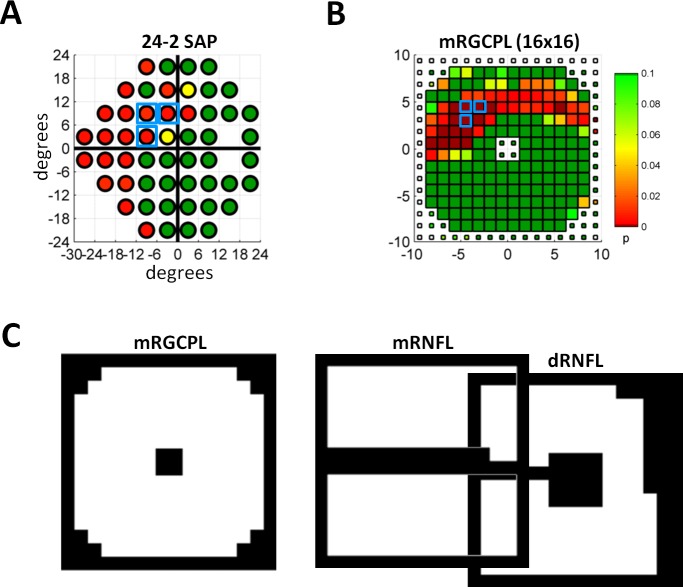
Both SAP and fdOCT data were analyzed for the presence of clusters of abnormal points that respected the horizontal midline. As a baseline metric, the common 5-5-1 cluster criterion was used, requiring a contiguous set of three or more points, all of which were significant at P ≤ 0.05, with at least one significant at P ≤ 0.01.⁴⁶ For instance, Figure 3A shows a 24-2 SAP with an example of a 5-5-1 cluster (blue squares). (Note that there are many possible 5-5-1 clusters, but only one is indicated.)

Figure 3.

Cluster analysis and ROIs. (A) The 24-2 SAP data as in Figure 2C with a set of points meeting the 5-5-1 cluster criterion outlined by light blue boxes. (B) Probability values from mRGCPL thickness data downsampled into a 16 × 16 grid. Data are from the same eye shown in Figure 2C. The small squares indicate values outside the ROI. White squares indicate missing data (which often occurs at scan edges after centering the scan). A set of points meeting the 5-5-1 cluster criterion is outlined by light blue boxes. (C) The ROIs shown in white for the mRGCPL, mRNFL, and dRNFL data. The dRNFL is offset from the mRNFL data based on anatomy, as shown in Figure 1D.^17,42

For the fdOCT, the data was first downsampled from 128 × 512 pixels to a 16 × 16 grid and then this reduced dataset was converted from thickness to probability values (see Fig. 3B). Next, a region of interest (ROI) was determined a priori for each fixation and thickness combination (see Fig. 3C) based on exclusion of regions that were relatively thin (e.g., fovea or raphe) or regions that were near the edge (1 pixel border) of the scan.^17,42 Data outside the ROI were ignored for cluster evaluation (e.g., smaller squares in Fig. 3B, at the center and edges, corresponding to the black regions in Fig. 3C, indicate data ignored when evaluating clusters). Figure 4 shows the complete set of downsampled fdOCT data for the patient in Figure 2C, including thickness probabilities (Fig. 4A), the PD analysis (Fig. 4B), and the HA analysis (Fig. 4C).

Figure 4.

Sample data from a glaucomatous eye. (A) The downsampled mRGCPL, mRNFL, and dRNFL fdOCT data, as well as the 24-2 SAP data from the same glaucomatous eye shown in Figure 2C. The white squares near the center of the dRNFL data represent data missing due to the optic disc. (B) The fdOCT data after the PD analysis in a similar format as (A). (C) The fdOCT data after the HA analysis in a similar format as (A).

In addition to the 5-5-1 cluster criterion, a novel continuous cluster metric was used. Unlike the 5-5-1, which returned a binary (yes/no) value for each hemifield or hemiretina based on whether or not a cluster was found, the continuous cluster metric returned a continuous value (p_cc). This value is related to the probability of observing a particular cluster of points. Similar to the 5-5-1, the p_cc required a contiguous set of points, all of which were significant at P ≤ 0.05 (the threshold probability). However, the p_cc metric also considered the number of contiguous points as well as the actual probabilities of these points.

For the fdOCT, the continuous cluster metric generated the p_cc value by first assessing, through computer simulation, the probability of observing a set of n contiguous points in a 16 × 16 grid of points (equivalent to the downsampled fdOCT), where the set of points respected the previously defined ROIs and was contained entirely within one hemiretina. For computational simplicity, the maximum tested value for n was 6. Note that the simulation was based on a randomly generated grid of 16 × 16 points and ignored any correlation between the points, which does exist in fdOCT from healthy controls. Thus, this value should not be thought of as a true probability of observation, but rather as a quantitative metric of convenience that ranks the relative probability. To further distinguish between the probabilities of different clusters of points, particularly when the number of points n is the same, the probability of the lowest observed P value in the set was also taken into account when determining p_cc by using a separate set of computer simulations. Thus, for each hemiretina, the value of p_cc was assigned by multiplying the simulation-determined probability value based on the largest number of n contiguous points found by the simulation-determined probability value based on the lowest observed P value in that set. (If no contiguous set of abnormal points was found [i.e., n = 1], then p_cc was defined based on the point within the ROI with the lowest probability value, also adjusted based on computer simulations.) For the SAP, the p_cc metric was determined in the same manner, although the values of p_cc were based on the set of 24-2 SAP points rather than a 16 × 16 grid, requiring a separate set of computer simulations.

Combining Structure and Function

Although there are several reasonable ways to combine structural and functional measures, the analysis here was confined to using the p_cc metric in a very simple manner. First, structure and function were “combined” by simply multiplying the p_cc of the inferior or superior retinal mRGCPL with the p_cc of the correspondent hemifield of the SAP. Then, a metric combining the mRGCPL and SAP (mRGCPL&SAP p_cc) was defined as the minimum value of the two hemifields. Finally, a more generic combination of fdOCT and SAP data (fdOCT&SAP p_cc), using both the mRGCPL and dRNFL, was defined as the minimum of the mRGCPL&SAP p_cc and dRNFL&SAP p_cc. To separate the effect of using the p_cc metric from the combination of structure and function, a “baseline” metric for combining structure and function (fdOCT&SAP p_MT/MD), based on the mean thickness of the OCT and the MD of the visual field, was defined as the minimum of the mRGCPL p_MT, the dRNFL p_MT, and the SAP p_MD.

Data Analysis and Evaluation

Data were analyzed using custom code written in MATLAB (version 2012a; MathWorks, Inc., Natick, MA). For cluster simulations, cloud-based computing resources were used (EC2 Elastic Compute Cloud; Amazon.com, Inc., Seattle, WA). A generalized estimating equation (GEE) approach, which accounts for intereye correlations, was used to compare means among groups (as in Table 1). When calculating thickness probability in any of the fdOCT metrics, the control group was also used as the normative database. However, to prevent a bias in the reported specificity, a “leave-one-out” approach was used when analyzing the control group. To evaluate the classification of subjects as either normal or glaucomatous, areas under receiver operator characteristic curves (AROC scores) were determined. An AROC score of 1 represents perfect discrimination of the two groups, whereas an AROC of 0.5 indicates performance no better than chance. Standard error (SE) of AROC scores and statistical tests between AROC scores of different classification metrics were performed (as in Tables 2 and 3) according to the method of Obuchowski.⁴⁷ This method is based on the nonparametric method of DeLong et al.,⁴⁸ but also adjusts for intereye correlations. (This approach has been used in previous studies using similar data [e.g., Ref. 21]) Sensitivity at an arbitrary fixed specificity value of greater than or equal to 85% was also determined. An α level of 0.05 was used to determine statistical significance.

Table 2.

Performance of Classification Metrics

Metric	AROC ± SE*	% SN at ≥85% SP
SAP alone
SAP pMD	0.768 ± 0.029	62
SAP p5-5-1	0.760 ± 0.030	62
SAP pcc	0.797 ± 0.034	72
fdOCT alone
cpRNFL pMT	0.718 ± 0.041	56
mRGCPL pMT	0.775 ± 0.038	56
mRGCPL p5-5-1	0.758 ± 0.034	59
mRGCPL pcc	0.818 ± 0.035	62
mRGCPL (PD) pcc	0.644 ± 0.046	34
mRGCPL (HA) pcc	0.676 ± 0.043	37
dRNFL pMT	0.724 ± 0.041	56
dRNFL p5-5-1	0.681 ± 0.034	31
dRNFL pcc	0.739 ± 0.037	49
dRNFL (PD) pcc	0.619 ± 0.043	38
dRNFL (HA) pcc	0.520 ± 0.043	24
fdOCT & SAP combined
mRGCPL&SAP pcc	0.868 ± 0.032	78
fdOCT&SAP pcc	0.859 ± 0.032	78
fdOCT&SAP pMT/MD	0.831 ± 0.034	62

SN, sensitivity; SP, specificity.

^* Standard error based on the method of Obuchowski,⁴⁷ accounting for intereye correlations.

Table 3.

Comparison of Classification Metrics

Metric	AROC ± SE*	Compared Metric	AROC ± SE*	Significance, P*
Entire population (n = 52 control eyes, 156 glaucoma/suspect eyes)
mRGCPL&SAP pcc	0.868 ± 0.032	SAP pMD	0.768 ± 0.029	<0.001
		SAP pcc	0.797 ± 0.034	0.003
		cpRNFL pMT	0.718 ± 0.041	<0.001
		mRGCPL pMT	0.775 ± 0.038	0.001
		mRGCPL pcc	0.818 ± 0.035	0.005
		fdOCT&SAP pMT/MD	0.831 ± 0.034	0.038
SAP (PSD) used as inclusion and exclusion criteria (n = 49 control eyes, 73 glaucoma/suspect eyes)
mRGCPL&SAP pcc	0.975 ± 0.014	SAP pMD	0.897 ± 0.026	<0.001
		SAP pcc	0.942 ± 0.024	0.066
		cpRNFL pMT	0.809 ± 0.045	<0.001
		mRGCPL pMT	0.867 ± 0.034	<0.001
		mRGCPL pcc	0.922 ± 0.025	0.004
		fdOCT&SAP pMT/MD	0.931 ± 0.025	0.003

^* Significance and SE based on the method of Obuchowski,⁴⁷ accounting for intereye correlations.

Results

Evaluation of Structure and Function Independently

The performance of the metrics in classifying subjects as either controls or glaucomatous was evaluated using AROC scores (see Table 2), although the sensitivity at an arbitrary fixed specificity of greater than or equal to 85% is also provided for context. First, consider only the SAP data. An example of a clearly abnormal 24-2 SAP, with an MD of −6.74 dB, is shown in Figure 4A (right). Using only the baseline metric of SAP p_MD yielded an AROC of 0.768 ± 0.029. The 5-5-1 cluster criterion was applied to the SAP data and resulted in a similar AROC score (0.760 ± 0.030). The continuous cluster criterion, p_cc, yielded a slightly higher AROC of 0.797 ± 0.034 and a greater sensitivity of 72% (vs. 62% for SAP p_MD). The difference in the AROC scores between the SAP p_cc cluster criterion and the SAP p_5-5-1 cluster criterion was statistically significant (P = 0.018), although the difference between the SAP p_cc and SAP p_MD was not (P = 0.063).

Consider next the fdOCT data alone. Figure 4A shows an example of mRGCPL, mRNFL, and dRNFL data from a patient with clear glaucomatous damage. In general, the mRNFL data performed slightly worse than either the mRGCPL or the dRNFL, so for the sake of simplicity, the mRNFL data have been omitted from the quantitative results (e.g., Table 2); however, when considering an individual subject, as in Figure 4, the data are still shown for context. The performance of the baseline metrics of mean circumpapillary RNFL thickness and mean optic disc volume RNFL thickness yielded AROC scores lower than those for the MD of the SAP (cpRNFL p_MT AROC = 0.718 ± 0.041 and dRNFL p_MT = 0.724 ± 0.041, as compared with SAP p_MD 0.768 ± 0.029), whereas the AROC score of the mRGCPL p_MT (0.775 ± 0.038) was higher than the SAP p_MD. However, none of these differences were statistically significant.

Perhaps surprisingly, the PD and HA analyses (see Figs. 4B, 4C for an example), which are similar in concept to the pattern deviation and glaucoma hemifield test analyses commonly used with the SAP, performed worse than the mRGCPL p_MT and the dRNFL p_MT, which were baseline global metrics based only on mean thicknesses (see Table 2 for AROC scores). Furthermore, although the dRNFL p_cc (AROC = 0.739 ± 0.037) performed better than the dRNFL p_MT, the sensitivity at 85% specificity was worse and the difference in AROC scores was not statistically significant (P = 0.312). However, the mRGCPL p_cc (AROC = 0.818 ± 0.035) did perform better than the mRGCPL p_MT (P = 0.040), with a greater sensitivity of 62% (vs. 56% for mRGCPL p_MT).

Evaluation of Combined Structure and Function

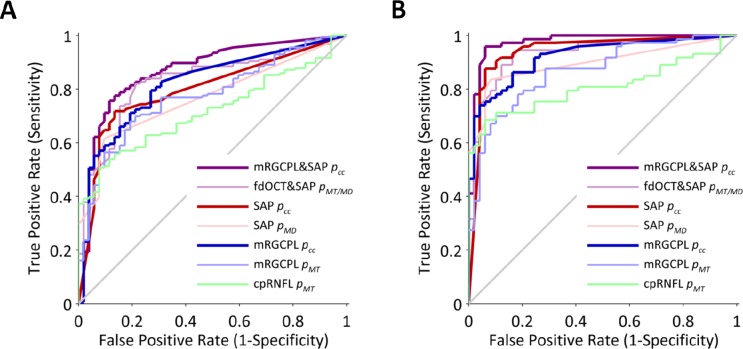
The performance of the best fdOCT global metric, mRGCPL p_MT, was similar to the SAP global metric, SAP p_MD. Likewise, the performance of the overall best fdOCT metric, mRGCPL p_cc, was similar to the best SAP metric, SAP p_cc. To assess the value-added from combining structure and function, we incorporated the best structural and functional metrics (the p_cc metric for both mRGCPL and SAP) into a single metric, mRGCPL&SAP p_cc. This combined structure-function technique yielded an AROC of 0.868 ± 0.032. We then compared the performance of this metric to the baseline (global) and p_cc (local patterns) metrics of structure and function considered independently (Table 3). As shown in Figure 5A, the mRGCPL&SAP p_cc had a significantly higher AROC than the SAP p_MD (P < 0.001) and the SAP p_cc metrics (P = 0.003) as well as the cpRNFL p_MT (P < 0.001), mRGCPL p_MT (P = 0.001), and mRGCPL p_cc metrics (P = 0.005).

Figure 5.

Receiver operator characteristic curves for various metrics. (A) Receiver operator characteristic curves for the entire population. (B) Receiver operator characteristic curves for a subpopulation in which SAP was used as inclusion and exclusion criteria.

However, because our combined structure-function metric relies on the continuous cluster method, we wanted to determine to what extent the higher AROC of the combined structure-function metric could be explained by merely using both fdOCT and SAP data, independent of the p_cc metric. Therefore, we tested a structure-function “baseline” metric based on the minimum of the SAP p_MD, mRGCPL p_MT, and dRNFL p_MT; this “baseline” method (fdOCT&SAP p_MT/MD) can be thought of as classifying a subject as abnormal if either structure or function is abnormal (simple logical rules on global measures), without testing for subtle patterns (as with the p_cc) and without combining the structural and functional information in a weighted and spatially correspondent manner (see Methods for details of the mRGCPL&SAP p_cc). When we compared the mRGCPL&SAP p_cc AROC (0.868 ± 0.032) to the fdOCT&SAP p_MT/MD AROC (0.831 ± 0.034), the p_cc structure-function metric performed better (P = 0.038) than the “baseline” structure-function metric (Fig. 5A).

Evaluation of a Subpopulation Selected Based on SAP

SAP was not used as inclusion or exclusion criteria for the control or glaucomatous groups to avoid biasing the AROC scores in favor of SAP-based metrics and, more importantly, to allow for inclusion of subtle cases. However, to allow for a comparison with studies that use SAP as inclusion criteria, we analyzed a subpopulation in which a SAP criterion (PSD P ≤ 0.05) was used as exclusion criteria for the control group and inclusion criteria for the glaucoma group. As expected, the AROC scores increased for each metric, with the mRGCPL&SAP p_cc metric now yielding an AROC of 0.975 ± 0.014. The mRGCPL&SAP p_cc metric performed significantly (P < 0.001 to P = 0.004) better than all the other methods that were previously tested on the full population (see Table 3 and Fig. 5B), with the exception of the SAP p_cc metric (P = 0.066), which is not surprising given that this subpopulation was defined based on SAP. For structural measurements considered independently, the p_cc metric performed better than the p_MT metric for the mRGCPL, mRNFL, and dRNFL, although this difference was statistically significant only for the mRGCPL (P = 0.005) and mRNFL (P = 0.012). For functional measures considered independently, the SAP p_cc metric performed better than the SAP p_MD metric (P = 0.019).

Discussion

Our purpose here was to combine structural and functional data, to make better use of the individual OCT and SAP measures, and to assist with glaucoma detection. We found that combining structure and function by taking into consideration spatially correspondent patterns of damage improved the proper classification of the control and glaucomatous groups. In general, the techniques used in this study improved the diagnostic capabilities of the fdOCT and SAP data in two steps. First, we considered structural and functional measures independently by using a novel technique that searches for many different types of spatially contiguous clusters of abnormal points and then converts the result into a single, continuous value (i.e., the p_cc metric). Next, we combined the structural and functional information in a spatially correspondent manner. Both steps offer value-added, although in different ways, as discussed below.

Evaluation of Structure and Function Independently

The continuous cluster (p_cc) metric has theoretical advantages when compared with similar techniques used in the past. When evaluating SAP data, the common cluster criterion of three contiguous points significantly abnormal at P ≤ 0.05, with at least one point significant at P ≤ 0.01 (i.e., the 5-5-1 cluster criterion), has been shown to offer classification performance that is on par with or better than other commonly used SAP metrics.⁴⁶ However, this criterion yields a binary response (whether or not a cluster is found) rather than a continuous metric and, at times, this rule can seem arbitrary. For instance, the 5-5-1 criterion does not consider the number of contiguous points nor the actual probabilities. As long as there are three or more contiguous points significant at P ≤ 0.05, the 5-5-1 does not distinguish between, for example, three contiguous points versus six contiguous points, even though the latter is much less likely to be observed due to chance alone. Thus, a set of six contiguous points at P = 0.02 would not meet the 5-5-1 criterion (because not a single point has P ≤ 0.01), despite being less probable than three contiguous points with two points at P = 0.05 and one point at P = 0.01. Likewise, the 5-5-1 criterion treats two points at P = 0.05 and one point at P = 0.01 the same as three points at P < 0.001, even though, again, the latter is much less likely.

Our use of the p_cc metric does involve some assumptions. For the fdOCT data, the appearance of abnormal points may be correlated (i.e., spatially clustered) in controls due to interindividual variability. For example, if a control has an RNFL distribution at the optic disc that differs from most other controls, a pattern of contiguous abnormal points may appear. One way to address this issue is the use of “superpixels” to group correlated areas.¹⁰ Another approach is to better understand factors leading to interindividual variability among controls and to attempt to correct or control for these underlying factors in the fdOCT data. In this study, we simply take the p_cc metric applied to the fdOCT data as an approximate “score” that ranks relative probabilities of observing clusters of abnormal points. Because the metric yields continuous values, an ROC curve can be generated by varying the threshold for considering a p_cc value as abnormal, which yields an empirical result for the optimal value in our population (without making any assumptions regarding the true probabilities of observing particular clusters of abnormal points in the fdOCT data). In the future, an independent study with a larger number of controls or a more advanced simulation might yield a better understanding of how the p_cc metric relates to true probabilities of observation in the fdOCT data. In any case, empirically, the p_cc metric performs better than the other methods tested in this study.

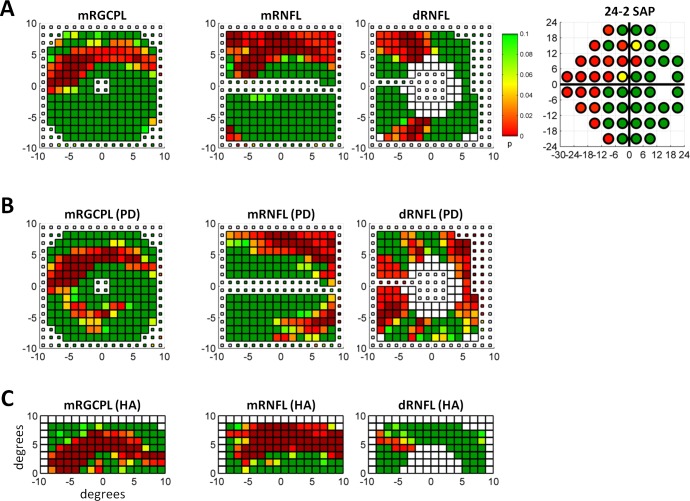
A specific example illustrating the advantage of the p_cc metric when applied to fdOCT data can be seen in Figure 6. The average thickness of the mRGCPL for this eye lies near the 32nd percentile for the eyes in the control group. Although the mRGCPL p_MT classifies this eye as a control when using the optimal point of the ROC curve, the mRGCPL p_cc metric classifies this eye as glaucomatous. Surprisingly, the PD and HA analyses did not perform very well overall. (It is important to realize that the focal loss volume metric,²¹ although it makes use of a pattern deviation analysis for the mGCC, is implemented differently from the PD method tested here. For details, see Ref. 15.) Certainly, there are some specific cases in which these strategies would be helpful. For instance, Figure 7A shows a control mRGCPL that had considerably fewer abnormal points once the PD analysis was applied. Similarly, Figure 7B shows the mRNFL of a patient (same eye as Fig. 6) in whom the abnormal points within an arcuate became more statistically significant when using the HA analysis. However, overall, these strategies did not offer much value-added beyond mean thickness. It is possible that the PD analysis removed some diffuse thinning that assisted with classifying the glaucomatous eyes when using mean thickness. Similarly, it is possible that symmetric damage was removed when using the HA analysis. It is also possible that in most cases the defects enhanced by the HA technique would already be detected using analyses based on mean thickness. In other words, perhaps early glaucomatous damage in the macula is always either diffuse (symmetric across the horizontal midline) or focal damage in the form of a deep, thin arcuate (as in Fig. 6). If true, then the HA technique would not offer much of an advantage in either of these cases. Notably, recent studies^24–26 using an HA strategy in fdOCT do not offer comparisons to the performance of macular measurements based simply on mean thickness. In any case, it is clear that there are some advantages to the PD and HA strategies on a case-by-case basis (as seen in Fig. 7).

Figure 6.

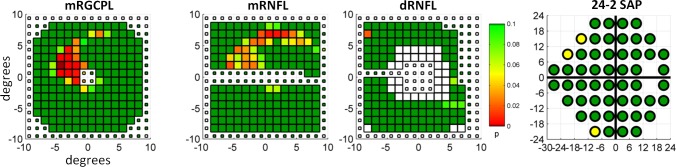
Example of an eye, belonging to the glaucomatous group, with a subtle arcuate defect in the macula. Data are in the same form as shown in Figure 4A.

Figure 7.

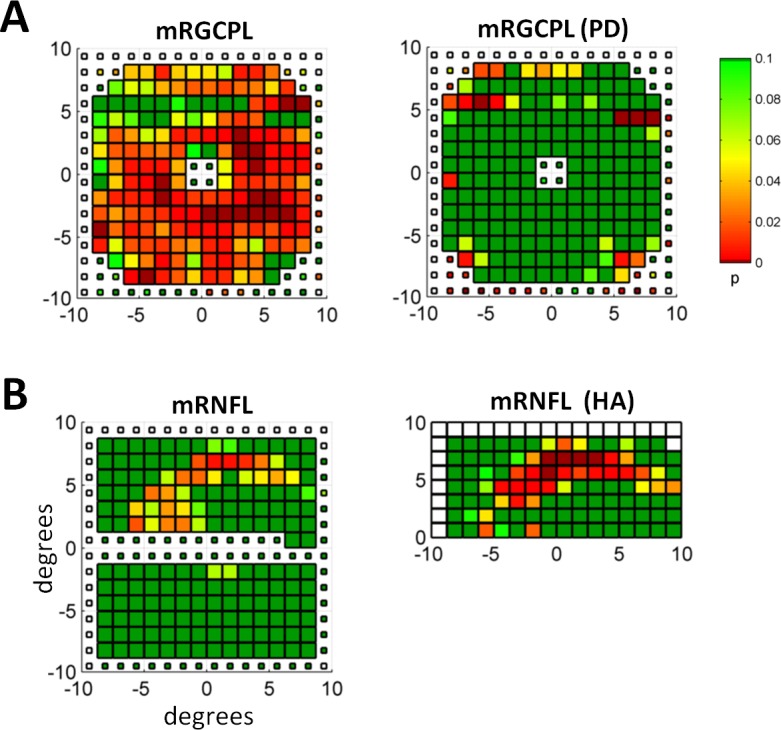
Examples of PD and HA analyses. (A) The mRGCPL probability values based on thickness (left) and the PD analysis (right) for an eye belonging to the healthy control group. (B) The mRNFL probability values based on thickness (left) and the HA analysis (right) for an eye belonging to the glaucomatous group. Same eye as shown in Figure 6.

Whereas our use of the mRGCPL thickness distinguishes our study from previous reports combining structure and function, recent studies^18–20 have also considered the diagnostic value of the mRGCPL (separate from the mGCC) when considering structure alone. In particular, Mwanza et al.¹⁸ and Takayama et al.¹⁹ have used a “minimum spoke” approach to analyzing the mRGCPL. Although minimum probability values performed worse than the p_cc metric in our study (data not shown), the “minimum spoke” approach is more complex than the analysis we used, so it is difficult to make a meaningful comparison. Further work would be needed to compare these methods in a fair manner. In any case, the p_cc metric is a more general approach that can be applied to the thickness of any layer at various regions of the retina, whereas the “minimum spoke” approach is probably most applicable to mRGCPL thickness.

Prior studies considering the diagnostic power of the macular region in fdOCT have almost always found performance similar to cpRNFL or dRNFL (see Refs. 13 and 16 for reviews). However, in our study, the best mRGCPL parameter performed considerably better than cpRNFL or the best dRNFL parameter. The reason for this discrepancy is not entirely clear; it may be due to population differences or other factors. Regardless, although our population may include more glaucomatous individuals with central defects than in other studies, the lack of a large source of bias suggests that a fair number of these individuals do exist and would therefore benefit from better analysis of the macular fdOCT data.

Evaluation of Combined Structure and Function

Combining structure and function yielded an improvement beyond using structural and functional measures independently, in agreement with many of the previous studies combining structure and function to aid in glaucoma detection.^27–41 Although some of these studies have evaluated the benefit of combining structure and function in comparison with simple independent measures, such as the average cpRNFL thickness, here we followed the logic of those studies that tested the combined structure-function method against the best independent measures of structure and function (i.e., the p_cc metric in this study). Additionally, previous studies that have used machine-learning classifiers or a priori models have often neglected to include a simple combination of structure and function to test for the value-added of using a more complex technique to combine structure and function. Here, we compare our best combined structure-function metric (mRGCPL&SAP p_cc) against a simpler model of combining structure and function (fdOCT&SAP p_MT/MD) to provide a more rigorous test for the value-added of our technique. It is important to note that even our “simple” model of combining structure and function involves more than the simple logical rules used in past studies. For instance, if we were to consider an individual glaucomatous if either the SAP p_MD or the mRGCPL p_MT or the dRNFL p_MT were abnormal at a significance level of P ≤ 0.05, then the corresponding AROC score would be 0.785 ± 0.033 (compare with values in Table 2), slightly better than simple metrics using structure or function alone, but considerably worse than even our “baseline” combination of structure and function (fdOCT&SAP p_MT/MD), which merely uses the minimum value of either the SAP p_MD or the mRGCPL p_MT or the dRNFL p_MT to provide a continuous metric.

Many of the previous attempts to combine structure and function used machine-learning approaches,^30–39 including an early study by Caprioli.³⁰ (Here, we include linear discriminant analysis under the umbrella of machine learning.) Two recent studies by Bowd et al.³⁶ and Bizios et al.³⁸ used tdOCT and SAP. Bizios et al.³⁸ found that their artificial neural network approach tested on a moderate glaucomatous population (SAP MD = −11.0 ± 8.2 dB) yielded better discrimination than cpRNFL or SAP MD alone, although not better than using their machine-learning approach on cpRNFL alone. Bowd et al.³⁶ found that their Bayesian machine-learning classifiers using both structure and function, tested on a mild glaucomatous population (SAP MD = −3.1 ± 3.4 dB), performed better than cpRNFL or SAP MD alone and also performed better than the best machine-learning approach on independent structural and functional measures, although the difference between the best functional measure and the combined structure and function approach was not statistically significant. Other studies using machine-learning approaches on data other than OCT have also reported improvements when combining structure and function as opposed to the best independent structural or functional measure.^33,34,37,39 Ultimately, the philosophy behind machine-learning approaches differs fundamentally from the approach used in this study. There is no clear “right answer”; both machine-learning and a priori models involve trade-offs.

Even relatively simple logical rules to combine structure and function have been shown to be useful in previous studies.^27–29 In particular, the study of Shah et al.²⁷ concluded that combining structure and function offered a statistically significant advantage over the best independent structural and functional measures, even though their method of combining structure and function did not require spatial correspondence. The study of Hirashima et al.²⁹ is, to the best of our knowledge, the only previous work combining structure and function to aid in glaucoma detection that uses 2-dimensional fdOCT data; however, when combining structure and function, the authors do not account for spatial correspondence and also use very simple global measures, such as average cpRNFL thickness, average mGCC thickness, and MD.

Two recent studies^40,41 have used more complex a priori models to combine structure and function in glaucoma while taking into account spatial correspondence. Boland and Quigley⁴⁰ created a simple model that relates the probability of abnormality in both confocal scanning laser ophthalmoscopy and SAP data to the probability that these abnormal data points are spatially correspondent, based on an extension of a structure-function spatial map created by Garway-Heath et al.⁴⁹ Although the Boland and Quigley⁴⁰ approach to relating structure and function is elegant, we used a coarser approach for spatial correspondence for two reasons: the Garway-Heath et al.⁴⁹ map in its current form does not fully apply to 2-dimensional fdOCT dRNFL data and the lack of 10-2 SAP data on all subjects prevented precise spatial relationships in the macula. In any case, the Boland and Quigley⁴⁰ model combining structure and function did not perform better than using the MD of SAP alone; however, their study attempted the more difficult task of separating glaucoma patients from glaucoma suspects (rather than from healthy controls).

Another important a priori model, which combines 1-dimensional cpRNFL fdOCT data with SAP, has been presented in a recent study by Medeiros et al.⁴¹ Their work attempts the much more ambitious task of relating fdOCT to SAP by first converting both datasets to estimated ganglion cell counts based on a model by Harwerth et al.⁵⁰ The Medeiros et al.⁴¹ model for combining structure and function performed better than simple global independent measures, such as average cpRNFL thickness and SAP MD, and this difference was statistically significant. However, the authors did not test their model against more complex independent measures of structure and function or against a simple model combining structure and function. Additionally, it is worth noting that the weighting function applied to the combination of structure and function is heavily biased toward the structural measure for mild glaucomatous defects (as defined by the SAP). The relative weighting for the fdOCT-derived estimated ganglion cell counts is 90% when the MD of the 24-2 SAP is −3 dB and 80% when the MD of the 24-2 SAP is −6 dB. Thus, it is not surprising that the performance of the Medeiros et al.⁴¹ combined structure-function metric was equivalent to average cpRNFL thickness for their preperimetric glaucoma group (admittedly a difficult group for glaucoma detection). Although the weighting function of Medeiros et al.⁴¹ makes their combined structure-function metric largely dependent on structural measures for mild glaucomatous damage (as defined by the SAP), in fairness, their metric appears to be aimed more at progression than early glaucoma detection. Indeed, further work by this group has framed this combined structure-function metric in the context of progression.^51,52 Although their combined structure-function metric is limited by the assumptions and validity of the Harwerth et al.⁵⁰ model (as mentioned by Medeiros et al.⁴¹ in their discussion), the conversion of structural and functional measures to estimated ganglion cell counts allows for interesting speculations regarding disease mechanisms in glaucoma.⁵¹

While combining only fdOCT dRNFL and SAP data (data not shown) in this study performed better than using dRNFL or SAP data alone, the best performance was achieved by combining mRGCPL, dRNFL, and SAP data or simply mRGCPL and SAP data. Although it may seem unusual that the dRNFL seems to add little to the combination of mRGCPL and SAP, the lack of 10-2 SAP data probably makes the 24-2 SAP and dRNFL somewhat redundant, whereas the mRGCPL offers complementary information pertaining to macular damage. The dRNFL may also be subject to interindividual variability to a higher degree than the mRGCPL. Because 10-2 SAP is not routinely collected in many clinical settings and is not officially a part of the protocol for the data collected by many important multisite studies, the mRGCPL data may serve as an important indicator of macular damage that might otherwise go unnoticed in glaucoma suspects and patients.

Inclusion and Exclusion Criteria

By not using more stringent inclusion and exclusion criteria at the outset, we allowed for the inclusion of more subtle cases. For instance, we included the fellow eye of glaucoma suspects even if there was no evidence of glaucomatous optic neuropathy or abnormal visual fields in that eye. Our rationale here is similar to the arguments made by Bowd et al.³⁶ in their study combining SAP and tdOCT data using machine-learning classifiers. The MD of the SAP in our glaucomatous group was similar to their study and notably higher than some other studies (e.g., Refs. 33 and 38) combining structure and function. In particular, 87% of the eyes in our glaucomatous group had an MD greater than −6 dB, suggesting “mild” glaucoma according to the Hodapp-Anderson-Parrish classification system.⁵³ An example of an interesting subtle case that would not have been included otherwise can be seen in Figure 6. However, although our population more closely resembles a screening population, the AROC scores we report (e.g., Table 2) are probably lower because our population is not strictly defined. Thus, when assessing the AROC scores in Table 2, it is important to realize that the maximum possible AROC is probably less than 1 in this context.

To illustrate the differences in the AROC scores, as well as to demonstrate the performance of these methods on a more well-defined population, we repeated our analyses on a subpopulation using SAP as part of the inclusion and exclusion criteria (see Table 3 and Fig. 5B). Although the performance of SAP-based metrics is likely to be favorably biased in this subpopulation, it is important to note that the performance of different metrics within a particular modality (i.e., structure or function) will not be affected by such a bias. For example, regarding the mRGCPL or the SAP data, there is no compelling reason to believe that the better performance of the p_cc metric was affected by a bias in how the subpopulation was selected. Ultimately, the lack of a “gold standard” for glaucoma diagnosis means there will be a certain amount of ambiguity in interpreting AROC scores, particularly in studies attempting to combine structure and function, regardless of how the populations are defined.

Future Directions

The methods used here could benefit from a more refined model for spatial correspondence between structural and functional measures. Although a precise local point-to-point multiplication of probabilities between structure and function yielded performance better than structure or function alone (data not shown), the lack of 10-2 SAP data led us to use a simpler method of combining structure and function. Additionally, continuous probability values for the SAP data in this study,⁵⁴ as opposed to the discrete values derived from machine-based normative data, may further enhance the performance of the combined structure-function techniques shown here. Finally, although we used a priori assumptions in this study to derive the ROIs for the fdOCT data, optimization based on our current dataset may yield better performance in future studies with independent datasets.

Conclusions

A combined structure-function metric, taking into consideration spatially correspondent patterns of damage, improved the detection of glaucomatous eyes. Overall, evaluation of the techniques used in this study suggests that the primary sources of value-added stem from the continuous cluster search (the p_cc), the mRGCPL data, and the combination of structure and function.