Abstract
It is generally accepted that oligomers of aggregating proteins play an important role in the onset of neurodegenerative diseases. While in silico aggregation studies of full length amyloidogenic proteins are computationally expensive, the assembly of short protein fragments derived from these proteins with similar aggregating properties has been extensively studied. In the present work molecular dynamics simulations are performed to follow peptide aggregation on the microsecond time scale. By defining aggregation states we identify transition networks, disconnectivity graphs and first passage time distributions to describe the kinetics of the assembly process. This approach unravels differences in the aggregation into hexamers of two peptides with different primary structures. The first is GNNQQNY, a hydrophilic fragment from the prion protein Sup35, and the second is KLVFFAE, a fragment from amyloid β-protein, with a hydrophobic core delimited by two charged amino acids. The assembly of GNNQQNY suggests a mechanism of monomer addition, with a bias towards parallel peptide pairs and a gradual increase in the amount of β-strand content. For KLVFFAE a mechanism involving dimers rather than monomers is revealed, involving a generally higher β-strand content and a transition towards a larger number of antiparallel peptide pairs during the rearrangement of the hexamer. The differences observed for the aggregation of the two peptides suggests the existence of a sequence–aggregation relationship.
Introduction
Amyloid protein aggregation is one of the main factors involved in the onset of several neurodegenerative conditions, including Alzheimer’s, Parkinson’s, and prion diseases. The aberrant assembly of proteins such as amyloid-β (Aβ), α synuclein, and the prion protein into fibrils has been associated with the death of neuronal cells. There is increasing evidence that oligomers, present in the early stages of aggregation, are the neurotoxic species, rather than highly organized fibrils.1-4 The prion protein and Aβ are two examples of amyloidogenic proteins whose early assembly mechanisms have been investigated using both experimental3,5,6 and computational tools.7-10 Two short fragments from these proteins exhibit aggregation behavior and cross-β structures similar to the ones specific to fibrils formed by the full length proteins. One is the GNNQQNY fragment from the N-terminal prion determining region of the yeast protein Sup35 (abbreviated GNN). The second is the KLVFFAE fragment from Aβ (abbreviated KLV). The motivation for studying these shorter fragments of amyloidogenic proteins is the hypothesis that their behavior captures essential features of the original proteins.11 Moreover, these two peptides have very different primary structures: GNN is polar, while KLV has a hydrophobic core. They are therefore likely to exhibit different aggregation pathways, whose elucidation would contribute to a better understanding of the sequence–aggregation relationship.
Current stochastic models that describe the aggregation process12 are mostly applicable to simple cases involving the attachment or detachment of a monomer to a larger aggregate, without any information about the conformational structure. A different method for describing stochastic biological processes involves kinetic transition networks13,14 and disconnectivity graphs15,16 and has already been applied to the study of conformational dynamics of peptides or protein folding17-20 and recently to aggregation.21 In the present work we characterize the assembly of six monomers into one hexamer for GNN and KLV, based on molecular dynamics (MD) simulations, and compare the pathways. Hexamers were chosen because previous experimental22 and theoretical23,24 studies suggest a classical nucleation process for the aggregation of GNN with a critical nucleus of four to six monomers. To obtain a general picture of the complex aggregation process we first derive coarse-grained transition networks (CGTNs) showing the transitions between oligomers of different sizes. In order to provide a more detailed picture of the aggregation process, we introduce so-called aggregation states defined on the basis of certain structural characteristics in addition to oligomer size, and derive kinetic transition networks (KTNs) revealing the population and transitions between these states.13 As these KTNs are rather complex, we apply the max-flow min-cut procedure allowing to remove less important nodes and edges of the KTNs while preserving the maximum flow within the network.17,25-27 The resulting networks, which we denote mincut transition networks (MTNs), provide a concise picture of the aggregation pathway in terms of stable aggregation states and transitions between them. However, they lack kinetic information, which we derive in a next step by describing the free energy landscape of aggregation through disconnectivity graphs (DGs)15,16 using the node and edge data from the MTNs. Finally, we provide information regarding the dynamics of aggregation through first passage time distributions (FPTDs) for reaching the most populated aggregation states. Although both peptides have been previously studied with both coarse-grained23,24,28,29 and all-atom models,14,21,30-32 we believe this is the first comparison of their aggregation behavior using a kinetic description that involves transition networks (TN).
Materials and Methods
MD Simulations
For both GNN and KLV we performed five independent all-atom MD simulations of six peptides inserted in a cubic box with side length 10 nm filled with explicit SPC water,33 resulting in a concentration of about 10 mM. Each simulation was 500 ns long, producing a total of 2.5 μs per sequence. The simulations were performed with the Gromacs 4.5.5 parallel software package34 and the GROMOS96 43A1 force field.35 Hydrogen atoms were treated as virtual interaction sites, permitting an integration time step of 5 fs while maintaining energy conservation.36 The system was maintained at 310 K and 1 bar via velocity rescaling with a stochastic term algorithm37 and the Berendsen barostat,38 respectively. Electrostatic interactions were described using the particle mesh Ewald algorithm39,40 with a cutoff of 0.9 nm. Van der Waals interactions were cutoff at 1.4 nm with a switching distance of 0.9 nm. During each MD simulation, structures were saved every 5 ps, resulting in 500,000 collected snapshots per peptide.
Definition of Aggregation States
The aggregation state is defined as a number with five digits, N1N2N3N4N5, where each digit corresponds to a structural feature or to an oligomeric state. N1 represents the oligomeric size, identified using a cutoff distance of 0.5 nm between any two atoms belonging to different peptides. N2 is the number of peptides connected by at least one hydrogen-bond. Hydrogen-bonds are defined based on distance and angle cutoffs of 0.41 nm and 40°, respectively. N3 and N4 are the number of antiparallel and parallel peptides within the oligomer. Two chains are antiparallel or parallel if they are connected by at least two hydrogen-bonds involving two unique amino acids from each peptide. N5 is the average number of amino acids in β-strand conformation per peptide in the oligomer. An amino acid is defined to be in a β-strand conformation if the dihedral angles ϕ and ψ (in degree) of the backbone are contained in the polygon with vertices (−180, 180), (−180, 126), (−162, 126), (−162, 108), (−144, 108), (−144, 90), (−50, 90), (−50, 180).41
Transition Matrix
To calculate the transition matrix that includes all pairwise transitions between aggregation states we first identified all the aggregation states and the number of transitions between states along the 2.5 μs trajectory using a lag time of 5 ps. Using these states and transitions we built an N×N matrix, where N is the number of states encountered. Each element of the matrix represents the population of a particular transition between two states. After normalizing the rows, each element represents the probability for a particular transition to occur. The transition matrix did not change significantly for longer lag times.
Kinetic Transition Networks
The row normalized transition matrices were converted into KTNs using the software Visone42 and the minimum stress algorithm. In the KTN plots, the nodes represent aggregation states, the area of each node is proportional to the population of the state, and the color of the node indicates the average number of amino acids in the β-strand conformation (N5). The color of network edges corresponds to the value of the transition probability. The CGTNs were constructed using oligomeric states with the thickness of the edges encoding the total number of transitions between pairs of states. Based on KTNs we have derived networks that preserve the maximum flow using the mincut procedure, which we denote as MTNs.17,25-27 In the case of MTNs the thickness of the edges corresponds to the number of transitions and the color of the nodes to the quantity (N3 – N4).
Representative States and Conformations
For each KTN we selected representative aggregation states and illustrate representative conformations in Fig. 2. To select representative states we first sorted by decreasing population and then identified the states with the highest population for each N1 value (or oligomer). For each state we selected a structure that reflects characteristics of the aggregation state. The snapshots were generated with the software package VMD.43
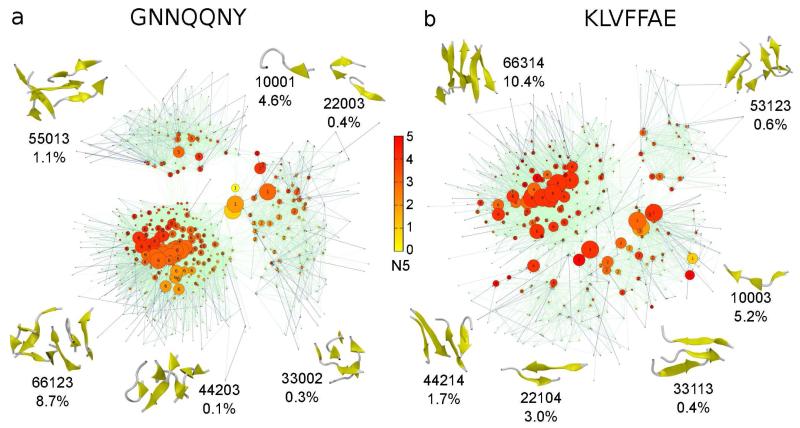
Figure 2.
Kinetic transition networks for GNN (a) and KLV (b). For both peptides the aggregation states N1N2N3N4N5 are shown as nodes connected by edges that represent transition probabilities. The size of each node corresponds to the population and the color corresponds to the average number of β-strand amino acids, N5. The color of the edges reflects the value of the transition probability, from light green for small probabilities to dark blue for high probabilities. For each oligomer size, N1, we illustrate representative conformations corresponding to the aggregation state with the highest population, together with the population of that state in percentage.
Disconnectivity Graphs
The number of times state i was visited during the simulations was used to define the partition function as Zi = Σj nij, where nij is the number of transitions from state j to state i.17,26 The free energy (FE) of state i was derived from Zi as Fi = −kT ln Zi, where k is the Boltzmann constant and T is the temperature. To calculate the FE barrier between two states we performed the following steps: (1) we derived the undirected graph with edge capacities cij ~ (nij + nji)/2, (2) we applied the mincut algorithm to the new undirected network to obtain the new transition capacities c′ij = c′ji, which reflect the maximum flow through the network, (3) we derived the partition function Zij = c′ij (h/kT)(1/ts), where h is the Planck constant, T is 310 K and ts is the sampling time interval of 5 ps, (4) we estimated the FE barriers as Fij ~ − kT ln(Zij).26 Using the FE minima and barriers we constructed FE DGs based on the method developed by Becker and Karplus.15
First Passage Time Distributions
The first passage time is defined as the time interval needed to reach a certain aggregation state along the MD trajectory. For a particular aggregation state, we calculated all the first passage times for each of the five trajectories and then constructed a histogram. FPTDs starting from specific states were calculated by considering only the time intervals originating at positions where the specific states occurred.
Results and discussion
Coarse-grained Transition Networks
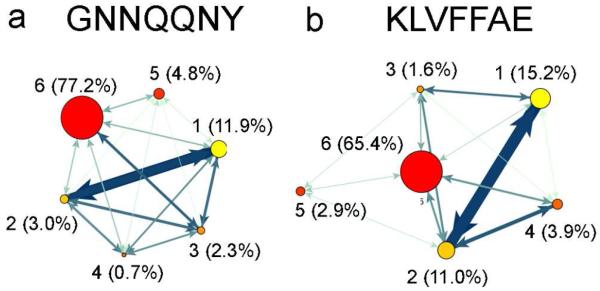
To obtain a general picture of the assembly process we have derived CGTNs that describe the dynamics of the system at the oligomer level (Fig. 1). In the case of GNN (Fig. 1a), hexamers are the dominant oligomers at 310 K, with a population of 77.2%, followed by monomers (11.9%), pentamers (4.8%), dimers (3%), trimers (2.3%), and tetramers (0.7%). For KLV (Fig. 1b), the hexamers are also the most populated oligomeric state (65.4%), followed by monomers (15.2%), dimers (11.0%), tetramers (3.9%), pentamers (2.9%), and trimers (1.6%). The high hexamer population indicates a fast initial assembly of small oligomers into a hexamer that undergoes slower rearrangements. This result may reflect the concentration (10 mM) used in our simulations. Studies using higher concentrations of around 100 mM report a spontaneous collapse into one disordered aggregate.44 The fact that GNN has a larger population of hexamers (77.2%) than KLV(65.4%) indicates faster assembly, which might result from the presence of a tyrosine residue.30
Figure 1.
Coarse grained transition networks for GNN (a) and KLV (b). The oligomeric states are shown as nodes connected by edges that represent the total number of transitions between two oligomeric states. The area of each node corresponds to the population while the color corresponds to the oligomeric state. The color and thickness of the edges changes from light green to dark blue and thin to thick, respectively, and corresponds to changes from fewest to most transitions between oligomeric states.
¿From the number of transitions between oligomeric states, encoded in the thickness of the edges between the nodes, it is clear that the largest number of transitions occurs between monomers and dimers in both systems. An important observation in the case of KLV is the lack of transitions from monomers to pentamers. This result indicates that pentamers are formed mainly through the combination of dimers and trimers. In the case of GNN, monomers contribute to all oligomeric states, suggesting a growth/breakage of the oligomer by the addition/removal of a monomer. This mechanism is supported by recent coarse-grained studies,23,29 which emphasize the role of monomer addition/loss up to oligomers of size 5 or 6 at 300 K. Beyond that size, the main aggregation mechanism involved oligomers rather than monomers. The CGTNs described above indicate significant differences between the aggregation of the two peptides. To obtain a better picture of the assembly process we now consider more detailed kinetic transition networks.
Kinetic Transition Networks
KTNs for GNN and KLV, based on the aggregation state definition (N1N2N3N4N5) from the Materials and Methods section, are shown in Fig. 2a and b, respectively. In both cases there are three distinct interconnected clusters: C1 for states with N1 (oligomer size) values of 1 to 4, C2 for states with N1 = 5, and C3 for N1 = 6. For KLV the clusters are more interconnected than for GNN, which suggests a more dynamic assembly process, with larger oligomers breaking into smaller ones more frequently. The coloring of the nodes is based on the average number of β-strand amino acids per peptide, encoded in N5. This information reveals an overall higher β-strand content in KLV relative to GNN, even for the states with low N1 values, indicating a higher degree of organization during the early assembly stages for KLV. It is important to note the central location of the states with N1 = 1 (e.g. 10001) in the case of GNN, but not for KLV. This result agrees with the CGTNs, where we observed that monomers contribute to all oligomeric states for GNN but not for KLV.
While both C1 clusters include states with different N1 values, the structure for GNN is more compact and has fewer transitions to cluster C3 than for KLV. Representative aggregation states for GNN are 10001 with a population of 4.6%, 22003 (0.4%), 33002 (0.3%), and 44203 (0.1%). Representative conformations for each state are shown in Fig. 2a. They generally have a small number of parallel or antiparallel peptide pairs and an average number of β-strand amino acids below 3. In the case of KLV representative aggregation states from cluster C1 are 10003 (2.5%), 22104 (3.0%), 33113 (0.4%), and 44214 (1.7%). For most of these states the number of parallel and antiparallel peptide pairs is larger than for GNN and the number of antiparallel pairs is higher than the number of parallel peptide pairs. In addition, the higher average number of β-strand amino acids indicates more ordered small oligomers for KLV (Fig. 2b).
The C2 clusters contain only states with N1 = 5, with a larger population for GNN. The representative aggregation states for this cluster are 55013 with a population of 1.1% for GNN and 53123 (0.6%) for KLV. Both states have more parallel pairs than antiparallel, with more pairs in total for KLV (antiparallel:parallel = 1:2) than for GNN (0:1) and thus more β-sheet-like structures. However, GNN has more chains connected by hydrogen-bonds. The most populated cluster for both fragments is C3, containing states with N1 = 6. The most representative aggregation states for this cluster are 66123 (8.7%) for GNN and 66314 (10.4%) for KLV. GNN samples a higher average number of parallel pairs (1:2), while for KLV the states with more antiparallel pairs are more frequent (3:1). In terms of β-strand content cluster C3 shows a gradual transition from low to high for GNN, while KLV has a more uniform distribution of higher β-strand content. State 66314 of KLV has 4 β-strand amino acids on average.
Mincut Transition Networks
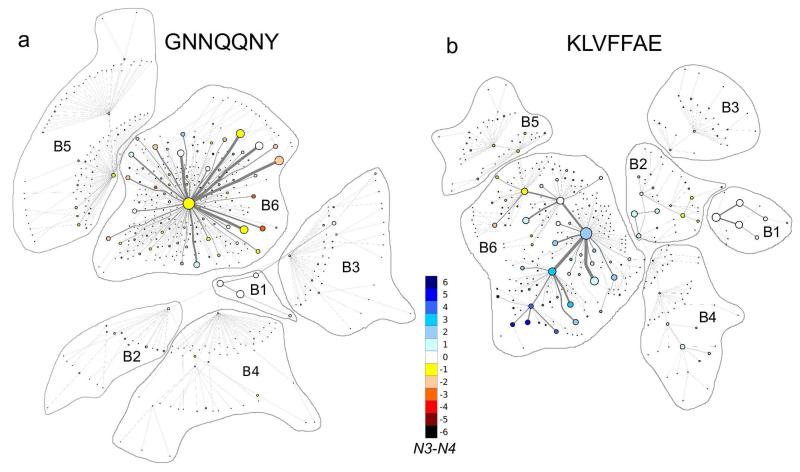
The KTNs described in the previous section provide a detailed picture of the aggregation process. However, the large number of transitions and nodes make it difficult to pinpoint the main pathways that dominate the assembly process. To identify the maximum flow in the transition network we applied the minimum cut method (mincut) and derived MTNs.
The MTNs of the two peptides are shown in Fig. 3, where we identify the states with the same value of N1 as basin Bi, with i = 1, …, 6. For GNN basin B6 has one central node corresponding as state 66123, which is connected radially to the other states. The highly populated states from B6 have an edge of high capacity in direct contact with the central node, and some of them have one to three edges directly connected to less populated nodes. The GNN assemblies from basin B6 have a higher propensity to form parallel pairs, but also contain a significant number of antiparallel pairs. State 66123 is also the one that connects B6 to the other basins. An important observation is that the transition to/from B6 from/to B2, B3 and B4 occurs through B1, specifically through state 10002, which is not the highest populated state within B1. This observation indicates the central role of monomers in the assembly process for GNN.
Figure 3.
Mincut transition networks for GNN (a) and KLV (b). The coloring of the nodes reflects N3 – N4, which indicates the excess number of antiparallel peptide pairs relative to parallel peptide pairs. Edges shown in gray represent the number of transitions returned by the mincut algorithm. Clusters of states with identical values of N1 have been outlined and identified as basin Bi, where i takes the value of N1.
The MTN of KLV is shown in Fig. 3b. The topology of basin B6 is very different from that of GNN. Rather than having one central node surrounded radially by the other nodes, KLV displays several nodes that are at the center of local clusters. One can identify five such nodes interconnected with the central node, corresponding to state 66314. Three of four nodes are among the top ten states with the highest population (Table 1). The difference in antiparallel to parallel pairs (N3 – N4) shows a clear shift from negative to positive values for the five local clusters. This shift corresponds to a gradual transition from more parallel to more antiparallel pairs. Overall, the nodes in basin B6 have a higher propensity for antiparallel pairs. Interestingly, the nodes with more parallel pairs are connected to basin B5 through state 66124, while the the majority of nodes with more antiparallel pairs are closer and connected to basins B1-B4 through state 66314. Basins B1, B3 and B4 are connected to basin B6 through B2 (state 22103), suggesting that dimers play a central role in the pathway to hexamers.
Table 1.
The ten aggregation states with the highest populations for GNNand KLV. For each peptide the aggregation state N1N2N3N4N5 is shown in the left column with the percentage population in the right column
| GNNQQNY | KLVFFAE | ||
|---|---|---|---|
| Aggregation State | Population [%] | Aggregation State | Population [%] |
| 66123 | 8.6 | 66314 | 10.4 |
| 66023 | 6.2 | 10003 | 5.2 |
| 66124 | 5.6 | 66214 | 5.0 |
| 66013 | 5.2 | 66304 | 4.4 |
| 66113 | 4.9 | 66224 | 4.0 |
| 10001 | 4.6 | 10004 | 3.9 |
| 66223 | 3.7 | 10002 | 3.6 |
| 10002 | 3.3 | 66124 | 3.2 |
| 66213 | 2.9 | 66324 | 3.1 |
| 66033 | 2.1 | 22104 | 3.0 |
One major difference between the above networks is the complex nature of basin B6, which suggests distinct paths for evolution of the collapsed hexamer in the two peptides. The distribution of parallel and antiparallel pairs is another characteristic of the two B6 basins. Numerous studies have reported a preference for parallel β-strands in GNN23,29-31 and antiparallel β-strands in KLV,32 in agreement with our findings. The central role of monomers in the assembly of small oligomers into hexamers is also clear from the MTN of GNN, in contrast to the importance of dimers for KLV. A two stage “dock-lock” mechanism32 for monomer addition to preformed structured oligomers was previously proposed for KLV fibril formation. Our results suggest that pathways involving dimers might also be relevant. To explore the role of electrostatic interactions during oligomer formation we identified salt bridges between amino acids K and E from different KLVpeptides. We found one, two and three salt bridges present in the system 23.6%, 4.3% and 0.2% of the simulation time, respectively. Given the fact that we did not observe in-register antiparallel β-sheets as in the KLVFFAE fibrils45 and that the salt bridges are not as abundant as in a computational study of pre-formed KLVFFAE fibrils46 we suggest that salt bridges play a secondary role in the early aggregation of KLVFFAE, i.e., they are not as important as in fibril formation and stability.
While we did not observe actual fibrils stabilized by steric zippers in our simulations, we did find KLVFFAE hexamers resembling β-barrel structures (Fig. 2b, state 66314). A similar type of hexamer conformation has been recently observed in experiments performed by Laganowsky et al. and Liu et al.47,48 when studying the aggregation of segments of the amyloid-forming protein αB crystallin. In these studies they report cylindrical oligomers (cylindrins) formed by six out-of-register β-sheets as early oligomers o pathway towards in-register fibril formation, but on pathway towards less stable out-of-register fibrils. The oligomers reported by Laganowsky et al. were found to be toxic and the β-barrel conformation was suggested as a possible template for toxic amyloidogenic oligomers. The stability of the cylindrins was later studied computationally by Berhanu et al.49 A recent computational study confirmed the existence of β-barrel oligomers containing eight KLVFFAE peptides,50 similar to the hexamers observed in our study. In the case of KLVFFAE the out-of-register arrangement of β-sheets has been observed experimentally and shown to lead to stable nanotubular structures, rather than the classical amyloid fiber with cross-β structure.51 The fact that we don not observe fibrils as in the work of Berhanu et al.46 is probably due to the limited number of peptides used in our study and also to the relatively short simulation time compared to the time necessary for fibril formation, which in vitro occurs within minutes or even hours. Moreover, the hexamers with β-barrel like structure observed in our study are indeed o pathway towards in-register fibrils, and there might be a rather high energy barrier towards the in-register β-sheet fibrils as indicated by Laganowsky et al.47
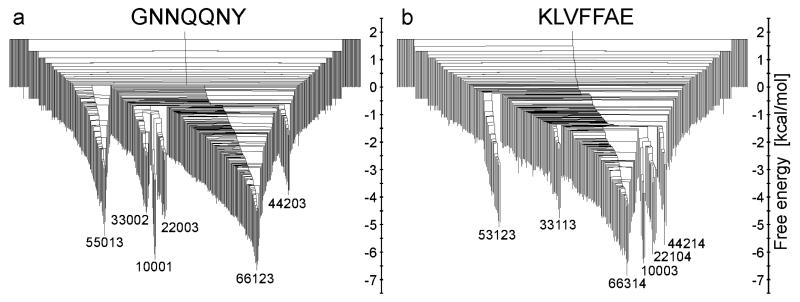
Disconnectivity Graphs
DGs were originally introduced to describe the dynamics of a small peptide15 and were subsequently employed to gain insight into the emergence of observable properties from the underlying potential energy landscape in a wide variety of systems.16 In the present work we have constructed DGs for each peptide based on the method described by Krivov et al.26 (Fig. 4). In Fig. 4a one can identify several free energy minima for GNN with the lowest value at 310 K for state 66123, followed in order of increasing FE by 10001, 55013, 22003, 33002, and 44203. For KLV the state with the lowest FE at 310 K is 66314, followed by states 10003, 22104, 44214, 53123 and 33113. Our DGs indicate a FE barrier for the GNN trimer formation from monomers, or to state 33002 from state 10001, of ~5.4 kcal/mol. This value is slightly higher than the FE barriers (around 3 kcal/mol) between disordered aggregates and in-register mixed parallel/antiparallel aggregates reported by Gsponer et al.30 In the case of dimer formation, or transitions to state 22003 from 10001, the FE barrier is around 5.1 kcal/mol. Barriers of 2 kcal/mol and 3 kcal/mol for GNN dimer formation have been reported previously by Reddy et al.52 and Strodel et al.14 The higher FE barrier observed in our simulations might be due to the fact that the monomers are initially spatially separated in explicit solvent. Overall, GNN has higher barriers for transitions to the most stable aggregation state than KLV in all cases, except for states with N1 = 2 and 4. This is an interesting result in the context of the earlier observation that monomers and dimers are central to the assembly process in GNN and KLV, respectively. In the case of GNN the higher FE barrier for aggregation might be due to the polar nature of the peptide, while for KLV the fact that the FE barrier is higher for dimers and tetramers might be related to the reduced hydrophobic surface compared to monomers.
Figure 4.
Mincut disconnectivity graphs for GNN (a) and KLV (b). The vertical axis is Fi ~ −kT ln Zi and Fij ~ −kT ln Zij for minima and barriers, respectively. Representative aggregation states for the lowest free energy minima are labelled and corresponding structures are shown in Fig. 2.
First Passage Time Distributions
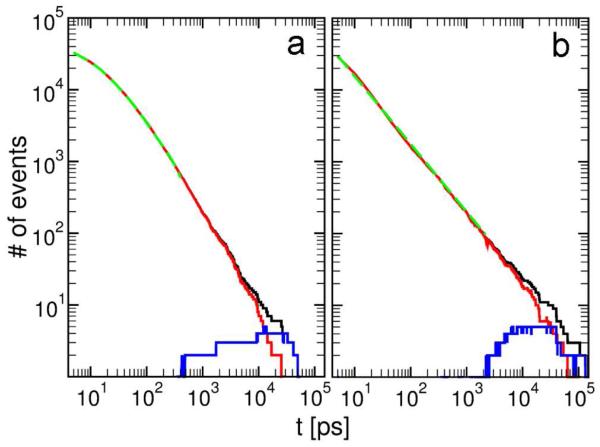
To provide further insight into the underlying dynamics we have calculated FPTDs for the states with the highest populations, i.e. 66123 for GNN and 66314 for KLV (Fig. 5). The distributions differ in two important aspects: for time intervals below 1 ns GNN displays significant curvature, while the FPTD of KLV is practically linear, and for longer times the distribution decays faster for GNN, reaching one event per time interval around 60 ns, compared to 200 ns for KLV. To understand these differences we calculated FPTDs starting from states with N1 = 6 and with N1 < 6. The two curves are shown in red (N1 = 6) and blue (N1 < 6) in Fig. 5. For both peptides, the FPTD is dominated by transitions between states with N1 = 6, equivalent to the rearrangement of the hexamer. The FPTs starting from states with N1 < 6 occur only at lag times of around 400 ps to 50 ns for GNN and 2 ns to 200 ns for KLV, and remain below 4 events per time interval. These time ranges indicate faster assembly of hexamers for GNN than for KLV, confirmed by the larger number of hexameric states observed in the CGTN. A previous study reported a mean first passage time to form an ordered KLV trimer from monomers of 244 ns with extremes between 7 and 600 ns at 300 K at monomer concentrations of 40-70 mM.32 We estimate a FPT from KLV monomers to state 66314 below about 200 ns. The two values are not directly comparable due to different concentrations (10 mM in the present work), different temperatures (310 K here), and the fact that state 66314 contains six peptides and is not as ordered as the trimer studied in reference 32. A trimer in a large bath of oligomers might exhibit a shorter FPT and might not reach a more ordered state due to interactions with other oligomers.
Figure 5.
First passage time distributions for the most populated aggregation states 66123 and 66314 of GNN (a) and KLV (b). The black, red and blue curves correspond to FPTDs from all times, from any time at which a state with N1 = 6 is present, and from any time at which a state with N1 < 6 occurred. The green curves are non-linear fitting functions for the FPTD for the time intervals with N1 = 6 that do not overlap with the blue curve. For (a) the fitting function is y = a1e−t/b1 + a2e−t/b2 + a3e−t/b3 with parameters a1 = 26620, b1 = 8.9 ps, a2 = 15878, b2 = 36.5 ps, a3 = 3854, and b3 = 216 ps. For (b) the fitting function is y = ct−d with parameters c = 137294 and d = 0.94 ps.
Power law behavior for the FPTD is associated with a barrierless process and exponential behavior indicates a barrier for the rate limiting process.18 In Fig. 5 we selected time ranges corresponding to FPTs starting from N1 = 6 and excluding overlapping states with FPTs starting from N1 < 6. For these time ranges, 0 to 400 ps for GNN and 0 to 1600 ps for KLV, we fitted different combinations of exponential (a·e−t/b) and power law (c·t−d) functions. While for GNN the best fit was obtained using a combination of at least three exponentials, a single power law function was sufficient for KLV. Although it is difficult to attribute the three exponential functions for GNN to a particular state or group of states, it is clear that the dynamical processes involved in the rearrangement of the GNN and KLV hexamers are different. To obtain further insight into this difference we analyzed the states that contribute most to the FPTD, starting from N1 = 6.
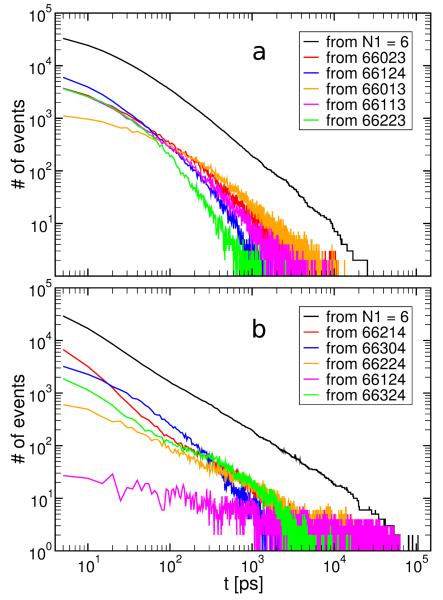
Since the FPTs starting from N1 = 6 dominate the distribution we identified all the contributing states and ranked them according to their populations. For each of the top five states we recalculated the FPTD originating from that state and ending in 66123 for GNN and 66314 for KLV. These distributions are included in Fig. 6 together with the total FPTDs starting from states with N1 = 6. For GNN the FPTD from state 66124 dominates very short time intervals below 100 ps. Since the target state is 66123, this result suggests that the decrease of N5 from four to three or backbone reorganization is the rate limiting process for the hexamer rearrangement at short time intervals. Beyond 100 ps the FPTD from states 66013, 66023 and 66113 makes the largest contribution, indicating the creation/breakage of antiparallel (N3) and parallel (N4) pairs as the rate limiting process. For KLV the five states with the highest populations are of type 66XX4, where X= 0, …, 6. Since the target state is 66314 this observation suggests that the formation and breakage of antiparallel (N3) and parallel (N4) pairs is the rate limiting process in the evolution of the KLV hexamer.
Figure 6.
First passage time distributions for the most populated aggregation states 66123 and 66314 of GNN (a) and KLV (b). The black curve corresponds to FPTDs from any time at which a state with N1 = 6 is present. The colored curves correspond to FPTDs started from specific states. The specific states are the top five with the highest population that contribute most to the distribution from the black curves and are arranged in order of decreasing population from top to bottom.
Conclusions
In this work we have highlighted differences between the aggregation pathways of two peptides with alternative amino acid sequences. While the two fragments might reflect the aggregation behavior of the full proteins, the relation between sequence and assembly mechanism is also of general interest. The early aggregation process of the two protein fragments from a large number of monomers has been studied before in silico, mostly using coarse-grained methods.23,24,28,29 More detailed all-atom studies have focused on the assembly of two or three monomers,14,21,30,32,52,53 the addition of monomers to a preformed oligomer,32,54,55 or the stability of preordered fibrilar structures.31,56,57 Here we investigated the aggregation of six monomers using all-atom MD simulations in explicit solvent.
We have considered both coarse-grained and more detailed kinetic transition networks, which identify monomers as the most important species in the aggregation of GNN. The kinetic transition networks indicate a higher β-strand content for all KLV assemblies compared to GNN, due to the hydrophobic residues, while in the case of the GNN hexamer a gradual transition from low to high β-strand content is observed. Mincut transition networks reveal a radial distribution of aggregation states of GNN for hexamer rearrangements dominated by parallel peptide pairs, and a modular distribution in the case of KLV, with a gradual increase in the relative number of antiparallel to parallel peptide pairs. Disconnectivity graphs reveal higher FE barriers for hexamer formation from monomers, trimers and pentamers of GNN compared to KLV, and from dimers and tetramers of KLV compared to GNN. This result is probably due to the hydrophilic/hydrophobic nature of the two peptides and emphasizes the importance of the stability of monomers and dimers for the aggregation of GNN and KLV, respectively. The first passage time distributions indicate an assembly process dominated by the rearrangement of the hexamer for both peptides, with faster aggregation for GNN, perhaps due to the presence of the tyrosine residue.
We find that monomers play a key role in the aggregation of GNN, consistent with previous studies indicating that the main pathway for the prion protein Sup35 propagation is monomer addition.58 Moreover, the reduced β-strand content in the intermediate oligomers of GNN observed in our study agrees with a previous observation that oligomers of Sup35 lack β-strand structure before being incorporated into fibrils.59 For KLV the observation that the dimers play an important role in aggregation process is consistent with the contribution of dimers and hexamers to aggregation of Aβ protein (1-42).6,7 Furthermore, the high β-strand content of the KLV oligomers in our study is consistent with a higher β-strand propensity in Aβ protein oligomers.7 The antiparallel nature of the fragment KLV, even though in contrast to the in-register parallel fibrils formed by the full-length Aβ protein,60 might play an important role in unstructured toxic oligomers that most probably lack the in-register β-sheet structure.61,62
In conclusion, our study highlights key differences in the assembly process of two aggregation-prone peptides with contrasting amino acid sequences, as well as connections to the aggregation of the corresponding full-length proteins. Furthermore, the present study is proof of concept that our method introduced here allows a concise description of the thermodynamics and kinetics of protein aggregation. In future studies it will be applied to more biologically relevant peptides, such as full-length Aβ, for which the results obtained for KLV will be of great value for understaning the aggregation of Aβ. Finally, our newly introduced method reveals for the first time in a one-to-one comparsion of KLV and GNN their different aggregation pathways, highlighting the importance of sequence for the aggregation mechanism.
Acknowledgement
B.B. and B.S. gratefully acknowledge the Jülich Supercomputing Centre for the computer time made available through grants JICS61 and JICS62. D.J.W. gratefully acknowledges financial support from the EPSRC and the ERC. We also thank Prof. Gerhard Stock for fruitful discussions.
References
- (1).Hardy J, Selkoe DJ. Science. 2002;297:353–356. doi: 10.1126/science.1072994. [DOI] [PubMed] [Google Scholar]
- (2).Kirkitadze MD, Bitan G, Teplow DB. J. Neurosci. Res. 2002;69:567–577. doi: 10.1002/jnr.10328. [DOI] [PubMed] [Google Scholar]
- (3).Silveira JR, Raymond GJ, Hughson AG, Race RE, Sim VL, Hayes SF, Caughey B. Nature. 2005;437:257–261. doi: 10.1038/nature03989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Haass C, Selkoe DJ. Nat. Rev. Mol. Cell. Biol. 2007;8:101–112. doi: 10.1038/nrm2101. [DOI] [PubMed] [Google Scholar]
- (5).Klein WL, Stine WB, Teplow DB. Neurobiol. Aging. 2004;25:569–580. doi: 10.1016/j.neurobiolaging.2004.02.010. [DOI] [PubMed] [Google Scholar]
- (6).Bitan G, Kirkitadze MD, Lomakin A, Vollers SS, Benedek GB, Teplow DB. Proc. Natl. Acad. Sci. 2003;100:330–335. doi: 10.1073/pnas.222681699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Urbanc B, Betnel M, Cruz L, Bitan G, Teplow DB. J. Am. Chem. Soc. 2010;132:4266–4280. doi: 10.1021/ja9096303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Barz B, Urbanc B. PLoS ONE. 2012;7:e34345. doi: 10.1371/journal.pone.0034345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Melquiond A, Dong X, Mousseau N, Derreumaux P. Curr. Alzheimer. Res. 2008;5:244–250. doi: 10.2174/156720508784533330. [DOI] [PubMed] [Google Scholar]
- (10).Sekijima M, Motono C, Yamasaki S, Kaneko K, Akiyama Y. Biophys. J. 2003;85:1176–1185. doi: 10.1016/S0006-3495(03)74553-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Balbirnie M, Grothe R, Eisenberg DS. Proc. Natl. Acad. Sci. 2001;98:2375–2380. doi: 10.1073/pnas.041617698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Yvinec R, D’Orsogna MR, Chou T. J. Chem. Phys. 2012;137:244107. doi: 10.1063/1.4772598. [DOI] [PubMed] [Google Scholar]
- (13).Wales DJ. Curr. Opin. Struc. Biol. 2010;20:3–10. doi: 10.1016/j.sbi.2009.12.011. [DOI] [PubMed] [Google Scholar]
- (14).Strodel B, Whittleston CS, Wales DJ. J. Am. Chem. Soc. 2007;129:16005–16014. doi: 10.1021/ja075346p. [DOI] [PubMed] [Google Scholar]
- (15).Becker OM, Karplus M. J. Chem. Phys. 1997;106:1495–1517. [Google Scholar]
- (16).Wales DJ, Miller MA, Walsh TR. Nature. 1998;394:758–760. [Google Scholar]
- (17).Krivov SV, Karplus M. Proc. Natl. Acad. Sci. 2004;101:14766–14770. doi: 10.1073/pnas.0406234101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Rao F, Karplus M. Proc. Natl. Acad. Sci. 2010;107:9152–9157. doi: 10.1073/pnas.0915087107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Baba A, Komatsuzaki T. Proc. Natl. Acad. Sci. 2007;104:19297–19302. doi: 10.1073/pnas.0704167104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Gfeller D, Rios PDL, Caflisch A, Rao F. Proc. Natl. Acad. Sci. 2007;104:1817–1822. doi: 10.1073/pnas.0608099104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Riccardi L, Nguyen PH, Stock G. J. Chem. Theory Comput. 2012;8:1471–1479. doi: 10.1021/ct200911w. [DOI] [PubMed] [Google Scholar]
- (22).Nelson R, Sawaya MR, Balbirnie M, Madsen A, Riekel C, Grothe R, Eisenberg D. Nature. 2005;435:773–778. doi: 10.1038/nature03680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Nasica-Labouze J, Mousseau N. PLoS Comput. Biol. 2012;8:e1002782. doi: 10.1371/journal.pcbi.1002782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Nasica-Labouze J, Meli M, Derreumaux P, Colombo G, Mousseau N. PLoS Comput. Biol. 2011;7:e1002051. doi: 10.1371/journal.pcbi.1002051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Ford LR, Fulkerson DR. Canad. J. Math. 1956;8:399–404. [Google Scholar]
- (26).Krivov SV, Karplus M. J. Chem. Phys. 2002;117:10894–10903. [Google Scholar]
- (27).Gomory RE, Hu TC. J. Soc. Ind. Appl. Math. 1961;9:551–570. [Google Scholar]
- (28).Cheon M, Chang I, Hall CK. Biophys. J. 2011;101:2493–2501. doi: 10.1016/j.bpj.2011.08.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Osborne KL, Bachmann M, Strodel B. Proteins. 2013;81:1141–1155. doi: 10.1002/prot.24263. [DOI] [PubMed] [Google Scholar]
- (30).Gsponer J, Haberthr U, Caflisch A. Proc. Natl. Acad. Sci. 2003;100:5154–5159. doi: 10.1073/pnas.0835307100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Vitagliano L, Esposito L, Pedone C, De Simone A. Biochem. Biophys. Res. Commun. 2008;377:1036–1041. doi: 10.1016/j.bbrc.2008.10.039. [DOI] [PubMed] [Google Scholar]
- (32).Nguyen PH, Li MS, Stock G, Straub JE, Thirumalai D. Proc. Natl. Acad. Sci. 2007;104:111–116. doi: 10.1073/pnas.0607440104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Berendsen HJC, Postma JPM, Gunsteren W. F. v., Hermans J. In: Pullman B, editor. Intermolecular Forces; The Jerusalem Symposia on Quantum Chemistry and Biochemistry 14; Springer Netherlands. 1981.pp. 331–342. [Google Scholar]
- (34).Hess B, Kutzner C, van der Spoel D, Lindahl E. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- (35).Scott WRP, Hnenberger PH, Tironi IG, Mark AE, Billeter SR, Fennen J, Torda AE, Huber T, Krger P, van Gunsteren WF. J. Phys. Chem. A. 1999;103:3596–3607. [Google Scholar]
- (36).Feenstra KA, Hess B, Berendsen HJC. J. Comp. Chem. 1999;20:786–798. doi: 10.1002/(SICI)1096-987X(199906)20:8<786::AID-JCC5>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- (37).Bussi G, Donadio D, Parrinello M. J. Chem. Phys. 2007;126:014101–014101-7. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- (38).Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- (39).Darden T, York D, Pedersen L. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- (40).Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- (41).Klimov DK, Thirumalai D. Structure. 2003;11:295–307. doi: 10.1016/s0969-2126(03)00031-5. [DOI] [PubMed] [Google Scholar]
- (42).Brandes U, Wagner D. Visone Analysis and Visualization of Social Networks. GRAPH DRAWING SOFTWARE. 2003:321–340. [Google Scholar]
- (43).Humphrey W, Dalke A, Schulten K. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- (44).Baftizadeh F, Pietrucci F, Biarns X, Laio A. Phys. Rev. Lett. 2013;110:168103. doi: 10.1103/PhysRevLett.110.168103. [DOI] [PubMed] [Google Scholar]
- (45).Colletier J-P, Laganowsky A, Landau M, Zhao M, Soriaga AB, Goldschmidt L, Flot D, Cascio D, Sawaya MR, Eisenberg D. Proc. Natl. Acad. Sci. 2011;108:16938–16943. doi: 10.1073/pnas.1112600108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Berhanu WM, Hansmann UHE. Prot. Sci. 2012;21:1837–1848. doi: 10.1002/pro.2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Laganowsky A, Liu C, Sawaya MR, Whitelegge JP, Park J, Zhao M, Pensalfini A, Soriaga AB, Landau M, Teng PK, Cascio D, Glabe C, Eisenberg D. Science. 2012;335:1228–1231. doi: 10.1126/science.1213151. WOS:000301225100046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Liu C, Zhao M, Jiang L, Cheng P-N, Park J, Sawaya MR, Pensalfini A, Gou D, Berk AJ, Glabe CG, Nowick J, Eisenberg D. Proc. Natl. Acad. Sci. 2012;109:20913–20918. doi: 10.1073/pnas.1218792109. PMID: 23213214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Berhanu WM, Hansmann UHE. Proteins. 2013;81:1542–1555. doi: 10.1002/prot.24302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Xie L, Luo Y, Wei G. J. Phys. Chem. B. 2013;117:10149–10160. doi: 10.1021/jp405869a. [DOI] [PubMed] [Google Scholar]
- (51).Mehta AK, Lu K, Childers WS, Liang Y, Dublin SN, Dong J, Snyder JP, Pingali SV, Thiyagarajan P, Lynn DG. J. Am. Chem. Soc. 2008;130:9829–9835. doi: 10.1021/ja801511n. [DOI] [PubMed] [Google Scholar]
- (52).Reddy AS, Chopra M, de Pablo JJ. Biophys. J. 2010;98:1038–1045. doi: 10.1016/j.bpj.2009.10.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Hwang W, Zhang S, Kamm RD, Karplus M. Proc. Natl. Acad. Sci. 2004;101:12916–12921. doi: 10.1073/pnas.0402634101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Meli M, Morra G, Colombo G. Biophys. J. 2008;94:4414–4426. doi: 10.1529/biophysj.107.121061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Zhang Z, Chen H, Bai H, Lai L. Biophys J. 2007;93:1484–1492. doi: 10.1529/biophysj.106.100537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Berryman JT, Radford SE, Harris SA. Biophys. J. 2009;97:1–11. doi: 10.1016/j.bpj.2009.03.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Park J, Kahng B, Hwang W. PLoS Comput. Biol. 2009;5 doi: 10.1371/journal.pcbi.1000492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Collins SR, Douglass A, Vale RD, Weissman JS. PLoS Biol. 2004;2:e321. doi: 10.1371/journal.pbio.0020321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Narayanan S, Walter S, Reif B. Chem. Bio. Chem. 2006;7:757–765. doi: 10.1002/cbic.200500382. [DOI] [PubMed] [Google Scholar]
- (60).Petkova AT, Leapman RD, Guo Z, Yau W-M, Mattson MP, Tycko R. Science. 2005;307:262–265. doi: 10.1126/science.1105850. PMID: 15653506. [DOI] [PubMed] [Google Scholar]
- (61).Bernstein SL, Dupuis NF, Lazo ND, Wyttenbach T, Condron MM, Bitan G, Teplow DB, Shea J-E, Ruotolo BT, Robinson CV, Bowers MT. Nat. Chem. 2009;1:326–331. doi: 10.1038/nchem.247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Ahmed M, Davis J, Aucoin D, Sato T, Ahuja S, Aimoto S, Elliott JI, Van Nostrand WE, Smith SO. Nat. Struct. Mol. Biol. 2010;17:561–567. doi: 10.1038/nsmb.1799. [DOI] [PMC free article] [PubMed] [Google Scholar]