A Functional Model of Cortical Gyri and Sulci

Abstract

Diffusion tensor imaging (DTI) and high angular resolution diffusion imaging (HARDI) have been broadly used in the neuroimaging field to investigate the macro-scale fiber connection patterns in the cerebral cortex. Our recent analyses of DTI and HARDI data demonstrated that gyri are connected by much denser streamline fibers than sulci. Inspired by this finding and motivated by the fact that DTI-derived fibers provide the structural substrates for functional connectivity, we hypothesize that gyri are global functional connection centers and sulci are local functional units. To test this functional model of gyri and sulci, we examined the structural and functional connectivity among the landmarks on the selected gyral/sulcal areas in the frontal/parietal lobe and in the whole cerebral cortex via multimodal DTI and resting state fMRI (R-fMRI) datasets. Our results demonstrate that functional connectivity is strong among gyri, weak among sulci, and moderate between gyri and sulci. These results suggest that gyri are functional connection centers that exchange information among remote structurally-connected gyri and neighboring sulci, while sulci communicate directly with their neighboring gyri and indirectly with other cortical regions through gyri. This functional model of gyri and sulci has been supported by a series of experiments, and provides novel perspectives on the functional architecture of the cerebral cortex.

1. Introduction

Due to the complexity and variability of the structure and function of the cerebral cortex (e.g. Rakic 1988; Scannell 1997; Kandel et al. 2000; Passingham et al. 2002; Rettmann et al. 2002; Zilles et al. 2009; Liu 2011), studying the functional mechanisms of the human brain has been very challenging. Consequently, the functional working mechanisms of the human brain and their structural underpinnings remain largely unknown. Despite significant achievements in cortical gyri/sulci segmentation/parcellation from structural MRI images in the past few decades (e.g. Thirion 1996; Fischl et al. 1999; Lohmann et al. 2000; Rettmann et al. 2002; Shi et al. 2008; Li et al. 2009; Li et al. 2010a), the structural connection patterns and the functional roles of gyri and sulci still remain to be elucidated. Thanks to recent advancements of modern in-vivo multimodal neuroimaging techniques, in particular, diffusion tensor imaging (DTI) (e.g. Basser and Pierpaoli 1996; Mori 2006) and functional magnetic resonance imaging (fMRI) (e.g. Fox et al. 2007; Logothetis et al. 2008), we are now able to quantitatively measure the brain’s macro-scale fiber wiring diagrams and functional activities with decent spatial and temporal resolutions (e.g. Honey et al. 2009; Stephan et al. 2009; Zhang et al. 2011; Zhu et al. 2011; Li et al. 2012). The multimodal DTI/fMRI data offers unparalleled opportunities to investigating the structural architectures and functional mechanisms of the human brain (e.g. Vincent et al. 2007; Rilling et al. 2008; Bullmore et al. 2009; Stephan et al. 2009; Zhang et al. 2011; Zhu et al. 2011; Zhu et al. 2012). Particularly, the joint representation and modeling approach of multimodal DTI/fMRI neuroimaging data has demonstrated its advantages in elucidating the structural brain architectures and possible functional mechanisms (e.g. Honey et al. 2009; Stephan et al. 2009; Bullmore et al. 2009; Zhang et al. 2011; Zhu et al. 2011; Li et al. 2012; Zhu et al. 2012).

Along the direction of using a joint representation and modeling approach, our macro-scale neuroimaging and micro-scale bioimaging studies recently revealed an interesting finding: diffusion imaging derived streamline fiber terminations mainly concentrate on gyri (Nie et al. 2012; Chen et al. 2012). That is, a dominant percentage of DTI-derived fibers are connected to gyral regions, rather than sulcal regions. This finding has been replicated in DTI and HARDI data (Nie et al. 2012) of human, chimpanzee, and macaque brains (Nie et al. 2012; Chen et al. 2012). Furthermore, a joint representation of cortical gyral folding and streamline fiber connection patterns was applied to the analyses of a number of primate/human brains. The experimental results consistently suggested that gyral regions are connected by much denser DTI-derived fiber tracts than sulcal regions in the whole cerebral cortex in all brains we studied (Nie et al. 2012; Chen et al. 2012), suggesting a common principle of structural brain architecture: gyri are structural connection centers of the cerebral cortex.

However, the abovementioned studies (Nie et al. 2012; Chen et al. 2012) only revealed the structural connection patterns in cortical gyri and sulci, while the functional implications of these findings remain unclear. As a follow-up study, in this paper, we hypothesize and examine a functional mechanism of the cerebral cortex: gyri are global functional connection centers and sulci are local functional units. Specifically, the hypothesized functional model of cortical gyri and sulci is illustrated in Fig. 1. The main idea here is that gyral regions are the functional connection centers that exchange information between distant structurally-connected gyral regions via dense fibers (black curves in the gray ribbon in Fig. 1), while sulcal regions communicate directly with their neighboring gyri through inter-column cortico-cortical fibers (yellow curves in Fig. 1, Kandel et al. 2000; Ghosh et al., 1988; Keller and Asanuma, 1993; Mountcastle 1997; Broman and Fletcher, 1999; Thomson et al. 2007) and communicate indirectly with remote cortical regions via the gyri and their dense fiber connections. It should be noted that the local inter-column cortico-cortical fibers cannot be imaged and revealed by the in-vivo DTI techniques used in this work (Mori 2006; Nie et al. 2012; Chen et al. 2012), but they do play important roles in inter-column neural communications (Kandel et al. 2000; Ghosh et al. 1988; Keller and Asanuma, 1993; Mountcastle 1997; Broman and Fletcher, 1999; Thomson et al. 2007).

Figure 1.

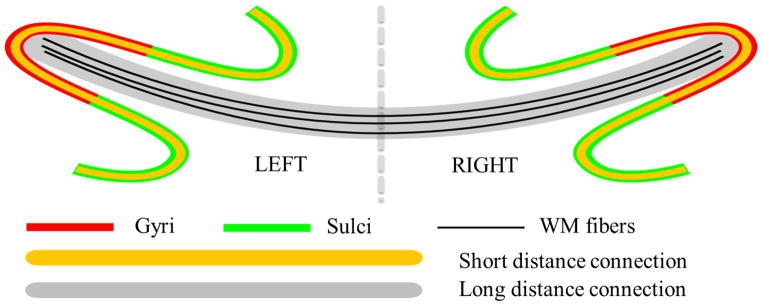
Illustration of the proposed functional model of cortical gyri and sulci. Gyri serve as the global functional connection centers that receive/send information between distant structurally-connected cortical regions via fibers (black curves in gray ribbon). Sulci directly exchange information with their neighboring gyri through inter-column cortico-cortical fibers (yellow curves) and indirectly communicate with remote cortical regions via gyri that are connected by dense fibers.

In order to test the above hypothesized functional model of cortical gyri and sulci, we qualitatively and quantitatively analyzed two independent multimodal DTI/R-fMRI datasets. First, as a test bed example to demonstrate the experiment methodologies and analysis approaches, we labeled the pre-central gyrus (PCG), post-central gyrus (POG), central sulcus (CS), and post-central sulcus (PCS) on both of the left and right hemispheres, and examined their structural and functional connectivity based on multimodal DTI/R-fMRI data. Our rationale is that the PCG, POG, CS and PCS include the primary motor and primary somatosensory systems and are known to possess structural and functional connections (e.g. Miller 1988; Asanuma 1989; Kandel et al. 2000). Thus, this well-characterized sub-system of the cerebral cortex can serve in this paper as a test-bed to investigate the functional working mechanisms of cortical gyri and sulci and to demonstrate our analysis approaches. Second, we conducted a whole cortex analysis, in which we manually labeled 555 cortical landmarks on 68 major cortical gyri/sulci of each subject. Then, the structural and functional connectivity patterns among these large-scale landmarks in the whole cerebral cortex are examined and quantified. Furthermore, the whole-cortex functional connectivity to the landmarks on eight selected gyri/sulci (PCG, POG, CS and PCS on both hemispheres) are also measured and examined. These experimental results from two independent multimodal DTI/R-fMRI datasets have consistently demonstrated the following finding: functional connectivity is strong among gyri, weak among sulci, and moderate between gyri and sulci. These results thus support our hypothesized functional model of cortical gyri and sulci: gyri serve as the global functional connection centers, while sulci function as the local functional units. The remaining three sections will provide details on data acquisition and computational methods, experimental results and their interpretation, as well as discussions and conclusions.

2. Materials and Methods

2.1. Data acquisition and preprocessing

Dataset 1

Eleven healthy volunteers were scanned in a GE 3T Signa MRI system (GE Healthcare, Milwaukee, WI) using an 8-channel head coil at the Bioimaging Research Center (BIRC) of the University of Georgia (UGA) under IRB approval. The experiments were undertaken with the understanding and written consent of each subject. DTI data was acquired using the spatial resolution 2 mm × 2 mm × 2 mm; parameters are TR 15.5s and TE min-full, b-value=1000 with 30 DWI gradient directions, and 3 B0 volumes were acquired. R-fMRI data was acquired using dimensionality 128×128×60×100, spatial resolution 2 mm × 2 mm × 2 mm, TR 5s, TE 25 ms, and flip angle 90 degrees (Li et al. 2012). The subjects kept their eyes closed and rested during the scans. All DTI and R-fMRI scans were aligned to the AC-PC line. For the DTI data, pre-processing includes brain skull removal, motion correction, and eddy current correction (Li et al. 2012). Fiber tracts were generated from the DTI data by using MedINRIA (http://www-sop.inria.fr/asclepios/software/MedINRIA/). Brain tissue segmentation was also performed on DTI data via the approaches in Liu et al. 2007. Then the GM/WM cortical surfaces were reconstructed using the methods in Liu et al. 2008. Pre-processing of the R-fMRI data includes brain skull removal, motion correction, spatial smoothing, temporal pre-whitening, slice time correction, global drift removal, and band pass filtering (0.01 Hz to 0.1 Hz) (Li et al. 2012).

Dataset 2

The second multimodal DTI/R-fMRI dataset includes eight healthy brains from the publicly available NA-MIC dataset released at http://hdl.handle.net/1926/1687. The multimodal DTI/R-fMRI imaging parameters are as follows. Both DTI and R-fMRI scans were acquired on a 3 Tesla GE system using echo planar imaging sequences. An eight-channel coil was used to perform parallel imaging using ASSET (Array Spatial Sensitivity Encoding Techniques, GE) with a SENSE-factor (speed-up) of 2. The DTI parameters are: 51 directions with b=900, 8 baseline scans with b=0, TR 17000 ms, TE 78 ms, FOV 24 cm, 144×144 encoding steps, and 1.7 mm slice thickness. Totally, 85 axial slices parallel to the AC-PC line covering the whole brain were acquired. The R-fMRI scan is 10 minutes long, and contains 200 repetitions of a high resolution EPI scan. The parameters are: 96 × 96 in plane, 3 mm thickness, TR=3000 ms, TE=30, 39 slices, and ASSET. During R-fMRI scans, the subjects kept their eyes closed and rested. Pre-processing of this DTI/R-fMRI dataset is similar to that of the first dataset (Li et al. 2012). This second dataset is used as an independent dataset to replicate the findings from the first dataset.

Dataset 3

The HARDI dataset was obtained in our prior studies in Nie et al., 2012. Specifically, diffusion gradients were applied in 120 non-collinear directions with diffusion weighting b = 2000 s/mm². The imaging matrix was 128 × 128 with a rectangular FOV of 256 × 256 mm². 80 contiguous slices with a slice thickness of 2 mm covered the whole brain. The software package MEDINRIA was used (q-ball model is adopted) for pre-processing and analysis of this HARDI dataset. Gray matter/white matter tissue segmentation and the GM/WM cortical surface were generated via the methods in Nie et al., 2012.

2.2. Labeling landmarks on cortical gyri and sulci

Cortical segmentation of gyri and sulci based on structural MRI images has been extensively studied in the neuroimage analysis literature (e.g. Thirion 1996; Fischl et al. 1999; Lohmann et al. 2000; Rettmann et al. 2002; Shi et al. 2008; Li et al. 2009; Li et al. 2010a), and a variety of algorithms and software tools are available. In this paper, however, we used the cortical surfaces reconstructed from DTI images to reduce the misalignment between fMRI images and structural images due to the geometric distortions that are commonly expected in EPI sequences (e.g. Andersson et al. 2003; Liu et al. 2007; Li et al. 2012; Nie et al. 2012). The reconstructed surfaces, however, are of lower quality because of the lower resolution of DTI data (2 mm isotropic) in comparison with structural T1-weighted MRI images (1 mm isotropic). Another reason is that the susceptibility artifacts and distortions of EPI data are not present in T1-weighted MRI data. The automatic methods might not be able to robustly extract gyral/sulcal patches. To ensure good quality of landmark labeling, we used visual inspection to interactively determine the gyral and sulcal surface patches with the open-source ParaView software (http://www.paraview.org/). Then, a series of structural landmarks (the number ranges from five to ten) were placed on those identified gyri and sulci, as shown in Figs. 2a–2b as examples.

Figure 2.

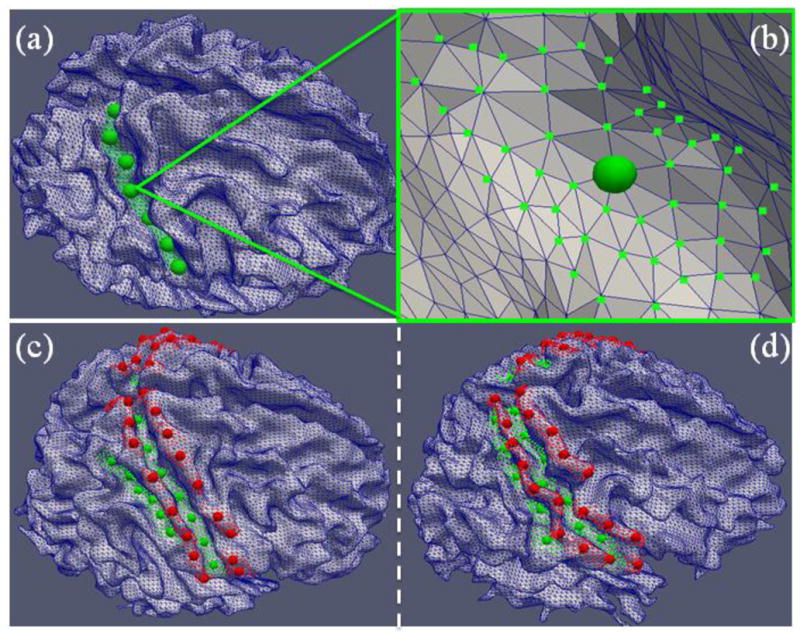
(a) As an example, the initial landmarks (green bubbles) were selected manually on the central sulcus for a roughly uniform distribution. (b) For each initial landmark in (a), the neighboring vertices in the range of 3-rings, as shown by the green dots, will be randomly chosen by algorithms as additional sampling points. (c)–(d) Placements of landmarks on two subjects. Red and green bubbles represent the initial landmarks on gyri and sulci, respectively. Other algorithm-generated sample landmarks are shown in small red/green dots.

It should be noted that at the current stage, there are no structural and/or functional correspondences between the landmarks (highlighted by the red and green bubbles in Figure 2) in different subjects due to the lack of mature algorithms or tools (as far as we know) that can reliably achieve those correspondences. Thus, the structural and functional correspondences across different brains have to be established at the gyrus/sulcus level, instead of the landmark level. As a consequence, the proposed functional mechanism is at the level of cortical gyri and sulci as well. Due to this lack of correspondences of cortical landmarks across different brains, examining the functional connectivity of cortical gyri/sulci based solely on the manually extracted cortical landmarks could potentially be biased. That is, the manually placed landmarks (ranging from 5 to 10 per cortical gyral/sulcal region in this paper) and their representative fMRI time series might not be sufficient to represent the functional activities of a whole gyrus or sulcus. In addition, due to the variability, nonlinearity, and inhomogeneity of the cerebral cortex, a slightly displaced landmark, even by only a few surface vertices, could have quite different structural and/or functional connectivity profiles, as demonstrated in Zhu et al. 2011, and Li et al. 2012. Therefore, in order to reduce the potential bias and to ensure sufficient statistical power, we algorithmically generated additional 100 different sets of sample landmarks for each subject based on the manually-labeled landmarks, as illustrated in Figs. 2a–2b. Specifically, this procedure serves as a repeated uniform sampler on the three-ring surface mesh neighborhoods in terms of graph connectivity of the original manually-labeled landmarks. In each repetition, the procedure randomly picks one vertex within the three-ring surface mesh neighborhood of each landmark with equal probability. The newly selected vertices form a new set of landmarks with the same number of elements as the original manually-labeled landmarks, as represented by the red and green dots in Figs. 2c–2d. From these figures, it can be seen that the sampled landmarks/points constitute a dense coverage of the whole gyrus/sulcus. Even if some of the manually-labeled landmarks were misplaced, the above sampling procedure can substantially reduce the potential bias by including many more additional neighboring sampled landmarks and ensures the statistical power. These sampled landmarks were then used to localize the R-fMRI time series under structural guidance, as detailed in Li et al. 2012. To increase signal-to-noise ratio, each sampled landmark is represented by the average of R-fMRI time series within a one-ring surface mesh neighborhood. Additional details about the methods for landmark labeling are provided in Supplemental Methods. The numbers of labeled landmarks in the gyri/sulci in two independent datasets are provided in Supplemental Table 1.

2.3. Joint multimodal representation methodology

Our previous studies (Nie et al. 2012; Chen et al. 2012) have shown that DTI-derived fiber connections closely follow the gyral folding patterns. This observation has been replicated in all of the DTI datasets of human, chimpanzee, and macaque brains we analyzed (Nie et al. 2012; Chen et al. 2012). Therefore, for each gyral or sulcal landmark defined in Fig. 2, the emanating fibers connected to the landmark in consideration can be readily extracted from the results of whole-brain streamline tractography via a similar method detailed elsewhere (Zhu et al. 2011, Li et al. 2012; Zhu et al. 2012). In addition, the R-fMRI signals can also be extracted for each vertex within the neighborhood of the landmark in consideration, and then averaged to represent the functional activity of that landmark (Li et al. 2012). As a result, the structural fiber connections and R-fMRI signals for each gyral and sulcal landmark are co-localized on and jointly represented by the same cortical surface patch. This joint representation of cortical shape, structural connection, and functional activity effectively takes the advantage of the fact that multimodal DTI and R-fMRI data are in the same DTI space and exhibit much less geometric misalignment (Li et al. 2012). That is, the geometric distortions in EPI (echo planar imaging)-based DTI and R-fMRI tend to be similar (Li et al. 2012), which substantially reduces the misalignment between traditionally used structural MRI and DTI/fMRI images (Liu et al. 2007; Nie et al. 2012; Chen et al. 2012). Additionally, this joint multimodal representation methodology enables and facilitates simultaneous modeling of structural and functional connectivity of cortical landmarks (in the next section), thus contributing to offering important insights into the structural and functional brain architectures and their functional mechanisms.

2.4. Structural and functional connectivity among gyral/sulcal landmarks

For a pair of the gyral/sulcal regions, their functional correlation strength was calculated by averaging the functional connectivity between any possible pairs of landmarks on two cortical regions. Here, the Pearson correlation (Zhu et al. 2012) between two extracted R-fMRI signals from two cortical landmarks was considered as their functional connectivity. In order to gain robustness and full coverage of the whole gyrus/sulcus, 100 sets of sampled landmarks (Section 2.2) were randomly selected in the 3-ring surface mesh neighborhood of the corresponding landmark (e.g. Fig. 2). This procedure created 100 functional connectivity matrices for each subject and they were averaged element-wise to suppress noises and outliers, resulting in a final functional connectivity matrix for each subject (detailed in the Supplemental Methods). It should be noted that the distributions of functional correlation values could vary largely from subject to subject, as demonstrated in Supplemental Figs. 1 and 3 (for two different datasets). Therefore, the mean functional correlation value and the standard deviation per subject were used to normalize the corresponding subject’s functional connectivity correlation matrix as follows. For each subject, the functional connectivity value, represented by FC, in the averaged functional connectivity matrix is normalized by:

$$\overline{FC(X,Y)}=1+\frac{FC(X,Y)-\mu }{4\sigma }$$ (1)

where μ is the average FC of the corresponding subject; σ is the standard deviation; 4σ, as commonly used in statistics, is considered as a cut-off threshold of the Gaussian distribution (experimental results suggested that the histograms of the FC are similar to Gaussian distributions within one subject). Within this normalization scheme, a functional connection with strength equivalent to the average level of the subject will have a value of 1.0. As a result, this normalization procedure provides much more consistent and comparable individual distributions, as shown in Supplemental Figs. 2 and 4 (for the same two datasets), and enables fair comparisons of functional connectivity between different subjects. Notably, the FC values are Gaussian-likely distributed within a subject and the distribution patterns are too different from each other to be compared, therefore, $\overline{FC}$ is used to normalize FC values across subjects. The normalized functional connectivity matrices were then used in the subsequent analyses in Section 3. Intuitively, a value of 1.0 represents an average functional connection level, and the larger the value is, the stronger the functional connectivity will be.

To extract the DTI-derived white matter fibers connecting to a certain gyral/sulcal landmark, the fibers in the 3-ring surface mesh neighborhood of each landmark were collected via a similar approach in Zhu et al. 2011 and Li et al. 2012. Then, the structural connectivity strength between two cortical regions is represented by the number of fibers connecting both regions (Zhang et al. 2011; Li et al. 2012; Zhu et al. 2012). Similar to the normalization procedure in measuring functional connectivity, the structural connection strength was normalized by the average number of fibers between any pair of cortical landmarks in this study to reduce the individual variability. Thus, a value of 1.0 represents the average structural connectivity; the larger the value is, the stronger the structural connectivity will be. Finally, the structural or functional connection strength between any pair of cortical gyri/sulci is defined as the averaged connection strength between all possible combinational pairs of the landmarks on two gyri/sulci (please see additional details in the Supplemental Methods).

3. Results

We designed and performed a series of experiments to test the hypothesized functional model of cortical gyri and sulci. These experiments and the results are detailed in Sections 3.1–3.3 respectively.

3.1. Structural/functional connectivity among major gyri/sulci in the whole cortex

In this section, we analyzed the structural and functional connectivity among major gyri and sulci in the whole cortex. First, by using similar methods in Section 2.2, we labeled 555 landmarks on 68 major gyri/sulci in the whole cortex (e.g. Fig. 3a) of each subject in dataset 1 according to the Talairach atlas (Talairach & Tournaux, 1988) used in the BrainVoyager Brain Tutor (http://www.brainvoyager.com) (Figs. 3b and 3c). We took the advantage of this software, that is, the atlas is mapped onto the surface in order to facilitate our landmark selection. More details about the landmark labeling have been discussed in Section 2.2. For each corresponding gyrus/sulcus in different brains (e.g. Figs. 3b and 3c), a certain number (ranging from 3–20) of landmarks are placed at cortical surface mesh vertices that are roughly distributed evenly along the gyral ridges or sulcal valleys. The distributions of landmarks are sufficiently dense to ensure the full coverage of the whole gyrus/sulcus. Fig. 3a shows an example of the placements of 555 landmarks on 68 gyri/sulci of one subject.

Figure 3.

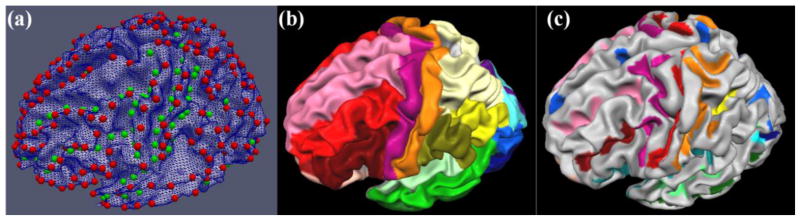
(a) Placements of landmarks of 68 gyri/sulci on one example subject. Red and green bubbles represent the initial landmarks on gyri and sulci, respectively. (b) All of the delineated gyri on the template brain. Different gyri are labeled by separate colors. The gyral delineations were obtained from the BrainVoyager software package. (c) All of the delineated sulci on the template brain. Different sulci are labeled as separate colors. It is noted that we labeled all cortical landmarks at the gyral ridges and sulcal valleys.

Then, the structural/functional connectivity was calculated between any pair of gyrus/gyrus, gyrus/sulcus, and sulcus/sulcus using the same methods in Sections 2.3 and 2.4. To measure the overall structural/functional connectivity of gyrus/gyrus, gyrus/sulcus, and sulcus/sulcus pairs, respectively, we defined the overall structural/functional connectivity value as the ratio of the survived number of pairs after thresholding (t=1.0, which is the mean value for normalization as explained in Section 2.4) to the total number of pairs. The result is shown in Table 1. It is evident that the overall gyrus-gyrus functional connectivity value (average: 0.48) over the whole cortex is significantly stronger than the overall sulcus-sulcus functional connectivity value (average: 0.37) (p-value=1.21e-04), while the overall gyrus-sulcus functional connectivity value (0.44) is moderate and in-between. The detailed distribution histograms of three types (gyrus/gyrus, gyrus/sulcus, and sulcus/sulcus pairs) of functional connectivity are shown in Fig. 4. It is evident that the gyri-gyri connectivity has higher bars on the right side (larger connectivity magnitude) of the histogram, while sulci-sulci connectivity has higher bars on the left side (smaller connectivity magnitude). Meanwhile, the gyri-sulci connectivity bars are in-between. The above findings suggest that gyri are global functional connection centers and sulci are local functional units. For structural connectivity, it is also clear that the overall gyrus-gyrus structural connectivity value (average: 0.15) over the whole cortex is significantly stronger than the overall sulcus-sulcus structural connectivity value (average: 0.03) (p-value=5.75e-10), while overall gyrus-sulcus structural connectivity value (0.07) is moderate and in-between. These results demonstrate the structural substrates of the functional connectivity results in the left panel of Table 1.

Table 1.

Overall functional and structural connectivity value of all gyrus-gyrus, gyrus-sulcus, and sulcus-sulcus pairs in dataset 1. Statistically significant items are underlined (p-value<0.05, mean=1.0). Con stands for connectivity, Stdev stands for standard deviation, and p stands for p-value.

Con	Overall Functional Connectivity Value			Overall Structural Connectivity Value
Sub	Gyrus-Gyrus	Gyrus-Sulcus	Sulcus-Sulcus	Gyrus-Gyrus	Gyrus-Sulcus	Sulcus-Sulcus
1	0.54	0.41	0.29	0.19	0.09	0.03
2	0.40	0.37	0.33	0.15	0.06	0.01
3	0.50	0.43	0.35	0.16	0.07	0.03
4	0.56	0.46	0.35	0.13	0.05	0.01
5	0.53	0.47	0.38	0.14	0.06	0.02
6	0.48	0.47	0.44	0.14	0.05	0.02
7	0.42	0.40	0.32	0.12	0.06	0.03
8	0.59	0.53	0.43	0.12	0.05	0.01
9	0.39	0.40	0.34	0.15	0.14	0.10
10	0.49	0.46	0.41	0.21	0.09	0.03
11	0.42	0.44	0.40	0.19	0.09	0.01
Mean	0.48	0.44	0.37	0.15	0.07	0.03
Stdev	0.07	0.04	0.05	0.03	0.03	0.03
Two-sample statistical significance test without equal variance assumption
Test	Gyrus-Gyrus>Gyrus-Sulcus	Gyrus-Gyrus>Sulcus-Sulcus	Gyrus-Sulcus>Sulcus-Sulcus	Gyrus-Gyrus>Gyrus-Sulcus	Gyrus-Gyrus>Sulcus-Sulcus	Gyrus-Sulcus>Sulcus-Sulcus
p-value	0.04	1.21e-04	9.39e-04	9.57e-07	5.75e-10	3.52e-04

Figure 4.

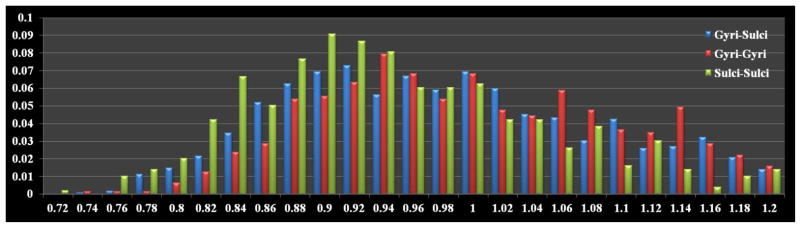
Histograms of the functional gyri-gyri (red), gyri-sulci (blue), and sulci-sulci (green) connectivity strengths.

In addition to the above whole cortex analysis, we performed global functional connectivity analyses of selected gyral or sulcal voxels. First, we randomly picked three landmarks in the gyral and sulcal regions, respectively, as shown in Fig. 5. Then, we measured the functional connectivity strength between other cortical voxels and the picked landmarks in consideration, and mapped them on the cortical surfaces (Fig. 5). It is evident that the gyral landmarks have much more long-distance functional connectivity than the sulcal voxel, consistent with our hypothesis that there are many more long-distance functional connections on gyral regions than sulcal regions.

Figure 5.

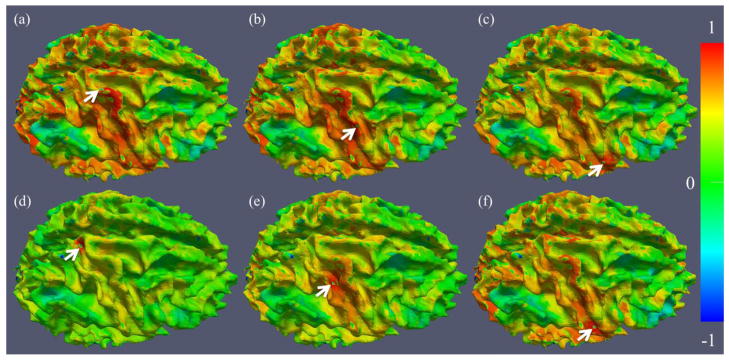
Examples of cortical connectivity maps of selected landmarks (pointed by white arrows). (a)–(c): three landmarks on the RPCG; (d)–(f): three landmarks on the RCS. The color bar is on the right. The results shown in this figure are in agreement with the proposed functional model.

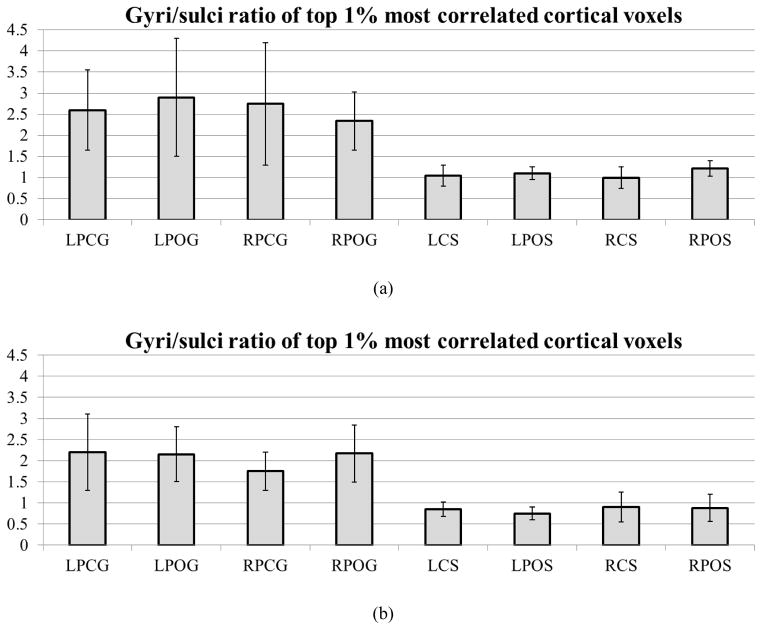
In addition to the above individual landmark-wise analysis in Fig. 5, a whole-brain functional connectivity analysis was performed for all of the cortical landmarks in the two datasets in Section 2.1. Specifically, the functional correlation strengths between the aforementioned landmarks in Fig. 2 and other cortical voxels in the whole brain were measured. From the top 1% of the most correlated cortical landmark/voxel pairs, we collected the ratios of the number of gyral voxels over that of sulcal voxels as shown in Fig. 6a. On average, for those strongly connected cortical voxels on gyral regions (LPCG, LPOG, RPCG, and RPOG), e.g., the highlighted dots on gyri in Fig 5a, 72.76% of the cortical voxels on the other ends of these connections are located on gyri and only 27.24% of them are located on sulci (a ratio of 2.67). As a comparison, for those strongly connected cortical voxels on sulcal regions (LCS, LPOS, RCS, and RPOS), e.g., the highlighted dots on sulcus in Fig. 5d, 51.14% of the cortical voxels on the other ends of these connections are located on gyri and 48.86% of them are located on sulci (a ratio of 1.05). These ratio differences are summarized in Fig. 6a and Fig. 6b for two different datasets. These results suggest that a majority of the strong functional connections to gyral regions originate from gyri too. This whole-brain analysis result further supports our functional model of cortical gyri and sulci: gyri are functional connection centers.

Figure 6.

(a) The ratio of the number of gyral voxels over that of sulcal voxels within the top 1% of the most functionally connected cortical voxels in the first dataset. (b) The ratios of the numbers of gyral voxels over those of sulcal voxels within the top 1% of the most functionally correlated cortical voxels in dataset 2.

3.2. Case studies of structural/functional connectivities among selected gyri and sulci

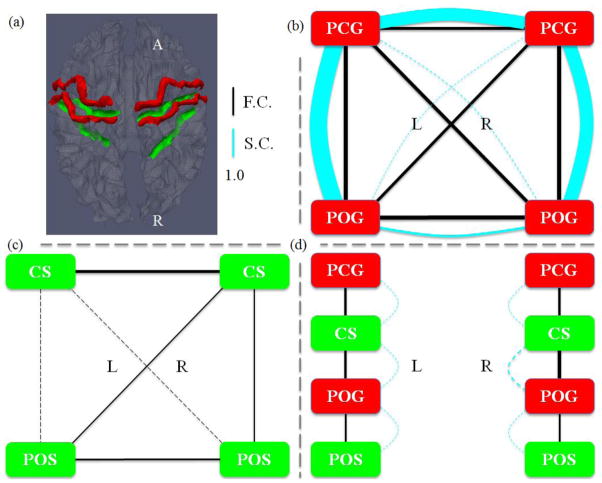
The structural and functional connection patterns among four gyri in the frontal/parietal lobe (red ribbons in Fig. 7a) are shown in Fig. 7b. A major observation obtained from the gyrus-gyrus connection patterns in Fig. 7b is that there exist both strong structural (cyan curves) and functional (blue lines) connectivity among these selected gyri. For instance, the DTI-derived structural fiber connections between PCG and POG on both hemispheres are quite strong, and their functional connections are strong as well. From a neuroanatomy perspective, this result is reasonable since the primary motor cortex (PCG) and primary somatosensory cortex (POG) are known to have strong connections (Miller 1988; Asanuma 1989; Kandel et al. 2000). This DTI study also demonstrated that there is strong structural connection between PCGs on two hemispheres, while the structural connections between LPOG and RPOG are relatively weak, as shown in Fig. 7b. However, it is interesting that the functional connection between LPOG and RPOG is still strong. Our interpretation is that this strong functional connection might be attributed to the strong indirect structural connections (e.g. Deligianni et al. 2011) through LPCG and RPCG.

Figure 7.

(a) Illustration of the four gyral regions (red) and four sulcal regions (green). In (b)–(d), the width of a functional connection edge (black) is proportional to the functional connectivity (F.C.). The width of a structural connection edge (cyan) is proportional to the structural connectivity (S.C.). Weak edges (width less than 1.0) are in dashed lines, which are significantly weaker than the average. (b) Joint representation of structural and functional connectivity among four gyri. Strong structural connectivity was observed in LPCG-LPOG, RPCG-RPOG, and LPCG-RPCG, which are significantly stronger than the average. (c) Joint representation of structural and functional connectivity among four sulci. No or very weak structural connectivity was observed in the DTI data. (d) Joint representation of structural and functional connectivity between adjacent gyri and sulci.

Quantitative measurements of these structural and functional connection strengths were also conducted. A one-way ANOVA was performed on any pair of gyri-gyri, gyri-sulci and sulci-sulci connection among PCG, POG, CS and PCS in dataset 1. The p-values are 4.18×10⁻¹⁵ and 4.7×10⁻⁴⁸ respectively for functional connectivity and structural connectivity, which demonstrates that the differences among gyri-gyri, gyri-sulci and sulci-sulci in terms of the two types of connections are significant. In addition, mean values, standard deviations and post-hoc t-tests between any pair of gyri in the eleven subjects in dataset 1 (Section 2.1) are shown in Table 2. It is apparent that the functional connection strength of any pair of gyri is above 1, meaning that the functional connection strengths between gyral regions are all above the average. In particular, four pairs exhibit statistical significance (p-value<0.05) and they are underlined in the left panel of Table 2. This result quantitatively demonstrates that gyral regions interact strongly with other gyral regions (e.g. the ones studied in this section), supporting our hypothesized functional model of cortical gyri. From the right panel in Table 2, it can also be found that there are strong or moderate structural connections among any pair of gyri. In particular, there are three pairs of strong direct structural connections (LPCG-RPCG, LPCG-LPOG, and RPCG-RPOG), as highlighted by the underlines in the right panel of Table 2. In comparison, other pairs of gyri (LPCG-RPOG, RPCG-LPOG, and LPOG-RPOG) exhibit relatively moderate structural connections. The functional connection strengths for these pairs, however, are still strong, as shown in the left panel of Table 2. Importantly, these above conclusions have been replicated in the second separate dataset, as shown in Supplemental Table 6. These results further suggest that: 1) strong indirect structural connections are possibly associated with strong functional connectivity (e.g. Deligianni et al. 2011); and 2) structural and functional connectivity are closely related (e.g. Brett et al. 2002; Passingham et al. 2002; Honey et al. 2009; Stephan et al. 2009; Li et al. 2012; Zhu et al. 2012). Notably, an important differentiation that should be made here is that the close relationship between strong functional connectivity and strong direct structural connections are particularly evident for gyrus-gyrus connections.

Table 2.

Functional and structural connection strengths among four gyri in dataset 1. Statistically significant elements are underlined (p-value<0.05, one-sample, two-tailed test, mean=1.0 for functional connectivity; one-sample, right-tailed test, mean=1.0 for structural connectivity). Con stands for connectivity, Stdev stands for standard deviation, and p stands for p-value. The individual subject’s data is referred to Supplemental Table 3.

Con	Functional Connectivity						Structural Connectivity
	LPCG RPCG	LPCG RPOG	LPCG LPOG	RPCG LPOG	RPCG RPOG	LPOG RPOG	LPCG RPCG	LPCG RPOG	LPCG LPOG	RPCG LPOG	RPCG RPOG	LPOG RPOG
Mean	1.11	1.17	1.22	1.08	1.24	1.26	6.57	0.71	8.93	0.29	6.84	1.32
Stdev	0.20	0.12	0.17	0.20	0.17	0.09	2.95	0.98	4.14	0.38	3.26	1.73
p	0.10	0.00	0.00	0.19	0.00	0.00	0.00	0.82	0.00	1.00	0.00	0.28

The structural and functional connection patterns among four selected sulci are shown in Fig. 7c. It is evident that there is no or very weak DTI-revealed direct structural connection among any pair of sulcal regions (no cyan curves in Fig. 7c). This result further replicates our prior results reported in Nie et al. 2012 and Chen et al. 2012 that DTI-derived fiber connection terminations concentrate on gyri, but not on sulci. Meanwhile, the functional connections of the sulci pairs of LCS-RPOS, LCS-LPOS, RCS-LPOS, and RCS-RPOS are week (black lines in Fig. 7c), suggesting that weak functional connections are associated with no or weak structural connections (quantifications in the right panels of Table 3 and Supplemental Table 4). This result supports our hypothesized functional cortical working model: sulci are the local functional units. It is interesting that the RCS-LCS pair has relatively higher functional connection. Our interpretation is that both RCS and LCS are connected to the RPCG and LPCG through local inter-column cortico-cortical fibers, and RPCG and LPCG are strongly connected by structural fibers (Fig. 7b). As a result, RCS-LCS has relatively stronger indirect structural connections (e.g., the structural LPCG-RPCG connection is 6.57 in Table 2), and therefore exhibits stronger functional connection. These results further suggest that functional connectivity has its structural underpinnings.

Table 3.

Functional and structural connectivity strengths among four sulci in dataset 1. Statistically significant elements are underlined (p-value<0.05, one-sample two-tailed test, mean=1.0 for functional connectivity; one-sample, right-tailed test, mean=1.0 for structural connectivity). Con stands for connectivity, Stdev stands for standard deviation, and p stands for p-value. The individual subject’s data is referred to Supplemental Table 4.

Con	Functional Connectivity						Structural Connectivity
	LCS RCS	LCS RPOS	LCS LPOS	RCS LPOS	RCS RPOS	LPOS RPOS	LCS RCS	LCS RPOS	LCS LPOS	RCS LPOS	RCS RPOS	LPOS RPOS
Mean	1.14	0.67	0.76	0.82	0.83	1.02	0.00	0.00	0.01	0.00	0.00	0.00
Stdev	0.20	0.17	0.17	0.18	0.29	0.21	0.00	0.00	0.03	0.00	0.00	0.00
p	0.05	0.00	0.00	0.01	0.07	0.77	1.00	1.00	1.00	1.00	1.00	1.00

The quantitative measurements of these structural/functional connection strengths are provided in Table 3. It is evident that in all of these eleven subjects we studied, there is no or very weak structural connections between any pair of sulci, which is consistent with our previous reports in Nie et al. 2012. Also, the functional connection strengths between LCS-RPOS, LCS-LPOS, RCS-LPOS, and RCS-RPOS are substantially lower than the average of these eight cortical regions, and three of them are statistically significant, as underlined in the left panel of Table 3. The LCS-RCS pair has higher functional connection, which was already interpreted and explained in the above paragraph. Notably, these conclusions have been replicated in the second separate dataset, as shown in Supplemental Table 7. Therefore, the results in this section have demonstrated that sulcal regions have much less remote functional interactions with other sulcal regions (Fig. 7c and the left panel of Table 3) or other gyral regions. Instead, sulcal regions mainly interact with locally connected neighboring gyral regions, which will be explained in details in the next section.

The structural and functional connection patterns between adjacent gyri and sulci are shown in Fig. 7d. We can see that there are moderate functional connections between sulcal regions and their neighboring gyral regions (solid black lines in Fig. 7d) in spite of the very weak structural connections (dashed cyan curves in Fig. 7d) that can be revealed by the in-vivo DTI data. However, a large number of neuroscience literature publications have demonstrated the cortico-cortical fiber connections within neighboring cortical regions (e.g. Kandel et al. 2000; Ghosh et al., 1988; Keller and Asanuma, 1993; Mountcastle 1997; Broman and Fletcher, 1999; Thomson et al. 2007) that cannot be revealed by in-vivo DTI at the current stage, and these cortico-cortical connections may explain the moderate functional connections between neighboring sulcal and gyral regions in Fig. 7d. The quantitative measurements of the structural and functional connection strengths between adjacent gyri and sulci shown in Fig. 7d are provided in Table 4. It is evident that the DTI-derived structural connections between adjacent gyri and sulci pairs are weak, in comparison with the structural connection strengths between gyri pairs in Table 2. In contrast, the functional connection strengths between adjacent gyri and sulci are moderate, which are in-between the functional connection strengths between gyrus-gyrus pairs (Table 2) and those between sulcus-sulcus pairs (Table 3). These above results have been replicated in the second separate dataset, as shown in Supplemental Table 8.

Table 4.

Functional and structural connectivity strengths of neighboring gyrus-sulcus pairs in dataset 1. Statistically significant items are underlined (p-value<0.05, one-sample two-tailed test, mean=1.0 for functional connectivity; one-sample, right-tailed test, mean=1.0 for structural connectivity). Con stands for connectivity, Stdev stands for standard deviation, and p stands for p-value. The individual subject’s data is referred to Supplemental Table 5.

Con	Functional Connectivity						Structural Connectivity
	LPCG LCS	LCS LPOG	LPOG LPOS	RPCG RCS	RCS RPOG	RPOG RPOS	LPCG LCS	LCS LPOG	LPOG LPOS	RPCG RCS	RCS RPOG	RPOG RPOS
Mean	1.04	1.03	1.00	1.06	1.20	0.99	0.73	0.62	0.40	0.46	0.92	0.21
Stdev	0.22	0.15	0.27	0.17	0.15	0.27	0.47	0.63	0.40	0.53	1.24	0.43
p	0.59	0.54	0.97	0.26	0.00	0.95	0.95	0.96	1.00	1.00	0.59	1.00

The results in Figs. 7c–7d and Tables 3–4 have demonstrated two major points about structural and functional connectivity of cortical sulci: 1) both structural and functional connection strengths between sulci and other remote cortical regions (except the RCS-LCS pair) are relatively weak; 2) sulcal regions mainly interact directly with their neighboring gyri, and at the same time, they communicate indirectly with other remote gyral/sulcal regions via their neighboring gyri. Also, we interpret that the moderate functional connectivity between adjacent sulci and gyri has its structural underpinnings, that is, the cortico-cortical fiber projections that cannot be revealed by DTI data. Therefore, these results further support our hypothesized functional model of cortical gyri and sulci: gyri are global functional connection centers, and sulci are local functional units.

3.3. Overall structural/functional connectivity among selected gyri and sulci and reproducibility study

To provide an overview of the findings discussed so far, the sub-figures in Figs. 7b–7d are integrated and summarized in Fig. 8a, that is, all of the structural/functional connection patterns are represented by the colored curves/lines in Fig. 8a. Based on the visualizations in Fig. 8a, it becomes even more evident that gyri (red boxes in Fig. 8a) are the functional connection centers, while the sulci serve as the local functional units. Quantitatively, we measured the graph edge degrees of the functional connection networks for all of the gyri and sulci, as shown in Table 5. The graph degrees are normalized to [0, 1], where 0 means no connection at all and 1 means the corresponding landmark connects to all possible nodes. Notably, the normalized metric is used here for better understanding of the contrast/difference between the average edge degrees of gyri/sulci nodes within the selected model system. It is evident that the graph edge degrees of the gyri nodes are significantly higher than those of the sulci nodes (overall p-value=1.90E-30, two-sample, right-tailed test without equal variance assumption). In addition, the averaged total functional connection strengths of the gyri nodes are significantly higher than those of sulci (p-value=0.004). Altogether, the quantitative results in this section further support our hypothesis from a graph theory perspective: gyri are global functional connection centers and sulci are local functional units.

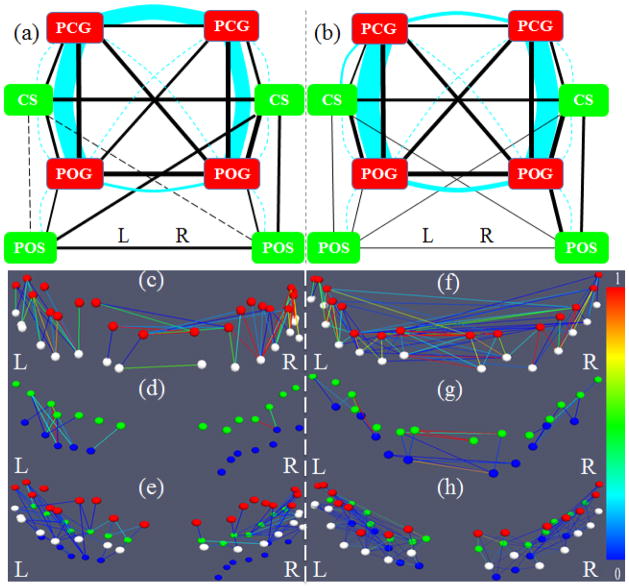
Figure 8.

(a) Overall joint representation of structural and functional connectivity of selected gyri and sulci in the frontal/parietal lobe. Edges colored in cyan represent structural connections, and those colored in black represent functional connections for gyrus-gyrus, sulcus-sulcus, and gyrus-sulcus patterns, respectively. The scales are the same as those in Fig. 7. The connections significantly stronger or weaker than the average are the same as those in Fig. 7. (b) The replication of the overall joint representation of structural and functional connectivity of gyri and sulci in the second dataset. (c)–(h): Examples of structural fiber connectivity patterns using DTI data (c–e) and HARDI data (f–h). Red, white, green, and blue bubbles represent the landmarks on PCG, POG, CS, and POS, respectively. The edges are colored based on the structural connectivity strength according to the color bar on the right. (c) and (f) are gyrus-gyrus pairs; (d) and (g) are sulcus-sulcus pairs; (e) and (h) are adjacent gyrus-sulcus pairs.

Table 5.

Average graph edge degrees of the functional networks in Fig. 7a in the dataset 1 with a threshold 1.0 (mean correlation). The degree values are normalized to [0, 1] where 0 means no connection at all and 1 means the corresponding node connects to all possible nodes. Stdev stands for standard deviation. The results of using lower thresholds, such as 0.9, 0.8 and 0.7, are shown in Supplemental Tables 9–11. The reproducibility study results for the dataset 2 are provided in Supplemental Table 12.

Gyri	Mean	Stdev	Sulci	Mean	Stdev
LPCG	0.66	0.20	LCS	0.50	0.18
LPOG	0.65	0.17	LPOS	0.43	0.21
RPCG	0.65	0.19	RCS	0.55	0.15
RPOG	0.68	0.15	RPOS	0.41	0.22
Two-sample statistical significance test without equal variance assumption
Test	Mean of gyri and sulci
p-value	0.004

Interestingly, the findings obtained in the first multimodal DTI/R-fMRI dataset in Fig. 7 and Fig. 8a were well replicated in a separate dataset (dataset 2 in Section 2.1), as shown and explained in Fig. 8b and Supplemental Fig. 5. Additionally, all of the quantitative measurements in Tables 2–4 obtained from the first dataset were also reproducible in the second publicly available dataset (http://hdl.handle.net/1926/1687), as shown in Supplemental Tables 6–8. Furthermore, the reproducibility studies of selected gyri and sulci in the frontal lobes (Supplemental Materials) have suggested similar conclusions. These results suggest that our data analysis results in Sections 3.1–3.3 are reproducible in independent datasets, strongly supporting the hypothesized functional model of cortical gyri and sulci.

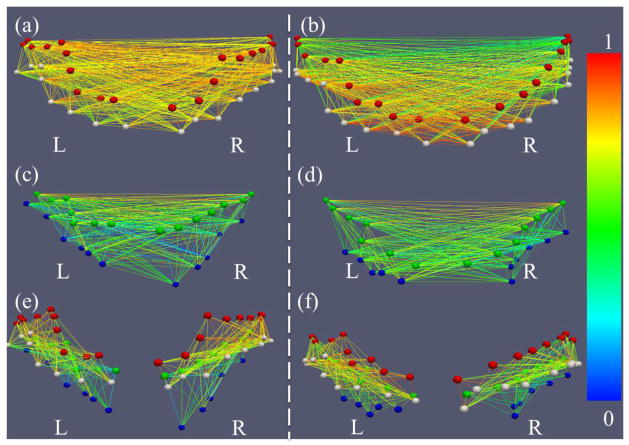
To provide an illustrative and intuitive visualization of the results discussed in Sections 3.1–3.3 so far, Figs. 8c–8h and Fig. 9 shows examples of the structural and functional connectivity patterns between the landmarks on gyrus-gyrus, sulcus-sulcus, and adjacent gyri-sulci pairs. It is evident that the gyrus-gyrus fiber connections (Figs. 8c and 8f), sulcus-sulcus fiber connections (Figs. 8d and 8g), and adjacent gyri-sulci fiber connections (Figs. 8e and 8h) are strong, weak, and moderate, respectively. Similarly, the gyrus-gyrus functional connections (Figs. 9a and 9b), sulcus-sulcus functional connections (Figs. 9c and 9d), and adjacent gyri-sulci functional connections (Figs. 9e and 9f) are strong, weak, and moderate, respectively. These visualizations illustrate the major findings in Sections 3.1–3.3.

Figure 9.

Examples of functional connectivity patterns for two randomly selected subjects (left and right panels, respectively). Red, white, green, and blue bubbles represent the landmarks on PCG, POG, CS, and POS, respectively. The edges are colored based on the functional connectivity strength according to the color bar on the right. (a) and (b) are gyrus-gyrus pairs; (c) and (d) are sulcus-sulcus pairs; (e) and (f) are adjacent gyrus-sulcus pairs.

4. Discussion and Conclusion

This paper presents two lines of experimental and computational studies to formally hypothesize a functional mechanism of cortical gyri and sulci. First, we defined a series of cortical landmarks on both gyri and sulci in the frontal/parietal lobe, and analyzed the structural and functional connectivity among these gyral and sulcal landmarks. In particular, we assessed the differences of structural and functional connectivity strengths among gyral-gyral, gyral-sulcal and sulcal-sulcal landmark pairs over all of the selected areas. Second, we performed whole cortex analyses to measure the strengths of structural and functional connections on gyral and sulcal regions. To examine the reproducibility of our studies, two independent multimodal DTI/R-fMRI datasets were used to examine the above hypothesized functional working mechanisms. Collectively, these studies and the experimental results (Sections 3.1–3.3) have supported a common functional model based on the common structural brain architecture: gyri are global functional connection centers and sulci are local functional units.

Conceptually, the studies of the fundamental functional working mechanism of cortical gyri and sulci in this paper are rooted in the following two methodological considerations. First, DTI is a useful macro-scale neuroimaging technique that can quantitatively map fiber connections in vivo (Basser and Pierpaoli 1996; Mori 2006). Our prior DTI studies (Nie et al. 2012; Chen et al. 2012) have revealed that streamline fiber wiring patterns closely follow cortical gyral folding pattern and fiber terminations concentrate on gyri. Importantly, this finding has been replicated by both DTI and HARDI data (dataset 3) and in the brains of three primates including human, chimpanzee and monkey (Nie et al. 2012; Chen et al. 2012). Thus this finding provides a solid structural basis for the proposed functional model of the brain, that is, gyri are functional connection centers in that DTI-derived fibers are the structural substrates of functional connectivity of the brain. Second, R-fMRI is a powerful functional neuroimaging technique that can reveal the functional architecture of the brain (Fox et al. 2007). In particular, multimodal DTI and R-fMRI data has the possibility of independently elucidating the common structural and functional brain architectures and their relationships. In addition to the investigation of the proposed functional mechanisms of cortical gyri and sulci via multimodal DTI/R-fMRI data, this work also provides additional evidence to the literature (e.g., Passingham et al. 2002; Stephan et al. 2009; Honey et al., 2009) that structural connections are the structural underpinnings of functional connectivity, as demonstrated extensively in Tables 1–4. Altogether, the studies in this paper offer further evidence to support the close relationships between structural and functional connectivity (e.g., Stephen et al. 2009; Honey et al., 2009; Zhu et al. 2012).

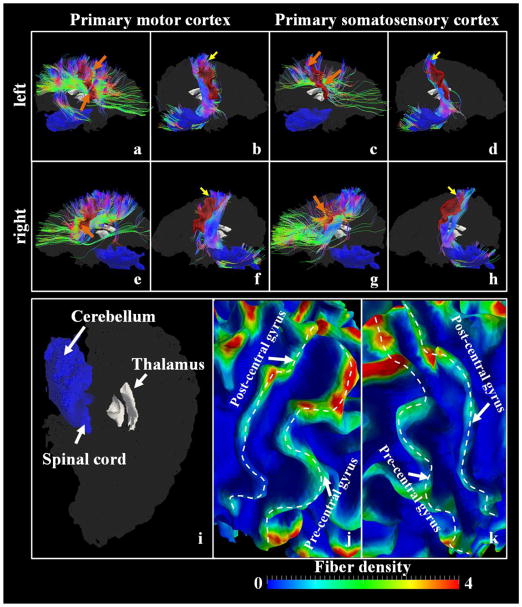
It should be noted that DTI data has limitations. Therefore, we chose the primary motor cortex and the primary somatosensory cortex as examples to further evaluate the structural basis of the proposed functional model. We examined the DTI-derived fibers emanating from the primary motor cortex and the primary somatosensory cortex and jointly visualized one subject as an example in Figure 10 in a qualitative manner. We also reported the quantitative statistical results in Table 6. Specifically, we firstly extracted the primary motor cortex/the primary somatosensory cortex surface patches from the white matter cortical surfaces. Since it is relatively difficult to locate the exact positions of Brodmann’s areas 3a, 3b, 1 and 2 and our results are reported using gyrus/sulcus as the basis, we extracted the patch expanding from the pre-central gyrus through the rostral wall to the depth of central sulcus root and used it to represent the primary motor cortex in that it covers most parts of the primary motor cortex (please see Figure 10(a), 10(b), 10(e) and 10(f) for example). As for the primary somatosensory cortex, we extracted the patch expanding from the depth of the central sulcus to the depth of the postcentral sulcus, crossing the crown of the post-central gyrus (please see Figure 10(c), 10(d), 10(g) and 10(h) for example). Then, the fibers emanating from one patch were extracted and manually split into two bundles, that is, the one connecting the spinal cord/thalamus regions (illustrated in Figure 10(i)) and the one connecting other cortical regions. Also, for each vertex of the surface, we calculated the number of fibers penetrating its 1-ring neighbor triangles, and associated the vertex with a fiber density value, which is defined as the fiber number divided by the area of 1-ring neighbor triangles. The surfaces with mapped fiber-densities are shown in Figure 10(j) and 10(k) in zoomed-in views. In Figure 10(j) and 10(k), we can clearly observe that the fiber density is substantially higher in regions near gyrus crest lines (the white dashed curves highlight the crest lines of the pre/post-central gyri) than those near central sulcus root. Quantitatively, we computed the ratio of each of the two bundles’ fiber number to the total fiber number extracted from the patch across five subjects in dataset 1 and reported the average ± standard deviation (std) ratios in Table 6. It is worth noting that the fibers connecting the other hemispheres are eliminated in Table 6.

Figure 10.

Joint visualization of the primary motor cortex/the primary somatosensory cortex (red color patches) and white matter fibers emanating from them. (a) The left primary motor cortex patch and fibers connecting other cortical regions; (b) The left primary motor cortex patch and fibers connecting the spinal cord/thalamus; (c) The left primary somatosensory cortex patch and fibers connecting other cortical regions; (d) The left primary somatosensory cortex patch and fibers connecting the spinal cord/thalamus; (e) The right primary motor cortex patch and fibers connecting other cortical regions; (f) The right primary motor cortex patch and fibers connecting the spinal cord/thalamus; (g) The right primary somatosensory cortex patch and fibers connecting other cortical regions; (h) The right primary somatosensory cortex patch and fibers connecting the spinal cord/thalamus; The yellow arrows highlight the regions where fibers connecting the spinal cord/thalamus penetrate the cortex, while the orange arrows highlight the regions penetrated by fibers derived from other cortical regions. The whole brain surfaces are shaded as a background with the thalamus regions detailed in (i). The fiber density, defined as the number of fibers penetrating 1-mm² area on the surface, is mapped onto the surfaces. The zoomed-in views of the left central sulcus and the right central sulcus regions are shown in (j) and (k), respectively. The dashed white curves highlight the gyral crest lines.

Table 6.

The ratio of fiber bundles extracted from the primary motor cortex/the primary somatosensory cortex patch. Results on the left/right hemispheres are reported separately and the fiber bundles extracted from one cortex patch are split into two parts: the bundle connecting the spinal cord/thalamus (spinal cord, for short) and the one connecting other cortical regions. The results are obtained on five subjects in dataset 1. The method used to obtain the ratio is referred to the main text.

	Left Hemisphere		Right Hemisphere
	Spinal cord	Other regions	Spinal cord	Other regions
Primary motor cortex	0.30 ± 0.09	0.48 ± 0.01	0.34 ± 0.04	0.46 ± 0.01
Primary somatosensory cortex	0.41 ± 0.18	0.47 ± 0.09	0.23 ± 0.02	0.60 ± 0.13

From both visual observations in Figure 10 and quantitative results in Table 6, we can evidently see that fibers connecting the spinal cord/thalamus regions are more likely to penetrate the patches in the superior parts of both of the primary motor cortex and the primary somatosensory cortex (highlighted by the yellow arrows in Figure 10) and account for around 30% of all fibers derived from the two cortex surface patches. On the other hand, fibers connecting other cortical regions within the same hemisphere account for around 50% of all fibers and they are concentrated on the lower parts of both cortex patches. These results provide the supporting evidence in terms of structural substrate of our exploration of structural/functional connections between the pre-central gyrus and the post-central gyrus.

It should also be noted that resting state fMRI data has spatial resolution limitations. To demonstrate that the pre/post-central gyri and central/post-central sulci used in this paper (Figure 2 in main text) are far enough in the fMRI volume image space, we used one subject as an example, represented the four crest lines and sulcal roots (Figure 2 in main text) in curves, and transformed them into the fMRI volume images via the transformation matrix generated by a linear registration between DTI and fMRI data. We jointly showed the four curves and the original fMRI volume image at time point #1 in Figure 11 with a 64×64×30 volume grid (dark blue mesh) used as the background. The opacity of the fMRI volume image was carefully adjusted to make the four curves visible. Generally, by eyeballing the distances among the four curves using the background grid as reference, several voxels can be easily spotted among any pair of two curves. To quantitatively validate this observation, we computed the average minimal distances between any two curves. Specifically, taking the pre-central gyrus and the post-central gyrus for example, for each node of the pre-central gyrus (red bubble in Figure 2 of the main text), we searched the nearest nodes on the post-central and computed the voxel-wise distance, defined as the minimal distance, and averaged the minimal distances and assigned it to (PCG, POG) cell in an average minimal matrix. The matrices are shown in Figure 12. In general, the average minimal distance between any two curves is about 3.5 voxels. Therefore, we believe the fMRI signals are distinct enough to reflect the functional segregation in neighboring gyri and sulci.

Figure 11.

Joint visualization of the original fMRI volume data (time point 1), the pre/post-central gyrus crest lines (white curves) and the central/post-central sulcus fundi (purple curves). The 64×64×30 volume grid (dark blue mesh) is used as the background to facilitate visual observation. The gyral crest lines and sulcus fundi are extracted on the cortical surface reconstructed from DTI data and transformed in fMRI volume image space via FSL FLIRT. The original fMRI volume image is color-coded according to the ‘voxel value’ color bar at the right bottom.

Figure 12.

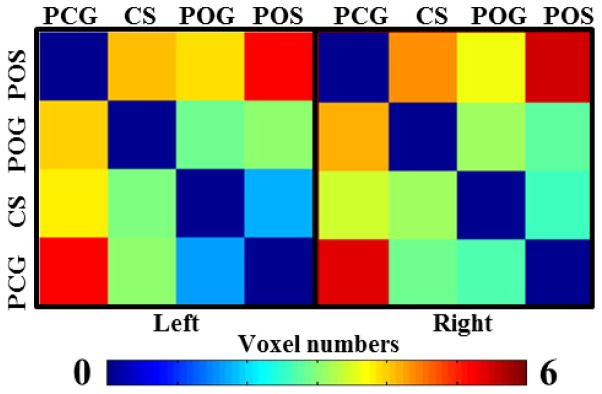
The average minimal distance matrices among four curves in Figure 11 on two hemispheres. The distance is measured voxel-wise in the fMRI volume image space. The color bar is at the bottom.

We envision that the proposed functional model of cortical gyri and sulci and its supporting experiment results could provide a foundation for future elucidation of fine-scale structural organization (Scannell 1997) and functional mechanisms of the cerebral cortex, for instance, how the gyri and sulci functionally interact with subcortical regions in resting state (Fox et al. 2007), during task performance (Logothetis 2008), or under natural stimulus of movie watching (Hasson et al. 2010; Sun et al. 2012). Also, the verified functional model and its associated computational approaches could possibly enable and facilitate many novel studies and applications in neuroimaging, cognitive neuroscience, and clinical neuroscience. For instances, the differentiation of the functional roles of gyri and sulci can help achieve better localization and selection of brain regions in different functional neuroimaging and cognitive neuroscience studies, and the functional interactions among gyral-gyral, gyral-sulcal, and sulcal-sulcal landmarks could be used to elucidate the potential dysfunctions in many neurological or psychiatric diseases/conditions.

In general, the work in this paper can be extended and enhanced in the following directions in the future. First, in this work, the cortical landmarks manually labeled on gyri and sulci do not possess structural and functional correspondences across individuals and populations. As a consequence, the different functional roles of cortical landmarks have to be analyzed at the gyri/sulci scale. In the future, we plan to use our recently developed cortical landmark optimization approaches (Zhu et al. 2011; Zhu et al. 2012) to define and optimize these cortical landmarks so that they will have correspondences at finer scales in different brains. For instance, in our recently developed Dense Individualized and Common Connectivity-based Cortical Landmark (DICCCOL) system (Zhu et al. 2012), 358 consistent cortical landmarks were discovered and replicated in over 240 individual brains. In the future, these DICCCOL landmarks could be initialized and optimized along the major gyri or sulci so that these newly discovered landmarks possess correspondences and could be used to examine the proposed functional model of gyri and sulci at the cortical landmark scale. In this case, the structural and functional connectivity patterns among large-scale landmarks can be integrated and compared across populations, which could potentially provide additional supporting evidence to the proposed functional model of gyri and sulci. Second, the experiments performed in this paper can be replicated and validated in other multimodal neuroimaging datasets with higher resolution and better quality. For instance, the ongoing Human Connectome Project (HCP) (http://www.humanconnectome.org/ and http://www.humanconnectomeproject.org/) plans to release high-quality DTI/HARDI/DSI and/or fMRI datasets, which can be used to test the reproducibility of the models presented in this paper in the near future. Once verified in these HCP datasets, the functional model of gyri and sulci can be used to facilitate the construction of structural and functional connectomes among gyri, sulci or the whole cortex, respectively. Finally, it should be noted that future elucidations of micro-scale structural connectivity patterns of neural circuitries at the cellular level, as well as their molecular mechanism, in the cerebral cortex might provide more biological explanations to the macro-scale DTI/HARDI/DSI derived observations reported in this work.

Finally, we would like to mention that the results obtained in this study should be interpreted with caveat that diffusion imaging including DSI and HARDI and R-fMRI are limited to structural and functional connectivity mapping at the macro-scale. For instance, current DTI/HARDI techniques have limitations in spatial resolution, the capability of dealing with crossing fibers, and the accuracy in mapping fibers around the gray matter and white matter boundaries. That is, current DTI/HARDI techniques can only map coarse-scale major fiber pathways, and they are far from being capable of mapping the complex fine-granularity fiber pathways and connectional architectures of the cerebral cortex (Schmahmann and Pandya, 2006). In the future, micro-scale biological imaging techniques such as the recently developed series two-photon tomography imaging (Ragan et al., 2012) should be considered to further examine cellular-scale fiber connection patterns among cortical gyri and sulci. Similarly, the spatial resolution of the R-fMRI data used in this study is limited and thus only coarse-scale functional connectivities among gyral and sulcal regions can be examined at the current stage. In the future, high-resolution R-fMRI data that can be acquired on ultra-high field (e.g. 7T) MRI systems should be used to verify the results obtained in this study. Additionally, several recent studies demonstrated the temporal dynamics of functional connectivity in R-fMRI datasets (Chang and Glover, 2010; Majeed et al., 2011; Bassett et al., 2011; Smith et al., 2012; Deco and Jirsa, 2012; Li et al., 2012b). Therefore, improved measurements of functional connectivity that can account for temporal dynamics should be considered in the future to replicate the functional connectivity models of cortical gyri and sulci presented in this work.