Abstract
A slackening to zero tension by large length release (~20 %) and a restretch of active muscle fibres cause a fall and a redevelopment in tension. According to the model of Brenner (Proc Natl Acad Sci USA 85(9):3265–3269, 1988), the rate constant of tension redevelopment (kTR) is the sum of attachment and detachment rate constants, hence is limited by the fast reaction. Here we propose a model in which, after restretch, cross-bridges cycle many times by stretching series elastic elements, hence kTR is limited by a slow reaction. To set up this model, we made an assumption that the stepping rate (v) decreases linearly with tension (F), which is consistent with the Fenn effect. The distance traveled by a cross-bridge stretches series elastic elements with stiffness σ. With these assumptions, we set up a first order differential equation, which results in an exponential time course with the rate constant kTR = ση0v0(1 – λ)/F1, where λ = v1/v0, η = step size, the subscript 0 indicates unloaded condition, and the subscript 1 indicate isometric condition. We demonstrate that the ATP hydrolysis rate (=[myosin head]/v0) is proportionate to kTR as the ambient temperature is changed, and that the published data fit to this relationship well if λ = 0.28. We conclude that kTR is limited by the cross-bridge turnover rate; hence it represents the rate constant of the slowest reaction of the cross-bridge cycle, i.e. the ADP isomerization step before ADP is released.
Keywords: Cross-bridge cycle, ATP hydrolysis rate, Tension transient, Rate constant, Posas fibres
Introduction
Muscle contraction occurs through cyclic attachment/detachment of myosin cross-bridges to/from actin in the thin filament, thereby pulling the thin filament toward the center of sarcomeres. In order to characterize the cross-bridge kinetics, Brenner and his colleague (Brenner and Eisenberg 1986; Brenner 1988) developed a simple mechanical method, in which the length of an active muscle fibre is released by ~20 % to induce slackness in fibres. Tension in the fibre falls to zero simultaneously with the length release owing to the shortening of series elastic elements. After being held at the short length for 20–50 ms, the fibre is then restretched to its original length. With the restretch, attached cross-bridges detach instantly, tension in fibers (if any) drops to zero again, hence the series elastic elements are still at the shortened stage. Thereafter, cross-bridges start attaching to the thin filament. This is the point of synchronization of all cross-bridges, which otherwise perform stochastic chemical transitions. As the number of force-generating cross-bridges increases, an exponential time course of tension redevelopment follows with the apparent rate constant kTR (Brenner 1988). With the tension increase, a restretch of the shortened series elasticity occurs.
In the two-state model proposed by Brenner, the rate constant of cross-bridge attachment to actin is defined as fapp, and that of detachment from actin is defined as gapp after applying the two-state model originally proposed by Huxley (1957). From these, it follows that the apparent rate constant of the system is: fapp + gapp, hence it was thought that the kTR reflects the kinetics of cross-bridge attachment and detachment (Brenner and Eisenberg 1986; Brenner 1988). The subscript “app” was used to signify that the rate constants are not limited to a single reaction step, but rather a composite of the rate constants of several steps in the cross-bridge cycle (Brenner 1990). In this report, “app” is shortened to “a” for simplicity. In the original formalism, it must be recognized that kTR is limited by the fast reaction. This is because, if , then it follows that kTR = fa + ga ≈ ga. Therefore, kTR is sensitive to the fast reaction (ga), but not sensitive to the slow reaction (fa).
In spite of the common use of kTR, there have been problems in the interpretation of kTR. One problem has been that the observed kTR is never faster than 40 s–1, whereas many rate constants of tension transients observed with various techniques are in the range 100–1,000 s–1, which suggested thatkTRmay be limited byone or more slow reactions (Gordon et al. 2000). Another problem has been that the length release needed to measure kTR is ~20 %, which corresponds to ~250 nm at the cross-bridge level when the half sarcomere length is 1,250 nm. If the step size is 9.7 nm (Sherwood et al. 2004), change of length by ~250 nm corresponds to ~26 cross-bridge steps. Therefore, kTR may represent the kinetics of the multiple cross-bridge cycles, and is very likely limited by the slow reaction(s) in cross-bridge cycle.
Here we propose a model, in which cross-bridges cycle many times during the tension recovery period by stretching series elastic elements, hence kTR is limited by the slowest reaction instead of the fastest reaction of the cross-bridge cycle. Because the contractile apparatus is made of proteins, it has been known that the series elasticity is present in thick and thin filaments (Huxley et al. 1994; Wakabayashi et al. 1994), myosin heads, Z-disks, and in tendon when present. Figure 1 represents a visual representation of the model we propose. A preliminary account of the present results was presented at a recent Biophysical Society meeting Kawai and Wang (2013).
Fig. 1.
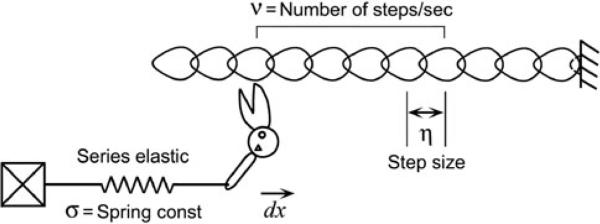
A graphic representation of the proposed cross-bridge model, in which cross-bridges cycle many times in the tension recovery period by stretching series elastic elements. Z-line is to the right, and M-line to the left
Materials and methods
Skinned skeletal muscle fibres from New Zealand white rabbit were used. The use of rabbits conformed with the current Guide for the Care and Use of Laboratory Animals (NIH publication DHSS/USPHS), and was approved by the University of Iowa's Animal Care and Use Committee. Rabbit of 3.5–5 kg weight was euthanized by injecting 150 mg/kg sodium pentobarbital into an ear vein. Strips of psoas, extensor digitorum longus (EDL) and tibialis anterior (TA) muscles were excised. Fibre bundles of ~15 mm in length and 2 mm in diameter were tied to wooden sticks at the in situ length using cotton thread and placed in the ice-cold Na skinning solution for 15–30 min. This was followed by K skinning solution for 30 min, and finally placed in the storage solution on ice for overnight. Next day the storage solution was replaced once again. The compositions of these solutions are found in Table 1 of our previous publication (Wang et al. 2013). The muscle bundles were then stored at –20 °C until used for experiments. On the day of experiments, skinned fibres (~3 mm in length and ~75 μm in diameter) were dissected from the bundles. Psoas fibres were used in the experiments to study the correlation between kTR and the ATP hydrolysis rate (ATPase). All three kinds of fibres (psoas, EDL, and TA) were used to study the correlation between kTR and the slow rate constant 2πa. The data of ATPase was taken from our previous publication (Zhao and Kawai 1994), which was measured on psoas fibres by the NADH fluorescence method with coupled enzyme systems, pyruvate kinase and lactate dehydrogenase.
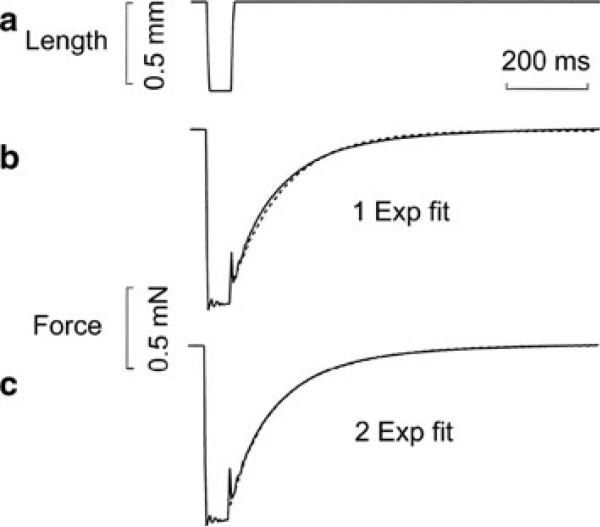
After mounting fibres to the experimental apparatus, the sarcomere length was adjusted to 2.5 μm using He–Ne laser (wavelength: 0.6328 μm) diffraction, and the fibre length (L0) and cross-sectional area were determined. The fibres were activated by the standard activating solution (6 mM CaEGTA, 5 mM MgATP, 1 mM Mg2+, 8 mM Pi, ionic strength 200 mM with KAc (Ac = acetate), pCa 4.6, pH 7.00). When the tension plateau developed, the length was suddenly released by 20 % L0, and restretched to the original length after 50 ms (Fig. 2a). Sinusoidal analysis was performed before the release-and-restretch experiment, because the latter disturbs fibres much more than the sinusoidal analysis. The method of sinusoidal analysis was described previously (Kawai and Brandt 1980; Wang et al. 2013). All the standard activations were performed at 20 °C, except for the temperature study. All data are expressed as mean ± standard error (SE).
Fig. 2.
Length (in a) and tension (in b and c) time courses. A rabbit psoas single muscle fibre was activated in the standard activating solution at 20 °C. When the tension plateau was reached, the length was suddenly released by 20 % L0 and restretched to L0 after 50 ms. The solid lines are the actual record, and the dotted lines are exponential fits (one exponential fit in b, and two exponential fit in c) with the following parameters: b kTR = 8 s–1, A = 0.93 mN; c kTR(slow) = 5.7 s–1, Aslow = 0.58 mN, kTR(fast) = 16.3 s–1, Afast = 0.42 mN; where kTR is the rate constant and A is its amplitude
The model
The model is depicted in Fig. 1. Here, x is the location of a myosin head, t is time, η is the step size, and v is the number of steps/sec (stepping rate, turnover rate, or cycling rate). From these definitions, it follows that
| (1) |
| (2) |
where dx is the distance traveled by the cross-bridge in time dt. This stretches the series elasticity with the spring constant σ by dx. The associated force increase (dF) for cross-bridges is:
| (3) |
Note that σ includes series elasticity of the thin filament, the thick filament, the myosin head, Z-line, and tendon if present. Our basic premise is that during force redevelopment (dF), the series elasticity elongates (dx), and filament sliding occurs according to Eq. 3.
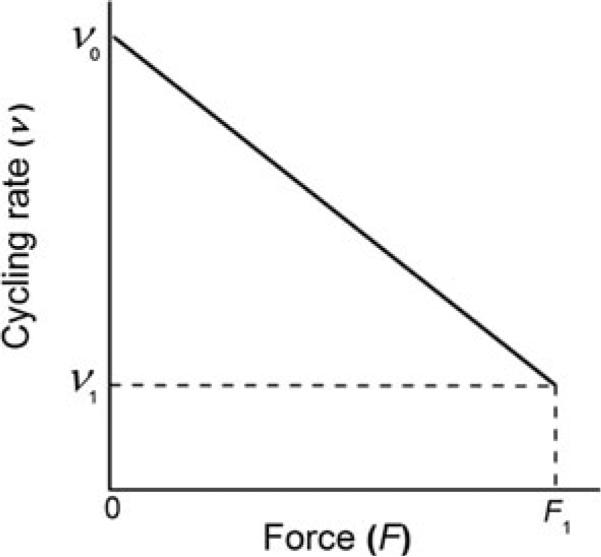
For the model we are proposing, one assumption needed is that the stepping rate (v) decreases linearly with an increase in force in the following way (Eq. 4).
| (4) |
where v1 is isometric cycling rate at F = F1, v0 is unloaded cycling rate at F = 0, and 0 ≤ F ≤ F1. We define λ : v1/v0 (0 < λ<1). The step size (η) is a constant (η0) for F < F1, but it becomes 0 for F = F1 (Eq. 5):
| (5) |
where subscript 0 indicates the unloaded condition, and 1 indicates the isometric condition. From Eqs. 4 and 5,
| (6) |
Eq. 6 corresponds to the linearized force–velocity relationship.
Equation 4 (Fig. 3) represents one interpretation of the Fenn (1923) effect , i.e. the stepping rate becomes less as force develops. There is experimental evidence for Eq. 6 by using skeletal muscle fibres (Piazzesi et al. 2007) and single molecules (Greenberg and Moore 2010).
Fig. 3.
A graphic representation of the Fenn effect (Eq. 4 in the text), i.e. the rate of stepping (v) becomes increasingly less as force develops
| (7) |
| (8) |
Equation 7 can be solved with the initial condition F(0) = 0 to result:
| (9) |
In a practical data fitting of the exponential time course, a constant (C) must be added to Eq. 9:
Because F(∞) = F1, we set
| (10) |
Equation 10 is the force time course, which approximates (dotted line) the data (solid line) in Fig. 2; see also (Brenner and Eisenberg 1986; Regnier et al. 1995; Stehle et al. 2002; Piroddi et al. 2003), where k ≡: kTR. The ATP hydrolysis rate is:
| (11) |
where Mc is the concentration of the myosin head.
Isometric values
Here we set F = F1. Then, v1 = λv0,
| (12) |
Two-state model
The two-state model (Huxley 1957; Podolsky 1968; Julian 1969; Brenner 1988) has been extensively used because of its simplicity. In this model (Brenner 1988),
| (13) |
where Det is the detached state and Att is the attached state. fa is the apparent rate constant of attachment, and ga is the apparent rate constant of detachment. The total concentration of myosin (Mc) equals the sum of concentrations of the detached and attached states.
| (14) |
Because of the steady-state,
| (15) |
| (16) |
Except for Mc, all the variables in Eq. 16 depend on F. The average time cross-bridges spend in the Det state (t̄det) is:
| (17) |
as expected (t̄det is the time constant of the attachment step). Similarly the average time in the Att state (t̄att) is:
| (18) |
One cycle time is the sum of the time spent in the two states:
If this equation and Eq. 16 are multiplied, then Eq. 11 results, confirming the derivation of t̄total. After combining Eqs. 12 and 16, we arrive at Eq. 19.
| (19) |
where fa1 and ga1 represent isometric values.
The model thus proposed is one of the simplest, because it does not consider non-linear filament compliance (Edman 2009; Nocella et al. 2013). The strain sensitivity of the rate constant is considered in Eq. 4, that the stepping rate (v) decreases linearly with an increase in force. The model proposed is also a simplified version, because it does not consider multiple attached states, and transitions between them are generally considered to be strain sensitive (Huxley and Simmons, 1971; Kawai and Halvorson, 2007). The case we have considered applies to shortening and isometrically held muscles as does the Fenn (1923) effect, but its applicability to lengthening muscle remains to be seen. The model assumes that the filament sliding occurs during force redevelopment, and this sliding stretches the series compliance.
Results
One or two exponential functions were fitted to the tension time course
The tension time course at standard activation from rabbit psoas fibres recorded by the experimental computer is plotted in Fig. 2b, c with solid lines. When this time course was fitted to one exponential function (Fig. 2b, broken line), we obtained the following results: k = 8.0 s–1, A = 0.93 mN, where k = kTR is the rate constant and A is the amplitude. When the same time course was fitted to two (fast and slow) exponential functions (Fig. 2c), the results are as follows: kslow = 5.7 s–1, Aslow = 0.58 mN, kfast = 16.3 s–1, and Afast = 0.42 mN. In Fig. 2b, there is a small departure between the data and fitted curve, whereas Fig. 2c the departure is almost absent.
The effect of temperature on fast and slow rate constants of kTR
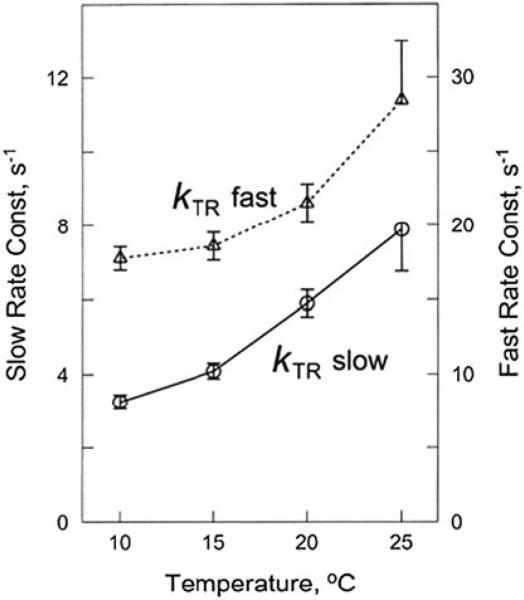
With skinned psoas muscle fibres, we studied kTR at temperatures in the range of 10–25 °C in every 5 °C. The effect of temperature on fast and slow rate constants of kTR is shown in Fig. 4. As expected, the temperature-rate constant plots show increasing functions with concave upward. Here we obtained Q10 = 1.8 for the slow component, and Q10 = 1.4 for the fast component.
Fig. 4.
The effect of temperature on fast and slow rate constants of kTR in rabbit psoas fibres
Relationship between kTR and ATPase at different temperatures
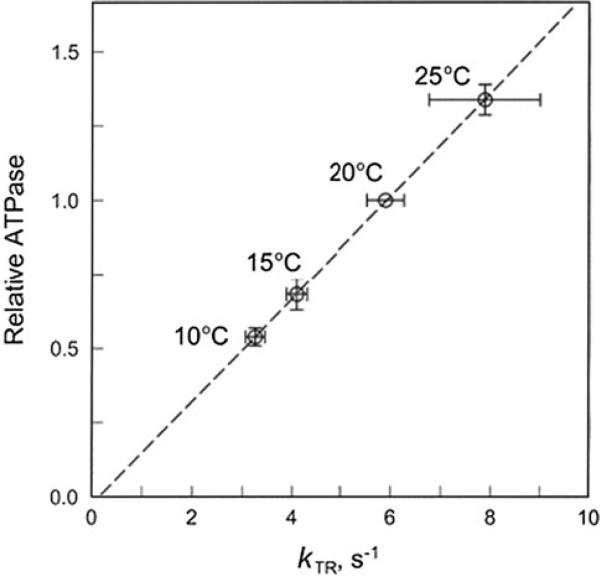
Through combining our published data on the isometric ATP hydrolysis rate (ATPase1) (Zhao and Kawai 1994) and the rate constant of the slow components in Fig. 4, ATPase is plotted against kTR in Fig. 5. This plot demonstrates nearly a perfect linear relationship with the intercept going through the origin, demonstrating that kTR and ATPase1 are proportionately related, and as predicted by Eq. 12.
Fig. 5.
Correlation between the ATP hydrolysis rate (ordinate) and the slow component of kTR (abscissa) in rabbit psoas fibres in the standard activating solution as the temperature is changed between 10 °C and 25 °C. The ATPase data were taken from our earlier publication (Zhao and Kawai, 1994), and normalized to that at 20 °C
Relationship between kTR and the rate constant 2πa
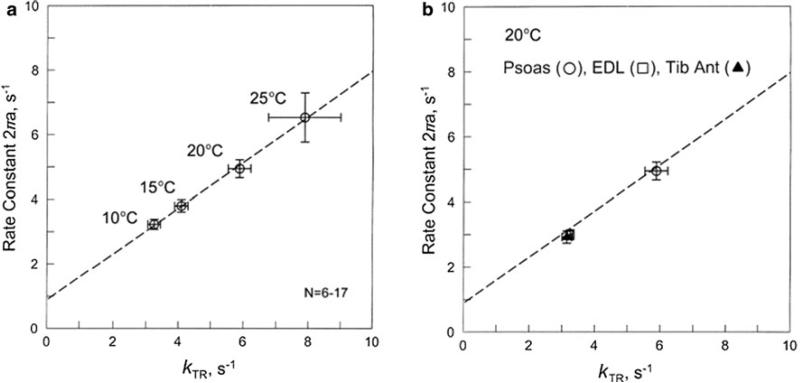
Sinusoidal analysis was performed immediately before the kTR measurement on the same preparations. The complex modulus Y(f) of fast twitch skeletal muscle fibres were fitted to the equation with three exponential processes, that included exponential processes A, B, and C (Eq. 2 in (Kawai and Brandt 1980)). The results are plotted in Fig. 6a for rabbit psoas fibres in which temperature was changed between 10 °C and 25 °C. Our results demonstrate that kTR deduced from release-restretch experiments and 2πa deduced from sinusoidal analysis are linearly related. Their empirical equation is:
| (20) |
Fig. 6.
Correlation between the apparent rate constant 2πa (sinusoidal analysis) and kTR as temperature is changed between 10 °C and 25 °C in rabbit psoas fibres in a, or different muscle fibres (psoas open circle, EDL open square, TA filled triangle) are compared at 20 °C in b. The points for EDL and TA overlap. From the regression line in a, Eq. 20 was deduced as the empirical relationship. The same line is drawn in b
This regression line in entered in Fig. 6a as a broken line. The correlation of kTR and 2πa was repeated for two other muscle types (EDL and TA) at 20 °C, and the results are plotted in Fig. 6b. The same regression line as in Fig. 6 a is entered in Fig. 6b. It is apparent that the data from two additional fast twitch fibres fall on the same regression line, except that the values for EDL and TA are about half of that of psoas fibres (Galler et al. 2005). As is well known, psoas contains 100 % type IID fibres, whereas EDL and TA contain significant amount of type IIA fibres (Hamalainen and Pette 1993; Galler et al. 2005) and may also contain a small amount of type I fibres (Lexell 1994). The experiments on EDL and TA, such as shown in Fig. 6b, were performed only on type IIA fibres by judging from the plot of complex modulus Y(f) (Galler et al. 2005).
Discussion
The cross-bridge model that account for kTR
Owing to its simplicity, kTR has been frequently used to characterize cross-bridge kinetics for ~25 years since its inception (Brenner 1988), but very little effort was spent on how to relate this parameter to the elementary steps of the cross-bridge cycle. In this report, we reexamined the tension redevelopment time course, and found that there are no differences in the results compared to those reported earlier. However, our interpretation of the time course is different, and we presented additional evidence. Based on these results, we propose a cross-bridge model that can provide both the theoretical and experimental bases for kTR. In the original model, kTR = fa + ga (Brenner 1988), hence it is limited by the fast reaction. That is, in the two-state model, if one rate constant is very much faster than the other, kTR measures primarily the faster rate constant of the two. However, it has been realized that kTR is never larger than ~40 s–1, while the rate constants of tension transients can be as large as 100–1,000 s–1 (Huxley and Simmons 1971; Heinl et al. 1974; Kawai 1978; Goldman and Simmons 1984; Fortune et al. 1991), hence it has been suggested that kTR may measure a slow reaction in the cross-bridge cycle (Gordon et al. 2000). The model we proposed in this report is consistent with this idea, and our result demonstrates that kTR is limited by the slowest forward rate constant of the cross-bridge cycle. Eq. 12 can be rewritten as:
| (21) |
Equation 21 demonstrates that kTR is proportionate to the turnover rate (v1), which is faga/(fa + ga) in the two-state model (Eq. 19). This quantity is limited by the slower reaction, if the two rate constants are very different. Therefore, it can be concluded that kTR = fa + ga as originally proposed (Brenner 1988) does not hold.
The best evidence comes from the proportionate relationship between kTR and the ATP hydrolysis rate when temperature was altered (Fig. 5). Because ATPase requires the cross-bridges to go through the entire cycle, it is easy to understand that ATPase is limited by the slowest reaction of the cycle. Eq. 21 forms the theoretical bases for this explanation.
Other evidence comes from the numerical evaluation of Eq. 21. The step size (η0) was reported to be 5.3 nm with the papain digested chicken skeletal muscle myosin S1 and rabbit skeletal actin (Kitamura et al. 1999), 9.7 nm in chicken pectoralis muscle (Sherwood et al., 2004), 12.6 nm in frog skeletal muscle (Wu and Nakamura, 2005), hence if we use the average value, η0 = 9.2 nm. The isometric ATPase rate was reported to be ATPase1 = 0.61 ± 0.04 mM s–1 at 20 °C (Kawai et al. 1987), and the myosin S – 1 concentration Mc = 0.21 ± 0.02 mM (Murakami and Uchida 1985) in rabbit psoas. Therefore, the isometric turnover rate is v1 = ATPase1/Mc = 2.90 s–1. The value for force:stiffness is reported to be F1/σ = 9.8 nm in rabbit psoas fibres at 19 °C (Linari et al. 2007). By using single myofibrils, kTR was reported to be 8 s–1 in rabbit psoas myofibrils at 15 °C (Piroddi et al. 2003). Our value for kTR (slow) is 6 s–1 for 20 °C (Fig. 4). Thus, the median value is kTR = 7 s–1. Therefore, Eq. 17 is satisfied if λ = 0.28, which is reasonable. Consequently, an agreement is obtained to validate Eq. 21, which further validates Eq. 12. In the case of the two-state model, these constants make Eq. 19 as follows:
| (22) |
The above analyses demonstrate that a measurement of kTR provides an estimate of the cross-bridge cycling rate (Eq. 21 and Fig. 5). Brenner and Eisenberg (Brenner and Eisenberg 1986) found that the time course of force redevelopment was fitted well by a single exponential function at the low level of Ca2+ activation (Brenner 1988), implying that force redevelopment is a first-order process. Metzger et al. also found, at all levels of Ca2+ activation the rate of tension redevelopment was well fitted by a single exponential function, which was recorded under sarcomere length control (Metzger et al. 1989). However, several other studies with rabbit psoas fibres found better fitting of the tension time course at high [Ca2+] by the sum of two exponential functions than by a single exponential function (Swartz and Moss 1992; Chase et al. 1994; Burton et al. 2005), although fitting with more than two exponentials did not provide a further improvement (Burton et al. 2005). The reason for the two exponentials is presumably because (1) nonlinear series elasticity (Edman 2009; Nocella et al. 2013), (2) possible nonlinear stepping rate (cf. Eq. 4), and/or (3) Eq. 5 may be more continuous than indicated. The nonlinearity introduces imperfectness in solving Eq. 7, resulting in a time course that is not a perfect exponential function, which makes the two exponential fit a better approximation.
The temperature effects
With our experiments, both fast and slow rate constant of kTR exhibited an increasing function of temperature (Fig. 4): the fast rate constants increased ~1.7 times (Q10 = 1.4), and the slow rate constant increased ~2.4 times (Q10 = 1.8) at the maximal Ca2+ activation in the temperature range 10–25 °C. When the temperature increases, both v0 (stepping rate) and kTR increase, but η0 (step size) and σ (stiffness of series elasticity) remain approximately unchanged. At the level of elementary steps of the cross-bridge cycle, the force generation step 4 (K4) increases with temperature, because it involves hydrophobic interaction (Zhao and Kawai, 1994), hence this step is an endothermic process. The increase in K4 results in an increase in the number of force-generating cross-bridges AM*ADP·Pi and AM*ADP (AM = actomyosin). This, in turn, results in an increase in the ATP hydrolysis rate, because ATPase = k6 [AM*ADP]. k6 is the rate constant of the ADP isomerization to AM ADP before ADP release, which is the slowest rate of the cross-bridge cycle where much of the work is performed (Kawai and Halvorson 2007), hence this step limits the cross-bridge cycling rate (v of Eq. 4).
The relationship between kTR and ATPase
The linear correlation between ATPase activity and kTR has been shown previously in single isolated human cardiomyocytes from atrial and ventricular tissues (Narolska et al. 2005). There is a roughly linear relationship between kTR and the unloaded shortening velocity over a tenfold range of shortening velocities in a variety of muscles at different conditions [reviewed by (Gordon et al. 2000)]. At the same time the shortening velocity was shown to have a linear relationship with actomyosin ATPase (Barany 1967), which implies a linear relationship between kTR and ATPase. Our results (Fig. 5) demonstrate that they are not only linear, but proportionately related, and as predicted by Eq. 21. Therefore, we conclude that kTR directly measures the steady-state cross-bridge turnover rate.
The relationship between kTR and kact
In single myofibril experiments, the rise of tension on Ca2+ activation (kact) and the tension redevelopment time course after release/restretch experiment (kTR) are remarkably similar, and kact = 7.9 s–1, and kTR = 8.0 s–1 were reported (Piroddi et al. 2003). This experiment was interpreted to mean that the same mechanochemical events take place in both time courses. If we combine the myofibril observation and our new interpretation of kTR, then it follows that the tension time course on Ca2+ activation likewise represents a stretching of the series elastic elements by multiple cross-bridge cycles, just as in the release-re-stretch experiment. In another words, when tension increases, it accompanies a stretch of series elastic elements, which would account for a difference in the Pi transients when [Pi] was decreased (tension increases) and [Pi] was increased (tension decreases) to result in the same [Pi] (Tesi et al. 2000) in myofibril experiments. Tension decrease is faster, because it can occur simultaneously with the cross-bridge detachment, whereas tension increase is slower, because it requires multiple cross-bridge cycles which is limited by a slow reaction. The rate constants of myofibril experiments are in the range 5–18 s–1 on rabbit psoas. In contrast, the asymmetric tension transient discussed by Huxley and Simmons (Huxley and Simmons 1971) or by Ranatunga et al. (2002) has a very fast time course (~500 s–1), and it likely represents an elementary step in the cross-bridge cycle. When one performs experiments at the slow time scale, such as carried out in this report, the fast signal is lost in the data collection process, hence not the subject of this report.
Relationship between kTR and slow exponential process A (phase 4) of tension transients
In addition to the two exponential processes present in the three-state model and detected by the perturbation analysis method, we have observed that the presence of series compliance results in an extra exponential process with the rate constant 2πa of process A, which is present in fast-twitch fibres (Galler et al. 2005; Kawai and Halvorson 2007). There have been suggestions that this process may represent the rate limiting step of the cross-bridge cycle [step 6 in Scheme 8 in Kawai and Halvorson (2007)]. This possibility has not been considered previously, because the transient analysis method in principle cannot resolve the slowest step of the cycle. However, this condition is lifted by introducing the series elasticity in the model. The linear relationship between kTR and 2πa has been demonstrated experimentally as the temperature was changed (Fig. 6a) or different muscle types were employed (Fig. 6b). Because the intercept value in Fig. 6 is small, and the slope is close to the unity, we can further approximate this relationship by 2πa ≈ kTR for simplicity and for practical purposes. Both kTR and 2πa values for EDL and TA fibres are about half compared to that for psoas fibres, because EDL and TA carry MHC IIA isoform, whereas psoas belongs to type IID fibres and carry only MHC IID isoform; type IID fibres respond more quickly than do type IIA fibres (Galler et al. 2005). The linear relationship between kTR and 2πa demonstrates that 2πa is also limited by the cross-bridge turnover rate.
Conclusions
In this paper, we have developed a cross-bridge model, in which during the force development, a cross-bridge cycles many times to stretch the series compliance to increase the force. It is a more comprehensive model than the earlier one described in Sect. 19 of Kawai and Halvorson (2007), and presented here together with new experimental evidence.
kTR is limited by the slowest reaction of the cross-bridge cycle, which is the ADP isomerization step 6 before its release, and not by the fastest reaction of the cycle as originally proposed (Brenner 1988). Previous model was not applicable for contracting muscle, because it assumed equilibrium between the two states, which did not consider multiple cross-bridge cycles and a consequent elongation of series elasticity. The slow component of kTR and the ATP hydrolysis rate are proportionately correlated when temperature is changed; hence kTR is proportionate to the cross-bridge cycling rate.
kTR and 2πa are linearly correlated based on the studies of different temperatures and different muscle types. kTR and 2πa are approximately the same.
Acknowledgments
This work was supported by grants from the National Institutes of Health HL070041 and The American Heart Association 13GRNT16810043. The content is solely the responsibility of the authors and does not necessarily reflect the official views of the National Center for Research Resources or the funding organizations.
References
- Barany M. ATPase activity of myosin correlated with speed of muscle shortening. J Gen Physiol. 1967;50(6 Suppl):197–218. doi: 10.1085/jgp.50.6.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner B. Effect of Ca2+ on cross-bridge turnover kinetics in skinned single rabbit psoas fibers: implications for regulation of muscle contraction. Proc Natl Acad Sci USA. 1988;85(9):3265–3269. doi: 10.1073/pnas.85.9.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner B. Muscle mechanics and biochemical kinetics. In: Squire JM, editor. Molecular mechanisms in muscular contraction. CRC; Boca Raton: 1990. pp. 77–149. [Google Scholar]
- Brenner B, Eisenberg E. Rate of force generation in muscle: correlation with actomyosin ATPase activity in solution. Proc Natl Acad Sci USA. 1986;83(10):3542–3546. doi: 10.1073/pnas.83.10.3542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton K, White H, Sleep J. Kinetics of muscle contraction and actomyosin NTP hydrolysis from rabbit using a series of metal-nucleotide substrates. J Physiol. 2005;563(Pt 3):689–711. doi: 10.1113/jphysiol.2004.078907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase PB, Martyn DA, Hannon JD. Isometric force redevelopment of skinned muscle fibers from rabbit activated with and without Ca2+. Biophys J. 1994;67(5):1994–2001. doi: 10.1016/S0006-3495(94)80682-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edman KA. Non-linear myofilament elasticity in frog intact muscle fibres. J Exp Biol. 2009;212(Pt 8):1115–1119. doi: 10.1242/jeb.020982. [DOI] [PubMed] [Google Scholar]
- Fenn WO. A quantitative comparison between the energy liberated and the work performed by the isolated sartorius muscle of the frog. J Physiol. 1923;58(2–3):175–203. doi: 10.1113/jphysiol.1923.sp002115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortune NS, Geeves MA, Ranatunga KW. Tension responses to rapid pressure release in glycerinated rabbit muscle fibers. Proc Natl Acad Sci USA. 1991;88(16):7323–7327. doi: 10.1073/pnas.88.16.7323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galler S, Wang BG, Kawai M. Elementary steps of the cross-bridge cycle in fast-twitch fiber types from rabbit skeletal muscles. Biophys J. 2005;89(5):3248–3260. doi: 10.1529/biophysj.104.056614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman YE, Simmons RM. Control of sarcomere length in skinned muscle fibres of Rana temporaria during mechanical transients. J Physiol. 1984;350:497–518. doi: 10.1113/jphysiol.1984.sp015215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon AM, Homsher E, Regnier M. Regulation of contraction in striated muscle. Physiol Rev. 2000;80(2):853–924. doi: 10.1152/physrev.2000.80.2.853. [DOI] [PubMed] [Google Scholar]
- Greenberg MJ, Moore JR. The molecular basis of frictional loads in the in vitro motility assay with applications to the study of the loaded mechanochemistry of molecular motors. Cytoskeleton. 2010;67(5):273–285. doi: 10.1002/cm.20441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamalainen N, Pette D. The histochemical profiles of fast fiber types IIB, IID, and IIA in skeletal muscles of mouse, rat, and rabbit. J Histochem Cytochem. 1993;41(5):733–743. doi: 10.1177/41.5.8468455. [DOI] [PubMed] [Google Scholar]
- Heinl P, Kuhn HJ, Ruegg JC. Tension responses to quick length changes of glycerinated skeletal muscle fibres from the frog and tortoise. J Physiol. 1974;237(2):243–258. doi: 10.1113/jphysiol.1974.sp010480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233(5321):533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- Huxley HE, Stewart A, Sosa H, Irving T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys J. 1994;67(6):2411–2421. doi: 10.1016/S0006-3495(94)80728-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julian FJ. Activation in a skeletal muscle contraction model with a modification for insect fibrillar muscle. Biophys J. 1969;9(4):547–570. doi: 10.1016/S0006-3495(69)86403-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M. Head rotation or dissociation? A study of exponential rate processes in chemically skinned rabbit muscle fibers when MgATP concentration is changed. Biophys J. 1978;22(1):97–103. doi: 10.1016/S0006-3495(78)85473-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M, Brandt PW. Sinusoidal analysis: a high resolution method for correlating biochemical reactions with physiological processes in activated skeletal muscles of rabbit, frog and crayfish. J Muscle Res Cell Motil. 1980;1(3):279–303. doi: 10.1007/BF00711932. [DOI] [PubMed] [Google Scholar]
- Kawai M, Halvorson HR. Force transients and minimum cross-bridge models in muscular contraction. J Muscle Res Cell Motil. 2007;28(7–8):371–395. doi: 10.1007/s10974-008-9131-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M, Wang L. Biophysical Journal. Philadelphia: 2013. A new theory on k(TR) with series elastic elements. Biophysical society meeting abstracts. p. 308a. [Google Scholar]
- Kawai M, Guth K, Winnikes K, Haist C, Ruegg JC. The effect of inorganic phosphate on the ATP hydrolysis rate and the tension transients in chemically skinned rabbit psoas fibers. Pflugers Arch. 1987;408(1):1–9. doi: 10.1007/BF00581833. [DOI] [PubMed] [Google Scholar]
- Kitamura K, Tokunaga M, Iwane AH, Yanagida T. A single myosin head moves along an actin filament with regular steps of 5.3 nanometres. Nature. 1999;397(6715):129–134. doi: 10.1038/16403. [DOI] [PubMed] [Google Scholar]
- Lexell J, Jarvis JC, Currie J, Downham DY, Salmons S. Fibre type composition of rabbit tibialis anterior and extensor digitorum longus muscles. J Anat. 1994;185(Pt 1):95–101. [PMC free article] [PubMed] [Google Scholar]
- Linari M, Caremani M, Piperio C, Brandt P, Lombardi V. Stiffness and fraction of myosin motors responsible for active force in permeabilized muscle fibers from rabbit psoas. Biophys J. 2007;92(7):2476–2490. doi: 10.1529/biophysj.106.099549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzger JM, Greaser ML, Moss RL. Variations in cross-bridge attachment rate and tension with phosphorylation of myosin in mammalian skinned skeletal muscle fibers. Implications for twitch potentiation in intact muscle. J Gen Physiol. 1989;93(5):855–883. doi: 10.1085/jgp.93.5.855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murakami U, Uchida K. Contents of myofibrillar proteins in cardiac, skeletal, and smooth muscles. J Biochem. 1985;98(1):187–197. doi: 10.1093/oxfordjournals.jbchem.a135257. [DOI] [PubMed] [Google Scholar]
- Narolska NA, van Loon RB, Boontje NM, Zaremba R, Penas SE, Russell J, Spiegelenberg SR, Huybregts MA, Visser FC, de Jong JW, van der Velden J, Stienen GJ. Myocardial contraction is fivefold more economical in ventricular than in atrial human tissue. Cardiovasc Res. 2005;65(1):221–229. doi: 10.1016/j.cardiores.2004.09.029. [DOI] [PubMed] [Google Scholar]
- Nocella M, Bagni MA, Cecchi G, Colombini B. Mechanism of force enhancement during stretching of skeletal muscle fibres investigated by high time-resolved stiffness measurements. J Muscle Res Cell Motil. 2013;34(1):71–81. doi: 10.1007/s10974-012-9335-4. [DOI] [PubMed] [Google Scholar]
- Piazzesi G, Reconditi M, Linari M, Lucii L, Bianco P, Brunello E, Decostre V, Stewart A, Gore DB, Irving TC, Irving M, Lombardi V. Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell. 2007;131(4):784–795. doi: 10.1016/j.cell.2007.09.045. [DOI] [PubMed] [Google Scholar]
- Piroddi N, Tesi C, Pellegrino MA, Tobacman LS, Homsher E, Poggesi C. Contractile effects of the exchange of cardiac troponin for fast skeletal troponin in rabbit psoas single myofibrils. J Physiol. 2003;552(Pt 3):917–931. doi: 10.1113/jphysiol.2003.051615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podolsky RJ. Deposit formation in muscle fibers following contraction in the presence of lead. J Cell Biol. 1968;39(1):197–201. doi: 10.1083/jcb.39.1.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW, Coupland ME, Mutungi G. An asymmetry in the phosphate dependence of tension transients induced by length perturbation in mammalian (rabbit psoas) muscle fibres. J Physiol. 2002;542(Pt 3):899–910. doi: 10.1113/jphysiol.2002.019471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regnier M, Morris C, Homsher E. Regulation of the cross-bridge transition from a weakly to strongly bound state in skinned rabbit muscle fibers. Am J Physiol. 1995;269(6 Pt 1):C1532–1539. doi: 10.1152/ajpcell.1995.269.6.C1532. [DOI] [PubMed] [Google Scholar]
- Sherwood JJ, Waller GS, Warshaw DM, Lowey S. A point mutation in the regulatory light chain reduces the step size of skeletal muscle myosin. Proc Natl Acad Sci USA. 2004;101(30):10973–10978. doi: 10.1073/pnas.0401699101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stehle R, Kruger M, Scherer P, Brixius K, Schwinger RH, Pfitzer G. Isometric force kinetics upon rapid activation and relaxation of mouse, guinea pig and human heart muscle studied on the subcellular myofibrillar level. Basic Res Cardiol. 2002;97(Suppl 1):127–135. doi: 10.1007/s003950200041. [DOI] [PubMed] [Google Scholar]
- Swartz DR, Moss RL. Influence of a strong-binding myosin analogue on calcium-sensitive mechanical properties of skinned skeletal muscle fibers. J Biol Chem. 1992;267(28):20497–20506. [PubMed] [Google Scholar]
- Tesi C, Colomo F, Nencini S, Piroddi N, Poggesi C. The effect of inorganic phosphate on force generation in single myofibrils from rabbit skeletal muscle. Biophys J. 2000;78(6):3081–3092. doi: 10.1016/S0006-3495(00)76845-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakabayashi K, Sugimoto Y, Tanaka H, Ueno Y, Takezawa Y, Amemiya Y. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys J. 1994;67(6):2422–2435. doi: 10.1016/S0006-3495(94)80729-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Muthu P, Szczesna-Cordary D, Kawai M. Diversity and similarity of motor function and cross-bridge kinetics in papillary muscles of transgenic mice carrying myosin regulatory light chain mutations D166V and R58Q. J Mol Cell Cardiol. 2013;62C:153–163. doi: 10.1016/j.yjmcc.2013.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu TC, Nakamura A. Step-size of net filament sliding of muscle contraction. Int J Biol Macromol. 2005;36(1–2):128–130. doi: 10.1016/j.ijbiomac.2005.03.015. [DOI] [PubMed] [Google Scholar]
- Zhao Y, Kawai M. Kinetic and thermodynamic studies of the cross-bridge cycle in rabbit psoas muscle fibers. Biophys J. 1994;67(4):1655–1668. doi: 10.1016/S0006-3495(94)80638-1. [DOI] [PMC free article] [PubMed] [Google Scholar]