Estimating Time to Disease Progression Comparing Transition Models and Survival Methods - an Analysis of Multiple Sclerosis Data

Summary

This paper reports an analysis that aims to quantify the effect of fingolimod, an oral treatment for relapsing remitting multiple sclerosis (MS), on disability progression. The standard approach utilizes survival analysis methods, which may be problematic for MS studies that assess disability at only a few time points and include as a cardinal feature both relapses and remissions. Instead, a Markov transition model, originally developed in the framework of longitudinal data, is fit, and its special probabilistic properties are used to estimate survival curves for time to disability progression. The transition approach models the whole disability process and uses all available transition data for inference, while survival methods concentrate on a single event of interest and use only time to event data. This paper compares the transition model approach to survival analysis methods, and discusses the differences in the interpretations of the estimated parameters. It applies both models to data obtained from two phase 3 clinical trials and finds that both yield positive effects for the new treatment compared to placebo, and provide similar estimates for the probability of disability progression over time. The transition model enables calculation of covariate-specific transition matrices that describe the short-term effect of treatment and other covariates on the disability process.

1. Introduction

Multiple sclerosis (MS) is a chronic inflammatory disease of the central nervous system whose clinical neurological symptoms include weakness, gait disturbance, ataxia, sensory loss, visual symptoms, and sphincter dysfunction. The Relapsing Remitting (RR) form of MS is characterized by periods (usually days or weeks) of neurologic symptoms (relapses) after which partial or complete resolution takes place, followed by periods (usually months or years) of clinical stability (remissions). Many treatments for MS aim at reducing the frequency of relapses, which is the main endpoint of many clinical trials. However, an equally important endpoint is the accumulation of disability. The latter is measured by the ordinal expanded disability status scale (EDSS) that ranges from 0, a normal neurological examination, to 10, death due to MS (Kurtzke, 1983). A key endpoint in many clinical trials is sustained or confirmed progression defined as an increase of at least one point in EDSS that lasts for at least 3 months.

In 2010, the U.S. Food and Drug Administration (FDA) and the European Medicines Agency (EMA) approved the first oral treatment for RRMS patients. The approval was based on the findings of two multi-national parallel-group phase 3 trials evaluating oral fingolimod, a sphingosine-1-phosphate receptor modulator that prevents the egress of lymphocytes from lymph nodes (Kappos et al., 2010; Cohen et al., 2010). These studies included a total of approximately 2500 patients randomized to placebo, fingolimod 0.5mg once daily, fingolimod 1.25mg once daily or interferon beta-1a 30µg (Avonex), a standard approved once weekly treatment administered by intramuscular route. The protocols required patients to visit the clinic every 3 months for one year in the active-controlled study (Cohen et al., 2010) and for two years in the placebo-controlled study (Kappos et al., 2010) for clinical evaluation and independent EDSS rating by a blinded assessor. In addition, all relapses occurring during the study period were confirmed and recorded. The studies concluded that fingolimod significantly reduces the annual relapse rate (the primary endpoint) in RRMS patients compared with either placebo or intramuscular interferon beta-1a.

The original analysis of fingolimod effect on EDSS (a secondary endpoint) followed the standard approach and utilized survival analysis methods, which may be inefficient for several reasons. First, confirmed progression requires a period of 3 months, which shortens the effective study periods of 12 and 24 months to 9 and 21 months, respectively. This, together with an often observed slow progression rate of MS, results in a small number of events over a period of two years (the duration of clinical studies in RRMS), potentially leading to low power for assessing the treatment effect. Second, the EDSS is an ordinal measure for which an increase of one point has different meanings at different EDSS levels. An increase from EDSS of 1 to EDSS of 2, for instance, does not carry the same clinical implication as an increase from EDSS 4 to 5. This requires stratified analysis which further reduces the effective sample size. Third, not all patients experience sustained progression before the end of study and by considering such individuals as censored important information is lost (Mandel et al., 2007). Fourth, although quantifying disability progression (i.e. worsening of the patient status) is of primary interest to patients and clinical community, some functional disability might be reversible, especially in a relapsing-remitting MS population. Studying the improvement in patient disability status may also provide some hints on the effect of a medicinal treatment. This possibility for EDSS to worsen (increase) and improve (decrease) complicates the definition of the endpoint and the corresponding analysis, but is disregarded in standard survival methods.

These difficulties, together with the study design of collecting EDSS data at pre-specified time points (3 month intervals) rather than continuously, suggest the use of methods tailored for longitudinal data analysis. In particular, methods based on transition models (Diggle et al., 2004) are natural alternatives for survival methods that circumvent the above-mentioned difficulties through modeling of the repeated categorical EDSS values, that is, the transition data from one state to another. In the context of MS, this approach was suggested and applied by several authors (Albert, 1994; Mandel et al., 2007; Gauthier et al., 2007; Mandel and Betensky, 2008). Essentially, the models adopt the Markov assumption of conditional independence that enables relatively simple estimation and interpretation of model parameters, and flexible ways to derive clinically relevant quantities, such as the distribution function of time to a certain EDSS level.

The aims of the current paper are to demonstrate the utility of transition models in analyzing disease progression in RRMS patients, and to assess the effect of fingolimod on EDSS using this method. Specifically, we aim to: (I) Assess how strongly fingolimod influence the probability to switch from one disability state to higher states, as compared to Avonex or placebo. (II) Assess the influence of baseline characteristics on the probabilities of transitioning from one state to another, which may help in identifying patients more likely to stay in low disability state vs. those more prone to disability progression. (III) Compare the results and clinical value of EDSS analysis performed using transition models and Cox proportional hazard models.

2. Methods

2.1 Modeling the EDSS Process

EDSS data were collected every 3 months for up to two years on n independent subjects. Let Y_it, denote the ordinal outcome (EDSS category) for patient i (i = 1,…, n) at time t (t = 0, …, T_i), where Y_it can take one of the values {1, …, J}, and let x_i, denote an m-dimensional baseline covariate vector measured for patient i. We use the modeling approach of Mandel et al. (2007), and Mandel and Betensky (2008) assuming a first order Markov dependency structure, that is, given all the history, the response Y_it depends on the vector of covariates x_i and on the response in the previous visit, Y_it−1, only. The following partial proportional odds model (PPOM) is used:

$$\text{Logit}\{P(Y_{\mathit{\text{it}}}\le j|x_i,Y_{\mathit{\text{it}}-1}=k)\}={\alpha }_{kj}+x_i^T\beta$$ (1)

where α_kJ = ∞. The EDSS value at the previous visit (lag-EDSS) is introduced as a covariate whose effect depends on both j and k, so that the model contains one intercept per pair of [EDSS, lag-EDSS]. However, the model maintains the proportional odds property for the m covariates, so that the total number of parameters is J(J − 1) + m. Note that the model is defined on the cumulative probability, hence enforces α_k1 ≤ α_k2 ≤ … ≤ α_kJ; the transition probability from state k to state j is given by:

$$P(Y_{\mathit{\text{it}}}=j|x_i,Y_{\mathit{\text{it}}-1}=k)=\frac{\text{exp}({\alpha }_{kj}+x_i^T\beta )}{1+\text{exp}({\alpha }_{kj}+x_i^T\beta )}-\frac{\text{exp}({\alpha }_{kj-1}+x_i^T\beta )}{1+\text{exp}({\alpha }_{kj-1}+x_i^T\beta )}$$ (2)

for k, j = 1, …, J, where we define α_k0 = −∞. If no covariates are used, the model imposes no restrictions on the transition probabilities from one state to another. Later on we will restrict some of the α_kJ values in order to reduce the number of parameters.

The model can be easily extended to handle time-dependent covariates or time-varying effects (Mandel et al., 2007). Such extensions are useful for long-term studies and less so for short ones where the covariates and their effects are not expected to change much.

A different path of extension is suitable when important subject-specific covariates are either not known or not measured. In such cases, the fixed-effects model (1) explains only part of the true heterogeneity in the data and can be extended by incorporating random effects into the transition matrix. Specifically, we assume that a latent random variable u_i having a density g satisfies the same proportional odds property as the observed covariates, so that

$$\text{Logit}\{P(Y_{\mathit{\text{it}}}\le y_{\mathit{\text{it}}}|{\{Y_{\mathit{\text{is}}}=y_{\mathit{\text{is}}}\}}_{s=0}^{t-1},x_i,u_i)\}=\text{Logit}\{P(Y_{\mathit{\text{it}}}\le y_{\mathit{\text{it}}}|Y_{\mathit{\text{it}}-1}=y_{\mathit{\text{it}}-1},x_i,u_i)\}={\alpha }_{y_{\mathit{\text{it}}-1}{y}_{\mathit{\text{it}}}}+x_i^T\beta +\gamma u_i,$$ (3)

where y_is is the EDSS of subject i as measured in her s’th visit. Conditionally on the covariate vector x_i and the EDSS at baseline, Y_i0, the likelihood of subject i with observed data (y_i0, …, y_iTi; x_i) is given by

$$\int \prod _{t=1}^{T_i}P(Y_{\mathit{\text{it}}}=y_{\mathit{\text{it}}}|Y_{\mathit{\text{it}}-1}=y_{\mathit{\text{it}}-1},x_i,u)g(u|Y_{i0}=y_{i0},x_i)du.$$ (4)

As discussed by Aitkin and Alfó (1998), the latent variable u is shared by all subject i’th responses Y_it, including the baseline state, and therefore is dependent of Y_i0. Moreover, as can be seen in (4), the random effect distribution may depend on the covariate vector x_i as well. Following Aitkin and Alfó (1998), we consider the natural location shift model $g(u|Y_{i0}=j,x_i)={\sigma }^{-1}{g}_0([u-{\zeta }_{0,j}-x_i^T\eta ])$ with ζ_0,1 = 0 and g₀ being the standard normal distribution, that is, $u_i=\sigma (z_i+{\zeta }_{0,y_{\mathit{\text{it}}-1}}+x_i^T\eta )$, where z_i ~ N(0, 1). Using this in (3), the model reduces to

$$\text{Logit}\{P(Y_{\mathit{\text{it}}}\le y_{\mathit{\text{it}}}|{\{Y_{\mathit{\text{is}}}=y_{\mathit{\text{is}}}\}}_{s=0}^{t-1},x_i,z_i)\}={\alpha }_{y_{\mathit{\text{it}}-1}{y}_{\mathit{\text{it}}}}+x_i^T\beta +\gamma \sigma (z_i+{\zeta }_{0,y_{\mathit{\text{it}}-1}}+x_i^T\eta )$$ (5)

Equation (5) clarifies an identification problem with the model, which was noted by Mandel and Betensky (2008); β itself is not identifiable, while β + γση is. However, the following two important observations enable effective inference: First, for a given z_i, the linear predictor $x_i^T\beta +\gamma \sigma [z_i+{\zeta }_{0,j}+x_i^T\eta ]$ is identifiable, and this suffices for valid inference regarding transition probabilities and progression, as discussed below. Second, when assignment of treatments to patients is independent of the random effect u, given the vector of covariates and the initial EDSS value, then the effect of treatment is identifiable and can be estimated and tested consistently. The latter independence requirement clearly holds in double blinded clinical trials. Thus, in our phase 3 data, testing for treatment effect and predicting time to sustained progression are both possible.

We will fit the model

$$\text{Logit}\{P(Y_{\mathit{\text{it}}}\le j|x_i,Y_{\mathit{\text{it}}-1}=k,u_i)\}={\alpha }_{kj}+x_i^T\beta +\sigma u_i,u_i~N(0,1),$$ (6)

where the treatment effect and the baseline EDSS value are contained in the vector x_i. Possible extensions of model (6) include dependence between the random effects and some of the covariates. Perhaps the most interesting extension in our framework takes the form $\text{Logit}\{P(Y_{\mathit{\text{it}}}\le j|x_i,Y_{\mathit{\text{it}}-1}=k,u_i)\}={\alpha }_{kj}+x_i^T\beta +u_{ki}$ with u_i = (u_1i, …, u_Ji)^T ~ N(0, Σ), in which a separate random effect is associated with each state of the process. Fitting such a model requires long sequences of EDSS in order to estimate Σ reasonably well. Since our data contain sequences of at most 9 observations, we consider an extension of model (6) with σ replaced by σ_k:

$$\text{Logit}\{P(Y_{\mathit{\text{it}}}\le j|x_i,Y_{\mathit{\text{it}}-1}=k,u_i)\}={\alpha }_{kj}+x_i^T\beta +{\sigma }_k{u}_i,~N(0,1),$$ (7)

In this model, heterogeneity of the population depends on the current state, where the larger ${\sigma }_k^2$, the larger the heterogeneity.

Maximum likelihood estimates and standard errors for parameters in Models (1), (6) and their extensions can be calculated using SAS procedure nlmixed; a sample code is given in Web Appendix A.

2.2 Prediction

Estimated transition probabilities for a typical patient can be obtained from equation (2) by using the patient’s covariates and the parameter estimates from model (1). Moreover, properties of Markov chains enable calculations of various derived quantities, and especially, the probability of transition from one state to another and the probability of progression over time. For example, let p_kj(x) = P(Y_it = j | x, Y_it−1 = k) be the transition probability from state k to state j for a typical patient with a covariate vector x, as described in (2), and let P(x) = (p_kj(x)) be the corresponding transition matrix whose k’th row contains the transitions from state k to the other states, then the probability of a patient who is now in state k to be in state j after 3 × s months is given by the (k, j) entry of P^s(x), the s’th power of P(x). Such matrix manipulations and operations can be easily performed using programming languages such as R or Matlab.

Similarly, for model (6), let p_kj(x, u) = P(Y_it = j | x, Y_it−1 = k, u) be the transition probability from state k to state j for a patient with a covariate vector x and a latent random effect u, and let P(x, u) = (p_kj(x, u)) be the corresponding transition matrix, then the s-step transition probabilities are given by ∫ P^s(x, u)σ⁻¹ϕ(u/σ), where ϕ is the standard normal density and the integration is conducted for each term of the matrix separately (for more details see Mandel and Betensky, 2008).

To estimate the probability of confirmed progression before time t, the technique described above can be used with the transition matrix being replaced by a ‘working matrix’. The working matrix is characterized by having an absorbing ‘artificial’ state to which the patient enters in case of a sustained progression at two consecutive visits. Construction of the working transition matrix is done by defining a new absorbing state, J + 1, and shifting all the probability between states larger than k to state J +1. For example, for k = 4 and J = 6, we define a new state ‘7’ and let p₅₇ = p₅₅ + p₅₆, p₆₇ = p₆₅ + p₆₆, and p₅₅ = p₅₆ = p₆₅ = p₆₆ = 0. It is easy to see that the entry in the 4’th row and 7’th column of the s’th power of this working matrix (or its integral if the random effects model is used) is the probability of a confirmed progression occurring at 3 × s months or before.

2.3 Choice of the Transition Probability Matrix

The large numbers of patients and transitions contained in the phase 3 fingolimod data enable a much more flexible modeling of the EDSS than in previous studies (Mandel et al., 2007; Gauthier et al., 2007; Mandel and Betensky, 2008). In particular, these earlier studies combined EDSS values of 3 and higher in one group and focused on transitions between the EDSS categories 0–1.5, 2–2.5 and 3+, whereas the current study has the opportunity to model and examine the transition rate between a larger range of EDSS values. We therefore partitioned the 3+ group to four groups: 3–3.5, 4–4.5, 5–5.5, and 6+. From knowledge on the natural history of MS and the definition of the EDSS categories, it was expected that transitions between distant states would be rare. Estimating the extremes of transition from states 1 to (4, 5, 6), or 2 to (5, 6), or 3 to (6), and vice versa, would therefore be challenging and in case of convergence, the estimates would probably be associated with relative large uncertainty. Therefore, it was decided to fix these estimates at 0 in the regression models and to use a 5-band transition matrix (18 constants instead of 30), that is, a 6 × 6 matrix with p_kj = 0 for |k − j| > 2.

It is worth noting that considering this simplified transition matrix is equivalent to removing extreme transitions in a data-driven manner. This approach could be criticized as the “0 entries” under-estimate the corresponding transition rates, which are rare but exist nonetheless. However, the bias is very small and it is of the order of the proportion of these “rare” events.

2.4 Model Evaluation

The transition model approach is very flexible and enables estimation of many derived quantities of interest as discussed briefly at the end of Section 2.1 and in more detail by Mandel et al. (2007). However, it involves matrix operations and numerical integration (when incorporating random effects), which complicates the calculation of standard errors and the construction of confidence intervals. Further, as quite strong parametric assumptions underpin the model, goodness-of-fit methods are essential to evaluate the quality of the inferences drawn from it.

Considering for simplicity model (1) and assuming the estimators satisfy the standard large sample property $\sqrt{n}({\mathrm{\alpha ̂}}_n-\alpha ,{\mathrm{\beta ̂}}_n-\beta )\to N(0,\Sigma )$, it is possible to derive confidence intervals for the probability of progression over time or any other derived quantity of interest, h(α, β), by:

1. Sampling B (e.g. B = 10,000) realizations (α₁, β₁), …, (α_B, β_B) from the N ((α̂_n, β̂_n), Σ̂/n) distribution.

2. Deriving h(α₁, β₁), …, h(α_B, β_B), the quantities of interest.

3. Calculating the variance of the realized h values and constructing normal based confidence intervals, or extracting the corresponding 2.5th and 97.5th percentiles.

For example, h(α, β) = h(α, β; x) could be either the 3-month transition probability from state k to state j, the 2-year transition probability, or the probability of confirmed progression before time t. All these quantities are functions of the estimated parameter vector (α̂_n, β̂_n), as discussed at the end of Section 2.2.

Note that α̂_n, β̂_n and Σ̂ are obtained in the maximization of the likelihood and are included in the output of the SAS procedure. The other steps are quite easy to perform in any language that supports matrix manipulations.

For goodness-of-fit purposes, it is natural to compare the ability of the model to predict the observed data. For this, the expected proportion of transitions from each type is compared graphically to the observed probabilities. This is done by comparing the one- and two-year transition proportions to the estimated probabilities based on the 3-month data. To describe uncertainty around observed probabilities of transition, binomial confidence intervals are also calculated.

3. Data

As aforementioned, we analyze data from two multi-center, randomized, double-blind phase 3 clinical trials. The TRANSFORMS trial (Cohen, 2010) was a 12-month study that compared two doses of fingolimod (p.o. 0.5mg and 1.25mg / day) to Avonex (i.m. 30µg / week), an approved MS therapy. The FREEDOMS trial (Kappos, 2010) was a 24-month study that compared the same two fingolimod doses to placebo. The entry criteria in both studies were similar: male and female patients, between 18 and 55 years of age, with active RRMS. The analysis includes all patients with EDSS data at two or more time points.

Baseline characteristics were similar in both studies and in all arms: average age of 37 years (SD=9), male to female ratio of 1:2, an average baseline EDSS of 2.3 (SD=1.4), and on average 2.2 (SD=1.2) documented relapses within two years prior to study start. In both studies, EDSS scores were determined every 3 months, but actual visits were allowed to deviate slightly from the schedule for logistical purposes. In order to address the problem of informative deviations from scheduled visit times, we removed EDSS data collected at a date deviating from schedule by more than 30 days.

Section B of the web appendix presents the distribution of baseline EDSS in the different treatment groups, which is a key measure of disease severity at the start of study. Table 1 presents the 3-month transition data for the four arms. Each row corresponds to transitions from one EDSS state to another and shows the percentages of transitions to the different states. In addition, the total number of transitions from each state is given (column entitled ‘No. row’). The table provides a crude estimate of the transition matrix for each arm without accounting for covariate effects. To estimate the 5-band matrix, we assign zeroes to cells as described in Section 2.3.

Table 1.

Transition percentages by arm and the numbers of transitions from each state.

Placebo
no. subjects = 387, no. transitions = 2619
Lag			EDSS				No. row
EDSS	0–1.5	2–2.5	3–3.5	4–4.5	5–5.5	6+
0–1.5	87.0	11.2	1.1	0.7	0	0	892
2–2.5	12.5	77.2	8.7	1.0	0.6	0	795
3–3.5	3.3	17.1	65.0	13.8	0.7	0.2	457
4–4.5	1.0	1.6	16.1	69.8	9.6	1.9	311
5–5.5	0	0.9	7.1	12.5	59.8	19.6	112
6+	0	0	3.8	5.8	15.4	75	52
Oral Fingolimod 0.5mg / day
no. subjects = 806, no. transitions = 4318
Lag			EDSS				No. row
EDSS	0–1.5	2–2.5	3–3.5	4–4.5	5–5.5	6+
0–1.5	88.4	10.3	1.2	0.2	0	0	1834
2–2.5	17.7	72.8	7.8	1.5	0.3	0	1165
3–3.5	3.0	14.3	71.9	9.8	0.6	0.4	694
4–4.5	1.1	3.2	17.5	72.2	5.0	0.9	439
5–5.5	0	0.7	2.0	10.8	73.6	12.8	148
6+	0	0	0	0	26.3	73.7	38
Oral Fingolimod 1.25mg / day
no. subjects = 763, no. transitions = 3956
Lag			EDSS				No. row
EDSS	0–1.5	2–2.5	3–3.5	4–4.5	5–5.5	6+
0–1.5	89.9	9.1	1.0	0	0	0	1646
2–2.5	16.2	72.6	9.8	1.0	0.3	0.1	1102
3–3.5	3.5	20.7	64.0	10.9	0.8	0.2	605
4–4.5	0.3	3.7	17.7	71.6	6.2	0.6	356
5–5.5	0	0.5	2.3	11.9	76.1	9.2	218
6+	0	0	3.4	3.4	34.5	58.6	29
Intra-muscular injected Interferon beta-1a (Avonex) 30µg / week
no. subjects = 392, no. transitions = 1441
Lag			EDSS				No. row
EDSS	0–1.5	2–2.5	3–3.5	4–4.5	5–5.5	6+
0–1.5	85.0	13.4	1.2	0.3	0	0	641
2–2.5	25.1	57.8	13.1	3.4	0.6	0	358
3–3.5	6.0	19.7	61.5	11.5	1.3	0	234
4–4.5	0.6	5.5	13.5	73.0	6.1	1.2	163
5–5.5	0	2.3	4.5	11.4	81.8	0	44
6+	0	0	0	0	100	0	1

Most patients have low EDSS values (i.e., EDSS<3) at baseline (see web appendix B) and as a consequence, the number of transitions from low EDSS levels are much larger than from higher levels (Table 1). Conclusions from an analysis ignoring these facts may be biased toward the lower scale of the EDSS. The high rate of staying in the same state (the main diagonals in Table 1) reflects the relatively slow progression of disease in RRMS patients. Also of note is the small number of 3-month transitions from low to high EDSS values, and vice versa, that supports the choice of the 5-band matrix. Such extreme transitions comprise less than 0.5% of our data.

4. Analysis

4.1 Transition Models

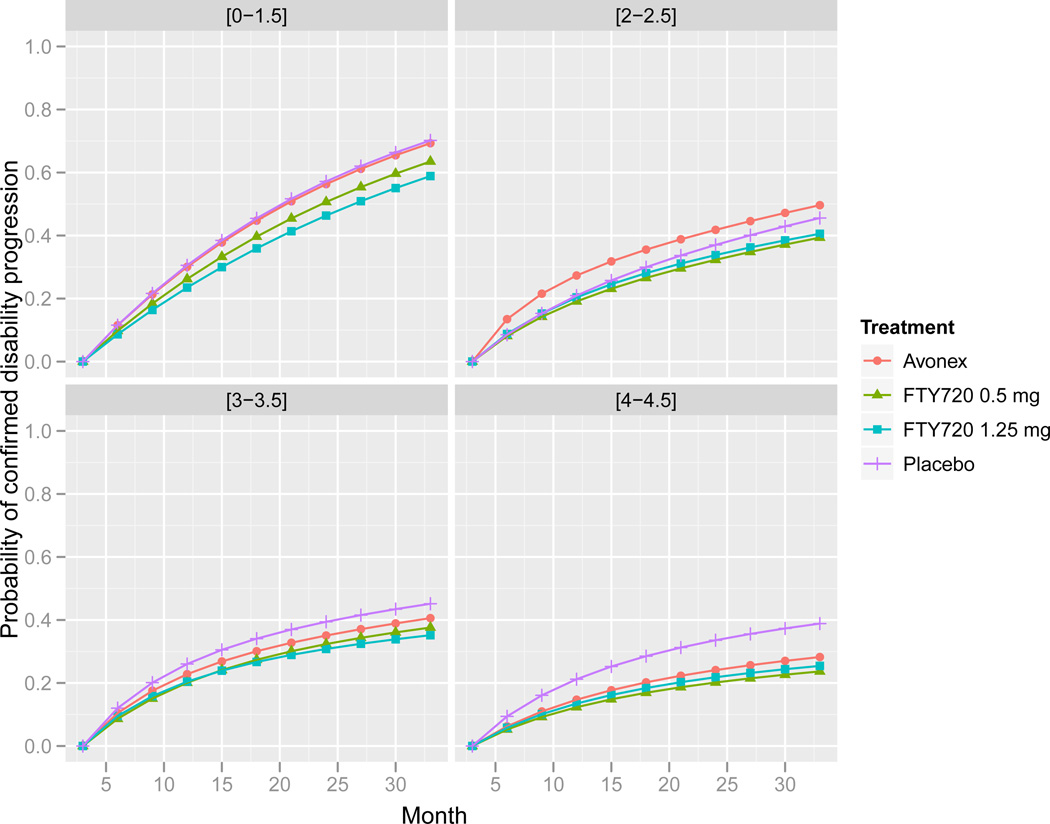
Table 1 gives crude estimates of the 3-month transition matrices for the different treatments. The worsening direction (entries above the diagonal) looks less severe in the treatment groups compared to placebo. For example, the crude probability of a patient having EDSS in the range 2–2.5 to experience worsening in the next three months is 0.103 in the placebo group and 0.096 in the fingolimod 0.5mg group (sum of entries to the right of the diagonal), while the corresponding probabilities of improvement are 0.125 and 0.177 (entries to the left of the diagonal). These transition matrices can be used to construct crude prediction curves for time to worsening or confirmed progression over time (see Section 2.2); Figure 1 presents such curves for patients with different baseline EDSS levels. The Figure shows that placebo patients tend to progress faster compared to patients treated with either fingolimod or Avonex. When comparing baseline EDSS levels, patients in the 0–1.5 group progress faster compared to the other EDSS groups; the group with the longest time to progression is 4–4.5.

Figure 1.

Probability of confirmed progression as a function of time stratified by treatment arm and baseline EDSS.

To account for observed and unobserved risk factors, we fit partial proportional odds models (1), (6),and (7) assuming the 5-band transition matrix described in Section 2.3. The following covariates were included in the model: Treatment group (4 groups), EDSS at baseline (5 categories), volume of brain T2 lesions at baseline (binary, cutoff=median), and duration of MS disease since first symptoms (binary, cutoff=5 years). Covariates that were excluded were: sex, which was considered as non relevant by the clinical advisors prior to the analysis; and age, which was found strongly correlated with MS duration. The number of relapses in the past two years and the number of Gadolinium-enhanced lesions at baseline were excluded in the model-building stage, using the Akaike information criterion.

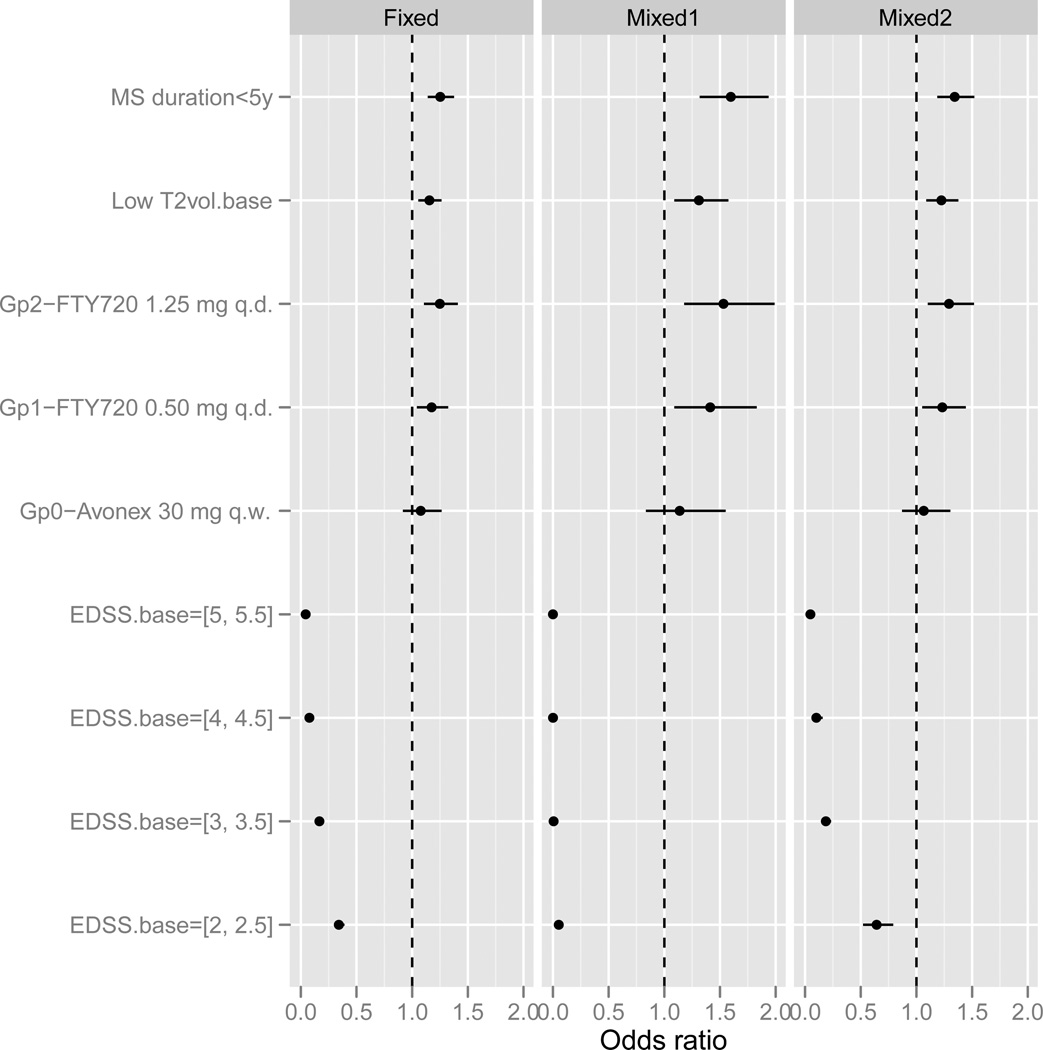
Because of the small number of transitions from state 6 and the difficulty of estimating the corresponding constants α_6j reliably, we excluded these parameters from the analysis; hence, only transitions to state 6 were calculated, but not transitions from 6 to other states. The estimated odds ratios (OR=exp(β)) of the fixed and random effects models are given in Figure 2 accompanied by the respective 95% confidence intervals. The fixed and random effects models show similar results, with the random effects estimates being slightly larger and having larger confidence intervals. The most important covariate in both models is baseline EDSS with a large negative effect, suggesting that patients with a more severe disease at baseline have a stronger tendency to deteriorate (conditional on the current EDSS level).

Figure 2.

Estimates and 95% confidence intervals for the fixed and random effects transition models. Odds ratio>1 indicates a protective covariate. Mixed1 - results of model (6), Mixed2 - results for model (7).

The results for baseline EDSS are seemingly inconsistent with those of Figure 1. However, care should be taken when interpreting the effect of baseline EDSS: The transition model controls for current disability status (effect given by the constants α_kJ), hence the β coefficients should be interpreted conditionally on the current status, while Figure 1 shows the marginal effect of baseline EDSS. Thus, the transition model compares patients having the same current EDSS level and hence the higher the baseline EDSS the larger the probability of progression, whereas the crude model (Figure 1) shows the marginal effect of baseline EDSS which depends on the clinical definition of the disability scale. That is, Figure 1 indicates that subjects are more likely to increase by one point on the EDSS scale if they start at 0–1.5 than at a higher level. Figure 2 indicates that subjects are more likely to increase by one point if they start at a high level of EDSS versus a low level, given their current level.

Fingolimod treatment, short disease duration and low lesion volume are significantly associated with slower rate of progression. Both fingolimod arms show a significant positive effect, with the 1.2mg arm estimated to be better than the 0.5mg arm (though the difference is not statistically significant). The Avonex effect is positive, but smaller than the fingolimod effects and not significantly different from placebo.

Comparing the two random effects models (6) and (7), we found the results of the latter to be quite similar to the fixed effects model. The variance terms, ${\sigma }_k^2$ are estimated to be 1.74, 0.92, 1.92, 0.05, and 2.24, for k = 1, …, 5, indicating a moderate difference in heterogeneity for different disability status.

To examine the sensitivity of the results to the choice of the 5-band transition matrix, we fit the fixed effects model (1) without any restriction on the transition matrix. The results are very similar to those obtained for the 5-band model; see Section C of the web-appendix.

The estimated transition models are used to generate subject-specific transition matrices that provide estimates for the probability of moving from one EDSS value to another in 3-month intervals. Transition matrices for subjects having the same vector of covariates are similar under the fixed-effects model, but are different under the mixed-effects model because different individuals have different values of the latent variable u. In Section D of the web appendix, we present transition matrices obtained by models (1) and (6) for several sets of covariates and for different values of u: u = 0 representing the ‘median’ transition matrix, and u = ± 1, representing matrices of ‘one standard deviation’ from the median. The matrices illustrate the effect of covariates on transition probabilities, either to higher or lower states, e.g., fingolimod 0.5mg reduces the rate of three month progression compared to placebo. They also show the large effect of baseline EDSS, where the probability of returning to the baseline level is always large. This is expected for our short term followup data as MS is a relapsing remitting disease that progresses slowly, and recruitment criterions required patients to have active disease and did not allow to enroll patients during a relapse. Finally, the three representative matrices calculated under the random effects model describe the heterogeneity of the disease. If the data contained long EDSS sequences, then the subject-specific random effect variables u_i could be estimated reliably, providing subject-specific transition matrices. However, for short EDSS data, this is not practical (see Mandel and Betensky, 2008).

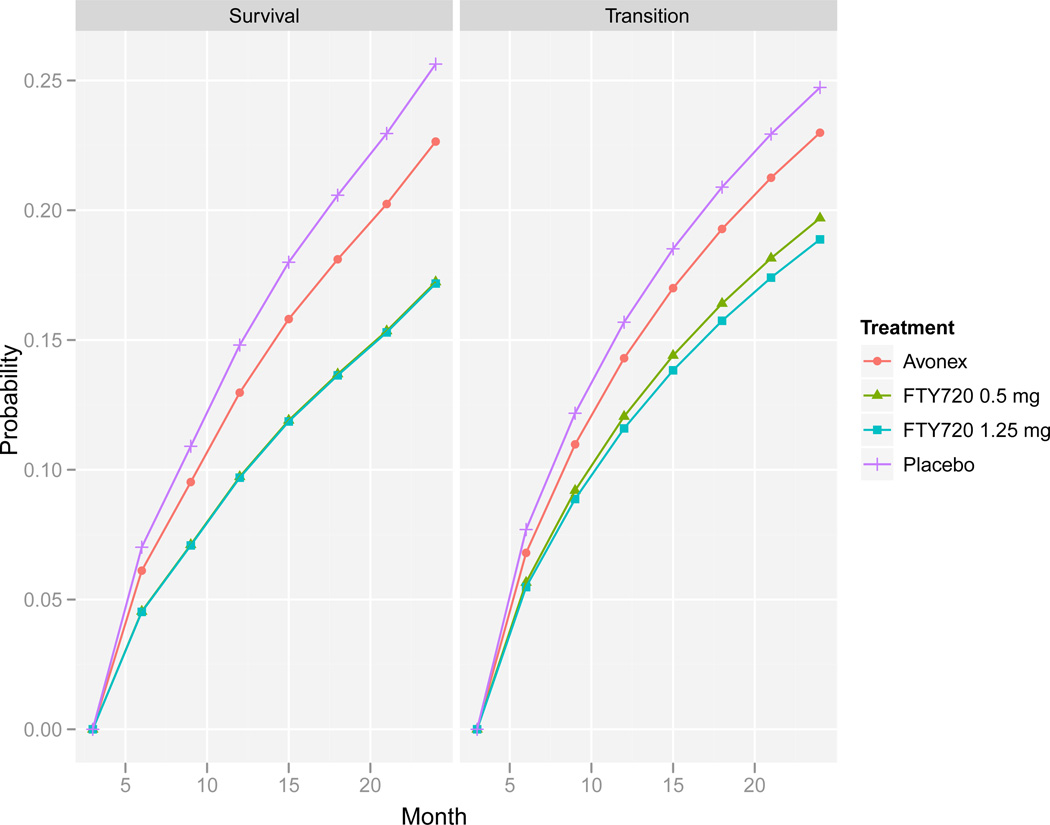
The model results are then used to calculate the probability of sustained progression as a function of time. For given baseline EDSS level, lesion volume and disease duration, a transition matrix is calculated using the estimated parameters, and probability curves are obtained by selecting the appropriate cell from powers of a modified transition matrix as discussed in Section 2.2. These estimated curves are comparable to covariate-specific probabilities obtained in survival regression analysis. The right panel of Figure 3 compares the estimated probabilities of sustained progression for the different arms for patients in the lowest EDSS group at baseline, having a disease duration <5 years and a lesion volume <median (this is the most frequent covariate profile in our data). The curves are based on the random effects model (6) and were calculated by averaging the results of 5000 simulations from the estimated distribution of the random effects. After 24 months, the model estimates the average probability of sustained progression for patients treated by fingolimod 0.5mg and fingolimod 1.25mg to be slightly less than 0.2 compared to placebo patients whose probability is estimated to be 0.25. Theoretically, such graphs can be used to calculate the probability for any time point and to calculate and compare the median time to progression for the different treatment arms. However, estimation of long-term progression is not recommended as the long-term performance of the model cannot be assessed from the data.

Figure 3.

Probability of confirmed progression over time by treatment arm based on the random effects transition model (right) and the Cox proportional hazard model (left). Covariates: EDSS at baseline 0–1.5, disease duration <5 years and lesion volume <median.

Goodness of fit of models (1) and (6) is examined as described at the end of Section 2.4. Figure 1 in web appendix E displays the expected proportions of one- and two-year transitions between pairs of states and compares them to the observed proportions. The overall performance is satisfactory, though the figure shows some disagreement, especially for transitions from state 5 to other states. This may be due to differential effects of covariates in different phases of the disease. As the number of transitions from state 5 is relatively small, we did not try to fit a model with covariates-lag EDSS interactions, though this may be an important extension of our model when more data are available.

As model based P-values may be inaccurate when the underlying parametric assumptions do not hold, we calculated exact p-values using a permutation test (Berger, 2000) by assigning patients randomly to the four arms, keeping the group sizes fixed, and fitting the fixed effects model to the generated data. We repeated this process 1000 times and calculated the percentage of times the estimates of the treatment effects were larger than the one obtained in the original data. We obtained one sided p-values of 0.023, 0.001 and 0.164 for the fingolimod 0.5mg, fingolimod 1.25mg, and Avonex arms, respectively, which confirmed our previous finding (see Figure 2).

4.2 Survival Analysis

We analyzed the data using standard survival analysis methods, similar to the ones performed in the original phase 3 studies, with the difference being that data from the two phase 3 studies are now pooled. As in the original studies, the endpoint is time to first confirmed progression defined as the time to first increase of 1 point in EDSS relative to baseline (0.5 point for baseline EDSS of 5.5) that lasts for two consecutive visits separated by at least 3 months. Table 2 presents the Kaplan-Meier survival estimates and the corresponding standard errors for the confirmed progression time. The survival curve for the Avonex arm is estimated only up to 12 months as this treatment was included only in the one-year study. The analysis suggests a significant reduction in the probability of progression from 0.24 for confirmed progression over two years in the placebo arm to 0.15–0.16 in the fingolimod groups.

Table 2.

Kaplan-Meier survival estimates (standard errors), and p-value of the Log Rank test against the placebo arm.

arm	6m	9m	12m	15m	18m	21m	24m	P-val
Placebo	0.945 (0.012)	0.913 (0.015)	0.871 (0.017)	0.842 (0.019)	0.817 (0.020)	0.796 (0.022)	0.761 (0.024)
FTY 0.5	0.961(0.007)	0.933 (0.009)	0.910 (0.010)	0.886 (0.013)	0.866 (0.015)	0.849 (0.016)	0.842(0.017)	0.008
FTY 1.25	0.948(0.008)	0.925 (0.010)	0.904 (0.011)	0.889 (0.013)	0.877 (0.014)	0.864 (0.015)	0.845 (0.018)	0.011
Avonex	0.944 (0.012)	0.914 (0.014)	0.880 (0.017)					0.166

We also fit a proportional hazard (Cox) model to the data in order to control for covariate effects. We considered the same covariates as in the transition models, using baseline EDSS once as a categorical covariate and once as a strata. The results are summarized in Table 3. The two models (stratified and not) give almost identical results, with both fingolimod arms significantly reducing the risk of progression. As in the transition models, both short disease duration and low lesion volume at baseline are protective factors, but not statistically significant here while they were significant under the transition models. The results for baseline EDSS differ from those of the transition model because the transition model controls for current disability status (see the discussion in the previous section regarding the marginal and conditional effect of baseline EDSS). In fact, the Cox model results are consistent with Table 1 and Figure 1 that show that patients in the EDSS group 0–1.5 tend to progress faster compared to patients in the other groups.

Table 3.

Results of proportional hazard models.

	Baseline EDSS as a covariate		Baseline EDSS as strata
	Hazard Ratio	95% CI	Hazard Ratio	95% CI
MS duration < 5y	0.855	(0.669, 1.094)	0.856	(0.669, 1.095)
Low T2.vol base	0.910	(0.718, 1.152)	0.911	(0.719, 1.154)
FTY 0.5mg	0.639	(0.470, 0.868)	0.637	(0.469, 0.866)
FTY 1.25mg	0.636	(0.465, 0.870)	0.633	(0.462, 0.866)
Avonex	0.867	(0.587, 1.281)	0.859	(0.787, 1.721)
EDSS.base=[5, 5.5]	1.218	(0.752, 1.974)
EDSS.base=[4, 4.5]	0.636	(0.416, 0.973)
EDSS.base=[3, 3.5]	0.600	(0.422, 0.854)
EDSS.base=[2, 2.5]	0.636	(0.475, 0.852)

The left panel of Figure 3 compared the probability of confirmed progression over time estimated by the Cox proportional hazard model for the four treatment groups in patients with low baseline EDSS, disease duration <5 years and lesion volume <median. The results are very similar to those shown in the right panel, which are based on the transition model. The two fingolimod arms are hardly distinguished with estimated two-year probability of progression of about 0.17. The respective estimated probabilities of progression in patients treated with placebo and Avonex are 0.26 and 0.22, respectively.

5. Discussion

This paper analyzes the effect of fingolimod on clinical disability of RRMS patients using transition models and compares the results to the more standard survival models. We found that both fingolimod arms decrease the disability progression rate compared to placebo after controlling for baseline covariates. This positive effect was found in the fixed and random effects transition models as well as in the Cox proportional hazard model. The most important covariate for short-term progression was baseline EDSS. Other important factors influencing EDSS are short disease duration and low T2 lesion volume at baseline, which were found to be protective. Avonex showed a smaller positive effect than the fingolimod arms and the effect was not significantly different from placebo. However, Avonex was only tested for one year and therefore there were low numbers of transitions (see Table 1). As a consequence, the estimate of its effect size is most variable.

Estimators obtained by transition models and by survival analysis techniques should show similar results when the Markov assumption holds (at least approximately) and when data are complete and comprise long EDSS sequences. However, these requirements are rarely satisfied. When considering which analysis to conduct, one point to keep in mind is the different data used by the survival and transition model approaches. Survival analysis is based on time to first confirmed progression data and the analysis ignores any changes in the EDSS that are not sustained and cannot account for intermittent missingness, whereas the transition model estimates the transition rate and does not distinguish between confirmed and temporary progression. In the current study, the outcomes from the Cox proportional hazard model and the transition model are highly concurrent as both approaches provide similar results for the treatment effects. The similarity of the prediction curves constructed by the two approaches and presented in Figure 3 illustrates this point. As transition models use the whole EDSS sequence, they are deemed to be more appropriate than survival methods to analyze longitudinal categorical data, especially when long-term follow-up is limited and data are subject to intermittent missingness. In addition, such models provide important information about the EDSS process by estimating short term probabilities for both improvement and deterioration. However, they are based on parametric assumptions that may fail to hold. Further study is needed in order to compare the methods in terms of power and sample-size/patient-years under different designs and effect sizes and to identify scenarios in which the transition model is substantially more powerful.

Three transition models were fit to the data, one fixed effects model and two models with a random component. The latter models are more general, relax the Markov assumption on the sequence of EDSS values and can be used to predict patient-specific transition matrices by predicting the latent variable u_i (but see Mandel and Betensky 2008 for the limitation of prediction in this framework). They are especially attractive for heterogeneous populations, e.g., MS patients, in which unobserved latent variables may explain part of the heterogeneity. However, estimation of random effects models involves maximization of a complicated function, and despite the existence of powerful procedures convergence problems often arise. We have found that using estimates of a fixed effects model as initial values for estimation of the random effects model often overcome convergence problems.

It is important to examine the sensitivity of the model to the underlying assumptions. We therefore extended the transition models in different directions such as including different sets of covariates, relaxing the proportional odds assumptions, and replacing the first-order Markov assumption with a second-order model. In all of our models, the findings of a positive effect of fingolimod on progression remain with only small changes in the size of the effect. Furthermore, we calculated exact p-values using a robust permutation test that confirmed our model based finding.

As part of checking the assumptions, a separate model has been fit to each arm. This resulted in better fit according to a likelihood ratio test, and showed good graphical fit. However, there are drawbacks for such an approach that limited its use. First, the number of parameters is much larger as a separate set of coefficients has to be estimated for each arm. This makes the estimates more variable and the goodness of fit test less reliable. More important, there is no simple way of comparing treatments as there is no one coefficient corresponding to treatments in this modeling approach. This is of main concern as comparison of treatments is the primary goal of clinical trials. One way to compare treatment groups is by comparing the estimated probabilities of progression after, say, two years on treatment. However, these probabilities depend on the covariate vector and may lead to different conclusions for different profiles. In fact, when trying this approach, we found that for most covariate profiles, fingolimod reduced progression compared to placebo, but for a few profiles, the probability of progression for the placebo patients was slightly smaller than that of fingolimod; though the differences were not statistically significant. More data and further explorations into these treatment-by-covariate interactions would be required in order to identify and characterize differential effects of the new treatment in various sub-populations.