Incorporating Network Structure in Integrative Analysis of Cancer Prognosis Data

Abstract

In high-throughput cancer genomic studies, markers identified from the analysis of single datasets may have unsatisfactory properties because of low sample sizes. Integrative analysis pools and analyzes raw data from multiple studies, and can effectively increase sample size and lead to improved marker identification results. In this study, we consider the integrative analysis of multiple high-throughput cancer prognosis studies. In the existing integrative analysis studies, the interplay among genes, which can be described using the network structure, has not been effectively accounted for. In network analysis, tightly-connected nodes (genes) are more likely to have related biological functions and similar regression coefficients. The goal of this study is to develop an analysis approach that can incorporate the gene network structure in integrative analysis. To this end, we adopt an AFT (accelerated failure time) model to describe survival. A weighted least squares approach, which has low computational cost, is adopted for estimation. For marker selection, we propose a new penalization approach. The proposed penalty is composed of two parts. The first part is a group MCP penalty, and conducts gene selection. The second part is a Laplacian penalty, and smoothes the differences of coefficients for tightly-connected genes. A group coordinate descent approach is developed to compute the proposed estimate. Simulation study shows satisfactory performance of the proposed approach when there exist moderate to strong correlations among genes. We analyze three lung cancer prognosis datasets, and demonstrate that incorporating the network structure can lead to the identification of important genes and improved prediction performance.

Introduction

In high-throughput cancer studies, it has been noted that results from the analysis of single datasets can be unsatisfactory. For example, the identified markers may have low reproducibility. Multiple factors may contribute to the unsatisfactory performance, including for example the highly noisy nature of cancer genomic data, technical variations of profiling techniques and, more importantly, small sample sizes of individual studies. Recent studies have shown that pooling and analyzing multiple studies may effectively increase sample size and improve properties of the identified markers [Guerra and Goldsterin 2009; Liu et al. 2012; Ma et al. 2011]. Multi-dataset methods include meta-analysis and integrative analysis methods. Integrative analysis pools and analyzes raw data from multiple studies and can be more informative than meta-analysis, which analyzes multiple studies separately and then pools summary statistics (lists of identified genes, p-values, effect sizes, etc). In this article, we analyze cancer prognosis studies with survival outcomes and gene expression measurements, but note that other types of outcomes and genomic measurements may be studied in a similar manner.

In the existing integrative analysis studies, it has been assumed that gene effects are interchangeable. Biomedical studies have suggested that there exists inherent interplay among genes. For example, genes belonging to the same pathways tend to have similar biological functions and correlated expressions. Transcription factors and their downstream regulated target genes can be highly correlated. Since transcription factors can up-regulate (promote) or down-regulate (suppress) the expressions of their downstream target genes, the correlations among them can be both positive and negative. Other examples involve tumor suppressor genes and genes that code enzyme. There are multiple ways of describing the interplay among genes, one of which is the network structure. In network analysis, a node represents a gene. Two nodes are connected if the corresponding genes are biologically or statistically “correlated”. The strength of connection depends on the strength of correlation. In the analysis of single datasets, network analysis has been conducted. For example, Li and Li [2008] proposed a network-constrained regularization approach to analyze genomic data. Huang et al. [2011] proposed a sparse Laplacian shrinkage method for variable selection and estimation. A two-step sparse boosting approach was developed in Ma et al. [2012]. Bayesian approaches have also been developed [Edwards et al. 2012]. However, to the best of our knowledge, network-based analysis has not been pursued in the context of integrative analysis.

In this article, we conduct integrative analysis of multiple cancer prognosis datasets with gene expression measurements. Our goal is to incorporate the gene network structure in the selection of cancer-associated genes. To this end, we describe cancer survival using an AFT (accelerated failure time) model. Compared with alternatives such as the Cox model, the AFT model has a significantly simpler objective function and hence lower computational cost, which is especially desirable with high-throughput data. In addition, its regression coefficients may have more lucid interpretations. For gene selection, we adopt penalization, which has been extensively used in cancer genomic studies. The proposed penalty is built upon the MCP (minimax concave penalty) [Zhang 2010], which, in single-dataset analysis, has been shown to have performance better than or comparable to Lasso, adaptive Lasso, elastic net, SCAD and others [Huang et al. 2012; Breheny and Huang 2011]. In the integrative analysis of multiple datasets, the effects of a gene are represented with a vector of regression coefficients. Thus, a group MCP approach is adopted for gene selection. To incorporate the network structure, a second, Laplacian penalty is added. The goal of the Laplacian penalty is to smooth the differences between regression coefficients of tightly-connected genes. The overall penalty and proposed approach are hence referred to as sparse group Laplacian shrinkage or SGLS. A group coordinate descent (GCD) algorithm is developed for implementing the SGLS.

Integrative Analysis of Cancer Prognosis Studies

Data and model settings

Assume that there are M independent studies, and there are n^m iid observations in study m(= 1, . . . , M). The total sample size is n = ∑_m n^m. In study m, denote T^m as the logarithm (or another known monotone transformation) of the failure time. Denote X^m as the length-p vector of gene expressions. For simplicity of notation, assume that the same set of genes are measured in all M studies. For the ith subject, the AFT model assumes that

$$T_i^m={\beta }_0^m+X_i^{m\prime }{\beta }^m+{∊}_i^m,$$ (1)

where ${\beta }_0^m$ is the intercept, ${\beta }^m\in {\mathbb{R}}^p$ is the length-p vector of regression coefficients, and ${∊}_i^m$ is the error term. When $T_i^m$ is subject to right censoring, we observe ($Y_i^m$, ${\delta }_i^m$, $X_i^m$), where $Y_i^m=\min \{T_i^m,C_i^m\}$, $C_i^m$ is the logarithm of the censoring time, and ${\sigma }_i^m=\mathrm{I}\{T_i^m\le C_i^m\}$ is the event indicator.

When the distribution of ${∊}_i^m$ is known, the parametric likelihood function can be easily constructed. Here we consider the more flexible case where this distribution is unknown. In the literature, multiple estimation approaches have been developed, including for example the Buckley-James and rank-based approaches. In this study, we adopt the weighted least squares estimation approach [Stute 1996], which has the lowest computational cost. This property is especially desirable with high-throughput data.

Let F̂^m be the Kaplan-Meier estimator of the distribution function F^m of T^m. F̂^m can be written as ${\widehat{F}}^m\left(y\right)={\sum }_{i=1}^{n^m}{\omega }_i^m\mathrm{I}\{Y_{\left(i\right)}^m\le y\}$, where ${\omega }_i^m$ are the jumps in the Kaplan-Meier estimator and can be expressed as

$${\omega }_1^m=\frac{{\delta }_{\left(1\right)}^m}{n^m},{\omega }_i^m=\frac{{\delta }_{\left(i\right)}^m}{n^m-i+1}\prod _{j=1}^{i-1}{\left(\frac{n^m-j}{n^m-j+1}\right)}^{{\delta }_{\left(j\right)}^m},i=2,\dots ,n^m.$$

${\omega }_i^m\mathrm{s}$ are also referred to as the Kaplan-Meier weights. Here $Y_{\left(1\right)}^m\le \cdots \le Y_{\left(n^m\right)}^m$ are the order statistics of $Y_i^m\mathrm{s}$, and ${\delta }_{\left(1\right)}^m\dots ,{\delta }_{\left(n^m\right)}^m$ are the associated censoring indicators. Similarly, let $X_{\left(1\right)}^m,\dots ,X_{\left(n^m\right)}^m$ be the associated gene expressions of the ordered $Y_i^m\mathrm{s}$. Stute [1996] proposed the weighted least squares estimator (${\widehat{\beta }}_0^m$, ${\widehat{\beta }}^m$) that minimizes

$$\frac{1}{2}\sum _{i=1}^{n^m}{\omega }_i^m{(Y_{\left(i\right)}^m-{\beta }_0^m-X_{\left(i\right)}^{m\prime }{\beta }^m)}^2.$$ (2)

We center $X_{\left(i\right)}^m$ and $Y_{\left(i\right)}^m$ using their ${\omega }_i^m$-weighted means, respectively. Define

$${\stackrel{‒}{X}}_w^m=\sum _{i=1}^{n^m}{\omega }_i^m{X}_{\left(i\right)}^m∕\sum _{i=1}^{n^m}{\omega }_i^m,{\stackrel{‒}{Y}}_w^m=\sum _{i=1}^{n^m}{\omega }_i^m{Y}_{\left(i\right)}^m∕\sum _{i=1}^{n^m}{\omega }_i^m.$$

Let $X_{\omega \left(i\right)}^m=\sqrt{{\omega }_i^m}(X_{\left(i\right)}^m-{\stackrel{‒}{X}}_w^m)$ and $Y_{\omega \left(i\right)}^m=\sqrt{{\omega }_i^m}(Y_{\left(i\right)}^m-{\stackrel{‒}{Y}}_w^m)$. With the weighted centered values, the intercept is zero. The weighted least squares objective function can be written as

$$L^m\left({\beta }^m\right)=\frac{1}{2}\sum _{i=1}^{n^m}{(Y_{\omega \left(i\right)}^m-{X_{\omega \left(i\right)}^m}^{\prime }{\beta }^m)}^2.$$ (3)

Denote ${\mathbf{Y}}^m={(Y_{\omega \left(1\right)}^m,\dots ,Y_{\omega \left(n^m\right)}^m)}^{\prime }$ and ${\mathbf{X}}^m={(X_{\omega \left(1\right)}^m,\dots ,X_{\omega \left(n^m\right)}^m)}^{\prime }$. Further denote Y = (Y^1′, . . . , Y^M′)′, X = diag(X¹, . . . , X^M) and β = (β^1′, . . . , β^M′)′.

With M independent studies, consider the overall objective function $L\left(\beta \right)={\sum }_{m=1}^M{L}^m\left({\beta }^m\right)$. Note that with this objective function, larger datasets have more contributions. When desirable, normalization by sample size can be applied.

Construction of network adjacency measure

In network analysis, a node corresponds to a gene. The most important characteristic of a network is perhaps the adjacency measure, which quantifies how closely two nodes are connected. The adjacency measure is often defined based on the notion of similarity (between nodes). In this section, we describe several adjacency measures used in our numerical study. These measures have been motivated by their counterparts in single-dataset analysis [Zhang and Horvath 2005; Huang et al. 2011]. The main difference between this study and published ones is that here we conduct the integrative analysis of multiple independent datasets, and so the similarity measure needs to be computed using multiple datasets. For the similarity measure between two nodes, the simplest possibility is to use the absolute value of the Pearson's correlation coefficient. Here the underlying assumption is that the correlation structures among genes are similar across datasets. Denote r̂_jk as the Pearson's correlation coefficient between gene j and gene k computed using the M datasets. Other correlation measures such as the Spearman's correlation can also be used. A drawback of this approach is that it cannot directly accommodate missingness of gene expressions. An alternative is to use the canonical correlation, which can easily accommodate missingness. Denote ${\widehat{\pi }}_{jk}$ as the canonical correlation between gene j and gene k computed using the M datasets.

Consider a_jk, which measures the strength of connection between nodes (genes) j and k. Here we focus on undirected network where a_jk = a_kj for j, k = 1, . . . , p. Based on the similarity measure defined above, we construct the adjacency matrix, whose (j, k)th element is a_jk, as follows. (N.1) a_jk = I{|r̂_jk| > r}, where r is the cutoff calculated from the Fisher transformation [Huang et al. 2011]; (N.2) $a_{jk}=\mathrm{I}\{{\widehat{\pi }}_{jk}>\pi \}$, where π is the cutoff calculated from permutation which corresponds to the null that all genes are not associated with cancer survival; (N.3) $a_{jk}=\frac{1}{1+e^{-\alpha ({\widehat{\pi }}_{jk}-\pi )}}$, where α > 0 can be determined by the scale-free topology criterion [Zhang and Horvath 2005] and π is defined in N.2; (N.4) $a_{jk}={\widehat{\pi }}_{jk}^{\alpha }$, where α is defined in N.3; (N.5) $a_{jk}={\widehat{\pi }}_{jk}^{\alpha }\mathrm{I}\{{\widehat{\pi }}_{jk}>\pi \}$, with α and π defined in N.3 and N.2, respectively; (N.6) a_jk = |r̂_jk|I{|r̂_jk| > r} with r defined in N.1; (N.7) $a_{jk}={\widehat{\pi }}_{jk}\mathrm{I}\{{\widehat{\pi }}_{jk}>\pi \}$ with π defined in N.2. Among the above definitions, N.1 and N.2 are unweighted and only measure whether two nodes are connected or not, whereas the rest are weighted and also measure the strength of connection. N.1, N.2, N.5, N.6 and N.7 are sparse in that some components may be exactly zero. N.3 and N.4 are two “soft” adjacency measures [Zhang and Horvath 2005]. N.5 is the sparse version of N.4. N.6 and N.7 are closely related to N.1 and N.2, respectively, defined based on similar measures.

With undirected network, there are other ways of defining the similarity measure and so adjacency matrix. The above options have been motivated by published single-dataset studies. Undirected network and adjacency matrix may not provide a complete description of the interplay among genes. We conjecture that it is possible to extend the proposed approach and accommodate information beyond the above adjacency matrix. Such an extension is nontrivial and not pursued in this article.

Sparse Group Laplacian Shrinkage

Denote ${\beta }_j^m$ as the jth component of β^m. Then ${\beta }_j={({\beta }_j^1,\dots ,{\beta }_j^M)}^{\prime }$ represents the effects of gene j across M datasets. Consider the penalized estimate

$$\widehat{\beta }=argmin\left\{\frac{1}{n}L\left(\beta \right)+P_{\lambda ,\gamma }\left(\beta \right)\right\},$$

where

$$P_{\lambda ,\gamma }\left(\beta \right)=\sum _{j=1}^p\rho \left(\Vert {\beta }_j\Vert ;\sqrt{M_j}{\lambda }_1,\gamma \right)+\frac{1}{2}{\lambda }_{2}d\sum _{1\le j<k\le p}{a}_{jk}{\left(\frac{\Vert {\beta }_j\Vert }{\sqrt{M_j}}-\frac{\Vert {\beta }_k\Vert }{\sqrt{M_k}}\right)}^2.$$ (4)

Here λ = (λ₁, λ₂) with λ₁ ≥ 0 and λ₂ ≥ 0 are tuning parameters, ρ is the MCP with tuning parameter λ₁ and regularization parameter γ, ∥ · ∥ is the L₂ norm, and M_j is the “size” of β_j. When the M datasets have matched gene sets, M_j ≡ M. We keep M_j so that the formulation can directly accommodate partially matched gene sets. In numerical study, when gene j is not measured in dataset k, we take the convention ${\beta }_j^k\equiv 0$. d ≡ max_j M_j.

Denote $\theta ={({\theta }_1,\dots ,{\theta }_p)}^{\prime }={(\frac{\Vert {\beta }_1\Vert }{\sqrt{M_1}},\cdots ,\frac{\Vert {\beta }_p\Vert }{\sqrt{M_p}})}^{\prime }$. We express the nonnegative quadratic form in the second penalty term in (4) using a positive semi-definite matrix L, which satisfies

$${\theta }^{\prime }L\theta =\sum _{1\le j<k\le p}{a}_{jk}{({\theta }_j-{\theta }_k)}^2,\forall \theta \in {\mathbb{R}}^p.$$ (5)

Let A = (a_jk, 1 ≤ j, k ≤ p) and G = diag(g₁, . . . , g_p), where $g_j={\sum }_{k=1}^p{a}_{jk}$. In a network where a_jk is the weight of edge (j, k), g_j is the degree of vertex j. We then have ∑_1≤j<k≤p a_jk(θ_j – θ_k)² = θ′(G – A)θ . Thus, L = G – A.

With the matrix notation, the SGLS penalty (4) can be written as

$$P_{\lambda ,\gamma }\left(\theta \right)=\sum _{j=1}^p\rho ({\theta }_j;{\lambda }_1,\gamma )+\frac{1}{2}{\lambda }_{2}d{\theta }^{\prime }L\theta .$$ (6)

Here the Laplacian matrix is not normalized, meaning that the weight g_j is not standardized to 1. In problems where predictors should be treated without preference with respect to network connectivity, we can first normalize the Laplacian such that L* = I_p – A* with A* = G^–1/2AG^–1/2 and use the following penalty function

$$P_{\lambda ,\gamma }\left(\theta \right)=\sum _{j=1}^p\rho ({\theta }_j;{\lambda }_1,\gamma )+\frac{1}{2}{\lambda }_{2}d{\theta }^{\prime }{L}^{\ast }\theta .$$

A normalized Laplacian L* can be viewed as a special case of the general L. In this study, we focus on formulation (6). In network analysis of gene expression data, it has been suggested that genes with higher connectivity tend to have more important biological implications [Zhang and Horvath 2005; Ma et al. 2012]. It is therefore sensible to consider the unnormalized Laplacian.

Rationale

Formulation (4) has been motivated by the following considerations. In our analysis, genes are the functional units for selection. Thus the first penalty imposes p individual penalties, with one for each gene. For gene j, its effects in the M datasets are represented by a group of regression coefficients, where the group size is M_j. Thus, the penalty is imposed on the group norm of regression coefficients. For gene selection, we adopt the MCP defined as

$$\rho (t;{\lambda }_1,\gamma )={\lambda }_1{\int }_0^{\mid t\mid }{\left(1-\frac{x}{{\lambda }_1\gamma }\right)}_{+}dx,$$ (7)

where for any a ∈ R, a₊ = aI{a ≥ 0}. The rationale of the MCP has been well discussed in Zhang [2010], Huang et al. [2012], Liu et al. [2012] and others, and will not be repeated here. The second penalty accommodates the network structure. In particular, tightly-connected genes (with large a_jks) are expected to have closely related biological functions and similar regression coefficients [Zhang and Horvath 2005]. We impose penalty on the difference between ∥β_j∥ and ∥β_k∥ to promote smoothness of estimated regression coefficients of connected genes. We note that there exist other ways of promoting smoothness. We have experimented with a few other formulations and found that the proposed one has the best performance.

In single-dataset analysis, adopting the sum of two penalties (with the first for selection, and the second to accommodate finer structure) has been proposed. Examples may include the fused Lasso, elastic net, sparse group Lasso [Friedman et al. 2010], and the approach in Huang et al. [2011]. The main difference between SGLS and these approaches is that it is developed for the integrative analysis of multiple datasets. In addition, censored survival data is analyzed, which can be more complicated than simple continuous data in the published studies. Another difference is that fused Lasso only smoothes between adjacent covariates. In this study, there is no spatial structure, and SGLS smoothes over all pairs of genes. The network adjacency measure is accounted for, which also differs from fused Lasso and elastic net.

Computation

Prior to analysis, for each dataset, we standardize each gene expression to have marginal mean zero and variance one. For computation, we consider a group coordinate descent (GCD) algorithm. This algorithm optimizes the objective function with respect to one gene at a time, and iteratively cycles through all genes. The overall cycling is repeated multiple times until convergence.

Denote X_j as the submatrix of X that corresponds to β_j. Consider the overall objective function

$$\tilde{L}(\beta ,\lambda ,\gamma )=\frac{1}{2n}{\Vert \mathbf{Y}-\sum _{j=1}^p{\mathbf{X}}_j{\beta }_j\Vert }^2+\sum _{j=1}^p\rho (\Vert {\beta }_j\Vert ;\sqrt{M_j}{\lambda }_1,\gamma )+\frac{1}{2}{\lambda }_{2}d\sum _{1\le j<k\le p}{a}_{jk}{\left(\frac{\Vert {\beta }_j\Vert }{\sqrt{M_j}}-\frac{\Vert {\beta }_k\Vert }{\sqrt{M_k}}\right)}^2.$$ (8)

For j = 1, . . . , p, given the group parameter vectors β_k (k ≠ j) fixed at their current estimates ${\tilde{\beta }}_k^{\left(s\right)}$, we seek to minimize L̃(β, λ, γ) with respect to the jth group parameter β_j. Here only terms involving β_j in L̃(β, λ, γ) matter. This is equivalent to minimizing

$$R\left({\beta }_j\right)=\frac{1}{2}a{\beta }_j^{\prime }{\beta }_j-{\mathbf{b}}^{\prime }{\beta }_j+c\Vert {\beta }_j\Vert +C\left(\tilde{\beta }\right),$$ (9)

where C is a term free of β_j, and a, b and c are defined as follows.

• For $\Vert {\beta }_j\Vert \le \gamma {\lambda }_1\sqrt{M_j}$,

$$\begin{array}{c}\hfill a=1+{\lambda }_2\sum _{k:k\ne j}\frac{a_{jk}}{M_j}-\frac{1}{\gamma },\mathbf{b}=\frac{1}{n}{\mathbf{X}}_j^{\prime }\mathbf{r}+{\tilde{\beta }}_j^{\left(s\right)},\hfill \\ \hfill c={\lambda }_1\sqrt{M_j}-\frac{{\lambda }_{2}d}{\sqrt{M_j}}\sum _{k:k\ne j}\frac{a_{jk}}{\sqrt{M_k}}\Vert {\tilde{\beta }}_k\Vert .\hfill \end{array}$$ (10)

where r is the working residual evaluated at the current estimate (to be defined below).

• For $\Vert {\beta }_j\Vert >\gamma {\lambda }_1\sqrt{M_j}$,

$$a=1+{\lambda }_2\sum _{k:k\ne j}\frac{a_{jk}}{M_j},c=-\frac{{\lambda }_{2}d}{\sqrt{M_j}}\sum _{k:k\ne j}\frac{a_{jk}}{\sqrt{M_k}}\Vert {\tilde{\beta }}_k\Vert .$$

while b remains the same as under the previous situation.

It can be shown that the minimizer of R(β_j) in (9) is

$${\tilde{\beta }}_j=\frac{1}{a}{\left(1-\frac{c}{\Vert \mathbf{b}\Vert }\right)}_{+}\mathbf{b}.$$ (11)

This explicit solution facilitates implementation of the GCD algorithm described below.

Let ${\tilde{\beta }}^{\left(0\right)}={({\tilde{\beta }}_1^{\left(0\right)\prime },\dots ,{\tilde{\beta }}_p^{\left(0\right)\prime })}^{\prime }$ be the initial value. A convenient choice for the initial value is zero (component wise). With fixed γ, λ₁ and λ₂, the GCD algorithm proceeds as follows:

1. Set s = 0. Initialize the vector of residuals $\mathbf{r}=\mathbf{Y}-{\sum }_{j=1}^p{\mathbf{X}}_j{\tilde{\beta }}_j^{\left(0\right)}$.

2. For j = 1, . . . , p,

   1. Calculate a, b and c as in expression (9);
   2. Update ${\tilde{\beta }}_j^{(s+1)}$ using expression (11);
   3. Update $\mathbf{r}\leftarrow \mathbf{r}-{\mathbf{X}}_j({\tilde{\beta }}_j^{(s+1)}-{\tilde{\beta }}_j^{\left(s\right)})$;

3. Update s ← s + 1;

4. Repeat Steps 2 and 3 until convergence.

Convergence of this algorithm follows from Theorem 4.1(c) of Tseng [2001]. It is achieved with all simulated data and the lung cancer data. The objective function can be rewritten as $f\left(\beta \right)=f_0\left(\beta \right)+{\sum }_{j=1}^p{f}_j\left({\beta }_j\right)$ where

$$f_0\left(\beta \right)=\frac{1}{2n}{\Vert \mathbf{Y}-\sum _{j=1}^p{\mathbf{X}}_j{\beta }_j\Vert }^2+\frac{1}{2}{\lambda }_{2}d\sum _{1\le j<k\le p}{a}_{jk}{\left(\frac{\Vert {\beta }_j\Vert }{\sqrt{M_j}}-\frac{\Vert {\beta }_k\Vert }{\sqrt{M_k}}\right)}^2,$$

and $f_j\left({\beta }_j\right)=\rho (\Vert {\beta }_j\Vert ;\sqrt{M_j}{\lambda }_1,\gamma )$. Since f₀ is regular in the sense of Tseng [2001] and ${\sum }_{j=1}^p{f}_j\left({\beta }_j\right)$ is separable (group-wise), the GCD solution converges to a coordinatewise minimum point of f, which is also a stationary point. Research code written in R is available at http://works.bepress.com/shuangge/43/.

Tuning parameter selection

The SGLS approach involves three tuning parameters: λ₁, λ₂ and γ. In our numerical study, we search for optimal tunings using V-fold cross validation (V = 5). More specifically, we apply two-dimensional search for λ₁ and λ₂, with λ₂ ∈ (0, 0.001, 0.01, 0.1, 1, 10). λ₁ and λ₂ control the shrinkage and smoothness of group predictors, respectively. Let λ_1max be the smallest λ₁ for which all regression coefficients are shrunk to zero. From the update step 2a, ${\lambda }_{1max}={\max }_j\Vert n^{-1}{\mathbf{X}}_j^{\prime }\mathbf{Y}\Vert ∕\sqrt{M_j}$. For preset ∊(= 0.01), we are able to generate a sequence of λ₁ values from λ_1max to ∊λ_1max. For a fixed number of steps, we can have a sequence that is equal-spaced in logarithm, since the difference of summarized prediction error in V-fold cross-validation is small at large λ₁. It is expected that λ₁ cannot go down to very small values which correspond to regions not locally convex. The cross validation criteria over non-locally convex regions may not be monotone. Generally speaking, smaller values of γ are better at retaining the unbiasedness of the MCP penalty for large coefficients, but they also have the risk of creating objective functions with a nonconvexity problem that are difficult to optimize and yield solutions that are discontinuous with respect to λ. It is therefore advisable to choose a γ value that is big enough to avoid this problem but not too big. In our numerical study, we consider values including 1.8, 3, 6 and 10, as in published studies. In practice, to reduce computational cost, one may fix the value of γ (for example, γ = 6 as suggested by published studies). However searching over λ₁ and λ₂ has to be conducted. As the GCD algorithm only involves simple calculations, cross validation is computationally affordable. For example, the analysis of one simulated dataset (details described below), including tuning parameter selection and estimation, takes less than ten minutes on a desktop PC.

Numerical Study

Simulation

We conduct simulation to better gauge performance of the proposed approach. We simulate three datasets, each with 100 subjects. For each subject, we simulate the expressions of 500 genes. The gene expressions are jointly normally distributed, with marginal means equal to zero and variances equal to one. The 500 genes belong to 100 clusters, with 5 genes per cluster. We consider the following correlation scenarios. Scenario 1: genes in different clusters have independent expressions, and expressions of genes i and j within the same cluster have correlation coefficient ρ^|i–j|; Scenario 2: expressions of genes i and j have correlation coefficient ρ^|i–j|; Scenario 3: genes in different clusters have independent expressions, and expressions of genes i and j within the same cluster have correlation coefficient ρ. Scenarios 1 and 2 correspond to the auto-regressive correlation, whereas scenario 3 corresponds to the compound symmetric correlation. Under scenarios 1 and 3, important and noisy genes are independent, whereas under scenario 2, they are correlated. We consider three levels of correlation with ρ = 0.1, 0.5, 0.9, standing for weak, moderate and strong correlation, respectively. Among the 500 genes, the first 20 (4 clusters) have nonzero regression coefficients. The nonzero coefficients are randomly generated from the uniform distribution on [0.25, 0.75]. The log event times are generated from the AFT models with zero intercept and N(0, 1) random errors. The log censoring times are independently generated from normal distributions. The average censoring rate is about 50%.

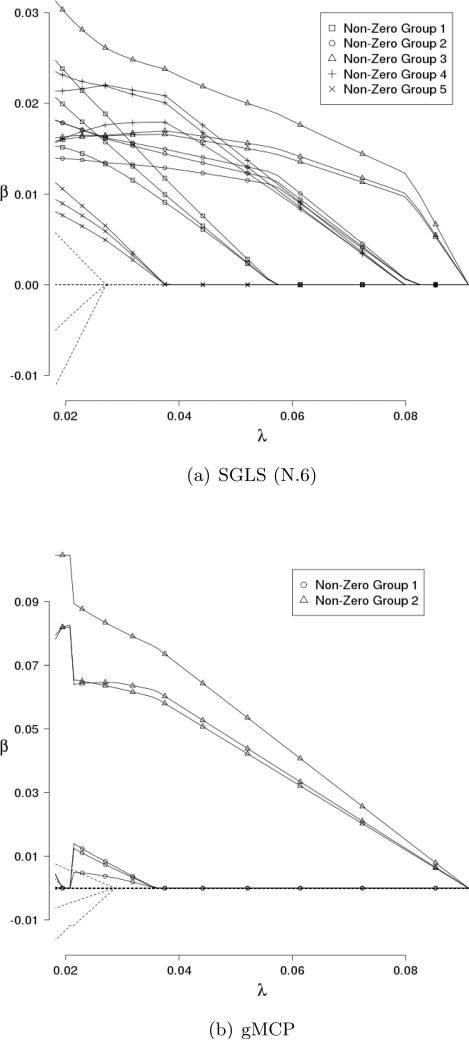
We first explore the solution paths – estimates as a function of tuning parameters. We simulate one set of data under scenario 1 with ρ = 0.5. Multiple parameters are involved in SGLS. Here, we fix γ = 3 and λ₂ = 0.1, and show the estimates as a function of λ₁ under adjacency measure N.6 in Figure 1. For comparison, we also consider the approach with λ₂ = 0. Under this approach, there is no smoothness over connected genes, and gene selection is achieved using the group MCP (gMCP) approach [Ma et al. 2011]. Figure 1 shows that the SGLS solution paths are similar to those of other penalization methods. It may be able to select more true positives than gMCP. It shows the merit of adding the Laplacian penalty and smoothing over connected genes. More definitive results are generated below using large scale simulations.

Figure 1.

Solution paths for a simulated dataset under scenario 1. Solid lines are for nonzero gene effects, and dotted lines are for zero effects. Solid lines with the same symbols are for the same gene.

In our simulation, we are interested in evaluating gene identification accuracy, which can be measured using the number of true positives and number of false positives. In addition, prediction performance is also of interest. For this purpose, for each set of simulated data, we simulate a set of independent testing data under the same settings. We conduct cross validation (for tuning parameter selection) and estimation using the training set only, and then make prediction for subjects in the testing set and compute the PMSE (prediction mean squared error). Summary statistics (means and standard deviations) based on 200 replicates are shown in Table 1.

Table 1.

Simulation study: the first row is number of true positives (standard deviation), the second row is number of false positives (standard deviation), and the third row is PMSE (standard deviation).

			SGLS
	ρ	gMCP	N.1	N.2	N.3	N.4	N.5	N.6	N.7
Scenario 1	0.1	19.5(0.7)	19.5(0.9)	19.3(1.1)	19.7(0.6)	19.4(1.1)	19.4(1.5)	19.4(1.6)	19.5(0.9)
		11.8(3.9)	13.3(4.2)	13.3(4.8)	16.8(4.5)	16.2(5.2)	12.9(3.7)	13.5(4.5)	14.1(3.9)
		4.5(0.9)	4.6(1.1)	4.6(1.1)	4.4(0.9)	4.5(1.2)	4.5(1.4)	4.7(2.0)	4.6(1.3)
	0.5	18.9(1.2)	19.9(0.4)	20.0(0.1)	19.1(1.1)	19.9(0.4)	19.9(0.5)	20.0(0.2)	20.0(0.2)
		11.3(4.0)	18.4(8.6)	11.0(7.6)	16.0(3.4)	16.7(5.6)	9.9(7.8)	17.8(8.3)	12.3(9.4)
		4.5(1.2)	3.7(0.5)	3.7(0.5)	4.1(0.6)	3.7(0.5)	3.8(0.6)	3.7(0.6)	3.7(0.5)
	0.9	11.1(1.5)	19.6(1.2)	20.0(0.0)	19.3(2.0)	19.9(0.7)	19.8(1.2)	20.0(0.2)	20.0(0.1)
		7.5(4.1)	7.8(8.9)	3.5(8.8)	21.1(8.8)	5.1(9.6)	2.5(7.7)	7.1(10.6)	2.5(5.4)
		4.9(0.8)	3.9(0.7)	3.8(0.5)	4.2(0.7)	3.7(0.6)	3.9(0.6)	3.7(0.5)	3.8(0.6)
Scenario 2	0.1	19.2(1.4)	19.6(0.8)	19.2(1.4)	19.8(0.5)	19.7(0.7)	19.7(0.6)	19.4(1.1)	19.7(0.5)
		12.4(3.5)	13.3(4.5)	13.2(3.7)	15.7(4.6)	15.4(5.6)	12.7(3.9)	14.4(5.4)	13.5(4.3)
		4.5(1.1)	4.3(1.1)	4.6(1.3)	4.3(0.9)	4.3(1.0)	4.3(0.8)	4.4(1.1)	4.6(1.1)
	0.5	18.0(1.9)	20.0(0.1)	19.9(0.2)	19.2(1.1)	19.7(0.8)	19.9(0.4)	20.0(0.4)	20.0(0.1)
		11.7(3.9)	16.7(9.5)	12.0(9.5)	16.1(5.9)	16.8(7.2)	13.4(9.3)	19.1(10.0)	13.5(9.0)
		4.5(0.8)	3.6(0.5)	3.8(0.7)	4.2(0.6)	3.9(0.7)	3.6(0.4)	3.7(0.5)	3.7(0.4)
	0.9	12.2(2.3)	19.2(1.8)	19.2(1.8)	20.0(0.1)	19.6(1.3)	19.8(0.5)	19.8(1.1)	20.0(0.3)
		4.3(2.9)	13.0(9.7)	10.6(9.8)	16.1(9.5)	9.3(10.2)	4.2(4.0)	9.5(8.2)	6.7(5.9)
		4.9(1.0)	4.1(0.9)	4.1(0.7)	4.0(0.8)	4.1(1.0)	4.4(1.1)	3.9(0.7)	3.9(0.7)
Scenario 3	0.1	19.7(0.6)	19.7(0.6)	19.6(0.6)	19.9(0.4)	19.9(0.5)	19.7(0.9)	19.7(0.7)	19.6(0.6)
		12.0(4.1)	13.7(4.1)	11.9(5.2)	15.2(5.3)	15.2(6.6)	12.7(3.6)	12.5(4.3)	11.0(3.5)
		4.6(1.0)	4.5(0.9)	4.4(1.0)	4.3(1.1)	4.4(1.0)	4.2(0.8)	4.4(1.0)	4.2(0.9)
	0.5	17.2(1.6)	20.0(0.0)	20.0(0.0)	19.7(0.7)	19.9(0.2)	20.0(0.3)	20.0(0.0)	20.0(0.1)
		8.7(4.1)	11.8(9.8)	8.0(11.0)	22.1(11.4)	15.7(9.1)	5.5(8.6)	11.6(8.3)	11.6(11.5)
		5.1(1.0)	3.6(0.4)	3.7(0.4)	4.2(0.8)	3.6(0.6)	3.6(0.5)	3.7(0.6)	3.7(0.5)
	0.9	6.7(1.3)	20.0(0.0)	19.6(1.3)	19.9(0.3)	19.7(1.0)	19.2(1.5)	20.0(0.0)	20.0(0.0)
		10.6(6.0)	4.9(7.1)	3.6(7.0)	18.8(7.9)	8.7(11.2)	1.5(5.4)	2.5(6.0)	2.2(6.5)
		6.8(1.1)	3.9(0.7)	3.8(0.6)	4.1(0.8)	3.9(0.6)	3.9(0.5)	3.9(0.7)	4.0(0.7)

Table 1 suggests that the SGLS approach can effectively identify the majority or all of the true positives. When the correlations are weak, the gMCP approach can also identify the majority of true positives. However, its performance can be significantly less unsatisfactory when the correlations are strong. When looking at the false positives, the differences between gMCP and SGLS and between different adjacency measures are more dramatic. Here we observe that the performance of different approaches is data-dependent. For example, under scenario 1 with ρ = 0.9, gMCP on average identifies 7.5 false positives, SGLS with N.3 identifies 21.1, and SGLS with N.7 identifies 2.5. Under scenario 3 with ρ = 0.9, gMCP on average identifies 10.6 false positives, SGLS with N.3 identifies 18.8, and SGLS with N.5 identifies 1.5. Table 1 suggests that there is no dominating approach. In practice, researchers may need to experiment with multiple approaches. This finding has also been made in single-dataset studies. When the correlation is moderate to strong, the prediction performance of SGLS is better than that of gMCP, although the difference is not significant. We have experimented with a few other simulation settings and reached similar conclusions.

Analysis of lung cancer prognosis studies

Lung cancer is the leading cause of death from cancer for both men and women in the United States and in most other parts of the world. Non-small-cell lung cancer (NSCLC) is the most common cause of lung cancer death, accounting for up to 85% of such deaths. Gene profiling studies have been extensively conducted on lung cancer, searching for markers associated with prognosis. Xie et al. [2011] described three lung cancer prognosis studies. The UM (University of Michigan Cancer Center) study has a total of 175 patients, among whom 102 died during follow-up. The median follow-up is 53 months. The HLM (Moffitt Cancer Center) study has a total of 79 subjects, among whom 60 died during follow-up. The median follow-up is 39 months. The CAN/DF (Dana-Farber Cancer Institute) study has a total of 82 patients, among whom 35 died during follow-up. The median follow-up is 51 months. We refer to Xie et al. [2011] and references therein for more details on study design, subjects’ characteristics and profiling protocols. 22,283 probe sets were profiled in all the three studies. To reduce computational cost and remove noisy genes, we rank the probe sets using their variations and select the top 1,000 probes for downstream analysis.

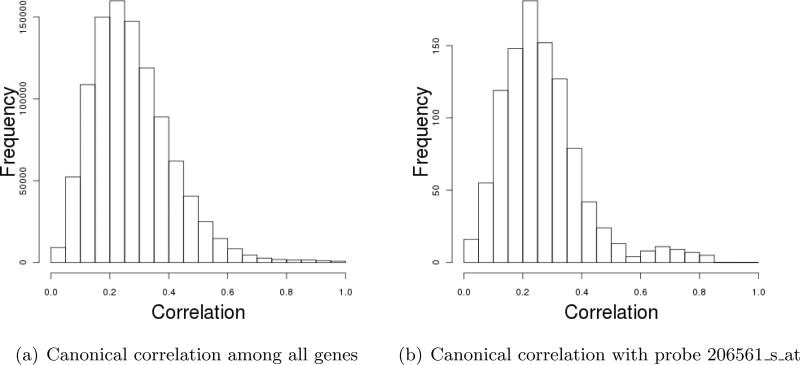
In some previous analyses, it has been assumed that gene effects are interchangeable [Xie et al. 2011]. Genes belong to different functional pathways. In addition, there exist strong correlations among some genes. The frequency of canonical correlations among all genes from multiple studies is given in Figure 2(a), and that of one randomly selected gene is given in Figure 2(b). In our analysis, we accommodate such correlations using the network structure and SGLS.

Figure 2.

Data analysis: frequency of canonical correlations.

Genes identified using SGLS under adjacency measures N.1-N.7 are presented in Tables 3-9 (Appendix). For comparison, we also employ gMCP (results presented in Table 10, Appendix). The numbers of identified genes and overlaps using different approaches are shown in Table 2. We can see that by accommodating the interplay among genes, SGLS identifies more genes. Such an observation is reasonable, considering that there are a considerable number of weak correlations and what is observed in simulation. Although there exist considerable overlaps, SGLS identifies different sets of genes.

Table 2.

Data analysis: numbers of genes and overlaps identified by SGLS (N.1–N.7) and gMCP.

	N.1	N.2	N.3	N.4	N.5	N.6	N.7	gMCP
N.1	22	19	22	13	14	13	13	9
N.2		20	19	14	15	14	14	8
N.3			25	14	15	14	14	9
N.4				15	15	14	14	5
N.5					16	15	15	5
N.6						19	19	4
N.7							20	4
gMCP								9

Unlike in simulation, with real data, it is difficult to objectively compare gene identification accuracy. We conduct evaluation of prediction performance using a random sampling approach [Ma et al. 2009]. Prediction evaluation may provide a partial evaluation of identification performance. Specifically, we generate training sets and corresponding testing sets with sizes 2:1 by random splitting. Estimates are generated using the training sets only. We then make prediction for subjects in the testing sets. For each split, with the predicted linear risk scores $\mathbf{X}\widehat{\beta }$, we dichotomize at the median, create two risk groups, and compute the logrank statistic, which measures the difference in survival between the two groups. The average logrank statistics over 100 splits are calculated as 4.47 (N.1), 4.30 (N.2), 4.77 (N.3), 4.93 (N.4), 4.23 (N.5), 5.13 (N.6) and 4.03 (N.7) for SGLS and 3.77 for gMCP. Under all adjacency measures, SGLS has improved prediction performance, as has been observed in simulation. The adjacency measure N.6 leads to the best prediction performance.

We now more closely examine genes identified by SGLS under N.6 but not by gMCP. Among the fifteen probes, fourteen belong to genes, and one is out from “gene desert”. These fourteen genes are SCGB1A1 (secretoglobin, family 1A, member 1 (uteroglobin)), GPX2 (glutathione peroxidase 2 (gastrointestinal)), ABP1 (amiloride binding protein 1 (amine oxidase (copper-containing))), CST1 (cystatin SN), TSPYL5 (testis-specific Y-encoded-like protein 5), ID1 (inhibitor of DNA binding 1, dominant negative helix-loop-helix protein), TUBB2A (tubulin, beta 2A class IIa), GEM (GTP binding protein overexpressed in skeletal muscle), KAL1 (Kallmann syndrome 1 sequence), PAH (phenylalanine hydroxylase), LYZ (lysozyme), PNMAL1(paraneoplastic Ma antigen family-like), ETS2 (v-ets erythroblastosis virus E26 oncogene homolog 2 (avian)) and C4BPB (complement component 4 binding protein, beta). Searching published literature suggests that these genes may have important implications. Gene SCGB1A1, also known as CCSP or CC10, encodes a member of the secretoglobin family of small secreted proteins. Previous studies have shown that Clara cells are discriminated in rodent lung epithelia by their expression of the secretoglobin. Sullivan et al. [2010] suggested that while variant Clara cells and PNECs possess the ability to expand and self-renew, only variant Clara cells have the capacity for multi-potent differentiation. Gene GPX2 is a member of the glutathione peroxidase family and encodes a selenium-dependent glutathione peroxidase that is one of two isoenzymes responsible for the majority of the glutathione-dependent hydrogen peroxide-reducing activity in the epithelium of the gastrointestinal tract. Hann et al. [2008] found up-regulation of GPX2 in small cell lung cancer. Gene ABP1 encodes a membrane glycoprotein that is expressed in many epithelium-rich and/or hematopoietic tissues and oxidatively deaminates putrescine and histamine. Bonner et al. [2003] found that ABP1 is on the list of genes associated with the embryonicpseudoglandular transition transcription factors. Gene CST1 is located in the cystatin locus and encodes a cysteine proteinase inhibitor found in saliva, tears, urine, and seminal fluid. Moreb et al. [2008] found that CST1 is down-regulated in non-small cell lung cancer. Gene TSPYL5 is involved in modulation of cell growth and cellular response to gamma radiation probably via regulation of the Akt signaling pathway and also involved in regulation of p53/TP53. It suppresses p53/TP53 protein levels and promotes its ubiquitination. Vachani et al. [2007] identified that TSPYL5 was among a panel of genes that accurately distinguished head and neck squamous cell carcinoma and lung squamous cell carcinoma. The protein encoded by gene ID1 is a helix-loop-helix (HLH) protein that can form heterodimers with members of the basic HLH family of transcription factors. Cheng et al. [2011] found an elevated ID1 expression level in lung cancer cell lines as well as lung cancer tissues. Tubulin (TUBB2A) is the major constituent of microtubules. It binds two moles of GTP, one at an exchangeable site on the beta chain and one at a non-exchangeable site on the alpha-chain. Previous studies suggest that β-tubulin isotype protein levels could be useful as indicators of NSCLC aggressiveness, and Cucchiarelli et al. [2008] found significantly higher fractions of β-tubulin classes II and V mRNA compared to the other isotypes in all lung tumor samples. The protein encoded by gene GEM belongs to the RAD/GEM family of GTP-binding proteins. It is associated with the inner face of the plasma membrane and can play a role as a regulatory protein in receptor-mediated signal transduction. Recent evidence indicates that Gemcitabine may modulate ERCC1 nucleotide excision repair activity and down-regulation of DNA repair activity. Mutations in gene KAL1 cause the X-linked Kallmann syndrome. Gene KAL1 is among the list of genes that are associated with NSCLC [Lacroix et al. 2008]. Gene PAH encodes the enzyme phenylalanine hydroxylase that is the rate-limiting step in phenylalanine catabolism. Armstrong et al. [2004] conducted meta-analysis and discussed lung cancer risk after exposure to PAH. Gene LYZ encodes human lysozyme, whose natural substrate is the bacterial cell wall peptidoglycan. Chiba et al. [2008] showed that LYZ was overexpressed in PA-MPCs. Gene ETS2 encodes a transcription factor which regulates genes involved in development and apoptosis. In Agathanggelou et al. [2003], protein analysis of six genes (ETS2, Cyclin D3, CDH2, DAPK1, TXN, and CTSL) showed that the changes induced by RASSF1A at the RNA level correlated with changes in protein expression in both NSCLC and neuroblastoma cell lines. Gene C4BPB encodes a member of a superfamily of proteins composed predominantly of tandemly arrayed short consensus repeats of approximately 60 amino acids. Chang et al. [2010] identified that C4BPB with other seven genes are down-regulated in at least three cisplatin-resistant cell lines, indicating that down-regulation of these genes is frequent across cancer cell lines from different tissue types.

Discussion

In cancer genomic research, integrative analysis of multiple datasets has been conducted and shown to outperform single-dataset analyses. In this study, we develop a Laplacian-penalization integrative analysis approach, which can accommodate the gene network structure in marker selection. The proposed approach is intuitively reasonable and computationally feasible. Simulation and the analysis of three lung cancer prognosis studies show that the proposed approach may have improved performance when there exist moderate to strong correlations among genes.

In single-dataset analysis, multiple ways of accounting for the interplay among genes have been developed. Data analysis shows that performance of different methods is data-dependent. In this study, we experiment with seven ways of constructing the adjacency matrices, which is by no mean complete. In practical data analysis, it may be of interest to follow similar strategies and extend the proposed approach under other network construction methods. Our simulation study suggests that performance of different adjacency matrices is data-dependent, which re-confirms findings in single-dataset analysis. With practical data, it has been conjectured that there is no optimal adjacency matrix and researchers may have to experiment with multiple choices. In this study, we focus on methodological development. Theoretical development is expected to be highly nontrivial and postponed to future research. In the analysis of lung cancer data, for genes identified by SGLS (under N.6 which has the best prediction performance) but missed by gMCP, our preliminary search suggests that they may have important implications, which partly support the validity of the proposed approach. Some genes identified under other adjacency matrices may also be meaningful (results omitted). More bioinformatics research is needed to fully comprehend implications of those genes. We note that multiple approaches can be employed to analyze the simulated and lung cancer data. We focus on the gMCP for comparison as it can directly establish the merit of adding the Laplacian penalty, and as the comparison of gMCP versus single-dataset and other integrative analysis approaches has been conducted in published studies [Huang et al. 2012; Liu et al. 2012; Ma et al. 2011]. We expect that it is possible to replace the gMCP penalty (first term in the proposed penalty) with, for example, group elastic net or group SCAD. As gMCP has comparable performance with those approaches, such an extension is not pursued.

Appendix

Table 3.

Analysis of lung cancer data using SGLS (N.1): identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
205725_at	SCGB1A1	−0.001	0.001	−4.2E-04
206754_s_at	CYP2B6	0.004	0.001	0.005
AFFX-CreX-5_at		0.001	4.7E-04	−9.4E-05
205048_s_at	PSPH	8.4E-05	−4.8E-04	−2.6E-04
209921_at	SLC7A11	−1.6E-04	−0.003	0.001
205776_at	FMO5	0.002	0.003	0.004
203559_s_at	ABP1	−0.003	0.007	0.004
206224_at	CST1	0.001	−0.002	−2.5E-04
215867_x_at	CA12	−0.001	−0.004	−4.4E-04
208937_s_at	ID1	−0.002	−0.003	−0.001
208025_s_at	HMGA2	−0.009	0.004	−0.009
204141_at	TUBB2A	0.002	0.004	−0.001
207850_at	CXCL3	−0.002	−0.020	0.005
219764_at	FZD10	−0.003	−0.007	−0.003
201242_s_at	ATP1B1	0.001	−0.002	0.001
208451_s_at	C4A	−4.0E-04	0.006	0.002
208078_s_at	SIK1	−3.2E-04	−0.001	−6.0E-05
213975_s_at	LYZ	−2.6E-04	0.001	0.001
218824_at	PNMAL1	0.001	4.5E-04	−4.0E-05
200965_s_at	ABLIM1	−4.9E-04	−3.8E-04	0.001
222303_at	ETS2	−0.001	−0.001	0.001
208209_s_at	C4BPB	4.9E-04	0.003	−2.4E-04

Table 4.

Analysis of lung cancer data using SGLS (N.2): identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
205725_at	SCGB1A1	−0.001	0.001	−0.001
206754_s_at	CYP2B6	0.005	0.001	0.006
205048_s_at	PSPH	7.8E-05	−4.1E-04	−2.1E-04
AFFX-r2-Ec-bioD-3_at		0.001	3.0E-04	−1.8E-04
209921_at	SLC7A11	−1.1E-04	−0.003	4.8E-04
205776_at	FMO5	0.002	0.003	0.003
203559_s_at	ABP1	−0.004	0.008	0.004
206224_at	CST1	0.001	−0.003	−2.9E-04
215867_x_at	CA12	−0.001	−0.004	−4.6E-04
208937_s_at	ID1	−0.003	−0.004	−0.001
208025_s_at	HMGA2	−0.011	0.006	−0.011
204141_at	TUBB2A	0.002	0.004	−0.001
207850_at	CXCL3	−0.002	−0.022	0.006
219764_at	FZD10	−0.003	−0.007	−0.003
201242_s_at	ATP1B1	0.001	−0.002	0.001
208451_s_at	C4A	−4.7E-04	0.006	0.002
213975_s_at	LYZ	−3.6E-04	0.001	0.001
218824_at	PNMAL1	0.001	0.001	−2.5E-05
222303_at	ETS2	−0.001	−0.002	0.001
208209_s_at	C4BPB	0.001	0.005	−4.3E-04

Table 5.

Analysis of lung cancer data using SGLS (N.3): identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
205725_at	SCGB1A1	−0.002	0.002	−0.001
206754_s_at	CYP2B6	0.005	0.001	0.006
AFFX-CreX-5_at		0.001	0.001	−2.5E-04
202831_at	GPX2	−1.3E-06	−3.0E-05	−1.1E-05
205048_s_at	PSPH	3.2E-04	−0.002	−0.001
209921_at	SLC7A11	−1.8E-04	−0.003	0.001
205776_at	FMO5	0.002	0.004	0.004
203559_s_at	ABP1	−0.004	0.008	0.004
206224_at	CST1	0.001	−0.003	−3.7E-04
215867_x_at	CA12	−0.001	−0.004	−0.001
208937_s_at	ID1	−0.003	−0.003	−0.001
209031_at	CADM1	2.3E-04	−4.8E-05	1.6E-04
208025_s_at	HMGA2	−0.009	0.004	−0.009
204141_at	TUBB2A	0.001	0.003	−4.6E-04
207850_at	CXCL3	−0.001	−0.018	0.005
219764_at	FZD10	−0.003	−0.007	−0.003
201242_s_at	ATP1B1	0.002	−0.003	0.001
208451_s_at	C4A	−3.9E-04	0.006	0.002
208078_s_at	SIK1	−1.2E-04	−2.6E-04	−3.0E-05
212814_at	AHCYL2	2.9E-04	−0.001	−1.0E-04
213975_s_at	LYZ	−4.8E-04	0.001	0.001
218824_at	PNMAL1	0.002	0.001	−4.9E-05
200965_s_at	ABLIM1	−0.001	−4.8E-04	0.001
222303_at	ETS2	−0.002	−0.003	0.001
208209_s_at	C4BPB	0.001	0.004	−3.8E-04

Table 6.

Analysis of lung cancer data using SGLS (N.4): identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
205725_at	SCGB1A1	−0.001	0.001	−3.6E-04
206754_s_at	CYP2B6	0.007	0.001	0.009
202831_at	GPX2	−7.5E-05	−0.004	−0.001
AFFX-r2-Ec-bioD-3_at		0.001	2.0E-04	−1.4E-04
203559_s_at	ABP1	−0.004	0.008	0.005
206224_at	CST1	0.001	−0.002	−1.9E-04
208937_s_at	ID1	−0.004	−0.005	−0.001
208025_s_at	HMGA2	−0.012	0.007	−0.012
204141_at	TUBB2A	0.002	0.007	−0.001
207850_at	CXCL3	−0.002	−0.031	0.007
219764_at	FZD10	−0.003	−0.006	−0.003
208451_s_at	C4A	−3.4E-04	0.004	0.001
213975_s_at	LYZ	−0.001	0.002	0.001
222303_at	ETS2	−0.001	−0.001	0.001
208209_s_at	C4BPB	0.001	0.006	−2.5E-04

Table 7.

Analysis of lung cancer data using SGLS (N.5): identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
206754_s_at	CYP2B6	0.007	0.001	0.009
202831_at	GPX2	−3.1E-05	−0.004	−0.001
AFFX-r2-Ec-bioD-3_at		0.002	0.001	−3.6E-04
203559_s_at	ABP1	−0.005	0.010	0.006
206224_at	CST1	0.001	−0.004	−3.9E-04
208937_s_at	ID1	−0.005	−0.007	−0.002
208025_s_at	HMGA2	−0.013	0.008	−0.013
204141_at	TUBB2A	0.003	0.007	−0.001
207850_at	CXCL3	−0.002	−0.032	0.007
219764_at	FZD10	−0.003	−0.006	−0.003
208451_s_at	C4A	−2.2E-04	0.002	0.001
213975_s_at	LYZ	−0.001	0.002	0.001
218824_at	PNMAL1	1.7E-04	4.6E-05	8.4E-06
222303_at	ETS2	−0.002	−0.004	0.002
208209_s_at	C4BPB	0.001	0.008	−0.001

Table 8.

Analysis of lung cancer data using SGLS (N.6): identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
205725_at	SCGB1A1	−0.001	0.001	−4.1E-04
206754_s_at	CYP2B6	0.006	2.5E-04	0.009
202831_at	GPX2	6.7E-05	−0.002	−0.001
AFFX-r2-Ec-bioD-3_at		0.004	0.001	−0.001
203559_s_at	ABP1	−0.005	0.010	0.007
206224_at	CST1	0.002	−0.006	−5.0E-04
213122_at	TSPYL5	0.002	−0.001	0.001
208937_s_at	ID1	−0.004	−0.006	−0.002
208025_s_at	HMGA2	−0.014	0.009	−0.013
204141_at	TUBB2A	0.004	0.009	−0.001
207850_at	CXCL3	−0.003	−0.043	0.008
219764_at	FZD10	−0.002	−0.005	−0.003
204472_at	GEM	−0.001	−0.004	0.001
205206_at	KAL1	0.001	0.001	0.001
205719_s_at	PAH	2.0E-04	−0.001	−0.001
213975_s_at	LYZ	−0.001	0.002	0.001
218824_at	PNMAL1	3.7E-04	7.5E-05	2.7E-05
222303_at	ETS2	−0.001	−0.001	0.001
208209_s_at	C4BPB	0.002	0.013	−0.001

Table 9.

Analysis of lung cancer data using SGLS (N.7): identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
205725_at	SCGB1A1	−0.001	0.001	−0.001
206754_s_at	CYP2B6	0.007	1.6E-04	0.009
202831_at	GPX2	8.7E-05	−0.003	−0.001
AFFX-r2-Ec-bioD-3_at		0.004	0.001	−0.001
205267_at		1.3E-04	1.6E-04	1.6E-04
203559_s_at	ABP1	−0.006	0.011	0.008
206224_at	CST1	0.002	−0.006	−0.001
213122_at	TSPYL5	0.002	−0.001	0.001
208937_s_at	ID1	−0.005	−0.007	−0.002
208025_s_at	HMGA2	−0.014	0.009	−0.014
204141_at	TUBB2A	0.004	0.009	−0.001
207850_at	CXCL3	−0.002	−0.042	0.008
219764_at	FZD10	−0.002	−0.005	−0.003
204472_at	GEM	−0.001	−0.003	0.001
205206_at	KAL1	4.5E-04	4.6E-04	3.4E-04
205719_s_at	PAH	2.3E-04	−0.001	−0.002
213975_s_at	LYZ	−0.001	0.003	0.001
218824_at	PNMAL1	0.001	1.5E-04	6.2E-05
222303_at	ETS2	−0.002	−0.003	0.001
208209_s_at	C4BPB	0.002	0.012	−0.001

Table 10.

Analysis of lung cancer data using gMCP: identified genes and their estimates.

Probe Set	Gene	UM	HLM	CAN/DF
206754_s_at	CYP2B6	0.001	4.E-04	0.002
209921_at	SLC7A11	−2.E-05	−2.E-04	4.E-05
205776_at	FMO5	0.003	0.007	0.007
215867_x_at	CA12	−0.001	−0.003	−2.E-04
208025_s_at	HMGA2	−0.004	0.002	−0.005
207850_at	CXCL3	−0.002	−0.017	0.004
219764_at	FZD10	−0.001	−0.002	−0.001
208451_s_at	C4A	−1.E-04	0.004	0.001
208078_s_at	SIK1	−0.001	−0.002	5.E-08