The pH-Dependent Picosecond Structural Dynamics in the Distal Pocket of Nitrophorin 4 Investigated by 2D IR Spectroscopy

Abstract

Nitrophorin 4 (NP4) belongs to a family of pH-sensitive, nitric oxide (NO) transporter proteins which undergo a large structural change from a closed to an open conformation at high pH to allow for NO delivery. Measuring the pH-dependent structural dynamics in NP4–NO around the ligand binding site is crucial for developing a mechanistic understanding of NO binding and release. In this study we use coherent two-dimensional infrared (2D IR) spectroscopy to measure picosecond structural dynamics sampled by the nitrosyl stretch in NP4–NO as a function of pH at room temperature. Our results show that both the closed and open conformers of the protein are present at low (pD 5.1) and high (pD 7.9) pH conditions. The closed and open conformers are characterized by two frequencies of the nitrosyl stretching vibration labeled A₀ and A₁, respectively. Analysis of the 2D IR lineshapes reveals that at pD 5.1, the closed conformer experiences structural fluctuations arising from solvation dynamics on a ∼3 ps timescale. At pD 7.9, both the open and closed conformers exhibit fluctuations on a ∼1 ps timescale. At both pD conditions, the closed conformers maintain a static distribution of structures within the experimental time window of 100 ps. This is in contrast to the open conformer, which is able to interconvert among its sub-states on a ∼100 ps timescale. Our results directly measure the timescales of solvation dynamics in the distal pocket, the flexibility of the open conformation at high pH, and the rigidity of the closed conformers at both pH conditions. We discuss how the pH dependent equilibrium structural fluctuations of the nitrosyl ligand measured in this study are related to the uptake and delivery of nitric oxide in Nitrophorin 4.

I. Introduction

Nitrophorins (NPs) are a particular class of nitrosyl binding heme proteins found naturally in the saliva of blood feeding insects. In these proteins, NO is stored in the low pH environment of the salivary gland (pH ∼5) and is released in the higher pH environment of the host tissue (pH ∼7.5) to induce vasodilation and prevent blood coagulation.^1,2 Nitric oxide is a reactive messenger molecule implicated in regulating the immune, nervous and cardiovascular systems of mammals.³ Given the importance of NO in biology, the NPs serve as excellent models to probe the interplay of structure, dynamics and function for a naturally occurring NO delivery system. Nitrophorin 4 is a widely studied protein of the Nitrophorin family. Figure 1 shows a high-resolution crystal structure of the NP4-NO protein acquired at pH 5.6. The protein structure consists of an eight-stranded antiparallel β-barrel with a heme buried at one end. The protein is known to undergo a conformational change upon binding to NO, such that the A-B (residues 31-37) and the G-H (residues 125-132) loops pack tightly together to form a hydrophobic pocket preventing NO escape.^4-6 Crystal structures of NP4 reveal a distal pocket with structurally distinct closed and open conformations.⁶ The closed conformation is characterized by a dynamic hydrophobic cavity with a network of hydrogen bonds between the residues of the A-B and G-H loops. The hydrogen bond network is disrupted in the open conformation resulting in a more hydrophilic cavity with the presence of water molecules and flexible loop regions. The two conformations are found to exist at all pH conditions by X-ray crystallography, with the fraction of the open conformation increasing at higher pH.⁶

Figure 1.

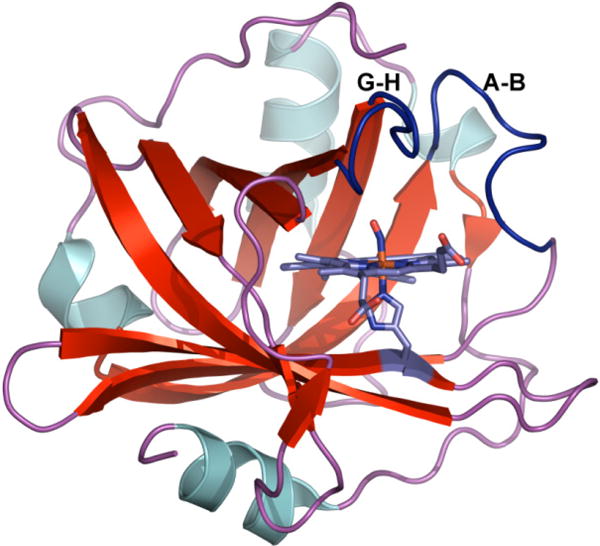
Cartoon showing the NP4-NO protein at pH 5.6 (PDB ID: 1X8O). The positions of the loops A-B and G-H are highlighted in dark blue.

Kinetic studies of the binding and dissociation of NO using histamine displacement and laser photolysis have revealed multi-exponential pH-dependent NO release rates across a wide range of timescales.^7-10 The pH dependence of the NO release is completely eliminated for the double mutant D129A/L130A confirming that the conformational flexibility of the loop regions is responsible for the pH-dependent NO release in NP4.⁷ However, the cause for the non-exponential NO release rates remains an open question. There have been several molecular dynamics simulations on the NO release dynamics of NP4.^11-15 These simulations have revealed the importance of the flexibility of the loop regions, the protonation state of Asp 30 and the equilibrium of the closed and open conformers to the pH dependent NO release mechanism in the NP4 protein.

While the structural flexibility of the A-B and G-H loops and the polarity of the distal pocket have been extensively discussed in experimental and theoretical studies of NP4-NO, there have been no measurements of the timescales of equilibrium structural fluctuations of the nitrosyl ligand. The time-dependent frequency fluctuations (δω(t)) of an IR active vibration (ω₀) are encoded in the frequency-frequency correlation function (FFCF, 〈δω(t)δω(0)〉). Two-dimensional (2D) IR spectroscopy has been used effectively to measure the FFCF of carbonyl and nitrosyl ligands in heme proteins to characterize the structural fluctuations around the ligand binding sites.^16-24 There is a growing body of literature on how the frequency shifts of the nitrosyl stretching vibration (ν_NO) in heme proteins are a sensitive reporter of the local electric field and Fe-NO bonding interactions.^25-27. The goal of this study is to measure the equilibrium structural dynamics in the distal pocket of NP4–NO as a function of pH using 2D IR spectroscopy to measure the FFCF of the ν_NO. Our experiments sample the conformational heterogeneity and directly measure the timescales of equilibrium structural fluctuations in the vicinity of the Fe–NO bond. We discuss how the spectroscopic data reveal a dynamic distal pocket environment that is crucial for the binding, release and regulation of NO in NP4.

II. Methods

Sample preparation

Nitrophorin 4 was overexpressed from an Escherichia coli strain and refolded from inclusion bodies supplemented with heme, as described previously.⁴ In order to resolve the weak mid-IR absorption band of the NO stretching vibration at ∼1905 cm^-1 from the absorbance of H₂O in the same spectral region, samples of purified ferric NP4 underwent a buffer exchange process to replace the 20 mM sodium phosphate buffer (at pH 7.0) with a deuterated buffer. Acidic (pD 5.1) and basic (pD 7.9) 20 mM potassium dideuterium phosphate (KD₂PO₄) buffer solutions were prepared in D₂O. Centrifugal filter devices (Amicon Ultra-0.5) were used to exchange the aqueous buffer as well as to concentrate the protein samples. In order to prepare the ferric NP4–NO complex, fresh NO gas was generated by mixing ascorbic acid (880 mg in 25 mL of water) and sodium nitrite (40-60 mg) after degassing each of them under Ar for at least 30 minutes. The sample was also degassed for at least 15 minutes prior to flushing with the generated NO gas using an airtight syringe. Linear FTIR (Jasco FT/IR-4100) and UV-Vis (Jasco V-630) spectra of the samples were obtained (sample path length = 50 μm) before and after each 2D IR scan to ensure that the protein had not degraded during the experiment. The final concentrations of the protein sample at the start of each scan were determined by the intensity of the alpha and beta bands in the UV-Vis spectra of ferric NP4-NO.²⁸ The final concentrations were 6.4 mM and 4.1 mM for the acidic and basic samples, respectively. These concentrations yield an OD of 0.046 and 0.037 for the ν_NO peak at 1905 cm^-1.

2D IR Experiment

Femtosecond pulses of mid-IR light were generated from a combination of commercial equipment, beginning with a regenerative amplifier (Spectra Physics Spitfire Pro-35F-XP), which outputs 3 W, 800 nm, 35 fs pulses of light at 1 kHz. Approximately 1 W of the 800 nm output is sent to an optical parametric amplifier (OPA-800C) to produce the near-IR signal and idler pulses. The two near IR fields undergo difference frequency mixing in a 0.5 mm AgGaS₂ crystal to generate 80 fs mid-IR pulses with a spectral bandwidth of ∼200 cm^-1 at a center wavelength of 5.1 μm.

The mid-IR pulse is sent into a five-beam interferometer to generate three input pulses, a tracer beam and a local oscillator field as described previously.^29,30 The three input IR beams have parallel polarizations and are arranged in a “boxcar” geometry, temporally overlapped, and focused onto the sample with a spot-size of ∼150 μm. Each of the input beams has 0.2 μJ of energy per pulse. The home-built sample cell is equipped with two 1 mm CaF₂ windows and a 50 μm Teflon spacer. The resulting background-free signal field is overlapped with the local oscillator field on a beamsplitter for heterodyne detection. The reflected and transmitted combined signal and local oscillator fields are π out of phase with respect to each other and are detected at the focal plane of a spectrometer (Triax 190, Horiba Jobin Yvon, 150 1ines/mm grating) using a 2 × 64 mercury cadmium telluride (MCT) array detector (IR0144, Infrared Systems Development). We subtract signals from the two linear MCT arrays to perform “balanced detection” on a shot-to-shot basis as explained in Ref 30.

The evolution (τ₁) and waiting (τ₂) time delays between the consecutive pairs of pulses 1,2 and 2,3 are accurately controlled by Newport XMS50 linear stages. Rephasing and non-rephasing experiments were performed at each τ₂ delay in order to construct absorptive 2D IR correlation spectra. The τ₁ delay was scanned in 4 fs steps from 0 to 4(3) ps for the rephasing (non-rephasing) experiments. The τ₂ delay was scanned in unequal time steps from 0 to 70 ps in unequal time steps with each data point representing 2000 laser shots. The raw experimental data was zero padded to 32.8 ps and Fourier transformed along τ₁ to obtain the ω₁ axis. The final 2D IR spectrum is corrected for the phase ambiguities corresponding to drift of the relative timing between the local oscillator and signal fields by comparing the projection of the 2D IR spectrum along the ω₁ axis to a two-beam dispersed pump-probe spectrum collected for the same values of τ₂.³¹

2D IR spectral fitting

The experimental 2D IR spectra were fit by iteratively calculating the third-order nonlinear signal field as a function of τ₁ and τ₃ in the time domain and then Fourier transforming it to obtain theoretical spectra as described previously.²⁹ 2D IR spectra of NP4 under both pH conditions were simulated using a six-level system for two non-interacting NP4-NO populations, each with a ground, first-excited and second-excited vibrational state (0, 1, 2) using the nonlinear response formalism detailed previously.^32,33 In our system, there are a total of 12 response functions for the rephasing and non-rephasing signals. We ignore any cross correlation terms between the two non-interacting NP4-NO populations since the experiment does not reveal the presence of any cross-peaks. We assume a separation of timescales for the vibrational and rotational dynamics for calculating the third-order nonlinear response functions.

The goal of the spectral fitting procedure is to extract parameters of the FFCF of the ν_NO in NP4-NO as a function of pH. We modeled the 2D lineshapes using the following form for the FFCF:

$$C_{11}(t)=\sum _{n=1}^2{\Delta }_n^{2}exp\left(-\frac{t}{{\tau }_{cn}}\right)+\frac{\delta (t)}{T_2^{\ast }}$$ (1)

In the above expression, Δ_n and τ_cn describe the amplitude and timescales of the frequency fluctuations in the Kubo model, δ(t) is the Dirac delta function and $T_2^{\ast }$ represents the timescales of fast dynamics determining the homogenous linewidth of the ν_NO in NP4-NO. Analytical expressions for the nonlinear dephasing functions in terms of the correlation functions are obtained using the methodology described in Ref. 33. The contribution of the rotational correlation functions to the 2D IR lineshape was not included because of the long time scales associated with orientational rearrangement of the protein. We accounted for the effects of vibrational population relaxation by introducing exponential relaxation rates into the vibrational response functions during all three time periods using harmonic scaling rules. For example, if the vibrational lifetime for the first excited state of ν_NO is T₁, then the vibrational lifetime of the second excited state is 1/2T₁. The vibrational lifetime of the first excited state of ν_NO for both the sub-populations of NP4-NO was determined to be 30 ps using IR pump-probe experiments. Harmonic scaling was used for the energy gap fluctuations in our two separate 3-level systems to relate the FFCFs of the first (1) and second (2) vibrational states of our three level system, such that: C₂₂(t) = 2C₂₁(t) = 2C₁₂(t) = 4C₁₁(t). For each pH condition, the experimental 2D IR spectra for all τ₂ points were fit simultaneously by floating the parameters in the FFCFs, the vibrational anharmonicity $({\Delta }_{12}=2{\nu }_{\mathrm{N}\mathrm{O}}^{1\leftarrow 0}-{\nu }_{\mathrm{N}\mathrm{O}}^{2\leftarrow 0})$, and the transition dipole moment between the first and second excited states(|μ₁₂|) for each of the sub-populations of NP4-NO. The best-fit values are listed in Table 2. The simulated and experimental spectra were fit using a nonlinear least squares fitting routine written in MATLAB.

Table 2.

Best fit parameters of the FFCF for the ν_NO in NP4-NO extracted from fitting the 2D IR data.

	Δ1 (ps-1)	τc1 (ps)	Δ2 (ps-1)	τc2 (ps)	$T_2^{\ast }$ (ps)	Δ12 (cm-1)
pD 5.1
A0	0.55±0.04	3.0±0.1	0.57±0.05	∞	7±2	30±2
A1	0.40±0.06	0.9±0.6	1.4±0.1	130±15	7±2	29±2
pD 7.9
A0	0.3±0.1	1.4±0.2	0.36±0.04	∞	7±2	30±2
A1	0.57±0.07	0.8±0.2	1.2±0.1	70±15	7±2	29±2

A. pH-Dependent FTIR Spectra and conformational sub-states of NP4-NO

The FTIR spectrum of NP4–NO in the ν_NO region is shown in Figure 2 as a function of pH. The spectra show two peaks in the ν_NO region centered at ∼1905 and ∼1917 cm^-1. We see that the peak at 1917 cm^-1 increases in amplitude under higher pH conditions. The shaded areas represent fits to the two peaks using Voigt lineshapes and the best-fit parameters are listed in Table 1. The two peaks in the ν_NO region indicate the presence of two conformational sub-states of the NP4-NO protein which exist under acidic and basic pH conditions. Previous FTIR and Raman studies of NP4-NO have assigned the peak centered at ∼1905 cm^-1 to the closed conformation where the NO ligand is in a hydrophobic environment and the peak at ∼1917 cm^-1 to the open conformation with a hydrophilic distal pocket.^8,25,34 The shift of the ν_NO vibration to higher frequencies in more hydrophilic/polar environments is also seen in other Fe–NO complexes like sodium nitroprusside.^29,35 In this work, we label the peak at ∼1905 cm^-1 as A₀ and the peak at ∼1917 cm^-1 as A₁. The labeling scheme follows from the FTIR spectroscopy of ferric myoglobin-NO (Mb^IIINO) under various pH conditions.^36,37

Figure 2.

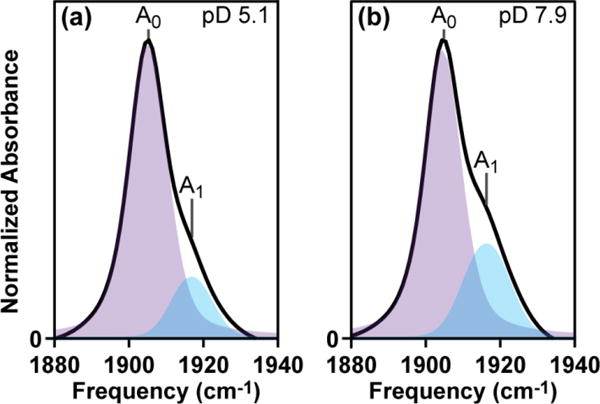
pH-dependent FTIR spectra of NP4-NO. The shaded areas represent the fits of the two peaks using a Voigt lineshape.

Table 1.

Spectral characteristics of the ν_NO region in NP4-NO. The error bars correspond to a 95% confidence interval.

Peak	Sample pD	νNO (cm-1)	ΔνFWHM (cm-1)
A0	5.1	1904.9±0.2	11.7±0.4
A1	5.1	1917±1	14±2
A0	7.9	1904.3±0.2	12.1±0.4
A1	7.9	1916±1	12±1

High-resolution crystal structures of NP4-NO at pH 5.6 and 7.5 have revealed the presence of at least two major conformers and considerable loop disorder at higher pH.⁶ Figures 3(a-b) display the distal pocket configuration for the closed and open conformational sub-states of NP4-NO at pH 5.6. We see that in the closed conformation the hydrogen bonding interaction between the residues of the A-B and G-H loops is preserved, the non-polar residues are packed into the binding pocket providing favorable non-polar interactions with the NO ligand. In contrast, the open conformation shows that Leu 130 has moved away from the distal pocket, providing room for several solvent molecules. The position of the electron density of Leu 130 in the open conformer matches closely with the NP4-NH₃ crystal structure at pH 7.4, which shows the presence of several (∼5) water molecules in the distal pocket.⁶ In the refined crystal structure of NP4-NO at pH 5.6, the open conformer was found to have an occupancy of 0.29. Based on the crystal structures and the pH-dependent FTIR spectra, we assign the A₀ and A₁ peaks in Figure 2a to the closed and open conformational sub-states of NP4-NO at pH 5.6.

Figure 3.

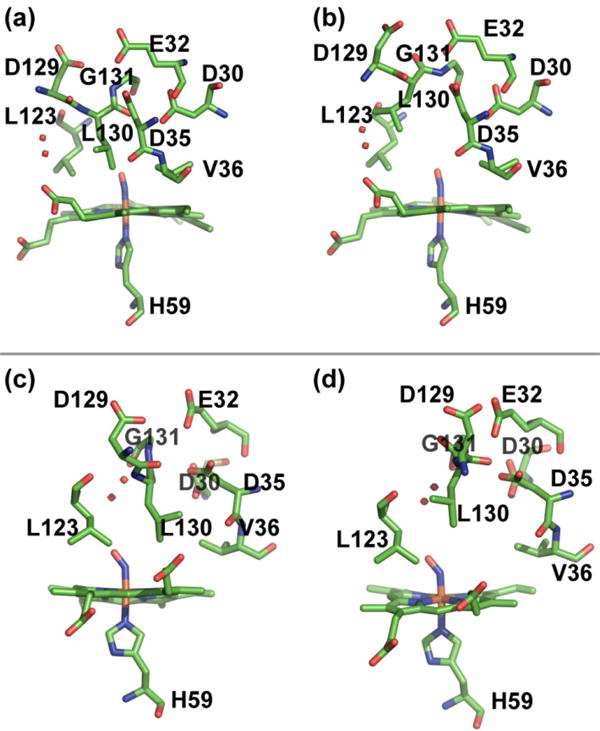
Multiple conformers of NP4-NO determined by X-ray crystallography. The top panel shows the closed (3a) and open (3b) conformers at pH 5.6 (PDB ID 1X8O). The bottom panel shows the closed (3c) and open (3d) conformers at pH 7.5 (PDB ID 1X8N).

The closed and open conformers of the high resolution crystal structure of NP4-NO at pH 7.5 are shown in Figures 3c-d. The x-ray study has noted the difficulty in modeling loops A-B and G-H because of considerable disorder. The structural distinction between the closed and open conformers is seen in the residues 129-131. Leucine 130 flips its position between the closed and open conformational sub-states in a manner similar to the crystal structure obtained at pH 5.6. Water molecules are seen in the distal pocket within ∼3.8 Å of the nitrosyl ligand in the crystal structure at higher pH. Given that the frequencies of the ν_NO peaks are very similar at both pH conditions, we assign the A₀ and A₁ peaks in Figure 2b to the closed and open conformational sub-states of NP4-NO at pH 7.5.

The ν_NO peak assignments described above agree with the studies on ferric Mb-NO and DFT calculations.^25,36,37 In wild type Mb^IIINO at room temperature, a major peak at ∼1927 cm^-1 and a weak feature at ∼1902 cm^-1 are observed in the ν_NO region at neutral pH.³⁸ The mutant, H64L, of Mb^IIINO shows a single peak at 1904 cm^-1. The negative polar interaction of the nitrosyl ligand with a tautomeric form of the distal histidine has been proposed for the protein conformer giving rise to the peak at 1927 cm^-1 in wild type Mb^IIINO.³⁷ The absence of this interaction in the H64L mutant, results in the downshift of the ν_NO frequency to 1904 cm^-1, which is very similar to the frequency of the A₀ peak in NP4-NO. The DFT calculations have shown how the frequency of the ν_NO in ferric heme proteins reports on the polarity of the heme protein and interactions of the NO moiety with nearby Lewis base donors.²⁵ The same DFT study has assigned an increase in frequency of the ν_NO in open conformer of NP4-NO to lone pair interactions of the NO with a water molecule.

The fits of peaks in the ν_NO region reveal that the fraction of the A₁ peak is 16% and 26% at pD 5.1 and 7.9 respectively. Previous FTIR studies of NP4-NO had measured a ratio of 0.2 at cryogenic temperatures for NP4-NO at pH 7.5.⁸ The linewidths of the peaks in the FTIR spectra range from 12-14 cm^-1 and are governed by the frequency-frequency correlation function (FFCF) of the ν_NO vibration, which measures the timescales of structural dynamics around the NO binding site for the open and closed conformations. Using 2D IR lineshape analysis we can measure the timescales of frequency fluctuations, which dictate the linewidth of the ν_NO in NP4-NO as a function of pH.

B. pH-dependent 2D IR spectra and extraction of the FFCF parameters

The top panel of Figure 4 displays a series of experimental 2D IR spectra of the ν_NO in NP4–NO plotted as a function of τ₂ at pD 5.1. In each of the spectra, the positive diagonal peaks correspond to vibrational transitions between the ground and first excited state of the ${\mathrm{\nu }}_{\mathrm{N}\mathrm{O}}({\nu }_{\mathrm{N}\mathrm{O}}^{0\to 1})$. The off-diagonal negative peaks involve transitions between the first and second excited states of the ${\mathrm{\nu }}_{\mathrm{N}\mathrm{O}}({\nu }_{\mathrm{N}\mathrm{O}}^{1\to 2})$. The separation of the two peaks in the ω₃ dimension of the 2D IR plots is a direct measure of the vibrational anharmonicity of the ν_NO in NP4–NO. Focusing on the strong positive 2D peaks in Figure 4a, we note that they are elongated along the diagonal axes at τ₂=0.2 ps representing a distribution of structures for the closed (A₀) and open (A₁) conformations of NP4-NO at low pH. As τ₂ increases, structural fluctuations cause the vibrational frequencies to lose correlation and results in the 2D lineshapes becoming more symmetric. It is important to note that the A₀ peak remains elongated along the diagonal even at τ₂ = 70 ps. A qualitative comparison between the A₀ and A₁ peaks at τ₂ = 70 ps suggests that the latter peak undergoes faster frequency fluctuations. The evolving 2D lineshape is a direct measure of the FFCF and provides information on the amplitude and timescales of the structural fluctuations in the open and closed conformations of NP4–NO.

Figure 4.

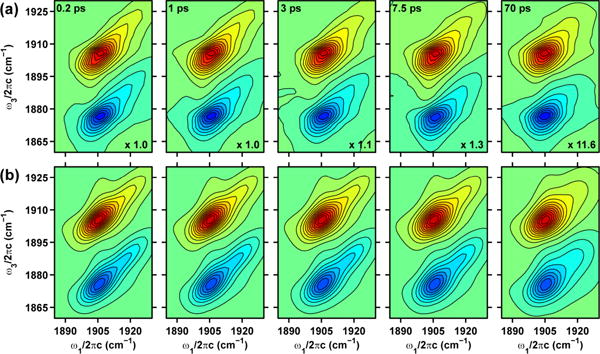
(a) Experimental 2D IR spectra of the ν_NO in NP4-NO at pD 5.1. (b) Best fits to the experimental 2D IR spectra. Contour levels are drawn at 5% intervals. The τ₂ values and the normalization factors for each 2D plot are given in the top left and bottom right corners, respectively.

We fit the 2D IR spectra to extract the parameters of the FFCF as described in the Methods section. In this paper we focus our efforts on understanding the 2D IR lineshape of the fundamental transition of the ν_NO in NP4–NO. The bottom panel in Figure 4 displays the 2D IR spectra resulting from the best fits of the experimental spectra assuming the form of the correlation functions given by Equation 1. The resulting parameters of the FFCF are listed in Table 2. We find that the homogenous dephasing time $(T_2^{\ast })$ for the A₀ and A₁ peaks of the ν_NO in NP4-NO at pD 5.1 is 7 ps. While the homogenous contribution to the spectral linewidth is similar for the A₀ and A₁ peaks, the timescales for structural diffusion (τ_c1 and τ_c2) are very different. The ν_NO of the closed conformer exhibits fast structural fluctuations on a 3 ps timescale (τ_c1). Significant portions of the dynamics are too slow to be measured on our experimental timescale of ∼100 ps. This is represented as τ_c2=∞ in Table 2. The ν_NO of the open conformer exhibits structural fluctuations on a 0.9 ps and a 130 ps timescale. The ratio of the amplitudes of the structural fluctuations $(\stackrel{{\Delta }_2}{}/\underset{{\Delta }_1}{})$ is 1 and 3.5 for the A₀ and A₁ peaks.

Figure 5 shows the experimental and best fit 2D IR spectra for the ν_NO in NP4-NO obtained at pD 7.9. At τ₂=0.2 ps, the A₀ and A₁ peaks are elongated along the diagonal indicating the presence of structural inhomogeneity in the two conformational sub-states. Similar to the 2D IR data taken at pD 5.1, the A₁ peak loses its frequency correlation faster than the A₀ peak as evidenced by their different 2D lineshapes at τ₂=25 ps. Our best fits to the 2D IR data (see Table 2) find that the vibrational anharmonicity is pH independent and is ∼30 cm^-1 for peaks A₀ and A₁ peaks. The ν_NO of the closed conformer exhibits fast structural fluctuations on a 1.4 ps timescale (τ_c1) and on timescales longer than our experimental time window of ∼100 ps. This is represented as τ_c2=∞ in Table 2. The ν_NO of the open conformer exhibits structural fluctuations on a 0.8 ps and a 70 ps timescale. The ratio of the amplitudes of the structural fluctuations $(\stackrel{{\Delta }_2}{}/\underset{{\Delta }_1}{})$ is 1 and 2 for the A₀ and A₁ peaks.

Figure 5.

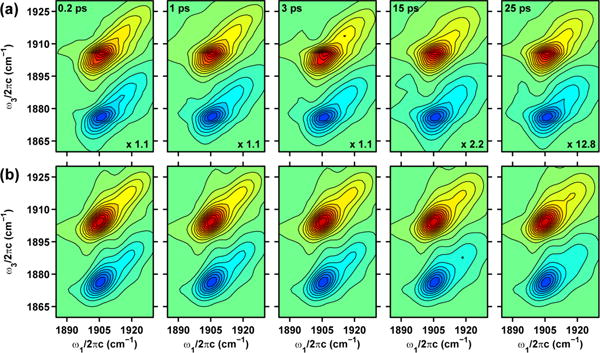
(a) Experimental 2D IR spectra of the ν_NO in NP4-NO at pD 7.9. (b) Best fits to the experimental 2D IR spectra. Contour levels are drawn at 5% intervals. The τ₂ values and the normalization factors for each 2D plot are given in the top left and bottom right corners, respectively.

The homogenous contribution to the IR linewidth is governed by protein and solvent fluctuations much faster than the experimental time window of a 2D IR experiment. The measured homogenous timescale $(T_2^{\ast })$, falls within the range of 5–12 ps for the ν_CO in myoglobin-CO, neuroglobin-CO and for cyt-P450_cam-CO substrate complexes.^16,20 In particular, the homogenous dephasing time for the H64V mutant of myoglobin-CO was measured to be 7.7 ps. In contrast, the homogenous dephasing time for the ν_NO of sodium nitroprusside (Na₂Fe(CN)₅NO⋅2H₂O, SNP) dissolved in various polar solvents was measured to be ∼2 ps.^29,39 These comparisons suggest that the dephasing timescales are slower in non-polar environments such as the distal pocket of NP4-NO in contrast to the polar solvent environments experienced by the ν_NO of sodium nitroprusside. The vibrational anharmonicity value of ∼29.5 cm^-1 for the A₀ and A₁ peaks extracted from the fits of the 2D IR spectra is not affected by pH. This value is similar to the measured anharmonicity of 29 cm^-1 for the ν_NO in wild-type Mb^III NO and 28 cm^-1 for the ν_NO in ferric cytochrome C-NO.²⁴

The closed conformer at acidic pH is characterized by a well packed distal pocket where the NO is surrounded by non-polar residues held together by hydrogen bonding interaction between the A-B and G-H loops as seen in Figure 3a. In contrast, the open conformation at the acidic pH is characterized by greater disorder in the A-B and G-H loops and displays room for several water molecules in the distal pocket.⁶ The FFCF of the A₀ and A₁ peaks exhibits spectral diffusion on 3 and 1.4 ps timescales, respectively. The crystal structures of the distal pocket at a higher pH are characterized by a greater degree of loop flexibility and the presence of several water molecules near the nitrosyl binding site. The FFCF of the A₀ and A₁ peaks in the pD 7.9 sample exhibits spectral diffusion on a 1.4 and 0.8 ps timescales, respectively. We assign the fast timescales to fluctuations of the local electric field around the nitrosyl ligand in NP4-NO for the closed and open protein conformers. Our previous work on characterization of the FFCF of the ν_NO in SNP found a negative correlation between the solvent polarity and the timescale for spectral diffusion.²⁹ The solvent polarity was defined by the empirical solvent parameters: ${\mathrm{E}}_{\mathrm{T}}^{\mathrm{N}}(30)$ and the acceptor number (AN).⁴⁰ It is interesting to note that the τ_c1 timescale of the ν_NO in NP4-NO mentioned above are very similar to the measured τ_c1 values of ν_NO in SNP dissolved in ethanol (3.2 ps), methanol (2.3 ps), D₂O (1.4 ps) and H₂O (0.84 ps). Based on the above comparison, we propose that the polarity of the protein distal pocket in the closed and open conformers at pD 5.1 can be characterized by a maximum ${\mathrm{E}}_{\mathrm{T}}^{\mathrm{N}}(30)$ value corresponding to that of ethanol $({\mathrm{E}}_{\mathrm{T}}^{\mathrm{N}}(30)=0.65)$ and water $({\mathrm{E}}_{\mathrm{T}}^{\mathrm{N}}(30)=1)$, respectively. The timescale for spectral diffusion of the closed conformer changes from 3 to 1.4 ps on increasing the sample pH. This can be explained by the presence of water molecules reported in the crystal structure resulting in an increase in the polarity of the distal pocket upon increasing the sample pH.

The 2D IR lineshape study also reveals the presence of slow (τ_c2) frequency fluctuations of the closed and open conformers. The frequency fluctuations of the ν_NO in the closed conformer under all pH conditions are too slow to be measured on the timescale of our experiment and appear static. In contrast the ν_NO in the open conformer undergoes frequency fluctuations on the 130 ps and 70 ps timescale for the pD 5.1 and 7.9 samples respectively. We attribute these long timescale dynamics to the structural dynamics of the loop regions of NP4-NO. These dynamics appear to be frozen for the closed conformers on the 100 ps timescale. However, the loop dynamics are faster for the open conformers. Our finding is consistent with X-ray crystallography studies, where it has been found that the A-B and G-H loops are poorly modeled for the open conformers of the NP4-NO protein.⁶

The carbonyl ligand has been used extensively as a vibrational probe in 2D IR studies to measure structural dynamics in the active site of several heme proteins.^16-22 These studies have measured timescales for spectral diffusion on 1-10 ps timescales and also slower timescales ranging from 60-300 ps. The fast timescales can be characterized as local structural fluctuations around the CO probe and the slower fluctuations have been attributed to global motions involving the entire protein. For example, molecular dynamics simulations have demonstrated that the experimentally measured timescales in the FFCF of the ν_CO in wild type and mutant myoglobin-CO are governed by the dynamics of the distal histadine ligand, and protein-water interactions.^18,22,41,42 2D IR studies of the ν_NO in wild-type Mb^IIINO and ferric cytochrome C-NO have measured vibrational frequency fluctuation timescales of 3.3 ps and 5.2 ps, respectively.^23,24 The ν_NO in the H64Q-NO mutant of Mb^IIINO exhibits a slower timescale of ∼10 ps in the measured FFCF.²⁴ A reduction in polar interactions with the nitrosyl ligand in the mutant without the distal histidine, results an increase in the timescale of frequency fluctuations which is in keeping with the trend seen in NP4-NO.

C. Relating structure, function and dynamics in Nitrophorin 4

The results and discussion of the 2D IR lineshape analysis reveals a picture of a dynamic distal pocket with structural fluctuations on a range of timescales. We next discuss how our measurement of the equilibrium structural fluctuations in the distal pocket of the open and closed conformers of NP4–NO at two different pH conditions shed light on the function of this NO transporter protein. The binding and release of NO from the heme has been described as the following two step process:⁷

$$\mathrm{N}\mathrm{P}\text{-}\mathrm{N}\mathrm{O}\underset{{\mathrm{k}}_{\mathrm{o}\mathrm{n}}}{\overset{{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}1}/{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}2}(\text{pH dep.})}{\rightleftarrows }}[\mathrm{N}\mathrm{P}\text{:}\mathrm{N}\mathrm{O}]\underset{{\mathrm{k}}_{-1}}{\overset{{\mathrm{k}}_1}{\rightleftarrows }}\mathrm{N}\mathrm{P}+\mathrm{N}\mathrm{O}$$

In this model, NO dissociation occurs with two pH-dependent rates (k_off1,2) involving a slow protein conformational change of the protein and a faster rate (k₁) representing release from the open conformation. It has been shown that the pH dependence of the slower off-rates can be attributed to the flexibility and dynamics of the loop regions from various mutant studies which have destabilized the closed conformation and altered the pH dependence of the equilibrium populations of the open and closed conformers.^7,10 Ultrafast rebinding studies following photodissociation of NO from ferric NP4-NO have measured a 10-25 ps and a >150 ps timescale for geminate recombination.⁹ The faster timescale has been attributed to NO rebinding from a hydrophobic closed conformer and the longer timescale has been attributed to rebinding from the hydrophilic open conformer.

Our results demonstrate that there is a static distribution of the closed conformers at both pH conditions and a distribution of interconverting open conformers on the ∼100 ps timescale. These heterogeneous structures arising from different interactions of the NO and its local environment in the distal pocket, would allow for slightly different rates of thermal bond cleavage resulting in a truly non-exponential ligand release process. The results in this study provide experimental verification for MD simulations which have suggested that the structural loops in NP4 should not be viewed as rigid cages that confine NO, but rather as a “dynamical oil droplet” that contains NO within the fluctuating nonpolar pocket.^6,11 We directly measure timescales of 3 ps and ∼1 ps for fast structural fluctuations in a hydrophobic and hydrophilic environment of the distal pocket.

We plan to perform 2D IR studies on mutants of NP4 where several key residues in the A-B and G-H loops have been replaced to affect the binding and release rates of NO, in the future. Measuring the FFCF of the ν_NO in these mutants will allow us to directly probe the correlation between equilibrium structural fluctuations in the distal cavity and the function of this NO transporter protein. The rates of NO binding/release to ferric myoglobin are 10/2000 fold faster than those for NP4, in addition to being described by a single phase.⁴³ A recent study has measured the FFCF of the ν_NO in wild-type Mb^IIINO to have a timescale of 3 ps and significant portions of the dynamics were too slow to measure on the experimental timescale.²⁴ In comparison with the NP4-NO 2D IR results presented in this manuscript, the ν_NO in wild-type Mb^IIINO lacks equilibrium structural fluctuations on the 70-100 ps timescale. This suggests that the equilibrium frequency fluctuations arising from local electric field fluctuations in the distal pocket and the loop dynamics have a role to play in regulating the uptake and diffusion of the nitrosyl ligand in NP4.

IV. Summary

In summary, we use 2D IR spectroscopy to measure the picosecond structural dynamics in the distal pocket of NP4–NO. We assign the A₀ and A₁ peaks in the nitrosyl stretching region of the FTIR to the ν_NO of the closed and open conformers of NP4-NO present at pD 5.1 and 7.9. The assignment is in agreement with previous IR and Raman studies of NP4-NO and Mb^IIINO and DFT calculations. The measured timescales of the FFCF for the A₀ and A₁ peaks are a quantitative description of the structural heterogeneity and solvent dynamics in the vicinity of the heme. The ability of the open conformer to exchange among its sub-states in ∼100 ps measures the structural flexibility of the loop regions. The spectroscopic data provides a microscopic explanation for the previously observed kinetic heterogeneity in the release rates of NO from the protein at all pH conditions. This study highlights how picosecond structural dynamics in the distal pocket of NP4-NO are linked to its function and could hold implications for ligand binding and release in other NO transport and receptor proteins.