Abstract
Extracellular neuroelectronic interfacing is an emerging field with important applications in the fields of neural prosthetics, biological computation and biosensors. Traditionally, neuron-electrode interfaces have been modeled as linear point or area contact equivalent circuits but it is now being increasingly realized that such models cannot explain the shapes and magnitudes of the observed extracellular signals. Here, results were compared and contrasted from an unprecedented optimization based study of the point contact models for an extracellular ‘on-cell’ neuron-patch electrode and a planar neuron-microelectrode interface. Concurrent electrophysiological recordings from a single neuron simultaneously interfaced to three distinct electrodes (intracellular, ‘on-cell’ patch and planar microelectrode) allowed novel insights into the mechanism of signal transduction at the neuron-electrode interface. After a systematic isolation of the nonlinear neuronal contribution to the extracellular signal, a consistent underestimation of the simulated supra-threshold extracellular signals compared to the experimentally recorded signals was observed. This conclusively demonstrated that the dynamics of the interfacial medium contribute nonlinearly to the process of signal transduction at the neuron-electrode interface. Further, an examination of the optimized model parameters for the experimental extracellular recordings from sub- and supra-threshold stimulations of the neuron-electrode junctions revealed that ionic transport at the ‘on-cell’ neuron-patch electrode is dominated by diffusion whereas at the neuron-microelectrode interface the electric double layer (EDL) effects dominate. Based on this study, the limitations of the equivalent circuit models in their failure to account for the nonlinear EDL and ionic electrodiffusion effects occurring during signal transduction at the neuron-electrode interfaces are discussed.
Keywords: Neuroelectronic interface, nonlinear ionic electrodiffusion, whole-cell biosensors, microelectrode arrays
I. INTRODUCTION
Extracellular recording of electrophysiological signals from individual cells using microelectrode arrays (MEAs) or field effect transistors (FETs) has important applications in the fields of prosthetic devices, biological computation and whole cell biosensors for high throughput drug screening or toxin detection [1-6]. While the field of bioelectronic interfacing holds great promise, the recording of high fidelity signals from extracellular devices has long suffered from the problem of low signal to noise ratios which has made it difficult to correlate the extracellularly recorded signals with the intracellular signals recorded using conventional patch-clamp electrophysiology.
For bringing about an improvement in the signal to noise ratio of the signals recorded on the extracellular microelectrodes and to explore strategies for engineering the cell-sensor interface using surface chemical modification of electrodes [7-9], microelectrode design or new electrode materials [10, 11], there exists a need to simulate and model the cell-sensor interface to better understand the mechanism of signal transduction across the interface. In most studies to date, much of the effort on modeling the cell-sensor interface has focused on the use of point or area contact linear equivalent circuit models for a description of the interface with an assumption of passive linearity for the dynamics of the interfacial medium in the cell-electrode cleft [12-17]. Only recently, the use of equivalent circuit models for simulating the cell-sensor interface has been questioned based on arguments related to the physics of electrodiffusion of ions in the cleft between the electrically active cell and the sensor and a modulation of the surface potential on the sensor surface [18-20]. Although models based on a description of electrodiffusion of ions in the cell-biosensor interface have been advanced, to date there has been no systematic attempt to explore the limitations of linear equivalent circuit models for representing the cell-biosensor interface.
In this regard, a recent paper from our group indicated the presence of second order nonlinear effects that occur during the process of signal transduction across the planar neuron-microelectrode interface through the estimation of a Volterra-Wiener model of the neuron-electrode junction from experimental data [21]. Based on our observation of these effects, two hypotheses were proposed (i) the nonlinear contributions to the extracellular signals recorded from the neuron-sensor junction are from a nonlinear dynamic neuron interfaced to the microelectrode through a passively linear interface that can be modeled using point or area contact linear equivalent circuit models, or (ii) the extracellular signals recorded on the microelectrode have active nonlinear contributions from both the neuron and the dynamics of the interfacial medium in the cleft. It was, however, not possible from the Volterra-Wiener model to conclusively prove whether these nonlinear contributions were exclusively from the neuron or from a combination of the dynamics of the neuron and the nonlinear ionic electrodiffusion and dielectric relaxation of the extracellular medium in the neuron-electrode cleft.
Therefore, to test if a passively linear interface employed in point or area contact equivalent circuit models is a valid representation of the system and to ascertain if there is indeed any contribution to the extracellular signals from the dynamics of the interfacial medium in the neuron-microelectrode cleft that cannot be modeled based purely on the theory of linear equivalent circuit models, a systematic study based on an optimization of the parameters of an equivalent circuit model for the neuron-microelectrode interface was undertaken. Additionally, we compare and contrast our results from the optimization of parameters of equivalent circuit models for a neuron simultaneously interfaced to an ‘on-cell’ patch electrode and the planar microelectrode (fig. 1 A and B) by fitting the simulated results to the extracellularly recorded signals obtained by a stimulation of the neuron through an intracellular patch electrode.
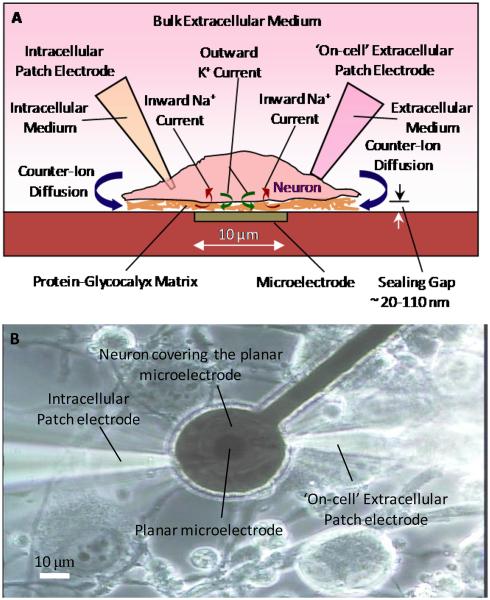
Fig. 1.
(A) An illustration of the experimental arrangement for the electrophysiological characterization of the ‘on-cell’ neuron-patch electrode and neuron-microelectrode interfaces. (B) An image of a NG108-15 neuron covering a planar microelectrode on an MEA interfaced simultaneously to intracellular and ‘on-cell’ extracellular Ag/AgCl patch electrodes.
As a control system, the ‘on-cell’ patch model of the neuron-patch electrode interface having a gigaOhm seal with the neuronal membrane would allow for a direct measurement of the cell-generated membrane potentials and also serve as a limiting case for the neuron microelectrode interface (fig. 1 A and B). The ‘on-cell’ patch would have a smaller area of attachment on the neuronal membrane compared to the cell-electrode contact at the planar neuron-microelectrode interface, but would be better defined. Also, at the extracellular neuron-patch electrode interface the cell membrane would be in direct contact with a large volume of the extracellular bath solution inside the patch electrode in sharp contrast to the small volume of the extracellular solution in the narrow (20-110 nm) neuron-microelectrode cleft. The two systems would also be different due to the presence of the porous protein-glycocalyx matrix and the extracellular matrix proteins deposited on the microelectrode due to a prolonged contact with the cell membrane. However, by understanding these differences we hoped to further understand this complicated system.
II. METHODS
Several different types of extracellular signal shapes recorded both with planar microelectrodes and field effect transistors have been reported in literature. On the basis of the recorded shapes the neuron-sensor junctions have broadly been classified into three major types: (a) capacitive, (b) ohmic and (c) anti-capacitive junctions characterized by a leading positive transient, direct proportionality to the intracellular signal and a leading negative transient respectively [12, 22-24]. Of these, the ohmic junction represents a strong coupling between the neuron and the sensor and its occurrence is the least common while most of the recorded extracellular signals fall under either the capacitive or the anti-capacitive category. The capacitive coupling has been interpreted on the basis of the linear junction conductance alone but the interpretation of the anti-capacitive coupling has required assumptions of a difference in the ion-channel distributions or a variance in their conductivity in the attached membrane compared to the free membrane [25]. However, there exists no conclusive evidence of either selective accumulation-depletion of ion-channels in the attached membrane or a difference in their conductance with respect to the free membrane [20]. Therefore, to test the hypothesis of the passive linearity of the neuron-electrode interface, in this paper we exclusively focused our attention on the extracellularly recorded signals that conformed to the ‘linear’ capacitive coupling of the neuron-electrode interface as previously reported in the literature [12, 22-24].
A. Cell culture and electrophysiological recording protocols
Briefly, NG108-15 neurons were cultured on top of substrate embedded microelectrode arrays and three-way electrophysiological recordings (fig. 1 A and B) were performed on them in voltage and current clamp modes. The culture of the NG108-15 neurons and extracellular and intracellular electrophysiological recordings from the neuron-electrode interfaces were carried out according to protocols and techniques described in [21, 26]. Whole-cell patch clamp recordings were performed using an intracellular electrode on neurons covering the microelectrodes completely while a second patch electrode filled with the extracellular solution was employed to form a seal with the neuronal membrane without breaking in to the cell.
NG108-15 cells are a cross between mouse neuroblastoma and rat glioma cells that unlike neurons do not form synapses among themselves but at the same time retain fully functional neuron-like ion-channels. The non-synapsing feature of the NG108-15 cells makes them ideally suited for use as whole-cell biosensors in high-throughput drug screening and toxin detection wherein an undesirable component of independent network-like behavior of neurons can be avoided while retaining the sensitivity advantage of neurons.
B. Mathematical models
NG108-15 neurons
A Hodgkin-Huxley type mathematical model of NG108-15 cells, based on the thermodynamic rate constant approach developed previously [27-29], was employed to extract the ion-channel parameters for the sodium, calcium and potassium ion channels. The dynamic membrane potential Vm in the mathematical model for the NG108-15 neuron was computed using
| (1) |
where Iinj is the external current injected into the neuron through the intracellular patch electrode and Cm the membrane capacitance. The total ionic membrane current Iionic and the leakage current IL were described in terms of the membrane potential Vm as
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
while the dynamics of the state variables for the ion-channels were given by
| (7) |
where gNa, gK, gCa, VNa, VK and VCa are maximum ion channel conductances followed by corresponding reversal potentials (sodium, potassium and calcium in that order); gL and VL are the leakage conductance and leakage reversal potentials respectively; m, h, n, and e are the state variables with m∞, h∞, n∞, and e∞ as their steady state values and the τ’s their voltage dependent time constants. The maximum conductance gL of the leakage current across the cell membrane was computed using
| (8) |
where and ionic are the membrane ionic currents at the holding potentials V1h and V2h respectively and Rm is the experimentally obtained membrane resistance. Membrane holding potentials V1h (−85 mV) and V2h (−80 mV) were chosen such that there was no significant contribution from the opening of the voltage-gated sodium, potassium and calcium ion channels at these potentials i.e. the membrane was in a hyperpolarized state. The leakage reversal potential VL was then computed using
| (9) |
This made use of the fact that the net membrane current at the resting membrane potential is zero. The superscript ‘ r ’ on the ion channel mediated currents represents the currents computed at the resting membrane potential. The voltage dependent steady state parameters and the time constants were computed using the general formulae
| (10) |
and
| (11) |
where the fitting parameters were: z, related to the number of moving charges during the opening and closing of the ion channels; V1/2, to the half activation/inactivation potential of the ion channel; A, related linearly to the activation or the inactivation time constant; and ξ, to the asymmetric position of the moving charge in the cell membrane. F, is the usual Faraday’s constant. The experimentally obtained parameters used in the model were: Rm, the membrane resistance; , the resting membrane potential; Cm, the membrane capacitance; and Iinj, the injected current.
‘On-cell’ neuron-patch electrode interface
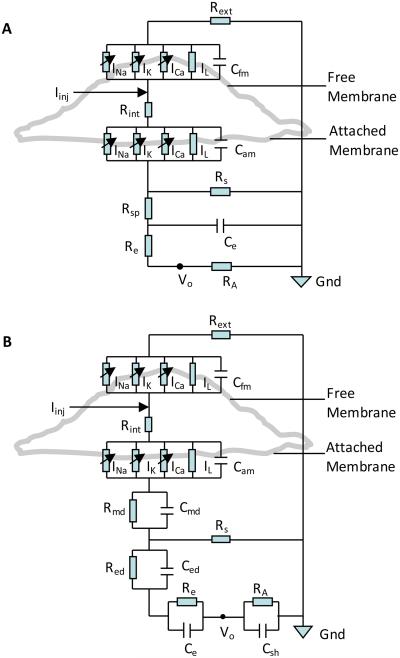
The neuron-patch electrode interface was modeled using a two compartment system as depicted in fig. 2 A. The physical significance of the equivalent circuit elements used in the model of the ‘on-cell’ neuron patch electrode interface was as follows: Rext, the resistance of the extracellular medium between the free membrane of the neuron and the ground electrode; Cfm, the free membrane capacitance; Rint, the internal cytoplasmic resistance to ionic current flow as seen by the ‘on-cell’ extracellular patch electrode; Cam, the capacitance of the portion of neuronal membrane interfaced to the extracellular patch electrode; Rs, the seal resistance between the inside of the ‘on-cell’ patch electrode and the bulk extracellular medium; Rsp, the spreading resistance between the cell and the extracellular patch electrode; Re and Ce, the resistance and the capacitance of the extracellular patch electrode respectively with Ce representing the capacitive coupling between the glass micropipette tip and the extracellular medium; and, RA, the input impedance of the recording amplifier. The attached and free membrane capacitances, Cfm and Cam, being in parallel, are directly proportional to the fractional surface areas of the attached and free membranes respectively and were computed based on the experimentally determined values for the membrane capacitance Cm using equations (12) and (13)
| (12) |
| (13) |
where aj is the fractional surface area of the attached membrane. The extracellular potential recorded with the ‘on-cell’ patch electrode for the circuit model depicted in fig. 2 A was computed using Kirchoff’s current and voltage law based set of time dependent linear first order ordinary differential equations that were coupled to the equations (7) for the Hodgkin-Huxley type linear thermodynamic model of the NG108-15 neuron.
Fig. 2.
Schematics of the point contact equivalent circuit models for (A) the ‘on-cell’ neuron-patch electrode interface and (B) the neuron-microelectrode interface. Vo represents the extracellular output.
Planar neuron-microelectrode interface
For modeling the neuron-microelectrode interface a more refined two compartment equivalent circuit model was employed (fig. 2 B) which included additional equivalent circuit elements to take into account the complexity arising from modeling the presence of EDL effects in the narrow 20-110 nm wide neuron-microelectrode cleft. The resistance and capacitance of the EDL associated with the protein-glycocalyx complex attached to the portion of the cell-membrane in contact with the microelectrode were modeled with circuit elements Rmd and Cmd respectively, while resistance Red and capacitance Ced modeled the equivalent resistance and capacitance of the EDL associated with the extracellular matrix deposited on the microelectrode. Resistor Re and capacitor Ce modeled the resistance and capacitance of the microelectrode and the parasitic shunt capacitance between the insulated connection leads (from the microelectrode to the amplifier) and the bulk electrolyte was modeled with the shunt capacitance Csh. The sealing resistance Rs simulated the resistance to ionic current flow between the center of the neuron-microelectrode cleft and the bulk extracellular medium. The dynamics of the neuron-microelectrode interface for the equivalent circuit model shown in fig. 2 B were simulated using coupled differential equations for the linear interface combined with equations (7) that modeled the ion-channel kinetics of the NG108-15 neuron.
C. Optimization of the model parameters
NG108-15 neurons
Previously estimated average values of the ion-channel parameters for NG108-15 neurons were used as starting values for the ion-channel parameter fitting procedure [28]. The fitting procedure was customized using a graphical user interface. The parameters for the sodium, potassium and calcium channels were obtained by fitting the simulated ionic currents and membrane potentials to the experimentally recorded ion-channel mediated membrane currents and potentials obtained from the voltage and current clamp recordings of the neuron respectively. Initially, the sodium currents were fitted in the range −65 mV to −35 mV followed by a fitting of the potassium currents in the −15 mV to +15 mV range. After this a simultaneous fitting of the ion-channel parameters was carried out to obtain a first estimate of the parameters for the sodium, potassium and calcium channels. Further, to overcome the limitations of the parameter fitting procedure with regard to the uniqueness of the large number of fitted parameters and to obtain a quasi-unique set, a second optimization of the estimated ion channel parameters was performed by fitting the simulated action potentials to the experimental current clamp signals.
Neuron-electrode interface
Optimization of the equivalent circuit parameters for the neuron-electrode interface was carried out in two steps. In the first step, all circuit parameters, including the fractional surface area of the attached membrane but excluding the experimentally determined total membrane capacitance Cm, were optimized by fitting the simulated extracellular signals to the experimental sub-threshold stimulation records obtained from the neuron-electrode interfaces. It is accepted that sub-threshold stimulation of a hyperpolarized neuron is not accompanied by an opening of the voltage gated membrane ion-channels responsible for the generation of action potentials and as a result there is no corresponding contribution from ionic electrodiffusion to the extracellular signals recorded on the electrodes. A sub-threshold stimulation pulse leads to a depolarization of the neuronal membrane through intracellular current injection and a consequent electromigration of the ions under the influence of an electric field. In this regime, the membrane conductance stays ohmic and is characterized by an ohmic leakage current across the membrane. As the sub-threshold stimulation pulse is not accompanied by an opening of the voltage gated ion-channels it does not induce significant ionic concentration gradients between the neuron-electrode interface and the bulk extracellular medium. In the case of the supra-threshold stimulation of the neuron, however, the opening of the voltage gated ion-channels leads to a significant difference in the ionic concentrations at the neuron-electrode interface relative to the ionic concentrations in the bulk extracellular medium. Therefore, the second step in the optimization of the equivalent circuit parameters for the neuron-electrode interface involved fixing the optimized invariant parameters obtained in step one and a re-evaluation of the remaining parameters of the model for the neuron-electrode interface by a fitting of the simulated signals to the experimental signals obtained from the supra-threshold stimulation of the neuron. This, as hypothesized, would enable quantification of the changes in the equivalent circuit parameters affected by the physics of ionic electrodiffusion upon opening of the voltage-gated ion-channels as one transitioned from the sub- to the supra-threshold regime of neuronal stimulation.
D. Numerical Methods
The coupled ordinary differential equations for the linear thermodynamic model of the neuron and the equivalent circuit representations of the neuron-electrode interfaces were numerically integrated in MATLAB (The MathWorks, Natick, MA) using its in-built differential equation solver ode15s for the solution of a set of stiff equations. The relative and absolute error tolerances of MATLAB’s ode15s solver were set to 10−4 and 10−7 respectively.
An in-built MATLAB optimization routine fmincon (employed for computing a constrained minimum of a function dependent on several variables within specified bounds and/or linear or nonlinear constraints) was first used for the estimation of the ion-channel parameters for the NG108-15 neurons and subsequently for the estimation of the equivalent circuit parameters for the neuron-electrode interfaces by fitting the simulated signals to the experimentally recorded signals. All parameter optimizations were carried out by minimizing the sum of squared residuals as shown in equation (14)
| (14) |
where S(tn) is the simulated data at time tn and R(tn) is the recorded value at that instant of time. However, for a comparison of the quality of fitting of the simulated signals to the experimental signals of differing magnitudes recorded from the three electrodes, the normalized sum of squared residual (nssr) values are reported here.
The ‘algorithm’ option in MATLAB for the optimization routine fmincon was set to the sequential quadratic programming (SQP), quasi-Newton line-search algorithm for all optimizations. An optimization termination tolerance of 10−8 for the minimizing function and the parameters being optimized was employed while the tolerance on constraint violation for the optimized parameters was fixed at 10−12. If a constraint violation on the upper or lower bounds for any parameter(s) was reported at the termination of the optimization routine then the limits were appropriately adjusted and the optimization procedure repeated for that case. The lower and upper bounds of the equivalent circuit model parameters were selected based on known typical values of the parameters from experiments and published literature [14, 30, 31]. The amplifier input impedance RA was fixed at 12 GΩ for all simulations.
III. RESULTS
A. Ion-channel parameters for the NG108-15 neurons
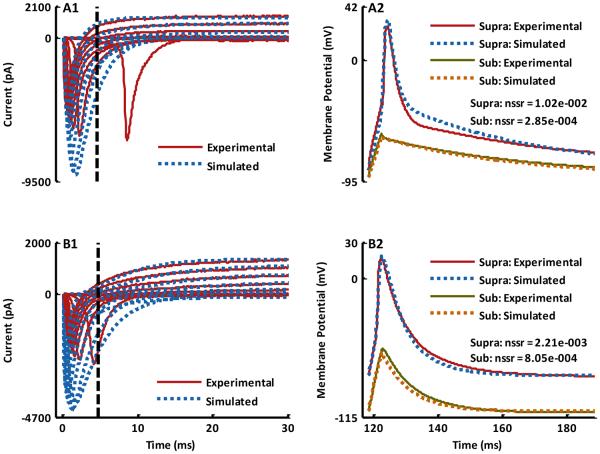
The results from the ion-channel parameter fitting procedure for the voltage and current clamp recordings are shown for a set of representative NG108-15 neurons, indicated by Cell 1 (fig. 3, A1 and A2) and Cell 2 (fig. 3, B1 and B2), selected from a group of neuron-electrode interfaces examined experimentally (n = 10). For the voltage clamp recordings an excellent fit to the experimental results was obtained for the potassium channel mediated ionic currents (fig. 3, A1 and B1 outward currents to the right of the dashed vertical black lines) but the fitted traces overestimated the sodium channel currents (fig. 3, A1 and B1, inward currents to the left of the dashed vertical black lines) due to space-clamping effects generated as a result of the large size of the NG108-15 neurons. An excellent fit to the experimentally recorded signals was obtained for the current clamp recordings for both the sub- and supra-threshold stimulation cases (fig. 3, A2 and B2). Table I, A and B, shows the optimized ion-channel parameter values for the recording data from the NG108-15 neurons reported here. The estimated ion-channel parameters were then fixed and employed further in the determination of the parameters of the equivalent circuit models for the neuron-electrode interface. Also, in all subsequent simulations of the two compartment equivalent circuit models of the neuron-electrode interface, a uniform spatial distribution of the different types of ion-channels in the attached and the free neuronal membranes was assumed.
Fig. 3.
A comparison of the simulated results with the experimentally recorded intracellular signals after an optimization of the ion-channel parameters. (A1 and B1) Experimental voltage clamp signals recorded using 10 mV potential steps starting from a holding potential of −85 mV (solid line) and their corresponding simulated voltage clamp signals (dotted line) using optimized ion-channel parameters for Cell 1 and Cell 2 respectively (See Table I, A and B). Currents to the left of the dashed black vertical lines represent inward sodium currents while to the right of the lines outward potassium currents are shown. (A2 and B2) Experimental sub- (solid line) and supra-threshold (solid line) intracellularly recorded current clamp signals from Cell 1 (Sub-threshold current injection, Iinj = 560 pA and supra-threshold current injection, Iinj = 760 pA, Δt = 4 ms ; membrane capacitance Cm = 70 pF ; and, resting membrane potential ) and Cell 2 (Sub- and supra-threshold current injection, Iinj = 1180 pA, Δt = 4 ms; membrane capacitance Cm = 80 pF ; and, resting membrane potential ) respectively. Simulated sub- (dotted line) and supra- threshold (dotted line) intracellular current clamp signals for Cell 1 and Cell 2 using optimized ion-channel parameters shown in Table I, A and B.
Table I.
Optimized ion channel parameters for (A) Cell 1 and (B) Cell 2 obtained by a fitting of the simulated current and voltage clamp intracellular signals to the experimentally recorded signalsa.
| A. |
| Activation |
Inactivation |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Channel | g | V rev | z | V 1/2 | ξ | A | z | V 1/2 | ξ | A |
| Sodium | 157.67 | 120.0 | 7.10 | −47.38 | −0.43 | 0.42 | −19.09 | −63.72 | 0.46 | 2.79 |
| Potassium | 16.05 | −80.0 | 3.16 | −14.43 | 0.13 | 8.65 | - | - | - | - |
| Calcium | 3.82 | 32.0 | 2.59 | −5.07 | −0.59 | 0.91 | - | - | - | - |
| Leakage | 1.61 | −54.6 | - | - | - | - | - | - | - | - |
| B. |
| Activation |
Inactivation |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Channel | g | V rev | z | V 1/2 | ξ | A | z | V 1/2 | ξ | A |
| Sodium | 51.56 | 120.0 | 7.48 | −56.00 | −0.38 | 0.42 | −20.25 | −58.65 | 0.46 | 2.97 |
| Potassium | 16.02 | −80.0 | 1.62 | −42.64 | 0.03 | 14.28 | - | - | - | - |
| Calcium | 3.82 | 32.0 | 2.59 | −5.11 | −0.59 | 0.91 | - | - | - | - |
| Leakage | 9.09 | −34.0 | - | - | - | - | - | - | - | - |
The ion-channel conductances and the electric potentials are reported in nano-Siemens and mV respectively.
B. ‘On-cell’ neuron-patch electrode interface
For the ‘on-cell’ neuron patch-electrode interface (fig. 2 A) the equivalent circuit parameters optimized using the extracellular signals recorded from sub-threshold stimulation of NG108-15 neurons included the internal cytoplasmic resistance Rint, the external resistance Rext, the spreading resistance Rsp, the sealing resistance Rs, the patch electrode resistance Re and capacitance Ce and aj, the fractional area of the cell membrane in contact with the extracellular patch electrode. The ‘on-cell’ extracellular signals employed in the parameter optimization corresponded to the sub-threshold intracellular potentials shown in fig. 3 A2 (Cell 1) and B2 (Cell 2). An excellent fit was obtained for the extracellular signals recorded on the patch electrodes corresponding to the sub-threshold stimulation of the neuron in the case of both the NG108-15 neurons employed in the study (fig. 4, A1 and B1). Table II, A and B indicate the sub-threshold values of the optimized parameters for Cell 1 and Cell 2.
Fig. 4.
A comparison of the simulated and the experimental results for the extracellular signals recorded from the ‘on-cell’ neuron-patch electrode interfaces for Cell 1 and Cell 2 after optimization of the point contact equivalent circuit model (fig. 2 A) parameters. (A1 and B1) Sub-threshold stimulation for Cell 1 and Cell 2 respectively. (A2 and B2) Supra-threshold stimulation for Cell 1 and Cell 2 respectively. (See Table II, A and B, for values of optimized equivalent circuit parameters.)
Table II.
Optimized parameters of the point contact equivalent circuit model for the ‘on-cell’ neuron-patch electrode interfaces for (A) Cell 1 and (B) Cell 2b.
| A. |
| a j | C e | R ext | R int | R s | R sp | R e | |
|---|---|---|---|---|---|---|---|
| Sub | 0.62 | 6.00 | 4.25e-5 | 5.20e-3 | 1.56e-1 | 5.00e-3 | O |
| Sup | O | O | 2.40e-6 | 1.65 | 5.39e-1 | 6.18e-2 | O |
| B. |
| a j | C e | R ext | R int | R s | R sp | R e | |
|---|---|---|---|---|---|---|---|
| Sub | 0.89 | 4.71e-1 | 1.28e-4 | 1.20e-1 | 6.75e-2 | 1.85e-1 | 3.31e-2 |
| Sup | O | O | 3.86e-4 | 1.17 | 1.28e-1 | 5.18e-3 | O |
The symbol ‘O’ stands for the point contact equivalent circuit model parameters fixed at values obtained from sub-threshold optimization of the model parameters for the neuron-electrode interfaces. The fractional surface area of the attached membrane is reported as a percentage of the total membrane surface area; all resistances are in gigaohms (GΩ) and the capacitances are in picoFarads (pF) . ‘Sub’ and ‘Sup’ refer to sub- and supra-threshold stimulations respectively.
Next, the optimized values of the invariant parameters - the ‘on-cell’ patch-electrode resistance Re, capacitance Ce and the fractional area of contact between the cell membrane and the ‘on-cell’ patch electrode aj obtained from the optimization of the sub-threshold signals were fixed while the rest of the parameters of the equivalent circuit model were then re-evaluated by fitting the simulated supra-threshold extracellular signals (corresponding to supra-threshold intracellular action potentials shown in fig. 3, A2 and B2) to experimental data from the neuron-electrode interface. For the two cells being reported here, the quality of the fitting of the simulated extracellular signal in the supra-threshold case to the corresponding experimentally recorded signal, although reasonably good, was not comparable to that obtained for the sub-threshold case and the optimized simulation results were observed to underestimate the amplitude of the extracellular signal when compared to the experimentally recorded signals as shown in fig. 4, A2 and B2. In the two NG108-15 neuron patch electrode interfaces considered it was observed that the internal cytoplasmic resistance, Rint, and the seal resistance, Rs (Table II, A and B) both increased in transitioning from the sub- to the supra-threshold stimulation of NG108-15 neurons indicating a change in these circuit parameters while no clear trend was discernible for the spreading resistance, Rsp, and the external resistance, Rext. This increase in the values of the internal cytoplasmic resistance, Rint, (as seen by the ‘on-cell’ patch electrode) and the seal resistance, Rs, in the supra-threshold case pointed to the presence of diffusion dominated ionic transport across the seal resistance formed by the ‘on-cell’ patch electrode with the neuronal membrane. Also, the high values of the seal resistance, Rs, (>1GΩ) obtained through the optimization procedure in the supra-threshold stimulation were consistent with the formation of a gigaseal for the extracellular patch electrodes as normally observed during conventional patch clamp electrophysiology.
Further, the impact of ionic electrodiffusion on the individual values of the equivalent circuit parameters employed for the supra-threshold optimization was systematically investigated by selectively fixing the equivalent circuit parameters at their sub-threshold values and optimizing the rest of the parameters to compare the normalized sum of squared residuals obtained for Cell 1 and Cell 2 (Table III, figures not shown here). It was determined that a selective elimination of the sealing resistance, Rs, and the internal cytoplasmic resistance, Rint, from the optimization procedure resulted in the highest normalized sum of squared residuals nssr (in that order) indicating that these two resistances were the most affected as a result of the ionic electrodiffusion induced by an opening of the voltage gated ion-channels in the supra-threshold regime of neuronal stimulation.
Table III.
nssr values for fitting of the simulated supra-threshold signal to experimental recordings after selective fixation of equivalent circuit parameter values at the sub-threshold level for the ‘on-cell’ patch electrode
| Circuit element | R s | R int | R ext | R sp |
|---|---|---|---|---|
| Cell 1 | 4.92e-1 | 1.64e-1 | 5.39e-2 | 5.82e-2 |
| Cell 2 | 6.89e-2 | 4.25e-2 | 2.35e-2 | 2.43e-2 |
It must be mentioned here that diffusion, within the framework of the point-contact equivalent circuit models, can only be simulated using a frequency dependent Warburg impedance [32] and thus, although the cytoplasmic internal resistance, Rint, and the seal resistance, Rs, did not simulate the Warburg impedance in this case, an increase in their values indicated the presence of ion transport mediated primarily by diffusion. Unlike linear impedance spectroscopy analyses, in this study, we employ a time domain composite model of the neuron-electrode interface that precludes the use of frequency dependent equivalent circuit elements for simulating interface dynamics.
C. Neuron-microelectrode interface
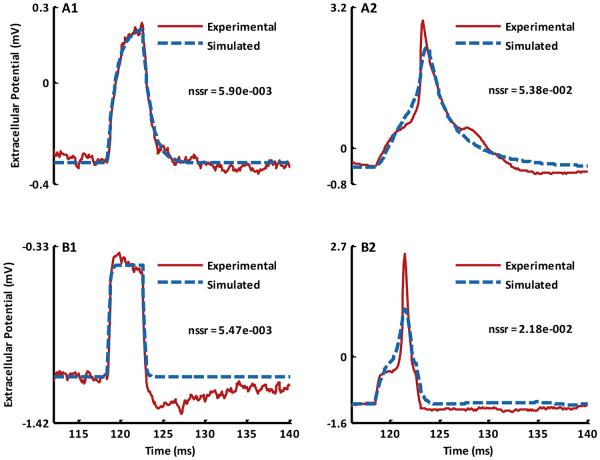
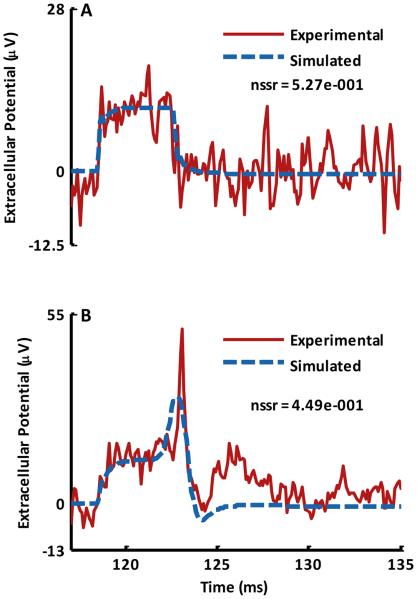
In the sub-threshold stimulation regime, capacitive type responses observed in the planar neuron-microelectrode interface for Cell 1 were analyzed. The equivalent circuit parameters of the neuron-microelectrode interface (fig. 2 B) included in the optimization for the sub-threshold stimulation were: resistor Rmd and capacitor Cmd, modeling the EDL associated with the protein-glycocalyx complex attached to the cell membrane, EDL resistance Red and capacitance Ced, associated with the microelectrode, resistance Re and capacitance Ce of the microelectrode, the parasitic shunt capacitance Csh, seal resistance Rs and the fractional area of the attached membrane in contact with the microelectrode aj. After an optimization of the equivalent circuit model parameters a reasonably good fit to the noisy extracellular signal corresponding to the sub-threshold stimulation of the neuron was obtained (fig. 5 A and Table IV). The related intracellular sub-threshold potential for the optimized extracellular signal is shown in fig. 3 A2.
Fig. 5.
A comparison of the simulated and the experimental extracellular signals recorded from the neuron-microelectrode interface corresponding to the supra-threshold stimulation of Cell 1 (fig. 3 A2) after optimization of the point contact equivalent circuit model (fig. 2 B) parameters. (A) Sub-threshold stimulation and (B) Supra-threshold stimulation. (See Table IV for the corresponding values of the equivalent circuit parameters.)
Table IV.
Optimized parameters of the point contact equivalent circuit model of the neuron-microelectrode interface for Cell 1b.
| a j | C md | C ed | C e | C sh | R ext | R int | R md | R s | R ed | R e | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub | 12.6 | 3.39 | 2.32e-1 | 5.00e+3 | 5.80e-3 | 4.91e-3 | 3.14e-2 | 2.82e-2 | 1.60e-4 | 4.44e-3 | 2.71e-4 |
| Sup | O | 3.37 | 2.22e-1 | O | O | 2.53e-5 | 2.95e-2 | 3.08e-2 | 1.38e-4 | 3.57e-3 | O |
The symbol ‘O’ stands for the point contact equivalent circuit model parameters fixed at values obtained from sub-threshold optimization of the model parameters for the neuron-electrode interfaces. The fractional surface area of the attached membrane is reported as a percentage of the total membrane surface area; all resistances are in gigaohms (GΩ) and the capacitances are in picoFarads (pF). ‘Sub’ and ‘Sup’ refer to sub- and supra-threshold stimulations respectively.
Again, as in the case of the ‘on-cell’ patch electrode interface, invariant parameters – the shunt capacitance Csh, the microelectrode resistance Re and capacitance Ce, and the area of the attached membrane in contact with the microelectrode aj, obtained from the sub-threshold optimization of the model parameters for the neuron-microelectrode interface, were fixed. The fitting of the simulated extracellular signals for the supra-threshold stimulation of the cell was performed by optimizing the values of the rest of the circuit elements in the equivalent circuit model of the neuron-microelectrode interface. Fig. 5 B shows a good fit of the simulated signal to the experimental signal recorded through the microelectrode (See fig. 3 A2 for the corresponding supra-threshold intracellular potential). In the case of the neuron-microelectrode interface, as also for the ‘on-cell’ neuron-patch electrode interface, the optimized signals underestimated the amplitude of the extracellular signals compared to the experimentally recorded signals from the planar microelectrode. But, unlike the neuron-patch electrode interface, Rs decreased in transitioning from the sub- to the supra-threshold regime of neural stimulation. A decrease in Rs in transitioning from the sub- to the supra-threshold stimulation was consistent with the enhanced conductivity of the overlapping EDLs in the neuron-microelectrode cleft region as a consequence of the increased ionic concentrations caused by an opening of the ion-channels during the supra-threshold stimulation of the neuron. A similar enhancement in the conductivity of the cell-sensor junction for HEK 293 cells interfaced to field effect transistors was also reported by Brittinger et al [18].
A further investigation of the impact of the change in circuit parameters due to ionic electrodiffusion on the fitting of the supra-threshold simulated signals to the experimental extracellular recordings was done by selectively fixing the circuit parameters at their sub-threshold values and optimizing the rest of the parameters to study its effect on the normalized sum of squared residuals. It was observed that selective fixation at sub-threshold values of all the parameters under consideration gave comparable nssr values (nssravg = (4.48 ± 0.03)×10−1) except in the case of the seal resistance, Rs (nssr = 4.63×10−1), and external resistance, Rext (nssr = 5.16×10−1), where it was noticeably higher than the rest. In the case of Rs, the increase in nssr value upon selective elimination was along expected lines for the reasons discussed in the preceding paragraph while for Rext it appeared that the optimization of the sub-threshold extracellular signal overestimated the value for the external resistance resulting in a high normalized sum of squared residuals. However, as Rext must not change between the ‘on-cell’ patch-electrode and the neuron-microelectrode interfaces (being a property of the bulk extracellular solution), the value of the external resistance (Rext = 2.53×10−5 GΩ, Table IV) obtained from the supra-threshold optimization for the planar neuron-microelectrode interface compared well with the average value obtained from an optimization of the equivalent circuit parameters for the corresponding ‘on-cell’ neuron-patch electrode interface (Table II A).
IV. DISCUSSION
Based on the optimization analysis presented here it was observed that for the ‘on-cell’ neuron patch electrode and the neuron-microelectrode interfaces the simulated post-optimization extracellular signals for the supra-threshold stimulations consistently underestimated the amplitude of the extracellular signal compared to the experimentally recorded signals. Since the current that flows through a microelectrode is negligible because of the high input impedance of the extracellular recording amplifier, a comparison can also be made with studies employing electrogenic cells interfaced to field effect devices that have comparable current flowing through the gate oxide. Earlier studies, by Wrobel et al and Brittinger et al [18, 20], that used field effect transistors, had also reported similar observations related to point contact equivalent circuit models of the cell-biosensor interface. Both studies attributed the underestimation of the amplitude of the simulated extracellular signal to the mechanism of ion-binding to the gate-oxide of the field effect transistor and concluded that diffusion or electrodiffusion alone could not explain the amplitude of the experimentally recorded extracellular signals.
Wrobel et al employed the Nernst-Planck equation reduced to a pure diffusion equation under assumptions of electroneutrality and thin EDLs to simulate the ion-accumulation in the cleft region which was then combined with the ion-sensitivity of the field effect transistor to reproduce the experimental signals by a fitting of the radius, R, of the attached membrane and the cleft height, h. Brittinger et al modeled electrodiffusion in the interfacial cleft by considering the Nernst potential arising from the ionic concentration difference between the bulk extracellular medium and the interfacial medium. But they could account for the total signal recorded on the transistor only after a superposition of the experimentally determined surface potential changes associated with the Gouy-Chapman-Grahame diffuse EDL on the silanized gate-oxide (arising due to a competitive binding of sodium and potassium ions) and the potential difference generated in the cleft region due to electrodiffusion of ions.
It is worth noting here that, despite the Debye length being much smaller than the width or height of the cleft (~ 20-110 nm), at the given ionic concentrations in the extracellular medium the electric double layer actually extends across the entire interface to the sensor surface due to the presence of fixed charges associated with the porous-protein glycocalyx matrix responsible for cellular adhesion on the sensor surface. The presence of overlapping EDLs in the cell-sensor interfacial cleft therefore renders the assumption of electroneutrality in the interfacial cleft incorrect. Also, the region within the overlapping EDLs is characterized by a nonlinear dependence of the electric potential on the ionic concentration profile accompanied by a presence of high electric fields. These studies thus indirectly pointed to the presence of nonlinear EDL effects in the process of signal transduction across the volume of the thin cell-sensor interfacial cleft.
Both these studies, however, considered a simplified system of recombinant K+ channels expressed in HEK 293 cells interfaced to the FETs and did not explicitly simulate the gating kinetics of the ion-channels coupled to their model for the cell-biosensor interface. In contrast, the coupled dynamics of the neuron and the linear equivalent circuit model for the interface were explicitly simulated in our study. Additionally, in our model for the NG108-15 neuron we estimated gating parameters of the ion-channel kinetics for sodium, potassium and calcium channels from the experimental current and voltage clamp recordings that realistically and uniquely accounted for the dynamics of the cells included in our study.
More recently, our laboratory experimentally characterized the neuron-microelectrode junction by an intracellular stimulation of the neuroelectronic interface with band-limited Gaussian white noise spanning the entire natural frequency and amplitude range of action potentials [21]. This approach of non-parametric ‘data-true’ nonlinear dynamic characterization of the neuroelectronic junction using Volterra-Wiener modeling allowed us to take into account all possible linear and second order nonlinear physicochemical processes, including ionic electrodiffusion, occurring at the neuron-microelectrode interface during the process of signal transduction. These results indicated that the linear part of the predicted output from the Volterra-Wiener model underestimated the extracellular signal but a summation of the linear and the nonlinear outputs accurately predicted the amplitude and shape of the experimentally recorded signal from the planar microelectrode. However, we were unable to separate the nonlinear contribution of the neuronal dynamics from the contribution of the interfacial medium to the recorded signal on the microelectrode.
It is notable that Buitenweg et al had also observed nonlinear components in the extracellular potentials recorded in their stimulation experiments with the neuron-electrode interface which could not be attributed entirely to the active neuronal contributions [33]. Their approach had focused on isolating the nonlinear component of the experimentally recorded response by a subtraction of the linear component from the total extracellular signal. For this purpose, the linear component of the extracellular response was simulated by employing an impedance model of the interface estimated earlier using linear impedance spectroscopy. However, they had not isolated the neuronal contribution from the interfacial contribution in the total nonlinear response detected in the extracellular signal. In the results presented here, we go a step further and systematically isolate the neuronal contribution to the nonlinearity in the extracellular response recorded through the microelectrodes using a prior independent estimation of the neuronal ion-channel parameters unique to the neuron-electrode interface under study.
V. CONCLUSIONS
In this study, concurrent electrophysiological recordings from a single neuron simultaneously interfaced to three distinct electrode configurations (intracellular, ‘on-cell’ patch and planar microelectrode) allowed novel insights into the mechanism of signal transduction at the neuron-electrode interface. Through an advanced optimization based analysis of the extracellular signals, our results clearly established the role of ionic electrodiffusion in the process of signal transduction across the neuron-electrode interface and identified the parameters of the point contact equivalent circuit models most affected. Our results, for the first time conclusively demonstrated that the mechanism of signal transduction across the neuron-electrode interface was nonlinear. Further, within the framework of a passively linear point or area contact equivalent circuit model of the neuron-electrode interface, it is therefore not possible to simulate and recover the correct amplitude and shape of the experimentally recorded extracellular outputs from supra-threshold stimulation of the neuron-electrode interfaces. This is especially significant because these models are now being actively extended to neural interfaces with nanoelectronic devices characterized, presumably, by still higher electric fields and the consequent nonlinear dynamics of the interfacial medium [34-36].
Engineering of neuroelectronic interfaces using surface-chemical modification of sensor surface, improved design or novel materials for device fabrication requires an understanding of the mechanism of signal transduction with its accompanying physicochemical changes at the cell-sensor interface and thus necessitates a further development of models based on the nonlinear physics of electrodiffusion of ions or unconventional techniques like the ‘data-true’ Volterra-Wiener characterization. However, equivalent circuit models with their simplicity of concept and ease of implementation will continue to be useful tools for the study and characterization of cell-sensor interfaces for applications in high-throughput drug screening and toxin detection, biological computation and neuroprosthetic devices.
ACKNOWLEDGMENTS
Manuscript received January, 2012. This work was supported by NIH grants R01NS050452 and R01EB005459. Vaibhav Thakore and Peter Molnar contributed equally to this work.
Authors gratefully acknowledge Professor Thomas DeMarse and Dr. Frank Sommerhage for their critical reading of the manuscript and useful suggestions.
REFERENCES
- 1.Rutten WLC, Smit JPA, Frieswijk TA, Bielen JA, Brouwer ALH, Buitenweg JR, Heida C. Neuro-electronic interfacing with multielectrode arrays - Selectivity and efficiency of motor-fiber stimulation, toward a cultured probe. IEEE Engineering in Medicine and Biology Magazine. 1999 May-Jun;18:47–55. doi: 10.1109/51.765188. [DOI] [PubMed] [Google Scholar]
- 2.Varghese K, Molnar P, Das M, Bhargava N, Lambert S, Kindy MS, Hickman JJ. A New Target for Amyloid Beta Toxicity Validated by Standard and High-Throughput Electrophysiology. PloS One. 2010 Jan;5:e8643. doi: 10.1371/journal.pone.0008643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Natarajan A, Molnar P, Sieverdes K, Jamshidi A, Hickman JJ. Microelectrode array recordings of cardiac action potentials as a high throughput method to evaluate pesticide toxicity. Toxicology in Vitro. 2006 Apr;20:375–381. doi: 10.1016/j.tiv.2005.08.014. [DOI] [PubMed] [Google Scholar]
- 4.Bousse L. Whole cell biosensors. Sensors and Actuators B-Chemical. 1996 Aug;34:270–275. [Google Scholar]
- 5.Bonomini MP, Ferrandez JM, Fernandez E. Searching for semantics in the retinal code. Neurocomputing. 2009 Jan;72:806–813. [Google Scholar]
- 6.Ingebrandt S, Yeung CK, Krause M, Offenhausser A. Neuron-transistor coupling: interpretation of individual extracellular recorded signals. European Biophysics Journal with Biophysics Letters. 2005 Mar;34:144–154. doi: 10.1007/s00249-004-0437-9. [DOI] [PubMed] [Google Scholar]
- 7.Ignatius MJ, Sawhney N, Gupta A, Thibadeau BM, Monteiro OR, Brown IG. Bioactive surface coatings for nanoscale instruments: Effects on CNS neurons. Journal of Biomedical Materials Research. 1998;40:264–274. doi: 10.1002/(sici)1097-4636(199805)40:2<264::aid-jbm11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 8.Jung DR, Cuttino DS, Pancrazio JJ, Manos P, Cluster T, Sathanoori RS, Aloi LE, Coulombe MG, Czamaski MA, Borkholder DA, Kovacs GTA, Bey P, Stenger DA, Hickman JJ. Cell-based sensor microelectrode array characterized by imaging x-ray photoelectron spectroscopy, scanning electron microscopy, impedance measurements, and extracellular recordings. Journal of Vacuum Science & Technology a-Vacuum Surfaces and Films. 1998;16:1183–1188. [Google Scholar]
- 9.Stelzle M, Wagner R, Nisch W, Jagermann W, Frohlich R, Schaldach M. On the chemical modification of pacemaker electrodes and patterned surface functionalization of planar substrates. Biosensors & Bioelectronics. 1997;12:853–865. doi: 10.1016/s0956-5663(97)00050-x. [DOI] [PubMed] [Google Scholar]
- 10.Mazzatenta A, Giugliano M, Campidelli S, Gambazzi L, Businaro L, Markram H, Prato M, Ballerini L. Interfacing Neurons with Carbon Nanotubes: Electrical Signal Transfer and Synaptic Stimulation in Cultured Brain Circuits. J. Neurosci. 2007 June 27;27:6931–6936. doi: 10.1523/JNEUROSCI.1051-07.2007. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Thein M, Asphahani F, Cheng A, Buckmaster R, Zhang MQ, Xu J. Response characteristics of single-cell impedance sensors employed with surface-modified microelectrodes. Biosensors & Bioelectronics. 2010 Apr;25:1963–1969. doi: 10.1016/j.bios.2010.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Weis R, Fromherz P. Frequency dependent signal transfer in neuron transistors. Physical Review E. 1997 Jan;55:877–889. [Google Scholar]
- 13.Offenhausser A, Knoll W. Cell-transistor hybrid systems and their potential applications. Trends in Biotechnology. 2001;19:62–66. doi: 10.1016/s0167-7799(00)01544-4. [DOI] [PubMed] [Google Scholar]
- 14.Martinoia S, Massobrio P, Bove M, Massobrio G. Cultured neurons coupled to microelectrode arrays: Circuit models, simulations and experimental data. IEEE Transactions on Biomedical Engineering. 2004 May;51:859–864. doi: 10.1109/TBME.2004.826607. [DOI] [PubMed] [Google Scholar]
- 15.Bove M, Martinoia S, Grattarola M, Ricci D. The neuron-transistor junction: Linking equivalent electric circuit models to microscopic descriptions. Thin Solid Films. 1996 Sep;285:772–775. [Google Scholar]
- 16.Buitenweg J, Rutten WLC, Marani E. Geometry-based finite-element modeling of the electrical contact between a cultured neuron and a microelectrode. IEEE Transactions on Biomedical Engineering. 2003 Apr;50:501–509. doi: 10.1109/TBME.2003.809486. [DOI] [PubMed] [Google Scholar]
- 17.Joye N, Schmid A, Leblebici Y. Electrical modeling of the cell-electrode interface for recording neural activity from high-density microelectrode arrays. Neurocomputing. 2009 Dec;73:250–259. [Google Scholar]
- 18.Brittinger M, Fromherz P. Field-effect transistor with recombinant potassium channels: fast and slow response by electrical and chemical interactions. Applied Physics a-Materials Science & Processing. 2005 Aug;81:439–447. [Google Scholar]
- 19.Pabst M, Wrobel G, Ingebrandt S, Sommerhage F, Offenhausser A. Solution of the Poisson-Nernst-Planck equations in the cell-substrate interface. European Physical Journal E. 2007 Sep;24:1–8. doi: 10.1140/epje/i2007-10204-6. [DOI] [PubMed] [Google Scholar]
- 20.Wrobel G, Seifert R, Ingebrandt S, Enderlein J, Ecken H, Baumann A, Kaupp UB, Offenhausser A. Cell-transistor coupling: Investigation of potassium currents recorded with p- and n-channel FETs. Biophysical Journal. 2005 Nov;89:3628–3638. doi: 10.1529/biophysj.104.049809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Thakore V, Behal A, Molnar P, Leistritz DC, Hickman JJ. Nanoscale Nonlinear Dynamic Characterization of the Neuron-Electrode Junction. Journal of Computational and Theoretical Nanoscience. 2008 Nov;5:2164–2169. doi: 10.1166/jctn.2008.1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jenkner M, Fromherz P. Bistability of membrane conductance in cell adhesion observed in a neuron transistor. Physical Review Letters. 1997 Dec;79:4705–4708. [Google Scholar]
- 23.Schatzthauer R, Fromherz P. Neuron-silicon junction with voltage-gated ionic currents. European Journal of Neuroscience. 1998;10:1956–1962. doi: 10.1046/j.1460-9568.1998.00205.x. [DOI] [PubMed] [Google Scholar]
- 24.Fromherz P. Extracellular recording with transistors and the distribution of ionic conductances in a cell membrane. European Biophysics Journal with Biophysics Letters. 1999;28:254–258. doi: 10.1007/s002490050206. [DOI] [PubMed] [Google Scholar]
- 25.Buitenweg JR, Rutten WLC, Marani E. Modeled channel distributions explain extracellular recordings from cultured neurons sealed to microelectrodes. IEEE Transactions on Biomedical Engineering. 2002 Dec;49:1580–1590. doi: 10.1109/TBME.2002.805555. [DOI] [PubMed] [Google Scholar]
- 26.Ma W, Pancrazio JJ, Coulombe M, Dumm J, Sathanoori R, Barker JL, Kowtha VC, Stenger DA, Hickman JJ. Neuronal and glial epitopes and transmitter-synthesizing enzymes appear in parallel with membrane excitability during neuroblastomaxglioma hybrid differentiation. Developmental Brain Research. 1998;106:155–163. doi: 10.1016/s0165-3806(97)00208-3. [DOI] [PubMed] [Google Scholar]
- 27.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mohan DK, Molnar P, Hickman JJ. Toxin detection based on action potential shape analysis using a realistic mathematical model of differentiated NG108-15 cells. Biosensors & Bioelectronics. 2006 Mar;21:1804–1811. doi: 10.1016/j.bios.2005.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Destexhe A, Huguenard JR. Nonlinear thermodynamic models of voltage-dependent currents. Journal of Computational Neuroscience. 2000 Nov;9:259–270. doi: 10.1023/a:1026535704537. [DOI] [PubMed] [Google Scholar]
- 30.Gabay T, Ben-David M, Kalifa I, Sorkin R, Abrams ZR, Ben-Jacob E, Hanein Y. Electro-chemical and biological properties of carbon nanotube based multi-electrode arrays. Nanotechnology. 2007 Jan;18:6. doi: 10.1088/0957-4484/18/3/035201. [DOI] [PubMed] [Google Scholar]
- 31. http://www.multichannelsystems.com.
- 32.Muralidharan VS. Warburg impedance - Basics revisited. Anti-Corrosion Methods and Materials. 1997;44:26–29. [Google Scholar]
- 33.Buitenweg JR, Rutten WLC, Marani E, Polman SKL, Ursum J. Extracellular detection of active membrane currents in the neuron-electrode interface. Journal of Neuroscience Methods. 2002 Apr 15;115:211–221. doi: 10.1016/s0165-0270(02)00021-3. [DOI] [PubMed] [Google Scholar]
- 34.Patolsky F, Timko BP, Yu GH, Fang Y, Greytak AB, Zheng GF, Lieber CM. Detection, stimulation, and inhibition of neuronal signals with high-density nanowire transistor arrays. Science. 2006 Aug;313:1100–1104. doi: 10.1126/science.1128640. [DOI] [PubMed] [Google Scholar]
- 35.Patolsky F, Zheng G, Lieber CM. Nanowire sensors for medicine and the life sciences. Nanomedicine. 2006 Jun;1:51–65. doi: 10.2217/17435889.1.1.51. [DOI] [PubMed] [Google Scholar]
- 36.Kotov NA, Winter JO, Clements IP, Jan E, Timko BP, Campidelli S, Pathak S, Mazzatenta A, Lieber CM, Prato M, Bellamkonda RV, Silva GA, Kam NWS, Patolsky F, Ballerini L. Nanomaterials for Neural Interfaces. Advanced Materials. 2009 Oct;21:3970–4004. [Google Scholar]