Acoustic signatures of sound source-tract coupling

Abstract

Birdsong is a complex behavior, which results from the interaction between a nervous system and a biomechanical peripheral device. While much has been learned about how complex sounds are generated in the vocal organ, little has been learned about the signature on the vocalizations of the nonlinear effects introduced by the acoustic interactions between a sound source and the vocal tract. The variety of morphologies among bird species makes birdsong a most suitable model to study phenomena associated to the production of complex vocalizations. Inspired by the sound production mechanisms of songbirds, in this work we study a mathematical model of a vocal organ, in which a simple sound source interacts with a tract, leading to a delay differential equation. We explore the system numerically, and by taking it to the weakly nonlinear limit, we are able to examine its periodic solutions analytically. By these means we are able to explore the dynamics of oscillatory solutions of a sound source-tract coupled system, which are qualitatively different from those of a sound source-filter model of a vocal organ. Nonlinear features of the solutions are proposed as the underlying mechanisms of observed phenomena in birdsong, such as unilaterally produced “frequency jumps,” enhancement of resonances, and the shift of the fundamental frequency observed in heliox experiments.

I. INTRODUCTION

Birdsong is one of the preferred animal models to study complex, learned, motor behavior [1]. Reasons for this choice lie on the parallels found, in many species of birds, between the mechanisms of acquisition of song and the learning of human speech [2]. Songbirds, as well as humans, must hear a tutor during a sensitive period of time in which they develop the adequate motor gestures that produce the proper vocalizations of the adult.

The complex vocalizations that compose the adult song come as a result of the interaction between a nervous system, which generates motor instructions, and a biomechanical periphery. Even though much progress has been made in understanding the motor control mechanisms at both levels [3,4], little is certain about how responsible for that complexity is the highly nonlinear biomechanical periphery or the neural activity generating the patterns.

The avian vocal organ, the syrinx, is composed in oscine birds of two sound sources. Each source has a set of tissues (labia) that enter a regime of sustained oscillations when driven by an airflow, which is in its turn controlled by the bird via the subsyringeal air sac pressure [5,6]. The human voice is produced in a very similar way: There is one source in the larynx, made up of a set of vocal folds that oscillate when driven appropriately [7].

The dynamics of the source, nonlinear in its nature, exhibits complex phenomena that might create complexities in the vocalizations even when driven by simple physiological instructions. In a recent work, Zollinger et al. investigated the occurrence of such nonlinear phenomena in the vocal organ of the northern mockingbird (Mimus polyglottos) in an attempt to assess to what degree the intrinsic nonlinearities of the vibratory sound-generating structures in the vocal organ contribute to song complexity [8]. Among their various findings, we highlight the unilateral occurrence of nonlinear phenomena, such as frequency jumps (i.e., jumps in the frequencies of the vocalizations). They observed that these events were consistent neither with fluctuations of the air sac pressure nor with the syringeal airflow, supporting the hypothesis that their occurrence did not require complex motor gestures.

Between the sound source and the environment stands the tract. The interglottal pressure, which provides the force driving the oscillations of the labia, depends on the pressure at the input of the tract. In this way, the tract is capable of affecting the labial motion. In humans, the dynamics of the vocal folds has been observed to be independent of the tract (except in some exceptional situations [9,10]). Beyond the sound source-filter hypothesis, however, the consideration of the interactions between the source and the filter adds a great deal of complexity to the biomechanical periphery responsible for sound generation [11,12].

A theoretical analysis of the nonlinear phenomena of the source-tract interacting system was carried out in a previous work [13]. One of the most popular models to account for the transfer of energy of an airflow to the tissue capable of displaying self-sustained oscillations is the two-mass model, introduced by Ishizaka and Flanagan [14], in which the dynamics of the vibrating tissue is described in terms of two masses and a set of springs. In Ref. [13], a sound source modeled as a two-mass system was coupled to a tract (modeled as a tube). A numerical exploration exhibited the characteristic features of a chaotic dynamical system [13]. When the coupling is strong enough, instabilities appear and bifurcations leading to, for instance, coexistence of periodic solutions are observed. In this kind of model it is difficult, however, to discern whether the complexity of the behavior is originated by the source-tract interaction. Since one deals with a four-dimensional model for the source (two dimensions for each of the masses), complex dynamics might occur even when the interaction with the tract is neglected. Additional difficulties arise in this approach when analytical calculations are attempted to unveil the dynamical origins of the nonlinear phenomena found in the numerical explorations.

With the aim of finding if complexity can occur only due to source-tract interaction, we presented in previous work a minimal model in which the source, when uncoupled to the tract, could only undergo a Hopf bifurcation [12]. In this way, any additional nonlinear phenomena taking place when the coupling was added to the model could be identified as a consequence of the interaction with the tract. In particular, by taking the system to a highly dissipative limit and studying the phase equations of the system, analytical expressions for the periodicity of the solutions could be found. Conditions for the coexistence of periodic solutions could be established for a parameter accounting for the length of the tract, and a mechanism for the occurrence of jumps in the frequency of vocalizations was proposed.

The motor gestures that determine the fundamental frequencies of vocalizations of songbirds are coordinated with the geometry of several parts of the vocal tract, such as the length of the trachea, the volume of the oropharyngeal-esophageal cavity, or the beak aperture [3,15,16]. In many of the reported experiments, however, this coordinated activity does not result in nonlinear effects as obvious as jumps in frequency. In order to determine the contributions of the source-tract coupling to the complexity of birdsong it is helpful to derive its effects on the amplitude of the sound, which is the most direct observable of birdsong.

Keeping this in mind, we study here the model presented in Ref. [12] in a way that allows us to observe nonlinear phenomena in the amplitude of the sound. This model holds the advantage that phenomena associated with the coupling are easily identified. Working in the weakly nonlinear limit, we derive analytical expressions for the amplitude of the sound. With these expressions we are able to explore systematically the effects on it introduced by the coupling, paying special attention to the regions where the frequencies of the sound produced in the source are close to the resonances of the tract.

The organization of this work goes as follows. In Sec. II, we describe our model and a selection of results, obtained by numerical exploration, which can be related to acoustic features of the solutions. In Sec. III, we deal analytically with the model in the weakly nonlinear limit. We discuss the acoustic properties of synthetic birdsong generated by our model in Sec. IV, focusing on the features that appear when going beyond the source-filter approximation. Finally, we present our conclusions in Sec. V.

II. THE MODEL

As we did in a previous work, we introduce a model for the source based on Titze’s “flapping mechanism,” in which the motion of the labia are ruled by a second-order equation [12]. This model is a simplified version of the one presented in Ref. [6], which was built on a previous model proposed by Titze to account for the oscillation of human vocal folds [17]. It assumes that each labium supports both an upward propagating surface wave, which is often observed as a phase difference between the upper and lower ends of the fold, and a lateral oscillation of its center of mass. Requiring that the labia have a more convergent profile when they are moving away from each other than when they are closing in, the force made on them by the glottal pressure will be greater in the opening phase than in the closing phase. In this way, the folds are capable of performing a “flapping” motion that enables a net transfer of energy from the airflow to sustain oscillations in the labia. This can be mathematically written in terms of Newton’s second law for the departure from equilibrium of the center of mass of a labium, x:

$$\{\begin{array}{l}\stackrel{.}{x}=y\hfill \\ \stackrel{.}{y}=-kx-\beta y-{cx}^{2}y+p_i+(p_s-p_i)f(x,y),\hfill \end{array}$$

where, in the second equation, the first term describes the elastic restitution of the labium, the second term represents dissipation, and the third term a nonlinear saturation that bounds the labial motion. The system is driven by the last two terms. They account for the average interglottal pressure, written in terms of the subsyringeal pressure p_s, and the pressure at the input of the tract p_i (all pressures in this work are defined per unit mass per unit area of the labium). In the driving term, f (x,y) is a function of the geometry of the folds that depends on the ratio of the cranial and bronchial areas of the labial valve. The experimentally observed phase difference between the upper and lower portions of the labia is introduced in this function [6,11,12,17]. An equivalent way of stating the requirements for flapping motion is that the average pressure between the labia is closer to the bronchial pressure when the labia present a convergent profile, and closer to atmospheric pressure when they are divergent. The force goes therefore in the same direction as the velocity of displacement of the labia, which might overcome the dissipation for high enough subsyringeal pressure. These requirements are met if f (x,y) is proportional to the velocity of the labia, i.e., f (x,y) = y/v_char, with v_char a characteristic velocity [6]. In contrast to the more detailed two-mass models, our system restricts the dynamics of the source to a simple spatial mode. In a previous work, we explored its dynamics in the (p_s,k) parameter space and found that it is capable of accounting for the mechanisms of sound production of the northern cardinal (Cardinalis cardinalis) [18]. Despite its simplicity, the simplified model proved realistic enough to synthesize birdsong when driven by actual physiological recordings of subsyringeal pressure and ventral muscular activity [19].

With the proposed f (x,y) = y/v_char, the system has a fixed point at (x,y) = (0,0). After a change of scales (t → t/γ and y → γy), and setting v_char = 1 for simplicity, we write

$$\{\begin{array}{l}\stackrel{.}{x}=y\hfill \\ \stackrel{.}{y}=-k{\gamma }^{2}x+\gamma (p_s-\beta )y-\gamma {cx}^{2}y+\gamma p_i(\gamma -y).\hfill \end{array}$$ (1)

To assume that the source-filter separation hypothesis holds means that the pressure at the input of the tract is considered negligible in the driving part of the system. This is expressed by setting p_i = 0 in (1). For certain values of the parameters (p_s,β), the driving force overcomes the dissipation, and a Hopf bifurcation occurs: The fixed point becomes unstable, and a limit cycle is born with zero amplitude and finite frequency [20]. Beyond the bifurcation, the midpoint of the labia oscillates around their equilibrium position.

Coupling between the source and the tract is introduced by p_i ≠ 0. When the dynamics of p_i = p_i (x,y,t) is introduced, complexity is added to the equations of motion of the labia. If the labial valve is coupled to a tube, the pressure at the input of the tract p_i will be affected by the reflections of the sound wave at its output. There is a contribution to the driving term that comes from a feedback that depends on the value of p_i at a previous time depending on the length L of the tract. We derived in Ref. [12] a functional form of p_i that accounts for this feedback. We assume two main contributions to the supraglottal pressure p_i: one due to the fluctuations originated in the glottis and injected into the tube, and the other one due to the feedback. For flow fluctuations of the order of kHz and tube section of the order of mm, the contribution of the fluctuating glottal flow U_g can be written as p₊ = ρ₀v_s U_g /A_i, where ρ₀ is the unperturbed air density, A_i the section of the input of the tract, and v_s the speed of sound. The average speed of the air in the glottis is given by a phenomenologically corrected Bernoulli’s law, $V_m=\sqrt{\frac{2p_s}{k_t{\rho }_0}}$, in which k_t stands for the trans-glottal pressure coefficient [17]. The glottal flow can be approximated as U_g = V_ma_m, where the glottal area a_m is proportional to the displacement from equilibrium of the midpoint of the labia x. We can therefore write the contribution to p_i due to fluctuations in the glottal flow as $p_{+}=\alpha \sqrt{p_s}x$, where α is inversely proportional to the area of the tube. The other contribution to the pressure at the input of the tract comes from the reflection at the output. We model the tract as a tube of length L, open at the end that is the furthest from the source. A sound wave entering the tube will be partially transmitted at the other end and partially reflected with a coefficient r. The reflection of a sound wave entering the tube at a given time will contribute to the pressure at the input of the tract with a delay of τ = 2L/v_s (the time it takes the wave to propagate to the other end and back), and opposite sign. Considering both contributions, the supraglottal pressure can be written as

$$p_i(t)=\alpha \sqrt{p_s}x-{rp}_i(t-\tau ).$$ (2)

In previous work [12], motivated by the experimentally observed coordination between the geometry of the avian vocal tract and the fundamental frequencies of vocalizations [1,15,21], we performed a numerical search for qualitatively different solutions of system (1) and (2) in the region where the resonant frequency of the tract was close to the fundamental frequency of the unperturbed source.

For strong enough coupling, we found a region of coexistence of periodic solutions. Working in the high-dissipation limit, a phase equation was derived for the dynamics of the source. Then, introducing the coupling to the tract as a perturbation to the phase dynamics, a bifurcation leading to the appearance of a coexistence region of periodic solutions was identified [12].

The coexistence of periodic solutions found was proposed as a mechanism by which frequency jumps can be achieved as a result of the coordination between the activities of the source and the tract. Beyond this effect in the frequencies of vocalizations, we are interested in nonlinear phenomena leaving their signature in the most direct observable of birdsong, i.e., the recorded sound amplitude.

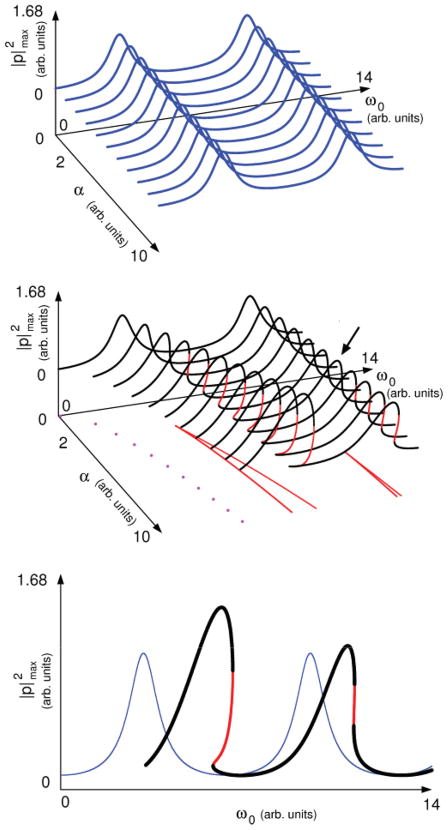
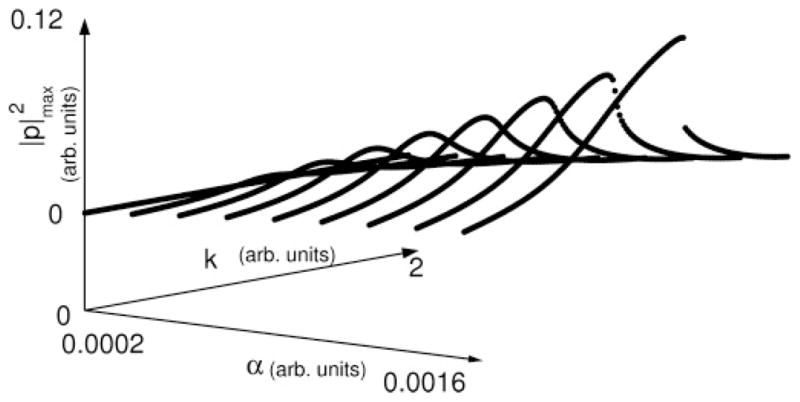
Here we search for qualitative changes introduced by the coupling in the amplitude of sounds generated in the system. The acoustic pressure at the input of the tract is p_i (t). Hence the partially transmitted wave at the output of the tract at a given time t is p(t) = (1 − r)p_i (t − τ/2). This quantity is the acoustic pressure at the output of the system. To find the amplitude of a synthesized sound we compute p(t) by numerically integrating Eqs. (1) and (2) and, after a long enough transient (i.e., long enough for oscillations with constant amplitude to be observed), find the maximum of its norm. This quantity, |p|_max, is hereafter called the “sound amplitude.” We focus on the region where the fundamental frequency of the sound produced by the unperturbed source f₀ = ω₀/2π is close to the resonance of the tract, which is where we previously found coexistence [12]. Since we focus on the qualitative changes introduced by the source-tract coupling in the dynamics of the system, we set the parameters to dimensionless values that enable us to spot bifurcations in the oscillatory solutions through the numerical exploration. We find a nontrivial behavior of the amplitude, depending on the strength of the coupling coefficient α. These findings are summarized in Figs. 1 and 2. In Fig. 1 we plot ${\mid p\mid }_{max}^2$ versus (k,α). Each point represents the value of ${\mid p\mid }_{max}^2$, computed for a grid of different initial conditions (x₀,y₀). When the coupling is considered, the values of k at which the maximum sound amplitude occurs shift, and their corresponding peaks grow. Both the shift and the enhancement of the peaks are observed even for smaller values of α than the ones required for the bifurcation leading to coexistence to take place. Consequently, phenomena associated with source-tract coupling are more likely to be identified in the amplitude of the vocalizations, where their signature is not restricted to a constrained region in the parameter space. A region of coexistence appears for strong enough coupling, as is evident in Fig. 2. In this picture, the squared amplitudes for a particular α are plotted for the coupled system, together with the results of computing the same quantity when the contribution of the supraglottal pressure is neglected in the forces driving the source. When the source-filter hypothesis is assumed, there is no bifurcation leading to coexistence. Moreover, no shift is observed in the frequency at which the peak occurs, and its corresponding amplitude is smaller than when the coupling is considered.

FIG. 1.

Sound amplitude against k for different values of the coupling coefficient α. As the coupling increases, the amplitude at the resonance grows. For large enough α, a coexistence region sets in, where two oscillatory solutions with different amplitudes are possible. Parameters used for numerical integration were (γ, p_s, β, c, r) = (7000π, 0.1, 0.01, 1 × 10⁻⁶, 0.71) in dimensionless units, τ = 1.43 × 10⁻⁴ s.

FIG. 2.

(Color online) Detail of sound amplitude against k and comparison with the source-filter uncoupled system. Crosses represent the amplitude of sounds originated in a source-filter system. Dots represent sounds generated in the source-tract coupled system. Empty dots highlight the region of coexistence of periodic solutions: At those values of k, the amplitude of the sound will be either of two values, depending on the initial conditions. Parameters used for numerical integration were (γ, p_s, β, c, r, α) = (7000π, 0.1, 0.01, 1 × 10⁻⁶, 0.71, 0.0014) in dimensionless units, τ = 1.43 × 10⁻⁴ s.

Numerical observations motivate analytical work. In order to find out the dynamical origin of the amplitude effects of source-tract coupling, we will reduce the system (1) and (2) to a simpler set of equations preserving the dynamics of the amplitude of oscillatory solutions. We propose here to study the weakly nonlinear limit of the system, in which the nonlinearities introduce a deviation from the periodic solutions of the linear part of the system [20,22]. In this limit we are able to obtain analytical expressions for the mentioned deviations, both in amplitude and in the phase of the oscillations. Different oscillatory solutions will appear when the nonlinear perturbations are introduced. Moreover, the types of solutions found when the nonlinearities include the source-tract coupling might be different from those found when the nonlinearities contain only the dynamics of the source. For this reason, we concentrate on the system

$$\ddot{x}+{\omega }_0^{2}x=\mu \left[\stackrel{.}{x}-\stackrel{\sim }{c}{x}^2\stackrel{.}{x}+(1-\stackrel{.}{x})\stackrel{\sim }{\alpha }\sum _{n=0}^{\infty }{(-r)}^{n}x(t-n\tau )\right],$$ (3)

which is essentially the same as the one described by Eqs. (1) and (2), with γ = 1, μ = p_s − β,c̃ = c/μ, $\stackrel{\sim }{\alpha }=\sqrt{p_s}\alpha /\mu ,{\omega }_0^2=k$.

III. ANALYSIS OF THE MODEL

The advantage of studying system (3) in the weakly nonlinear limit (μ ≪ 1) is that, as the nonlinear part is seen as a perturbation, trajectories will be deviations from harmonic oscillations. Conditions can be found for those trajectories to be oscillatory. Moreover, bifurcations can be found leading to, for instance, coexistence of oscillatory solutions. Equation (3) can be written equivalently as

$$\{\begin{array}{l}\stackrel{.}{x}=y\hfill \\ \stackrel{.}{y}=-{\omega }_0^{2}x+\mu [y-\stackrel{\sim }{c}{x}^{2}y+(1-y)\stackrel{\sim }{\alpha }{\sum }_{n=0}^{\infty }{(-r)}^{n}x(t-n\tau )].\hfill \end{array}$$ (4)

Before introducing any approximations, we begin by proposing the change of variables

$$\{\begin{array}{l}x={ae}^{i\omega t}+\overline{a}{e}^{-i\omega t}\hfill \\ y=i\omega {ae}^{i\omega t}-i\omega \overline{a}{e}^{-i\omega t},\hfill \end{array}$$

where a = a(t) is a new, complex variable, and ā stands for its complex conjugate. By replacing variables in system (4) we can derive an equation for ȧ:

$$2i\omega \stackrel{.}{a}=\left({\omega }^2-{\omega }_0^2\right)(a+\overline{a}{e}^{-2i\omega t})+\mu f(a,\overline{a},e^{i\omega t},e^{-i\omega t}).$$ (5)

At this point, no approximations have been made, and this last equation is identical to (4). If μ = 0, the system has a fixed point at ω = ω₀, where a is constant and oscillations are harmonic. When we consider the case where the dissipation and the nonlinearities are small μ ≪ 1, solutions at ω ≈ ω₀ The relation between a and its time derivative should read ȧ ≪ aω. In this way, the change in a over one period of oscillation can be neglected. If these assumptions hold, many terms in the system can be eliminated, leading to a simpler equation that retains the dynamics. Equation (5) can be written in the form

$$\stackrel{.}{a}=\frac{\mu }{2i\omega }\sum _{n=0}^{\infty }{F}_n(a,\overline{a})e^{i\omega nt},$$

where the right-hand side of the equation is the Fourier series of the right-hand side of (5), with coefficients

$$F_n=\frac{1}{T}{\int }_t^{t+T}\left[\frac{{\omega }^2-{\omega }_0^2}{\mu }(a+\overline{a}{e}^{-2i\omega t^{\prime }})+\mu f(a,\overline{a},e^{i\omega t^{\prime }},e^{-i\omega t^{\prime }})\right]e^{-in\omega t^{\prime }}{dt}^{\prime }.$$

This expansion is exact if a is constant. If a changes slowly, a = a(μt), its change over one period of the oscillation T is small, and we can consider it approximately constant when evaluating the integral. Since we are interested only in the slow changes in a, we keep only the nonoscillating terms in the expansion. By means of this standard procedure, we eliminate all the nonresonant terms in the equation, which are those that would have zero average over one cycle of oscillation of the slow varying a. After this and upon the introduction of the new The second change of variables is mistaken, it should read $a\to A=a\sqrt{\stackrel{\sim }{c}}$. dimensionless equation for the dynamics of the deviation from harmonic oscillations A(t′) = ρ(t′)e^iφ(t′):

$$\{\begin{array}{l}\stackrel{.}{\rho }=\rho \left[1+\frac{\alpha \sqrt{p_s}r}{(p_s-\beta )\omega }\frac{sin(\omega \tau )}{1+r^2+2rcos(\omega \tau )}\right]-{\rho }^3\hfill \\ \stackrel{.}{\phi }=\frac{{\omega }_0^2-{\omega }^2}{(p_s-\beta )\omega }-\frac{\alpha \sqrt{p_s}}{(p_s-\beta )\omega }\frac{1+rcos(\omega \tau )}{1+r^2+2rcos(\omega \tau )}.\hfill \end{array}$$ (6)

The search for oscillatory solutions to the system (1) and (2) now reduces to a search for fixed points in (6). Thus, observing the bifurcations in the fixed points of (ρ,φ), we can find qualitative changes in the oscillatory behavior of x, and by these means of the squared amplitude of the sound produced by the source-tract system per unit α,

$${\mid p\mid }_{max}^2={(1-r)}^2\frac{p_s{\rho }^{\ast 2}}{1+2rcos(\omega \tau )+r^2},$$ (7)

where ρ^* is the value of ρ at a fixed point:

$${\rho }^{\ast 2}=1+\frac{\alpha \sqrt{p_s}r}{(p_s-\beta )\omega }\frac{sin(\omega \tau )}{1+r^2+2rcos(\omega \tau )},$$

with ω satisfying

$${\omega }_0^2=g(\omega )={\omega }^2+\alpha \sqrt{p_s}\frac{1+rcos(\omega \tau )}{1+r^2+2rcos(\omega \tau )}.$$ (8)

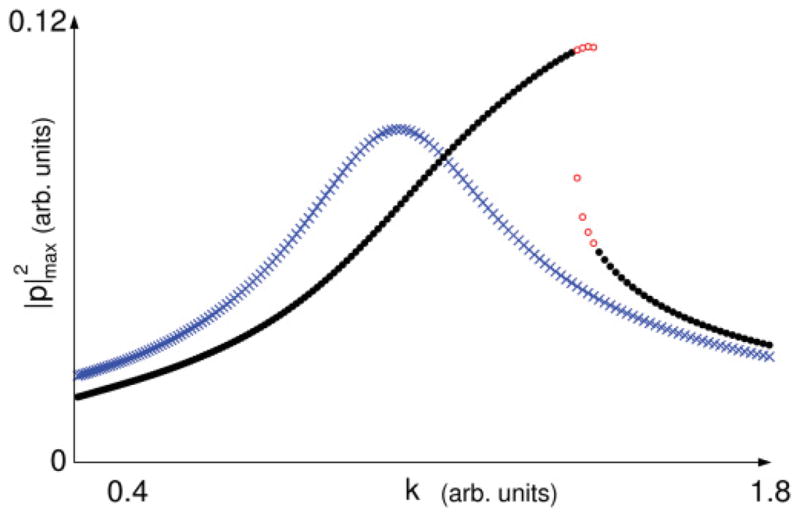
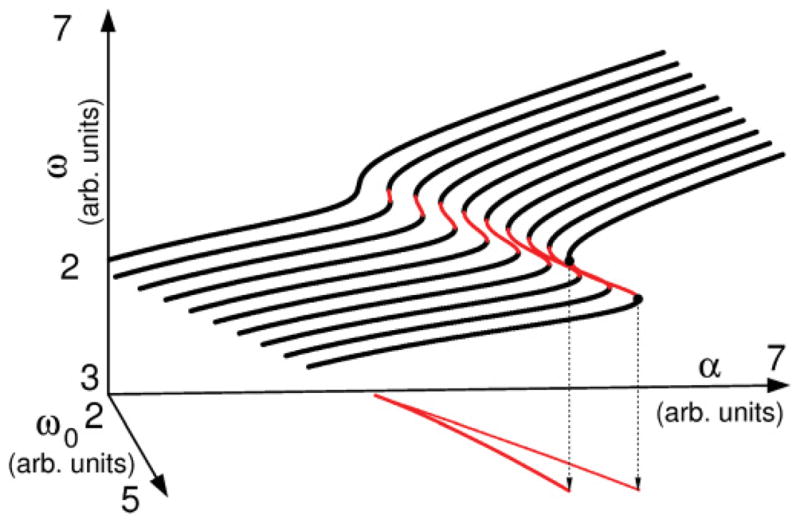
With these expressions we can identify the conditions under which three, one, or no fixed points exist for ω ≈ ω₀. Moreover, the stability of the solution can be determined analytically. These results are summarized in Fig. 3. Given a value of ω that satisfies condition (8), the system will present a stable fixed point if $\frac{\partial g}{\partial \omega }>0$, unstable if $\frac{\partial g}{\partial \omega }<0$. Function g(ω) increases from ω = 0, in a way that fixed points will be stable unless it happens that g(ω) presents a maximum at some value satisfying $\frac{\partial g}{\partial \omega }=0,\frac{{\partial }^{2}g}{\partial {\omega }^2}<0$. At this maximum, a saddle-node bifurcation occurs, and three fixed points coexist: two stable and one unstable. If that maximum is found, g(ω) also presents a minimum for a larger value of $\omega (\frac{\partial g}{\partial \omega }=0,\frac{{\partial }^{2}g}{\partial {\omega }^2}>0\text{at}\text{that}\text{point})$. A stable and an unstable fixed point will collide in a new saddle-node bifurcation. The existence of this pair of saddle-node bifurcations requires that g(ω) presents a maximum. Consequently, it is possible to find, for fixed (r,ω), the smallest value of α for which the conditions (8) and $\frac{{\partial }^{2}g}{\partial {\omega }^2}>0$ can be satisfied. These critical values of (α,ω₀) happen at a cusp bifurcation. For every fixed point of a, the source-tract system oscillates. In Fig. 4 we plot the square of the amplitude of the oscillations per unit α [computed via Eq. (7)] corresponding to the fixed points displayed in Fig. 3.

FIG. 3.

(Color online) Angular frequencies of fixed points of system (6). The dark bold lines indicate stable fixed points, where condition (8) is met and $\frac{\partial g}{\partial \omega }>0$. Thinner, lighter lines indicate unstable fixed points, at which $\frac{\partial g}{\partial \omega }<0$. The lines in the (α, ω₀) plane delimit the region of coexistence of fixed points. On these lines $\frac{\partial g}{\partial \omega }=0$, indicating the occurrence of saddle-node bifurcations of fixed points. The point where they meet is where a cusp bifurcation occurs: that is, the critical value for (α, ω₀) at which coexistence is possible. Parameters used were (p_s, β, r, τ) = (5.1, 0.1, 0.51, 1.0) in dimensionless units.

FIG. 4.

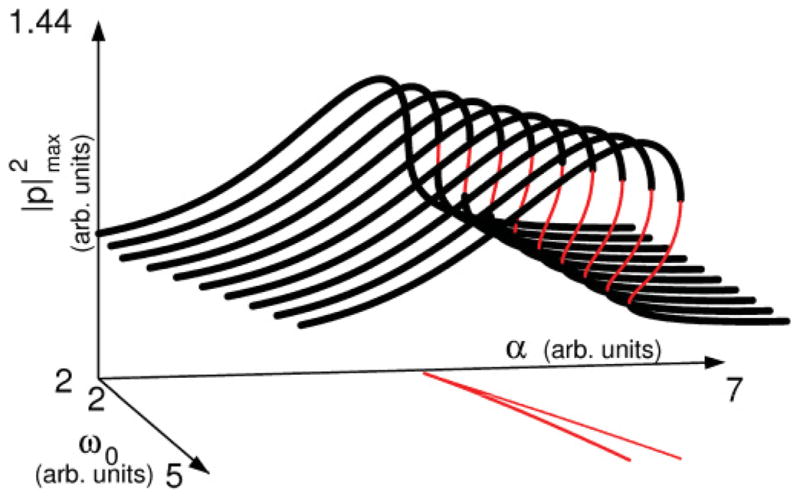
(Color online) Sound amplitude of stationary oscillatory solutions. The dark, bold lines indicate stable oscillatory solutions. Thinner, lighter lines indicate unstable limit cycles. The lines in the (α, ω₀) plane delimit the region of coexistence of fixed points. On these lines, $\frac{\partial g}{\partial \omega }=0$ indicating the occurrence of saddle-node bifurcations of fixed points. The point where they meet is where a cusp bifurcation occurs. Parameters used were the same as in Fig 3.

In the search for signatures of source-tract coupling in the amplitude of the sound generated by the complete system, we compare the previous results to those obtained when the source-filter independence is assumed to hold. In this latter case, fixed points of a occur at (ρ^* = 1, ω = ω₀). Consequently there are no bifurcations leading to coexistence of limit cycles. Moreover, the amplitude of oscillations per unit α does not depend on α. The resulting amplitudes are displayed in the top panel of Fig. 5. In the middle panel of the figure, the squared amplitudes, computed for the same values of parameters for the acoustically coupled system, are displayed together with the cusp lines in the same way we discussed in the previous paragraph. We also included in this panel a dotted line to illustrate another phenomenon originated by the coupling: the shift of phonation threshold. The existence of limit cycles in the coupled system depend on Eq. (8) to be satisfied. For a fixed set of (α,p_s,r,τ), values of ω₀ below a certain threshold do not lead to oscillations. These threshold values were computed and plotted as a dotted line on the (α, ω₀) plane. The bottom panel of the figure illustrates the qualitative differences between the sound amplitudes coming out of a coupled system and the ones produced in a source-filter sound generator. A value of α is selected, and the squared amplitudes per unit α plotted for both approximations. The coupled system displays coexistence of stable solutions with different amplitude, a shift and enhancement of the resonance peaks, and the introduction of an α-dependent phonation threshold.

FIG. 5.

(Color online) Amplitudes (squared, per unit α) of sounds originated in source-filter and source-tract coupled systems. Sounds coming out of a source-filter system (top panel). Sounds coming out of a source-tract coupled present coexistence of stable solutions. The thick, dark lines represent stable solutions, the thinner, lighter lines indicate unstable solutions. Regions of coexistence of solutions are indicated by the intersecting lines in the (α, ω₀) plane. Phonation thresholds are indicated by the dotted line in the (α, ω₀) plane (middle panel). Comparison of amplitudes of sounds elicited by both systems for α = 7.0, as indicated by the arrow in the middle panel (lower panel). Parameters used were the same as in Fig 3.

IV. ACOUSTIC FEATURES OF THE SOLUTIONS

Source-tract coupling introduces complexity in the system of equations describing the dynamics of the vocal organ. Even considering simple dynamics for the source, the source-tract coupled system presents a nontrivial bifurcation diagram, including a cusp bifurcation leading to a region of coexistence of periodic solutions. In the previous section, we also found dynamical mechanisms leading to phenomena affecting the amplitude of the oscillatory solutions, as well as a shift in the values of parameters required for a Hopf bifurcation to take place.

Characteristics of the oscillatory solutions depend on parameters accounting for physiological variables of the system. In this way, the complexity of the solutions, leaving their signature in the acoustic properties of the vocalizations produced, can be controlled by simple, coordinated motor gestures in the source-tract system.

The activity of the muscle syringealis ventralis vS is directly correlated to the fundamental frequency of the sound produced in the syrinx [23], in a way that leads to the hypothesis that this physiological variable is responsible for the active control of the stiffness of the labia [parameter k in Eq. (1)] [6,19]. In addition, the activity of the vocal tract has been reported to be coordinated with the frequency of the vocalizations [15,24]. Beyond the source-tract separation approximation, vocalizations with nontrivial acoustic features can be generated by simple paths in the space of the parameters accounting for motor gestures controlling the labial tension k, subsyringeal pressure p_s and vocal tract length L.

Among these vocalizations stand the unilaterally produced frequency jumps. These are syllables in which the fundamental frequency changes abruptly and have been observed in the northern mockingbird [25]. We proposed in a previous work a mechanism by which the bird exploits the coexistence of periodic solutions to produce them [12]. A region of coexistence in parameter space can be crossed by smoothly varying the parameter accounting for the length of the tract L, hence achieving the frequency jump with a simple motor gesture.

The coordination of the vocal tract and the syringeal activity is one of the mechanisms by which birds emphasize the fundamental frequency of the vocalization. By adjusting the length L of the trachea, the frequency of the sound produced by the vibrations of the labia in the syrinx is matched by the resonance of the tube through which the sound is filtered ν = v_s /(4L). The introduction of the source-tract coupling in the model predicts, for certain values of the parameters, an enhancement of this effect: Resonant sounds in the source-tract coupled system present higher amplitudes than in the source-filter approximation. In Fig. 2, synthetic sounds were generated with identical systems, one of them coupled, the other uncoupled. For a fixed L, the frequency of the oscillation generated in the labia was varied (by sweeping in the parameter accounting for their stiffness k), and the amplitude of the oscillation was computed. In the source-tract coupled system simulations, resonances occur at a higher fundamental frequency and are stronger.

To illustrate the differences in spectral content of vocalizations produced in both approximations, we synthesize vocalizations by numerical integration of system (1) and (2). (A modified version of Eq. (1) in which p_i = 0 is integrated to produce the source-filter vocalization.) We introduce a very simple pressure pattern, consisting merely of an increase beyond the value at which the folds begin to oscillate and, after a time interval, a return to subthreshold. During that time, vocalization takes place. The length of the tract remains fixed, adjusted so that its resonant frequency matches the fundamental frequency of the sound produced by the source alone. The vocalizations are plotted in Fig. 6 (acoustic pressure and sonogram). It is remarkable that the energy of the source-tract coupled system concentrates the energy in the fundamental frequency f₀ and in every harmonic (f₀,2f₀,3f₀, …). In contrast, the peaks of energy in the source-filter syllable occur as expected in a sound filtered by an open-closed tube with L = v_s /(4f₀), namely, at (f₀,3f₀, …). The quadratic term introduced by the feedback in the driving part of system (1) is responsible for this effect.

FIG. 6.

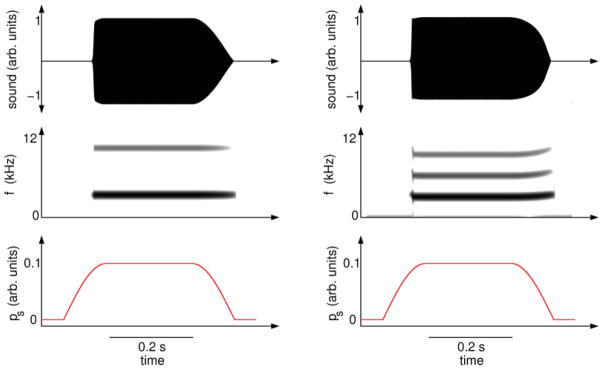
(Color online) Synthetic vocalizations produced by numerical integration of Eqs. (1) and (2), considering source-filter independence (left panels) and source-tract interaction (right panels). Sound (top panels) is produced when the system is driven by a simple pressure gesture (bottom panels). The sonograms (middle panels) show that the spectral content of the vocalizations are qualitatively different. Parameters used for numerical integration were (γ, β, c, r, α) = (7000π, 0.01, 1 × 10⁻⁶, 0.71, 0.0014) in dimensionless units, τ = 1.43 × 10⁻⁴ s.

Experiments have been performed in some species to study how the vocal pathway modifies the sound generated in the source, in which the ambient where the birds phonated was filled with heliox [24,26]. The change of atmosphere carries an increase in sound velocity of up to 550 m/s. If the source and the tract do not interact, the fundamental frequencies of the vocalizations recorded should not be modified as the velocity of sound increases. By simulating a heliox experiment with synthetic sounds generated by a source-tract coupled system, we expect to be able to make quantitative predictions on the changes in fundamental frequency and spectral content to be observed as the sound velocity is increased.

With this in mind, we generated a series of synthetic sounds with all the parameters of system (1) and (2) fixed except for v_s, which ranged from 341 to 520 m/s. The fundamental frequency of sounds originated in the uncoupled system remained constant over the simulated heliox experiment, as expected. No shift was observed in the fundamental frequency or the higher resonances, but only a change in the ratio of the peaks (see Fig. 7, left panels). The sounds synthesized using the source-tract coupled system increased in fundamental frequency as the sound velocity increased. Furthermore, the shift in the amplitude peaks became larger the higher the frequency at which they appeared (see Fig. 7, right panels).

FIG. 7.

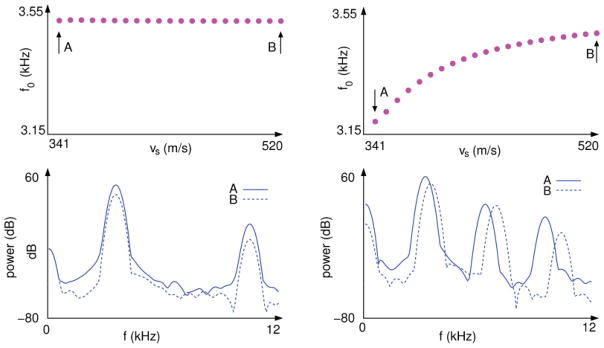
(Color online) Fundamental frequencies of synthetic vocalizations and power spectrum for varying medium density. Fundamental frequencies of sounds do not change with the air density if the source and the filter do not interact (top left panel). When the source is coupled to the tract, there is a drift in the fundamental frequency (top right panel). The arrows A and B in the upper panels indicate two different air densities, at which the power spectra of the synthetic sounds were computed (bottom panels). The power spectrum of the source-filter synthetic sound changes only the relative values between the resonance peaks when the density of the air is changed (bottom left panel), whereas a shift is observed in the peaks of the source-filter vocalizations (bottom right panel). Parameters used for numerical integration were (γ, β, c, r, α) = (7000π, 0.01, 1 × 10⁻⁶, 0.71, 0.0014) in dimensionless units, τ = 9.6 cm/v_s.

Small shifts in frequencies have been observed when the density of the air is reduced by mixing it with heliox [24]. We showed here that even with a simple description of the dynamics of the folds, a shift in frequency is to be expected upon a change in the density of the atmosphere; responsible for this effect is the delayed feedback introduced by the coupling to the tract.

V. CONCLUSIONS

In this work we have studied the dynamics of a simple interacting sound source-tract system. Our model consists of an oscillator coupled to a simple tube. Vocal tracts are actually much more complex and include, for instance, the beak and the oropharyngeal-esophageal cavity, whose activities have been reported to be coordinated with that of the sound source [15,27]. They affect, however, the filtering of the sound; their contributions to the feedback are negligible. We have found that when the frequencies of the sounds generated in the source are close to the resonant frequencies of the tube, a shift and an enhancement of the resonance peaks occur. For some values of the parameters, we also found coexistence of stable periodic solutions. This implies the possibility of having rapid changes in the acoustic output of the system, in both amplitude and frequency, even for smooth changes in the parameters.

The parameters accounting for the physiology of the sound source-tract system were set to dimensionless values at which the effects of the coupling were noticeable as qualitative changes in the dynamics. By these means, we were capable of finding bifurcations in the system leading to acoustic phenomena consistent with observations [8]. The difficulties in estimating labial mass, or values for the muscle tensions involved, make it difficult to advance beyond qualitative analysis.

The mathematical model proposed to account for the dynamics of the uncoupled sound source presents little complexity, namely, just the possibility of oscillating by going through a Hopf bifurcation. It is then the interaction between the source and the tract that is responsible for the additional phenomena discussed here.

Complexity is introduced in the acoustic features of the vocalizations when the interaction of the source and the tract is taken into consideration. In our model, the tract does not play the role of a passive filter, but it interacts with the source, introducing a delayed feedback p_i in the driving term of the fold oscillations. The delayed feedback introduced by the interaction of the tract and the source is responsible for quantifiable effects in the acoustic properties of the vocalizations, such as the position and relative intensities of the resonant peaks when the fundamental frequency of the sound produced is close to the frequency associated to the tube. The weakly nonlinear approximation made in this work pursued the goal of determining the underlying dynamical mechanisms leading to these effects, as well as proposing ways to quantify the degree of source-tract coupling from the observed vocalizations. The use of a minimal model pursued the goal of identifying what part of the complexity of the sounds was due to the nonlinearities of the source, and which was due to the interaction with the tract.

The complex vocalizations elicited by songbirds come as the result of the interaction of a nervous system and a biomechanical periphery. In this work, we contribute to the task of determining where such complexity is originated. This issue has been addressed in Refs. [1,4,8]. It is hypothesized that complexity in vocalizations might not require complex active neural control, but can be achieved by the driving of a highly nonlinear periphery with simple motor instructions. The mechanism proposed here supports the idea that, in order to understand the complexity of birdsong, it is necessary to study in parallel the central neural control and the dynamics of the periphery.