Anniversary Paper: Development of x-ray computed tomography: The role of Medical Physics and AAPM from the 1970s to present

Abstract

The AAPM, through its members, meetings, and its flagship journal Medical Physics, has played an important role in the development and growth of x-ray tomography in the last 50 years. From a spate of early articles in the 1970s characterizing the first commercial computed tomography (CT) scanners through the “slice wars” of the 1990s and 2000s, the history of CT and related techniques such as tomosynthesis can readily be traced through the pages of Medical Physics and the annals of the AAPM and RSNA/AAPM Annual Meetings. In this article, the authors intend to give a brief review of the role of Medical Physics and the AAPM in CT and tomosynthesis imaging over the last few decades.

INTRODUCTION

As the AAPM celebrates its 50th anniversary, it is natural to pause and take stock of the contribution its members, meetings, and publications have made to the field of medical physics. Entire modalities, such as computed tomography (CT) and magnetic resonance imaging, have been conceived and developed into powerful clinical tools in the half century since the founding of the AAPM, often with substantial involvement from AAPM members and journals. In particular, CT and related techniques such as tomosynthesis have been the subject of over 200 publications in the AAPM’s flagship journal Medical Physics.

Certainly, the attempt to trace the role of a single journal and professional organization in the development of an imaging modality such as CT cannot provide a complete and definitive history of the modality itself. Many significant developments in CT were published in other journals or took place at companies who may or may not have divulged proprietary information in the scientific literature. However, the broad outlines of the modality’s history are quite clear from its treatment in the pages of Medical Physics.

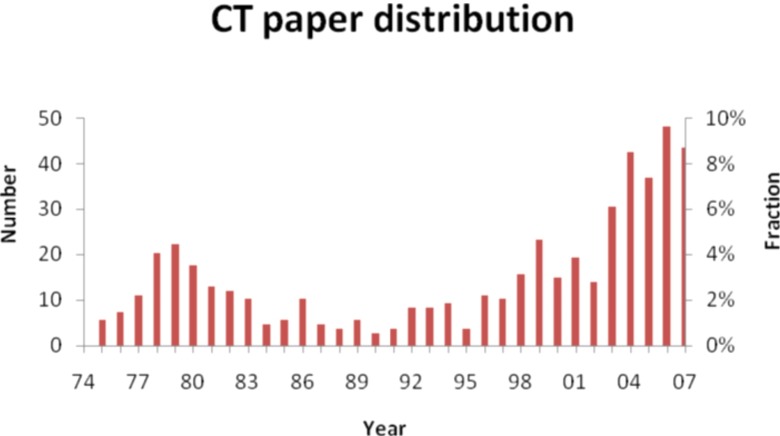
For instance, to gain a sense of the scope of the work that has been published in Medical Physics, we searched the archives of Medical Physics for articles related to x-ray CT and tomosynthesis. Figure 1 shows the number of such papers published per year for the past 35 years.

Figure 1.

Approximate distribution of papers relevant to CT and tomosynthesis published in Medical Physics over the past 35 years. Left axis: Approximate number of araticles. Right axis: Approximate percentage of articles.

The bimodal nature of the plot succinctly tells a story of waxing and waning interest in x-ray tomography, beginning with the initial excitement following the commercial introduction of CT in 1972 by EMI, and then trailing off through the 1980s as the technology matured and emerging technologies, such as magnetic resonance imaging (MRI), won attention from researchers and clinicians alike. The introduction of spiral/helical scanning at the 1989 RSNA/AAPM annual meeting, followed by the introduction of multislice scanners in the mid 1990s, led to a resurgence of interest in CT technology and has also enabled entirely new applications that were impractical with the slower scanners of the past. Similarly, an expanded scope of detector technologies and applications for x-ray tomography is evident in the last decade—e.g., in the use of flat-panel detectors for tomosynthesis and cone-beam CT.

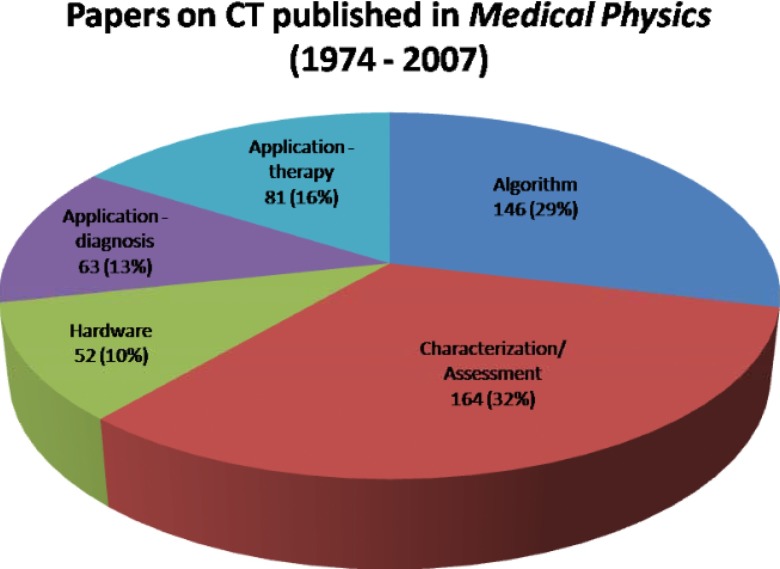
The focus of the x-ray CT papers published in Medical Physics can be divided into five principal categories: hardware, system assessment, algorithm development, diagnostic applications, and therapeutic applications (largely radiation therapy treatment planning and image-guided interventions). Figure 2 illustrates the fraction of the published articles between 1974 and 2007 falling into each category.

Figure 2.

Distribution of topic categories for CT-related papers published in the Medical Physics. Within each sector, the two numbers represent the approximate number and percentage of the articles published for a given category.

Similarly, the AAPM has commissioned a number of Task Groups on the topic of CT, mostly related to the quality assurance and dosimetry of CT or its application in radiation therapy simulation. In fact, the first AAPM Task Group (TG) Report¹ was on the topic of quality assurance in CT, which formalized the now familiar concepts of “head” and “body” phantoms as soft-tissue-equivalent cylinders of different diameters. While many Task Group Reports involve CT as integral to the medical imaging arsenal, those dealing specifically with CT in either diagnostic or therapy contexts are summarized in Table 1.

Table 1.

Summary of AAPM Task Group Reports related to CT.

Year	Report No.	TG No.	Title	Reference
1977	1	N/A1	Phantoms for performance evaluation and quality assurance of CT scanners	1
1978	4	N/A2	Basic quality control in diagnostic radiology	2
1991	31	8	Standardized methods for measuring diagnostic x-ray exposures	3
1991	35	6	Recommendations on performance characteristics of diagnostic exposure meters	4
1993	39	2	Specification and acceptance testing of computed tomography scanners	5
1994	46	40	Comprehensive QA for radiation oncology	6
1998	60	4	Instrumentation requirements of diagnostic radiological physicists	7
1998	62	53	Quality assurance for clinical radiotherapy treatment planning	8
2002	74	12	Quality control in diagnostic radiology	9
2003	83	66	Quality assurance for computed-tomography simulators and the computed-tomography-simulation process: Report of the AAPM Radiation Therapy Committee Task Group No. 66	10
2004	86	N/A3	Quality assurance for clinical trials: A primer for physicists	11
2006	91	76	The management of respiratory motion in radiation oncology	12
2007	95	75	The management of imaging dose during image-guided radiotherapy	13
2006	108	108	AAPM Task Group 108: PET and PET/CT shielding requirements	14
2008	96	23	The Measurement, Reporting, and Management of Radiation Dose in CT	15

¹Work predates AAPM Task Group enumeration—Diagnostic Radiology Committee Task Force on CT Scanner Phantoms.

²Work pre-dates AAPM Task Group enumeration—Diagnostic Radiology Committee Task Force on Quality Assurance Protocol.

³Reported by the Subcommittee on Quality Assurance Physics for Cooperative Trials, Radiation Therapy Committee.

FOUR DECADES OF X-RAY COMPUTED TOMOGRAPHY

Pre-1970s and 1970s: The Dawn of CT

The 1972 introduction of the first commercial CT scanner by Hounsfield led to a flurry of publications in Medical Physics and other journals by academic and industrial researchers who sought to characterize, improve, and apply the new technology. This accounts for the first peak seen in Fig. 1, and the concerns of the time are well summarized in two review articles on fundamental photon attenuation physics¹⁶ and the basic aspects of early CT technology and systems.¹⁷ Although CT technology was still in its infancy, researchers of the day were quick to identify and lay the groundwork for new applications, some of which are only just coming to fruition, like dual-energy CT.

Researchers in this era devoted substantial effort to characterizing the physical properties of CT scanners that affect image quality. While much proprietary research took place within the numerous companies developing scanners, a number of academic groups investigated these effects and reported their findings in Medical Physics. They evaluated various physical properties of CT systems that affect image quality, including x-ray beam characteristics,^{18, 19, 20} focal-spot effects,²¹ collimators,^{21, 22} the system modulation transfer function (MTF),^{23, 24} and image noise properties.²⁵ Additional metrics based on information and detection theory such as noise-power spectrum (NPS), noise equivalent quanta (NEQ), and signal detectability were also developed and applied to evaluating CT image quality.^{26, 27}

Image artifacts also occupied an important body of early research. The deleterious effect of the polychromatic spectrum of conventional x-ray sources on CT image quality—the so-called beam hardening effect—was recognized and described early in this era, along with a number of correction algorithms.^{28, 29, 30, 31} Meanwhile, other investigators realized that the differences between the polychromatic spectra obtained when the tube is run at two different kVp could be used to develop dual-energy techniques that allow one to extract effective atomic number and electron density information.^{19, 32} The noise properties of the dual-energy technique were studied first in 1979.³³ In fact, these techniques remain the foundation of energy-spectral-based algorithms for modern CT scanners. An article on image reconstruction from truncated data and its implication for metal artifact correction was also published in Medical Physics in 1979.³⁴ Naturally, researchers sought to determine and reduce the radiation dose delivered to the subject during CT imaging. In particular, careful experiments were designed and carried out to measure and calculate exposure/dose in CT imaging.^{35, 36, 37} Strategies for reducing dose were proposed by Moran³⁸ and Lewitt.³⁴

The original EMI system was a dual-slice first-generation system, acquiring one ray for each of two slices at a time. The source and detector needed to be translated along each section of the patient and then rotated, with the process repeated for 180 projection views. During the 1970s, a more time-efficient fan-beam imaging system involving rotation only was developed. One of the first articles on fan-beam CT published in Medical Physics described a convolution backprojection algorithm, which is now referred to as the fan-beam filtered backprojection (FBP) algorithm.³⁹ This algorithm can fully exploit the data acquired in the divergent-beam scanning configuration and is still used for image reconstruction from data acquired with modern fan-beam CT scanners. Moreover, it forms the basis for the derivation of approximate algorithms for image reconstruction from CT data acquired with the cone-beam configurations introduced later.

Owing to the accurate anatomical information depicted in CT images, CT scans soon became routinely used in many radiation oncology centers for treatment planning, including Co-60 radiotherapy⁴⁰ and electron beam therapy.⁴¹ In fact, Cormack’s original motivation in the “discovery” of CT (contemporary to and independent of Hounsfield) was to image and quantify the electron density within the body for purposes of more accurate dose calculation in radiation therapy. Holden and co-workers studied imaging the continuously-changing distribution of the object, which later evolved into the important technique of four-dimensional CT.⁴² Overall, CT had established itself as a prime imaging modality in modern radiology by the end of the 1970s.

It deserves mention and has become of topical interest lately that, while so much attention was being devoted to CT, some groups continued to pursue classical tomography, which seeks, through coordinated motion of the source and film, to create x-ray images in which some chosen plane was in focus, with other planes providing a blurred background. Classical tomography is the forebear of the currently thriving tomosynthesis technique. Orphanoudakis and colleagues proposed the mathematical model based on transfer function analysis⁴³ and later validated the assumption of system linearity.⁴⁴ Harding and colleagues used transfer function analysis to address the problem of optimized blurring.⁴⁵

The late 1980s: The Doldrums of CT

Following the booming period of CT research in the late 1970s, momentum persisted through the early years of the 1980s before falling off substantially after 1983.

One of the most interesting articles appearing in Medical Physics during this period is Hounsfield’s Nobel address, in which he reviewed the development of CT before the 1980s and predicted the growing importance of MRI.⁴⁶ In many ways, it is precisely the growth in MRI that accounts for the decline in publications related to CT, as many of the original CT researchers found themselves drawn to this new technology. Moreover, the major focus of the research that was performed on CT in this decade suggested a fairly mature technology, with articles on image artifact reduction, system assessment, and new applications dominating the literature.

Building on work from the 1970s, researchers continued to develop a solid understanding of methods and metrics of system evaluation, with an eye to improving image quality. Glover and Pelc elucidated the nature of CT image artifacts and methods for reducing their impact on image quality, including partial volume effects,⁴⁷ metal artifacts,⁴⁸ and x-ray scatter artifacts.⁴⁹ Understanding the spatial resolution and noise characteristics of CT included evaluation of the MTF,^{50, 51} noise, NPS, NEQ,⁵² and signal to noise ratio in CT image for lesion detection.⁵³ Duerinckx analyzed the second order statistics (covariance and correlations) in CT images,⁵⁴ while Parker tried to relate the amplitude of measurement errors to the maximum image error so that a cost-benefit relationship can be established.⁵⁵

Naturally, many of these image quality metrics are intimately related to the radiation dose delivered to the patient, and researchers continued to develop new dose figures-of-merit,^{56, 57} a new ion chamber for dose measurement,⁵⁸ Monte Carlo simulation for dose calculation,⁵⁹ and a novel dose calculation approach for heterogeneous media.⁶⁰ While Table 1 suggests somewhat of a dearth of activity in CT quality assurance and dosimetry during the 1980s, over the course of the decade, ion chambers specifically designed for CT dose measurement had been developed, and dose descriptors such as the CT dose index came to be recognized by federal regulatory bodies and the AAPM.⁶¹

Interest in novel system configurations continued, as Drost reported using a xenon detector to obtain dual energy information from a single scan.⁶² Edwards reported a treatment planning system running on the GE whole body CT scanner.⁶³ A prototype megavolt CT system for clinical use was reported by Simpson and Swindell,^{64, 65} which appears to be the earliest report of such a system in Medical Physics. On the algorithmic front, researchers began to investigate so-called short scan fan beam trajectories involving rotations less than 360 deg, and one of the earliest articles about short scan was published by Parker.⁶⁶ The weighting scheme Parker proposed has become a widely used standard. Characterization and algorithmic correction of artifacts expanded into scatter, beginning with the article by Johns and Yaffe⁶⁷ for fan beam CT and growing to include a number of other approaches.^{47, 49, 66, 67, 68, 69, 70, 71} Prospective gating was applied to cardiac CT imaging by Moore.^{72, 73} Finally, this era saw the introduction of the classic Siddon algorithm for calculating the exact radiological path through a three-dimensional (3D) CT array.⁷⁴

Two important new applications of CT introduced during the 1980s were blood flow measurements and bone mineral measurements. Works pertaining to flow measurement have been reported in Medical Physics.^{75, 76, 77, 78, 79, 80, 81} Good et al. studied the effect of CT noise and tissue heterogeneity on cerebral blood flow determination for xenon-enhanced CT.⁸⁰ Articles in Medical Physics addressing bone and cortical mineral measurement typically employed a dual-energy approach.^{82, 83, 84, 85} Another novel application suggested during this period was to use CT to measure temperature,⁸⁶ which had potential applications in the area of hyperthermia therapy.

The 1980s also saw the development of early, practical cone-beam CT reconstruction techniques that would capture increased attention in following decades. The now familiar “Feldkamp” algorithm for circular orbit reconstruction made its debut in 1984 and spurred a considerable research effort throughout the field concerning methods for exact reconstruction, cone-beam artifacts, and alternative (noncircular) orbits. By the end of the decade, the ability to reconstruct 3D images from divergent beams—e.g., using 3D filtered backprojection, maximum likelihood estimation, etc.—had become firmly established, and applications in microtomography began to develop.

Finally, in the realm of tomosynthesis, Buonocore reported reconstructing limited angle CT data by using a fast minimum variance estimator.⁸⁷ Ruttimann designed a new sampling scheme for circular tomosynthesis.⁸⁸ Two other articles about blood vessel reconstruction from limited-view data also appeared.^{89, 90}

The 1990s: CT Goes Spiral/Helical

As can be seen in Fig. 1, CT research activity continued to be modest in the early nineties, but it began to expand again in the late nineties leading to the second peak in the 2000s. The articles published in the early 1990s, while few in number, were highly significant, as they introduced the spiral, later also referred to as helical, scanning that energized the CT research community and revolutionized radiological practice during the late 1990s.

The new scanning protocols and geometries arising due to spiral/helical and multislice technology demanded new algorithms and new approaches to evaluation. In the early 1990s, the research focus was on validating the use of a spiral/helical scan instead of a step-and-shoot scan for single-slice image acquisition. There was concern that spiral/helical scanning would yield new artifacts since it deliberately introduced motion inconsistencies into the tomographic data set. However, these inconsistencies could be cured through interpolation, and the benefits of the fast volume coverage soon became apparent. Spiral/helical CT was established as the standard CT scan mode by the end of 1990s.

Analysis of the image artifacts resulting from data inconsistency and algorithms to correct for them were described in Medical Physics.^{91, 92} Later articles deepened the understanding of image-quality issues, including noise, longitudinal resolution, and contrast.^{93, 94, 95, 96, 97, 98, 99, 100} As the image quality improved due to these investigations, spiral/helical CT scanning began to replace conventional CT scanning in clinics. Patient dose delivered by spiral/helical CT scanning and the methods to reduce dose attracted considerable interest at this point.^{101, 102, 103, 104}

Single-slice spiral/helical CT scanners soon evolved into multislice volume scanners with small voxel size, large scanning range, isotropic spatial resolution, and high speed. Dual-slice spiral/helical CT was first described in Medical Physics by Liang and Kruger, who characterized a two-slice system from Elscint.¹⁰⁵ Later, Taguchi and Hu reported advanced interpolation algorithms for multislice spiral/helical CT with careful attention to optimizing the helical pitch.^{106, 107} McCollough evaluated and systematically compared the performance of a multislice CT system to a single-slice scanner in terms of a variety of image quality and dose parameters and dose.¹⁰⁸ Meanwhile, Corrigan et al. described a multirow helical microtomography system for specimen imaging.¹⁰⁹ These articles are a prelude to the slice wars that followed in the early 2000s. Interest in dual-energy imaging also continued in this period.^{110, 111, 112} The faster scanners made possible new applications especially for cardiac,¹¹³ lung,¹¹⁴ bone,¹¹⁵ liver,¹¹⁶ and blood flow imaging.¹¹⁷

CT also played an important role in radiation therapy during the 1990s, helping to fuel a revolution in computerized 3D radiotherapy planning. Early interest in the use of CT in radiation therapy was captured in an AAPM symposium edited by Ling et al.,¹¹⁸ and the technology became firmly established in the following decade. With CT scanners developed specifically for radiotherapy planning and integrated with various treatment planning systems, CT provided the important benefits of 3D target and normal tissue delineation, dose calculation (including the dose-volume histogram), and simulation that have become standard to modern radiation therapy. For guidance of radiotherapy as well, CT pointed to more precise delivery through improved soft-tissue localization at the time of treatment. Early interest in megavoltage CT^{119, 120, 121} suggested the potential for treating the “target-of-the-day” in a manner not possible with two-dimensional portal images, and interest in image-guided radiation therapy continued through the next decade using both megavoltage and kilovoltage CT systems integrated with the treatment machine.

The CT hardware developments reported in Medical Physics during the 1990s mostly relate to detector technology. An image intensifier coupled with a digital TV for tomography¹²² and a solid-state x-ray detector array consisting of scintillators coupled to Si-photodiodes¹²³ were developed. Holdsworth pursued a related development by coupling an image intensifier to a charge coupled device camera in a benchtop CT scanner.¹²⁴ Fahrig reported the use of a C-arm CT system with x-ray image intensifiers for vascular imaging and intervention.¹²⁵ Synchrotron radiation sources began to be investigated and used for CT either in a conventional absorption contrast mode¹²⁶ or by exploiting different physical phenomena such as refraction.¹²⁷

Digital tomosynthesis based on a multiple projection method was also investigated,^{128, 129} along with related studies on sparse object image reconstruction from few-view data sets.^{130, 131, 132} Finally, Zwicker performed a feasibility study investigating transverse tomosynthesis on a digital radiotherapy simulator with conventional isocentric rotational geometry.¹³³

The 2000s: The Slice Wars and the Renaissance of CT

The CT slice wars began in earnest in the 2000s as manufacturers added more rows to the detectors in an effort to increase the volume that could be scanned in a given time. For example, 16-slice diagnostic CT scanners became available in 2001, and some of the first evaluation studies were reported in Medical Physics.¹³⁴ At present, state-of-the art clinical scanners have 256 or 320 rows and the first such prototype was developed by Toshiba in 2004. This prototype was compared to a then-standard 16-slice system¹³⁵ and physical factors such as scatter were investigated.¹³⁶ As all manufacturers added physical rows to the detector, some also explored further increases in sampling through the use of a z-flying focal spot strategy,¹³⁷ which makes use of a periodic motion of the focal spot in the longitudinal direction to double the number of simultaneously acquired slices.

An important CT advance in 2000s was the development and widespread applications of CT systems with a flat-panel detector for cone-beam CT imaging. A flat-panel detector eliminates the need for acquiring data slice by slice, thus allowing the acquisition of fully volumetric images. Most CT systems with flat-panel detectors generally do not use a slip-ring technology, thus enjoying a high degree of imaging flexibility, making such systems particularly attractive for applications in image-guided radiation therapy and interventional procedures.^{138, 139, 140, 141, 142} For image-guided radiation therapy, researchers incorporated flat-panel detector systems on the treatment machine for kilovoltage and megavoltage cone-beam CT and tomosynthesis, now a fairly widespread technology.^{143, 144, 145, 146} For image-guided surgery and interventional radiology, C-arms featuring flat-panel detectors have been developed for intraoperative cone-beam CT.^{147, 148, 149, 150}

Small-animal imaging has become increasingly important as transgenic and knockout mice are produced to model human diseases. Since the late 1990s, microcomputed tomography (micro-CT) has become a standard imaging technology for in vivo imaging of small animals as well as in vitro imaging of small specimens. For example, micro-CT has been used for imaging vascular specimens with different contrast agents.¹⁵¹ One of the challenges of small animal imaging is that most of their physiological parameters, such as heart rate and respiration rate, are much higher than those of humans while the scanners, for a variety of reasons, typically have worse temporal resolution than human scanners. Johnson and Badea have developed respiratory and cardiac gating techniques that allow for in vivo imaging of cardiopulmonary structures.¹⁵²

Another important area of application of cone-beam CT over the current decade has been volumetric imaging of the breast. Using benchtop prototype and early clinical cone-beam CT imaging systems, numerous investigators^{153, 154, 155, 156, 157, 158} have demonstrated exquisite fat-to-fibroglandular soft-tissue discrimination in cone-beam CT images of the breast with total radiation dose no greater than that of a conventional two-view mammogram. Systems developed for early clinical studies utilize a pendant breast geometry, with studies underway to examine the diagnostic performance in breast cancer screening and diagnosis.

In all areas of CT, dose remains an important issue, and because the beam coverage of volumetric imaging devices in the z direction has increased significantly, traditional CT dose metrics and measurement techniques are no longer applicable. New dose metrics have been proposed and they are also appropriate for a direct comparison with the traditional CT dose metrics.^{159, 160}

Another issue of increasing concern in CBCT imaging is the large quantity of scattered radiation generated in the patient and reaching the detector. In some imaging geometries, the scatter fluence may even exceed the primary fluence at the detector. Such a large scatter fraction reduces contrast and creates significant artifacts in the resulting reconstructions.^{161, 162} The use of postpatient antiscatter grids and the development of robust scatter correction algorithms remain important areas of research.

As discussed above, spiral/helical CT scanners began to adopt multiple detector rows in the late 1990s. At that time the interpolation-based methods approximated the x-ray beams as multiple, parallel fan-beams for up to four-slice scanners. However, when the number of the detector rows increased, the interpolation algorithms became inadequate due to the cone-beam artifacts introduced by the cone-beam angle subtended by the detector rows.¹⁶³ Since late 1990s, a number of articles have been published in Medical Physics on approximate algorithms based on the FDK algorithm for image reconstruction on spiral/helical CT scanners with multirow detectors.¹⁶⁴ These modifications of the FDK algorithm have been quite successful and form the backbone of the current reconstruction algorithms on virtually all commercial diagnostic multislice spiral/helical CT scanners. In parallel to the effort of developing approximate algorithms, active effort has been devoted to exact image reconstruction in spiral/helical cone-beam CT.

In 2001, a breakthrough FBP-based algorithm, now called Katsevich’s algorithm, was introduced for exact reconstruction in spiral/helical cone-beam CT. The original derivation of the Katsevich algorithm was nicely explained in an article published in Medical Physics,¹⁶⁵ which also provides an alternative derivation of the Katsevich algorithm. The Katsevich algorithm was subsequently extended to address image reconstruction from spiral/helical cone-beam data acquired with a large detector.¹⁶⁶ An alternative approach to reconstructing images on PI-lines or chords was later developed by Zou and Pan for spiral/helical cone-beam CT.¹⁶⁷ An important feature of the approach is that algorithms such as the backprojection filtration algorithm can be derived for reconstruction of images within regions of interest from truncated projection data.¹⁶⁷ This approach has also sparked considerable effort in the investigation and development of chord-based algorithms for image reconstruction for cone-beam CT.¹⁶⁸

The development of algorithms for the correction or suppression of image artifacts remains active in the 2000s. Additional empirical methods have been proposed for scattering correction for flat-panel detector,^{169, 170} geometric misalignment correction,^{171, 172, 173} beam-hardening correction,^{174, 175} and motion-artifact reduction.¹⁷⁶ An interesting investigation on local tomography from megavoltage CT may find some applications in radiation therapy.¹⁷⁷

After a steady stream of papers on tomosynthesis and classical tomography in the 1970s, 1980s, and 1990s, there was a new surge of interest starting in the 2000s, reflecting the growing availability of digital flat panel x-ray detectors suitable for these techniques.^{178, 179, 180, 181, 182, 183, 184, 185} The primary application interest in tomosynthesis is in breast imaging, as an extension to mammography, where it may offer better detection rates, with little increase in radiation exposure. Several reconstruction algorithms have been investigated,^{177, 178, 179, 180, 181, 182, 183} including the backprojection method, FBP algorithm, the simultaneous algebraic reconstruction technique (SART), and a maximum likelihood method. The anisotropy in imaging performance caused by oblique x-ray incidence in detectors for breast tomosynthesis was also investigated.^{184, 185} The application of tomosynthesis for chest imaging has been proposed.^{186, 187} Optimization of a tomosynthesis system in terms of system response and lung nodules detection has been investigated in Medical Physics. Recently, there has been increased interest in applying digital tomosynthesis to radiation therapy for localization of radioactive seeds,¹⁸⁸ as well as imaging of joints¹⁸⁹ and 3D structures of therapy.¹⁹⁰ The on-board imager mounted on a treatment system has recently been evaluated as a potential tomosynthesis system for use in image guided radiation therapy.¹⁹¹

DISCUSSION AND A LOOK TO THE FUTURE

While this brief survey of x-ray tomography publications in Medical Physics from the 1970s through the present gives a picture of the history of CT and related modalities, a look at a few recent articles gives a sense of some potential future directions for x-ray tomography.

As summarized above, although there have been tremendous advances in CT technologies and applications in the last two decades, there remains a strong desire and need to develop innovative x-ray detector and source technologies, high performance CT systems dedicated to specific imaging tasks, and advanced applications. As an example, a great deal of effort has been invested to develop highly compact, multiple x-ray sources with sufficient flux. Recently, a new x-ray source has been developed that utilizes carbon nanotubes as “cold cathodes” to replace the thermionic cathode used in the conventional x-ray tube. This development could find important applications in medicine, security scanning, and other fields, as discussed in several presentations at the 2007 AAPM Annual Meeting. It is worth noting that there have also been research efforts on the development of bench-top x-ray sources with (quasi) monochromatic, strong flux for various practical applications. One of the intriguing new directions—inverse geometry volumetric CT—turns traditional CT on its head, by using an extended scannable source or multiple disjoint sources to illuminate a relatively small detector. Pelc’s group has investigated the feasibility of such a system for acquiring volumetric images with negligible cone-beam artifacts.^{192, 193} While technical challenges remain to develop sources of sufficient flux, the approach has the premise to allow for fast and flexible imaging in a variety of clinical applications.

Another emerging direction seeks to exploit the remarkable physical properties of synchrotron radiation (monochromatic, high-flux, coherent) to optimize traditional absorption CT or to explore whole new forms of contrast based, for example, on detecting phase shifts in the coherent (and even incoherent) beams after passing through a sample. The comparison of conventional micro-CT and synchrotron-radiation CT has been performed by assessing trabecular bone microarchitecture in a large subset of human bone specimens.¹⁹⁴

While synchrotron sources are obviously much less widely available than x-ray tubes, there has been emerging interest in simulating some of the properties of synchrotron sources by suitable modification of x-ray tube sources. For instance, quasimonochromatic CT systems using a conventional x-ray source with different filters have been developed with the aim of improving image quality without increasing patient dose. McKinley and co-workers performed a simulation study to compare the image quality obtained with different filter materials and system configurations, thereby showing the feasibility of such a system used for computed mammotomography.¹⁹⁵ Saito built such a system using the combination of tungsten target and Er/Yb filters and demonstrated its advantages with phantom images.¹⁹⁶

An area that deserves continued research and diligent clinical practice is the radiation dose associated with CT. As indications for diagnostic CT examination have grown, CT has come to contribute an increasingly significant portion of population dose. Thus, as our understanding of biological response to low radiation doses improves, it is incumbent upon the medical physics community not only to develop rigorous quantitative dosimetry techniques suitable to all forms of CT but also to ensure that the radiation dose associated with each exam is as low as reasonably achievable such that the resulting image is sufficient for the imaging task. Improved dosimetry techniques and metrics are under investigation.^{197, 198, 199, 200, 201} Improved CT scanner technologies, reconstruction techniques, and increasingly task-specific examination will be key to reducing dose in a broad range of applications.^{202, 203, 204, 205} The tendency toward lower kVp techniques appears a promising direction (e.g., 80 kVp abdominal or chest techniques in place of conventional 100–120 kVp techniques). Patient body habitus—particularly in light of an increasingly overweight population with increased demand on diagnostic medicine—needs to be more rigorously considered in technique selection and better accounted in patient dosimetry.^{206, 207, 208, 209} Low-dose thoracic CT provides an initial example of the potential for significant dose reduction in task-specific CT examination, motivated by the desire for early cancer detection.^{210, 211} Similar efforts beckon in all applications of CT—most immediately in head^{212, 213} and pediatric CT.^{214, 215, 216, 217}

In order to improve the dose efficiency and image quality in CT, the utilization of photon-counting detectors has been proposed. Photon-counting image acquisition has a number of advantages over conventional charge integrating detector. It may allow for image acquisition with effective elimination of electronic noise and Swank noise, and could potentially allow for energy-resolved x-ray imaging. Rejection (either complete or in part) of the scattered radiation would be possible, depending on the spectrum of the input x-ray beam. In the case of a polychromatic x-ray source, signal to noise ratio is further improved due to the fact that the photon-counting detector assigns a more optimal energy-weighting factor to the detected photons.²¹⁸ At present, photon-counting detectors cannot achieve the count rates necessary for medical CT, but with improvements they could come to replace the energy-weighted, current integrating detectors used at present.

Some of these new directions are certain to flourish and others to fade away. While it is not possible to predict which will suffer which fate without further investigation, it is certain that such research will continue to appear in the pages of Medical Physics and at the Annual Meetings of the AAPM.