Dose calculation with respiration-averaged CT processed from cine CT without a respiratory surrogate

Abstract

Dose calculation for thoracic radiotherapy is commonly performed on a free-breathing helical CT despite artifacts caused by respiratory motion. Four-dimensional computed tomography (4D-CT) is one method to incorporate motion information into the treatment planning process. Some centers now use the respiration-averaged CT (RACT), the pixel-by-pixel average of the ten phases of 4D-CT, for dose calculation. This method, while sparing the tedious task of 4D dose calculation, still requires 4D-CT technology. The authors have recently developed a means to reconstruct RACT directly from unsorted cine CT data from which 4D-CT is formed, bypassing the need for a respiratory surrogate. Using RACT from cine CT for dose calculation may be a means to incorporate motion information into dose calculation without performing 4D-CT. The purpose of this study was to determine if RACT from cine CT can be substituted for RACT from 4D-CT for the purposes of dose calculation, and if increasing the cine duration can decrease differences between the dose distributions. Cine CT data and corresponding 4D-CT simulations for 23 patients with at least two breathing cycles per cine duration were retrieved. RACT was generated four ways: First from ten phases of 4D-CT, second, from 1 breathing cycle of images, third, from 1.5 breathing cycles of images, and fourth, from 2 breathing cycles of images. The clinical treatment plan was transferred to each RACT and dose was recalculated. Dose planes were exported at orthogonal planes through the isocenter (coronal, sagittal, and transverse orientations). The resulting dose distributions were compared using the gamma $\left(\gamma \right)$ index within the planning target volume (PTV). Failure criteria were set to $2\%∕1\mathrm{mm}$. A follow-up study with 50 additional lung cancer patients was performed to increase sample size. The same dose recalculation and analysis was performed. In the primary patient group, 22 of 23 patients had 100% of points within the PTV pass γ criteria. The average maximum and mean γ indices were very low (well below 1), indicating good agreement between dose distributions. Increasing the cine duration generally increased the dose agreement. In the follow-up study, 49 of 50 patients had 100% of points within the PTV pass the γ criteria. The average maximum and mean γ indices were again well below 1, indicating good agreement. Dose calculation on RACT from cine CT is negligibly different from dose calculation on RACT from 4D-CT. Differences can be decreased further by increasing the cine duration of the cine CT scan.

INTRODUCTION

Four-dimensional computed tomography (4D-CT) is becoming increasingly popular for radiotherapy simulation of thoracic lesions. Studies have shown its efficacy in contouring gross tumor volume for treatment planning,^{1, 2, 3} specifically in stereotactic radiotherapy (SRT),^{4, 5} and proton therapy.^{6, 7} Calculation of dose, however, is often performed on a free-breathing helical CT, but artifacts during helical or axial acquisition due to respiratory motion are well-known.^{8, 9}

Dose calculation using 4D-CT has been explored.^{1, 10, 11, 12} These calculation methods generally apply a 3D treatment plan to each phase of the 4D-CT, equally divide the number of monitor units among each of the phases, and register the resulting dose distributions to a reference phase using rigid or deformable registration. Though not truly 4D treatment planning, this calculation methodology should provide a more accurate estimate of how dose is distributed over a respiratory cycle than calculation on a single, presumably stationary image set. Currently, however, this methodology is not commonly used clinically.

Guckenberger et al. compared dose calculation on 3D and 4D image sets by recalculating dose on different phases of the 4D-CT and comparing these distributions to 4D dose calculation described above. This study demonstrated minimal dosimetric differences for gross tumor and the internal target volume,¹⁰ suggesting that 4D imaging may not be necessary to account for motion in dose calculation. Producing 3D image sets which reflect respiratory motion, however, still requires 4DCT; end-inspiration and end-expiration scans are generally not reliable.¹³ Admiraal et al. demonstrated that dose calculation on the respiration-averaged CT (RACT), the pixel-by-pixel average of the ten phases of 4D-CT, produces similar results to the dose calculation methodology described above.¹⁴ The use of RACT for dose calculation has been adopted at our institution because RACT represents moving structures more accurately than free-breathing helical CT or end-inspiration/expiration imaging over a fraction of radiation.

Recently, we investigated the use of maximum intensity projection (MIP) and RACT processed from cine CT (the unsorted images from which 4D-CT is formed) for delineation of internal gross tumor volume for patients treated with SRT.¹⁵ MIP and RACT from cine CT (denoted ${\mathrm{MIP}}_{\text{cine}}$ and ${\mathrm{RACT}}_{\text{cine}}$ as per our previous convention) can be produced without a respiratory surrogate and sorting software, reducing the cost and complexity of incorporating motion information into the treatment planning process. Contours delineated on cine CT image sets were similar to or slightly larger than those delineated on 4D-CT, reflecting the nature of ${\mathrm{MIP}}_{\text{cine}}$ and ${\mathrm{RACT}}_{\text{cine}}$ image sets to more accurately reproduce total motion extent than 4D-CT, particularly when respiratory motion is irregular.¹⁵ This finding implies that one could substitute cine CT image sets for 4D-CT for some patients and produce treatment plans better encompassing motion due to regular and irregular respiration.

As ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ is currently used for dose calculation, the obvious choice to substitute for ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ in our cine-CT-based treatment planning paradigm is ${\mathrm{RACT}}_{\text{cine}}$. ${\mathrm{RACT}}_{\text{cine}}$, however, averages all the images at each couch position, which can over- or underemphasize different parts of the respiratory cycle in the CT number averaging process.¹⁶ This can be demonstrated with a simple example. From calculus, the mean of any function is

$$\overline{f\left(x\right)}=\frac{{\int }_a^{b}f\left(x^{\prime }\right)d{x}^{\prime }}{b-a}.$$ (1)

If we consider the respiratory trace as a simple sine function, the mean of the sine function is

$$\overline{f\left(x\right)}=\frac{1-\cos \left(x\right)}{x}.$$ (2)

This function, along with the sine function, is plotted in Fig. 1. Not surprisingly, $\overline{f\left(x\right)}=0$ when $x=2\pi k$, where k are integers. This is the case in ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$, where ten image sets are chosen to represent equally spaced phases of one respiratory cycle, like 1 period of a sine wave. Figure 1 illustrates that when $x⩾2\pi$, $\overline{f\left(x\right)}$ reaches a maximum at $x\approx 3\pi$ or 1.5 breathing cycles. This means that ${\mathrm{RACT}}_{\text{cine}}$ will be maximally different from ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ when the cine duration is approximately 1.5 breathing cycles, and that ${\mathrm{RACT}}_{\text{cine}}$ will be “weighted” towards one-half of the respiratory pattern more than the other. This change in CT number may have a significant impact on dose calculation.^{17, 18} Figure 1 also illustrates that $\overline{f\left(x\right)}$ generally decreases with increasing x. For cine CT, this means that increasing the number of images acquired at each couch position (e.g., increasing the cine duration) should make ${\mathrm{RACT}}_{\text{cine}}$ more similar to ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$.

Figure 1.

Plot of $\sin \left(x\right)$ and the average of $\sin \left(x\right)$. Note that the average is zero at integer multiples of $2\pi$. The variable x represents the cine duration of a cine CT exam. Increasing the cine duration decreases the variation from a one-period average. When $x>2\pi$, the maximum deviation from a one-period average is reached near $3\pi$.

The purpose of this study was to evaluate the difference in dose calculation on ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ and ${\mathrm{RACT}}_{\text{cine}}$. We hypothesized that there would be negligible differences between dose calculation on ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ and ${\mathrm{RACT}}_{\text{cine}}$. Furthermore, we hypothesized that differences between the dose distributions will decrease as cine duration increases and more imaging samples of the respiratory cycle are included in the averaging process. Successfully demonstrating that ${\mathrm{RACT}}_{\text{cine}}$ can replace ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ for dose calculation could provide centers without access to 4D-CT an image set which emulates 4D dose calculation.

METHODS

The respiratory wave forms of 23 4D-CT simulation patients (the “primary” patient group) who had an average of at least two breathing cycles per cine duration were classified as “regular” or “irregular” by calculating the coefficient of variation (COV) of the respiratory period over the duration of the scan. The COV was defined as the standard deviation over the mean expressed as a percentage. $\mathrm{COVs}<10\%$ were considered regular and those $>10\%$ were considered irregular. We anticipate that patients that breathe regularly will be more affected by the over/under-emphasis phenomenon because the same fraction of the breathing cycle will be averaged for every couch position, though the phase will be different (Fig. 2). Patient respiratory characteristics are shown in Table 1.

Figure 2.

Overemphasis of certain parts of the respiratory pattern at each couch position. The entire shaded region represents the duration of the “beam on” time, i.e., the portion of the respiratory cycle imaged at each couch position. The light shaded region is one period, the dark shaded region is any part of the breathing cycle beyond one period that will be included in the averaging and will “weight” the average towards that part of the respiratory cycle. Note that different phases of the respiratory pattern are captured each cine duration, weighting a different part of the pattern at each couch position.

Table 1.

Patient characteristics, first group. Patients were included in this group if they had 2 breathing cycles per cine duration. Abbreviations: Avg. $T=\text{average}$ breathing period, $\mathrm{CD}=\text{cine}$ duration, $\mathrm{COV}=\text{coefficient}$ of variance, $\mathrm{SD}=\text{standard}$ deviation, $Tx=\text{treatment}$ technique, IMRT=intensity-modulated radiation therapy, $\mathrm{SRT}=\text{stereotactic}$ radiotherapy, and $3\mathrm{DCRT}=3\mathrm{D}$ conformal radiation therapy.

PatientNo.	Location	Avg.T (s)	CD/avg. T	COV(%)	$Tx$
1	Lung	2.2	2.0	4.3	IMRT
2	Lung	2.7	2.2	4.4	IMRT
3	Lung	2.3	2.2	4.8	IMRT
4	Liver	2.5	2.2	6.4	3DCRT
5	Esophageal	1.8	2.5	6.7	IMRT
6	Lung	2.1	2.4	6.8	IMRT
7	Lung	2.7	2.2	7.8	SRT
8	Lung	1.9	2.1	7.9	SRT
9	Lung	1.6	2.5	8.0	IMRT
10	Lung	2.1	2.1	8.9	SRT
11	Liver	3.0	2.3	9.7	IMRT
12	Lung	2.6	2.2	11.2	IMRT
13	Lung	2.3	2.2	12.9	SRT
14	Lung	2.2	2.3	13.0	IMRT
15	Lung	3.5	2.1	16.1	IMRT
16	Lung	3.2	2.2	18.9	3DCRT
17	Lung	2.7	2.2	20.5	IMRT
18	Esophageal	1.9	2.3	20.5	IMRT
19	Lung	3.1	2.3	22.6	IMRT
20	Esophageal	2.6	2.3	26.2	3DCRT
21	Lung	2.2	2.3	34.0	IMRT
22	Lung	2.3	2.3	37.0	IMRT
23	Lung	2.6	2.5	37.2	IMRT
Average		2.4	2.3
SD		0.5	0.1

At the time of simulation, all imaging was performed on an eight-slice General Electric Discovery ST PET/CT scanner (GEMS, Waukesha, WI) in cine mode with $2.5\mathrm{mm}$ slice thickness, $50\mathrm{cm}$ field-of-view, and 512 by 512 image matrix. ${\mathrm{RACT}}_{\text{cine}}$ was processed from the same cine CT images from which the simulation 4D-CT was formed. A different number of images were included in each ${\mathrm{RACT}}_{\text{cine}}$ to simulate fractions of the breathing cycle being captured at each couch position (1, 1.5, and 2 breathing cycles). These image sets will be denoted ${\mathrm{RACT}}_{\text{cine}1}$, ${\mathrm{RACT}}_{\text{cine}1.5}$, and ${\mathrm{RACT}}_{\text{cine}2}$ in this report.

The clinical treatment plan was copied to each ${\mathrm{RACT}}_{\text{cine}}$ image set and dose was recalculated using collapsed cone convolution on a $4\mathrm{mm}$ isotropic grid with Pinnacle³ version 7.6 (Philips Medical Systems, Madison, WI). Dose planes for all plans were interpolated to $1\mathrm{mm}$ pixels and exported at coronal, sagittal, and transverse orientations through the isocenter. ${\mathrm{RACT}}_{\text{cine}}$ plans were compared to the ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ plan using the gamma $\left(\gamma \right)$ index.^{19, 20, 21} Equations for the γ index are shown in Eqs. 3, 4. The variables $r_e$ and $r_r$ represent points on the evaluated and reference distributions, respectively, where d and D are the user-selected pass/fail criteria

$$\Gamma (\overrightarrow{r_e},\overrightarrow{r_r})=\sqrt{\frac{r^2(\overrightarrow{r_e},\overrightarrow{r_r})}{\Delta d^2}+\frac{{\delta }^2(\overrightarrow{r_e},\overrightarrow{r_r})}{\Delta D^2}},$$ (3)

$$\gamma \left(\overrightarrow{r_r}\right)=\min \left\{\Gamma (\overrightarrow{r_e},\overrightarrow{r_r})\right\}\forall \left\{\overrightarrow{r_e}\right\}.$$ (4)

Clinical γ index criteria are typically $5\%∕3\mathrm{mm}$ or $3\%∕3\mathrm{mm}$ (Refs. ^{19, 20, 21}) for comparing calculated distributions to film measurements. Since we compared two calculated distributions, we have tightened the criteria to $2\%∕1\mathrm{mm}$ to reflect a lower percent dose difference limit of dose calculation accuracy²² and the spatial resolution of the scanner in the transverse plane.

Gamma indices were computed using DoseLab software.^{23, 24} Dose planes contained the full extent of the dose grid. Maximum and mean γ indices and percentages of points passing the γ criteria were measured for the area formed by the intersection of the clinically contoured planning target volume (PTV) and the dose planes (Fig. 3). At the time of planning, the PTV was formed by first identifying the “motion envelope” of the gross tumor using the MIP and confirming this volume using 4D-CT phase data, similar to the method used by Rietzel et al.²⁵ This volume was expanded to a clinical target volume generally using an $8\mathrm{mm}$ expansion, and expanded again to the PTV with a 5 or $3\mathrm{mm}$ expansion, generally depending on the type and frequency of image guidance utilized in treatment. If the PTV contained multiple regions, a weighted average of the γ index in each region was calculated. Gamma indices for ${\mathrm{RACT}}_{\text{cine}1}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$, ${\mathrm{RACT}}_{\text{cine}1.5}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$, and ${\mathrm{RACT}}_{\text{cine}2}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ were compared using a one-way analysis of variance (ANOVA) for correlated samples with a post-ANOVA Tukey HSD test to detect any statistically significant differences between the dose calculations on image sets of increasing cine duration.²⁶

Figure 3.

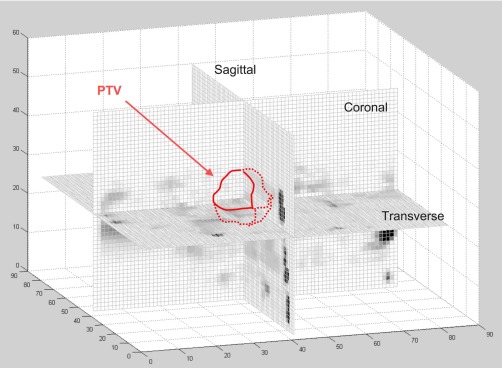
Intersection of orthogonal dose planes with PTV. Mean and maximum gamma $\left(\gamma \right)$ indices were calculated on each of these intersections for all patients.

Due to the small number of patients fitting our two-breathing-cycle-per-cine-duration criteria and their relatively short average breathing period (Table 1), we performed a follow-up study with a larger number of patients and longer breathing periods more typical of clinical exams. Fifty lung cancer patients whose clinical dose calculation was performed on ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ were included for comparison (the “follow-up” patient group). Patient characteristics are shown in Table 2. Of these 50 patients, 25 received SRT and 25 received intensity modulated radiation therapy (IMRT). As before, ${\mathrm{RACT}}_{\text{cine}}$ was reconstructed using the same cine CT data as the 4D-CT simulation. Averaging, however, was only performed with the maximum number of images at each couch position. As before, the clinical plan was copied to the ${\mathrm{RACT}}_{\text{cine}}$ image set, dose was recalculated, and dose distributions on ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ and ${\mathrm{RACT}}_{\text{cine}}$ were compared inside the PTV using the γ index.

Table 2.

Patient characteristics, follow-up group. All patients’ lesions were located in the lung. Note: The respiratory trace could not be retrieved for patient 31. Abbreviations: Avg. $T=\text{average}$ breathing period, CD=cine duration, SD=standard deviation, $Tx=\text{treatment}$ technique, IMRT=intensity-modulated radiation therapy, and SRT=stereotactic radiotherapy.

Patient No.	Avg. T (s)	CD/avg. T	$Tx$
1	7.0	1.3	IMRT
2	6.2	1.2	IMRT
3	6.2	1.1	IMRT
4	6.2	1.2	IMRT
5	6.2	1.2	IMRT
6	6.2	1.2	IMRT
7	6.1	1.2	IMRT
8	5.8	1.3	IMRT
9	5.5	1.3	IMRT
10	5.3	1.3	IMRT
11	5.2	1.1	IMRT
12	5.2	1.3	IMRT
13	5.1	1.4	IMRT
14	5.1	1.5	IMRT
15	5.0	1.4	IMRT
16	4.8	1.3	IMRT
17	4.7	1.3	IMRT
18	4.7	1.3	IMRT
19	4.6	1.3	IMRT
20	4.5	1.1	IMRT
21	4.4	1.4	IMRT
22	4.4	1.6	IMRT
23	4.4	1.4	IMRT
24	4.4	1.4	IMRT
25	4.3	1.4	IMRT
26	3.4	1.6	SRT
27	4.6	1.7	SRT
28	3.1	1.6	SRT
29	4.9	1.3	SRT
30	5.2	1.2	SRT
31	…	…	SRT
32	4.2	1.4	SRT
33	5.6	1.3	SRT
34	5.7	1.6	SRT
35	4.5	1.6	SRT
36	2.6	1.9	SRT
37	6.0	1.6	SRT
38	4.6	1.9	SRT
39	7.9	1.5	SRT
40	7.6	1.2	SRT
41	5.9	1.0	SRT
42	5.2	1.3	SRT
43	4.9	1.1	SRT
44	4.8	1.3	SRT
45	4.7	1.2	SRT
46	4.7	1.3	SRT
47	4.7	1.7	SRT
48	4.6	1.4	SRT
49	4.4	1.3	SRT
50	4.1	1.4	SRT
Average	5.1	1.4
SD	1.0	0.2

RESULTS

Primary patient group

For the ${\mathrm{RACT}}_{\text{cine}1}$ and ${\mathrm{RACT}}_{\text{cine}1.5}$ comparisons, 22 of 23 patients demonstrated 100% of points within the PTV on coronal, sagittal, and transverse planes passing our $2\%∕1\mathrm{mm}$γ criteria. The lone patient who demonstrated any failing points had 1.4% and 0.3% of points fail on coronal and sagittal planes respectively for the ${\mathrm{RACT}}_{\text{cine}1}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ comparison. Though already extremely low, the failures decreased to 0.6% and 0% on coronal and sagittal planes respectively in the ${\mathrm{RACT}}_{\text{cine}1.5}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ comparison, then disappeared completely in the ${\mathrm{RACT}}_{\text{cine}2}$ comparison. All patients demonstrated 100% passing points within the PTV for all geometrical orientations in the ${\mathrm{RACT}}_{\text{cine}2}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ comparison.

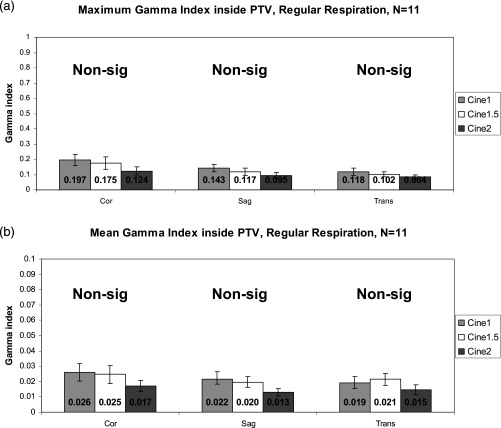
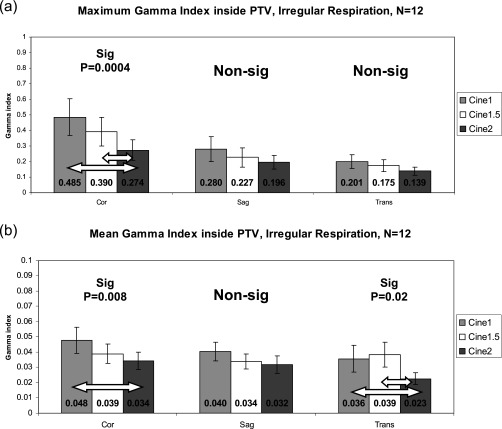
Figure 4 illustrates the maximum and mean γ index for the ${\mathrm{RACT}}_{\text{cine}1}$, ${\mathrm{RACT}}_{\text{cine}1.5}$, and ${\mathrm{RACT}}_{\text{cine}2}$ comparisons within the PTV for patients with regular respiratory patterns. Figure 5 contains the results for irregular respiratory patterns. Maximum and mean values are very low, well under 1, which demonstrates that dose calculation on ${\mathrm{RACT}}_{\text{cine}}$ is very similar to dose calculation on ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$, regardless of how many breathing cycles are used for averaging. The data show, however, that increasing the cine duration does, in general, decrease the γ index to even lower levels. The γ indices from the ${\mathrm{RACT}}_{\text{cine}2}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ comparison are significantly lower for several irregular respiration comparisons, but no regular respiration comparisons (indicated by arrows in Fig. 5). The ${\mathrm{RACT}}_{\text{cine}1.5}$ versus ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$γ indices were not significantly higher for regular respiration, contrary to what we had anticipated.

Figure 4.

Gamma $\left(\gamma \right)$ indices inside the PTV for the primary patient group, regular respiratory patterns. (a) Maximum γ. (b) Mean γ (note the y-axis scale). Error bars are standard error $(N=11)$. Note that γ generally decreases as cine duration increases.

Figure 5.

Gamma $\left(\gamma \right)$ indices inside the PTV for the primary patient group, irregular respiratory patterns. (a) Maximum γ. (b) Mean γ (note the y-axis scale). Error bars are standard error $(N=12)$. Arrows indicate statistically significant differences by ANOVA/Tukey HSD tests. Again, note that γ generally decreases as cine duration increases.

Follow-up patient group

Gamma criteria were met for 100% of points within the PTV for 49 of 50 patients. Patient 22 had 1% of points within the PTV fail our criteria on the coronal γ distribution.

Figures 6a, 6b shows the maximum and mean γ indices within the PTV for the three geometrical orientations. All are well below 1, again supporting that calculation on ${\mathrm{RACT}}_{\text{cine}}$ is very similar to calculation on ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$. Figures 6c, 6d compares maximum and mean γ indices within the PTV considering SRT and IMRT treatment techniques separately. The maximum γ index is higher in IMRT treatment techniques, but the mean γ index is higher in SRT treatment techniques. This discrepancy is most likely caused by the small PTVs utilized in SRT. Dose was calculated using $4\mathrm{mm}$ isotropic grid size which was interpolated to $1\mathrm{mm}$ on each dose plane for γ analysis. A $4\times 4\times 4{\mathrm{mm}}^3$ cube occupies a larger percentage of the total volume for a small volume than a large volume, thereby weighting the mean towards the higher γ index.

Figure 6.

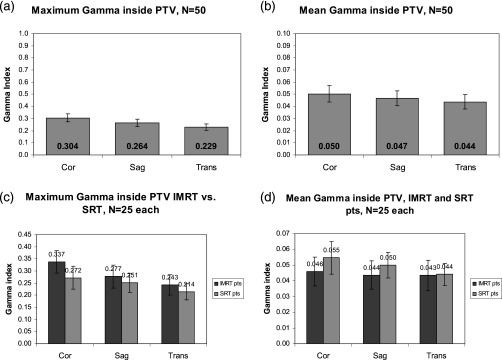
Gamma $\left(\gamma \right)$ indices inside the PTV for the follow-up patient group. (a) Maximum γ. (b) Mean γ (note the y-axis scale). (c) Maximum γ, separated by treatment technique. (d) Mean γ, separated by treatment technique. Error bars are standard error.

DISCUSSION

Preliminary studies in 4D dose calculation have been performed,^{1, 10, 11, 12} but the technique is not yet commonly used for clinical purposes. Dose calculation with ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ is currently used at our institution for treatment planning of thoracic lesions. Admiraal et al. have shown that this technique can produce similar results to 4D dose calculation.¹⁴ We have developed a technique to create RACT image sets directly from the cine CT images which does not require a respiratory trace or sorting into phase or amplitude bins. An early paper by Geise et al., however, cites that a 4%–10% change in electron density may produce a 2% error in dose.¹⁸ In the case of regions highly affected by motion, especially irregular motion, CT number fluctuation may exceed this limit. The current study has shown that calculating dose on these ${\mathrm{RACT}}_{\text{cine}}$ image sets is negligibly different than calculating dose on ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$, and that including more than one period of a respiratory pattern can decrease this difference even further (Figs. 45). Indeed, patient 22 in the primary group was the only patient to demonstrate any points failing the $2\%∕1\mathrm{mm}$γ criteria in the ${\mathrm{RACT}}_{\text{cine}1}$ and ${\mathrm{RACT}}_{\text{cine}1.5}$ comparisons, but these failing points disappeared as the cine duration increased. Our findings suggest that ${\mathrm{RACT}}_{\text{cine}}$ could replace ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ for the purposes of dose calculation with negligible differences in resulting dose distributions.

${\mathrm{RACT}}_{\text{cine}}$ could be a very useful tool for dose calculation in the future. Already used for attenuation correction of PET,²⁷ and recently used for contouring in conjunction with maximum intensity projection,¹⁵${\mathrm{RACT}}_{\text{cine}}$ is relatively easy to generate on a GE Lightspeed CT scanner because cine scanning is a standard operating mode and images can be processed using simple software on a PC. A respiratory surrogate and sorting software are not required to generate ${\mathrm{RACT}}_{\text{cine}}$. The use of ${\mathrm{RACT}}_{\text{cine}}$ for contouring and dose calculation could provide access to image sets that present sufficient motion information for planning purposes without performing 4D-CT.

The cine duration of a 4D-CT (or cine CT) exam is determined by the operator. Pan et al. recommend using the average breathing period of a patient and adding the length of one gantry rotation,²⁸ which is the procedure at our institution. Accordingly, the number of patients with imaging of two or more breathing cycles is rare. Often, these patients are breathing rapidly and the period of the respiratory cycle is small, which necessitates acquiring data for more than one breathing cycle and lengthening the cine duration. Indeed, the average breathing period of patients used in the first part of the study was less than $3\mathrm{s}$, while most patients have a breathing period between 4 and $5\mathrm{s}$.²⁷ Consequently, the first set of patients suffers from several problems: First, the sample size is small; second, though the majority of patients were lung cancer patients, some patients with esophageal or liver malignancies were used to increase sample size; third, the average respiratory periods of these scans are not representative of the whole population.

To remedy these issues, we included a second set of 50 lung cancer patients whose respiratory periods were closer to the population average. Multiple ${\mathrm{RACT}}_{\text{cine}}$ image sets, however, could not be reconstructed because less than two breathing cycles were captured at each couch position. The results of this second patient group, being similar to results of the first, support the conclusion that ${\mathrm{RACT}}_{\text{cine}}$ is sufficiently similar to ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ for dose calculation.

Patient 40, the only patient to show failing points in the follow-up group of patients, demonstrated a substantial shift in anatomy from ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ to ${\mathrm{RACT}}_{\text{cine}}$. This shift caused the observed disagreement in dose distributions, particularly at the superior and inferior regions of the tumor, which was located near the diaphragm (Fig. 7). The change in dose is due to substantially different CT density distributions within the moving lesion from one RACT to the other. Regardless, the regions of disagreement were small and the points failing within the PTV represented only 1% of the PTV volume. Other patients demonstrated similar differences, often near high contrast boundaries.

Figure 7.

Patient 40, follow-up group. (a) Coronal ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$. (b) Coronal gamma $\left(\gamma \right)$ distribution, ${\mathrm{RACT}}_{\text{cine}}$ vs ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$. This was the only patient in the follow up group to have any points inside the PTV fail our criteria (1%). Note the regions of high γ at the inferior and superior regions of the tumor.

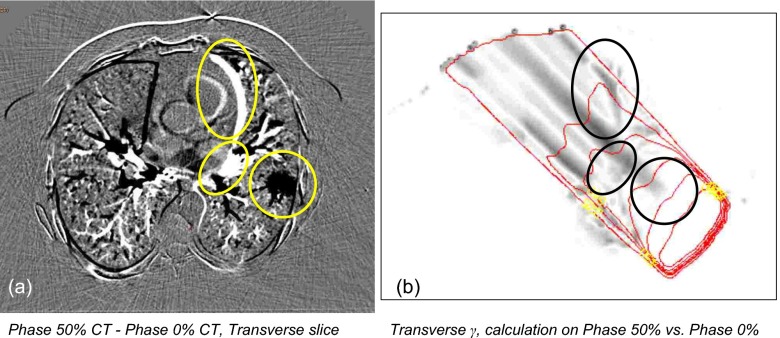
Even when the motion blur does not change significantly within target volumes, changes in high-motion areas can still affect dose agreement within the PTV. Moving structures in the beam path can modulate the depth dose curves, which cause “shadows” of dose disagreement behind the moving anatomy. Examples of this phenomenon are shown in Figs. 89. Figure 8 uses the extreme phases of a 4D-CT to demonstrate this effect, and Fig. 9 shows images and γ distributions from patient 20 of the primary group where this effect can be observed. “Shadowing” effects transverse slices more than coronal or sagittal slices due to beam entry parallel to the transverse plane and may explain why, in Figs. 4b, 5b, the ${\mathrm{RACT}}_{\text{cine}1.5}$ mean γ index is greater, though not significantly, than the ${\mathrm{RACT}}_{\text{cine}1}$ mean γ index inside the PTV for regular and irregular respiration on transverse slices only, not coronal or sagittal.

Figure 8.

Shadowing effect, illustrated by calculating dose on the end-inspiration and end-expiration phases of 4D-CT for one oblique beam. (a) Difference CT image, taken by subtracting the end-inspiration image from the end-expiration image. Circled structures show large differences in CT number. (b) The gamma $\left(\gamma \right)$ distribution obtained by comparing the two distributions. Circles have been redrawn on the γ distribution to highlight the effect of the large change in CT number. Note the long shadows of disagreement behind the moving anatomy. The two extremes of respiratory motion were chosen to exaggerate the difference in anatomical position and subsequent dose calculation.

Figure 9.

Patient 20, primary group. (a) Coronal ${\mathrm{RACT}}_{\text{cine}1.5}$. (b) Transverse ${\mathrm{RACT}}_{\text{cine}1.5}$. (c) Coronal gamma $\left(\gamma \right)$, ${\mathrm{RACT}}_{\text{cine}1.5}$ vs ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$. (d) Transverse γ, ${\mathrm{RACT}}_{\text{cine}1.5}$ vs ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$. This patient exhibits the shadowing effect described. Note the vague stripe behind the area of high disagreement on the superior/lateral edge of the PTV on the coronal view [(a), (c)]. The transverse view [(b), (d)] was taken through this area of high disagreement. Again, note the stripes behind the structures highlighted by arrows. The γ index on both views was still far below our $2\%∕1\mathrm{mm}$ failure criteria.

This geometric ambiguity could be remedied by performing a true 3D γ analysis. The γ index analysis used in this study was based on three orthogonal planes of dose through the isocenter, not a full 3D γ analysis. Presently, no such analytical tool exists at our institution. It is possible to approximate a 3D γ analysis by performing a 2D γ analysis on successive dose planes and “stacking” the slices to form a 3D γ distribution.²⁹ It has been shown, however, that indices in a full 3D γ distribution are less than indices in a “stack” of 2D γ distributions.^{29, 30, 31} Given the low γ indices encountered in this study, we do not expect a “stacked” 3D analysis or a true 3D analysis (which would produce lower values than a stacked analysis) to yield significant (if any) failures using our established criteria.

Originally, we had anticipated that regular respiratory patterns would be more affected by the overemphasis averaging than irregular respiratory patterns because the same fraction of the respiratory cycle would be emphasized at each $2\mathrm{cm}$ couch position (though the actual phase that was overemphasized would be different each time). Our data have shown this to be untrue: Disagreement was approximately twice greater for irregular respiratory patterns for 1, 1.5, and 2 breathing cycle ${\mathrm{RACT}}_{\text{cine}}$ image sets (Figs. 45). Respiratory frequency and amplitude are often correlated,³² and the higher disagreement on irregular respiratory patterns (which were classified by variability in period) can most likely be attributed to extreme changes in respiratory amplitude, which can produce severe artifacts on RACT images.³³ These artifacts are localized to the $2\mathrm{cm}$ “slabs” of tissue imaged at each couch position, but may occur at multiple couch positions if the irregularity persists through the entire exam.

Though increasing cine duration increases dose agreement on ${\mathrm{RACT}}_{\text{cine}}$ and better samples an irregular respiratory cycle,¹⁵ lengthening beam-on time increases patient dose. Our experience with cine CT has shown that RACT and MIP can be produced with good image quality using as little as $40\mathrm{mA}$, which could drastically reduce patient dose from a cine CT scan.³⁴

While the similarity between ${\mathrm{RACT}}_{\text{cine}}$ and ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ for dose calculation is encouraging, it should be noted that the similarity of ${\mathrm{RACT}}_{\text{cine}}$ to ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ for dose calculation does not necessarily imply similarity of ${\mathrm{RACT}}_{\text{cine}}$ to 4D dose calculation. We did not explicitly compare ${\mathrm{RACT}}_{\text{cine}}$ to 4D dose calculation, but this is a topic of future research. Given the low γ indices produced in spite of our conservative γ criteria, however, we do not expect that additional differences would be significant.

CONCLUSIONS

Dose calculation is a critical part of the treatment planning process. For thoracic tumors that are influenced by respiratory motion, RACT generated from unsorted cine CT images can provide a similar environment for dose calculation as RACT generated from sorted, ten-phase 4D-CT images. Substituting ${\mathrm{RACT}}_{\text{cine}}$ for ${\mathrm{RACT}}_{4\mathrm{D}\text{-}\mathrm{CT}}$ for the purposes of dose calculation can provide centers without 4D-CT access to an image set that may emulate 4D dose calculation.