Estimating parsimonious models of longitudinal causal effects using regressions on propensity scores

Abstract

Parsimony is important for the interpretation of causal effect estimates of longitudinal treatments on subsequent outcomes. One method for parsimonious estimates fits marginal structural models by using inverse propensity scores as weights. This method leads to generally large variability that is uncommon in more likelihood-based approaches. A more recent method fits these models by using simulations from a fitted g-computation, but requires the modeling of high-dimensional longitudinal relations that are highly susceptible to misspecification. We propose a new method that, first, uses longitudinal propensity scores as regressors to reduce the dimension of the problem and then uses the approximate likelihood for the first estimates to fit parsimonious models. We demonstrate the methods by estimating the effect of anticoagulant therapy on survival for cancer and non-cancer patients who have inferior vena cava filters.

1. Introduction

In many studies, the goal is to estimate the effect of a longitudinal treatment on a subsequent outcome. Often, these treatment regimes are given in non-randomized fashions. Data arising in such a study must be analyzed carefully to address the non-randomized longitudinal nature of the treatment, the severe bias resulting from the naive application of inappropriate statistical methods, and variability that can arise in estimates due to the large dimension of the problem.

We are motivated by a study of patients who had received inferior vena cava filters (IVCF) due to risk for pulmonary embolism (PE). These filters often prevent blood clots from traveling to the lung. However, there are two factors whose impact requires investigation. First, because the filters may lead to more clots being formed in the legs [1], it is important to estimate whether additional pharmaceutical anticoagulant (AC) therapy administered immediately after filter placement is effective for prolonging life for IVCF patients. In particular, little is known about the relationship between AC therapy and survival after the first 30 days when IVCF patients are at highest risk of mortality. Second, because some IVCF patients who also have cancer have been observed to have increased bleeding and clotting [2], it is important to assess if the presence of cancer for such patients affects survival by possibly interacting with AC therapy.

In our study, we consider a retrospective cohort of patients who had an IVCF placed at our medical center as part of standard clinical care. Some patients in the study had cancer, whereas others did not have cancer but were otherwise at high risk for a blood clot. Each of the patients was subsequently considered for AC therapy on the basis of both their cancer status and baseline variables. Although cancer temporally preceded the IVCF placement, our interest is in the population of patients who receive an IVCF, and thus, we restricted our study design to include only patients with an IVCF; this yields the population of interest (namely patients who currently receive IVCF in clinical settings). Using data collected about this cohort, our interest is in assessing the relationship between the two exposures, cancer and AC therapy, and mortality.

A first challenge in estimating the effect of cancer and AC therapy is that the processes that lead to cancer and the assignment of AC are multifactorial and not simple. In particular, there is a multitude of factors in which cancer and non-cancer patients differ. Moreover, for each of the cancer and no cancer groups (and for each of the background factors that predicted that group), there is also a multitude of factors in which AC versus no AC patients can differ.

A second challenge arises from the estimation of cancer and AC effects for many time points (e.g., days) for an extended period as these survival outcomes may be estimated with high variability and may be difficult to interpret. In particular, it is important to be able to assess whether simpler relations exist for these many effects. If such relations are shown to hold, they can improve understanding and simplify treatment decisions. To address this, one should be able to assess also the plausibility of parsimonious causal models for such studies.

To accomplish this, Robins et al. [3] proposed that marginal structural models (MSMs) be fitted using inverse probability weighting techniques. This methodology allows for a parsimonious model to be specified in terms of the causal target of interest while avoiding the intermediate variables in the causal model. However, because these estimation techniques are based on inverse propensity score weighting, which differs from g-computation [4,5], they are prone to exaggerated variability and instability that are uncommon in likelihood-based approaches, even if they are adjusted through augmentation [6].

Neugebauer and van der Laan [7] considered fitting such models through the simulation of counterfactuals estimated from g-computation, a procedure that provides clarity in the process of model fitting. Neugebauer and van der Laan [7] also developed alternative procedures that are computationally feasible in more complex data sets. Additionally, a case study of this methodology was recently published [8]. Van der Wal et al. [9] considered a case where a factorization allows for a simplified algorithm for the g-computation. All of these methods require, however, the specification and fitting of models for the conditional distributions in the g-computation formula. Such models are complex and difficult to specify when the adjustment for many covariates is necessary, and the resulting model fits are prone to severe misspecification.

In this paper, we propose a new method that, first, uses longitudinal propensity scores as regressors to reduce the dimension of the problem and then uses the approximate likelihood for the first estimates to fit parsimonious models. This method is appropriate in cases where treatments are assigned over a small number of time points so that the total number of possible treatment regimens is manageable.

In the next section, we quantify the goal and the design, and in Section 3, we describe the methodology. In Section 4, we describe how we use the methodology to address the questions of the IVCF study. Section 5 concludes with a discussion.

2. Goal and design

Consider a group of individuals i, each of whom can be potentially exposed to a sequence of discrete treatments, Z₁, …, Z_L, during a treatment period. We are interested in the distributions of the potential outcomes Y_i,t (z₁, …, z_L) [4] at time t after assignment to treatment levels z₁, …, z_L. With no loss of generality, we restrict attention to the case with only two treatment assignments (L = 2), each treatment is binary, and Y binary, as our arguments apply directly to the more general case. We thus wish to estimate the potential outcome distributions

$$Pr(Y_{i,t}(z_1,z_2)=1)$$ (1)

and, more specifically, to assess the plausibility of a model that relates these quantities across different treatments and times, (z₁, z₂, t), in a parsimonious fashion. For conciseness, we omit the subscript i in our notation. In particular, we are interested in relations of the form

$$\mathbf{g}\{Pr(Y_t(z_1,z_2)=1)\}=\mathbf{f}(z_1,z_2,t;\mathit{\beta }),$$ (2)

where f and g are specified functions such that the derivative ∇g exists. We intend g to be contrasts, for example, log odds ratios between the probabilities Pr(Y_t(z₁, z₂) = 1) across different treatments z₁, z₂; and we intend f to express possible parsimonious relations for those contrasts. For example, in our IVCF study, we consider model (11), which we introduce in detail in Section 4.

To begin, we assume the design satisfies the three standard assumptions that are required for the original g-computation relation to connect the target (1) to the observed data distributions. First, treatments of one individual do not affect the outcomes of another individual, an assumption known as no interference [10, 11]. Second, we have available the information used by the assignments of treatments Z; this can be expressed by the conditional independence

$$Y_t(z_1,z_2)\perp Z_1\mid X_1,\text{and}{Y}_t(z_1,z_2)\perp Z_2\mid X_1,Z_1,X_2,$$ (3)

also known as sequential ignorability [12]. Here, we denote covariates observed at baseline by X₁ and X₂ that consist of covariates observed after assignment of Z₁ but before Z₂. Finally, we also assume positive probabilities of assignment for each treatment.

3. Parsimonious models using regression on longitudinal propensity scores

Under the aforementioned design assumptions, Robins [5] showed that the target distributions (1) are recoverable from the distributions of observed data through the following, the so-called g-computation relation:

$$Pr(Y_t(z_1,z_2)=1)=\sum _{x_1^{\prime }}\sum _{x_2^{\prime }}Pr\left(Y_t^{\text{obs}}=1\mid Z_1=z_1,X_1=x_1^{\prime },Z_2=z_2,X_2=x_2^{\prime }\right)\times Pr\left(X_2=x_2^{\prime }\mid X_1=x_1^{\prime },Z_1=z_1\right)\times Pr\left(X_1=x_1^{\prime }\right).$$ (4)

In practice, large dimensions of X₁ and X₂ make positing models for the regressions in the preceding relation subject to severe misspecification. In contrast, methods that use the propensity scores can be preferable when there is some existing knowledge on the assignments of the treatments. However, the use of the propensity scores as weights is known to be associated with unstable estimation even if augmented with outcome regressions [6]. For these reasons, we wish to assess models (2), first by estimating the potential outcome distributions (1) using regressions on treatment propensity scores to summarize the information into approximately unbiased estimators and second by using the empirical approximate distribution of the first stage estimators as a likelihood to fit the more parsimonious models (2).

In order to achieve our first goal, we use the results of Achy-Brou et al. [13], who showed that the longitudinal propensity scores can be used also as regressors. Specifically, for a patient with baseline covariate values X₁, consider the propensity score e₁(X₁) to be the probability Pr(Z₁ = 1 | X₁) that the patient receives treatment Z₁ = 1; and for a patient with baseline covariate values X₁, initial treatment Z₁, and subsequent covariates X₂, consider the propensity score e₂(X₂, Z₁, X₁) to be the probability Pr(Z₂ = 1 | X₂, Z₁, X₁) that the patient receives treatment Z₂ = 1. Then Achy-Brou et al. [13] showed that if the sequential ignorability holds conditionally on the original and possibly high-dimensional covariates, namely (3), then it also holds if these covariates are replaced by the longitudinal single dimension propensity scores, namely

$$Y_t(z_1,z_2)\perp Z_1\mid e_1,\text{and}{Y}_t(z_1,z_2)\perp Z_2\mid e_1,Z_1,e_2.$$ (5)

As a result, we have that the g-computation in (4) can actually be simplified through the use of the propensity scores:

$$Pr(Y_t(z_1,z_2)=1)=\sum _{e_1^{\prime }}\sum _{e_2^{\prime }}Pr\left(Y_t^{\text{obs}}=1\mid Z_1=z_1,e_1=e_1^{\prime },Z_2=z_2,e_2=e_2^{\prime }\right)\times Pr\left(e_2=e_2^{\prime }\mid e_1=e_1^{\prime },Z_1=z_1\right)\times Pr\left(e_1=e_1^{\prime }\right).$$ (6)

We estimate this by first estimating the propensity scores e₁ and e₂ and finding the following: (i) a coarse discretization of e₁ that balances X₁ and (ii) a coarse discretization of e₂ that balances X₁ and X₂ within levels of Z₁. We then stratify individuals by the cross-classified discretized propensity scores e₁ and e₂ within both the Z₁ = 0 and Z₁ = 1 groups. Next, we estimate $Pr\left(Y_t^{\text{obs}}=1\mid Z_1=z_1,e_1,Z_2=z_2,e_2\right)$ using a nonparametric estimator (e.g., for the marginal assessment of survival, empirical proportions if survival is fully observed, or Kaplan–Meier estimators if survival is censored administratively). Using these empirical analogues of the components of (6), we obtain estimates, say p̂(z₁, z₂, t), that are consistent for Pr(Y_t(z₁, z₂) = 1).

To achieve the second goal, that is, to assess the plausibility of simpler relationships (2) between probabilities Pr(Y_i,t (z₁, z₂) = 1) in the different treatment groups across time, the key observation is that we can easily find the joint distribution for the estimators p̂(z₁, z₂, t). In other words, we can now regard the vector of estimators p̂ := (p̂(z₁, z₂, t), over z₁, z₂, t) as condensed data that have a likelihood that connects these data to the vector of true probabilities p := (p̂(z₁, z₂, t), over z₁, z₂, t). This likelihood is the induced joint distribution of the estimators and is approximately normal

$$\widehat{\mathbf{p}}\mid \mathbf{p},{\mathrm{\sum }}_p~N(\mathbf{p},{\mathrm{\sum }}_p),$$ (7)

by the central limit theorem and the delta method, because the estimators in each component of (6) are sample averages. An estimate Σ̂_p of the variance covariance matrix Σ_p can be obtained analytically with the delta method or empirically by the bootstrap.

The preceding discussion indicates how one can estimate contrasts g() among the probabilities p and assess a parsimonious model (2) for those contrasts. Specifically, with no further assumptions, the contrasts can be estimated by using the delta method on (7),

$$\mathbf{g}(\widehat{\mathbf{p}})\mid \mathbf{p},{\widehat{\mathrm{\sum }}}_g~N\left(\mathbf{g}(\mathbf{p}),{\widehat{\mathrm{\sum }}}_g\right),$$ (8)

with Σ̂_g = (∇g(p̂)′Σ̂_p(∇g(p̂))), whereas, if model (2) is assumed, the same likelihood applies but with the model form for the contrasts g(p):

$$\mathbf{g}(\widehat{\mathbf{p}})\mid \mathit{\beta }~N\left(\mathbf{f}(\mathit{\beta }),{\widehat{\mathrm{\sum }}}_g\right).$$ (9)

Thus, the parameters β̂ of the parsimonious model can be estimated by maximizing the empirical likelihood (9), that is, minimizing the quadratic form

$$\{\mathbf{g}(\widehat{\mathbf{p}})-\mathbf{f}(\mathit{\beta })\}{\widehat{\mathrm{\sum }}}_g^{-1}{\{\mathbf{g}(\widehat{\mathbf{p}})-\mathbf{f}(\mathit{\beta })\}}^{\prime }.$$ (10)

The estimated covariance matrix Σ̂_p of p̂ is block diagonal as the empirical proportions are calculated from independent groups, which facilitate computation in many cases. It is easy to see that (10) is a case of generalized least squares and that β̂ is asymptotically normal. We may thus calculate confidence intervals (CIs) directly or use a bootstrap.

4. The inferior vena cava filters study

To study the relationship between death and AC, and cancer in patients with ICVF, an extensive medical records search was conducted at the Johns Hopkins Hospital in Baltimore, Maryland. A cohort of 702 patients who had an IVCF placed between 1 January 2002 and 31 December 2006 was analyzed. Through patient records and the Social Security Death Index, cancer status z₁, AC therapy assigned immediately following filter placement z₂, and time to death were measured for each patient. More details about this study and the subjects are available upon request in Narayan et al. [14]. All statistical calculations were performed using the R statistical package [15].

In this application, the goal of Section 2 is t estimate the effect that cancer, which is ‘treatment’ (z₁), and subsequent assignment to AC, which is ‘treatment’ (z₂), have on survival up to time t(Y_t = 1). Although standard survival modeling [16] often centers on the regression of hazard rates, our interest is in the marginal survival distribution as a clinical assessment. As the cancer patients have a different distribution of baseline covariates compared with non-cancer patients, and AC therapy is non-randomized, we apply the techniques described in the previous sections to recalibrate the various treatment groups in terms of their covariates. Specifically, the first step is the estimation of the propensity scores. We first modeled the probability e₁ of having cancer (Z₁ = 1) using background variables X₁ (observed in all subjects before adjudication for cancer) through a logistic regression model. We found that there was a nonlinear relationship of age with cancer status.

We similarly modeled the probability, e₂, of being assigned to AC, separately in cancer and non-cancer patients using the variables X₁, and clot history and basic hematological biomarkers that the physicians consider before assigning AC, X₂ (for details, see the Appendix of Narayan et al. [14]). For cancer patients, we found there to be a nonlinear relationship between age and AC assignment such that older patients were more likely to have received AC. We also found that patients with brain involvement were less likely to have received AC, but those with prior PE or general venous thromboemboli were more likely to receive AC. In addition, patients who underwent IVCF installation as a result of prior complications with AC were less likely to receive AC in our study. In non-cancer patients, those who received the IVCF for prior failure of AC or thrombolysis were more likely to receive AC. In addition, gender, hypercoagulable state, and prior PE were predictors of AC assignment.

Fifty eight out of the 702 patients had propensity scores outside the area of overlap between treatment groups and were excluded. Both of the propensity scores were discretized by coarsening to quintiles of e₁ and e₂ | Z₁, e₁. The appropriateness of this discretization was confirmed by checking that the quintiles balance the corresponding covariates between cancer groups (for e₁) and AC groups given cancer groups (for e₂). There was one cell in the table of e₁ × e₂ × cancer × AC in which comparisons were not possible because of an empty cell in one of the cancer × AC groups, and thus the 26 subjects from this e₁ × e₂ cell were excluded, with 618 subjects remaining in the final analysis. Although this modifies the population mix, this new mix is precisely known by the covariates of the patients kept in the study. Table I shows the comparison of the original sample and the reduced sample after exclusions in terms of several clinically relevant variables.

Table I.

Comparison of original cohort sample and the analyzed sample after exclusion of subjects in areas of nonoverlap of the propensity scores and empty comparison cells.

	Original cohort (702 patients)	After exclusion (618 patients)
Age (years), median (IQR)	58 (25)	60 (23)
Female, number (%)	328 (53)	300 (49)
Race, number (%)
Caucasian	422 (60)	392 (63)
African-American	251 (36)	204 (33)
Other	29 (4)	22 (4)
Chemotherapy, number (%)	39 (5)	38 (6)
Congestive heart failure, number (%)	42 (6)	40 (6)
Estrogen-containing medication, number (%)	4 (0.6)	4 (0.6)
History of recent trauma, number (%)	90 (13)	60 (10)
History of stroke, number (%)	43 (6)	39 (6)
History of venous thromboembolism, number (%)	124 (18)	108 (17)
Hypercoagulable state, number (%)	18 (3)	12 (2)
Pregnant, number (%)	6 (0.8)	4 (0.6)
Respiratory failure, number (%)	28 (4)	28 (5)
Surgery within last 3 months, number (%)	157 (22)	143 (23)

IQR, interquartile range.

Consider the three assumptions that are required for the design that validates the methods. No interference holds trivially here, as a patient’s assignment is independent of all other patients’ variables. We argue that the assumption of sequentially ignorable treatment assignment is also useful here. First, even though we may be missing confounders for cancer incidence, the result of the methods we proposed still has a useful meaning—that of comparing survival distributions between cancer and non-cancer groups after having recalibrated the distribution of the covariates between the groups so that they be the same. Second, AC therapy is given to patients on the basis of their diagnoses and a set of observed variables selected in collaboration with the clinicians who assigned patients to treatment groups. As these variables included the clinical indicators important for this assignment, sequential ignorability for AC is plausible. Indeed, although the relatively high dimension of the observed covariates complicates the analysis, it helps to reinforce the plausibility of sequential ignorability. Furthermore, it is reasonable to assume that cancer could have affected any subject in our study and that practices in terms of prescribing AC therapies differ across physicians, in which cases the assumptions 0 < e₁(X₁) < 1 and 0 < e₂(X₂, z₁, X₁) < 1 are reasonable.

To estimate survival probabilities beyond time t for each of the e₁ × e₂ × cancer × AC cells, we used Kaplan–Meier estimators. As some cells were small because of sample size, we redistributed subjects from these smaller cells into neighboring cells based on the (continuous) propensity scores until only five cells remained. In each of these condensed cells, survival was estimated. Survival in each of the smaller cells in the original table was estimated as an average of the survival estimated in the condensed cells weighted by the number of subjects redistributed from the smaller cell to each of the condensed cells. A sensitivity analysis of the number of condensed cells was also conducted.

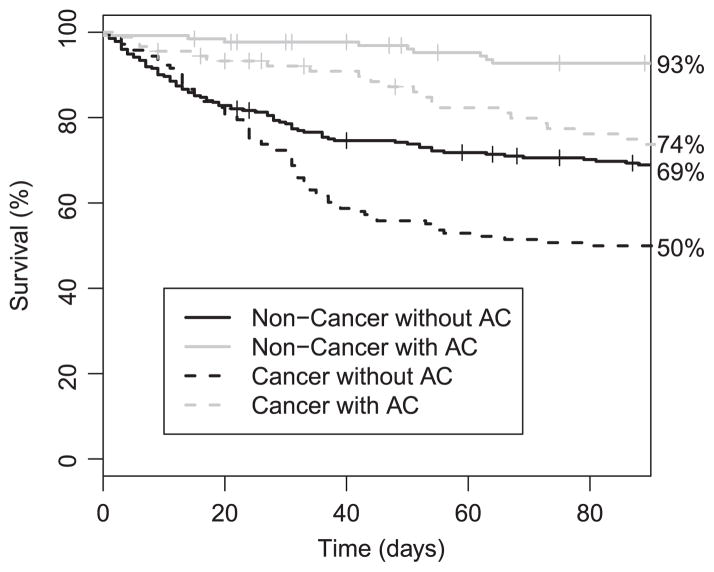
As the interest in this study was in short-term survival, we only consider the time from IVCF placement until 90 days after placement. Over this period, there were many observed deaths; we show in Figure 1 the unadjusted nonparametric estimators of survival in each stratum of cancer and AC treatment.

Figure 1.

Kaplan–Meier estimates of survival observed in each of the treatment by cancer groups. Tick marks show censoring times that are not also failure times.

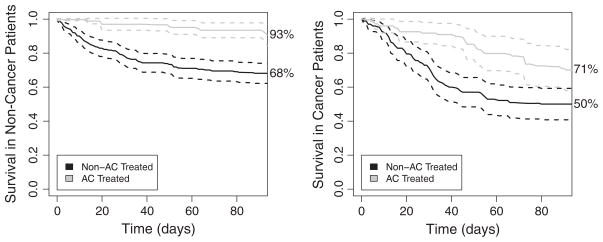
From this figure, it is clear that the groups who received AC had better survival, whereas those who had cancer tended to die earlier. These differences are difficult to interpret, however, as attributable to cancer or AC because patients across groups also differed in other characteristics, and thus confounding by indication may be present. To address this, we also estimated survival by first using the empirical analogue of Pr(Y_t(z₁, z₂, t)) in (6) on the basis of the sequential propensity scores e₁ and e₂. We plot in Figure 2 the results of this analysis, and the dotted lines indicate bootstrap-based CIs. The bootstrap was conducted by resampling individuals within condensed levels of the propensity scores. Although many of the curves look similar, the AC-treated cancer patients have lower survival in Figure 2 compared with that in Figure 1. This indicates that there is indeed a selection bias of cancer patients who are more healthy to the AC group.

Figure 2.

Estimates of survival in each of the treatment by cancer groups calculated by the propensity score-based g-computation formula. Dashed lines indicate pointwise 95% confidence intervals.

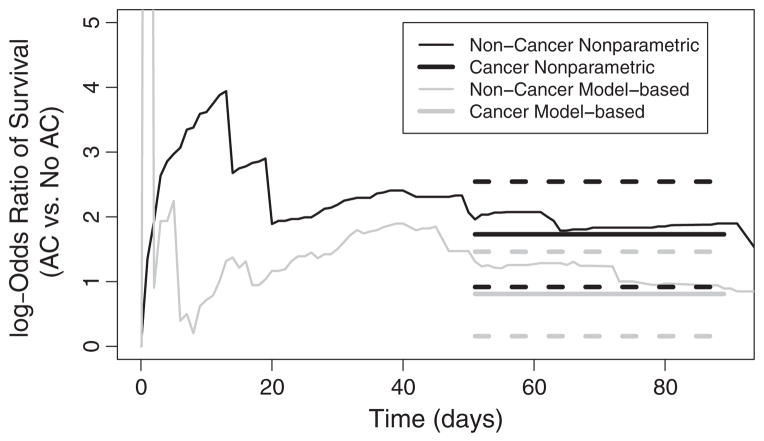
We wanted to explore whether a more parsimonious modeling of survival was plausible. We considered the odds ratios of having survived until each time point, as estimated from the aforementioned method (log odds shown in Figure 3). Using thin lines, we show the log odds ratio of survival for AC in cancer and non-cancer patients separately. Note that because of estimated probabilities of survival being very close to 1 shortly after filter placement, there is a great deal of variation in the estimated log odds ratios before 10 days. However, our interest in this work lies in the survival behaviors after the first 30 days following IVCF receipt, as little is known about survival behavior later on. Thus, we focused our attention on this later period. Figure 3 suggested the log odds ratio for AC is approximately constant from 50 to 90 days after IVCF installation. We therefore assessed the fit of the more parsimonious model

Figure 3.

Comparison of the log odds ratio for death comparing AC with no AC therapy for cancer and non-cancer patients. Using thin lines, the nonparametrically estimated log odds ratios are shown. On the right, the thick solid black and gray lines indicate the fitted parsimonious model for a common log odds ratio between 50 and 90 days. Thick dashed lines indicate 95% confidence intervals.

$$\text{logit}\widehat{\mathbf{p}}(z_1,z_2=1,t)-\text{logit}\widehat{\mathbf{p}}(z_1,z_2=0,t)={\mathit{\beta }}_1\text{for}{z}_1=0,1;t\in [50,90].$$ (11)

To simplify computation, we considered a subgrid of time points in the interval between 50 and 90 days. This model is a special case of (2), where the contrast function g is the log odds ratio comparing cancer followed by AC with cancer followed by no AC, and the parsimonious function f is the constant β₁. We therefore appealed to the properties (8)–(9) and obtained the estimator β̂₁ by minimizing (10), using the estimated covariance matrix Σ_g from the delta method. The fit from this model is shown in thick lines on top of the nonparametric estimates on the right of Figure 3. The fitted log odds ratio of survival comparing the AC to non-AC patients after in the time interval of interest was 0.82 (95%CI 0.17–1.47) for non-cancer patients and 1.74 (95%CI 0.93–2.55) for cancer patients. In order to assess the fit of this model, we computed the likelihood ratio test of $\{\mathbf{g}(\widehat{\mathbf{p}})-\mathbf{f}(\widehat{\mathit{\beta }})\}{\widehat{\mathrm{\sum }}}_g^{-1}{\{\mathbf{g}(\widehat{\mathbf{p}})-\mathbf{f}(\widehat{\mathit{\beta }})\}}^{\prime }$ on the basis of the log odds ratios over the time points in 50–90 days (p > 0.45). Thus, as also suggested by the figure, the data are consistent with a constant odds ratio effect of AC therapy between 50 and 90 days, for both cancer and non-cancer patients.

In this study, our primary interest is in the relationship between survival after the first month and the exposures of interest. In the preceding modeling, we consider the log odds ratio of survival in the period of 50 to 90 days after the filter is installed. We present this model after inspection of the data, and the same model fitted to the 20-to-90-day period results in a rejected goodness-of-fit test for cancer patients.

5. Conclusion

In this paper, we have developed techniques for the fitting of parsimonious models in a causal framework. The key distinction between our methodology and standard fitting of MSMs is that we use regressions on propensity scores to summarize the information into approximately unbiased estimators. This avoids the use of inverse probability-weighted estimating equations, which can be unstable. Similar techniques have also been suggested in other estimation problems [17]. Additionally, the two-stage approach presented here allows for transparency in the modeling process; in particular, the estimates from the g-computation may be interpreted and compared with results from more parsimonious modeling. In comparison, model building in the case of standard fitting of MSMs can be more complex [18, 19].

To assess the uncertainty of our estimates, we used a bootstrap of subjects in Section 4. For the results presented in this paper, we resampled within levels of the propensity score, although we also implemented a more comprehensive bootstrap that involved re-estimating the propensity score within each iteration. This bootstrap yielded similar results in the period of interest.

The aforementioned methodology is quite general and may be applied in cases where there are more than two states (alive versus dead); for example, it may be of interest to additionally consider the process of developing clots. In such a scenario, a clot may be observed before death but not after a death, posing a semi-competing risk problem [20]. This problem may be addressed by applying the methodology introduced in this paper to the induced multi-state model [14]. Such techniques are also applicable in standard competing risk scenarios and other more complex contexts in which each individual is susceptible to more than two events. In addition, our methodology applies directly to problems in which there are more than two treatment assignments or multi-level treatments, but the total number of possible treatment regimens is manageable.

Our method uses stratification of the propensity score for simplicity and transparency. Such stratification methods have been widely used in the scientific literature and have shown to have desirable statistical properties. For example, Senn et al. [21] showed that for normally distributed outcomes, the coarsening seemingly obtained by propensity score stratification does not reduce variability and, on the contrary, will yield the same results as a fully saturated linear model for the outcome in special cases. Senn et al. [21] further advised caution during the estimation of the propensity score to avoid over-fitting, a concern that our method may generally inherit. In our case, we model the process through which patients receive treatments in consultation with clinical collaborators who make treatment decisions. This motivates plausible and parsimonious propensity score models, whereas outcome regression validity depends on processes whose variation is more difficult to understand.

Odds ratio estimation and the variance associated with stratification for propensity scores have also been studied previously. The work of Stampf et al. [22] studies various estimators of an odds ratio treatment effect for the case where a single treatment is assigned, and found delta method-based variance estimation for a marginal effect (similar to our proposed technique) to have reasonable performance. Williamson et al. [23] described variance estimation in the context of propensity score stratified modeling techniques and advocate the use of a bootstrap. Furthermore, they note that the estimation of variance conditionally on the propensity score, as proposed earlier, generally results in conservative inference.