Abstract
This paper proposes a novel formulation to model and analyze the statistical characteristics of some types of segmentation problems that are based on combining label maps / templates / atlases. Such segmentation-by-example approaches are quite powerful on their own for several clinical applications and they provide prior information, through spatial context, when combined with intensity-based segmentation methods. The proposed formulation models a class of multiatlas segmentation problems as nonparametric regression problems in the high-dimensional space of images. The paper presents a systematic analysis of the nonparametric estimation’s convergence behavior (i.e. characterizing segmentation error as a function of the size of the multiatlas database) and shows that it has a specific analytic form involving several parameters that are fundamental to the specific segmentation problem (i.e. chosen anatomical structure, imaging modality, registration method, label-fusion algorithm, etc.). We describe how to estimate these parameters and show that several brain anatomical structures exhibit the trends determined analytically. The proposed framework also provides per-voxel confidence measures for the segmentation. We show that the segmentation error for large database sizes can be predicted using small-sized databases. Thus, small databases can be exploited to predict the database sizes required (“how many templates”) to achieve “good” segmentations having errors lower than a specified tolerance. Such cost-benefit analysis is crucial for designing and deploying multiatlas segmentation systems.
1 Introduction and Background
The strategy of segmenting an image using other examples of similar segmentations has lead to various approaches in a spectrum of clinical applications over the last two decades. This paper considers segmentation methods, e.g. [1,5,11], using a combination of (i) a set of template images that depict the anatomy and (ii) a set of tissue probability maps or segmentations that give, for each template, the true probability of each voxel belonging to a specific anatomical structure. A pair comprising a template image and its true segmentation is termed an atlas. For segmenting structures in biomedical images where boundary parts of the anatomy are not readily apparent in the image data, atlases can infuse crucial prior information, strongly influenced by anatomical context, and thereby complement solely-data-driven segmentation methods.
For segmenting anatomical structures having weakly-visible boundaries, atlas-based methods leverage information within the spatial configuration of those surrounding structures whose boundaries are well defined in the image. This relies on the assumption that the geometry (i.e. location, pose, size, and shape) of the weakly-visible structure is a function of the geometry of these surrounding structures. Subsequently, atlas-based segmentation methods register pre-segmented template images to match the target image containing the structure we want to segment. Assuming reliable matching of the surrounding structures, registration methods yield a deformation to best match the weakly-visible structure of interest. Subsequently, template segmentations are deformed to the target.
Large collections of medical images, and associated expert-defined segmentations, are becoming ubiquitous as public resources, and within specific clinical practices. This has lead to multiatlas, nonparametric atlas, or label-fusion approaches [1,2,5,10,11,13,15,16] to segmentation that leverage information in the entire database of atlases. Multiatlas approaches can exploit methods for fast selection [18] of a small subset of templates that are most similar to the target. They independently register the selected templates to the target and, then, deform database segmentations to the target space. A weighted average [1] of the deformed segmentations produces a nonparametric estimate of the segmentation of the target. Instead of using the entire database, the carefully selected subset produces better estimates, as shown for brain [1] and cardiac [5] images. The proposed theoretical framework and the results shed light on this behavior, indicating that an optimal subset size depends on the database size.
The spirit of the proposed framework differs significantly from that of methods focussing on estimating rater-performance parameters (particularly, rater bias) [17] and the parameters’ confidence intervals [4] or compensating for inter-voxel label correlations [15]. Unlike such methods, the proposed approach models and predicts segmentation error as a function of database size and provides per-voxel confidence measures on the segmentation.
This paper makes many contributions. It proposes a novel statistical non-parametric regression framework to model a class of multiatlas segmentation approaches and analyze the convergence behavior of segmentation error with respect to database size. It shows that the error convergence rate as a function of database size has an analytic form with parameters fundamental to the segmentation problem. By measuring these parameters, it characterizes multiatlas segmentation problems (i.e. chosen anatomical structure, imaging modality, etc.) and a class of approaches (i.e. registration algorithm, label-fusion algorithm, etc.) in terms of (i) the complexity of the function mapping the geometry of (clearly-visible) surrounding structures to the geometry of the structure of interest, (ii) the inherent anatomical randomness in the structure’s geometry, (iii) number of atlases available in the database, and (iv) some algorithm parameters. In this way, the framework offers new methods to evaluate the efficacy of a particular database of atlases, modality, algorithm, etc. It can provide per-voxel confidence measures for segmentations. We demonstrate that the segmentation error for large database sizes can be predicted using small-sized databases. Thus, small databases can be exploited to predict the database sizes required (“how many templates”) to achieve “good” segmentations having errors lower than a specified tolerance. Such cost-benefit analysis is crucial for designing and deploying multiatlas segmentation systems.
2 Methods
This section presents a novel statistical framework, relying on nonparametric regression, to model and analyze a class of multiatlas segmentation approaches.
Consider the problem of estimating the unknown segmentation for a target image, using a database of atlases (templates and their segmentations). Treating each atlas as a member of a family of atlases under constrained diffeomorphisms (e.g. constrained under limited deformation norm), we first transform the database to factor out a diffeomorphism between the geometrical configurations of anatomical structures within the target and each template; better matches of the two geometries would usually lead to better matches of the segmentations. We assume that multiatlas segmentation methods can compute an optimal smooth diffeomorphism using image registration on the raw intensities or on derived geometry-capturing features and, later, deform each template and segmentation, in the database, to the target-image physical space. Thus, we propose to (i) model multiatlas segmentation as a regression problem where the independent variable represents the deformed template images and the dependent variable represents the deformed segmentation images and (ii) analyze the rate of convergence of the error in multiatlas segmentation with respect to increasing database sizes to characterize the diffculty for a specific segmentation problem.
2.1 Statistical Modeling and Analysis of Multiatlas Segmentation
Consider a vector random variable F that models a (deformed) biomedical image with V voxels. Observed images f ∈ ℝV are drawn from the probability density function (PDF) P (F). For a specific anatomical structure in the image, let S be a V -dimensional vector random variable modeling the (deformed) true probabilistic-segmentation image. Segmentations s are drawn from P (S). Let S[v] denote the random variable at the v-th component of S (i.e. voxel v in image); ∀s∀v, s[v] ∈ [0, 1]. Assume that the joint random variable (F, S) has a PDF P (F, S) capturing dependencies between images f and segmentations s.
Consider a database aM ≜ {(fm, sm)}m=1,…,M of M atlases, i.e. template images {fm}m=1,…,M paired with their true segmentations {sm}m=1,…,M, where each observed image pair (fm, sm) is drawn independently from the PDF P (F, S). For a given target image f0 whose true segmentation s0 is unknown, we get an estimate ŝ0 of the true segmentation, using database aM.
We treat the multiatlas segmentation problem as that of statistical non-parametric regression [8,14]. Let r(F) be a regression function of S (dependent variable) on F (independent variable). We choose r(F) as the regression function that minimizes the mean squared error (MSE) risk function EP(F,S) [||S − r(F)||2] = EP(F)[EP(S|F)[||S − r(F)||2]. For any target f, the MSE-minimizing regression function is the conditional expectation r(f) ≜ EP(S|f)[S]. Let r̂(F, aM) be an estimator of r(F).
We want to characterize the behavior of conditional-expectation regression estimators over (i) varying images f ~ P (F) and (ii) varying databases aM comprising M image pairs. Hence, we treat the database as a random variable
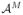 , assume a joint PDF P (F, S,
, assume a joint PDF P (F, S,
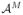 ), and then define a new MSE function:
), and then define a new MSE function:
| (1) |
| (2) |
The second term in the MSE(M, f) expression leads to EP(F)EP(
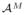 |F)[||r(F) − r̂(F,
|F)[||r(F) − r̂(F,
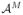 )||2], which is the mean integrated squared error associated with regression estimators [14]. We consider P(
)||2], which is the mean integrated squared error associated with regression estimators [14]. We consider P(
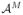 |F) = P (
|F) = P (
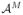 ).
).
Let r(f)[v] denote the v-th component of r(f) and let r̂ (f,
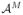 )[v] denote the v-th component of r̂(f,
)[v] denote the v-th component of r̂(f,
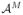 ). Then, the linearity of expectation gives:
). Then, the linearity of expectation gives:
| (3) |
| (4) |
We now analyze all three terms in the expression for MSE(M, f)[v]:
For the conditional-expectation regression function r(f), the first term is the variance of the conditional PDF P (S[v]|f). This term (i) depends on the inherent (beyond human control) randomness in the segmentation, at voxel v, given image data f and (ii) is independent of the estimator r̂(f,
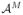 ).
).The second term relates to the quality of approximation of the estimator r̂(f,
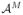 ) to the true conditional-expectation regression function r(f). This term depends on the database size M and the characteristics of the marginal distribution P (F) and the regression function r(·) in the locality of f [8]. This term equals the sum of the squared bias and variance of the estimator.
) to the true conditional-expectation regression function r(f). This term depends on the database size M and the characteristics of the marginal distribution P (F) and the regression function r(·) in the locality of f [8]. This term equals the sum of the squared bias and variance of the estimator.The third term vanishes because it is equal to EP (
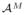 )EP(S|
)EP(S|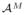 ,f)[2(S[v] − r(f)[v])(r(f)[v] − r̂ (f,
,f)[2(S[v] − r(f)[v])(r(f)[v] − r̂ (f,
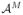 )[v])] where the inner expectation is zero (decomposition of random variable S[v] − r̂(F,
)[v])] where the inner expectation is zero (decomposition of random variable S[v] − r̂(F,
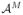 )[v]).
)[v]).
Thus, MSE(M, f)[v] is the sum of the variance of the conditional PDF, the squared bias of the estimator, and the variance of the estimator:
| (5) |
We now choose a specific regression estimator. A consistent estimator for the conditional-expectation regression function r(f) is the generalized k-nearest-neighbor (kNN) estimator [12] r̂(f, aM):
| (6) |
where g(·, ·) is some distance metric in the space of f, Rk is the distance between f and its k-th nearest neighbor in the set {fm}m=1,…,M, and w(·) : ℝ ↦ ℝ is a bounded non-negative generalized weight function satisfying ∫ w(u)du = 1 and w(u) = 0 for ||u||> 1. In this paper, w(u) is constant ∀u : ||u|| ≤ 1.
For the class of generalized kNN estimators [12],
| (7) |
| (8) |
where (i) D is the dimension of the independent variable; (ii) φ(r(·)[v], P(F), f, D) depends on the values and differential properties of the PDF P (F) in the locality of the fixed image f, the local differential properties of the v-th component of the true regression function r(·), and dimension D; (iii) ψ(w(·), D) depends on the chosen weight function w(·) and the dimension D. Indeed, the kNN estimator converges to the true conditional-expectation regression function asymptotically as the database size M → ∞ and the number of nearest neighbors k → ∞ at an appropriate rate such that (k/M) → 0.
It is important to note that the rate of convergence of the bias and variance depends on (i) the dimensionality D associated with the independent random variable F, (ii) the values and the differential properties of the PDF P (F) of images, and (iii) the differential properties of the regression function r(f).
2.2 Practical Interpretation Using the Statistical Analysis
This section leverages the theory described in Section 2.1 to get practically useful measures of the difficulty of multiatlas segmentation for a specific segmentation problem. It describes how to empirically characterize the typical behavior of the regression-based segmentation scheme for an anatomical structure of interest.
Empirically Computing MSE
For a chosen k and database size M, we propose to empirically compute MSE(M) in Equation 1 by: (i) Monte-Carlo sampling of target images f to compute EP(F)[·], (ii) for each f, Monte-Carlo sampling of databases aM, from a large database with size N > M, to compute EP(
 |f)[·], and (iii) computing the MSE terms at each voxel v and summing them over all voxels. We repeat this process for a range of M values.
|f)[·], and (iii) computing the MSE terms at each voxel v and summing them over all voxels. We repeat this process for a range of M values.
Parametric Form for MSE
When the class of signals F is unconstrained, D equals the number of image voxels, which is typically very large. However, consistent with empirical evidence in the signal-processing literature that the intrinsic dimension [9] of real-world multivariate data is far less than the number of variables, we consider D as the intrinsic dimension of the independent variable (template images) and estimate it empirically. Note that each voxel v can have a different value for the intrinsic dimension Dv.
Tracing our way back, we (i) substitute Equations (7) and (8) for voxelwise regression estimator’s bias and variance, respectively, into Equation (5), (ii) substitute that into Equation (3), and (iii) substitute the resulting equation into Equation (1). This gives the following parametric forms for the MSEs:
| (9) |
| (10) |
These equations captures the characteristics of a specific segmentation problem and approach through parameters α, δ, β, D, whose significance we describe next:
-
α denotes the intrinsic randomness in the segmentations s as a function of the image data f. α is independent of the regression estimator and hence is the lowest possible achievable MSE.
δ closely relates to α and captures the lowest possible MSEs for the chosen generalized-kNN estimator (i.e. w(·)) and k, which is achieved when the database size M → ∞. As M → ∞, we make the kNN estimator converge to the true conditional expectation, by letting k go to ∞ at such a rate so that (k/M) → 0; in that case, δ → α.
Assuming that f lies in a Euclidean space, at each voxel, ψ(w(·), Dv) = c(Dv) ∫ w2 (u)du, where c(Dv) is the volume of the unit sphere in Dv dimensions [12]. For the chosen kNN scheme with constant w(·) within the unit sphere, ψ(w(·), Dv) = 1, αv = γv = δv/(1 + 1/k), and α = γ = δ/(1 + 1/k).
β represents the overall complexity of multiatlas segmentation in terms of the (i) differential properties of the true regression function r(f) and (ii) values and differential properties of the image PDF P (F). For example, r(·) is harder to estimate when β is increased when: (i) larger gradients and curvatures in r(·) lead to larger values of φ; (ii) around a target f0, low values of P (F) make it harder to obtain databases comprising sufficiently-many templates near f0; (iii) around a target f0, locally-varying P (F) leads to databases where the templates near f0 pull the segmentation estimate towards that for the local higher-probability templates.
D in the exponent represents the overall intrinsic dimension associated with the entire anatomical structure. Larger D increases the difficulty of multiat-las segmentation by requiring estimation of a higher-dimensional regressor.
Parameter Estimation (α, β, δ, D)
To estimate parameters δ, β, D (for a specific segmentation problem and approach) we (i) empirically evaluate MSE(Mj) for a range of database sizes Mj (e.g. M1 = 10, Mj+1 = Mj + 10) and then (ii) solve a weighted nonlinear least-squares curve-fitting problem
| (11) |
where weights Wj are the computed variances of the squared errors for each Mj. Interestingly, effects of changing k are absorbed by changes in δ and β, leaving D unchanged. As described before, for chosen kNN estimator, α = δ/(1 + 1/k). Parameter estimates for any voxel v are obtained by curve fitting to MSE(Mj)[v].
3 Experiments and Results on a Clinical Database
This section describes some practical considerations and shows results on a large clinical database. The results demonstrate the validity of the proposed model for multiatlas segmentation and the utility of the proposed analysis in clinical applications. Section 3.1 shows that several anatomical structures in the brain exhibit the parametric trends determined by the model, which in turn shows that the model is well-suited for real applications. Section 3.2 shows that the segmentation error for large database sizes can be predicted using small-sized databases. Thus, small databases can be exploited to predict the database sizes required to achieve a specified maximum tolerable MSE in segmentation.
Practical Considerations
The proposed formulation is based on the independent variable being the deformed templates in the entire database. However, multiatlas approaches require only a few most-similar templates (k in kNN) and registration between the target and thousands of templates in a large database can be very expensive. Thus, this paper uses an extremely-fast approximate search for similar templates relying on affine registration followed by spatial pyramid matching on coded geometry-capturing features (canny edges clustered and coded based on orientation and curvature) [18]. This implicitly induces a distance metric in the space of deformed images f, underlying kNN regression. The fast lookup makes multiatlas schemes viable for large databases. Next, we compute the optimal deformations, between each selected template and the target, using constrained diffeomorphic registration using [7].
Clinical Database
We evaluate the proposed methods on a large clinical database obtained from the National Alliance for Medical Image Computing (www.na-mic.org) comprising 186 T1 MR brain images (dimensions ≈ 256×256×240; voxel size ≈13mm3) with expert segmentations for the caudate, putamen, thalamus, hippocampus, and globus pallidus in both hemispheres.
3.1 Error Convergence in Multiatlas Segmentation in Brain MRI
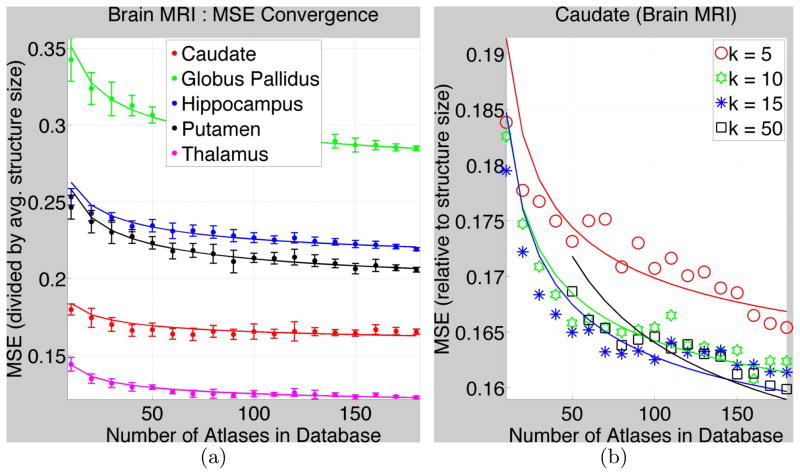
We selected 20 random target images f. For each f, we performed 50 random Monte-Carlo simulations of databases aM, ∀M. We chose k = 10. Figure 1(a) shows MSE values (divided by the average size of the structure in the database), and fitted curves, for various database sizes. Corresponding structures in the left and right brain hemisphere structures are combined.
Fig. 1. MSE Convergence for Subcortical Structures in Brain MR images.
(a) The dots and the error bars show MSE(Mj) and the standard deviation, respectively, (divided by the average true size of structures in database) for k = 10. The parametric fitted curves are shown by solid lines. Table 1 gives the parameter values. (b) shows MSEs and fitted curves for the caudate (as an example) for varied k.
The size-normalized MSE values relate to Dice, both measuring degree of (dis)similarity relative to size. While the Dice measure takes values in [0, 1], size-normalized MSE takes values in [0, η] where η is twice the ratio of (i) the size of the largest structure in the database to (ii) the average size of the structure in the database. For example, for thalamus segmentation, using the largest database M = 186, averaged over 20 target images, Dice = 0.91 and MSE = 0.11.
Table 1 shows the parameters underlying the fitted curves. Values for δ (inherent randomness) indicate the lowest possible MSE achievable with k = 10 and the chosen generalized-kNN estimator. Values for β (regression complexity) and D (intrinsic dimension) indicate (i) the size of databases needed to achieve small MSEs, e.g. MSE closer to δ, and (ii) the amount of benefit, in terms of a decrease in MSE, obtained for the cost of an increase in database size. Such cost-benefit analyses are crucial for designing clinical support systems. Interestingly, the range of our estimates for D, for probabilistic segmentations, is similar to that found for fuzzy digit images [9] and texture [3,6].
Table 1.
Parameters indicating difficulty of multiatlas segmentation and the underlying convergence behavior (of segmentation MSE with increasing database sizes Mj) for anatomical structures in brain MR images (using 186 atlases)
| Parameters | Caudate | Globus Pallidus | Hippocampus | Putamen | Thalamus |
|---|---|---|---|---|---|
| δ: randomness | 0.15 | 0.26 | 0.20 | 0.18 | 0.11 |
| β: complexity | 0.03 | 0.10 | 0.06 | 0.08 | 0.03 |
| D: dimension | 10.1 | 10.0 | 10.0 | 10.0 | 10.0 |
The globus pallidus has probably the weakest boundaries and is the most difficult to segment (for its very small size) leading to the highest values for MSE, δ, β, D. The hippocampus is the second most difficult to segment probably because of its elongated thin shape and small size. The thalamus gives the lowest MSEs probably due to its large size, despite the part of its boundary next to the gray matter being quite weak.
Figure 1(b) shows MSEs and fitted curves for the caudate (as an example) for varied k. Consistent with the theory of kNN-estimator convergence (Section 2), large k leads to lower MSE for large database sizes M, but can increase MSE for lower M. Indeed, for the kNN estimator to converge asymptotically to the true conditional expectation, as M increases, k must increase at an appropriate rate [8]. Thus, Figure 1(b) is consistent with the regression theory in the sense that the MSE-minimizing k does depend on the database size M.
Figure 2 shows a hippocampus and parameter values associated with curves fitted to MSE values obtained at each voxel, i.e. without the summation Σv(·) for δ, β in Equation 10. Zero values for MSE and δ for voxels well inside or well outside the hippocampus indicate the ease of segmentation for such voxels. Voxels where the segmentation is the most difficult (highest β, D; high δ) lie near the hippocampus head (near the amygdala; very low contrast) and the tail (perhaps larger shape variability leads to inaccurate registration). As described in Section 2.2, for the chosen kNN estimator and k = 10, α = δ/(1+1/k) = δ/1.1.
Fig. 2.
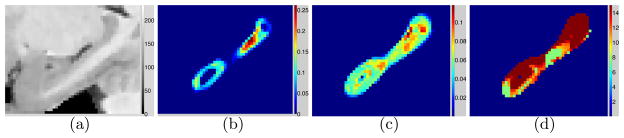
Parameter values per voxel for multiatlas hippocampus segmentation from T1 MR images. (a) MR image, sagittal slice with voxels {v}. (b) δv = inherent randomness. (c) βv = complexity of regression function. (d) Dv = intrinsic dimension.
3.2 Predicting Error Convergence Using Small Databases of Atlases
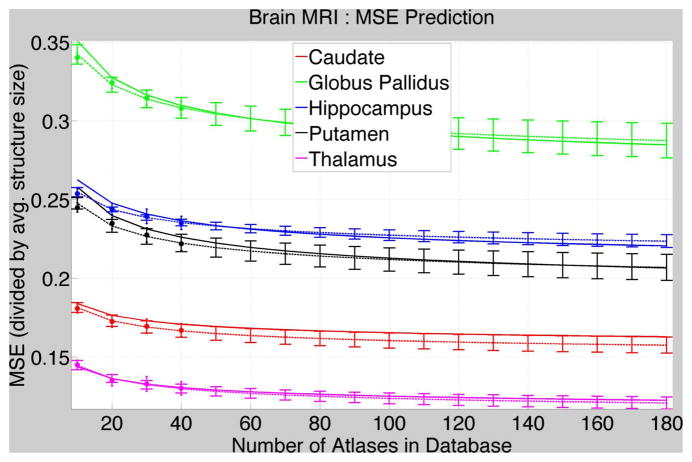
Figure 3 shows the results of experiments where we first randomly picked 40 atlases from the brain database, then computed MSE values for Mj = 10, 20, 30, 40 using the 40-atlas database, and finally fitted the parametric curves for these 4 values of Mj. We then compare these fitted curves to the fitted curves in Figure 1 that were obtained using the full-sized database. Figure 3 shows that the curves using small-sized databases predict the MSEs at large database sizes quite well.
Fig. 3. Predicting MSE for Large Database Sizes using Small Databases.
MSEs (dot = mean value; error bar = standard deviation) and fitted curves (dashed lines; error bars = standard deviation on the fitted curve) using small databases (40 atlases) compared with the fitted curves (solid lines) using large databases in Figure 1.
Table 2 shows the mean and standard deviation of the parameters estimated using random 40-sized databases for brain MR images. It shows that these parameter estimates, using 40-sized databases, are very close to the parameters estimated using the full 186-sized database in Table 1.
Table 2.
Parameters obtained using small-sized databases (each with 40 atlases) of brain MR images. The numbers indicate the mean and standard deviation (in parenthesis) of the parameters over different randomly selected 40-sized atlas databases.
| Parameters | Caudate | Globus Pallidus | Hippocampus | Putamen | Thalamus |
|---|---|---|---|---|---|
| δ: randomness | 0.15 (0.01) | 0.26 (0.01) | 0.21 (0.01) | 0.19 (0.01) | 0.11 (0.01) |
| β: complexity | 0.03 (0.01) | 0.08 (0.02) | 0.05 (0.01) | 0.06 (0.01) | 0.04 (0.01) |
| D: dimension | 10.1 (0.05) | 10.0 (0.03) | 10.0 (0.03) | 10.1 (0.06) | 10.0 (0.02) |
Figure 3 and Table 2 show that the error-convergence curves as well as the underlying parameters predicted using small-sized databases are a good approximation to those observed using much larger databases. Thus, small databases, which require fewer expert segmentations and lesser time and effort to construct, can be exploited to predict the much-larger database sizes required to achieve a specified maximum tolerable error in segmentation. Such cost-benefit analysis is crucial for designing and deploying multiatlas segmentation systems, potentially comprising a few thousand atlases.
4 Discussion and Conclusions
This paper presents a new statistical modeling and analysis framework for measuring the difficulty of multiatlas segmentation (for a specific anatomical structure, imaging modality, registration method, label-fusion strategy, etc.) in terms of the convergence behavior of segmentation error as a function of database size. It captures these properties using parameters fundamental to the underlying nonparametric regression and extends the analysis to give per-voxel estimates. It shows results using a large clinical database. Furthermore, it shows that small databases, requiring expert segmentations of only a small number of atlases, can be exploited to make valid predictions of the (much-larger) database sizes required to achieve a specified maximum tolerable error in segmentation.
Future work will deal with empirically determining how small can atlas databases be before they start losing their power of predicting MSE convergence for much larger database sizes. Some preliminary evidence indicates that the prediction needs significantly fewer atlases (perhaps just 15 or 20) than those used in this paper. Another interesting aspect unexplored in this paper is the applicability of the proposed framework to anatomical structures outside the brain where our initial experiments are quite promising.
The experiments in this paper use simple averaging for label fusion even though the proposed theoretical framework relies on generalized-kNN regression and thus allows for generalized weighting schemes. Some recent approaches to label fusion have found that generalized weighting schemes can perform better [16]. In the future, the proposed framework can be exploited to analyze approaches with sophisticated weighting schemes.
Recent works [2,10,13] in multiatlas segmentation have found improvements in performance by using local averaging approaches where the tissue probability at a voxel is determined by using only that information in the (registered) atlases which lies within the locality of that voxel. The proposed framework can be extended to model local label fusion by modeling a separate regression problem at each voxel in the image, i.e. the set of k nearest neighbors can be different at each voxel and will be determined by local similarities between the target and the templates, instead of global similarities proposed in this paper. Indeed, this is an important part of future work. Nevertheless, this paper makes significant contributions by establishing a brand new principled theoretical framework for modeling and analysis. Furthermore, this paper shows how the proposed framework coupled with a small set of atlases (requiring few expert segmentations) can be utilized to predict the much-larger database sizes (“cost”) required to achieve a specified maximum tolerable error (“benefit”) in segmentation. Such “cost-benefit” analysis is crucial for designing and deploying multiatlas segmentation systems comprising, potentially, several hundreds or thousands of atlases.
Acknowledgments
The authors gratefully acknowledge the support of this work through the National Alliance for Medical Image Computing (NAMIC) and the NIH/NCRR Center for Integrative Biomedical Computing (CIBC) grant P41-RR12553.
References
- 1.Aljabar P, Heckemann R, Hammers A, Hajnal J, Rueckert D. Multi-atlas based segmentation of brain images: Atlas selection and its effect on accuracy. NeuroImage. 2009;46(3):726–738. doi: 10.1016/j.neuroimage.2009.02.018. [DOI] [PubMed] [Google Scholar]
- 2.Artaechevarria X, Munoz-Barrutia A, Ortiz-de-Solorzano C. Combination strategies in multi-atlas image segmentation: application to brain MR data. IEEE Trans Med Imaging. 2009;28(8):1266–1277. doi: 10.1109/TMI.2009.2014372. [DOI] [PubMed] [Google Scholar]
- 3.Carter K, Raich R, Hero A. On local intrinsic dimension estimation and its applications. IEEE Trans Signal Proc. 2010;58(2):650–663. [Google Scholar]
- 4.Commonwick O, Warfield S. Estimation of inferential uncertainty in assessing expert segmentation performance from STAPLE. IEEE Trans Med Imag. 2010;29(3):771–780. doi: 10.1109/TMI.2009.2036011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Depa M, Sabuncu MR, Holmvang G, Nezafat R, Schmidt EJ, Golland P. Robust atlas-based segmentation of highly variable anatomy: Left atrium segmentation. MICCAI Workshop Stat. Atlases Comp. Models Heart; 2010. pp. 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Felsberg M, Kalkan S, Krueger N. Continuous dimensionality characterization of image structures. Image and Vision Computing. 2009;27(6):628–636. [Google Scholar]
- 7.Ha L, Kruger J, Fletcher T, Joshi S, Silva C. Fast parallel unbiased dif-feomorphic atlas construction on multi-graphics processing units. Euro Symp Parallel Graph Vis. 2009:65–72. [Google Scholar]
- 8.Hardle W. Applied Nonparametric Regression. Cambridge Univ. Press; 1990. [Google Scholar]
- 9.Hein M, Audibert JY. Intrinsic dimensionality estimation of submanifoldsRd. Int Conf Mach Learn. 2005:289–296. [Google Scholar]
- 10.Isgum I, Staring M, Rutten A, Prokop M, Viergever M, Ginneken B. Multi-atlas-based segmentation with local decision fusion - application to cardiac and aortic segmentation in CT scans. IEEE Trans Med Imag. 2009;28(7):1000–1010. doi: 10.1109/TMI.2008.2011480. [DOI] [PubMed] [Google Scholar]
- 11.Lotjonen J, Wolz R, Koikkalainen J, Thurfjell L, Waldemar G, Soininen H, Rueckert D. ADNI: Fast and robust multi-atlas segmentation of brain magnetic resonance images. NeuroImage. 2010;49(3):2352–2365. doi: 10.1016/j.neuroimage.2009.10.026. [DOI] [PubMed] [Google Scholar]
- 12.Mack YP. Local properties of k-NN regression estimates. SIAM J Alg Disc Meth. 1981;2(3):311–323. [Google Scholar]
- 13.Sabuncu M, Yeo B, van Leemput K, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE Trans Med Imaging. 2010;29(10):1714–1729. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Takezawa K. Introduction to Nonparametric Regression. Wiley; 2005. [Google Scholar]
- 15.Wang H, Suh JW, Das S, Pluta J, Altinay M, Yushkevich P. Regression-based label fusion for multi-atlas segmentation. IEEE Conf Comp Vis Pattern Recog. 2011;1:1113–1120. doi: 10.1109/CVPR.2011.5995382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang H, Suh JW, Pluta J, Altinay M, Yushkevich P. Optimal weights for multi-atlas label fusion. Int Conf Info Proc Med Imag. 2011:73–84. doi: 10.1007/978-3-642-22092-0_7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Warfield S, Zou K, Wells W. Validation of image segmentation by estimating rater bias and variance. Phil Trans Roy Soc. 2008;366(1874):2361–2375. doi: 10.1098/rsta.2008.0040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhu P, Awate SP, Gerber S, Whitaker R. Fast Shape-Based Nearest-Neighbor Search for Brain MRIs Using Hierarchical Feature Matching. In: Fichtinger G, Martel A, Peters T, editors. MICCAI 2011, Part II. LNCS. Vol. 6892. Springer; Heidelberg: 2011. pp. 484–491. [DOI] [PubMed] [Google Scholar]