Mangarevan invention of binary steps for easier calculation

Significance

The paper describes the mixed counting system in Mangarevan, which is unique in that it had three binary steps superposed onto a decimal structure. In showing how these steps affect calculation, our analysis yields important insights for theorizing on numerical cognition: counting systems serve as complex cultural tools for numerical cognition, apparently unwieldy systems may in fact be cognitively advantageous, and such advantageous systems can be—and have been—developed by nonindustrialized societies and in the absence of notational systems. These insights also help to dismiss simple notions of cultural complexity as a homogenous state and emphasize that investigating cultural diversity is not merely an optional extra, but a must.

Abstract

When Leibniz demonstrated the advantages of the binary system for computations as early as 1703, he laid the foundation for computing machines. However, is a binary system also suitable for human cognition? One of two number systems traditionally used on Mangareva, a small island in French Polynesia, had three binary steps superposed onto a decimal structure. Here, we show how this system functions, how it facilitated arithmetic, and why it is unique. The Mangarevan invention of binary steps, centuries before their formal description by Leibniz, attests to the advancements possible in numeracy even in the absence of notation and thereby highlights the role of culture for the evolution of and diversity in numerical cognition.

At the onset of the 18th century, the polymath Gottfried Wilhelm Leibniz (1646–1716) described a binary (i.e., base 2) number system and its usefulness for calculations. He explained the advantages as follows (Fig. 1): “For here, it is as if one said, for example, that 111, or 7, is the sum of four, two, and one, and that 1101, or 13, is the sum of eight, four, and one. This property enables assayers to weigh all sorts of masses with few weights and could serve in coinage to give several values with few coins” (1). Besides these practical advantages, Leibniz continues, a binary system would also spare the individual from learning by heart any addition and multiplication tables—a benefit, however, that came with downsides such as longer number representations. The greatest impediment to switching from a decimal to a binary system was that we are accustomed to counting by ten and may feel no need to learn again what we have already learned by heart (1).

Fig. 1.

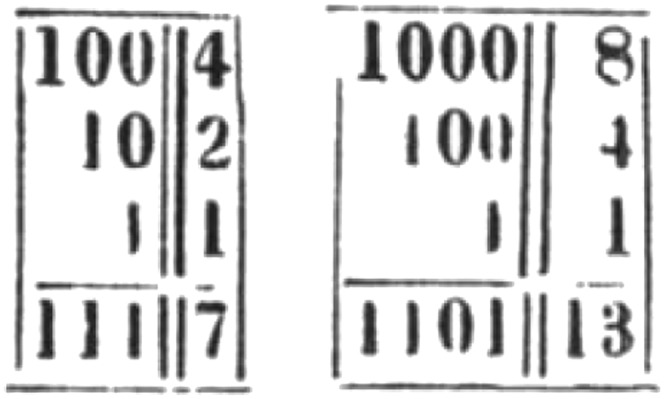
Two of Leibniz’s examples for binary notation and calculation (1).

The binary system, together with some of Leibniz’s original ideas, laid the foundation for computing machines but, besides this innovation, had virtually no effect on how humans themselves operate with numbers. This is not to say that binary systems were entirely odd to human thinking or absent from the world’s languages. Although the majority of verbal number systems have base 10, followed by 20 and 5 (2)—arguably motivated by body-based counting practices (3–6)—other bases are also observed, albeit rarely (7, 8). Among these, base 2 is particularly rare and most likely so for a practical reason. Systems of this type tend to count 1, 2, 2 + 1, 2 + 2, 2 + 2 + 1, etc. For illustration, take the case of Middle Watut, an Austronesian language spoken by about 1,350 people in Morobe Province of Papua New Guinea. Its counting sequence unfolds as follows (9):

• 1 = morots

• 2 = serok

• 3 = serok a morots [= 2 + 1]

• 4 = serok a serok [= 2 + 2]

• 5 = serok a serok a morots [= 2 + 2 + 1].

Systems like these make recursive use of base 2 and therefore qualify as base 2 systems. They do not, however, use specific numerals for the powers of the base and therefore suffer from being unable to keep track of the constituents in higher number words. Expressing a number like 77 in such a system is thus virtually out of question. However, even a full-fledged binary system with distinct symbols for the powers of the base translates 77 into a representation with seven signs (i.e., 1,001,101₂) that is considerably longer than its decimal counterpart with two signs.

Clearly, compactness of number representation suffers from small base size, thus rendering a pure binary system infeasible for many practical purposes. However, what if one combined binary and decimal bases? Would the combined benefits of the two bases offset their downsides? This question is not merely of academic interest but is warranted by the actual existence of such a system—invented centuries ago by the Polynesian inhabitants of Mangareva. Answering this question also highlights the potential for variability in numeration systems and thus emphasizes the role of culture for the evolution of numerical cognition.

Cultural Background

Mangareva is the main island of the Gambier group in French Polynesia, ∼1,650 km southeast of Tahiti and close to the Tropic of Capricorn (Fig. 2). The islands are of volcanic origin, clustered in a lagoon some 25 km across and surrounded by an extensive barrier reef, which provides a supply of seafood and partial protection against the currents (10, 11).

Fig. 2.

Mangareva and some of its trading relations.

Human settlers reached the island group in three waves. The first wave arrived between 500 and 800 of the common era (CE) from the West, presumably via the Marquesas and/or Tuamotus, and moved further to the eastward islands of Pitcairn, Henderson, and Easter Island (Rapa Nui). The second wave arrived between 1150 and 1450 CE from the Southeast Marquesas. And the third wave arrived in the 19th century in the wake of European colonialism (11–13).

In former times, fish and other seafood provided the principal sustenance and were held in high esteem compared with other poor people’s food. Octopus was even considered a gift for the king, as were turtles. The most valued vegetable food was breadfruit, supplemented by other root crops, various types of bananas, and coconuts. Provided there was sufficient rain, breadfruit was harvested four times a year, and most of it was fermented for storage in pits. Some of the larger storage pits were under the supervision of chiefs but were stocked in a communal effort and served as provision for ceremonial occasions (10, 14, 15). The population size was estimated at around 1,500 at European contact but may have amounted to several thousand and perhaps even 6,000–8,000 in earlier times, with occasional drops due to famines, wars, and ensuing emigration (10, 14).

The Mangarevan society was one of those Polynesian societies with substantial social stratification, based on seniority of descent and primogeniture. The chiefs secured a tight and dominant tenure over the typically scarce crop lands and requested tributes from their peasants, but also redistributed a considerable proportion of it during public feasts (10, 14, 16). For centuries, goods were also exchanged externally, as Mangareva kept close contact with the islands of the Pitcairn group to the East and was part of long-distance trading that included Hawai'i, the Marquesas and Tuamotus, the Austral and Cook Islands, and the island group around Tahiti (11, 13, 17) (Fig. 2). In this economic and cultural context, both tributes and trading goods were regularly due in larger quantities. Whereas the latter primarily involved material for tool fabrication and decoration, tributes largely consisted of food items, notably including breadfruit, turtles, fish, and octopus. Keeping track of these commodity cycles must have been a challenging task, especially in the absence of notation or literacy more generally. However, most Polynesian cultures had experts for oral tradition, whose task was memorization of genealogies and other verbally represented and transmitted information. In some cases, these specialists were also responsible for keeping track of the redistribution of goods during public presentations and feasts (18, 19). Information is lacking on whether this generalized to Mangareva, but the rongorongo—high-ranking experts for all tasks involving oral memory and ceremonial reciting (10)—would surely have been qualified to keep track of the provision, redistribution, and trading of goods and of the likely substantial numbers involved.

French influence on Mangareva began with proselytizing by Catholic padres in 1834 (10) and culminated in the annexation by France. Ever since, the Gambier Islands have been part of the overseas territory of French Polynesia. Regarding the counting systems, the padres played an ambivalent role: they documented them when they were still in use, at least to some extent, but, in their efforts to introduce literacy, they also contributed to their cessation. As a consequence, the more interesting specific counting systems in particular had already ceased to be used at the beginning of the last century (20).

The Mangarevan language, which belongs to the Nuclear Polynesian languages and thus to the Oceanic branch of the Austronesian language family (11, 12), was still spoken by about 1,600 people in 1987 (21). Although the ethnic population of the Gambier Islands has remained rather stable, the population of speakers had decreased to 600 by 2011. The language itself is now classified as “in trouble” because intergenerational transmission is in the process of breaking down although the child-bearing generation itself is still able to use the language (21).

Both the decrease in language proficiency more generally and the introduction of Arabic digits and French-based infrastructure set an end to traditional Mangarevan counting. Empirical studies on how exactly these systems were structured, how and when they were used, and which implications they entailed are thus no longer possible. Instead, investigations have to rely on conceptual analyses, set into context by ethnographic information and comparative data.

Mangarevan Counting in Context

If their cultural ecology does not require them to do so, human societies do not necessarily develop elaborate numeration systems, and some nonliterate societies in particular lack numeration systems altogether (22–25). Oceanic-speaking societies, however, and especially those in Polynesia and Micronesia are renowned for their ancestral interest in numbers—attested to both by cultural practices that involved large quantities of items such as tributes, competitive gardening, or feasting and by extensive numeration systems. These numeration systems were all derived from one common Proto-Oceanic system and were in place in the absence of literacy or industrialization and well before European contact.

Explicit statements on, or even detailed descriptions of, the relevance of counting are available for several of these cultures, including the Micronesian atoll of Woleai, the Polynesian outlier Rennell, and two Nuclear Polynesian groups, Tahiti and Hawai'i, which are closely related to Mangareva. These reports acknowledge, for instance, people’s “addiction to high numbers” (26) and their “emphasis on carefully counted quantity” as well as descriptions of public generosity and an ostentatious display of religious zeal (18). For Woleai, both the redistribution of more than 12,000 coconuts and its meticulous observation during a funeral have been documented (27), and Tahitians are reported to have played counting games for recreational purposes (28). In all of these instances, the context of counting is characterized in a way that leaves no room for doubt: counting was indeed important, and particularly so before Western influence (18), amounting to an interest even in abstract mathematics (29). As it was used particularly in contexts in which generosity and prestige were at stake, such as tribute giving and redistribution or competitive generosity, most counting and calculating was performed publicly (18, 27, 28, 30).

All Polynesian languages contained general counting systems, evolved from a common ancestor, which were regular and decimal, with terms for large powers of ten (8, 31, 32). Most Polynesian languages also contained, in pre-European times, distinct counting systems that were restricted to specific objects and based on diverging counting units, typically involving one or more of the factors 2, 4, 10, and 20. In other words, these objects were counted not singly, but for instance in pairs, in pairs of pairs, or even in scores. Differences across languages basically concern the number and value of power terms, the value of the specific counting units, and the objects specifically counted, but all of them were purely verbal (33, 34).

Like their Polynesian relatives, speakers of Mangarevan used a highly regular, decimal system with large power numerals (8, 31), supplemented by one or more object-specific or mixed systems (30, 33–36). The system that was used for general counting contained monolexemic numerals for the numbers 1 through 9 and for the powers of 10 up to at least 10,000,000 (maeaea). The mixed systems were confined to counting a small group of highly valued objects, namely turtles, fish, coconuts, octopuses, and breadfruit* (10, 20). In a nutshell, they contained the same monolexemic numerals for the numbers 1 through 9 as the general system, and distinct monolexemic numerals for 10, 20, 40, and 80 (Table 1). The numeral for 80 (varu) was counted with the basic numerals from 1 through 9 to generate multiples up to 720.

Table 1.

Numerals in the Mangarevan mixed system (adapted from ref. 10)

Basic numbers				Powers		Symbolized here as
n	Numeral	n	Numeral	P	Numeral
1	ta'i	6	ono	1	[tauga]
2	rua	7	'itu	10	takau	K
3	toru	8	varu	20	paua	P
4	'a	9	iva	40	tataua	T
5	rima			80	varu	V

Any composite number word N was construed by adding terms on different power levels as follows:

with n ∈ {1, …, 9} and P = power numeral (according to Table 1); subscript numbers indicate the power level, and square brackets indicate that terms are optional.

Importantly, the number word N did not necessarily indicate the number of single items, but the number of counting units (tauga) in which these items were counted. The size of tauga depended on the object counted. It was 1 for turtles, 2 for fish, 4 for coconuts and one particular type of breadfruits, and 8 for octopuses and another type of breadfruits (10, 37). For instance, a number word like that for 12 attained in counting fish referred to 12 tauga with 2 fish each (thus 24 fish) whereas, in counting coconuts, it would refer to 12 tauga with 4 coconuts each (thus 48 coconuts).

As detailed above, the objects that were counted specifically were also culturally salient, and some of them such as turtles or octopuses were even considered an appropriate gift for the king. In contrast to the general system used for the majority of mostly ordinary items, the specific systems therefore also served the purpose of emphasizing the special status of these objects. Here, however, we will focus on their cognitive purpose of facilitating mental arithmetic.

Arithmetic with the Mangarevan System

We will illustrate how one could calculate with a mixed system like that in Mangarevan for three elementary types of operation: addition (with subtraction ensuing by analogy), multiplication, and division (which ensues from multiplication by analogy). This selection is justifiable for at least two reasons. First, addition and multiplication are already inherent in number word construction. A word like “two hundred and seven” employs the multiplication principle for assessing the number of hundreds, and the addition principle for combining hundreds and single units. And second, even in a preliterate society like Mangareva, the frequent exchange of goods by way of tributes and redistribution within (10, 14, 16) and beyond island boundaries (11, 13, 17) generates a need for the aforementioned operations at least to some extent.

The prime precondition for any type of advanced arithmetic is the mastery of a counting sequence. Once this sequence is in place, abbreviation strategies lead almost automatically to certain types of basic arithmetic. For instance, adding two numbers by fact retrieval from memory abbreviates the process of taking one addend and counting upwards the size of the second addend. Likewise, multiplication abbreviates adding one factor to itself as often as the second factor indicates. As attested to by research in developmental psychology (38, 39), detecting or developing such abbreviation strategies is a matter of practice and emerging expertise, both of which were spurred on by the importance of numbers and the emphasis on carefully counted quantity in Polynesia. The heaviest constraint on mental arithmetic is exerted by the capacity of the working memory, estimated at 7 ± 2 elements. Working memory is required not only for processing itself, but also for keeping in mind the numbers to be processed and contingent intermediate results. The crucial question is therefore how computation with the mixed system affects the cognitive load involved in number representation and processing.

Addition.

For addition, three cases need to be distinguished: (i) addition in the decimal ranges for the basic numerals and for the multiples of varu (V), (ii) addition in the binary range for the multiples of 10 up to V, and (iii) addition of those numbers that are composed of both decimal and binary constituents.

• i)Adding basic numerals in the decimal ranges presupposes knowledge of the 55 addition facts given in Table 2A, and the same is true for the multipliers in the multiples of V. If you wish to add, for instance, 5 and 4, nothing about the respective number words tells you that this addition yields 9. You have to arrive at this fact by counting 4 beyond 5—or by ultimately memorizing its result.
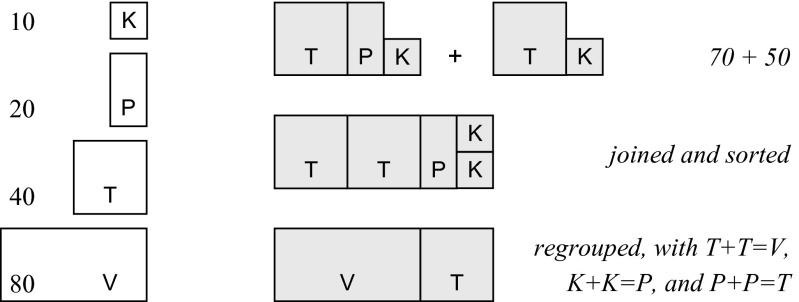
• ii)The addition facts in the binary range are given in Table 2B, but, other than in the decimal ranges, hardly any of these facts really need to be memorized. Here, the number words referring to a certain power level do not occur in different quantities (and thus lack multipliers)—they are either present or not present. In TK, for instance, T and K are present, whereas P is not. This is what Leibniz referred to as the simple summing-up of constituents (1). Adding a power term to itself yields the next power term in the sequence (e.g., K + K = P), whereas adding different power terms to each other yields a concatenation of these terms (e.g., P + K = PK). Virtually the only fact one needs to know is the sequence in which power terms follow each other: K + K = P, P + P = T, and T + T = V. Every other equation can be solved by the simple joining, sorting, and regrouping of terms, akin to adding Roman numerals (40); for an example, see Fig. 3. Addition in the binary range therefore indeed turns out to be easier than addition in a decimal context—as was envisaged by Leibniz (1).
• iii)Adding composite numbers (i.e., numbers that are composed of decimal and binary constituents) is achieved by a simple combination of decimal facts and binary transformations. For purposes of illustration, consider 273 + 219, which translates into the mixed system as toru varu paua takau toru (= 3V P K 3) + rua varu tataua takau iva (= 2V T K 9):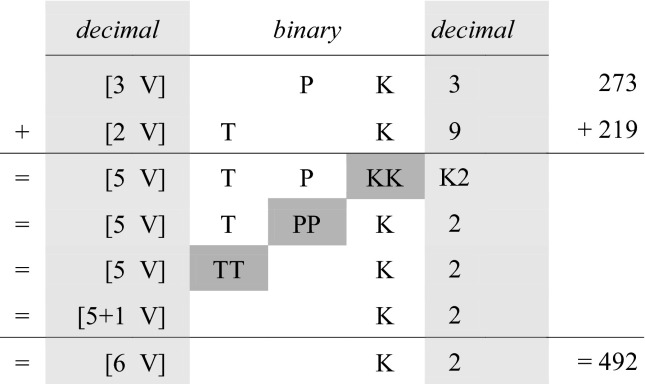In the binary range, 2 takau (K) are transformed into 1 paua (P), 2 paua into 1 tataua (T), and 2 tataua into 1 varu (V). This latter power term adds to the 3 + 2 varu already in place to produce 6 varu, according to the addition table for decimal numbers as described above. Adding, on the units level, the numbers 3 and 9 likewise yields 12 (= takau rua or K2). In other words, although the number words themselves may be mixed, the operations applied to their constituents follow the systematic patterns of either the decimal or the binary part.

Table 2.

Addition table for (A) the basic numbers from 1 through 10, and (B) the multiples of 10 up to 80

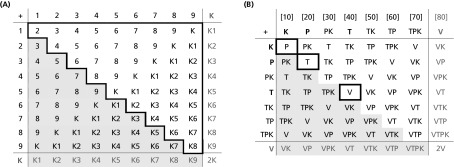Note: Basic numerals up to 9 are represented by digits, larger numerals by letters (monolexemic words are represented by monosymbolic letters, with K = takau, P = paua, T = tataua, and V = varu). Basic facts to be known for arithmetic are framed by bold lines (for half of the table only as addition is commutative; the remainder is shaded); the unmarked results are obtained by simple joining and/or transformation, as detailed in Addition.

Fig. 3.

Calculating 70 + 50 (= TPK + TK) by joining, sorting, and regrouping of terms.

This analysis reveals that, even if we include the most irregular cases, addition with the mixed system remains fairly simple and straightforward.

Multiplication.

Multiplication may be solved easily by recursive addition, performed as often as the multiplier requests. For instance, 3 · 6 can be solved as 6 + 6 + 6.

However, even more “multiplication-like” types of computations would still get by in the binary range of the mixed system with transformations rather than proper calculations, as will be illustrated for multiplying power terms by basic numbers. Multiplying a binary term (multiplicand m) by 2 simply shifts m one power level up, for example, 2 · K = P or 2 · P = T. Even for a composite term like PK, multiplication by 2 merely shifts each constituent one power level up, thus yielding TP. Multiplication by 4 shifts m two power levels up, and multiplication by 8 shifts m three power levels up, at least in principle. Here, however, a decimal range is entered, thus producing multiples of V, with 8 · K = V, 8 · P = 2V, 8 · T = 4V, etc. For the remainder of multiplications with other factors, such shifts are recursively applied and/or followed by an addition of m, according to the pattern displayed in Table 3.

Table 3.

Patterns of transformations during multiplication in the binary range

Task	Decomposition	Shifts	Example
2·m		= shift 1	2K = P
3·m	= 2·m + m	= shift 1 + m	3K = P + K
4·m		= shift 2	4K = T
5·m	= 4·m + m	= shift 2 + m	5K = T + K
6·m	= 4·m + 2·m	= shift 2 + shift 1	6K = T + P
7·m	= 4·m + 2·m + m	= shift 2 + shift 1 + m	7K = T + P + K
8·m		= shift 3	8K = V

Adopting these strategies, multiplication by 3, for instance, involves a shift of m one level up, followed by addition of the same m (e.g., 3 · K = 2K + K = PK). Analogously, multiplication by 5 involves two shifts, followed by addition of m, and so on.

Division.

Although division is analogous to multiplication, it is probably worth mentioning that the binary steps also facilitated division. To afford simple division in the absence of notation, two additional yet plausible assumptions are proposed, both of which are supported by their cultural salience (33, 34, 41).

The first assumption is that the power term varu (V = 80 basic units) was the preferred or principal counting unit of the mixed system. Eight, followed by four, is prominent as a mythological number across Polynesia and occurs frequently in contexts that are indicative of remarkable powers or superior rank (41). In Mangareva, for instance, the supreme god Tangaroa was conceived of as having eight sons, and the culture hero Maui-matavaru, who fished up an island and snared the sun, was conceived of as being the youngest of a family of eight and/or as having eight heads (10). When the mixed system was used in the redistribution of goods, prestige depended on large quantities for which varu would thus have been an appropriate—and culturally valued—size.

The second assumption is that the preferred divisor was likely an even number, if not a power of 2 (specifically 2, 4, or 8). All of these numbers, which also reemerge as a possible size of the basic counting unit tauga, are even numbers and thus suited the concern with symmetry that has been described as a recurrent theme across Polynesian societies^† (41–44).

This assumption also helps to solve a practical problem inherent in division. Whereas the outcomes of addition and multiplication always remain within the set of natural numbers (albeit perhaps exceeding the limits of the number system), division frequently produces fractions, some of which have infinite decimal places. Apart from the general question of whether algorithms for division may be discovered or developed in the absence of a notational system, their application in “real life” also necessitates a decision on how to treat the remainders of all of those equations that do not produce integers. We therefore propose that—if division was practiced in Mangareva—people likely either aimed at equations that produced no fractions at all or were willing to disregard the ensuing remainder.

Given the mixed-base structure that generates it, the principal unit varu can be divided without rest by 2, 4, 8, and 16 along a binary series and by 5, 10, 20, and 40 along a more decimal series (although divisions by 5 and 16 may have been less important). However, the size of varu is not only easy to divide by preferred numbers—these divisions also predominantly yield monolexemic terms:

• varu (V) divided by

• 2 yields 40 = tataua (T)

• 4 yields 20 = paua (P)

• 8 yields 10 = takau (K)

• 10 yields 8 = varu

• 20 yields 4 = 'a

• 40 yields 2 = rua

Even the division of an uneven amount of V (say 7V) units by a preferred divisor (say 4) is less complicated than it might sound:

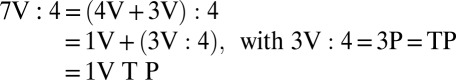In other words, although we cannot prove that division was performed in Mangareva, it would have been possible and, in fact, rather straightforward—if one accepts the two assumptions laid out above. These procedures may not have amounted to unrestricted division in an abstract sense, but they would have been division nonetheless.

Conclusion

Summarizing our results, it seems clear that superposing a decimal system with binary steps is indeed advantageous, as described by Leibniz (1) because it allows arduous calculations and retrieval of addition facts to be replaced by simple transformations in the binary range. Crucially, these advantages are not vitiated by the downside of longer number representations also anticipated by Leibniz. The decimal basis of the system guarantees that number representations remain relatively compact. The mixed system thus neutralizes the tradeoff associated with base size (45) by combining the benefits of a small base (fewer or no addition facts) with the benefits of a larger base (compact representation). Actually, both of these implications adjust to the constraints on working memory and thereby benefit mental arithmetic: the more compact representation relieves cognitive load in retaining information, and the reduction in addition facts relieves cognitive load in processing.^‡ The main cost inflicted by this mixing is an increase in irregularity, which requires additional lexemes and rules and thus affects the ease with which a system is learned and mastered.

Apparently, its users favored the benefits of the mixed system over the regularity of the general decimal system, as they developed the mixed system out of the purely decimal system in wide use across Polynesia (8, 33). Most likely, this development occurred after initial settlement of the island, as the system is distinct to Mangareva, but before the long-distance trading ceased in 1450 CE, which had connected Mangareva with the rest of Eastern Polynesia (11, 17, 32). This time frame suggests two inferences with implications for theorizing on cognitive evolution. First, although number systems do evolve as part of the linguistic system to which they belong, changes in these systems need not be constrained to random processes—their users may also take an active part in actually adapting them to shifting cognitive needs. The invention of binary steps in an otherwise decimal system, and coexistent with a perfectly regular decimal system, is just too ingenious to have occurred by chance. And second, cultural evolution need not result in homogeneous complexity. Although specific cultural–ecological conditions certainly do favor concurrent changes in correlated aspects (for examples, see refs. 46 and 47), the presence of any such condition may be neither necessary nor sufficient. The concern with large numbers and exact counting attested to in Polynesia neither correlated with advanced technology nor did it presuppose literacy, which for a long time were considered as cornerstones of the development of numerical cognition.

More recently, cross-cultural research on number systems has provided important insights into the evolution of and constraints on numerical cognition, but has focused to this end on the simpler instances (22–25, 48). Although these insights are important and fruitful, they should not obscure our view on what could be learned about numerical cognition when turning toward the more sophisticated instances. Only if we take the full range of cultural variability into account will we be able to uncover the full potential for diversity in numeration systems and to assess their role as powerful and complex cognitive–linguistic tools. These tools may vary on several dimensions: with regard to the contexts of applicability (18, 27, 49), with regard to their modality (i.e., whether implemented as number words, notational systems, or body-based expressions), or with regard to their properties, such as extent, base size, or regularity (6). Taking this variability into account will allow us to investigate how properties of these tools interact with the cognitive representation and processing of numerical information and how they may contribute to advancing numeracy.

One such instance has been analyzed in detail here: an advantageous change in number system, envisaged by Leibniz at the onset of the 18th century and yet also invented centuries earlier, literally on the other side of the world, in the absence of any number notation system and well before the requirements of advanced technology. Even more noteworthy, Mangarevans had found a way to compensate for the downsides of a purely binary system by mixing decimal and binary steps in a well-balanced manner, thus demonstrating numerical mastery on an advanced level. For this unique invention and the lessons it may teach us, Mangarevan deserves a prominent position in theorizing on numerical cognition.