Dynacortin contributes to cortical viscoelasticity and helps define the shape changes of cytokinesis

Abstract

During cytokinesis, global and equatorial pathways deform the cell cortex in a stereotypical manner, which leads to daughter cell separation. Equatorial forces are largely generated by myosin-II and the actin crosslinker, cortexillin-I. In contrast, global mechanics are determined by the cortical cytoskeleton, including the actin crosslinker, dynacortin. We used direct morphometric characterization and laser-tracking microrheology to quantify cortical mechanical properties of wild-type and cortexillin-I and dynacortin mutant Dictyostelium cells. Both cortexillin-I and dynacortin influence cytokinesis and interphase cortical viscoelasticity as predicted from genetics and biochemical data using purified dynacortin proteins. Our studies suggest that the regulation of cytokinesis ultimately requires modulation of proteins that control the cortical mechanical properties that establish the force-balance that specifies the shapes of cytokinesis. The combination of genetic, biochemical, and biophysical observations suggests that the cell's cortical mechanical properties control how the cortex is remodeled during cytokinesis.

Introduction

Cytokinesis is the mechanical process that cleaves a mother cell into two daughter cells and is essential for the propagation of cells across all phylogeny (Robinson and Spudich, 2000b). After more than 100 years of study, the fundamental mechanical bases for metazoan cytokinesis are still not understood, let alone the molecular bases for these mechanical elements (Rappaport, 1996). Two predominant models have been debated in recent decades: equatorial stimulation and polar relaxation (White and Borisy, 1983; Devore et al, 1989). The equatorial stimulation model assigns active force production to the contractile ring, which is considered a myosin-II-driven process (Robinson et al, 2002b). In contrast, the polar relaxation model assigns the polar cortex as the major source of active force production. As the volume of the mother cell is conserved during division, expansion of the polar cortex leads to cleavage furrow ingression. The role of myosin-II in the polar relaxation model is to serve as a dynamic actin crosslinker, increasing the equatorial stiffness so that the cleavage furrow ingresses.

Still, recent studies have been unable to clarify the mechanical mechanisms of cytokinesis. Myosin-II is required for cytokinesis in suspension culture, while adherent mitotic ameboid myosin-II mutant cells divide nearly normally (DeLozanne and Spudich, 1987; Knecht and Loomis, 1987). Pharmacological inhibition of the polar cortex with actin filament destabilizers inhibits furrow ingression, whereas introduction of the inhibitors in the furrow region accelerated ingression of the cleavage furrow (O'Connell et al, 2001). By atomic force microscopy, which measures the bending modulus perpendicular to the cell's surface, the mammalian cell equator was more stiff than the basal global stiffness of the cell, a property that is most likely ubiquitous among metazoan-like cytokineses (Matzke et al, 2001). These results suggest that the global and equatorial cortices have distinct and important roles in cytokinesis.

Force-balance is a principle fundamental to all mechanical shape changes. We have proposed a force-balance hypothesis in which the amount of contractile force generated by the contractile ring is specified by the mechanical resistance provided by the global cortex. A significant component of our hypothesis is that different mechanical elements are generated by specific proteins and that genetic interactions between these proteins reveal how they modulate different mechanical elements (Robinson and Spudich, 2000a; Robinson, 2001; Robinson et al, 2002b). In the force-balance hypothesis, at least three idealized mechanical elements are involved in cell shape changes. These elements include an active equatorial constricting force, cortical stretch modulus, and cytoplasmic viscosity. The active constricting forces for cytokinesis are proposed to be produced largely by equatorially localized myosin-II (Robinson and Spudich, 2000b). The cortical stretch modulus is the energy cost for deforming the cell. The stretch modulus is generated by cortical actin filaments and crosslinkers, and has been shown to be a strong predictor of how much myosin-II is recruited to the cleavage furrow cortex (Robinson et al, 2002a). As actin crosslinkers are dynamic, the cell's cortex is neither purely viscous nor elastic but has both viscous and elastic characteristics (Sato et al, 1987; Wachsstock et al, 1993, 1994; Xu et al, 1998). Cytoplasmic viscosity is the energy cost for bulk flow and the ratio of the stretch modulus to the cytoplasmic viscosity is predicted to set the rate of furrow ingression (Zhang and Robinson, in preparation).

Genetic studies using Dictyostelium discoideum have identified proteins that are predicted to influence cortical viscoelasticity during cytokinesis (Robinson and Spudich, 2000a; Weber et al, 2000). Efficient cytokinesis requires different actin filament crosslinking proteins with different cellular distributions (Robinson and Spudich, 2000a). Dynacortin is an actin filament bundling protein that was originally identified in a genetic selection for suppressors of mutants devoid of cortexillin-I, an actin crosslinking protein (Faix et al, 1996, 2001; Robinson and Spudich, 2000a). The suppression experiment was performed with a cDNA expression library and only the carboxyl-half (C181) of dynacortin suppressed cortexillin-I (Robinson and Spudich, 2000a). In contrast, overexpression of the full-length dynacortin not only failed to rescue cortexillin-I but it also induced a dominant cytokinesis defect (Robinson and Spudich, 2000a). Dynacortin is distributed around the cell cortex, while cortexillin-I is concentrated in the equatorial cortex (Weber et al, 1999; Robinson and Spudich, 2000a). The cellular distributions and the genetic interactions of cortexillin-I and dynacortin suggest that they cooperate with each other to modulate the cortical mechanics that drive the complex shape changes of cytokinesis.

In this paper, we combine biochemistry, genetics, direct observation of cytokinesis, and cellular biophysics to dissect the function of dynacortin and the basis for its genetic interactions with cortexillin-I. A significant new technical development is our ability to quantify the mechanical impact that dynacortin and cortexillin-I have on cell cortices, using a new noninvasive technology, laser-tracking microrheology (LTM) (Gittes et al, 1997; Mason et al, 1997; McGrath et al, 2000; Yamada et al, 2000). Several observations emerge from this study. First, we report the first loss-of-function phenotype for dynacortin, assigning a role for dynacortin, like cortexillin-I, in modulating the cortical viscoelasticity of interphase cells and specifying the shapes of cytokinesis. Second, dynacortin has two independent actin crosslinking domains, amino-half (N173) and C181, that crosslink with different relative activities. Third, our data suggest that the activities of proteins that are predicted to have different kinetics of actin crosslinking may be distinguished in vivo using LTM. Finally and most significantly, this study provides essential groundwork for determining how global and equatorial actin crosslinking specifies the shapes and ultimately the dynamics of cytokinesis.

Results

Dynacortin and cortexillin-I have quantitative effects on cell growth

To initiate this study, we characterized the growth effects of a dynacortin hairpin construct (dynhp) that silenced dynacortin expression. The expression of dynhp led to a complete loss of detectable dynacortin and resulted in mild changes in the rate of increase of cell number as compared to wild type and cortexillin-I controls (Figure 1C; Table 1). We examined the cell size and relative growth rates of cells expressing each of the dynacortin domains for direct comparison to dynhp (Figure 1B and C; Table I). By microscopy, full-length dynacortin induced a ‘big-cell' phenotype in wild type (Figure 1B) and cortexillin-I (data not shown), as observed previously (Robinson and Spudich, 2000a). Interestingly, N173 also induced a similar phenotype. C181 cells were uniform in size and rescued the growth rate as shown previously (Figure 1B, Table I; Robinson and Spudich, 2000a).

Figure 1.

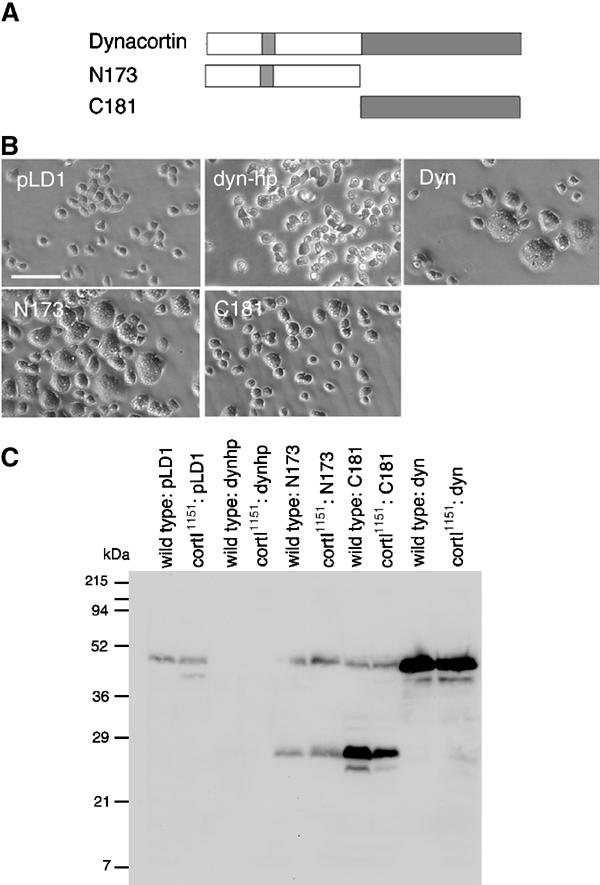
(A) The cartoon represents the dynacortin proteins studied. (B) Micrographs of wild-type (wt:pLD1) cells carrying the control plasmid pLD1A15SN or an expression plasmid for dynacortin hairpin (dynhp), full-length dynacortin (Dyn), N173, or C181; scale bar, 40 μm. (C) Western immunoblot using antidynacortin polyclonal antibodies of cells expressing various dynacortin constructs. pLD1 is the expression vector used to express each protein in Dictyostelium and control strains were transformed with the empty vector.

Table 1.

Quantification of cellular growth rates and cellular concentrations of dynacortin and its domains

Strain	Relative growth ratea (n)	% Total protein (n)	[monomer], μM	[dimer]b, μM
Wild type: pLD1A15SN	[100%] (12)	0.03% (4)	2	1
cortI1151: pLD1A15SN	54% (12)	0.03% (4)	2	1
Wild type: dynhp	110% (6)	0.0% (8)	—	—
cortI1151: dynhp	40% (6)	0.0% (8)	—	—
Wild type: N173	96% (8)	0.4% (2)	50	NA
cortI1151: N173	21% (6)	0.4% (4)	50	NA
Wild type: C181	88% (14)	0.5% (4)	60	30
cortI1151: C181	80% (10)	0.5% (2)	60	30
Wild type: dynacortin	61% (8)	0.3% (3)	20	10
cortI1151: dynacortin	35% (8)	0.2% (3)	10	5
aRelative growth rates were measured as the increase in cell number in suspension culture. All strains were normalized to wild type: pLD1A15SN controls, which is bracketed to indicate that fact.
bDynacortin and C181 form dimers while N173 exists as monomers (Supplementary Figure 1; Supplementary Table 1).

To compare directly the in vivo morphological, growth, and mechanical effects (below) with the affinities and activities measured in vitro, we quantified the expression levels of each dynacortin domain in wild-type and cortexillin-I mutant strains (see Materials and methods). The cellular concentrations are presented (Table I). Although some of the protein concentrations appear unusually high, in fact the cellular concentrations of each domain are consistent with the biochemical activities of each protein (below; compare Table I with Table II).

Table 2.

Summary of actin-binding parameters for dynacortin, N173, and C181

Protein	KD1app, μM (n)	KD2app, μM (n)	(KD1app)2KD2app, μM3	Half-maximal concentrationsa
				Fluorescence assay	Falling ball viscometry
Dynacortin	8.7±1.3 (6)	1.3±0.2 (17)	98	0.5 μM	0.5–1 μM
N173	9.4±1.3 (10)	6.1±0.9 (21)	540	60 μM	50–60 μM
C181	19±2.9 (7)	2.0±0.4 (20)	720	8 μM	15 μM
KD1app increased with increasing actin concentration. This is likely due to actin polymers getting buried in the actin bundle so that it was more difficult for dynacortins to saturate each available site. The listed KD1app data are based on 5-μM actin-binding isotherms. Data from first binding step fit a model of a single binding isotherm, and the same saturation stoichiometry was observed at every actin concentration. For the 5-μM actin data, the χ2 values obtained by comparing the data to a simulated square hyperbola using the measured KD1app value ranged from 0.05 to 0.1 (P>0.20). Thus, the model is not rejected and KD1 appears to be only [actin]-dependent, not [crosslinker]-dependent. KD2app is based on all data as this parameter did not appear to be [actin]-dependent over greater than an order of magnitude of actin concentrations. Both KD values are only apparent values as dynacortin proteins that are bound and forming crosslinks versus those that are only bound cannot be cleanly separated by cosedimentation analysis.
aConcentrations are for dimeric dynacortin and C181 and monomeric N173.

Dynacortin, N173, and C181 crosslink actin but with different activities

To elucidate dynacortin's molecular mechanisms, we analyzed dynacortin, C181, and N173 for their hydrodynamic properties and interactions with actin filaments (Table II, Supplementary Results and Supplementary Figures 1–3). Hydrodynamically, dynacortin is a rod-shaped dimer and the core of dimerization resides in the C181 domain (Supplementary Figure 1, Supplementary Table 1). Both N173 and C181 bind and crosslink actin in vitro with similar apparent thermodynamics, but with different overall activities as determined by falling ball viscometry and quantitative fluorescence microscopy (Table II; Supplementary Figures 2, 3). Using actin cosedimentation, falling ball viscometry, and the fluorescence microscopy assay, we determined an activity order for actin crosslinking as: Dynacortin>C181>N173 (Table II). The half-maximal concentrations for bundle formation determined from the fluorescence assay and falling ball viscometry are in good agreement with the actual amounts of each protein expressed in cells (Compare Tables I and II). As N173 and C181 had similar thermodynamics but C181 appeared to be a more effective crosslinker than N173, we hypothesize that N173 may have faster on and off rates to achieve the same actin crosslinking equilibrium.

Dynacortin and cortexillin-I have complementary distributions during cytokinesis; C181 and N173 are distributed between the cytoplasm and cortex

We examined the subcellular localization of dynacortin, N173, and C181 in interphase and dividing cells. Each protein was detected in two ways: GFP-fusions (GFP-dynacortin, GFP-N173 or C181-GFP) were imaged in live interphase cells (Figure 2A), and untagged proteins were imaged by immunocytochemistry in fixed dividing cells (Figure 2B). Both types of detection gave similar results for the localization of each protein. Only GFP-dynacortin and overexpressed untagged dynacortin showed clear enrichment in the cortex (Figure 2A and B). Cells expressing dynacortin-hairpin (dynhp), which had >99% reduction in the dynacortin level, had only a low level of background fluorescence when examined by immunocytochemistry (Figure 2B). Endogenous dynacortin is distributed between the cytoplasm and cortex in dividing cells (Figure 2B). Overexpressed full-length dynacortin showed a clear cortical enrichment in dividing cells (Figure 2B). N173 showed some cortical localization by both methods (Figure 2A and B), while C181 appeared to be distributed evenly between the cortex and cytoplasm (Figure 2A and B). To compare the localization of dynacortin to cortexillin-I, we examined the distribution of a GFP-tagged cortexillin-I expressed in a cortexillin-I mutant cell line (cortI¹¹⁵¹:GFP-cort; Figure 2C). Cortexillin-I localized to the contractile ring in agreement with previously published observations (Weber et al, 1999).

Figure 2.

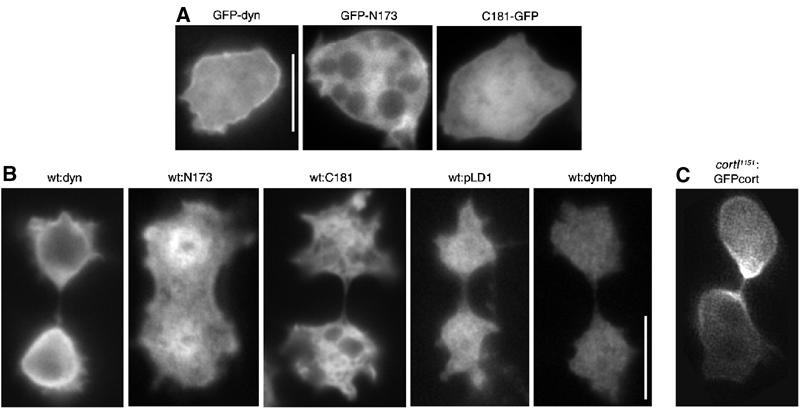
Dynacortin, N173, and C181 are globally distributed during cytokinesis. (A) GFP-dynacortin, GFP-N173, and C181-GFP were examined in live wild-type interphase cells; scale bar, 10 μm. (B) Total dynacortin was imaged by immunocytochemistry of dividing wild-type cells carrying episomal expression plasmids using antidynacortin polyclonal antibodies. Endogenous dynacortin (wt:pLD1) and wild-type cells expressing dynacortin-hairpin (wt:dynhp), which reduced dynacortin expression by >99%, are also presented. As the N173 and C181 domains are overexpressed, the pattern that is revealed is largely due to the transgene product. (C) A cortexillin-I mutant cell complemented with a GFP-cortexillin-I construct (cortI¹¹⁵¹:GFPcort) is shown to indicate the distribution of cortexillin-I during cytokinesis. Scale bar (10 μm) in B applies to B and C.

Dynacortin and cortexillin-I control the morphology of cytokinesis

To ascertain dynacortin's and cortexillin-I's role in cytokinesis, we examined the morphology of dividing cells (Figure 3). We monitored the velocity of furrow ingression, whether the cleavage furrow ingressed evenly from both sides and whether the daughter cells were equal in size (Table III). To monitor the kinetics of furrow ingression, we measured the time-dependent change of the furrow diameter and the length of the furrow, which ultimately formed a bridge before being severed (Figure 3A). Wild-type cells always formed a discrete bridge relatively early in the process, and the bridge length always started smaller than the furrow diameter (Figure 3B). As the furrow continued to constrict, at some point the cylindrical bridge length and diameter were equal to each other. The distance when the furrow length and diameter were equal is defined as the crossover distance (D_x). Subsequently, the bridge became longer than the diameter as the furrow diameter continued to decrease before being severed.

Figure 3.

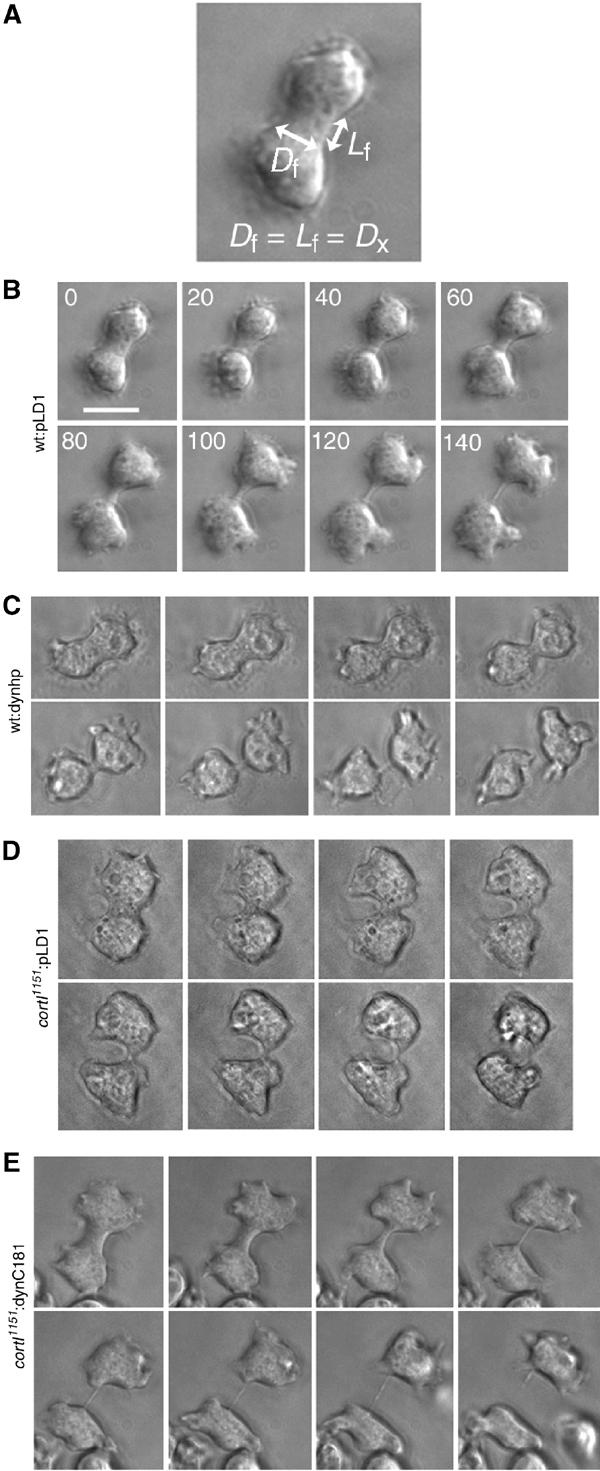
Analysis of the morphology of cytokinesis of wt:pLD1, wt:dynhp, cortI¹¹⁵¹:pLD1 and cortI¹¹⁵¹:C181 cells. (A) Diagram depicts the furrow diameter (D_f) and the furrow length (L_f), which were measured to determine the crossover distance, D_x. D_x is defined as the distance where D_f equals L_f. (B) Wt:pLD1 cells form a distinct bridge relatively early during the process. (C) Wt:dynhp cells form a distinct bridge at a later stage and appear more rounded in general. (D) This cortI¹¹⁵¹:pLD1 cell formed a bridge at a later stage and the furrow ingression was faster on one side than the other. (E) The morphology of the cortexillin-I mutant cytokinesis was rescued by dynacortin C181. The furrow ingressed symmetrically and a distinct bridge was formed at an earlier stage similar to wild type; scale bar, 10 μm.

Table 3.

Average velocity of furrow ingression and crossover distance for each strain

Strain	Velocitya (μm/s) (n)	Cross-over length, Dxb (μm) (n)	Symmetric daughtersc/symmetric furrowsd (n)
Wild type: pLD1	0.029±0.0032 (21)	2.7±0.16 (21)	100%/100% (24)
Wild type: dynhp	0.033±0.0023 (14)	1.5±0.20 (14)	88%/100% (17)
cortI1151: pLD1	0.032±0.0030 (16)	2.2±0.19 (16)	80% (30)/50% (22)
cortI1151: cortI	0.027±0.0027 (6)	2.5±0.068 (6)	100%/100% (6)
cortI1151: C181	0.037±0.0026 (19)	3.0±0.14 (19)	100%/95% (19)
aThe velocity is the average velocity of furrow ingression.
bCrossover length is an objective morpho-metric parameter in which the length of cleavage furrow bridge is equal to the diameter of the cleavage furrow. The crossover length serves to distinguish quantitatively morphologies between different strains. Values are mean±s.e.m. Wild type:pLD1, cortI1151: C181 and cortI1151:cortI are all statistically indistinguishable. Wild type: dynhp (P<0.00005) and cortI1151: pLD1 (P<0.05) are significantly less than the wild-type control. cortI1151: C181 is significantly greater than cortI1151: pLD1 (0.0005<P<0.005).
cThe cells were assessed qualitatively as to whether the daughter cells were symmetric in size.
d The furrows were assessed for being symmetrically positioned and whether they ingressed similarly from both sides.

Deletion of cortexillin-I or silencing of dynacortin altered the morphology of cytokinesis (Figure 3C and D; Table III). Silencing of dynacortin caused the cells to appear more rounded during division and led to a large decrease in the crossover distance (Figure 3C; Table III). Deletion of cortexillin-I reduced the efficiency of cytokinesis, leading to a higher rate of failures, unequal cleavage events, and asymmetric ingression of the furrow (Table III). We focused on successful divisions so that the morphology (crossover distance and symmetry of furrow ingression) and velocities of furrow ingression could be fully assessed. Therefore, our data likely under-represent the unequal cleavage rate and cytokinesis failure rate as compared to other studies of cortexillin-I mutants (Weber et al, 2000). The crossover distance and symmetry of the cleavage furrows of cortexillin-I mutants were rescued by cortexillin-I (Table III) and dynacortin C181 (Figure 3E; Table III). Thus, even though dynacortin C181 and cortexillin-I have different cellular distributions during cytokinesis (Figure 2), both proteins quantitatively rescue the morphology of dividing cortexillin-I mutant cells.

Laser-tracking microrheology allows quantitative analysis of cortical mechanics

To quantify the effects of dynacortin and cortexillin-I on cortical mechanics, we used laser-tracking microrheology (LTM) to measure cortical viscoelasticity of wild-type and mutant cell lines (Figure 4; Mason et al, 1997; McGrath et al, 2000; Yamada et al, 2000). With LTM, the viscoelasticity of materials may be measured across a frequency spectrum by monitoring the motions of a spherical bead immersed in the material. Typically, viscoelastic moduli are measured when all dimensions of the material are nearly infinite relative to the bead. As cell cortices are sheet-like and often much thinner than the particles, we chose to measure the frequency-dependent viscoelasticity, ∣μ^*∣, which is a phenomenological spring constant with viscous damping (see Methods for equations and rationale).

Figure 4.

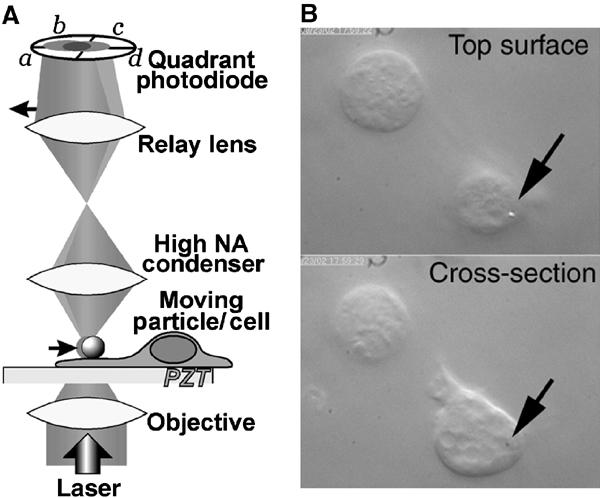
Laser-tracking microrheology (LTM) system for measuring cortical mechanics. (A) The LTM system utilizes a low-power laser that is focused by the objective on a 0.7 μm polystyrene bead resting on the surface of the cell. As thermal energy drives the motion of the bead, the laser beam is deflected. The deflections are relayed via a condenser and relay lens to a quadrant photodiode detector, which monitors bead position. (B) Upper panel: To measure the cortical mechanical properties, a negatively charged polystyrene bead (arrow) is allowed to settle onto the surface of the cell, attaching nonspecifically. By focusing on the top surface of the cell, the bead is visible. Lower panel: By focusing on a lower cross-section, pseudopods can be seen. An arrow marks the XY-position of the bead.

To determine cortical viscoelasticity, the thermal motions of a bead on a cell were monitored (at 6 kHz) for eleven 1-s intervals and then the viscoelasticity was calculated as the average of these 11 sequential measurements. For windows of time greater than 1 s, the bead's motions were often obscured by the cell's motion. Therefore, we restricted our observations to timescales shorter than 1 s. For physiological relevance, we focused on the longer timescales from 500-ms timescale (2 rad/s) to 5-ms timescale (200 rad/s).

To verify that LTM of beads placed on the cell's extracellular surface would report on the underlying cytoskeleton, we compared wild-type cells to wild-type cells treated with latrunculin B, a potent F-actin depolymerizing agent (Figure 5A and B). In all, 85% of the viscoelasticity of wild-type cells was lost upon treatment with latrunculin B. As latrunculin B treatment results in depolymerization of filamentous actin, the 15% of viscoelasticity that remains presumably is due to the lipid bilayer and underlying cytosol.

Figure 5.

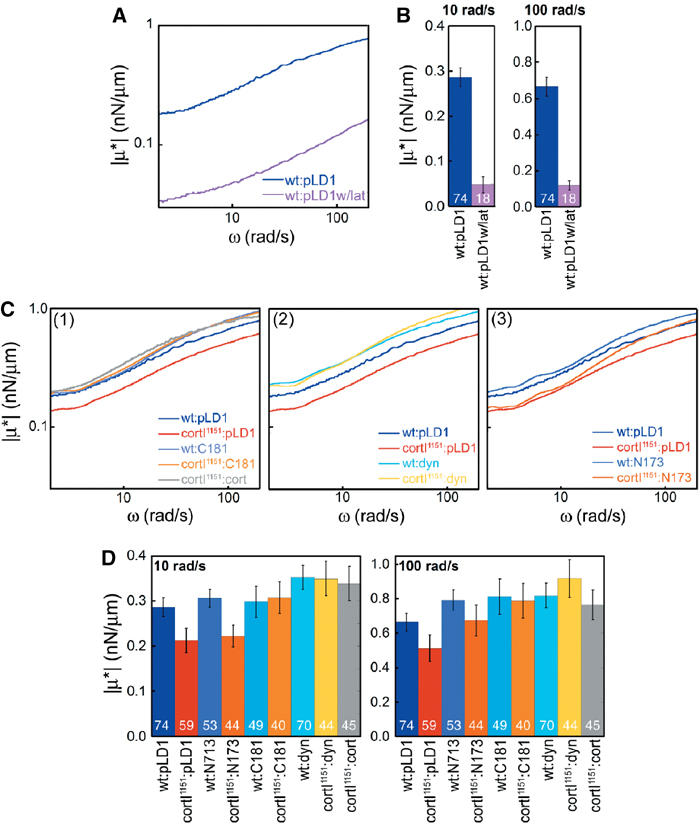
Dynacortin and its domains alter cortical viscoelasticity. (A) Frequency spectra of wild-type cells (wt:pLD1) and wt:pLD1 treated with latrunculin B show that actin filaments are necessary for 85% of cortical viscoelasticity. (B) Histograms of wt:pLD1 versus wt:pLD1 treated with latrunculin B at 10 and 100 rad/s for statistical comparison. n values are shown on bars. P-values from Student's t-test are <0.0001 at both frequencies. (C) Frequency spectra of viscoelasticity of wild-type and cortexillin-I mutant cells expressing dynacortin full-length, N173, C181, and cortexillin-I proteins. All spectra are the average spectra for each strain. The numbers of cells measured for each genetic strain are shown on the histrogram in part D. All measurements were made on ‘wild-type'-sized cells to prevent possible complications due to cell size differences. The wild-type control spectrum is shown in each panel for direct comparison. (D) Histograms of means (±s.e.m.) for the viscoelasticity at 10 and 100 rad/s. These values correspond to the frequency spectra in (A). n values for each strain are listed on the bars in the histograms. For significance, the P-values from pairwise Student's t-test are presented in Supplemental Table 2.

LTM also permits measurement of the phase angle, a property that reflects the solid-like or liquid-like nature of a material. As the material becomes more solid-like, the phase angle tends towards 0 and as the material becomes more liquid-like, the phase angle tends towards 90°. Pure actin networks and Cos7 lamellae have a characteristic phase angle of 22° (at 10 rad/s; Yamada et al, 2000). We extracted the phase angle data for each strain to determine how liquid- or solid-like the respective strains are. The average phase angles for all Dictyostelium strains ranged between 15 and 22°, which is similar to the phase angle of pure actin. In fact, none of the strains showed a difference greater than 2° across the full frequency range. In contrast, latrunculin B generally increased the phase angle (to around 30°) particularly at higher frequencies, indicating that the cell cortex was partially liquefied by the depolymerization of the actin filaments. Therefore, even though the beads are on the extracellular surface of the plasma membrane, the bead reports on a mechanical environment that is largely dependent on the cortical actin cytoskeleton and that has material properties (phase angle) similar to pure actin.

Loss of dynacortin or cortexillin-I reduces cortical viscoelasticity

By LTM analysis, removal of dynacortin and/or cortexillin-I had quantitative effects on cortical viscoelasticity (Figures 5 and 6; Supplementary Table 2). Deletion of cortexillin-I reduced the cortical viscoelasticity by approximately 30% across the full frequency spectrum as compared to the wild-type strain (Figure 5C, panel 1; 5D). The distribution of viscoelastic values of dynacortin silenced cells was much more heterogeneous with many more high-end outliers than wild-type parental cells were; therefore, we present histograms of viscoelastic measurements at two frequencies for wild-type and cortexillin-I mutant cells with and without dynacortin (Figure 6). Silencing of dynacortin in wild-type cells resulted in a 50% reduction in the median cortical viscoelasticity (Figure 6, panels 1, 2 versus 3, 4). Interestingly, the cortexillin-I background (Figure 6, panels 5, 6 versus 7, 8) seemed to be more resistant to the loss of dynacortin than the wild-type cells were. For example, silencing of dynacortin in wild-type cells reduced viscoelasticity from 0.28 to 0.14 nN/μm (at 10 rad/s), while in the cortexillin-I background, the numbers remained similar (0.17 versus 0.20 nN/μm at 10 rad/s). This resistance might reflect the antagonistic role proposed for these two proteins in promoting cytokinesis (Robinson and Spudich, 2000a). Alternatively, the cortexillin-I mutant cells may have adapted to the absence of cortexillin-I and the same safeguards protect the cell from the loss of dynacortin. Nevertheless, dynacortin and cortexillin-I modulate cortical mechanics and both may help keep the cortex relatively uniform in its mechanical properties.

Figure 6.

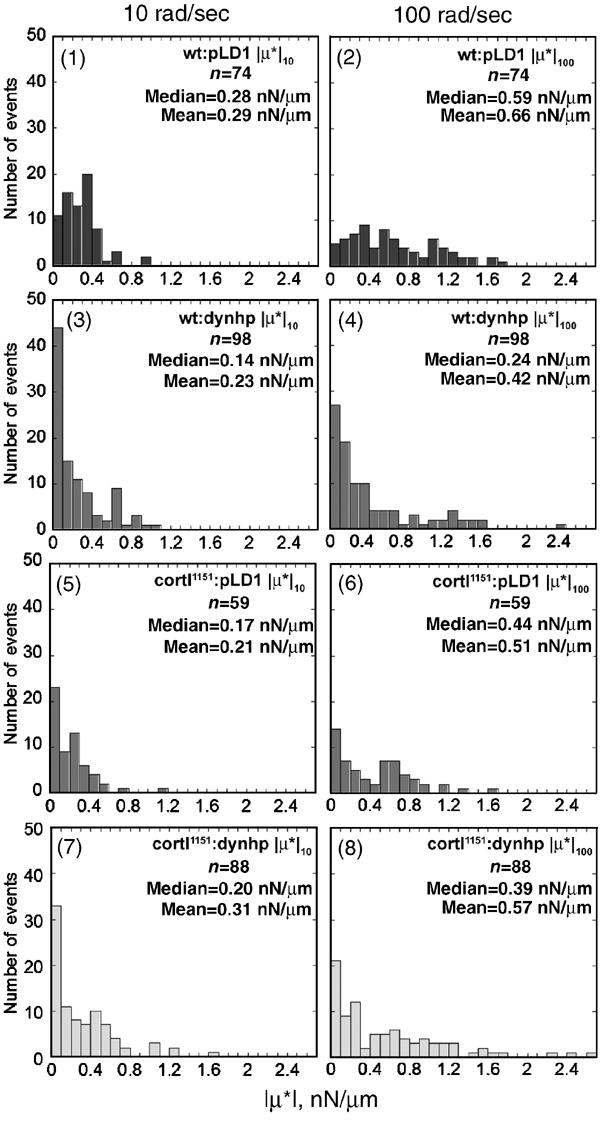
Dynacortin is required for normal cortical viscoelasticity. Silencing of dynacortin reduced the median cortical viscoelasticity and led to greater skewing of the frequency distribution, which is indicative of greater heterogeneity of the viscoelasticity of the cortex. As the mean is very sensitive to skewing and heterogeneity while the median is more resistant, the medians for each strain are emphasized. The means are presented for comparison. The frequency distribution of viscoelastic measurements from wild-type cells (wt:pLD1) at 10 rad/s was monomodal but was more broadly distributed at 100 rad/s. The wt:pLD1 medians were very similar to the means indicating monodispersity and therefore, greater homogeneity of the wild-type cortex. Wt:dynhp cells devoid of dynacortin showed a skewed distribution with increased heterogeneity at both frequencies. Cortexillin-I mutants (cortI¹¹⁵¹:pLD1) were intermediate between wt:pLD1 and wt:dynhp cells at both frequencies. The cortI¹¹⁵¹:dynhp (dynacortin/cortexillin-I double mutant) cells were similar to cortI¹¹⁵¹:pLD1 cells. As wt:dynhp, cortI¹¹⁵¹:pLD1, and cortI¹¹⁵¹:dynhp distributions were skewed, we compared the distributions to wt:pLD1 using a one-tailed, nonparametric Mann–Whitney–Wilcoxson U-test, which makes no assumptions about the shape of the distributions. ∣μ^*∣₁₀ and ∣μ^*∣₁₀₀ values for wt:dynhp (P<0.001) and cortI¹¹⁵¹:pLD1 (P<0.005) were significantly less than wt:pLD1. The distributions of ∣μ^*∣₁₀ and ∣μ^*∣₁₀₀ values for cortI¹¹⁵¹:dynhp were also smaller than the distributions of values for wt:pLD1 (∣μ^*∣₁₀; P=0.11 and ∣μ^*∣₁₀₀; P=0.01).

Overexpressing dynacortin, C181 and N173 reveal additional important cortical mechanical properties

We used LTM to examine the effects of C181 and cortexillin-I on the cortexillin-I mutant's cortical viscoelasticity (Figure 5C, panel 1; 5D). We found that C181 rescued cortical viscoelasticity to wild-type levels across all frequencies examined, while cortexillin-I actually restored the viscoelasticity to slightly above wild-type levels. The rescue of cortexillin-I mutant's cortical mechanics by cortexillin-I and C181 correlates well with their rescue of cortexillin-I mutant cells' cytokinesis morphology and ability to grow in suspension culture.

We also analyzed the cortical mechanics of dynacortin and N173 overexpressing cells (Figure 5C, panels 2 and 3; 5D). Previously, we showed that dynacortin overexpressers are variable in size, probably due to a defect in the efficiency of cytokinesis rather than a complete loss of cytokinesis. To avoid possible mechanical changes due to size differences rather than differences in dynacortin-mediated actin crosslinking, we restricted our LTM measurements to the sub-population of cells that were similar in size to wild-type cells. Overexpression of dynacortin increased cortical viscoelasticity to levels higher than wild type across the full range of frequencies examined, regardless of the genetic background, wild type or cortexillin-I (Figure 5C, panel 2; 5D). By contrast, N173 rescued the cortical viscoelasticity of the cortexillin-I mutant cells only at high frequencies (above 40 rad/s); at lower frequencies, cortexillin-I cells expressing N173 showed only a small increase in cortical viscoelasticity (Figure 5C, panel 3; 5D). N173's behavior of increasing cortical viscoelasticity at higher frequencies is consistent with a crosslinking protein that has faster kinetics. Indeed, our biochemical analysis of N173 has suggested that it crosslinks actin with faster kinetics than either full-length dynacortin or C181 do. Thus, our current data suggest that LTM can discriminate between different crosslinking kinetic properties in vivo.

It is notable that N173, C181, and dynacortin have larger relative effects in a cortexillin-I background than they do in a wild-type background. In fact, the cortexillin-I background is necessary for observing the frequency-dependent behavior of N173. However, the actual ∣μ^*∣ values achieved by each respective overexpressed dynacortin protein are similar in both genetic backgrounds. As the expression levels in each background are similar, the biochemical components that generate cellular mechanical properties may be saturable (Figure 5, Table I).

Discussion

In this paper, we present the first characterization of the loss-of-function phenotype of dynacortin, including its role in cytokinesis, characterize dynacortin's actin crosslinking mechanisms, and demonstrate that dynacortin and cortexillin-I control the viscoelastic properties of the cell cortex. We examine several aspects of the morphology of cytokinesis of mutant strains with altered dynacortin and/or cortexillin-I function and introduce a novel metric, D_x. This analysis reveals that dynacortin and cortexillin-I specify the dimensions and morphology of the cleavage furrow. Furthermore, from our biochemical analyses of dynacortin and actin interactions in vitro, we demonstrate that the specific molecular interactions quantitatively specify both morphology and mechanics.

LTM, a powerful technique for measuring cortical mechanics

We used LTM to measure the cortical viscoelasticity of wild-type and cortexillin-I mutant cells expressing dynacortin, N173, C181, or cortexillin-I. Quantitatively, our measurements by LTM agree with measurements from other techniques. Our LTM measurement of wild-type cortical viscoelasticity was 0.3 nN/μm (at 10 rad/s), which is in reasonable agreement with the cortical stretch modulus (1.5 nN/μm) measured by microcapillary aspiration (Gerald et al, 1998; Dai et al, 1999). Considering that the scale of the deformations from each technique differs by an order of magnitude, the agreement between values from the two techniques is remarkable. In principle, the cortical viscoelasticity measured by LTM and the cortical stretch modulus measured by microcapillary aspiration are similar parameters. However, LTM has the important advantage of generating time-dependent information that reflects the kinetics of actin crosslinking.

Across greater than two decades of mechanical frequency, silencing of dynacortin caused a severe reduction (50%) in cortical viscoelasticity, while deletion of cortexillin-I caused a significant reduction (30%) in cortical viscoelasticity. For cortexillin-I, the reduction we measured with LTM matches the reduction previously reported using nontime-resolved methods (Simson et al, 1998). Genetically rescuing cortexillin-I with either cortexillin-I or C181 restored cortical viscoelasticity to wild-type levels. In contrast, overexpressing dynacortin elevated the viscoelasticity of both wild-type and cortexillin-I mutant cells across all frequencies, possibly explaining the dominant cytokinesis defect induced by this construct. From our in vitro studies, we predicted that N173 would have differential effects, depending on the mechanical frequencies, because of its predicted faster binding kinetics. Indeed, N173 increased the viscoelasticity of wild-type and cortexillin-I mutant cells only slightly at a low mechanical frequency but restored the cortical viscoelasticity of cortexillin-I mutant cells to wild-type levels at higher frequencies. Thus, cortical mechanics are controlled biochemically, can be dissected genetically, and can be measured using LTM.

Crossover distance as a critical cytokinesis metric

The shapes of cytokinesis are very stereotypical and include a final bridge stage in which the bridge, connecting the two daughter cells, is cylindrical in shape. This regularity allows the bridge to be analyzed using means typical of highly quantitative studies of fluid breakup of viscoelastic fluids (Entov and Hinch, 1997; Zhang and Lister, 1999). The regularity is nicely reflected in the crossover distance, D_x, which appears to be a fingerprint for each genetic strain (Table III). Previously, we hypothesized that the amount of force required of the contractile ring may be related to the stretch modulus of the cortex; indeed, this relationship accurately predicts the myosin-II amounts sent to the contractile ring (Robinson et al, 2002a). In this working hypothesis (Figure 7), the size of the vectors reflects this balance. In our working model, we propose that D_x might reflect the magnitude of the restoring vector that counteracts the pulling force that the contractile ring exerts on the cell's cortex. We speculate that D_x is a balancing point where the forces of the contractile ring balance the largely elastic properties of the rest of the cortex. Higher values of viscoelasticity mean that the cortex deforms less in response to a force. Hence, the contractile ring does not constrict as much by the time D_x is reached. In contrast, if cells are softer, then the contractile ring advances further yielding a smaller D_x. After the balancing point defined by D_x, cells appear to enter a new phase where furrow thinning follows a different kinetic behavior (Zhang and Robinson, in preparation).

Figure 7.

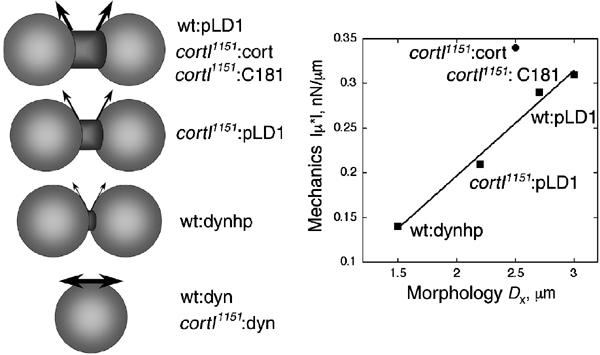
A hypothesis for how cortical mechanics might specify the shapes of cytokinesis. The morphology is schematized, and the arrows represent the restoring vectors that are hypothesized to counteract the contractile force. To summarize the data presented in this paper, we present a graph, comparing D_x measured by direct observation of cytokinesis and ∣μ^*∣ from the interphase mechanical measurements from LTM. The line is a linear fit (correlation coefficient of 0.99) to all points except the cortI¹¹⁵¹:cort (see Discussion).

To summarize the data from this paper into a framework, we present a plot of the measured D_x and ∣μ^*∣ values, which were correlated (Figure 7). Each of the ‘wild-type-like' strains has a larger D_x and ∣μ^*∣ than the loss-of-function cortexillin-I or dynacortin hairpin mutants. Cells overexpressing dynacortin have greater viscoelasticity. The viscoelasticity increase might be responsible for the dominant cytokinesis defect observed in these cells by making it more difficult for the contractile ring to contract. Due to the low frequency of division events in the dynacortin overexpressing strains, D_x has not yet been quantified. Interestingly, the cortI¹¹⁵¹:cort cells' ∣μ^*∣ versus D_x point falls somewhat off of the line, possibly as cortexillin-I enriches in the cleavage furrow cortex but is not excluded from the global cortex. Further, expression of cortexillin-I in a cortexillin-I mutant (cortI¹¹⁵¹:cort) elevates cortical viscoelasticity to above wild-type levels probably because expression from an episomal plasmid is not as well controlled as the endogenous locus. Thus, if cortexillin-I specifically increases the viscoelasticity of the cleavage furrow cortex to above wild-type levels, the furrow cortex may stretch less as it constricts, resulting in a slightly smaller D_x.

The interpretation of the correlation in Figure 7 currently remains a hypothesis, as viscoelastic measurements used interphase, rather than mitotic, cells. Currently, technical issues prevent us from measuring viscoelasticity of mitotic cells using LTM. Specifically, to get the beads to adhere to the cell surface, the cells must be plated in starvation buffer. This condition significantly reduces the frequency of cytokinesis events. In other work, we have quantified the dynamics of cleavage furrow ingression of wild-type, myosin-II, RacE, dynacortin, and cortexillin-I mutant strains (Zhang and Robinson, in preparation). By comparing the kinetics of furrow thinning to fluid mechanical models, we determined the function of each protein during cytokinesis. Further, from the cytokinesis dynamics analysis, we calculated cortical stretch modulus values that closely match the viscoelasticity values measured by LTM. Ultimately, the mitotic values for viscoelasticity may prove to be related to interphase values as the global cortex of dividing mammalian cells became uniformly four-fold more stiff than interphase levels (measured with atomic force microscopy, AFM) (Matzke et al, 2001). In the AFM study, the equatorial region continued to rise in stiffness beyond this four-fold increase, perhaps due to the activity of proteins providing a similar function as cortexillin-I does in Dictyostelium. If Dictyostelium cells are similar to mammalian cells, the correlation in Figure 7 may simply shift up (perhaps four-fold as in mammalian cells) to account for the different cell cycle stage.

C181 compensation for cortexillin-I

Previously, we showed that dynacortin C181 rescued the growth rate and gross cytokinesis defect of cortexillin-I (Robinson and Spudich, 2000a). Here, we demonstrate that C181 rescues the cleavage furrow morphology, including shape and dimensions, and the interphase cortical viscoelasticity of cortexillin-I mutant cells. With the mechanical and biochemical data in hand, three mechanisms might explain how C181 compensates for cortexillin-I. As cortexillin-I and myosin-II are not exclusively concentrated in the contractile ring, both proteins may contribute to global mechanical properties as well as equatorial contractility (reviewed in Robinson et al, 2002b). Dynacortin C181 might rescue cortexillin-I's role in global viscoelasticity, indicating a level of functional redundancy. Second, C181 may have an indirect effect on the contractile ring by stiffening the global cortex, thereby refocusing the equatorial contractility of cortexillin-I mutant cells. As C181 is reduced in the furrow region, the cleavage furrow cortex and cytoplasm may have lower viscoelasticity so that this region is more deformable, allowing the cortexillin-I mutant contractile ring to constrict through a softer region of the cell. A similar phenomenon has been observed in mammalian cells when disruption of the equatorial cytoskeleton by pharmacological inhibition accelerated the rate of cleavage furrow ingression (O'Connell et al, 2001). In addition, a third mechanism is suggested from the combination of our LTM, biochemical, and dynamics data (this paper; Zhang and Robinson, in preparation). In this hypothesis, global actin crosslinking mediated by dynacortin (and C181) and equatorial actin crosslinking mediated by cortexillin-I have distinct roles in governing the fluid dynamics of furrow ingression.

Cortical mechanics and dynamics of furrow ingression

Our mechanical measurements may also help explain the kinetics of shape changes. Quantitatively, the stretch modulus and cytoplasmic viscosity should combine to regulate the speed of cleavage furrow shape changes for a given force. As an initial model, the ratio of cortical stretch modulus to viscosity should determine the velocity of shape changes (such that v=S_c/3μ where v is the velocity, S_c is the stretch modulus, and μ is the viscosity) (Entov and Hinch, 1997). Using 0.3 nN/μm (wild type at 10 rad/s; this paper) or 1.5 nN/μm for S_c (Gerald et al, 1998; Dai et al, 1999) and the largest measured cytoplasmic viscosity (0.35 nN s/μm²; Feneberg et al, 2001), velocities in the 1–2 μm/s range are predicted. For furrow ingression, these velocities are 50-fold faster than observed for wild-type cells (Table III). However, bridge retraction (after the intercellular bridge is severed) velocities are on the 1–2 μm/s range and agree with these predictions (Zhang and Robinson, in preparation). Thus, the dynamics of bridge retraction can be described in terms of fluid mechanical properties. In contrast, we have identified Dictyostelium mutants where cleavage furrow ingression achieves velocities predicted from the pure fluid mechanical considerations (Zhang and Robinson, in preparation).

As it is the energy cost for deforming the cell, the cortical stretch modulus has two opposing roles that are separated temporally during cytokinesis. As the mother cell and two daughter cells are nearly spherical, these shapes may be thought of as equilibrium states. As the mother cell begins to elongate and form the furrow, it reaches a transition state that is an energy barrier between two equilibrium states. Therefore, the larger the stretch modulus, the larger the energy barrier. In contrast, once the cell overcomes the energy barrier, a larger stretch modulus will help drive the daughter cells to complete division to minimize their surface area. Increasing the cortical stretch modulus by overexpressing dynacortin should make the initial deformation more difficult, perhaps generating a cytokinesis defect. Softer cells such as the dynacortin mutants would still progress through cytokinesis. However, dynacortin mutants do have altered cytokinesis morphology. Cortexillin-I mutants complete cytokinesis relatively efficiently but also suffer from morphological defects. As the stretch modulus plays a dual role in cell shape changes, it is possible that there may be a window of acceptable viscoelasticity. The cell requires large enough viscoelasticity to maintain normal kinetic and shape control, but not so much that the contractile apparatus cannot overcome the energy barrier.

Historical perspective

Researchers have been interested in cytokinesis since the 19th century (reviewed in Rappaport, 1996). Certainly, it has been long appreciated that cytokinesis is a mechanical process that involves force generation and mechanical changes of the equatorial and global cortices. Biophysical studies of large echinoderm eggs (cells that are orders-of-magnitude larger than Dictyostelium) revealed that the cleavage furrow cortex became more stiff than the global cortex and that the cleavage furrow cortex generated nN-scale forces (for example, Hiramoto, 1963; Wolpert, 1966; Rappaport, 1967; Hiramoto, 1990). These previous studies are consistent with our observations in Dictyostelium that global and equatorial actin crosslinking specify the dimensions (D_x) of the cleavage furrow. Thus, this paper provides essential groundwork for developing a quantitative molecular and mechanical understanding of cytokinesis. Ultimately, by combining highly quantitative approaches with biochemistry and interaction genetics in a single cell type, we will dissect the complexity and robustness of cytokinesis, a process that serves as an elegant model cell shape change.

Materials and methods

Constructs and strains

Dynacortin (dynacortin aa 1–354), N173 (dynacortin aa 1–172) and C181 (dynacortin aa 173–354) were expressed using pLD1A15SN (Figure 1). We used the full-length dynacortin (pLD1A15SN:dynacortin) and C181 (pLD1A15SN:dynacortin 2B19) constructs, which were described previously (Robinson and Spudich, 2000a). pLD1A15SN:N173 was constructed using PCR with the addition of SalI and NotI sites at the ends flanking the initiator ATG and a stop codon, respectively. CortI 2A19 was described previously (Robinson and Spudich, 2000a). GFP-N173, C181-GFP, and GFP-cortexillin-I were constructed using our GFP-tagging cassette construct and the cortexillin-I cDNA was derived from cortI 2A19 cDNA, as previously described (Robinson and Spudich, 2000a).

pLD1A15SN:dynhp was engineered by first subcloning into pLD1A15SN a PCR product of the full-length dynacortin cDNA in which a Sal I site had been introduced at the 3′ end and a Not I site had been introduced at the 5′ end. Then, a PCR product that included the C181 region with 5′ Not I and 3′ Mlu I sites was subcloned. The dynacortin hairpin construct reduced the expression of dynacortin to undetectable levels in wild-type and cortI¹¹⁵¹ strains (Figure 1C). Wild-type (Ax3:orf7-3; HS1000) and cortI¹¹⁵¹ (HS1151) cells have been described previously (Robinson and Spudich, 2000a).

For quantification of growth rates, each strain was grown in suspension culture, and cell number was measured using a hemacytometer as described (Robinson and Spudich, 2000a). For quantification of the protein amounts in each strain, a dilution series of lysates and purified protein were prepared and analyzed by Western immunoblot analysis using antidynacortin antibodies as described previously (Robinson et al, 2002c). Each protein was compared to known amounts of the matching purified recombinant protein. Signal from the immunoblot was generated using Amersham's ECL reagent and collected and quantified using a BioRad Versadoc imaging system.

Immunocytochemistry

To assess the localization of endogenous dynacortin, overexpressed dynacortin, N173, and C181, mid-log phase cells were fixed and stained as described previously (Robinson and Spudich, 2000a), except that the fixation buffer used was 4% paraformaldehyde, 150 mM NaCl, 0.1% Triton X-100. Indirect detection was achieved using fluorescein isothiocyanate-conjugated donkey anti-rabbit secondary antibodies (Pierce). Cells were imaged using a Zeiss Axiovert 135 microscope with a 40X (NA1.3) oil immersion objective and a 1.6X optivar. Images were collected using IPLab software package (Scanalytics) and processed using Adobe Photoshop (Adobe Systems Inc.).

Live cell imaging

To image the GFP fusion proteins, log phase cells were plated in imaging chambers. After attachment, the media were replaced with MES starvation buffer (50 mM MES pH 6.8, 2 mM MgCl₂ and 0.2 mM CaCl₂). Cells were imaged using a 40X (NA1.3) oil objective and a 1.6X optivar on a Zeiss Axiovert microscope. Images were collected using IPLab software (Scanalytics).

To image cells undergoing cytokinesis, log phase cells were plated in imaging chambers in enriched HL-5 media. Imaging was performed with the same objective and optivar setting as for GFP-fusion proteins. Rather than the suggested phase ring, the phase 2 ring was used to give higher contrast while avoiding the ‘phase halo' that comes from the unmatched refractive index of the media. The phase halo subsequently obscures some of the fine details of the furrow and bridge as it proceeds. Images were collected every 2 s. Green, UV, and IR filters were added to eliminate phototoxicity and heating from the Köhler illumination.

Laser-tracking microrheology

To determine the viscoelasticity of cell cortices, we used laser-tracking microrheology (LTM). The LTM system has been described in detail elsewhere (Mason et al, 1997; McGrath et al, 2000; Yamada et al, 2000). Briefly, the mechanical properties of a material are inferred from the Brownian motions of embedded probe particles. Motions of probe particles are detected using a low-powered laser (0.13 mW, λ=670 nm) focused on the particle and a quadrant photodiode detector to detect off-axis motions of the forward-scattered light. To develop LTM for the study of cortical mechanics of D. discoideum cells, we monitored the motion of beads attached to the extracellular surface of the cell cortex. D. discoideum mutant strains were removed from the incubator during log-phase growth when 40–80% confluent, washed twice with 1 ml of 1 × PB (20 mM Na₂HPO₄, 20 mM NaH₂PO₄, pH 6.9), and resuspended at a final concentration of 1 × 10⁶ cells/ml. About 20 μl of washed cells were transferred to double-stick tape-glass slide flow cell, and 0.70-μm-diameter carboxylated polystyrene beads (Bangs Laboratories, Inc.) were then added. For latrunculin B-treated cells, 7.5-μM latrunculin B was added to the cells along with the polystyrene beads.

As particles are not fully embedded in a large cytoskeletal network, the original equations for extracting moduli from particle motions are no longer appropriate. Although models exist for extracting moduli of motions of spheres half-embedded in sheet-like materials (Bausch et al, 1998), key parameters cannot be measured in our system. Rather than making ad hoc geometric assumptions, we chose to measure the viscoelasticity, μ^*(ω), as a combination of a phenomenological spring (Re(μ^*)=μ′) and dashpot (Im(μ^*)=μ″), with both elements having frequency-dependent values. Hence, μ^*(ω)=[2 k_BT/〈ΔR²(τ)〉]_ω=1/τ, which is equivalent to μ^*(ω)=6πaG^*(ω) where a is the particle radius, thus removing any geometry-dependent assumptions. The phase angle, δ(δ=arctan(μ″/μ′)), relates the liquid- to solid-like properties of the material. In all LTM statistics, each tracking event represents one bead on a unique cell (i.e. average of 11 sequential 1 s acquisitions).

Supplementary Material

Supplementary Material