Abstract
Levofloxacin is a broad-spectrum fluoroquinolone used in the treatment of both acute and chronic bacterial prostatitis. Currently, the treatment of bacterial prostatitis is still difficult, especially due to the poor distribution of many antimicrobials into the prostate, thus preventing the drug to reach effective interstitial concentrations at the infection site. Newer fluoroquinolones show a greater penetration into the prostate. In the present study, we compared the unbound levofloxacin prostate concentrations measured by microdialysis to those in plasma after a 7-mg/kg intravenous bolus dose to Wistar rats. Plasma and dialysate samples were analyzed using a validated high-pressure liquid chromatography-fluorescence method. Both noncompartmental analysis (NCA) and population-based compartmental modeling (NONMEM 6) were performed. Unbound prostate tissue concentrations represented 78% of unbound plasma levels over a period of 12 h by comparing the extent of exposure (unbound AUC0–∞) of 6.4 and 4.8 h·μg/ml in plasma and tissue, respectively. A three-compartment model with simultaneous passive diffusion and saturable distribution kinetics from the prostate to the central compartment gave the best results in terms of curve fitting, precision of parameter estimates, and model stability. The following parameter values were estimated by the population model: V1 (0.38 liter; where V1 represents the volume of the central compartment), CL (0.22 liter/h), k12 (2.27 h−1), k21 (1.44 h−1), k13 (0.69 h−1), Vmax (7.19 μg/h), kM (0.35 μg/ml), V3/fuprostate (0.05 liter; where fuprostate represents the fraction unbound in the prostate), and k31 (3.67 h−1). The interindividual variability values for V1, CL, Vmax, and kM were 21, 37, 42, and 76%, respectively. Our results suggest that levofloxacin is likely to be substrate for efflux transporters in the prostate.
INTRODUCTION
Chronic bacterial prostatitis is frequently associated with recurrent urinary tract infections (UTIs) in young and middle-aged men and is caused mainly by Enterobacteriaceae family pathogens, especially Escherichia coli (1). Treatment of bacterial prostatitis is still difficult due to two main reasons. First, the biological status of the pathogens, which often become resistant by either producing biofilm or developing plasmid-mediated resistance to antimicrobials (2). Second, the physiological barrier for many antimicrobial agents, since only a few commonly used antimicrobials are able to penetrate sufficiently well the plasma-prostate barrier and reach the prostatic fluid (2). It is well established that poor drug distribution in the prostate is one of the factors contributing to antimicrobial resistance in bacterial prostatitis and may lead to pharmacotherapy failure or prolonged daily antimicrobial use, the latter increasing the chance of quinolone-related adverse effects. In addition, there is limited knowledge on the mechanisms involved in the transport of antimicrobial agents into the prostatic tissue and on the clinical significance of the results obtained (3).
Because of the broad antibacterial spectrum of fluoroquinolones, including Gram-positive bacteria for newer quinolones, and their favorable pharmacokinetics (PK) properties, such as high tissue distribution and urinary excretion as unchanged drug, these antimicrobials are currently the first choice drugs against bacterial prostatitis (4). Studies based on prostatic fluid concentrations have shown that newer generation quinolones such as gatifloxacin and moxifloxacin are able to penetrate into the prostate tissue to a more significant extent compared to older quinolones and to other antimicrobial agents such as β-lactams and cephalosporins (5, 6). It has been reported that levofloxacin, a broad-spectrum fluoroquinolone that was approved in the United States for the treatment of bacterial prostatitis in 2003, has a good distribution into prostatic fluid and ejaculate (7–9). Current guidelines on the treatment of chronic bacterial prostatitis suggest a 500-mg levofloxacin oral daily dose for 4 weeks, but the period may be extended to up to 6 weeks depending on the clinical outcome of each patient. These high daily antimicrobial doses for a long period of time may be associated with several quinolone-related adverse events and also with the development of drug-resistant strains (10).
A commonly used method of investigating antimicrobial prostate penetration described in the literature is biopsy sampling, in which the total tissue concentrations are compared to those in plasma (7). However, this method poses several disadvantages, especially because it is not able to distinguish between the unbound drug and the fraction bound to proteins. Furthermore, drug concentrations determined in tissue homogenates represent the total sum of blood, interstitial, and intracellular concentrations. Studies have shown that biopsy data may clearly overestimate target site concentrations for drugs that accumulate in the intracellular space, such as quinolones (11). In addition, the levels of drugs that tend to equilibrate exclusively with the interstitial fluid, such as β-lactams, are likely to be underestimated (11, 12).
Microdialysis is a semi-invasive sampling technique that selectively measures the unbound, pharmacologically active, drug concentrations in virtually any body tissue, creating a more realistic insight on antimicrobial penetration in the interstitial fluid, which is the defined target site for most bacterial infections (13). The free local drug concentrations in specific tissues of the body can differ from those found in the systemic circulation and possibly be more representative of the drug distribution at the active site (14). Our research group has been using microdialysis to investigate antibacterials and antifungals tissue penetration in healthy and infected rodents, including norfloxacin (15) and piperacillin (16) in skeletal muscle, gatifloxacin in muscle and lung (17), and voriconazole (18) and fluconazole (19) in renal cortex.
The aim of the present study was to investigate the local distribution of levofloxacin in the prostates of rats using microdialysis and to compare these results to the extent of exposure in the systemic circulation after intravenous (i.v.) administration. Afterward, a comprehensive population PK model was developed to describe the kinetic disposition of the drug in central and peripheral compartments. These findings lead to a better understanding of this quinolone prostate penetration and should be helpful to guide the development and to optimize antimicrobial therapies of new and already-in-use quinolones.
MATERIALS AND METHODS
Chemicals.
Levofloxacin hydrochloride, ciprofloxacin (internal standard [IS]), and urethane (ethyl carbamate, ≥99%) were purchased from Sigma-Aldrich (St. Louis, MO). High-pressure liquid chromatography (HPLC)-grade acetonitrile and methanol were purchased from Tedia (Fairfield, NJ). Formic acid was purchased from Fluka Chemie GmbH (Buchs, Switzerland), and triethylamine and phosphoric acid were purchased from Merck (Darmstadt, Germany). Heparin (5,000 IU/ml) was purchased from Cristália Produtos Químicos Farmacêuticos, Ltd.a (São Paulo, Brazil). Water was purified with a Millipore Milli-Q system (Bedford, MA). All of the other chemicals used were of pharmaceutical or analytical grade.
Microdialysis system.
The microdialysis system consisted of a PHD 2000 syringe pump (Harvard Apparatus, Holliston, MA). Gas-tight syringes (500 μl; Hamilton Company, Reno, NV) were used to provide the perfusion solution. CMA 20 concentric microdialysis probes (4-mm membrane length, 20-kDa cutoff; CMA Microdialysis, Kista, Sweden) were used. The perfusion fluid was composed of Ringer's solution (pH 7.2; 147 mM NaCl, 1.3 mM CaCl2, 4 mM KCl) prepared as described previously (20).
In vitro probe calibration.
Initially, in vitro microdialysis experiments were carried out in order to investigate the influence of the perfusate flow rate and drug concentration on the relative recovery (RR) determined by dialysis (recovery) and retrodialysis (delivery) methods. Different flow rates (1.5, 2.0, and 2.5 μl/min) were tested, whereas the levofloxacin concentration in Ringer's solution was fixed at 1,000 ng/ml. In the second experiment, the flow rate was fixed at 1.5 μl/min, whereas the levofloxacin concentration varied (150, 750, and 3,000 ng/ml). A flow rate (1.5 μl/min) was used for the final probes calibration using levofloxacin at 1,000 ng/ml in Ringer's solution.
In vitro calibration by dialysis consisted of perfusing blank Ringer's solution through probes immersed in levofloxacin solution in Ringer, while levofloxacin in Ringer was perfused through the probes, and the periprobe solution was blank Ringer for the retrodialysis experiment (n = 3/experiment). The peribrobe solution was maintained at 37 ± 1°C and under gentle magnetic stirring. The perfusate was allowed to equilibrate for 1 h prior to the collection of three 20-min samples, which were stored at −80°C in polypropylene tubes. The dialysis RR (RRD) and retrodialysis recovery (RRRD) were calculated according to equations 1a and b:
| (1a) |
| (1b) |
where Cdial is the dialysate concentration and Cperf is the perfusate concentration.
In vivo probe calibration.
The no-net-flux (NNF) method used for probe calibration in vivo involves both recovery and delivery experiments in the same trial (21). The recovery determined in vivo was used to correct the actual interstitial concentrations from the subjects. A group of rats (n = 3) was used and the procedures described in “Animal experiments” below were followed. A butterfly-type i.v. catheter coupled to a syringe pump was inserted in the lateral tail vein and levofloxacin was administered as a constant i.v. infusion of 1.13 mg/h (k0) with a flow rate of 4.7 μl/min. A loading dose (LD) of 2.1 mg/kg was administered previous to the start of the infusion to reach the steady state instantaneously. The LD and maintenance doses were calculated from the plasma data (pilot study) fitted to a two-compartment model using specific equations for constant i.v. infusion (22). Using this protocol, an average Cpss (average plasma concentration at steady state) of 1.56 μg/ml was kept during the experiment. Five different concentrations of levofloxacin in Ringer's solution (0, 250, 500, 1,500, and 2,000 ng/ml) were perfused through the tissue at a flow rate of 1.5 μl/min, and three dialysate samples were collected every 20 min for each perfusate concentration. After each change in the perfusate concentration, the probes were allowed to equilibrate for 1 h with the new solution before the dialysate samples were collected. If the drug diffuses equally from both sides of the semipermeable membrane, a linear relationship between the drug concentrations in the perfusate (Cperf) and the net loss or gain of the substance in the dialysate in relation to the perfusate concentration (Cdial – Cperf) can be established. The point of NNF corresponds to the concentration of the periprobe fluid and the slope to the relative recovery according to equation 2 (23):
| (2) |
where RRNNF is the relative recovery determined by the NNF calibration method and Ctfree is the free tissue concentration.
Levofloxacin plasma protein binding.
Levofloxacin plasma protein binding was determined in vitro by microdialysis using the dialysis method. Pooled blank rat plasma from five different rats was spiked with levofloxacin at three different concentrations (200, 1,000, and 4,500 ng/ml). The test tubes containing spiked plasma were placed in a water bath and maintained at 37 ± 1°C. The microdialysis probes (n = 3) were placed into the tubes and perfused with Ringer's solution at a flow rate of 1.5 μl/min. A 1-h equilibration period was allowed before three 20-min dialysate samples were collected for each probe. Levofloxacin free concentrations in the dialysate were corrected using the probe recovery determined in vitro. The fraction bound to plasma proteins (fbplasma) was calculated by the ratio between free and total levofloxacin plasma concentrations.
Animal experiments.
Study protocols were approved by UFRGS Ethics in Animal Use Committee (number 18330). Male Wistar rats weighing between 0.25 and 0.35 kg were obtained from FEPPS (Fundação Estadual de Produção e Pesquisa em Saúde, Porto Alegre, Brazil). Blood and prostate microdialysis sampling were performed simultaneously in the same group of rats (n = 7). Rats were anesthetized with urethane (1.25 g/kg, administered intraperitoneally) and immobilized in a supine position, and an FEP flexible cannula (1.19 mm [outer diameter] by 0.63 mm [inner diameter]) was inserted into the carotid artery for blood sampling. A heparinized saline solution (100 IU/ml) was maintained in the arterial cannula to prevent clotting. The group received an i.v. bolus dose of 7 mg/kg through the femoral vein of the left hind leg. This dose was derived from the daily dose of levofloxacin of 500 mg for humans, considering a 70-kg male adult. Blood samples (∼200 μl) were collected into heparinized Eppendorf tubes at predetermined time points (0.083, 0.25, 0.5, 0.75, 1, 1.5, 2, 4, 6, 8, and 12 h) after administration. Plasma was immediately separated by centrifugation and stored at −80°C until analysis.
For prostate microdialysis, the tissue was exposed with minimal dissection after an abdominal incision, and a microdialysis probe was inserted as described previously (24). Probes were flushed with Ringer's solution at a flow rate of 1.5 μl/min and allowed to equilibrate inside the tissue for 1 h before drug administration. After drug dosing, microdialysate samples (30 μl) were collected at 20-min intervals for up to 12 h and stored at −80°C until analysis. For data analysis purposes, the drug concentration measured in the sample was attributed to the midpoint of each sampling interval.
Levofloxacin quantification in plasma and dialysate samples.
Plasma and dialysate samples were analyzed using an in-house HPLC-fluorescence method. Chromatographic separation was carried out on an Atlantis T3 column (150 by 4.6 mm [inner diameter], 5-μm particle size; Waters, Milford, CT) coupled to a C18 guard cartridge (4.0 by 3.0 mm [inner diameter], 4-μm particle size; Shimadzu, Kyoto, Japan). The temperature of the column oven was maintained at 35°C during the analysis. The isocratic mobile phase was a mixture of 0.4% aqueous triethylamine (pH adjusted to 3.0 with phosphoric acid)-methanol-acetonitrile (75:22.5:2.5 [vol/vol/vol]), which was pumped at a flow rate of 1.0 ml/min. Detection was achieved with a Shimadzu RF-10AXL fluorescence detector (λexcitation = 292 nm, λemission = 494 nm). Data acquisition and integration were performed using Shimadzu CLASS-VP v6.12 software.
For the analysis of levofloxacin in rat plasma, 10 μl of IS solution (ciprofloxacin, 10 μg/ml) was added to 100-μl plasma samples, and the tubes were briefly vortex mixed. Then, 200 μl of ice-cold acetonitrile containing 0.5% formic acid was added, followed by 5 min of vortex mixing and 10 min of centrifugation at 4°C and 13,500 × g. Next, 40 μl was injected into the HPLC system. For the analysis of microdialysis samples, an aliquot of 25 μl of dialysate was added to 50 μl of 0.5% aqueous formic acid and briefly vortex mixed. The samples were directly analyzed by HPLC.
The HPLC-fluorescence method was validated according to current guidelines (25, 26). Pooled blank rat plasma from five different animals, including hemolytic plasma, was used to test the method specificity. The analytical curves were fitted by least-squares linear regression using the software Scientist v2.01 (MicroMath, Salt Lake City, UT). The lower limits of quantification of levofloxacin were 5 ng/ml for dialysate and 10 ng/ml for plasma samples. The method showed linearity in the range of 10 to 5,000 ng ml−1 in plasma and 5 to 1,750 ng ml−1 in dialysate with determination coefficients (r2) higher than 0.996 and 0.999, respectively. Levofloxacin plasma extraction recovery was high (>90%). The intra-assay accuracy was >85%, and the intra-assay imprecision was ≤15%. The long-term stability study showed that levofloxacin was stable in plasma and dialysate for at least 30 days at −80°C.
PK data analysis. (i) NCA.
Noncompartmental analysis (NCA) of the individual profiles was performed using WinNonlin v5.3 software (Pharsight Corp., St. Louis, MO). The pharmacokinetic parameters included the elimination rate constant (λz), the terminal half-life (t1/2), the maximum observed concentration (Cmax), the extrapolated concentration at t = 0 (C0), the area under the concentration-time curve (AUC) calculated by the linear trapezoidal rule, the total clearance (CL), the mean residence time (MRT), and the apparent volume of distribution during the terminal phase (Vz). The tissue distribution factor (fT) was calculated by the ratio of the area under the curve of the tissue concentration-time profile (AUCprostate,free) and the area under the curve of the total plasma concentration-time profile corrected for the fraction unbound to plasma proteins (fuplasma·AUCplasma,total). The PK parameters for the tissue data were compared to those for the plasma by one-way analysis of variance (ANOVA; α = 0.05) using Statistica v7 (StatSoft, Tulsa, OK).
(ii) Population PK model.
A population PK model that can simultaneously describe total drug concentrations in plasma and free drug concentrations in the prostate was developed in the nonlinear mixed effect modeling software NONMEM 6 (ICON Development Solutions, Dublin, Ireland). Different structural models varying in presence or absence of saturable distribution processes were tested. Saturable processes were modeled by Michaelis-Menten (MM) kinetics. Each model consisted of a central compartment (total plasma concentrations), a peripheral compartment (representing tissues other than the prostate), and a prostate compartment (free prostate concentrations). All models were parameterized as a system of differential equations (ADVAN 6 TRANS 1 subroutine). Individual PK parameters were assumed to follow a lognormal distribution with mean (θ; typical value) and variance (ω2; interindividual variability). It should be remarked that the volume of the prostate compartment (Vprostate) could only be estimated as a function of the fraction unbound in the prostate (fuprostate) since free drug concentrations were measured in the prostate. Different residual error models (e.g., constant coefficient of variation [CV], combined error) were tested. Separate residual error models were used for total plasma concentrations and free prostate concentrations. The first-order conditional estimation with interaction algorithm was applied for parameter estimation. Model comparison and selection of a final model were based upon numerical comparison of objective function values (log-likelihood ratio test; α = 0.05), visual assessment of basic goodness-of-fit plots, and visual predictive checks (VPCs). For the final model, nonparametric bootstrapping (Wings for NONMEM; n = 1,000) was performed to check model stability and to obtain the confidence intervals (CI) for the model parameters.
RESULTS
In vitro probe calibration.
A series of in vitro microdialysis probe recovery studies were performed viewing to establish the best conditions for the in vivo experiments. As expected, the in vitro recovery was inversely dependent on the perfusate flow rate. The RRs determined by the dialysis method were 24.2% ± 5.5%, 20.1% ± 3.8%, and 16.2% ± 2.1% for the 1.5-, 2.0-, and 2.5-μl/min perfusate flow rates, respectively. The RRs determined by retrodialysis were 25.2% ± 5.3%, 22.8% ± 4.1%, and 18.0% ± 5.7% for the 1.5-, 2.0-, and 2.5-μl/min perfusate flow rates, respectively. For the same perfusate flow rate, there was no statistical difference (α = 0.05) between the recoveries determined by dialysis and retrodialysis. The perfusion flow rate of 1.5 μl/min was chosen as the most suitable for the intended application and was used in all subsequent experiments.
The influence of drug concentration or relative recovery was also evaluated by both methods. The RRs determined by the dialysis were 22.8% ± 1.2%, 19.6% ± 0.6%, and 20.4% ± 1.6% for levofloxacin concentrations of 150, 750, and 3,000 ng/ml, respectively. The RRs determined by retrodialysis were 24.7% ± 5.5%, 26.7% ± 5.0%, and 29.7% ± 7.6% for the same concentrations, respectively, indicating that levofloxacin does not bind to the plastic probe materials, and thus diffusion occurs equally in both directions of the semipermeable microdialysis membrane.
In vivo probe calibration.
For the in vivo recovery, the NNF method was used, where the probe recovery was determined by the slope of the regression line of the [(Cdial – Cperf) versus Cperf] plot. The in vivo probe recovery was found to be 17.5% (y = −0.1753x + 0.067, r2 = 0.9456). The slightly lower RR for levofloxacin in vivo compared to in vitro can be attributed to the distinct characteristics of the tissue compared to the in vitro setup, such as drug uptake into cells, the active transport across membranes, the extent of tissue vascularization, and blood flow through the tissue, as previously reported for other drugs (20).
Levofloxacin plasma protein binding.
Since protein binding may sometimes be dependent on the plasma drug concentration, we assessed the in vitro protein binding of levofloxacin by testing it over three different plasma concentrations in the same range of levels found after administration of the 7-mg/kg i.v. dose to rats. The mean fraction bound to plasma proteins (fbplasma) was found to be 45.5% ± 9.4%, and no concentration dependence was seen. The ubound drug fraction in plasma was considered for the calculation of fT by correcting the total AUCplasma.
NCA of plasma and prostate profiles.
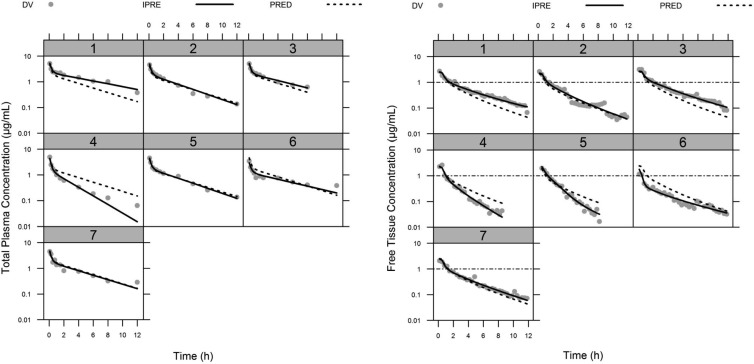
The mean pharmacokinetic parameters determined by NCA are summarized in Table 1. The MRT was slightly shorter in prostate than in the systemic circulation. The maximum observed prostate concentration (Cmax) was ca. 50% of that observed in plasma. If one compares the free prostate concentrations to the unbound plasma levels (Fig. 1), it can be seen that during the distribution phase (between 0 and 2 h after dosing), levofloxacin reaches unbound tissue concentrations higher than those in plasma, indicating that this fluoroquinolone distributes quickly and efficiently through the urinary tract organs, including the prostate. The tissue distribution factor fT was found to be 0.78, indicating that in fact the overall prostate concentrations are 22% lower than the free levels in plasma and the levels expected if only diffusion had driven levofloxacin distribution into prostate. In this context, no reliable prediction of free prostate concentrations was obtained when PK parameters determined from fitting total levofloxacin plasma levels to a two-compartment model taking into consideration protein binding was obtained. Hence, there was a need for a more complex population PK model that could adequately fit levofloxacin PK in plasma and prostate simultaneously.
TABLE 1.
PK parameters determined by NCA of the individual profiles
| Parametera | U | Mean ± SD (n = 7) |
||
|---|---|---|---|---|
| Plasmatotal | Plasmafree | ProstateISFb | ||
| λz | 1/h | 0.15 ± 0.05 | 0.33 ± 0.13* | |
| t1/2 | h | 5.0 ± 1.7 | 2.3 ± 0.7* | |
| Cmax | μg/ml | 4.58 ± 0.57 | 2.52 ± 0.31 | 2.31 ± 0.65† |
| C0 | μg/ml | 5.74 ± 0.82 | 3.16 ± 0.45 | |
| AUC0–12 | h·μg/ml | 9.4 ± 3.3 | 5.2 ± 1.8 | 4.6 ± 1.8† |
| AUC0–∞ | h·μg/ml | 11.7 ± 4.3 | 6.4 ± 2.4 | 4.8 ± 1.9† |
| MRT | h | 6.1 ± 2.7 | 3.0 ± 0.9* | |
| CL | Liter/h | 0.21 ± 0.08 | ||
| Vz | Liter | 1.4 ± 0.5 | ||
| Vss | Liter | 1.2 ± 0.4 | ||
| fT | 0.78 ± 0.25 | |||
λz, elimination rate constant; t1/2, elimination half-life; Cmax, maximum observed concentration; C0, extrapolated concentration at t = 0; AUC0–∞, AUC from zero to infinity; CL, total clearance; fT, tissue distribution factor; MRT, mean residence time; Vz, apparent volume of distribution at the terminal phase; Vss, apparent volume of distribution at steady state. The apparent volume of distribution (Vz) was calculated as CL × t1/2/ln(2), and the total clearance was calculated as the dose/AUC0–∞. The tissue distribution factor (fT) was calculated as [AUCtissue/(fuplasma × AUCplasma)], where fuplasma = 0.55.
Significant differences were determined by one-way ANOVA (α = 0.05) and Tukey's honest-significant-difference post hoc test. *, P < 0.05 (versus plasmatotal group); †, P > 0.05 (differences not statistically significant compared to the plasmafree group).
FIG 1.
Individual concentration-versus-time profiles after an i.v. bolus dose of levofloxacin at 7 mg/kg to rats (n = 7). Gray dots represent the observed total plasma concentrations (left panel) and the unbound prostate tissue concentrations measured by microdialysis (right panel), with a fitted solid line depicting the individual concentrations predicted by the PK model and a dashed line showing the population fits. In the right panel, the horizontal dash-dot line represents the reported levofloxacin susceptibility breakpoint (MIC ≤ 1 mg/liter) against Enterobacteriaceae (37). DV, dependent variable (observations); IPRE, individual model predictions; PRED, population model predictions.
Population PK model.
A three-compartment model comprising a saturable efflux transport from the prostate compartment into the central compartment and a combined residual error models for both total plasma and free prostate concentrations was selected as a final model. The system of differential equations for the final model is given in equations 3a to 3c.
| (3a) |
| (3b) |
| (3c) |
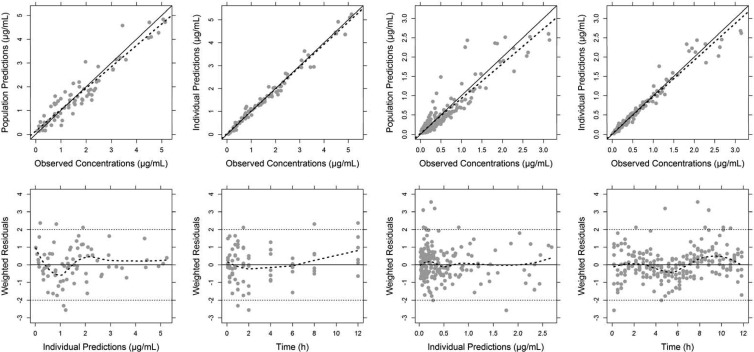
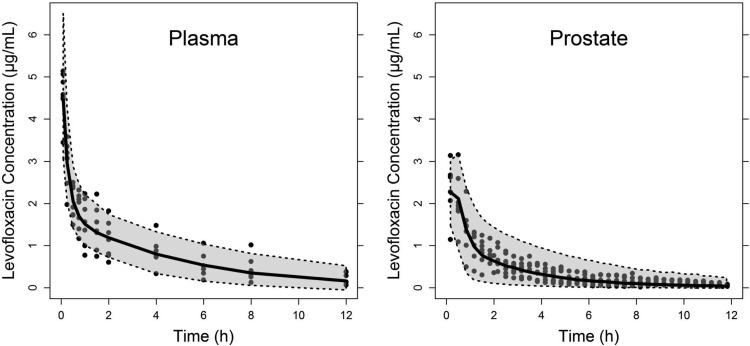
where X1, X2, and X3 are the drug amount in the central, peripheral, and prostate compartments, respectively, and k12, k21, k13, and k31 are the first-order distribution rate constants, k10 is the first-order elimination rate constant from the central compartment, Vmax is the maximum transporter velocity, kM is the MM constant, and V3* is Vprostate/fuprostate. The relationship CL = k10·V1 was considered, wherein V1 represents the volume of the central compartment. The final model, including a saturable (MM) and a nonsaturable (k31) transport process from the prostate compartment into the central compartment fit the data significantly better than models without any of the two transport processes (P < 0.001 for both models). Individual and population predictions adequately describe both total plasma and free prostate concentrations (Fig. 1). The basic goodness-of-fit plots and the results of the VPCs are displayed in Fig. 2 and Fig. 3, respectively. For both total plasma and free prostate concentrations, the predicted and observed concentrations are overall in good agreement (Fig. 2, top panels). For the total plasma concentrations, the model underestimates the observed concentrations slightly at later time points (Fig. 2, two left lower panels). For the free tissue concentrations, the model slightly underestimates the higher observed concentrations (Fig. 2, two top right panels). However, both are minor concerns since the adequateness of the final model is confirmed by the results of the VPC (Fig. 3) that shows that the model adequately predicts the observed concentrations with respect to the average (median) and the spread of the data (prediction interval), although one can infer that the model slightly underestimates the variability in tissue concentrations as most observations are within the 90% prediction interval. The point estimates and nonparametric CI for the model parameters of the final model are given in Table 2. The interindividual variability could only be estimated for CL, V1, kM, and Vmax and were dropped for the other PK parameters. The stability of the final model was confirmed by the results of bootstrapping analysis since all 1,000 runs resulted in reasonable estimates for the typical value parameters, and 40.2% of the bootstrapping runs were minimized successfully. It should be pointed out, however, that the reliability of the 90% CI is limited by the small number of subjects available for the bootstrap procedure.
FIG 2.
Goodness-of-fit plots for the plasma (four panels on the left) and tissue data (four panels on the right) using a nonlinear mixed-effect modeling approach. The data were simultaneously fitted to a three-compartment body model with first-order elimination from the central compartment. In the observed versus model-predicted concentration plots (upper panels), the solid and dashed line indicate the linear regression fit and identity line, respectively, whereas in the residual plots (lower panels), a trend dashed line was added using the local polynomial regression fitting (Loess smooth) in R.
FIG 3.
Visual predictive checks of the population modeling approach for the plasma and tissue data. The black circles indicate the observations, the solid black line represents the median of the simulations, and the gray-shaded area is the 90% prediction interval for 1,000 simulated rats based on the percentile method.
TABLE 2.
Parameter estimates of the final levofloxacin population PK model from the original data set and from 1,000 bootstrap replicatesa
| Parameter | U | Estimate | Nonparametric bootstrap |
|||
|---|---|---|---|---|---|---|
| Median | Relative bias (%)b | 5th percentile | 95th percentile | |||
| V1 | Liter | 0.38 | 0.37 | –1.6 | 0.30 | 0.43 |
| CL | Liter/h | 0.22 | 0.22 | 0.0 | 0.18 | 0.27 |
| k12 | 1/h | 2.27 | 2.23 | –1.8 | 1.43 | 3.51 |
| k21 | 1/h | 1.44 | 1.38 | –4.2 | 0.79 | 2.18 |
| k13 | 1/h | 0.69 | 0.60 | –13.9 | 0.01 | 3.84 |
| Vmax | μg/h | 7.19 | 6.50 | –9.6 | 3.64 | 13.2 |
| kM | μg/ml | 0.35 | 0.31 | –10.7 | 0.17 | 0.71 |
| V3/fuprostate | Liter | 0.05 | 0.04 | –11.5 | 0.00 | 0.23 |
| k31 | 1/h | 3.67 | 3.64 | –0.8 | 2.51 | 4.34 |
| Inter-individual variability | ||||||
| ω2(V1) | % CV | 21.0 | 19.5 | –7.0 | 0.3 | 27.1 |
| ω2(CL) | % CV | 36.7 | 33.0 | –10.1 | 12.6 | 47.9 |
| ω2(Vmax) | % CV | 41.6 | 39.0 | –6.3 | 4.2 | 53.8 |
| ω2(kM) | % CV | 76.0 | 71.8 | –5.6 | 0.3 | 106.3 |
| Residual variability | ||||||
| σ12 (proportional error, plasma) | % CV | 10.2 | 9.6 | –6.1 | 0.3 | 13.6 |
| σ22 (additive error, plasma) | μg/ml | 0.085 | 0.084 | –1.3 | 0.050 | 0.145 |
| σ32 (proportional error, tissue) | % CV | 15.2 | 14.6 | –3.7 | 11.9 | 19.2 |
| σ42 (additive error, tissue) | μg/ml | 0.015 | 0.013 | –9.6 | 0.009 | 0.023 |
fuprostate, unbound fraction in prostate tissue; % CV, percent coefficient of variation.
The accuracy in parameter estimation was assessed from the bias, which was calculated as follows: relative bias (%) = [(bootstrap median–original estimate)/original estimate] × 100.
DISCUSSION
Microdialysis has emerged as the state-of-the-art technique to measure free interstitial concentrations in many tissues in both preclinical and clinical studies, especially because it allows the distinction between the interstitial fluid space and other compartments. Particularly for antimicrobials, free tissue concentrations are of great relevance since they are more representative of the drug concentration at the site of infection. Free antimicrobial concentrations in prostate have not been reported thus far, although these drugs are used for long periods of time to treat prostatitis. We sought to compare here the free levofloxacin concentrations in prostate and plasma using in vivo microdialysis in rats. A PK model was developed to fit the kinetic distribution of levofloxacin in both compartments using a nonlinear mixed-effect modeling approach.
Good correlation between the plasma PK parameters determined by NCA and estimated by the population PK model was observed. Population CL of 0.22 liter/h estimated by the model was virtually the same found by noncompartmental analysis (Table 1). The plasma concentration at t = 0 h was estimated from the model fitted parameters by dividing the average amount given to rats (2.198 mg) by V1, yielding a C0 of 5.83 μg/ml, which is in close agreement with the value determined by NCA. From the relationship AUC0–∞ = dose/CL, the plasma AUC0–∞ was calculated to be 9.9 h·μg/ml, being in close agreement with the results presented in Table 1. The volume of the prostate tissue compartment (V3) was found to be 8-fold smaller than V1, and such small volume of distribution could be due to the small prostate volume compared to V1.
After i.v. administration, levofloxacin quickly distributes throughout the body, as evidenced by the fast exponential decay in the plasma concentrations (Fig. 1, left panel), reaching maximum prostate tissue levels within ∼15 min after dosing. A similar rapid distribution was observed for gatifloxacin in the skeletal muscles and lungs of rats (17). The efficient and rapid distribution of fluoroquinolones within the urinary tract is one of the reasons this class of antimicrobial agents are frequently used as drugs of first choice for the treatment of UTIs, associated with the fact that they are mostly excreted by renal elimination as unchanged drugs. These PK properties contribute to the concentration-dependent bactericidal killing effect against the most common uropathogens involved in UTIs.
Despite of the rapid distribution observed, levofloxacin free prostate concentrations were 22% lower than the respective free plasma concentrations in rats. A mean prostate tissue/plasma concentration ratio of 2.96 has been previously reported for levofloxacin using biopsy tissue of patients undergoing prostate resection after a 500-mg oral dose every 24 h prior to surgery, followed by a short i.v. infusion of 500 mg on the day of the surgery (3). The present findings are consistent with a previous report (11) showing that measurements in whole tissue homogenates can lead to overestimation of the target site concentrations and therefore its clinical efficacy, because it does not distinguish between interstitial, intracellular, blood, and prostatic fluid drug concentrations.
Our data are in good accordance with previous microdialysis studies with levofloxacin. Hutschala et al. (27) found a median AUCtissue/AUCplasma ratio of 0.6 (range, 0.4 to 0.9) in the lung tissues of patients undergoing cardiac surgery and that the Cmax in pulmonary fluid represented 38% of maximum plasma levels. Zeitlinger et al. (28) investigated the lung penetration of levofloxacin in patients who had undergone lung surgery, obtaining a fu·AUC/MIC90 ratio of 151 and a Cmax/MIC90 ratio of 12 for E. coli. The same group showed that levofloxacin concentrations in skeletal muscle interstitial space of patients with sepsis represent 85% of free plasma concentrations, with a high interindividual variability on tissue penetration (46% CV). Marchand et al. (29) studied levofloxacin PK in rat muscle and lung after continuous infusion and detected unbound AUCtissue/AUCplasma ratios virtually equal to unity (i.e., 1.00 and 1.06 in the muscle and lung, respectively), suggesting passive distribution of levofloxacin in these tissues. The downside of the latter report is, however, that the determinations were based on a single-point determination at steady state rather than multiple measurements after single administration; thus, it does not allow the fully characterization of the kinetics of levofloxacin distribution/elimination that occurs in the tissue prior and after steady state.
To mathematically predict levofloxacin free prostate concentrations observed experimentally, the equation assuming a two-compartment body model using fuplasma, the first-order rate constant from the tissue to the central compartment (k21), and the hybrid constants α and β for plasma distribution and elimination, respectively, was initially used without success because the model predictions underestimated tissue dialysate concentrations within the distribution phase and overestimated during the elimination phase (data not shown). Indeed, this model can only be applied when the unbound drug concentrations in plasma and tissue fluids are equal at equilibrium assuming that the driving force of distribution is passive diffusion only.
Prostate accumulation of fluoroquinolones was hypothesized to be governed by two main processes: passive diffusion, which is driven by drug's lipophilicity, and ion-trapping mechanisms (30). The first process is based solely on the drug capacity of permeating through cellular membranes by passive diffusion and is mainly governed by the molecule partition coefficient (log D). On the other hand, ion-trapping mechanisms are based on the fact that fluoroquinolones are amphoteric molecules that tend to be more or less charged depending on the compound pKa and the pH of the medium. Due to the increased alkaline pH of the prostatic fluid in men with prostatic infection (pH of ∼8.34) compared to the plasma, quinolones with an isoelectric point close to the plasma pH tend to concentrate toward fluids with a pH above plasma pH (3). The “fourth-generation” fluoroquinolone moxifloxacin was reported to reach a prostatic secretion/plasma concentration ratio of 1.57, especially due to its enhanced lipophilicity compared to older quinolones, such as norfloxacin and ciprofloxacin, enhancing its distribution and accumulation into different target tissues (30). Ion-trapping mechanisms were also hypothesized to remarkably influence this effect. Although both mechanisms would result in higher quinolones concentrations in the prostate, our data indicate that lower free levofloxacin concentrations were observed. In this sense, a third mechanism mediated by active efflux pumps is suggested to play a role in the prostate penetration of quinolones.
The involvement of carrier-mediated active transport for quinolones was evidenced in the renal distribution of levofloxacin and grepafloxacin in rats (31), and there are reports that these transporters are distributed in other tissues, including liver and small intestine. MPR4 drug efflux pumps were specifically localized in prostate and kidney (32). A previous study (33) have shown that the brain distribution of several quinolones, including levofloxacin, is limited due to the action of multiple efflux transporters, including MRP family drug efflux pumps and P-glycoprotein (P-gp). Comparatively, cellular overproduction of P-gp has been described as one of the major causes for multidrug resistance in prostate tumor cells, since P-gp acts as an efflux pump for various anticancer drugs with a wide variety of chemical structures, being an obstacle to the effective treatment of prostate cancer (34). However, the role of P-gp and other transporters on quinolone distribution in the prostate has not yet been a focus of investigation.
Even though the average 22% difference in tissue/plasma ratio from unity could be influenced by the experimental variability inherent to the study, we hypothesized that it could be due to a second mechanism in addition to passive diffusion. Assuming that the distribution of levofloxacin into prostate is governed by diffusion but an efflux transporter is involved, which would justify the lower free levels observed in prostate in comparison to plasma, we used a three-compartment model to individually model the total plasma and free prostate concentrations of levofloxacin observed in the animals here. The developed population PK model consisting of three compartments with both first-order and nonlinear distribution adequately fit levofloxacin PK in plasma and rats prostate interstitial fluid. Assuming that levofloxacin distribution to prostate is governed by diffusion and an active mechanism, and taking into consideration that the concentrations observed in prostate are higher than the kM determined by modeling (0.35 μg/ml), the AUC determined for the prostate (Table 1) is an overestimation of the tissue exposition to the drug and, consequently, the tissue penetration factor would be even lower than estimated.
Levofloxacin, like the other quinolones, is a concentration-dependent antimicrobial, and it has been suggested in the literature that the AUC/MIC index is a better predictor of its therapeutic outcome. The applicability of the PK/PD indices based upon in vitro MIC threshold values to predict therapeutic outcome is, however, limited since they may not accurately reflect the in vivo scenario (35). Recently, the use of more descriptive approaches, such as the PK/PD modeling of the free antimicrobial concentrations at the infection site against bacteria, gives a better indication of drug effectiveness. In this regard, the proposed PK model allows the prediction of unbound tissue levels for different levofloxacin dosing regimens and can be used to simulate dosing schemes and choose regimens in order to reach the desired free prostate ISF concentrations. Furthermore, the developed population PK model could be incorporated into a PK/PD model to describe and predict infection treatment outcome using levofloxacin.
A previous study has shown that norfloxacin levels in noninfected prostate are not significantly different than those in the presence of chronic bacterial prostatitis (36). However, the present study was conducted in healthy rats, and one cannot disregard the possible influence of the infection on levofloxacin PK in the inflamed prostate gland. If quinolone distribution is not affected by prostate infection and/or inflammation, our findings in uninfected rats could be extrapolated to the infected condition. This assumption remains to be confirmed.
Conclusions.
For the first time, to the authors' knowledge, we report here the prostate tissue distribution of an antimicrobial agent using microdialysis showing the feasibility of this method for investigating the penetration of drugs into the prostate. The developed population PK model was able to simultaneously fit levofloxacin concentration-time profiles in plasma and prostate tissue ISF and could also quantify the interindividual variability in the kinetic disposition of levofloxacin. In a clinical setting, the model may be applied to simulate therapeutically relevant unbound concentration-time profiles in the prostate resulting from doses other than the tested and multiple-dose regimens, aiming at optimizing levofloxacin therapy for bacterial prostatitis. Our findings suggest that levofloxacin is likely to be a substrate for efflux transporters in the prostate, but further studies are needed in order to confirm this hypothesis and identify the transporters involved in the distribution of this quinolone in the prostate.
ACKNOWLEDGMENTS
F.K.H. received a scholarship from CNPq/Brazil and CAPES/Brazil through the PDSE Program (Process 5339/11-1). This study was supported by CNPq/Brazil (Process 144816/2010-5) and FAPERGS/RS/Brazil (Process 11/0908-5). This study was approved by UFRGS Ethics Committee on Animal Use (Project 18330).
We thank Bibiana Verlindo de Araújo at UFRGS, who kindly demonstrated basic animal handling and microsurgery techniques in rats.
Footnotes
Published ahead of print 11 November 2013
REFERENCES
- 1.Wagenlehner FME, Naber KG. 2005. Fluoroquinolone antimicrobial agents in the treatment of prostatitis and recurrent urinary tract infections in men. Curr. Infect. Dis. Rep. 7:9–16. 10.1007/s11908-005-0018-9 [DOI] [PubMed] [Google Scholar]
- 2.Naber KG, Weidner W. 2000. Chronic prostatitis - an infectious disease? J. Antimicrob. Chemother. 46:157–161. 10.1093/jac/46.2.157 [DOI] [PubMed] [Google Scholar]
- 3.Naber KG, Sorgel F. 2003. Antibiotic therapy - rationale and evidence for optimal drug concentrations in prostatic and seminal fluid and in prostatic tissue. Andrologia 35:331–335. 10.1046/j.1439-0272.2003.00568.x [DOI] [PubMed] [Google Scholar]
- 4.Naber KG. 2008. Management of bacterial prostatitis: what's new? BJU Int. 101:7–10. 10.1111/j.1464-410X.2008.07495.x [DOI] [PubMed] [Google Scholar]
- 5.Naber CK, Steghafner M, Kinzig-Schippers M, Sauber C, Sorgel F, Stahlberg HJ, Naber KG. 2001. Concentrations of gatifloxacin in plasma and urine and penetration into prostatic and seminal fluid, ejaculate, and sperm cells after single oral administrations of 400 milligrams to volunteers. Antimicrob. Agents Chemother. 45:293–297. 10.1128/AAC.45.1.293-297.2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wagenlehner FME, Kees F, Weidner W, Wagenlehner C, Naber KG. 2008. Concentrations of moxifloxacin in plasma and urine, and penetration into prostatic fluid and ejaculate, following single oral administration of 400 mg to healthy volunteers. Int. J. Antimicrob. Agents 31:21–26. 10.1016/j.ijantimicag.2007.08.025 [DOI] [PubMed] [Google Scholar]
- 7.Drusano GL, Preston SL, Van Guilder M, North D, Gombert M, Oefelein M, Boccumini L, Weisinger B, Corrado M, Kahn J. 2000. A population pharmacokinetic analysis of the penetration of the prostate by levofloxacin. Antimicrob. Agents Chemother. 44:2046–2051. 10.1128/AAC.44.8.2046-2051.2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Croom KF, Goa KL. 2003. Levofloxacin: a review of its use in the treatment of bacterial infections in the United States. Drugs 63:2769–2802. 10.2165/00003495-200363240-00008 [DOI] [PubMed] [Google Scholar]
- 9.Bulitta JB, Kinzig M, Naber CK, Wagenlehner FME, Sauber C, Landersdorfer CB, Soergel F, Naber KG. 2011. Population pharmacokinetics and penetration into prostatic, seminal, and vaginal fluid for ciprofloxacin, levofloxacin, and their combination. Chemotherapy 57:402–416. 10.1159/000329520 [DOI] [PubMed] [Google Scholar]
- 10.Van Bambeke F, Tulkens PM. 2009. Safety profile of the respiratory fluoroquinolone moxifloxacin comparison with other fluoroquinolones and other antibacterial classes. Drug Safety 32:359–378. 10.2165/00002018-200932050-00001 [DOI] [PubMed] [Google Scholar]
- 11.Mouton JW, Theuretzbacher U, Craig WA, Tulkens PM, Derendorf H, Cars O. 2008. Tissue concentrations: do we ever learn? J. Antimicrob. Chemother. 61:235–237. 10.1093/jac/dkm476 [DOI] [PubMed] [Google Scholar]
- 12.Muller M, Stass H, Brunner M, Moller JG, Lackner E, Eichler HG. 1999. Penetration of moxifloxacin into peripheral compartments in humans. Antimicrob. Agents Chemother. 43:2345–2349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Joukhadar C, Derendorf H, Muller M. 2001. Microdialysis: a novel tool for clinical studies of anti-infective agents. Eur. J. Clin. Pharmacol. 57:211–219. 10.1007/s002280100301 [DOI] [PubMed] [Google Scholar]
- 14.Elmquist WF, Sawchuk RJ. 1997. Application of microdialysis in pharmacokinetic studies. Pharm. Res. 14:267–288. 10.1023/A:1012081501464 [DOI] [PubMed] [Google Scholar]
- 15.Freddo RJ, Costa TD. 2002. Determination of norfloxacin free interstitial levels in skeletal muscle by microdialysis. J. Pharm. Sci. 91:2433–2440. 10.1002/jps.10230 [DOI] [PubMed] [Google Scholar]
- 16.de Araujo BV, Diniz A, Palma EC, Buffe C, Costa TD. 2011. PK-PD modeling of beta-lactam antibiotics: in vitro or in vivo models? J. Antibiot. 64:439–446. 10.1038/ja.2011.29 [DOI] [PubMed] [Google Scholar]
- 17.Tasso L, Bettoni C, Oliveira L, Costa T. 2008. Evaluation of gatifloxacin penetration into skeletal muscle and lung by microdialysis in rats. Int. J. Pharm. 358:96–101. 10.1016/j.ijpharm.2008.02.023 [DOI] [PubMed] [Google Scholar]
- 18.de Araujo BV, da Silva CF, Haas SE, Dalla Costa T. 2009. Free renal levels of voriconazole determined by microdialysis in healthy and Candida sp.-infected Wistar rats. Int. J. Antimicrob. Agents 33:154–159. 10.1016/j.ijantimicag.2008.08.020 [DOI] [PubMed] [Google Scholar]
- 19.Azeredo F, Araujo B, Haas S, Torres B, Pigatto M, Andrade C, Dalla Costa T. 2012. Comparison of fluconazole renal penetration levels in healthy and Candida albicans-infected Wistar rats. Antimicrob. Agents Chemother. 56:5852–5857. 10.1128/AAC.01323-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.de Lange ECM, de Boer AG, Breimer DD. 2000. Methodological issues in microdialysis sampling for pharmacokinetic studies. Adv. Drug Deliv. Rev. 45:125–148. 10.1016/S0169-409X(00)00107-1 [DOI] [PubMed] [Google Scholar]
- 21.Whitaker G, Lunte CE. 2010. Investigation of microdialysis sampling calibration approaches for lipophilic analytes: doxorubicin. J. Pharm. Biomed. Anal. 53:490–496. 10.1016/j.jpba.2010.05.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shargel L, Wu-Pong S, Yu ABC. 2005. Applied biopharmaceutics and pharmacokinetics, 5th ed. McGraw-Hill Book Co, New York, NY [Google Scholar]
- 23.Plock N, Kloft C. 2005. Microdialysis: theoretical background and recent implementation in applied life-sciences. Eur. J. Pharm. Sci. 25:1–24. 10.1016/j.ejps.2005.01.017 [DOI] [PubMed] [Google Scholar]
- 24.Konety BR, Somogyi G, Atan A, Muindi J, Chancellor MB, Getzenberg RH. 2002. Evaluation of intraprostatic metabolism of 1,25-dihydroxyvitamin D3 (calcitriol) using a microdialysis technique. Urology 59:947–952. 10.1016/S0090-4295(01)01652-1 [DOI] [PubMed] [Google Scholar]
- 25.Bansal S, DeStefano A. 2007. Key elements of bioanalytical method validation for small molecules. AAPS J. 9:E109–E114. 10.1208/aapsj0901011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Food and Drug Administration 2001. Guidance for industry: bioanalytical method validation. U.S. Food and Drug Administration, Washington, DC [Google Scholar]
- 27.Hutschala D, Skhirtladze K, Zuckermann A, Wisser W, Jaksch P, Mayer-Helm B, Burgmann H, Wolner E, Muller M, Tschernko E. 2005. In vivo measurement of levofloxacin penetration into lung tissue after cardiac surgery. Antimicrob. Agents Chemother. 49:5107–5111. 10.1128/AAC.49.12.5107-5111.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zeitlinger MA, Traunmueller F, Abrahim A, Mueller MR, Erdogan Z, Mueller M, Joukhadar C. 2007. A pilot study testing whether concentrations of levofloxacin in interstitial space fluid of soft tissues may serve as a surrogate for predicting its pharmacokinetics in lung. Int. J. Antimicrob. Agents 29:44–50. 10.1016/j.ijantimicag.2006.08.045 [DOI] [PubMed] [Google Scholar]
- 29.Marchand S, Frasca D, Dahyot-Fizelier C, Breheret C, Mimoz O, Couet W. 2008. Lung microdialysis study of levofloxacin in rats following intravenous infusion at steady state. Antimicrob. Agents Chemother. 52:3074–3077. 10.1128/AAC.00242-08 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Perletti G, Wagenlehner F, Naber K, Magrid V. 2009. Enhanced distribution of fourth-generation fluoroquinolones in prostatic tissue. Int. J. Antimicrob. Agents 33:206–210. 10.1016/j.ijantimicag.2008.09.009 [DOI] [PubMed] [Google Scholar]
- 31.Ito T, Yano I, Masuda S, Hashimoto Y, Inui K. 1999. Distribution characteristics of levofloxacin and grepafloxacin in rat kidney. Pharm. Res. 16:534–539. 10.1023/A:1018871029244 [DOI] [PubMed] [Google Scholar]
- 32.Kruh GD, Belinsky MG. 2003. The MRP family of drug efflux pumps. Oncogene 22:7537–7552. 10.1038/sj.onc.1206953 [DOI] [PubMed] [Google Scholar]
- 33.Tamai I, Yamashita J, Kido Y, Ohnari A, Sai Y, Shima Y, Naruhashi K, Koizumi S, Tsuji A. 2000. Limited distribution of new quinolone antibacterial agents into brain caused by multiple efflux transporters at the blood-brain barrier. J. Pharm. Exp. Ther. 295:146–152 [PubMed] [Google Scholar]
- 34.Nobili S, Landini I, Mazzei T, Mini E. 2012. Overcoming tumor multidrug resistance using drugs able to evade P-glycoprotein or to exploit its expression. Med. Res. Rev. 32:1220–1262. 10.1002/med.20239 [DOI] [PubMed] [Google Scholar]
- 35.Mueller M, de la Pena A, Derendorf H. 2004. Issues in pharmacokinetics and pharmacodynamics of anti-infective agents: kill curves versus MIC. Antimicrob. Agents Chemother. 48:369–377. 10.1128/AAC.48.2.369-377.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nickel JC, Downey J, Clark J, Ceri H, Olson M. 1995. Antibiotic pharmacokinetics in the inflamed prostate. J. Urol. 153:527–529. 10.1097/00005392-199502000-00076 [DOI] [PubMed] [Google Scholar]
- 37.European Committee on Antimicrobial Susceptibility Testing 2013. Breakpoint tables for interpretation of MICs and zone diameters, version 3.1. European Committee on Antimicrobial Susceptibility Testing, Basel, Switzerland [Google Scholar]