Intracellular Dynamics of HIV Infection

Abstract

Early studies of HIV infection dynamics suggested that virus-producing HIV-infected cells had an average half-life of approximately 1 day. However, whether this average behavior is reflective of the dynamics of individual infected cells is unclear. Here, we use HIV-enhanced green fluorescent protein (EGFP) constructs and flow cytometry sorting to explore the dynamics of cell infection, viral protein production, and cell death in vitro. By following the numbers of productively infected cells expressing EGFP over time, we show that infected cell death slows down over time. Although infected cell death in vivo could be very different, our results suggest that the constant decay of cell numbers observed in vivo during antiretroviral treatment could reflect a balance of cell death and delayed viral protein production. We observe no correlation between viral protein production and death rate of productively infected cells, showing that viral protein production is not likely to be the sole determinant of the death of HIV-infected cells. Finally, we show that all observed features can be reproduced by a simple model in which infected cells have broad distributions of productive life spans, times to start viral protein production, and viral protein production rates. This broad spectrum of the level and timing of viral protein production provides new insights into the behavior and characteristics of HIV-infected cells.

INTRODUCTION

Untreated HIV infection usually involves an initial acute phase, followed by a long period of stable viral load and clinical latency, ending in severe CD4⁺ T cell depletion and AIDS. The long period of clinical latency initially led to the idea that the intracellular viral replication cycle may also be extremely slow. However, the subsequent studies of viral kinetics under treatment revealed a highly dynamic process of infection. Despite the apparent stability of viral loads and CD4⁺ T cell numbers during the observed clinical latency, there was a rapid turnover of both free virus (half-life [t_1/2] of ∼45 min) (1) and productively infected cells (∼0.7 per day, which translates to a half-life of ≈1 day) (2–4). The understanding of in vivo viral dynamics under therapy has been very helpful in elucidating the effects of antiretroviral treatment (ART), the rate of viral evolution, and the mechanisms of immune control. However, since the model was based upon the dynamics of total virus produced by all productively infected cells, it estimated the average death rate of infected cells or the average rate of viral production.

Although this averaged replication cycle of productively infected cells has proved extremely useful in understanding the overall dynamics of infection, it may be missing a number of important underlying features at the intracellular level, where the infected cells show a great variation in behavior (5). For example, it has been observed that the rate at which HIV-infected CD4⁺ T cells release new virions varies greatly across the cell population (6–8). The differences in viral protein production rates, on the other hand, could have an impact on infected cell death because of viral cytopathic effect, so the cells that produce viral protein at a higher rate would on average have shorter life spans (9, 10). In addition, differences in the rates of viral protein synthesis may also have implications for immune recognition and control of infection, since the level of viral protein and viral production may impact on factors such as CD8⁺ T cell recognition of infected cells. Finally, our concepts of “productively” and “latently” infected cells suggest a strict dichotomy. However, a spectrum of levels of viral production would have major implications for our understanding of HIV latency and attempts to purge the latent reservoir.

A number of studies have investigated the distribution of viral protein production across the population of infected cells. Studies of viral production have been performed on visna virus infection (11) and HIV-infected Jurkat cells (12–15). These studies suggested that the translation of viral proteins proceeds at a wide range of rates and seems to increase exponentially over time in individual cells (6, 11, 15). The start of protein production in HIV-infected Jurkat cells was also highly variable and seemed to negatively correlate with the level of produced viral protein, which has been linked to the position of the integration site within the nucleus (14). Details of the steps in HIV provirus transcription and translation leading to virus production in the SupT1 cell line during the first 24 h of infection have also been recently studied (16). However, the impact of viral protein production on cell death could not be seen in the immortalized cell lines, and it is not clear whether these observed dynamics of virus production and cell death are consistent with the dynamics found in primary cell infection.

The aim of this study was to understand the intracellular dynamics of HIV infection. In particular, we were interested in the time between virus entry and the start of viral protein production, distribution of viral protein production rates and life spans of productively infected cells, and a possible correlation between the distributions of virus protein production rates and death rates across the infected CD4⁺ T cell population. To this end, we have studied the dynamics of a single-round in vitro HIV infection of healthy peripheral blood lymphocytes (PBLs) from 8 donors with an HIV-enhanced green fluorescent protein (EGFP) reporter virus. The virus had egfp inserted within the nef coding sequence that is under the regulation of the HIV long terminal repeat (LTR) promoter. EGFP in infected cells was produced at the rate of translation of the Nef protein, so the production rate of EGFP is a measure for the production rate of viral proteins. After initialization of protein production, EGFP accumulated in the cell cytoplasm, with the fluorescence correlated to the amount of EGFP present in a cell. We followed the productively infected cell numbers and fluorescence distribution over 4 days after infection. In order to investigate the diversity in EGFP expression and its impact on cell fate, we also used a fluorescence-activated cell sorter (FACS) to sort the productively infected cells into two groups at 24 h postinfection according to their fluorescence level, EGFP-high and EGFP-medium, and followed them in parallel. We used statistical analysis and mathematical modeling to interpret the experimental results.

We found the results consistent with a picture in which infected cells had a broad distribution of times from infection to production of viral protein (what we call “silent phase”), with a similarly broad distribution of life spans from the start of production of viral protein. Protein production also varied across the infected cell population but was on average lower for the cells that started protein production later. However, life spans of productively infected cells were independent of viral protein production rates.

This study provides insights into the intracellular dynamics of HIV infection that underlie the observed in vivo dynamics of viral load after treatment. The observation of a wide distribution of time from initial infection to viral protein production has important implications for our understanding of cellular latency. Similarly, the decrease in viral protein production levels observed in cells that commenced producing later suggests that cells reactivating after prolonged treatment may behave differently from cells that commence viral production immediately after infection. Although our study relies on relatively short-term tracking of in vitro-infected cells, it suggests a reevaluation of our concepts of productive and latent infection.

MATERIALS AND METHODS

Experimental methods. (i) Virus production.

The pNLAD8-EGFP HIV-1 R5-tropic infectious clones contain the EGFP open reading frame inserted into the nef gene.

Virus was produced by transfection of 293T cells, which were obtained from the American Type Culture Collection and maintained in Dulbecco's modified Eagle's medium (DMEM) (Invitrogen, California) supplemented with 10% (vol/vol) cosmic calf serum (CCS) (HyClone, Toronga, New Zealand) and penicillin-streptomycin (Invitrogen, Carlsbad CA).

Transfections were carried out with polyethylenimine (Polysciences Inc., Warrington, PA), and transfection efficiencies were measured using a reverse transcriptase assay (17). Thirty-six hours posttransfection, virus-containing medium was harvested, clarified by centrifugation at 1,462 × g for 30 min, and then passed through a 0.45-μm-pore-size filter (Sartorius, Goettingen, Germany) to remove cellular debris. Purified virus was concentrated by ultracentrifugation using an L-90 ultracentrifuge (SW-31Ti rotor; Beckman Coulter, Fullerton, CA) at 100,000 × g for 1 h at 4°C through a 20% sucrose cushion and resuspended in phosphate-buffered saline (PBS). The concentrated viral stocks were quantified using the Vironostika HIV-1 antigen (p24 CA) microElisa (bioMérieux, Boxtel, Netherlands) according to the manufacturer's instructions and frozen in single-use aliquots at −80°C.

(ii) Cell culture.

Peripheral blood mononuclear cells (PBMCs) were isolated from buffy coats of random (identity-blocked) blood donors (supplied by the Red Cross Blood Bank Service, Melbourne, Australia) through density gradient centrifugation over Ficoll-Paque Plus (Amersham Biosciences, Piscataway, NJ) as previously described (18).These cells were then used for isolation of peripheral blood lymphocytes (PBLs) by incubating PBMCs in plastic tissue culture dishes to remove adherent cells. The purity of PBLs was assessed by flow cytometry (FACSAria; Becton, Dickinson, San Jose, CA) and determined to be >95% pure based on forward-scatter and side-scatter characteristics. The PBLs were stimulated in medium (2 × 10⁶ cells/ml) supplemented with 10 μg/ml phytohemagglutinin (PHA; Murex Diagnostics, Dartford, Kent, United Kingdom) for 3 days and then were transferred into fresh RPMI 1640 with 10% fetal bovine serum (FBS) (SAFC Biosciences, KS) and 50 μg/ml gentamicin (Pfizer, Bentley, WA, Australia) containing 10 units/ml interleukin-2 (Roche Applied Science, Mannheim, Germany) 24 h before infection. All biological samples were handled according to the Burnet Institute and the Alfred Hospital-approved ethics guidelines, in line with Australian Government regulation.

(iii) Virus infection.

Eight donor samples (one sample each from donors 13, 14, 15, 23, 81, and 85 and two samples, 98(1) and 98(2), from donor 98) were infected with 1 μg of p24 capsid protein (CA) equivalent of HIV/10⁶ cells. Stimulated PBLs were spinoculated with the virus at 30°C for 2 h at 1,200 × g and then incubated further for 1 h at 37°C and 5% CO₂. Subsequently, the cells were washed twice with PBS to remove unbound virus and incubated with media at 37°C and 5% CO₂ for 4 days. Antiretrovirals (20 μM raltegravir and 500 nM zidovudine [AZT] obtained from AIDS Research and Reference Reagent Program, Division of AIDS, National Institute of Allergy and Infectious Diseases, U.S. National Institutes of Health) were added to the culture media either 24 h before the infection (pretreatment control) or 18 h after the infection (posttreatment) and maintained throughout the experiment. Twenty-four hours postinfection, the number of viable cells was calculated, and cell concentration was adjusted across the different samples.

(iv) PKH-26 labeling.

We used PKH-26 labeling to check if infected cells were dividing. Five hours before HIV-1 infection, replicates of 2 × 10⁶ PBLs were collected, washed twice with PBS, and stained by following the manufacturer's instructions. Briefly, cells were resuspended in a solution of 2 μM PKH-26 (Sigma-Aldrich, St. Louis, MO) and mixed vigorously for 5 min. Then, RPMI 1640 and 10% FBS medium was added to stop the labeling reaction. The cells were subsequently washed twice with medium and finally resuspended in 2 ml RPMI 1640, 10% FBS, 50 μg/ml gentamicin, and 10 units/ml interleukin-2.

(v) FACS analysis.

Two samples (from donor 15 and donor 23) were FACS analyzed at 12, 15, 18, and 24 h postinfection. After 24 h, 7 donor samples [from donors 13, 14, 23, 81, 85, and 98(1) and 98(2)] were analyzed by FACS and then FACS sorted into EGFP-medium (3 < log F < 4) and EGFP-high (log F > 4). Unsorted and sorted samples were then FACS analyzed on day 2, day 3, and day 4.

Flow cytometry data were collected on a FACSAria flow cytometer (BD Biosciences, Franklin Lakes, NJ) and analyzed with Flow-Jo software (Tree Star, Ashland, OR) and FACSDiva (BD Biosciences, Franklin Lakes, NJ). Cell sorting of viable cells was performed by employing FACSAria. The PBL population was initially gated based on size (forward light scatter) and granularity (side angle light scatter) characteristics. On day 1 postinfection, viable cells were sorted according to the levels of EGFP expression into high, medium, and negative. Subsequently, cell density was adjusted to 1.5 × 10⁵ cell/ml, and cells were maintained in culture for a further 3 days. Samples were taken after 2, 3, and 4 days postinfection from the standardized cell cultures, to assess EGFP expression, cell number, and viability. When collecting the samples, cells were washed and resuspended in PBS-1% CCS, adding 5 μg/ml propidium iodide (Sigma-Aldrich, St. Louis, MO) to estimate the number of viable cells. Also, a known number of CountBright counting beads (Invitrogen, Carlsbad, CA) was added to the sample before analysis in order to calculate absolute cell numbers.

Data analysis. (i) Half-life of GFP⁺ cells.

Death rate δ of EGFP⁺ CD4⁺ T cells between two time points, t₁ and t₂, was calculated assuming exponential decline in the cell numbers between these two time points, N(t₂) = N(t₁)exp[−δ(t₂ − t₁)], where N(t) is a measured number of EGFP⁺ cells at time t. Death rate is then obtained from

$$\delta =\frac{\ln \hspace{0.17em}\left[N\left(t_1\right)/N\left(t_2\right)\right]}{t_2-t_1}$$ (1)

which corresponds to the half-life t_1/2 = ln2/δ.

(ii) Cell number balance in unsorted cell cultures.

The number of EGFP⁺ cells at the end of each 1-day period, which were not EGFP⁺ at the start of this period, can be estimated by balancing the cell numbers.

None of the EGFP⁺ cells present on day 1 were EGFP⁺ on day 0. Therefore, the number of new EGFP⁺ cells on day 1 is equal to N(1), i.e., the total number of EGFP⁺ cells on day 1.

The number of cells that were not EGFP⁺ on day 1 but were EGFP⁺ on day 2 can be estimated as follows. If N(1) is the number of EGFP+ cells on day 1, and the death rate between day 1 (=t₁) and day 2 (=t₂) is δ₁₂, then these cells will be reduced to N(1)exp(−δ₁₂) on day 2. Thus, the excess number of cells on day 2, coming from the cells that became EGFP⁺ in this period, is:

$$\Delta N_2=N\left(2\right)-N\left(1\right)\exp \hspace{0.17em}\left[-{\delta }_{12}\left(t_2-t_1\right)\right]$$ (2)

In principle, δ₁₂ should be determined from the decline of cell numbers in the sorted medium and high cultures, in which cells die and are not replaced. However, cell numbers were not measured immediately after sorting. Because of an observed decrease in death rate with time, for estimation purposes, we assume that the death rate is at least equal to δ₂₃ (but may be higher). Therefore, our estimate is that at least ΔN₂ new cells were EGFP⁺ on day 2.

We can similarly estimate the number of new cells that were not EGFP⁺ on day 2 but were EGFP⁺ on day 3 (ΔN₃) with the formula

$$\Delta N_3=N\left(3\right)-\Delta N_2\exp \hspace{0.17em}\left(-{\delta }_{12}\right)-N\left(1\right)\exp \hspace{0.17em}\left(-{\delta }_{12}\right)\exp \hspace{0.17em}\left(-{\delta }_{23}\right)$$ (3)

and the number of new cells that were not GFP⁺ on day 3 but were GFP⁺ on day 4 (ΔN₄) with the formula

$$\begin{array}{c}\Delta N_4=N\left(4\right)-\Delta N_3\exp \hspace{0.17em}\left(-{\delta }_{12}\right)-\Delta N_2\exp \hspace{0.17em}\left(-{\delta }_{12}\right)\exp \hspace{0.17em}\left(-{\delta }_{23}\right)\\ -N\left(1\right)\exp \hspace{0.17em}\left(-{\delta }_{12}\right)\exp \hspace{0.17em}\left(-{\delta }_{23}\right)\exp \hspace{0.17em}\left(-{\delta }_{34}\right)\end{array}$$ (4)

As before, we assumed δ₁₂ = δ₂₃ for estimation purposes.

(iii) Fluorescence distributions and MFI analysis.

Fluorescence distributions obtained from FACS were aligned for comparison purposes so that the autofluorescence peaks were at 10² relative fluorescence units (RFU). On day 1, fluorescence distributions from all donors had the minimum after the background peak between log F of 3.55 and log F of 3.65. We therefore chose log F of 3.6 as the threshold for defining the cells as EGFP positive. Death rates and mean fluorescence intensity (MFI) of EGFP⁺ cells in donor samples were obtained from aligned individual distributions using this threshold.

(iv) Estimating EGFP degradation and production rate.

We assume that EGFP is produced and degraded at constant rate,

$$dG/dt=p-{\delta }_{GFP}G$$ (5)

where G is EGFP level at time t, and p and δ_GFP are production and degradation rates, respectively. This would result in an exponential rise from detection threshold G₀ to a plateau G* = p/δ_GFP,

$$G\left(t\right)=G^{*}-\left(G^{*}-G_0\right)\exp \hspace{0.17em}\left(-{\delta }_{GFP}t\right)$$ (6)

Our aim was to estimate EGFP production and degradation rates (p and δ_GFP, respectively) for use in the mathematical model of the experiment.

For fitting purposes, we needed to combine MFI of the cell samples followed during the first 24 h (from donors 15 and 23) with the MFI of the cell samples measured on days 1, 2, 3, and 4 (from donors 13, 14, 23, 81, 85, and 98 [1] and 98 [2]). We used the average MFI of the unsorted samples at 12, 15, and 18 h and the averages of the direct measurements of MFI in the sorted high cultures on days 2, 3, and 4.

Because the EGFP⁺ cells in the medium EGFP fluorescence range on day 1 were only a small fraction of all EGFP⁺ cells, we assumed that the EGFP⁺ cells that appeared during the first 18 h gave rise to mostly EGFP-high cells. The averaged MFI in sorted EGFP-high cells on day 1 was found from the fluorescence distributions of unsorted samples on day 1 and the sorting threshold for EGFP-medium and EGFP-high. We then fitted equation 6 to the combined early (12 to 18 h) data and EGFP-high data to obtain the average EGFP degradation and average protein production in cells sorted high. The estimate of the protein production in cells sorted medium was obtained from the average EGFP level on days 2 to 4 and the obtained EGFP degradation rate.

Modeling details. (i) Simulation parameters.

In a simple model in which infected cells start producing viral proteins at a constant rate after a postinfection delay, and do so for the rest of their life span, some parameters could be estimated directly from the experiment, and the rest were determined so as to reproduce experimental results.

The distribution of life spans from the start of protein production was chosen as lognormal, with the mean and standard deviation chosen so that they result in the average cell death rates for days 2 to 3 and days 3 to 4, similar to those experimentally observed in medium- and high-sorted cells. The probability density function for the natural logarithm of life span lnt_l (where lifetime t_l is in days) was given by normal probability density (defined by the mean and the standard deviation in parentheses): f_n(lnt_l; ln0.5,1) (see Fig. 5B).

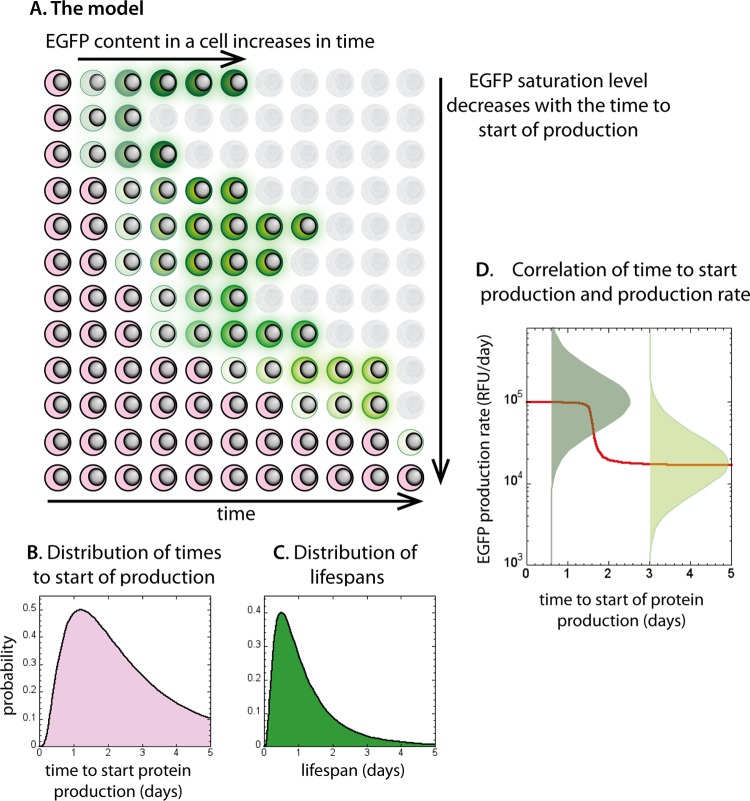
FIG 5.

The model and parameters used in simulation. Schematic representation of the model is shown in panel A. Cells with integrated HIV that have not yet started protein production are shown in pink. They start producing viral proteins at different, lognormally distributed times (B). Once cells have initiated viral protein production, they produce protein at a constant rate, and their EGFP content increases in time to a saturation level (cells turning green in panel A). EGFP saturation level is directly proportional to the rate of production of EGFP. The life spans for protein-producing cells are lognormally distributed (C) irrespective of their protein production rates. The distribution of protein production rates is negatively correlated with the production starting time (D). For each starting time, protein production rate has a lognormal distribution (green bell-shaped curves on log scale in panel D), but the peak of this distribution corresponds to a lower production for later starting times. This means that the cells that start producing protein later have lower average EGFP saturation levels (cells turning lighter green when starting producing later in panel A).

The number of new EGFP⁺ cells at the start of each day did not decay exponentially in time, which we would expect if all cells had the same probability of starting protein production after DNA integration. Therefore, we chose the probability density for time from infection to starting EGFP production (in days) to be lognormal, so that its natural logarithm lnt_p is distributed normally: f_n(lnt_p; ln1.2,0.8). The parameters for the start of protein production were chosen so that they give numbers of new EGFP⁺ cells as observed in the experiment, when combined with the average death rates (Fig. 5C).

EGFP half-life was set as 9 h from the estimate obtained by fitting.

Production rate had a lognormal distribution with the mean μ_p negatively correlated with the time between start of production and integration t_p. For the early producers, the mean early production rate p₀ was estimated from the exponential rise fit to the evolution of MFI in the high-sorted cell population. Standard deviation of lnp₀ was estimated as 0.8 from the width of the unsorted fluorescence distribution on day 1. The probability density function for the logarithm of the early production rate p₀ was f_n(lnp₀; 11.5,0.8), where production is in RFU/cell/day.

In order for the MFI of the fluorescence distribution in the unsorted samples to decrease after day 2, there has to be a negative overall correlation between the time to start production and production rate. We chose a steplike dependence of mean production rate and the start of production (a slow decrease until day 1.5, and then a fast decrease till day 2, and finally a slow decrease later) in order to reproduce the steplike decrease of MFI between day 2 and day 3. The results were not very sensitive on the exact choice of the function.

(ii) Simulation details.

In a typical simulation, we would have 2 × 10⁵ infected cells. At the start, each cell was assigned a time of virus entry (t_e) from a uniform distribution from 0 to 2 h (mimicking 2 h of spinoculation), fixed initial minimum delay (t_i) (6 h), time to start of production after the minimum delay (t_p), and life span (t_l) from the corresponding lognormal distributions, as well as a protein production rate (p) chosen from a positive normal distribution determined by its time to start production.

At the cell-dependent time, t₀ = t_e + t_i + t_p, a cell would start producing protein at its rate p, and its EGFP content would be updated according to equations 5 and 6 until its time of death, t_d = t₀ + t_l. Fluorescence distributions and EGFP⁺ cell numbers (with log F of >3.6) were collected at 12, 15, and 18 h and on days 1, 2, 3, and 4.

RESULTS

In an attempt to synchronize the infection, we spinoculated the stimulated peripheral blood lymphocytes (PBLs) from 7 donor samples with the HIV-EGFP virus for 2 h (see Materials and Methods for details). After 18 h of infection, AZT and raltegravir were added in order to prevent any second round of infection or delayed viral integration events, which could misalign the synchronized infection among different HIV-infected cells.

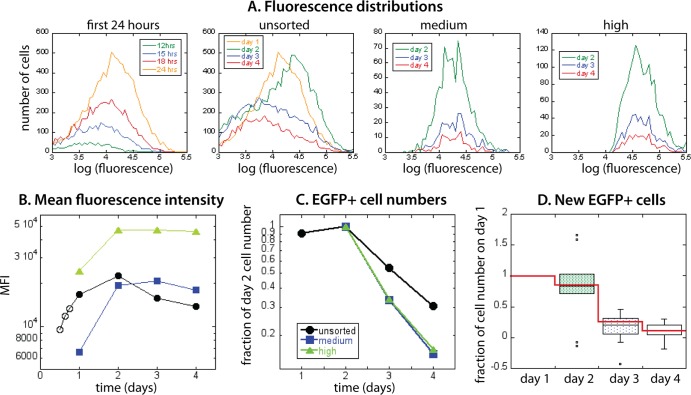
In order to study the early rate of EGFP production over the first day of infection, EGFP fluorescence was monitored every 3 to 6 h in two samples, starting at 12 h postinfection. As early as 12 h postinfection, we noticed a low peak in EGFP fluorescence appearing above the large autofluorescent peak (at 10² RFU in the cultures), representing the emergence of infected cells producing EGFP. From 12 to 24 h, we observed a steady increase in both the fraction and MFI of viable EGFP⁺ cells (we used viability dye to exclude dead cells), corresponding to an increasing number of cells commencing production of viral protein, as well as an increased EGFP content of infected cells already in the production stage (Fig. 1A).

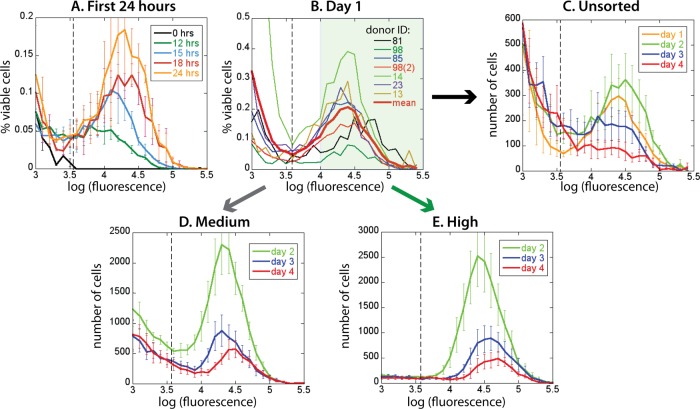
FIG 1.

Fluorescence distributions obtained in different phases of experiment. (A) The first EGFP⁺ cells appear 12 h postinfection, and their number and fluorescence increase during the first 24 h. (B) Fluorescence distributions of all donor samples on day 1 have similar positions of peaks, although they differ in the fraction of EGFP⁺ cells. On day 1, cells were FACS sorted into EGFP-medium (10³ < F < 10⁴; inside the white region in panel B) and EGFP-high (F > 10⁴; inside the green region in panel B). (C) Averaged fluorescence distributions of unsorted samples on day 1, day 2, day 3, and day 4 show that EGFP⁺ cell numbers and fluorescence first increase and later decrease (from day 2 onward). However, in the sorted EGFP-medium (D) and EGFP-high (E), cell numbers decline monotonically while fluorescence is not changing much. The dashed vertical lines in panels A to C represent the EGFP⁺ gate. Error bars represent variations in cell proportions (A) or numbers (C to E) across donor samples.

At 24 h, the samples varied in the absolute percentage of viable EGFP⁺ cells (reflecting the variability of permissiveness to infection across the donor population [5]) but had broad fluorescence distributions of similar width and mean fluorescence intensity (Fig. 1B). Following these infected cells over time, we observed that both MFI and number of productively infected cells were still somewhat increasing from day 1 to day 2, subsequently dropping in both MFI and cell number over days 3 to 4 (Fig. 1C).

Having a broad distribution of EGFP fluorescence at any time could have different origins. For example, in one picture, infected cells may increase their EGFP content to intrinsically different saturation levels, resulting in a distribution of fluorescence intensities. Alternatively, they may be increasing their fluorescence at different rates to an essentially similar final level or until death. By separating the EGFP⁺ cells with lower EGFP expression on day 1 from those with high EGFP fluorescence and following them over time, we could distinguish between these two possibilities.

The change of EGFP fluorescence distributions over time could also be an outcome of different scenarios. If the distribution of EGFP levels included cells that always have very low fluorescence, then the drop in mean fluorescence intensity on days 3 and 4 could be the result of the bright cells with high EGFP content dying earlier, leaving a larger proportion of the dimmer cells viable on later days. Another possibility is that all cells did not start viral protein (and EGFP) production at the same time after integration and that the cells that started producing later reached lower EGFP levels. Separating the cells that were EGFP positive on day 1 and then following their number and fluorescence would help us distinguish between these two processes.

In order to understand the variation in EGFP content, as well as untangle the possible correlations of viral protein production with infected cell death or start of viral protein and EGFP accumulation, we FACS sorted the viable cells into EGFP-medium (3 < log F < 4) and EGFP-high (log F >4) populations, as indicated in Fig. 1B. The proportion of infected cells was low (at most 3% of all viable CD4⁺ T cells), and although the sorting of cells on day 1 removed most of the cells not expressing EGFP, it still left part of the tail of the putatively uninfected peak. For consistency of the data analysis of EGFP⁺ cell numbers and MFI, we narrowed the definition of EGFP⁺ cells to the fluorescence interval 3.6 < log F < 4 (the dashed vertical line in Fig. 1 marks log F = 3.6, the EGFP⁺ threshold).

The changes in the averaged unsorted and sorted fluorescence distributions over time are shown in Fig. 1C to E. The sorting of cells into EGFP-medium and EGFP-high removed most of the background signal due to the putatively uninfected cells that did not express EGFP. Therefore, the sorted populations represent the cells that have started EGFP (and HIV protein) production before day 1, uncomplicated by the possible later appearance of new EGFP⁺ cells. By comparing the fluorescence and cell numbers in the unsorted and sorted productively infected cell populations over time, we could deduce how the start of viral protein production and cell death correlated with protein accumulation level and production rate.

Distribution of EGFP fluorescence.

The mean fluorescence intensity (MFI) of EGFP in unsorted and sorted cell cultures over 4 days, averaged over all donor samples, is shown in Fig. 2. We saw the first EGFP⁺ cells above background as early as 12 h postinfection (Fig. 1A and 2A). MFI then increased monotonically in the first 24 h (Fig. 2, open circles). At 24 h, we saw a broad distribution of EGFP levels across cells in each sample (Fig. 1). Upon sorting of EGFP⁺ cells into those with lower (“medium”) and higher (“high”) fluorescence, the MFI of medium-sorted EGFP⁺ cells (squares in Fig. 2A) was at sorting (on day 1) approximately 3 times lower than the MFI of the cells sorted as high (triangles in Fig. 2).

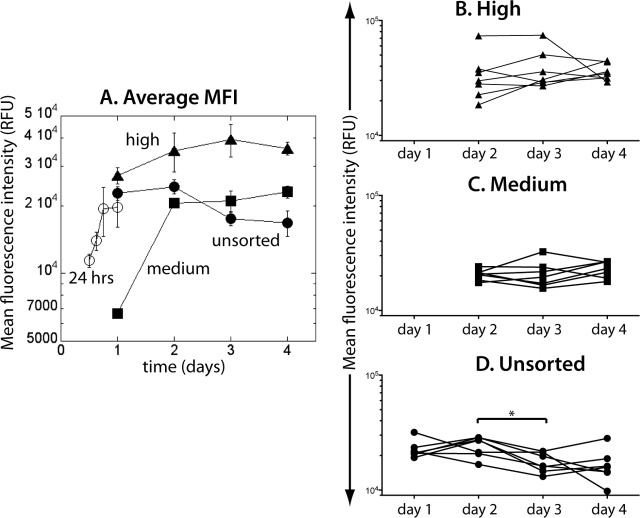
FIG 2.

Change of the average mean fluorescence intensity over time. During the first 24 h of infection, MFI increases monotonically (open circles in panel A). On day 1, cells were sorted into EGFP-medium (solid squares) and EGFP-high (solid triangles) and were followed in parallel with the unsorted cells (solid circles). (B and C) From day 2, neither MFI of EGFP-high nor of EGFP-medium changed significantly. (D) In the unsorted samples, MFI dropped significantly between day 2 and day 3.

However, 24 h later and over the next 2 days (days 2 to 4), both sorted cell populations had MFIs within the high range (>10⁴ RFU), suggesting that the early EGFP-medium state may have been transient. Although the cell numbers in the sorted cell cultures declined steadily over this period, their MFI appeared stable. Indeed, EGFP level in the sorted cultures did not change significantly over this period (high, Fig. 2B, P = 0.4861, Friedman test with Dunn's multiple comparison posttest; medium, Fig. 2C, P = 0.4861, Friedman test with Dunn's multiple comparison posttest, suggesting that the EGFP fluorescence had reached a plateau by day 2.

This is consistent with a picture of infected cells initially passing through a low/medium EGFP fluorescence stage and reaching a final fluorescence level that has an inherent broad distribution in the high range over the infected cell population. Interestingly, although EGFP-medium cells increased their MFI rapidly into the “high” range, they still had on average approximately 30% lower EGFP content than EGFP-high cells over the period from days 2 to 4.

In contrast, in the unsorted samples (black circles in Fig. 2A), after the initial increase, the average EGFP MFI decreased between day 2 and day 3 (P < 0.0145, Friedman test with Dunn's multiple comparison posttest; Fig. 2D).

As mentioned before, this could be either because the cells with a higher fluorescence died faster or because the cells becoming EGFP⁺ later had a lower final EGFP level. We shall investigate each scenario separately. However, in order to distinguish between these two possibilities, we first need to estimate the death rates of productively infected cells and the rates at which cells become EGFP⁺ on successive days.

Cell death and EGFP fluorescence.

To understand the interplay of EGFP content, viral protein production, and death of productively infected cells, we monitored the number of EGFP⁺-infected cells in sorted and unsorted cultures over time. However, in measuring cell death, we also needed to take into account the possibility of cell division. As a control experiment, we included in our analysis the cell dye PKH-26, in order to measure cell division by dye dilution. Consistent with previous studies (19), we found that EGFP-producing cells do not divide in culture (data not shown), which is most likely due to Vpr-induced cell cycle arrest, so we ignored division of infected cells as a factor in total infected cell number.

Figure 3A shows the average decay of the number of EGFP⁺ cells over a 3-day period, in the unsorted, EGFP-medium, and EGFP-high samples. Samples were standardized/scaled by the number of EGFP⁺ cells present on day 2. In the unsorted populations, EGFP⁺ cell numbers decayed more slowly than in the sorted populations. This is an indication that the EGFP-negative cells, which make up a large proportion of the unsorted cell cultures, could contain a potential source of new EGFP-positive cells (infected cells that are yet to start actively producing EGFP) that appear later. Because of this, the observed decay of the number of productively infected cells could reflect the balance of cell death and possible later appearance of new productively infected cells from the large EGFP-negative cell population. By FACS sorting cells into EGFP-medium and EGFP-high on day 1, we removed the majority of EGFP-negative cells, so the sorted cell cultures reflected the infected cell death dynamics more directly. We used the decay of EGFP⁺ cell numbers in the sorted cell cultures to estimate the death rate of productively infected cells.

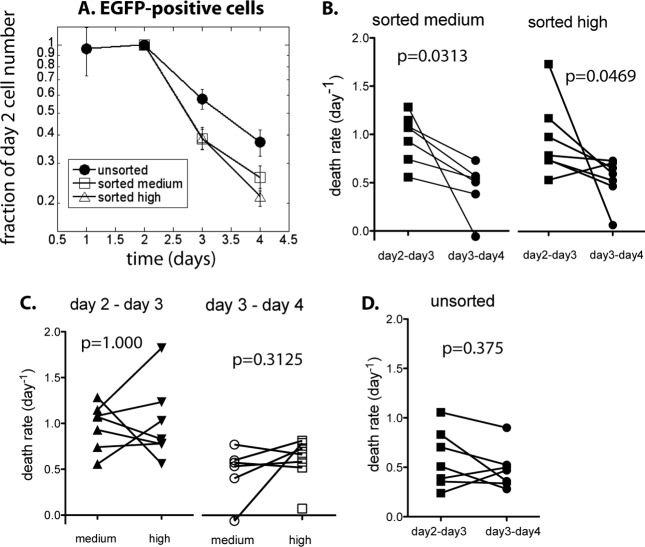
FIG 3.

Cell death in unsorted and sorted cell cultures. (A) Change in EGFP-positive cell numbers over time, scaled by the cell number on day 2. From day 2, cell numbers decline in all samples. Decline in the unsorted cell populations is slower than in the sorted. (B) In sorted cell cultures, the decline rate slows down in time significantly. (C) There is no difference in the rates of decay of cell numbers between EGFP-medium and EGFP-high cells in the same time period. (D) However, in the unsorted cell populations, EGFP⁺ cells are lost at the same rate between days 2 and 3 and between days 3 and 4.

Slowing down of death rate in time.

If the probability of the cells dying were the same in all cells and constant over time, then the decay would be a single exponential and a straight line on a logarithmic scale. However, Fig. 3A indicates that the death rates of productively infected cells could slow down over time.

As a first estimate, we compared the average decay rates of the number of EGFP⁺ cells between days 2 and 3 postinfection to the average decay rates between days 3 and 4 postinfection (Fig. 3A). In the first period (days 2 to 3), the decay rates are 0.973 day⁻¹ in the sorted medium and 1.004 day⁻¹ in the sorted high cultures (corresponding to half-lives of 0.71 days and 0.69 days, respectively), while in the second period (days 3 to 4), the decay rates are 0.445 day⁻¹ in the sorted medium and 0.564 day⁻¹ in the sorted high cultures (half-lives of 1.56 days and 1.23 days, respectively). This represents an average 50% reduction of death rate from the period between day 2 and 3 to the period between day 3 and 4.

The decay rates of EGFP⁺ cells in individual samples for the “medium” and “high” cells are shown in Fig. 3B. In both types of sorted cultures, the slowing down of the cell loss from the first 1-day period to the next was statistically significant (medium, P = 0.0313; high, P = 0.0469; Wilcoxon paired test), with cell death increasing in the later period only in one sample (from donor 81 in sorted EGFP-high).

These results suggest that the death rate of productively infected cells slows down in time since infection (or in other words, that the half-life of surviving cells increases in time). Our understanding of the HIV life cycle is based largely on estimates of average turnover of productively infected cells, which would imply that the life spans would be exponentially distributed, although they could still in principle vary widely over cell population. The apparent slowing down of turnover of productively infected cells means that infected cells are a heterogeneous set in terms of their intrinsic longevity, with a significant proportion of longer-lived cells (larger than expected from an exponential distribution of life spans). Such a distribution of life spans may be consistent with a lognormal distribution or a similar distribution with a “fat tail” (4, 20).

Death rate of productively infected cells is not correlated with EGFP level.

If the infected cells with higher expression of EGFP died faster, then we would expect that (i) in the fluorescence distributions for the sorted cell cultures (Fig. 1D and E), the cells with higher EGFP fluorescence would disappear faster, so the distributions would progressively lose the high-fluorescence part, (ii) consequently, MFI of both the unsorted and the sorted cell distributions would decrease in time, and (iii) the death rate of productively infected cells in the EGFP-medium samples would be lower than in the EGFP-high samples, because they have consistently lower MFI (Fig. 2A).

However, there is no evidence of the decrease of MFI in the sorted cell cultures. Instead, we have a consistent level or even a slight increase in MFI over time (Fig. 2B and C). The death rate of EGFP-medium cells is not significantly different from the death rate of the EGFP-high cells (Fig. 3C; P = 1.000 for medium compared to high on days 2 to 3, and P = 0.3125 on days 3 to 4; Wilcoxon paired test). This suggests that the distribution of productively infected cell life spans is the same for all cells once they start productive infection and that it is not related to the level of EGFP in a cell.

Time to becoming EGFP positive.

The decay of the EGFP⁺ cells in the unsorted samples from their peak at day 2 appeared exponential and slower than the decay of the cells in the sorted cultures (Fig. 3A). Indeed, the analysis showed that the difference in death rate between the two consecutive time periods in the unsorted population was not significant (Fig. 3D, P = 0.375, Wilcoxon matched pair test), while the EGFP⁺ cell decay in the unsorted samples was also significantly slower than in the sorted samples (P = 0.0027 for days 2 to 3 and P = 0.0289 for days 3 to 4, Friedman test with Dunn's multiple comparison posttest). The average decay rate was 0.532 day⁻¹, consistent with the half-life of productively infected cells estimated from in vivo studies of viral decay dynamics under therapy. Thus, the unsorted cell population behaved as expected from the in vivo studies of viral dynamics after treatment, with a constant decay rate of productively infected cells. However, this is quite different from initially rapid and then slowing death rate of sorted cells.

Since the main effect of sorting was to eliminate a large proportion of cells that were not expressing EGFP, it seems likely that the reason for this slower decline in EGFP⁺ cell numbers in unsorted cell cultures is that the death of productively infected cells is being compensated by the emergence of new EGFP⁺ cells over time. That is, although we added AZT and raltegravir to block integration 18 h postinfection, there may be a number of cells in the silent phase that have already integrated the HIV genome but did not immediately proceed to productive infection. Indeed, it seems highly likely that there might be a distribution in the times from provirus integration to significant EGFP production and positive expression of EGFP.

Using the EGFP⁺ cell numbers available for each day in the unsorted cell population belonging to each donor, and death rates found in the sorted cultures for each period, we can estimate how many cells would be present the next day if the changes in cell numbers were caused only by death. For all donors, there are more EGFP⁺ cells present the next day in the unsorted population than expected just from cell death. The excess cells present each subsequent day can be interpreted as new EGFP⁺ cells appearing during this period. The estimated number of new EGFP⁺ cells at the end of each 1-day period is shown in Fig. 4.

FIG 4.

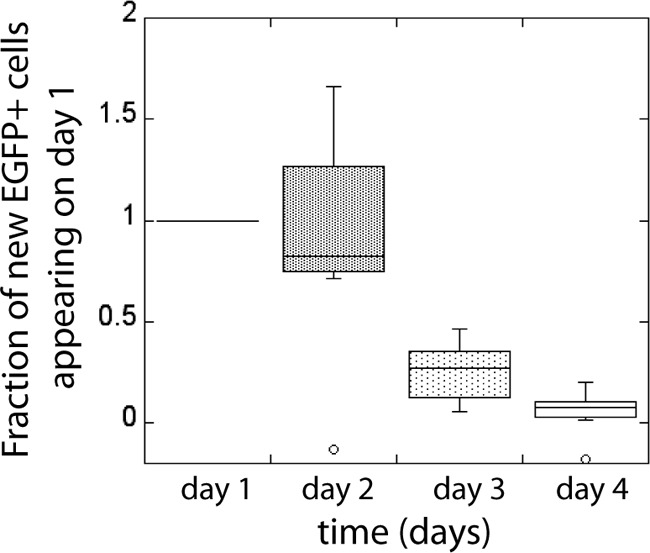
New EGFP⁺ cells in the unsorted samples appearing on each day. The number of new EGFP⁺ cells appearing on consecutive days is scaled by the number of new EGFP⁺ cells appearing on day 1.

Since at the time of infection there were no EGFP⁺ cells, all EGFP⁺ cells after 1 day were “new” EGFP⁺ cells. After 48 h, there were almost equally as many new EGFP⁺ cells that were not positive a day before. The number of new EGFP⁺ cells diminished after day 2, but new cells were still appearing on day 3 and day 4. The number of new EGFP⁺ cells on consecutive days did not decline exponentially, suggesting a lognormal (or other “fat-tailed”) distribution of times from infection to start of EGFP expression above the threshold (log F = 3.6).

Association between start of EGFP production and EGFP fluorescence.

We have found that the drop in EGFP fluorescence in the unsorted cell cultures between day 2 and day 3 could not be explained by increased death of the cells that had accumulated higher levels of EGFP. On the other hand, we have also found that cells can start EGFP and viral protein production a long time after provirus integration. The new EGFP⁺ cells that appear later than 24 h postinfection would contribute to the infected cell fluorescence distributions of the unsorted cultures on days 2 to 4 but not to the cultures that were FACS sorted on day 1. Therefore, the drop in MFI that appears only in the unsorted samples between day 2 and day 3 suggests that the cells that start producing EGFP⁺ later have reduced EGFP expression compared to that of the cells that started to produce earlier.

Since we could not directly measure the start of EGFP production and fluorescence of individual cells, we used mathematical modeling to investigate the plausibility of this scenario and to estimate the type of correlation between the time to start of EGFP production and EGFP production rate.

EGFP fluorescence and EGFP production and degradation rate.

FACS analysis measures the EGFP fluorescence of cells, which is directly proportional to the amount of EGFP protein in the cell cytoplasm at any time. If EGFP synthesis proceeded at a constant rate, and a fixed proportion of it were degraded per unit of time, the EGFP content would rise from zero to a plateau. The final plateau level of EGFP would then represent the balance between EGFP production and degradation and would be directly proportional to the ratio of the rate of synthesis to the degradation rate. The change in MFI in Fig. 2A supports this model: MFI increases over the first 24 h, and the cells sorted as EGFP⁺ on day 1 (sorted cultures) have a stable MFI level from day 2 onward.

The time taken to reach the plateau can give us an indication of the half-life of EGFP: fluorescence will reach the plateau faster for higher degradation rate (or shorter EGFP half-life). If we assume constant EGFP production and degradation rates, we can estimate these two parameters by fitting the exponential rise of MFI in the high-sorted cell population, as explained in Materials and Methods. This gives the estimate of the half-life of the Nef-EGFP fusion protein as approximately 9 h, which is much faster than 26 h that had been estimated as the half-life of free EGFP (21).

We estimated the mean EGFP production rates for the EGFP-high- and EGFP-medium-sorted cells as 6.0 × 10⁴ and 4.2 × 10⁴ RFU/day, respectively, meaning that the mean EGFP production rate in the medium-sorted culture was around 30% lower than in the samples sorted as EGFP-high. However, the distributions of EGFP fluorescence (and the associated EGFP production rates, since the production rates are proportional to EGFP fluorescence at the plateau) in these sorted cultures were broad and partly overlapped.

Assuming that the EGFP decay rate is relatively constant among cells from the start of production, cell fluorescence at the plateau is a measure of EGFP production rate (and thus the production rate of Nef protein). Our results suggest that viral protein production rates have a wide distribution among cells and that this distribution shifts toward lower average EGFP production rates for the cells becoming EGFP positive at later times.

The conceptual model we describe of the delay until EGFP production in an infected cell and then the sudden switch from no EGFP production to full production is likely an oversimplification of a true process. The delay from infection to EGFP production may in part occur because of the variation in the time to proviral integration, if the completely reverse-transcribed DNA can persist in activated cells for similarly long periods of time as in resting cells (22), without being degraded by cellular defense mechanisms. However, this delay cannot account for greater than an 18-hour delay, since raltegravir was added at this time. Following this, viral protein production may be delayed due to either a poor integration site or cellular factors inhibiting viral activation. Once viral protein production is initiated, it may increase at rates that could vary across cell population, until they reach, again variable, maximum levels. However, the fastest accumulation of EGFP would be after production had reached the plateau, and because of the high EGFP degradation rate, cells would cross the EGFP detection threshold when the production rate was constant. The delay time in our model would then consist of the time without any production and the time during which viral proteins were being translated but have not yet accumulated to detectable levels.

Modeling the dynamics of HIV protein production and cell fate during primary cell infection.

Our analysis separated different aspects of cellular and viral dynamics in order to explain the observed features of the experimental data. However, our estimates of different parameters of the HIV replication cycle were made by analyzing different aspects of infection independently and in isolation. A major question is whether the factors we considered, acting together as schematically represented in Fig. 5A, would reproduce the behavior of the system.

In setting up the simulation, we used the parameters estimated from experimental results. The distribution of EGFP production rates was taken to be lognormal in order to reproduce the bell-shaped appearance of the fluorescence distributions of sorted cells on log scale (Fig. 1D and E), with standard deviations roughly estimated from the width of the unsorted fluorescence distributions on day 1. Lognormal distributions were also used to represent the experimental fat-tailed distributions of EGFP⁺ cell life spans (Fig. 5C) and the times from infection to the start of EGFP production (Fig. 5B). The parameters for the lognormal distribution (the mean and the standard deviation of log-life span) of life spans were chosen so that they reproduce the observed average death rates between days 2 and 3 and between days 3 and 4. The distribution of times to start of production was chosen so that it approximately reproduced the average experimental values on days 1, 2, 3, and 4. Different types of fat-tailed distributions roughly following the same pattern at the experimental time points would have given the same result. EGFP degradation rate was taken as 2 day⁻¹, as estimated from the MFI of sorted cells. However, the results were not strongly sensitive on this particular choice of parameters. Thus, this simplified model could essentially be described by three distributions, for the delay between infection and the start of production of viral proteins, the life span of cells after starting protein production and protein production rate, and one constant parameter for EGFP degradation rate.

Using these three distributions and one parameter, where the means were chosen based upon experimental data, we modeled the changes in fluorescence and EGFP⁺ cell numbers over the first 24 h, the distribution of fluorescence on the first day, and the subsequent behavior of the cells sorted as EGFP-high and EGFP-medium.

A stochastic simulation consisted of 2 × 10⁵ infected cells in total, followed over 4 days. At the start, each infected cell was allocated parameters for the time to initiate EGFP production, the life span of productive infection (time from initial protein production to death), and the level of EGFP production, drawn from the lognormal distributions of these parameters. In each EGFP-producing cell, the fluorescence increased to a plateau, the increase described by exponential rise from the interplay of EGFP production and degradation (equation 6).

This simulation could reproduce the general shape of fluorescence distributions and the change in MFI in sorted cell cultures, as well as the appearance of new EGFP⁺ cells and the survival curves of EGFP⁺ cells in the sorted and unsorted samples. However, one aspect of cell behavior that could not be reproduced with such a minimalist model in which all parameters were uncorrelated was the decline in MFI in the unsorted population. That is, although the overall cell number in the unsorted population could be faithfully reproduced, we did not see the observed decrease in EGFP fluorescence between day 2 and day 3, but the MFI in the unsorted distribution stayed constant during this period. Even when we added the assumption that the cells that produce EGFP and viral proteins faster have shorter life spans, we were not able to reproduce the observed decline in MFI, but it drastically changed the decline of cell numbers and the appearance of the sorted distributions.

In the next set of simulations, we required that the cells that initiated protein production later also had on average a lower mean EGFP production rate. In this case, the mean of the lognormal distribution of production rates was a monotonically decreasing function of the time to start production, with the same standard deviation (Fig. 5D). Thus, in this set of simulations, the distributions were again estimated from experimental results, with only the correlation between the time of start and production rate adjusted in order to obtain the observed decrease in MFI in unsorted cells. For simplicity, we used a steplike decrease of production rate with time (Fig. 5D). The shape of MFI time dependence in sorted cells at later times is similar to the dependence of protein production rate on the start of production, because in our model of EGFP production and destruction, the final EGFP fluorescence of a cell is proportional to EGFP production rate.

The fluorescence distributions of the simulated infected cell population closely mimicked the observed unsorted and sorted infected cell behavior over time in shape, infected cell number, and fluorescence (Fig. 6A). Tracking of the cell numbers in the sorted cell populations after simulating the sorting protocol at 24 h postinfection also revealed a two-phase decay seen in vitro, while the unsorted population exhibited single-exponential decay (Fig. 6B), with new EGFP⁺ cells appearing in numbers similar to experimental numbers each day (Fig. 6C). Importantly, in the evolution of MFI over time, we obtained the drop of the MFI between day 2 and day 3 as in the experimental unsorted population (Fig. 6D). In the sorted cells, MFI of the cells sorted as medium increased into the high range but always stayed below the MFI of the cells sorted as EGFP-high. This effect in the sorted populations was not the result of the correlation between the timing of EGFP production and production rate (since the average production rate did not begin to decrease till after day 1) but was just a consequence of having a distribution of production rates, with the lower end of the distribution becoming EGFP⁺ later than the higher end. Thus, the observed infected cell dynamics can be explained by simple distributions of parameters, provided that the average protein production rate is negatively correlated in a steplike way to the timing of production. We note that although we used lognormal distributions for the different parameters in the model, any “fat-tailed” distribution (such as gamma distribution) would produce a similar result.

FIG 6.

Reproduction of the main experimental results by the model. (A) Fluorescence distributions have the same general appearance over time, with MFI of the unsorted distribution decreasing after day 2, and the sorted distributions stable after day 2. The EGFP⁺ cell numbers decline faster in the sorted (medium and high) cell populations than in the unsorted, with decline rate slowing down in time (C). The new EGFP⁺ cells appearing on each day (red line in panel D) closely follow the estimates from the experiment (box plot in the background of panel D).

DISCUSSION

Studies of in vivo HIV viral kinetics under therapy have provided significant insights into the average replication cycle of HIV in infected cells. The exponential decline of viral load observed in vivo on ART would at first glance imply a constant death rate of productively infected cells. However, it is possible that individual infected cells have nonexponential distributions of life spans and intracellular delays and still produce an overall dynamic of exponential decay (23). The nonexponential variation in the duration of the silent phase can lead to different estimates of the turnover of infected cells and free virus clearance (24) and cause slowing down of the decay of viral load in the late stages of drug treatment (25). Ignoring the variation in both the infected cell life spans and the intracellular delays can cause large underestimates of the basic reproductive ratio of the virus and of the efficacy of the antiretroviral therapy necessary to control the infection (23). If a large variation in viral protein production rates implies a similar variation in the rates of release of new virions, which then also on average negatively correlates with the timing of the start of production, this could further modify our estimates of the parameters of HIV infection and our understanding of viral decay during treatment.

Previous analyses of viral kinetics in vivo have presented a simplified model of the behavior of the average productively infected cell. In this in vitro study, we investigated the distribution of virus protein production rates, infected cell life spans, and silent-phase times across the infected CD4⁺ T cell population. Our analysis suggests that the simple average behavior may be at odds with some underlying complexities. In particular, our analysis suggests that cells differ in their susceptibilities to death, with an accumulation of longer-lived cells over time. On the surface, this seems inconsistent with the observed exponential decay of virus in vivo. However, we also show that the faster-dying, early-producing cells were replaced by infected cells with delayed viral protein production profiles over the first few days of infection. This resulted in exponential decay of productively infected cells in the almost synchronously infected cell culture and may contribute to the observed exponential decay of viral load in patients receiving drug treatment.

Despite every effort to ensure synchronized infection by adding raltegravir and AZT, cells appeared to switch on fluorescence after a wide range of postintegration times, with around 15% of cells that became EGFP⁺ 2 days or more postinfection. The rate of EGFP production seemed slower in the cells that initiated production later. This negative correlation is similar to the results observed in synchronously infected Jurkat cells, where the probability of starting translation of viral proteins has been associated with the position of the viral integration site, activation status, and availability of Tat protein. The activated infected CD4⁺ T cells with disadvantageous integration sites had lower probabilities of transactivation and also lower EGFP expression (14).

Our study suggests that only approximately 45% of all cells that became EGFP positive during 4 days had done so by 24 h postinfection. This has implications for studies wishing to separate virus-producing from transcriptionally silent infected cells (26), as just because a cell was not producing EGFP at 24 h does not mean it may not have done so later in the days immediately postinfection. Determining the mechanisms of the delay in viral protein production also has important implications for understanding latency in vivo. The delay may occur due to a disfavored integration site of the virus or alternatively because of a cellular activation state or a cofactor that inhibited viral activation. That there appears a wide distribution in times from infection to viral production, and a decrease in protein production in cells that produce virus later, suggests quite a different picture from the traditional concept of a simple dichotomy of productive versus latent infection. Understanding this distribution and the mechanisms behind it may have important implications for therapies aimed at activating and purging the latent reservoir (27).

Surprisingly, we found that the EGFP⁺ cell life span was not correlated to EGFP fluorescence and therefore to EGFP production in a cell. Since EGFP fluorescence and content was found to directly correlate with the quantity of p24 in the supernatant of Jurkat cells in a similar experiment (13), this might suggests that cell death is uncorrelated with viral protein content and viral protein production rate. However, the life span of infected cells since infection would be longer for the cells that have a longer silent phase, i.e., the cells that also have lower EGFP production rates. It has been shown recently that HIV integration can cause CD4 cell death and that integrase inhibitors such as raltegravir can rescue cells (28). The lack of correlation between viral protein production level and the death of productively infected cells may suggest that viral proteins may not be cytotoxic in the cells that have survived the integration events.

Our in vitro study did not incorporate immune mechanisms such as CD8⁺ T cells specific for the virus. The in vivo death rate of infected cells may be influenced by cell killing by host cytolytic effector mechanisms that are not represented in the in vitro model. Recognition of infected cells would depend on the viral protein expression and therefore on protein production rate, which could lead to the negative correlation between viral protein production rate and productive life span of infected cells in vivo. In addition, the in vivo dynamics may be different following infection of other cell types, including CD4 cells that are not recently activated. However, the similarity between the death rate of infected cells we observe in vitro and that estimated in vivo is consistent with arguments that CD8⁺ T cells may not affect the death rate of productively infected cells (29–31).

Our in vitro studies have a number of limitations. First, it was necessary to stimulate PBLs in vitro to achieve sufficient infection rates for sorting. This may have contributed to our observation of the relatively uniform EGFP content of sorted cells analyzed later in infection. This would seem initially to contradict the previous observation from confocal microscopy imaging (6–8) that a population of high- and low-virus-producing cells may coexist. However, we note that we also observed that cells becoming EGFP positive later in infection must have lower EGFP content. Thus, a cross-sectional analysis of images (as performed in references 6 and 7) might show a mix of recently infected cells that have higher virus production rates and cells infected some time ago. Identifying whether there are phenotypic differences between cells producing EGFP early and late in vitro may be helpful.

In this experiment, we measured the EGFP content in HIV-infected cells as a proxy for viral protein production but have not directly investigated production and release of new virions. Since FACS identifies only EGFP content in a cell, it is in principle possible that some cells produced high levels of viral protein but failed to efficiently assemble and release virus, whereas other cells released new virions more efficiently and therefore had lower protein content. In a single-cell experiment with HIV-EGFP-infected Jurkat cells, EGFP fluorescence and viral protein production positively correlated with the virion release rate (13), but this might not be true in healthy PBLs. In addition, since the new budding virions use the host cell membrane proteins to generate an envelope, it is possible that this process may increase the probability of cell death, so that cell death rate may correlate with the rate of release of new virions. One future challenge would be to directly measure virus release by normal EGFP-HIV-infected CD4⁺ T cells in a single-cell experiment.

The study of viral dynamics has been crucial for our understanding of HIV infection and has been used to challenge the way we treat infected individuals. In this study, we measured the dynamics of viral infection in vitro. We showed that this system recapitulates the average behavior of the total infected cell population, as expected from in vivo studies of viral dynamics. However, our study revealed that the behavior of the total infected cell population masks the inherent heterogeneity of the infection, which exhibits a broad range of different trajectories. The wide distribution of times from infection to viral protein production could combine with broad distributions in protein production levels and infected cell life spans to reproduce the average dynamics observed in vivo. Extrapolating from our results using short-term in vitro culture, we may speculate that infected cells could form a quasi-continuum of increasing silent phases and decreasing viral protein production rates, with productively infected and latently infected cells representing successive ranges within this continuum. Future studies will be needed to investigate the mechanisms underlying these broad distributions and whether this contributes to immune control in vivo.