Abstract
In nature, the protonation of oxo bridges is a commonly encountered mechanism for fine-tuning chemical properties and reaction pathways. Often, however, the protonation states are difficult to establish experimentally. This is of particular importance in the oxygen evolving complex of Photosystem II, where identification of the bridging oxo protonation states is one of the essential requirements toward unraveling the mechanism. In order to establish a combined experimental and theoretical protocol for the determination of protonation states, we have systematically investigated a series of Mn model complexes by Mn K pre-edge X-ray absorption spectroscopy. An ideal test case for selective bis-μ-oxo-bridge protonation in a Mn-dimer is represented by the system [MnIV2(salpn)2(μ-OH(n))2](n+). Although the three species [MnIV2(salpn)2(μ-O)2], [MnIV2(salpn)2(μ-O)(μ-OH)]+ and [MnIV2(salpn)2(μ-OH)2]2+ differ only in the protonation of the oxo bridges, they exhibit distinct differences in the pre-edge region while maintaining the same edge energy. The experimental spectra are correlated in detail to theoretical ly calculated spectra. A time-dependent density functional theory approach for calculating the pre-edge spectra of molecules with multiple metal centers is presented, using both high-spin (HS) and broken-symmetry (BS) electronic structure solutions. The most intense pre-edge transitions correspond to an excitation of the Mn-1s core electrons into the unoccupied orbitals of local eg character (dz2 and dxy based in the chosen coordinate system). The lowest by energy experimental feature is dominated by excitations of 1s-α electrons and the second observed feature is primarily attributed to 1s-β electron excitations. The observed energetic separation is due to spin polarization effects in spin-unrestricted density functional theory and models final state multiplet effects. The effects of spin polarization on the calculated Mn K pre-edge spectra, in both the HS and BS solutions, are discussed in terms of the strength of the antiferromagnetic coupling and associated changes in the covalency of Mn-O bonds. The information presented in this paper is complemented with the X-ray emission spectra of the same compounds published in an accompanying paper. Taken together, the two studies provide the foundation for a better understanding of the X-ray spectroscopic data of the oxygen evolving complex (OEC) in Photosystem II.
Keywords: X-RAY ABSORPTION SPECTROSCOPY, XANES, MN DIMERS, OEC, METALLOPROTEIN, TD-DFT, BROKEN SYMMETRY
INTRODUCTION
Protons are essential components of countless chemical reactions, but are often difficult to identify with widely employed structure determination techniques such as X-ray diffraction or EXAFS (extended X-ray absorption fine structure). This is particularly true for the active sites of metalloproteins, where knowledge of the proton count and protonation sites would provide required structural information for the formulation of feasible mechanisms. Examples for such cases are the water-splitting reaction of the oxygen evolving complex (OEC) of Photosystem II (PSII) or the hydrogen peroxide disproportionation reaction of Mn catalase.1,2,3,4,5,6,7,8 In these and other systems, oxo-bridges between metal atoms are known to be protonated and de-protonated in the catalytic steps, thus allowing the catalytic cycle to be completed under physiological conditions.9
For small molecules, it may be possible to identify protons in a crystal structure, however, in the vicinity of elements with much higher masses it is unlikely that the electron density that belongs to the hydrogen atoms can be resolved. Several spectroscopic methods are sensitive to protonation states including vibrational (IR, resonance Raman) and electron paramagnetic resonance (EPR) techniques (electron nuclear double resonance (ENDOR), electron spin echo envelope modulation (ESEEM), or hyperfine sublevel correlation, (HYSCORE)).1,10,11,12,13 These methods can potentially provide a direct probe of ligand protonation state. However, due to experimental complications, such as spin relaxation and spectral crowding, the desired information is often not attainable in practice. Thus, alternative methods of establishing protonation patterns are highly desirable.
In the following back-to-back studies,14 we explore X-ray absorption (XAS) and X-ray emission spectroscopy (XES) as means to experimentally establish ligand protonation states. X-ray based methods have the advantage of being element selective and independent of metal spin state. Thus the protocols established in the present studies have broad general applicability. The pre-edge region of metal K-edge XAS spectra is a well-known probe of metal oxidation state and site geometry. As such, indirect correlations between pre-edge intensities and the presence of terminal oxos vs. terminal hydroxos have been made.15 However, a detailed interpretation of the pre-edge region requires the close interaction between theory and experiment. Time-dependent density functional theory (TD-DFT) approaches for the prediction of Fe and Mn K pre-edges have been established for monomeric systems.16,17,18 However, applications to more complex multimetallic systems are relatively limited and have primarily focused on the rising edge.19,20,21
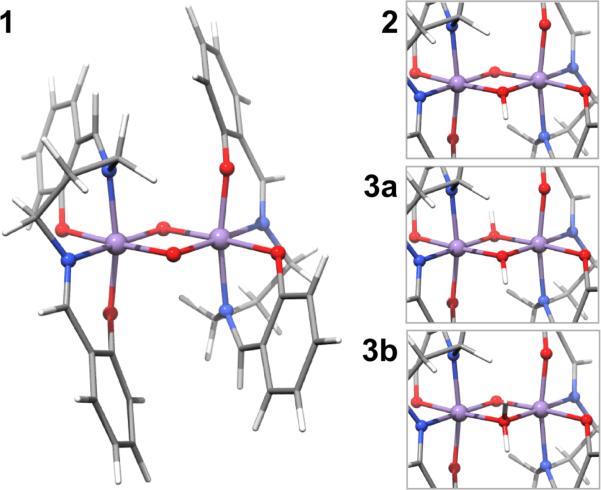
In order to rigorously assess the informatiton content of the metal K pre-edge region and its sensitivity to protonation state in more complex multimetallic systems, we have undertaken a systematic investigation of a series of Mn dimers. The three complexes were first reported by Baldwin and coworkers22 and can be described by the general formula [MnIV2(salpn)2(μ-OH(n))2](n+), where the protonation state of the bridging oxygen atoms are varied from a bis-oxo species (1) to an oxo/hydroxo (2) and finally to a doubly protonated species (3) (Figure 1, Chart 1). In principle the doubly protonated species may be described as either a bis-μ-hydroxo (3a) or a μ-oxo/μ-aquo species (3b). While the former is chemically more reasonable, we nevertheless assess the ability of XAS to distinguish between these two possibilities. We also note that this is relevant in view of proposed structural models for the OEC, which formulate an aquo bridge in the O5 position.23 Furthermore, we note that this series of model complexes represents the only set of Mn complexes where three protonation states of the oxo bridges could be isolated without changes in the oxidation state of the Mn centers. Thus, this series serves as an ideal test set for the present investigation.
Figure 1.
Optimized structures of compound 1 (left) and details of the protonated cores 2, 3a, and 3b (top to bottom on the right). Color code for the atoms as follows: Mn purple, O red, N blue, C grey, H white.
Chart 1.
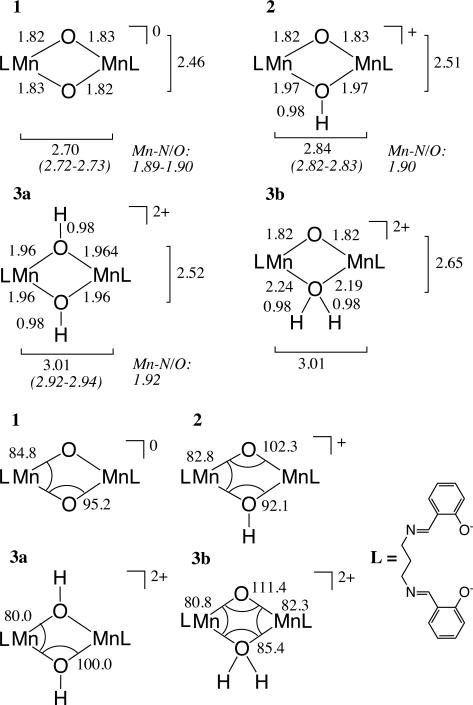
Interatomic distances in Å (top) and selected angles in degrees (bottom) of the MnIV dimer cores, distances from EXAFS measurements are given in italics. L represents the salpn ligand, which is depicted on the bottom right.
In this paper, DFT methods are used to explore the geometric and electronic structures, as well as the magnetism of these complexes. The geometries and electronic structures obtained here are then used for both the XAS (this paper) and the XES calculations (accompanying paper, Ref. 14). In the present paper, we establish the computational approach for the calculation of metal pre-K-edge XAS of antiferromagnetically coupled dimers. A time-dependent DFT approach is utilized implementing both high-spin and broken symmetry electronic structure solutions. The current study forms the foundation for future X-ray spectroscopic investigations of the OEC.
MATERIALS AND METHODS
Synthesis of sample preparation
The synthesis of compounds 1, 2 and 3 has been published22 and was followed in this work. To maximize the yield of 3 and avoid the presence of possible decomposition after reaction with water, it was synthesized at SSRL (Stanford Synchrotron Radiation Laboratory), immediately prepared for data collection and frozen in liquid N2. The samples, diluted with BN (< 5% weight) in Al holders sealed with Kapton tape, were stored under inert atmosphere until data collection in the He-filled cryostat. UV-visible signatures and XAS spectra of all compounds were compared to previously published data to establish sample purity.
XAS measurements
XAS data were collected at SSRL on beam-line 9-3 under ring condition of 3.0 GeV and 150 mA. The intensity of the incident X-rays were monitored by an N2-filled ion chamber (I0) in front of the sample. The radiation was monochromatized by a Si(220) double-crystal monochromator. A 9 keV cutoff mirror in combination with 50% detuning of the monochromator was utilized to minimize higher harmonics. Data were collected as fluorescence excitation spectra with a Ge element detector (Canberra). The energy was calibrated by assigning the pre-edge peak of KMnO4 (6543.3 eV). The standard was placed between two N2-filled ionization chambers (I1 and I2) after the sample. The sample was kept at a temperature of 10 K in a liquid helium flow cryostat to minimize radiation damage. The X-ray flux at 6.6 to 7.1 keV was 5.9 – 6.2 × 109 photons × s−1 × mm−2. For the sample most sensitive to radiation damage (3), the total number of photons deposited was 3.0 × 1013. For each sample, no XANES shift was observed from the first to the last scan (see Figure S3). The energy resolution, considering the natural line width of the 1s hole of ~1.16 eV and the instrumental resolution of ~0.87 eV, is ~1.45 eV. The experimental resolution is obtained with ΔEdivergence of 0.56 eV with a 2 mm vertical slit and a source distance of 18.5 m, ΔEmono/E for Si(220) of 1 × 10–4, and at the Mn K edge, ΔEmono is 0.66eV.
Analysis of XAS Spectra
The X-ray absorption XANES regions were fit using the program BlueprintXAS.24 Both the pre-edge and edge jump regions of the spectra were fit, and out of the 100 generated fits at least 24 reasonable fits were included for a statistically significant average. From these averages, peak areas and intensity-weighted average energies are reported (see Table 2). All of the spectra we re normalized to an edge intensity of 1 based on the intensity value of the edge region fit component. The pre-edge areas in Table 2 were obtained from the BlueprintXAS program and subsequently multiplied by 100.
Table 2.
Intensity-weighted average energies (IWAEs) and areas for the total pre-edge region and individual peaks from experiment and calculation (high spin and broken symmetry).
| Total | 1 | 2 | |||||
|---|---|---|---|---|---|---|---|
| Peak (eV) | Areaa | Peak (eV) | Areaa | Peak (eV) | Areaa | ||
| exp. | 1 | 6542.1 | 36.17 | 6541.0 | 11.68 | 6542.7 | 24.52 |
| 2 | 6542.1 | 26.02 | 6540.7 | 8.50 | 6542.7 | 17.53 | |
| 3 | 6541.8 | 17.28 | 6540.5 | 7.62 | 6542.7 | 9.66 | |
| calc, HS | 1 | 6542.1 | 1.72 | 6541.3 | 0.79 | 6542.9 | 0.93 |
| 2 | 6542.5 | 1.41 | 6541.1 | 0.51 | 6543.2 | 0.90 | |
| 3a | 6542.2 | 1.19 | 6541.5 | 0.84 | 6544.0 | 0.35 | |
| 3b | 6541.7 | 3.32 | 6541.0 | 2.47 | 6543.5 | 0.85 | |
| calc, BS | 1 | 6542.2 | 1.69 | 6542.2 | 1.69 | – | – |
| 2 | 6541.7 | 1.39 | 6540.9 | 0.39 | 6543.1 | 1.00 | |
| 3a | 6542.2 | 1.20 | 6541.5 | 0.84 | 6544.0 | 0.36 | |
| 3b | 6542.5 | 3.29 | 6541.0 | 2.31 | 6543.3 | 0.98 | |
Experimental areas are based on fits to the normalized data, values were multiplied by 100. Calculated areas are sums of oscillator strength and normalized to the number of donors.
Computational Details
The ORCA, program package25 was used for all DFT calculations in this paper, considering scalar relativistic effects on the basis of the 0th order regular approximation for relativistic effects (ZORA),26,27 and solvation effects using the conductor-like screening model (COSMO).28 A larger than the default integration grid (Grid4 in ORCA nomenclature) was used throughout. Geometry optimizations for the four molecules were based on the crystal structure of 1 with the respective number of protons added in the appropriate positions, as no crystal structures are available for either 2 or 3. Two sets of optimizations were carried out. In the calculations labeled ‘cryst’ only the positions of the hydrogen atoms were relaxed, while unconstrained geometry optimizations are labeled ‘opt’. Following procedures published previously,29,30 optimizations were performed at the high spin state with a dielectric constant of 8 and the van der Waals correction31 as implemented in ORCA. For these calculations, the functional BP86 was combined with the scalar-relativistically recontracted (SARC) version of the Karlsruhe triple-ζ def2-TZVP (-f)32 basis set33 together with the corresponding auxiliary basis. Using these structures, single point high spin and broken symmetry calculations, employing the TPSSh functional34 and the same basis set combination as above, were performed to extract the exchange coupling constants J as defined by Yamaguchi35,36
For the calculation of Mn K pre-edge XANES, the TD-DFT approach with the Tamm-Dancoff approximation37 as implemented in ORCA38 and established earlier for pre-edge calculations39,17 was chosen. The functional TPSSh and the ‘Split’ resolution of the identity40,41/chain of spheres42 (RIJCOSX) approximation were combined with the same basis set combination as for the broken symmetry calculations. Acetonitrile was chosen as the solvent to be modeled by COSMO in accordance with previous protocols employed.17 For each Mn center as many as 100 roots needed to be calculated in order to cover an energy range that is broad enough to allow for a reliable comparison between theory and experiment. According to the approach developed previously,39 the donor orbitals were localized and the virtual space was not truncated. As established previously, the spectra computed with TPSSh were shifted by 36.3 eV to higher energy to compensate for systematic shortcomings of the density functional, basis and relativistic approximations,17 and subsequently subjected to Gaussian broadening by 1.5 eV in order to facilitate the visual comparison between theory and experiment. To illustrate the shift of the MLCT peak to higher energies for larger percentages of HF exchange as first demonstrated in Ref. 17, we present Figure S5 with 10% – 16% HF exchange specified in the %method block of ORCA, as well as Figure 4 showing spectra with 13% HF exchange.
Figure 4.
Background-subtracted experimental pre-edge region (top) and calculated Mn K pre-edge spectra with 13% HF exchange in the TPSSh functional based on the high-spin solution (bottom). The color code is solid black trace for compound 1, dotted red trace for 2, and dashed blue trace for 3a. The calculated spectra are not shifted, since the shift for the TPSSh functional with 13% HF exchange is different from that of the pure TPSSh functional and has not been determined for reasons detailed in the text.
Details on the analysis of the calculated spectra and the correlation to experiment
The calculated pre-K-edge XAS were analyzed with procedures described previously,39,17 resulting in intensity-weighted average energies (IWAE) and calculated areas reported in Table 2. These are directly comparable to the respective experimental data, as was established in Ref.39 For the correlation plots, calculated dimer data were broadened by 1.0 eV (instead of 1.5 eV used for the visual comparison), in order to allow for a valid correlation with the monomer data which were also broadened by 1.0 eV. Since contributions from two donor sites are considered in the XAS calculations, the calculated intensities were divided by two in order to correctly correlate with experimental normalization procedures. ORCA input file examples are included in the SI.
RESULTS AND DISCUSSION
Structures
The complete oxo bridge protonation series of the MnIV-dimer [Mn2(IV,IV)(μ-O)2(salpn)2] was first published in 1994 by Baldwin et al.22 Prior to that, the crystal structure of the unprotonated compound, [Mn2(IV,IV)(μ-O)2(salpn)2] (1), had been established.43 Since the crystal structures of the singly protonated compound 2 are and the doubly protonated compound 3 are unknown, the XRD of 1 served as a starting point for the geometry optimizations of these complexes. It is chemically intuitive to doubly protonate 1 in a symmetric way, forming 3a, which is how this compound was characterized in the original publication. Nevertheless, the asymmetrically protonated form 3b was investigated computationally to explore the limits of structural differentiation of K pre-edge X-ray absorption spectroscopy (this work) and valence-to-core X-ray emission spectroscopy (Ref. 14).
Comparision of the DFT-derived structures with experimental data is possible based on the previously reported EXAFS data.22 These data, along with the interatomic distances and selected angles of the optimized core geometries, are presented in Chart 1. The optimized geometry of compound 1 has Mn-Mn and Mn-μ-O distances of 2.70 Å and 1.82/1.83 Å, which compare well with EXAFS and XRD data (2.72-2.73 Å, 1.89-1.90 Å and 2.73 Å, 1.81/1.82 Å, respectively). The Mn-O-Mn and O-Mn-O angles are predicted to be 95. 2° and 84.8°, respectively, compared to 97.7° and 82.3° in the XRD. Note that there is no displacement of the Mn centers from the plane defined by the oxo bridges and the N and O atoms of the salpn ligand. After the first protonation step, forming 2 with the asymmetrically protonated Mn2(μ-O)(μ-OH) core, the diamond core expands, with the Mn-Mn distance increasing to 2.84 Å in excellent agreement with the EXAFS distance of 2.82-2.83 Å. The asymmetry is reflected in the increased Mn-O-Mn angle of 102.3° and the compressed Mn-OH-Mn angle of 92.1°.
The symmetric Mn2(μ-OH)2 core 3a has a Mn-Mn distance which is increased by 0.17 Å relative to species 2, and increased by 0.31 Å relative to the unprotonated core. For the asymmetric double protonation of the core3b, Mn2(μ-O)(μ-OH2), the Mn-Mn distance is only 0.003 Å longer than in 3a. Comparison to EXAFS data shows that both structural proposals would match the reported Mn-Mn-distance of 2.92-2.94 Å for species 3. Comparison of the Mn-μ-O distances allow for a better discrimination of the two possible structures. The Mn-N and Mn-O vectors are found at an average value of 1.92 Å in the EXAFS data of 3. According to the calculations the average Mn-N/O distance in 3a is 1.93 Å, while in 3b the average is 1.95 Å. Given a resolution of ~0.16 Å in k = 2–12 Å–1 EXAFS data, one would expect the long 2.21 Å Mn-OH2 vectors in 3b to be separable from the shorter Mn-O/N distances at 1.90 Å. On this basis, the EXAFS data are in better agreement with structure 3a. However, we note it is also possible that such longer Mn-OH2 contributions would not contribute significantly to the EXAFS signal and/or could be strongly correlated with shorter first shell distances, thus making the assignment of structure 3, on the basis of EXAFS data alone, somewhat ambiguous.
Magnetic data
The experimental magnetic data was published previously and will only briefly be compared to the calculated isotropic exchange coupling constants. Calculations were performed both on the optimized geometries and on geometries taken from the crystal structure of 1 with hydrogen atoms added as appropriate and optimized. The calculated values for J are in good agreement with the experimentally obtained ones and in line with calculated data on idealized hydroxo-bridged species.44 The interaction between two magnetic centers bridged by two oxo ligands takes place via three π superexchange pathways, the overlap integrals Si of which are reduced by protonation of the bridges, leading to weaker isotropic coupling constants.44 The decrease in coupling magnitude by ~43 cm–1 after each protonation step is in line with an independent quenching of the oxo superexchange pathways due to protonation.44 In the calculations, this finding is reflected in both the x-ray-structure-based and the optimized data (see Table 1). Overlaps of ~0.25 per pathway are commonly found for metal centers that couple significantly, as for the first two pathways of compound 1 with the predicted J-value of –73 cm–1 (S1 = 0.25, S2 = 0.20, see Table 1). For compound 2, one of the two pathways is destroyed due to protonation (S1 = 0.25, S2 = 0.06), leading to a decreased J-value of –37 cm–1. The J-value for 3a is close to the experimentally determined one (–3 cm–1 compared to –6 cm–1 derived experimentally), which is reflected in the small overlap magnitude for the magnetic orbitals indicative of two inactivated magnetic exchange pathways (S1 = 0.06, S2 = 0.06). For 3b, the computed J-value is significantly larger than the experimental value (–55 cm–1 vs. –6 cm–1), in line with one unquenched and one partially quenched pathway (S1 = 0.25, S2 = 0.13). Here, the difference in coupling magnitude between 2 and 3b lies in the Mn-O-Mn angles of the dimer, which determine the overlap at the bridging atoms facilitating superexchange (see Chart 1).
Table 1.
Top: experimental isotropic exchange coupling constants from Ref. 22 and computed values for the fully relaxed structure and the crystal structure with optimized H atoms. Bottom: magnetic orbital overlaps Si from the broken symmetry solutions of the fully relaxed models 1, 2, 3a, and 3b.
| Compound | Jexp / cm−1 | Jcalc,opt / cm−1 | Jcalc,cryst / cm−1 |
|---|---|---|---|
| 1 | –92 | –73 | –101 |
| 2 | –48 | –37 | –46 |
| 3a | –6 | –3 | –16 |
| 3b | –55 | –28 | |
| S 1 | S 2 | S 3 | |
| 1 | 0.25 | 0.20 | 0.00 |
| 2 | 0.25 | 0.06 | 0.03 |
| 3a | 0.06 | 0.06 | 0.02 |
| 3b | 0.25 | 0.13 | 0.01 |
Judging from the computed magnetic data alone, the bridging motif of 3b is less realistic than that of 3a. The energetics of these two models render the same result: the asymmetrically protonated structure is 20.0 kcal mol–1 higher in energy than the symmetrically protonated model. Thus, structure 3b is strongly disfavored from classical analysis. However, in biological systems and model complexes, the chemical environment can alter the relative energies of protonation isomers.45 To assess the ability of Mn K pre-edge XAS (this paper) and valence-to-core XES (accompanying paper) to discriminate between 3a and 3b it is thus worthwhile to include both isomers in the analysis.
Experimental XAS data
The experimental XANES of compounds 1-3 are displayed in Figure 2. All complexes exhibit a steep rising edge feature at ~6553 eV which is dominantly due to dipole allowed 1s-4p transitions. To lower energies, between 6538 and 6545 eV, the K pre-edges corresponding to 1s-3d(+4p) transitions are observed. For the Mn dimers studied here, the intensities of the white line maxima at ~6560 eV vary, with the intensity of the unprotonated compound 1 being the lowest (~ 1.1), followed by the protonated compounds 2 (~1.2) and 3 (~1.25). This increase in white line intensity is consistent with typical observations for transition metal aquo species, which show very intense white line features.46 The edge energies do not change significantly across the series (≤ 0.12 eV based on both the first derivatives and the edge component of the fits), indicating that the Mn centers are at the same oxidation state in all three complexes. The absence of an energy shift in the edge is in contrast to what has been observed for a similar protonation series of Fe dimers (protonation of the oxo-bridge while maintaining the same ligand framework), where the edge shifts to lower energy upon protonation.46 However, in the case of the Fe complexes, there is a significant distortion of the Fe2(μ-oxo)(μ-acetato)2 core upon protonation: the Fe-Obridge bond lengths increase and the Fe atoms become less displaced from the ligand plane upon protonation.47 For the series of Mn dimers presented here, the only change in the geometry of the Mn2O2 core is a slight lengthening of the Mn-Obridge bond distances (vide supra).
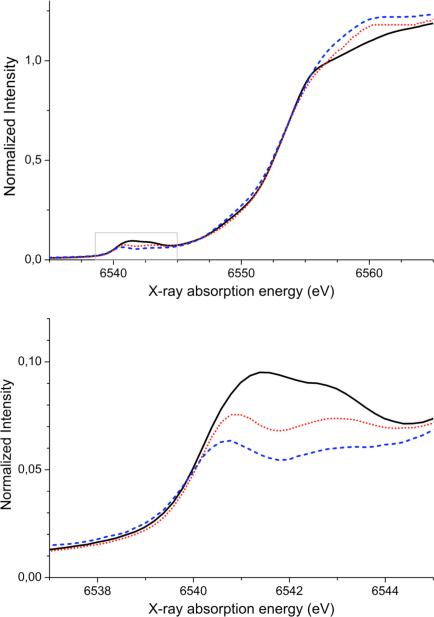
Figure 2.
Top: XANES of compounds 1 (solid black), 2 (dotted red) and 3 (dashed blue). Bottom: Expansion of the pre-edge. region.
This study focuses on the pre-edge region of the XAS spectra (see Figure 2, bottom). For each compound, two peaks between 6538 and 6545 eV appear, with decreasing intensity upon protonation. Quantitatively, the areas reduce from 36.2 for compound 1, to 26.0 for compound 2 and 17.3 for compound 3 (see Table 2). As can be seen in Table 2 and in Figure S2, the areas of the two features become more similar up on protonation. The intensity weighted average energy (IWAE) of the total pre-edge region decreases slightly (6542.1 to 6541.8 eV) upon protonation. The IWAEs of complex 1 and 2 are nearly unchanged (difference of 0.09 eV), whereas the major part of the decrease occurs for the second protonation step (0.30 eV). The larger part of this change can be attributed to the decrease in the area of the second feature upon protonation (see Table 2 and Figure S2).
Calculated K pre-edge XAS
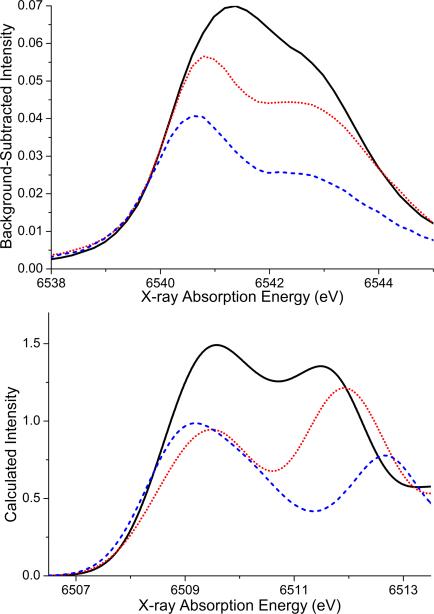
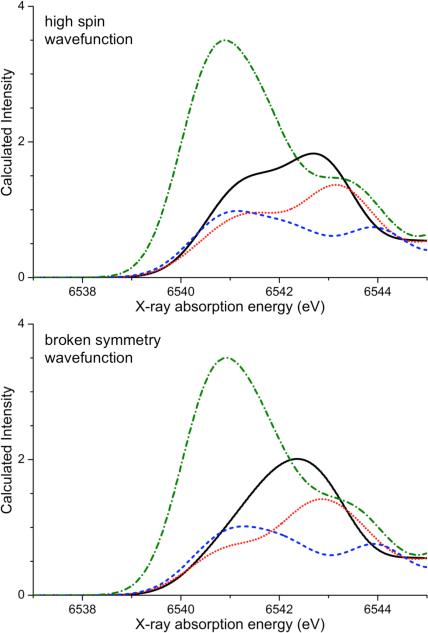
The calculated spectra based on the high spin solution have two features in the pre-edge region between 6538 and 6545 eV, as presented in Figure 3 (top). For the bis-μ-oxo bridging motif of complex 1, the first peak is less intense than the second peak. The intensity distribution differs from the one observed experimentally. This can in part be explained by artifacts arising from the description of charge-transfer states in time-dependent density functional theory.48,49 These artifacts are highly dependent on the density functional used and decrease with increasing amounts of Hartree-Fock exchange.17 Secondly, the improper description of multiplet effects in TD-DFT also leads to a slightly erroneous intensity distribution. (vide infra and Ref. 17). Upon protonation, the area of the whole pre-edge region (6539 – 6545 eV) decreases for the singly protonated and symmetric doubly protonated structures 2 and 3a, respectively. This follows the experimental trend. However, the first feature at 6541 eV in the calculated spectrum of 2 is of lower intensity than the second one at 6543 eV, whereas the spectrum of 3a has a broad first peak at 6541 eV that is of higher intensity than the second peak at 6544 eV. The calculated spectrum of the asymmetric doubly protonated core, structure 3b, has a first peak of nearly twice the intensity of the unprotonated structure 1. This does not follow the trend of the experimental data and thus the spectrum is far too intense for 3b to represent a realistic structure for the doubly protonated species 3. The exclusion of 3b based on the total calculated Mn K pre-edge area is consistent with the conclusions drawn from magnetic data and calculated total energies.
Figure 3.
TPSSh-calculated X-ray absorption spectra based on the high-spin solution (top) and the broken symmetry solution (bottom) fo r compounds 1 (solid black), 2 (dotted red) and 3a (dashed blue) and 3b (dash-dotted green).
To address the unsatisfactory intensity distribution, it is possible to reduce the artifacts associate with charge transfer transitions by adjusting the amount of Hartree-Fock exchange of the chosen functional. It has been discussed in some detail earlier that the CT-transitions overlap with the pre-edge manifold with 10% HF exchange as in the TPSSh functional, although they are found at much higher energies in the experimental spectra.17 To demonstrate the steep dependence of the results on the amount of HF exchange in the density functional, this parameter was systematically varied for the systems studied in the work. Figure S5 presents the calculated spectra of compound 1 with the factional HF exchange varying between 10% and 16%. It is important to understand that the adjustment of HF exchange does not change the information content of the spectra: the interpretation of the experimental data will remain exactly the same since the relative intensities and energetic splitting of the 1s-3d(+4p) transitions are virtually unchanged while the CT peaks strongly shift (see Figure S5). With 13% HF exchange the peak splitting and intensity distribution of the calculated K pre-edge spectrum for complex 1 is similar to the experimental one. Figure 4 shows the experimental background-subtracted pre-edge region and the calculated spectra for complexes 1, 2 and 3a based on the TPSSh functional with 13% HF exchange. With this choice, the intensity ratio of the two peaks for complexes 1 and 3a gives a better visual impression, while the maximum intensity of the first feature in the spectrum of complex 2 at 6509.5 eV remains less intense than that of its second feature at 6512 eV. We would like to stress here that the area of a broad signal with low maximum intensity can be the same as the area of a narrow signal with high maximum intensity, and thus the area correlation presented in Figure 7 is a better tool to assess the agreement with experiment.
Figure 7.
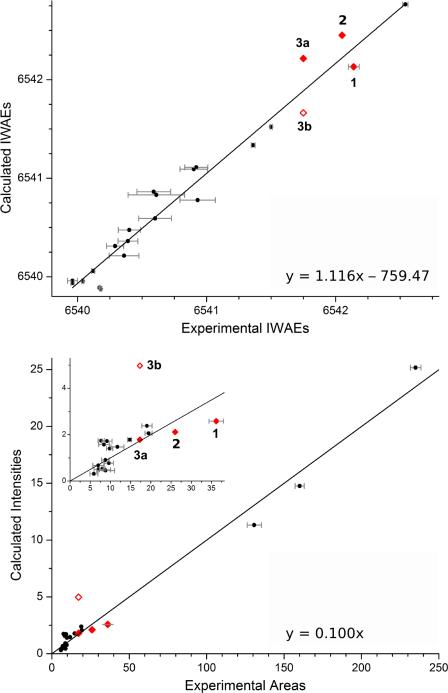
Correlation of experimentally determined areas and high-spin calculated oscillator strengths (top) and IWAEs (bottom) for the whole pre-edge region (see Table 2), shown as red diamonds. Unfilled red diamonds correspond to values for structure 3b. Black circles correspond to the Mn monomer data previously reported, and referred to in the text. For more information on monomer data and error bars, see Table S3. The regression lines are based on the monomer data and follow y = 1.116 × – 759.47 (IWAEs, adjusted R = 0.979) and y = 0.100 × (areas, adjusted R = 0.994, forced through 0).
In conclusion, a somewhat better visual appearance of the calculated spectra can be achieved by slightly altering the amount of HF exchange in the functional (e.g. only 3%). However, this number is not transferrable to other systems and no new insights arise from this numerical exercise. For example, a previous extensive study on Mn monomers demonstrated that the experimental transition energies and areas are well reproduced using the unaltered TPSSh functional.17 Hence, variation of the fractional HF exchange is not an approach we recommend or will pursue in the future. Secondly, the important issue of missing multiplet effects in the TD-DFT approach cannot be addressed by adjusting the fractional HF exchange (vide infra). Lastly, we feel that it is important to stick to standard functionals in order to draw on all the experience that has been gathered for them in chemical applications. In particular, TPSSh is known to yield excellent electronic structure descriptions for Mn compounds based on magnetic and spectroscopic data,29,30,50 and has been used successfully to judge the quality of structural models.3,51 It is particularly undesirable to use different functionals for different properties of the same system.
High spin vs. broken symmetry electronics structure
The calculated spectra based on the broken symmetry electronic reference structure look remarkably similar to the ones based on the high spin solution (see Figure 3). An exception is the calculated spectrum of 1, where instead of the two peaks only one resolved is prediced. More subtle differences can be observed for the relative intensities of the spectra for compound 2. Quantitatively, the similarities between the spectra based on the high spin and the broken symmetry solutions are also reflected in the intensity weighted average energies and the computed areas, see Table 2. A comparison of the HS and BS stick spectra is given in Figure S3.
In the TD-DFT approach, neither the ground state nor the excited determinants correspond to pure spins states, and thus are unable to adequately model the multiplet splitting responsible for the appearance of two peaks in the experimental K pre-edge spectra. However, the spin-polarization in open-shell TD-DFT calculations has been interpreted as a “poor man's approximation” to multiplet splitting, since it is responsible for the appearance of two peaks in the calculated pre-edge spectra.52,15 It is important to keep in mind that neither the high spin nor the broken symmetry electronic structure appropriately represent the ground state of an antiferromagnetically coupled MnIV dimer. Spin polarization occurs in both electronic structures; in the high spin solution the whole α set is shifted down in energy relative to the β-manifold through exchange stabilization,53,54,55,56 whereas in the broken symmetry solution the effect appears locally on each Mn center and is of opposite sign owing to the antiparallel spin alignment. This antiparallel spin alignment, which leaves net positive spin density on one center and net negative spin density on the other center in the broken symmetry solution, is an artifact in the sense that the spin density should be zero at every point in space in a singlet state. The physical content of the broken symmetry solution has been discussed in detail elsewhere.48,57,58 In the present context, the local spin polarization is a desired feature since it will aid to simulate the multiplet structure of the final state manifold as discussed before in the case of Fe(IV) centers.15,52
A further difference in the electronic structures is the amount of covalency in the Mn2O2 core: the BS solution in the strong coupling limit will lead to more covalent delocalization onto the bridging atoms than the respective HS solution, while for weak coupling the extent of covalency is comparable. This effect is of importance for the intensity of the transitions, since a more covalent description will have a stronger overlap of the Mn d-orbitals with the p-orbitals of the bridging oxygen atoms. From the calculated stick-spectra, (see Figure S4), one observes that for model 3a (weakly coupled), the HS and BS spectra are nearly indistinguishable, whereas for model 1 (strongly coupled), energetic shifts and intensity differences appear. The most important difference in the stick spectra of 1-HS and 1-BS is the larger energetic separation between the transitions into the α dz2 and dxy orbitals, and a smaller energetic separation between the transitions into the β dz2 and dxy orbitals. This can be explained through the altered spin polarization effects in the BS electronic structure as discussed above. The transition into the α dz2 dominated component in the BS case is less intense than in the high spin case, whereas more similarly intense transitions into the β dz2 and dxy based molecular are observed (vide infra and Fig. 5).
Figure 5.
Assignment of the calculated K pre-edge XAS spectrum based on the difference densities associated with the states for complex 1. The labels for the dominant local Mn are in accordance with a coordinate system with the x-axis along the Mn-Mn vector and the z-axis perpendicular to the Mn2O2 plane. The states the difference densities are associated with are degenerate; thus for each image there exists a mirror image with the largest contribution on the other Mn ion.
It is important to note that although the spectra from individual Mn centers should be identical for all compounds, in particular for the symmetrically protonated complexes 1 and 3a, the stick spectra show that subtle geometric differences (ligand distances and angles) can induce differences in intensity and energy between two “nearly equivalent” Mn centers. Since it is well known that DFT provides very good geometries,59,60 it is recommended to calculate transitions from all metal centers rather than relying on symmetry considerations.
Assignment of the calculated XAS spectra
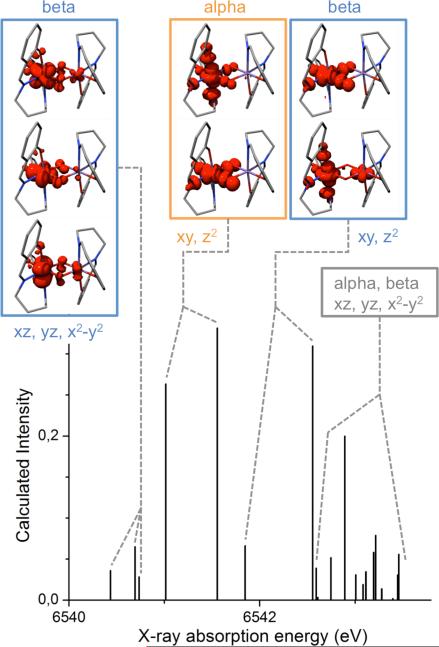
Using a hybrid functional (such as TPSSh in the present work) rather than functionals without added HF exchange, leads to admixture of off-diagonal matrix elements that result in contributions from more than one acceptor orbital to the transition. Since the calculated excited states in the present Mn dimers typically contain contributions from 4-6 acceptor orbitals, it is difficult to obtain an intuitive picture on the basis of the excited state compositions. It is hence more revealing to analyze the electronic difference density between the ground and excited electronic states. The shapes of these densities readily allow one to identify negative regions with the squares of ‘effective donor orbitals’ whereas regions of positive difference density correspond to the squares of ‘effective acceptor orbitals’. Since the donor orbitals in the case of XAS transitions are invariably highly localized, for highly compact Mn 1s orbitals, the difference densities are dominated by positive contributions that can be analyzed readily (Figure 5). The assignment of the peaks is presented only for the high spin solution since the BS based results are very similar.
In the MnIV2 system with a high-spin (d3)2 configuration, the β orbitals are all empty. In a coordinate system where the origin is in the center of the Mn2O2 diamond with the x-axis towards one Mn atom and the z-axis perpendicular to the plane, the occupied α orbitals are dominated by dxz, dyz and dx2-y2 character, leaaving the unoccupied α orbitals to be dz2 and dxy based. These orbital characters are the ‘local’ characters of the acceptor orbitals on the Mn centers, since the origin of the coordinate system does not coincide with either of the metal atoms. In the predicted XAS of species, 1 four groups of transitions can be identified (see Figure 5): the transitions into the empty β orbitals of predominant dxz, dyz and dx2-y2 character are at lowest energies followed by transitions into the empty α dz2 and dxy based molecular orbitals. The latter transitions are the most intense and account for the majority of the low energy feature in the convolution. The next transitions are those into β orbitals dominated by dz2 and dxy character. The last group of states has acceptor orbitals from both the α and β set best described as having dxz, dyz and dx2-y2 character mixed with contributions from the ligands. The same pattern can be observed for the other species, with modifications in the relative intensities and positions of the transitions. A quantification of the metal, oxo bridge and salpn ligand character is given in Table S2. Importantly, in the computed spectra of species 2 and 3a, groups of states can be identified that have dominantly metal-to-ligand charge transfer (MLCT) character.
The significantly elevated intensity of compound 3b can be attributed to two transitions in the pre-edge region (see also Figure S4). The first intense state is due to transitions into α orbitals dominated by dxy character, the second one due to transitions into β orbitals with dxz, dxy and dx2-y2 contributions. The difference densitites associated with these transitions show that the ligand atoms trans to the aquo bridge are more strongly involved than the ones trans to the oxo bridge, which contribute very little intensity.
Electric dipole, magnetic dipole and electric quadrupole contributions to the intensities
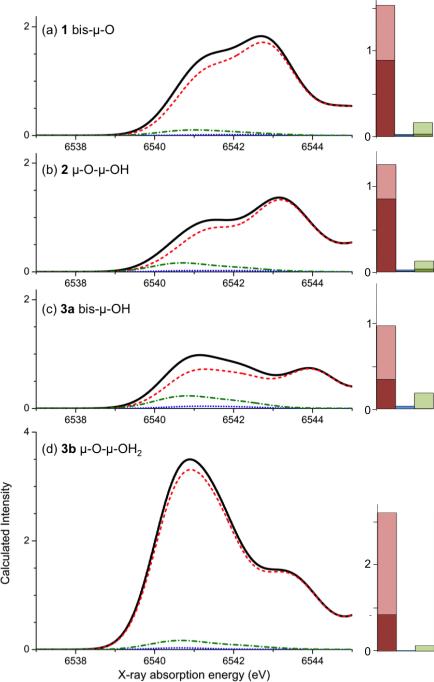
Transitions from the 1s to the 3d orbitals are dipole forbidden. However, through mixing of 4 p character into the molecular orbitals, these transitions can become partly allowed (1s-3d(+4p)). The relative intensities of the states depend on the amount of Mn p character in the donor orbitals. The electric dipole mechanism dominates electronic spectra, but two other mechanisms, the magnetic dipole and electric quadrupole, may also contribute to the total intensity.39 Figure 6 shows all contributions for the four complexes. As anticipated, the electric dipole mechanism dominates all spectra, followed by the electric quadrupole mechanism. The magnetic dipole mechanism has no significant contribution to the calculated spectra. The loss in total intensity on going from 1 to 2 to 3a is primarily due to the loss in electric dipole intesity.
Figure 6.
Electric dipole (dash red), magnetic dipole (dotted blue) and electric quadrupole (dash-green) contributions to the total spectrum (black) from the mechanisms for compounds 1, 2, 3b, 3a panels a, b, c, d. Quantitatively, the contributions are presented as bar diagrams on the right. The total height of a column represents the total sum of calculated oscillator strength to the pre-edge from each of the mechanisms. The lighter shading represents the contribution from the first peak, and the darker shading the contribution from the second peak. Note that the intensity scale for 3b is twice as high as for the other complexes.
The results are quantified by summing the contributions to the total intensity over the whole pre-edge range between 6538 and 6545 eV. This reveals a systematic decrease in the electric dipole contribution (red) for the protonation steps from 1 to 2 to 3a, and a dramatic increase for the asymmetric structure of 3b (see Table 3). The magnetic dipole mechanism (blue) leads to nearly the same negligible intensity for each complex, representing less than 3% of the calculated intensity. The electric quadrupole contribution is relatively constant (0.13-0.19). However, the relative contribution of EQ to the first peak is higher than for the second peak in each compound. This trend becomes more important upon protonation, as is shown in the bar diagrams of Figure 6 (and Table S1). Here, the lighter shades of the respective colors represent the intensity of the first peak, i.e. the sum of the oscillator strengths of the first five transitions for each structure, and the darker bars correspond to the intensity of the second peak. Examination of the ratios of the lighter colors, i.e. light green to light red, shows that the importance of the electric quadrupole mechanism relative to the electric dipole mechanism within the first peak increases upon protonation from 1 to 3a (numbers given in Table S1).
Table 3.
Electric dipole, magnetic dipole and electric quadrupole contributions to the calculated HS pre-edge intensities as sums of the respective calculated oscillator strengths.
| Compound | Total | ED | MD | EQ |
|---|---|---|---|---|
| 1 | 1.72 | 1.53 | 0.03 | 0.16 |
| 2 | 1.41 | 1.25 | 0.02 | 0.13 |
| 3a | 1.19 | 0.97 | 0.03 | 0.19 |
| 3b | 3.32 | 3.16 | 0.02 | 0.13 |
As is shown in the assignments of the computed K pre-edges, the first peak is the least impacted by ligand character in the difference densities. This is consistent with the electric dipole contribution being lower in this part of the spectrum relative to the other mechanisms. The mixing of ligand and metal character in the states corresponding to the first peak is clearly affected by the protonation of the bridges. This may be attributed to changes of the relative energetic positions of the orbitals with O character upon protonation. Similarly, the distortion of the Mn2O2 core leads to more asymmetry in the system for the asymmetric protonated species than for complexes 1 and 3a.
Correlation of experimental and calculated XAS intensities and energies
The experimental and calculated areas and intensity-weighted average energies (IWAEs) are compared for the dimers in the series. In order to better judge the correlation between experiment and theory, previously reported data on a series of Mn monomers,17 as well as additional data from the Mn(V)-monomers [Mn(V)(O)(taml)]1–, [Mn(V)(N)(CN)5]3– and [Mn(V)(N)(CN)4]2–.61,62
The regression lines in Figure 7 are based on the monomer data only. The IWAE data points of all compounds are in reasonable proximity to the monomer line (Figure 7, top). The average energies for the dimers are located at higher values than most of the monomers since their oxidation state is +4, and not +2 or +3 as for the monomers. The regression line follows y = 1.116 × – 759.47 with an adjusted R-value of 0.979, which changes only slightly to 0.982 upon inclusion of the total IWAE dimer data for compounds 1, 2 and 3a. The visual impression from Figure 7(top) is that the dimer data points are within the scatter of the monomer data around the regression line. Quantitatively, the deviation of the dimer data points from the regression line (in the y-direction) is less than 0.35 eV. The correlation for the total pre-edge areas is shown in the lower half of Figure 7. Here, the regression line is forced through 0 and follows y = 0.100 ×. The adjusted R-value of 0.994 indicates an excellent correlation between the experimental and calculated areas over a wide range of compounds. It remains unchanged upon inclusion of the data points for 1, 2 and 3a. Based on these data, model 3b can clearly be ruled out, since the data point is outside the scatter range of the monomer data around the regression line. The deviation of 3b from the regression line (in the y-direction) is significantly larger (3.25 ) than for 3a (0.06 ) and the average of 1, 2 and 3a (0.49). This is an important finding when considering different protonation patterns for the OEC. Overall, the area correlation is a more powerful tool than the energy correlation for the discrimination between bridging motifs.
CONCLUSIONS
In this paper, we have described the analysis of experimental and calculated K pre-edge XAS of [MnIV2(salpn)2(μ-O)2]H0-2 dimers and their theoretical interpretation in detail. The correlation of experiment and calculation is based on the pre-edge areas and the respective intensity weighted average energies. In combination with the visual inspection of experimental and calculated spectra, this approach allows one to distinguish the protonation patterns across the series. The analysis of the calculated spectra based on either high spin or broken symmetry density functional solutions provides nearly identical results: the most intense transitions are into acceptor orbitals from the local eg set; at lower energies from the 1s-α orbitals, at higher energies from the 1s-β orbitals. To the best of our knowledge, the analysis presented here represents the first calculation and analysis of metal pre-K- edge spectra for multi-nuclear complexes using a TD-DFT approach.
To best model the K pre-edge region of a metal, one needs a good value for the final state energies relative to the ground state energy, which is dominated by the energy difference of donor and acceptor orbitals but also strongly influenced by electron-electron interactions in the final state, i.e. multiplet effects. To predict the intensity, one needs descriptions for both quadrupolar and dipolar contributions to the spectrum, the latter of which requires the consideration of 3d-4p-mixing resulting from a good model for the molecular geometry and/or local symmetry. Several approaches have been used to predict metal K pre-edges: TD-DFT as presented here, FEFF and atomic multiplet models. The FEFF code uses a multiple-scattering wavefunction approach, and for XANES calculations includes only weakly bound orbitals that have energies higher than the muffin-tin potential's zero point energy. The energies are calculated from at omic total energy calculations using the Dirac-Fock-Desclaux atom code. The geometry and symmetry enter the calculation as a set of xyz coordinates so that no restrictions apply. Intensities are calculated as sums of scattering amplitudes, in the case of XANES by ‘implicit summation of full multiple scattering’. Multiplet theory includes, as the name suggests, multiplet effects, which are based on atomic models where a metal ion is placed in a ligand field with a 10Dq value estimated from an empirical formula.63 Although it is possible to include dipolar intensity mechanisms besides the standard quadrupole-derived intensities and symmetries lower than C4v, this is often not done in applications. In comparison to TD-DFT, the consideration of multiplet effects is an advantage of atomic multiplet calculations, but the often neglected dipolar intensity mechanisms and standardized chemical environments cannot take into account effects of complex ligand spheres. In FEFF models, the influence of the lowest-lying unoccupied MOs may be overlooked depending on the shape of the muffin-tin-potential. However, long-range effects can be considered in this approach. Interestingly, Farges found that for Mn(IV), Mn-Mn scattering vectors are indispensable to correctly model the pre-edge region in Mn oxides.64 However, we note that approaches that make use of MOs are closer to concepts used in chemistry.
Within the TD-DFT description multiplet effects are not explicitly accounted for, but rather approximated by spin polarization effects. Hence, the method should still be capable of describing the trends in intensity and IWAEs upon ligand protonation. The calculations are based on DFT optimized geometry as an input, leading to 3d-4p-mixing in the description of the acceptor MOs, which with in the TD-DFT implementation in ORCA allows for the determination of dipolar and quadrupolar intensities. For K-edges, the multiplet effects are expected to be relatively small. Within the limits of the energy determination for the transitions with TD-DFT, neglecting multiplet effects, one can vary the HF-exchange to compensate for erroneously predicted CT transitions, but we prefer not to do this for the reasons detailed above. With the comparison of the area and IWAE values for the salpn dimer protonation series to a large body of monomer data, we have shown that TD-DFT can reproduce and explain trends in ligand protonation in real systems.
The present studies thus form a basis for future quantitative investigations of the catalytic intermediate states in the OEC of PSII. While a 1.9 Å crystal structure is now available,65 and has been theoretical refined,3,66,67,68,69 many questions concerning the oxidation states and protonation patterns of the OEC remain unanswered. The present studies demonstrate that by combining experimental XAS data with calculations, a detailed picture of the ligand protonation pattern in model dimer systems can be derived. Although the erroneous prediction of CT transitions by TD-DFT has a notable impact on the visual comparison of the calculated spectra to the experimental ones, this does not compromise the interpretation of the 1s-to-3d transitions. Whether significant MLCT transitions should be expected for calculations on OEC models has yet to be systematically evaluated. We note, however, that the ligand sphere of the Mn4CaO5 complex consists of carboxylate ligands, water molecules and histidine ligands so that fewer and less intense MLCT transitions can be expected.
Higher resolution data such as provided by photon-in/photon-out measurements (KαHERFD, RIXS) are a more sensitive probe of the ligand environment and electronic structure. Such experiments may also be used in the future to assess the origin of transitions, i.e. to differentiate between 1s-3d(+4p) and MLCT or MMCT transitions. This will ultimately provide a more stringent test for the currently applied theoretical models and those to be developed in the near future. Studies along these lines are underway in our laboratories.
The accompanying paper on X-ray emission spectroscopy (XES) of the same compounds demonstrates that valence-to-core XES provides a complementary probe. Taken together, XAS and XES methods have promise for obtaining insight into the protonation changes which occur in the S states of the Kok cycle and hence ultimately the mechanism of photosynthetic water oxidation. These studies are currently underway in our laboratories.
Supplementary Material
ACKNOWLEDGMENT
This work was supported by the Director, Office of Science, Office of Basic Energy Sciences (OBES), Division of Chemical Sciences, Geosciences, and Bio-sciences (CSGB) of the Department of Energy (DOE) under Contract DE-AC02-05CH11231 (J.Y. and V.K.Y.) for instrumentation development and NIH Grant GM 55302 (V.K.Y) for Mn inorganic chemistry. Experiments were carried out at Stanford Synchrotron Radiation Lightsource (SSRL), BL 9-3 in Stanford. SSRL is supported by DOE OBER. VK, MAB, SD and FN acknowledge the Max Planck Society for funding. SD also acknowledges Cornell University and the Alfred P. Sloan Foundation.
ABBREVIATIONS
- XES
X-ray emission spectroscopy
- XAS
X-ray absorption spectroscopy
- IWAE
Intensity Weighted Average Energy
- OEC
Oxygen Evolving Complex
- PSII
Photosystem II
Footnotes
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Supporting Information. Second derivative spectra of experimental XAS (Figure S1). Representative fits of experimental XAS (Figure S2). Overlay of 1st and 4th XAS scans for all compounds to assess radiation damage (Figure S3). Comparison of HS and BS stick spectra (Figure S4). Table with contributions to calculated spectra (Table S1). Quantification of Mn, oxo-bridge and salpn character to calculated transitions (Table S2). Changes in calculated spectra for variation of HF exchange (Figure S5). Input file examples for XAS. Reference monomer data incl. standard deviations (Table S3). Coordinates of all structures.
REFERENCES
- 1.Rapatskiy L, Cox N, Savitsky A, Ames WM, Sander J, Nowaczyk MM, Rögner M, Boussac A, Neese F, Messinger J, Lubitz W. J. Am. Chem. Soc. 2012;134:16619–16634. doi: 10.1021/ja3053267. [DOI] [PubMed] [Google Scholar]
- 2.Siegbahn PEM. Chem.–Eur. J. 2008;14:8290–8302. doi: 10.1002/chem.200800445. [DOI] [PubMed] [Google Scholar]
- 3.Ames W, Pantazis DA, Krewald V, Cox N, Messinger J, Lubitz W, Neese FJ. Am. Chem. Soc. 2011;133:19743–19757. doi: 10.1021/ja2041805. [DOI] [PubMed] [Google Scholar]
- 4.Suzuki H, Sugiura M, Noguchi TJ. Am. Chem. Soc. 2009;131:7849–7857. doi: 10.1021/ja901696m. [DOI] [PubMed] [Google Scholar]
- 5.Cox N, Ogata H, Stolle P, Reijerse E, Auling G, Lubitz WJ. Am. Chem. Soc. 2010;132:11197–11213. doi: 10.1021/ja1036995. [DOI] [PubMed] [Google Scholar]
- 6.Whittaker JW. Arch. Biochem. Biophys. 2012;525:111–120. doi: 10.1016/j.abb.2011.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barynin VV, Whittaker MM, Antonyuk SV, Lamzin VS, Harrison PM, Artymiuk PJ, Whittaker JW. Structure. 2001;9:725–738. doi: 10.1016/s0969-2126(01)00628-1. [DOI] [PubMed] [Google Scholar]
- 8.Siegbahn PE. M. Theor. Chem. Acc. 2001;105:197–206. [Google Scholar]
- 9.Samples CR, Howard T, Raushel FM, DeRose VJ. Biochemistry. 2005;44:11005–11013. doi: 10.1021/bi0506270. [DOI] [PubMed] [Google Scholar]
- 10.Zheng M, Khangulov SV, Dismukes GC, Barynin VV. Inorg. Chem. 1994;33:382–387. [Google Scholar]
- 11.Stone KL, Behan RK, Green MT. Proc. Natl. Acad. Sci. 2006;103:12307–12310. doi: 10.1073/pnas.0603159103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sinnecker S, Neese F, Lubitz W. J. Biol. Inorg. Chem. 2005;10:231–238. doi: 10.1007/s00775-005-0633-9. [DOI] [PubMed] [Google Scholar]
- 13.McConnell IL, Grigoryants VM, Scholes CP, Myers WK, Chen P-Y, Whittaker JW, Brudvig GW. J. Am. Chem. Soc. 2011;134:1504–1512. doi: 10.1021/ja203465y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lassalle-Kaiser B, Boron III TT, Krewald V, Kern J, Beckwith MA, Schroeder H, Alonso-Mori R, Nordlund D, Weng TC, Sokaras D, Neese F, Bergman U, Yachandra V, De Beer S, Pecoraro VL, Yano J. Inorg. Chem. 2013 doi: 10.1021/ic400821g. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chandrasekaran P, Stieber SCE, Collins TJ, Que JL, Neese F, DeBeer S. Dalton Trans. 2011;40:11070–11079. doi: 10.1039/c1dt11331c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.DeBeer George S, Petrenko T, Neese F. J. Phys. Chem. A. 2008;112:12936–12943. doi: 10.1021/jp803174m. [DOI] [PubMed] [Google Scholar]
- 17.Roemelt M, Beckwith MA, Duboc C, Collomb M-N, Neese F, DeBeer S. Inorg. Chem. 2012;51:680–687. doi: 10.1021/ic202229b. [DOI] [PubMed] [Google Scholar]
- 18.Jaszewski AR, Stranger R, Pace RJ. J. Phys. Chem. A. 2008;112:11223–11234. doi: 10.1021/jp803286c. [DOI] [PubMed] [Google Scholar]
- 19.Jaszewski AR, Petrie S, Pace RJ, Stranger R. Chem.–Eur. J. 2011;17:5699–5713. doi: 10.1002/chem.201001996. [DOI] [PubMed] [Google Scholar]
- 20.Jaszewski AR, Stranger R, Pace RJ. Phys. Chem. Chem. Phys. 2009;11:5634–5642. doi: 10.1039/b900694j. [DOI] [PubMed] [Google Scholar]
- 21.Brena B, Siegbahn PEM, Ågren H. J. Am. Chem. Soc. 2012;134:17157–17167. doi: 10.1021/ja306794p. [DOI] [PubMed] [Google Scholar]
- 22.Baldwin MJ, Stemmler TL, Riggs-Gelasco PJ, Kirk ML, Penner-Hahn JE, Pecoraro VL. J. Am. Chem. Soc. 1994;116:11349–11356. [Google Scholar]
- 23.Gatt P, Petrie S, Stranger R, Pace RJ. Angew. Chem. 2012;124:12191–12194. doi: 10.1002/anie.201206316. [DOI] [PubMed] [Google Scholar]
- 24.Delgado-Jaime MU, Mewis CP, Kennepohl P. J. Synchrotron Radiat. 2010;17:132–137. doi: 10.1107/S0909049509046561. [DOI] [PubMed] [Google Scholar]
- 25.Neese F. WIREs Comput. Mol. Sci. 2012;2:73–78. [Google Scholar]
- 26.van Lenthe E, Baerends EJ, Snijders JG. J. Chem. Phys. 1993;99:4597–4610. [Google Scholar]
- 27.van Wüllen C. J. Chem. Phys. 1998;109:392–399. [Google Scholar]
- 28.Klamt A, Schüürman D. J. Chem. Soc., Perkin Trans. 1993;2:799–805. [Google Scholar]
- 29.Baffert C, Orio M, Pantazis DA, Duboc C, Blackman AG, Blondin G, Neese F, Deronzier A, Collomb M-N. Inorg. Chem. 2009;48:10281–10288. doi: 10.1021/ic901409y. [DOI] [PubMed] [Google Scholar]
- 30.Orio M, Pantazis DA, Petrenko T, Neese F. Inorg. Chem. 2009;48:7251–7260. doi: 10.1021/ic9005899. [DOI] [PubMed] [Google Scholar]
- 31.Grimme S, Antony J, Ehrlich S, Krieg H. J. Chem. Phys. 2010;132:154104–19. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 32.Weigend F, Ahlrichs R. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 33.Pantazis DA, Chen XY, Landis CR, Neese F. J. Chem. Theory Comput. 2008;4:908–919. doi: 10.1021/ct800047t. [DOI] [PubMed] [Google Scholar]
- 34.Staroverov VN, Scuseria GE, Tao J, Perdew JP. J. Chem. Phys. 2003;119:12129–12137. [Google Scholar]
- 35.Yamaguchi K, Takahara Y, Fueno T. In: Applied Quantum Chemistry. Smith VH Jr., Scheafer HF III, Morokuma K, editors. D. Reidel; Boston: 1986. p. 155. [Google Scholar]
- 36.Yamanaka S, Kawakami T, Nagao H, Yamaguchi K. Chem. Phys. Lett. 1994;231:25–33. [Google Scholar]
- 37.Hirata S, Head-Gordon M. Chem. Phys. Lett. 1999;314:291–299. [Google Scholar]
- 38.Neese F, Olbrich G. Chem. Phys. Lett. 2002;362:170–178. [Google Scholar]
- 39.DeBeer George S, Petrenko T, Neese F. Inorg. Chim. Acta. 2008;361:965–972. [Google Scholar]
- 40.Dunlap BI, Connolly JWD, Sabin JR. J. Chem. Phys. 1979;71:3396–3402. [Google Scholar]
- 41.Feyereisen M, Fitzgerald G, Komornicki A. Chem. Phys. Lett. 1993;208:359–363. [Google Scholar]
- 42.Neese F, Wennmohs F, Hansen A, Becker U. Chem. Phys. 2009;356:98–109. [Google Scholar]
- 43.Gohdes JW, Armstrong WH. Inorg. Chem. 1992;31:368–373. [Google Scholar]
- 44.Pantazis DA, Krewald V, Orio M, Neese F. Dalton Trans. 2010;39:4959–4967. doi: 10.1039/c001286f. [DOI] [PubMed] [Google Scholar]
- 45.Sinnecker S, Svensen N, Barr EW, Ye S, Bollinger JM, Neese F, Krebs C. J. Am. Chem. Soc. 2007;129:6168–6179. doi: 10.1021/ja067899q. [DOI] [PubMed] [Google Scholar]
- 46.Westre TE, Kennepohl P, DeWitt JG, Hedman B, Hodgson KO, Solomon EI. J. Am. Chem. Soc. 1997;119:6297–6314. [Google Scholar]
- 47.Armstrong WH, Lippard SJ. J. Am. Chem. Soc. 1984;106:4632–4633. [Google Scholar]
- 48.Neese F. Coord. Chem. Rev. 2009;253:526–563. [Google Scholar]
- 49.Neese F. J. Biol. Inorg. Chem. 2006;11:702–711. doi: 10.1007/s00775-006-0138-1. [DOI] [PubMed] [Google Scholar]
- 50.Pantazis DA, Orio M, Petrenko T, Zein S, Bill E, Lubitz W, Messinger J, Neese F. Chem.–Eur. J. 2009;15:5108–5123. doi: 10.1002/chem.200802456. [DOI] [PubMed] [Google Scholar]
- 51.Pantazis DA, Orio M, Petrenko T, Zein S, Lubitz W, Messinger J, Neese F. Phys. Chem. Chem. Phys. 2009;11:6788–6798. doi: 10.1039/b907038a. [DOI] [PubMed] [Google Scholar]
- 52.Berry JF, DeBeer George S, Neese F. Phys. Chem. Chem. Phys. 2008;10:4361–4374. doi: 10.1039/b801803k. [DOI] [PubMed] [Google Scholar]
- 53.Zhao XG, Richardson WH, Chen JL, Li J, Noodleman L, Tsai HL, Hendrickson DN. Inorg. Chem. 1997;36:1198–1217. doi: 10.1021/ic9514307. [DOI] [PubMed] [Google Scholar]
- 54.Noodleman L, Davidson ER. Chem. Phys. 1986;109:131–143. [Google Scholar]
- 55.Gebhard MS, Deaton JC, Koch SA, Millar M, Solomon EI. J. Am. Chem. Soc. 1990;112:2217–2231. doi: 10.1021/ja00226a047. [DOI] [PubMed] [Google Scholar]
- 56.Deaton JC, Gebhard MS, Koch SA, Millar M, Solomon EI. J. Am. Chem. Soc. 1988;110:6241–6243. doi: 10.1021/ja00226a047. [DOI] [PubMed] [Google Scholar]
- 57.Neese FJ. Phys. Chem. Solids. 2004;65:781–785. [Google Scholar]
- 58.Caballol R, Castell O, Illas F, de P. R. Moreira I, Malrieu JP. J. Phys. Chem. A. 1997;101:7860–7866. [Google Scholar]
- 59.Bühl M, Kabrede H. J. Chem. Theory Comput. 2006;2:1282–1290. doi: 10.1021/ct6001187. [DOI] [PubMed] [Google Scholar]
- 60.Minenkov Y, Singstad A, Occhipinti G, Jensen VR. Dalton Trans. 2012;41:5526–5541. doi: 10.1039/c2dt12232d. [DOI] [PubMed] [Google Scholar]
- 61.Yano J, Robblee J, Pushkar Y, Marcus MA, Bendix J, Workman JM, Collins TJ, Solomon EI, DeBeer George S, Yachandra VK. J. Am. Chem. Soc. 2007;129:12989–13000. doi: 10.1021/ja071286b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hall ER, C. J. P., Bendix J, Collins TJ, Glatzel P, DeBeer S. 2013 doi: 10.1021/ja504206y. manuscript in preparation. [DOI] [PubMed] [Google Scholar]
- 63.Glatzel P, Bergmann U, Yano J, Visser H, Robblee JH, Gu WW, de Groot FMF, Christou G, Pecoraro VL, Cramer SP, Yachandra VK. J. Am. Chem. Soc. 2004;126:9946–9959. doi: 10.1021/ja038579z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Farges F. Phys. Rev. B. 2005;71:155109. [Google Scholar]
- 65.Umena Y, Kawakami K, Shen J-R, Kamiya N. Nature. 2011;473:55–60. doi: 10.1038/nature09913. [DOI] [PubMed] [Google Scholar]
- 66.Pantazis DA, Ames W, Cox N, Lubitz W, Neese F. Angew. Chem., Int. Ed. 2012;51:9935–9940. doi: 10.1002/anie.201204705. [DOI] [PubMed] [Google Scholar]
- 67.Grundmeier A, Dau H. Biochim. Biophys. Acta Bioenerg. 2012;1817:88–105. doi: 10.1016/j.bbabio.2011.07.004. [DOI] [PubMed] [Google Scholar]
- 68.Luber S, Rivalta I, Umena Y, Kawakami K, Shen JR, Kamiya N, Brudvig GW, Batista VS. Biochemistry. 2011;50:6308–6311. doi: 10.1021/bi200681q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Galstyan A, Robertazzi A, Knapp EW. J. Am. Chem. Soc. 2012;134:7442–7449. doi: 10.1021/ja300254n. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.