Validation sampling can reduce bias in healthcare database studies: an illustration using influenza vaccination effectiveness

Abstract

Objective

Estimates of treatment effectiveness in epidemiologic studies using large observational health care databases may be biased due to inaccurate or incomplete information on important confounders. Study methods that collect and incorporate more comprehensive confounder data on a validation cohort may reduce confounding bias.

Study Design and Setting

We applied two such methods, imputation and reweighting, to Group Health administrative data (full sample) supplemented by more detailed confounder data from the Adult Changes in Thought study (validation sample). We used influenza vaccination effectiveness (with an unexposed comparator group) as an example and evaluated each method’s ability to reduce bias using the control time period prior to influenza circulation.

Results

Both methods reduced, but did not completely eliminate, the bias compared with traditional effectiveness estimates that do not utilize the validation sample confounders.

Conclusion

Although these results support the use of validation sampling methods to improve the accuracy of comparative effectiveness findings from healthcare database studies, they also illustrate that the success of such methods depends on many factors, including the ability to measure important confounders in a representative and large enough validation sample, the comparability of the full sample and validation sample, and the accuracy with which data can be imputed or reweighted using the additional validation sample information.

1. Introduction

Large health care databases are increasingly being used to study treatment effectiveness in medical research [1]. However, using data collected primarily for administrative and clinical purposes to conduct comparative effectiveness research poses many challenges. One major problem is that large databases can have limited ability to characterize important confounding differences in outcome risk between exposed and unexposed persons [2–4]. For instance, database confounder adjustment for health status is often accomplished by broadly defining medical conditions using binary International Classification of Disease (ICD-9) diagnosis codes, or risk score summary measures based on these codes, assigned by the medical provider during patient visits [5–7]. This relatively crude adjustment can lead to residual confounding in effectiveness estimates, because ICD-9 codes do not adequately measure disease severity or functional status [4, 8–12].

A prominent example of this problem is the estimation of influenza vaccine effectiveness (VE) among the elderly in large database studies, which have consistently found implausibly high risk reductions against all-cause mortality (~50%) when adjusting only for database information such as binary ICD-9 coded indicators of health status [13–15]. More recent research has indicated that residual confounding may account for some, if not all, of this observed effect [10–11]. Specifically, when examining the association between influenza vaccine and mortality in the pre-influenza control period prior to the circulation of influenza, even larger reductions in risk (~70%) have been found [10]. Any effect observed during the pre-influenza period represents bias, since no association between influenza vaccine and morbidity or mortality is biologically plausible when influenza virus is not circulating. This bias has been shown to be reduced by adjusting for functional limitations obtained from medical chart review [11], which suggests that unmeasured frailty is the most plausible unmeasured confounder in this setting. Such confounding would occur if seniors who are very close to dying are no longer given preventive therapies, such as influenza vaccine.

Although adjusting more comprehensively for additional confounders obtained by medical record review or in-person physical examination has the potential to reduce bias in traditional effectiveness estimates that adjust only for information available in database sources, it may be too expensive to collect these more costly confounders in large database studies, where sample sizes can reach tens or hundreds of thousands. One solution is to collect the more expensive data on a smaller validation sample or a subset of the full database cohort and use validation or two-phase sampling methods to incorporate this information into analyses. Here we implement two such approaches, a missing data imputation method and a survey sample reweighting method, to estimate influenza VE in the elderly. We use GHC administrative data from a prior influenza VE study [9] (full sample) supplemented by richer confounder data on a subset (validation subsample) that included in-person examinations as part of the Adult Changes in Thought (ACT) study [16]. We use the control time period prior to influenza season to evaluate each method’s ability to successfully reduce confounding bias compared to traditional adjustment approaches that rely solely on confounders from database sources.

2. Materials and methods

2.1 Study design, setting, and population

We used existing cohorts from two prior studies conducted among persons aged 65 years and older who were members of Group Health Cooperative (GHC), a managed care organization in Washington State with ~350,000 enrollees. The composition of the GHC population is representative of the surrounding region, which is primarily white, middle class, and well educated. The first was a large, retrospective database cohort study of influenza VE among 72,527 community-dwelling seniors from 1995–2002 [9] that captured data from GHC’s administrative systems on all-cause mortality (outcome of interest), influenza immunization (exposure of interest), and database confounders used in prior database studies of influenza VE [14–15], including health care utilization (e.g., number of outpatient visits) and ICD-9 diagnosis codes assigned to patient encounters and used to define binary health status indicators (e.g., heart disease). In the current study, we utilized data from two study years (September 1, 2000 – August 31, 2001 and September 1, 2001 – August 31, 2002), required that persons remain continuously enrolled during each study year, and defined this cohort as the full sample. Subjects were followed each study year from the September 1 start date until their death or August 31, whichever occurred first. Database confounders were captured in the one-year baseline period prior to each study year (September 1, 1999 – August 31, 2000 and September 1, 2000 – August 31, 2001). To make fuller use of available database information in the current study compared with prior studies, we also defined additional database covariates using a broader range of data, including medications, laboratory test results, other health care utilization (e.g., home health services), and disease severity measures, based on methods described previously [11].

The second sample was taken from the longitudinal ACT study, a prospective cohort study of aging and dementia among GHC seniors [16]. The original ACT cohort of 2,581 community-dwelling, dementia-free persons aged 65 years or older was enrolled from 1994 to 1996 and supplemented with 811 more members from 2000 to 2003. Extensive data from in-person interviews and physical examinations were collected at an initial visit and follow-up visits every two years thereafter, including self-reported demographics, activities, and instrumental activities of daily living (ADL and IADL), health behaviors, and disease conditions, as well as clinical assessments of physical function, dementia, and depression. Some interviews were conducted by proxy if study subjects were unavailable. Further study design details have been published previously [16–17]. In the current study, we used ACT data to more comprehensively characterize potential confounders on subjects who were also in the full sample. Confounder data were accessed on ACT enrollees with a follow-up visit during the baseline period in which database confounders were available from the full sample (September 1, 1999 – August 31, 2001 and September 1, 2000 – August 31, 2001). These ACT participants are a subset of the full cohort and are defined in the current study as the validation sample. In analyses, we linked the ACT data on validation sample members to their full sample database information, which contained their mortality status, influenza vaccine exposure status, and database confounders.

2.2 Statistical model

Our primary aim was to assess whether confounding bias in traditional database estimates of influenza VE against all-cause mortality, which naively adjust only for database confounders, can be reduced by incorporating adjustment for additional confounders measured in a validation sample. For each approach, we used data from both study years to fit a Cox proportional hazards model that estimated the RR of death for vaccinated versus unvaccinated individuals, treating vaccination status as a binary time-varying covariate defined for each subject as ‘unvaccinated’ from September 1 up to the date of vaccination and as ‘vaccinated’ for the rest of that study year (i.e., until August 31). To estimate the effect of vaccine during influenza season as well as control periods before and afterward, we included an interaction term between vaccine status and a three-category time period effect defined using local influenza viral surveillance data for each study year [10]: before (September 1 to December 16 in study year 1, and September 1 to December 15 in study year 2), during (December 17 to March 18 in study year 1, and December 16 to March 10 in study year 2), and after (March 19 to August 31 in study year 1, and March 11 to August 31 in study year 2) influenza season.

In each Cox model, propensity scores were used to consolidate confounders into a single summary measure for adjustment. The propensity score was defined as the probability of receiving influenza vaccine in each study year conditional on confounders measured in the year prior and was estimated using multivariable logistic regression. Two specific scores were created using confounders defined a priori based on expert clinical opinion: 1) An error-prone score (PS_ep) computed among the full cohort and based only on database confounders, and 2) A gold-standard score (PS_gs) computed in the validation cohort and based both on database and validation sample confounders. To prevent bias, propensity score models excluded variables related only to exposure and not outcome by inspecting the age and gender adjusted odds ratios (ORs) between each variable and outcome [18–19]. Using these propensity scores, we implemented four approaches: 1) an unadjusted model, 2) a naïvely adjusted model, 3) imputation, and 4) reweighting. The unadjusted and naïvely adjusted methods involved fitting a Cox model among the full sample that either did not adjust for any confounders or adjusted only for database confounders as measured by PS_ep, thus replicating traditional unadjusted and adjusted database study methods. The second two approaches, described further in the next sections, fit Cox models that incorporated confounders from the ACT validation sample.

2.3 Imputation

We first viewed the lack of more detailed confounder data (i.e., the lack of PS_gs) for some full cohort members from a missing data perspective [20] and applied the following steps [21]: 1) In the validation sample, use linear regression to estimate the association between the predictor PS_ep and outcome PS_gs, adjusted for influenza vaccination status; 2) Use this regression equation to predict PS_gs among full sample members not in the ACT validation sample; and 3) In the full sample, fit a Cox regression model estimating the RR of death for those vaccinated versus not vaccinated, adjusted for PS_gs (for those in the ACT validation sample) or its predicted value of PS_gs (for those not in the ACT validation sample) and use bootstrapping to estimate standard errors. Notably, when considering this problem in a measurement error context, where the propensity score based only on database confounders (PS_ep) is the quantity measured with error compared with a gold standard propensity score based on the more detailed confounder data (PS_gs), this imputation approach is equivalent to the regression calibration algorithm described by Carroll et al. [22]. Sturmer et al. referred to this specific application of regression calibration as propensity score calibration [21].

2.4 Reweighting

The second validation sampling approach we employed is a survey reweighting method called generalized raking [23–24]. Reweighting is often used when analyzing a subcohort sampled from a larger cohort using a two-phase stratified design. Subcohort analyses are then inverse probability–weighted based on the sampling probabilities (i.e., using Horvitz-Thompson estimation) so that subcohort inference reflects the larger cohort and is thus generalizable to the original population [25]. However, weights based only on the stratifying factors do not generally use all the available information on the larger cohort, information known as auxiliary data (V) [26]. To increase precision, standard weights can be adjusted using V so that the observed total of V in the larger cohort equals the weighted total of V in the subcohort, while keeping the adjustment as small as possible. This induced dependence of the weights on V, measured on the full cohort, drives the efficiency gain and is known as calibration [27–28]. To avoid confusion with the previously described imputation approach, which has also been called calibration, we refer to this reweighting method using an alternative survey terminology: generalized raking [24].

To implement raking in the influenza VE example, we fit a weighted Cox model in the validation sample that estimated the RR of death for those vaccinated versus not vaccinated, adjusted for PS_gs, where the weights were estimated as follows: 1) Define initial weights as the inverse probability of inclusion in the ACT validation cohort, and estimate them using logistic regression with age, gender, and their interaction as predictors, as if the ACT cohort was drawn from the full sample using an age and gender stratified design; and 2) Adjust the initial weights by using the additional auxiliary information, PS_ep, available on all full cohort members. Instead of directly using PS_ep as the raking variable (i.e., instead of using V=PS_ep), we used a variable based on PS_ep called a delta-beta, a quantity that reflects the estimated influence of each subject in a Cox regression and has been shown to estimate the optimally efficient choice of V [23,25–26]. We note that although the initial weights in Step 1 were based only on age and gender (in order to reflect stratifying factors that are commonly used in practice in two-phase designs), the final weights used in Step 2 for reweighting depend on all the auxiliary database information contained in the PS_ep thus fully leveraging the available database information.

3. Results

3.1 Characteristics of the study years and cohorts

The full sample and validation sample cohorts comprised about 44,000 and 1,000 seniors each year who contributed 86,400 and 1,936 person-years during the two-year study period, respectively (Table 1). Annual influenza vaccine coverage was about 72% and 77% in the full and validation samples, respectively, and about 3–4% died each year in each cohort. The percent who died in the periods before, during, and after influenza season were 0.9%, 0.8%, and 1.6%, respectively, with the highest percent observed after influenza season, which was roughly twice as long as the other periods. Most vaccinated seniors received vaccine in November of each study year (Figure 1). Tables 2 and 3 show the characteristics of the full and validation sample cohorts based on database confounders included in the PS_ep and the supplemental confounders included in the PS_gs, respectively. About 60% of members in both cohorts were female, and the full sample was slightly younger than the validation sample. Table 4 shows the ORs and 95% confidence intervals (CIs) quantifying the magnitude of the age and gender adjusted association between each confounder and death to provide further insight into the confounding mechanisms based on both database and validation sample information.

Table 1.

Study and subject characteristics by study year

	Full Sample		ACT Validation Sample
Study Year (September through August)	2000	2001	2000	2001
Number of cohort members evaluated	43,814	43,974	1,005	968
Total person-years assessed	43,140	43,260	984	952
Number of deaths	1,406	1,464	40	31
Number of vaccinations	31,417	32,005	789	745
Date by which at least x% of influenza vaccinations given to study cohort members during the study year had been administered
50%	11/21/2000	11/10/2001	12/1/2000	11/10/2001
75%	12/5/2000	11/15/2001	12/6/2000	11/15/2001
90%	12/11/2000	11/27/2001	12/9/2000	11/26/2001
Vaccination Coverage in the study cohort, as of December 31 (%)	70	72	76	76

Figure 1.

Timing of influenza circulation and distribution of influenza vaccine.

Table 2.

Study characteristics of the full database cohort and validation sample based on database confounders

Characteristic:	Full sample			ACT validation sample
	Vaccinated person-years (%)	Unvaccinated person-years (%)	Total person- years (%)	Vaccinated person-years (%)	Unvaccinated person-years (%)	Total person- years (%)
Total person-years	49,141	37,259	86,400	1,180	756	1,936
Age Group (year)*
65–74	49.8%	53.5%	51.4%	25.7%	24.9%	25.4%
70–84	40.7%	36.1%	38.7%	57.9%	54.5%	56.6%
85+	9.6%	10.4%	9.9%	16.4%	20.5%	18.0%
Sex
Male	42.5%	42.2%	42.3%	40.8%	38.8%	40.0%
Female	57.5%	57.8%	57.7%	59.2%	61.2%	60.0%
Prescriptions in previous year:
0–14	20.7%	31.2%	25.2%	16.1%	21.3%	18.1%
15–33	24.7%	24.8%	24.7%	23.6%	26.4%	24.7%
34–63	26.8%	22.9%	25.1%	29.4%	26.0%	28.1%
>=64	27.8%	21.1%	24.9%	30.9%	26.2%	29.0%
Prednisone	6.1%	4.9%	5.6%	5.8%	5.9%	5.9%
Isosorbide di- or mono-nitrate	3.0%	2.4%	2.7%	3.4%	3.0%	3.2%
Furosemide	12.7%	11.0%	12.0%	15.4%	14.4%	15.0%
ACE inhibitors	26.3%	22.8%	24.8%	25.3%	22.3%	24.1%
Verapamil, diltiazem or felodipine	16.0%	13.4%	14.9%	17.8%	15.1%	16.8%
Antidepressants	21.2%	18.9%	20.2%	23.2%	21.8%	22.7%
Oral narcotics	10.9%	9.5%	10.3%	20.3%	17.6%	19.2%
Benzodiazepine	17.6%	15.3%	16.6%	22.7%	18.7%	21.2%
Pulmonary medications	4.8%	3.6%	4.3%	4.7%	3.3%	4.2%
Medical services received in previous year:
Chemotherapy or radiation treatment	0.4%	0.4%	0.4%	0.4%	0.4%	0.4%
Home health care	8.3%	7.5%	7.9%	7.3%	7.4%	7.3%
Optometrist	54.4%	48.0%	51.6%	52.6%	46.2%	50.1%
Hospitalization:
none	84.5%	86.3%	85.3%	83.9%	86.8%	85.0%
1+	15.5%	13.7%	14.7%	16.1%	13.2%	15.0%
Total specialist visits:
none	66.1%	71.7%	68.5%	56.5%	63.7%	59.3%
1+	33.9%	28.3%	31.5%	43.5%	36.3%	40.7%
Days with ≥ 1 outpatient visits:
0–3	20.7%	30.4%	24.9%	14.2%	21.6%	17.1%
4–6	20.8%	21.4%	21.1%	16.2%	18.5%	17.1%
7–12	30.3%	26.7%	28.8%	34.7%	31.7%	33.5%
13+	28.2%	21.5%	25.3%	35.0%	28.3%	32.3%
Medical diagnosis in previous year:
Asthma	5.1%	4.1%	4.7%	5.4%	4.3%	4.9%
Congestive Heart Failure	6.2%	5.5%	5.9%	7.7%	7.2%	7.5%
COPD	11.4%	9.4%	10.5%	11.2%	9.8%	10.7%
Dementia	2.1%	2.6%	2.3%	3.0%	5.8%	4.1%
Depression	5.5%	4.9%	5.3%	5.4%	5.5%	5.5%
Peripheral vascular disease	3.0%	2.5%	2.8%	3.9%	2.7%	3.5%
Pneumonia	4.2%	3.8%	4.0%	4.4%	4.7%	4.5%
Diabetes:
none	84.8%	86.8%	85.6%	87.1%	88.9%	87.8%
untreated	4.3%	3.8%	4.1%	3.4%	2.5%	3.1%
oral meds only	5.0%	4.5%	4.8%	4.0%	3.8%	3.9%
insulin	1.6%	1.2%	1.4%	1.3%	0.7%	1.1%
complication	4.4%	3.7%	4.1%	4.1%	4.1%	4.1%
Cancer:
none	77.5%	80.5%	78.8%	76.4%	79.5%	77.6%
cancer	20.1%	17.2%	18.9%	21.2%	18.4%	20.1%
severe/multiple myeloma	2.5%	2.3%	2.4%	2.4%	2.1%	2.3%
Laboratory Values in previous year
Lowest Albumin
<3.39	1.3%	1.2%	1.3%	1.6%	1.2%	1.4%
3.4–3.59	1.5%	1.4%	1.5%	1.7%	2.5%	2.0%
3.6–3.89	7.6%	6.4%	7.1%	8.1%	7.2%	7.7%
3.9+	30.3%	28.1%	29.4%	28.6%	26.7%	27.9%
Lab data not assessed	59.2%	62.8%	60.8%	60.1%	62.4%	61.0%
Highest Creatinine
<1	26.7%	24.6%	25.8%	28.3%	26.1%	27.4%
1.1–1.39	25.9%	23.1%	24.7%	27.6%	26.1%	27.0%
1.4–2.39	8.2%	7.1%	7.7%	9.1%	8.8%	9.0%
2.4+	1.1%	1.0%	1.1%	1.3%	1.4%	1.3%
Lab data not assessed	38.0%	44.2%	40.7%	33.8%	37.6%	35.3%
Lowest Hematocrit
<29	1.5%	1.3%	1.4%	2.0%	1.4%	1.8%
29–33.9	3.9%	3.4%	3.7%	4.2%	4.9%	4.5%
34–37.9	11.0%	9.7%	10.4%	15.0%	13.6%	14.4%
38–39.9	10.6%	9.5%	10.1%	11.8%	11.5%	11.7%
40+	30.2%	28.0%	29.3%	29.2%	25.9%	27.9%
Lab data not assessed	42.7%	48.1%	45.0%	37.8%	42.6%	39.7%

Table 3.

Study characteristics of the validation sample based on supplemental confounders

Characteristic:	ACT validation sample
	Vaccinated person-years (%)	Unvaccinated person-years (%)	Total person-years (%)
Total person-years	1,180	756	1,936
65–74	25.7%	24.9%	25.4%
70–84	57.9%	54.5%	56.6%
85+	16.4%	20.5%	18.0%
Sex
Male	40.8%	38.8%	40.0%
Female	59.2%	61.2%	60.0%
Race
White	90.1%	89.1%	89.7%
Perceived Health:
Poor	2.7%	3.5%	3.0%
Fair	14.3%	15.4%	14.7%
Good	41.5%	38.8%	40.5%
Very good	31.5%	27.9%	30.1%
Excellent	10.0%	14.4%	11.7%
BMI
Underweight	0.9%	1.3%	1.1%
Adequate	32.5%	32.9%	32.7%
Overweight	39.1%	39.0%	39.0%
Obese	24.6%	23.2%	24.1%
Unavailable	2.9%	3.6%	3.2%
Lives Alone	37.1%	37.3%	37.2%
Any exercise in past 12 months	69.8%	64.8%	67.9%
Frailty measures:
Frail Grip Strength	38.5%	39.3%	38.8%
Frail Walking Speed	30.5%	35.0%	32.2%
Able to walk around house:
No difficulty	88.9%	88.5%	88.7%
Some difficulty	8.5%	8.5%	8.5%
A lot of difficulty/unable	2.6%	3.0%	2.7%
Able to walk half a mile:
No difficulty	68.1%	65.0%	66.9%
Some difficulty	10.6%	12.5%	11.3%
A lot of difficulty/unable	21.2%	22.5%	21.7%
Able to walk up stairs:
No difficulty	76.2%	73.7%	75.2%
Some difficulty	14.0%	15.6%	14.7%
A lot of difficulty/unable	9.8%	10.7%	10.2%
Able to get out of bed/chair:
No difficulty	79.0%	79.1%	79.0%
Some difficulty	17.5%	16.9%	17.2%
A lot of difficulty/unable	3.6%	4.0%	3.8%
Able to feed oneself:
No difficulty	98.2%	96.9%	97.7%
Some difficulty	1.8%	3.1%	2.3%
Able to dress oneself:
No difficulty	92.5%	91.7%	92.2%
Some difficulty	6.2%	6.3%	6.3%
A lot of difficulty/unable	1.2%	2.0%	1.5%
Able to bathe oneself:
No difficulty	92.9%	91.2%	92.2%
Some difficulty	4.7%	5.4%	5.0%
A lot of difficulty/unable	2.4%	3.4%	2.8%
Able to use toilet:
No difficulty	96.2%	95.2%	95.8%
Some difficulty	2.8%	3.6%	3.1%
A lot of difficulty/unable	0.9%	1.2%	1.0%
Receives home health care	8.0%	8.0%	8.0%
Uses handivan	4.3%	4.5%	4.4%
Difficulty on any IADL item	30.3%	33.9%	31.7%
Difficulty on any ADL item	28.8%	29.5%	29.0%
Medical diagnosis in previous year:
Congestive Heart Failure	6.9%	6.4%	6.7%
Hearth Rhythm Problems	29.5%	28.8%	29.2%
Heart Condition	24.5%	22.8%	23.8%
Diabetes:
none	87.7%	88.6%	88.1%
untreated	2.9%	2.8%	2.9%
with oral medication	3.5%	3.6%	3.5%
with complications	5.9%	5.0%	5.6%
Parkinson’s Disease	3.2%	3.0%	3.1%
Chronic Lung Condition	22.3%	22.9%	22.5%
Acute Lung Infection	55.1%	54.9%	55.0%
Kidney:
none	89.0%	88.6%	88.8%
disease	9.7%	10.3%	9.9%
failure	1.3%	1.1%	1.2%
Autoimmune disorder	6.3%	7.0%	6.6%
Any Fractures	10.4%	10.1%	10.3%
Dementia	5.1%	8.9%	6.6%
Cognitive Abilities Screening Instrument Score
0–89	18.8%	23.7%	20.7%
90–94	29.4%	29.8%	29.6%
95–96	18.8%	17.4%	18.3%
97+	32.5%	28.7%	31.0%
CES-D Depression score
0	28.5%	26.7%	27.8%
1–3	32.3%	34.0%	33.0%
4–6	13.9%	13.9%	13.9%
6+	25.0%	24.7%	24.9%

Table 4a.

Age and gender adjusted odds ratios of associations between database confounders and death in the full sample.

Full sample characteristic:	Association with Death Odds Ratio (95% CI)
Prescriptions in previous year:
0–14	referent
15–33	1.3 (1.13,1.49)
34–63	1.65 (1.45,1.89)
>=64	3.53 (3.13,3.98)
Prednisone	2.29 (2.05,2.57)
Isosorbide di- or mono-nitrate	1.77 (1.52,2.06)
Furosemide	3.15 (2.9,3.41)
ACE inhibitors	1.58 (1.46,1.71)
Verapamil, diltiazem or felodipine	1.36 (1.24,1.48)
Antidepressants	1.9 (1.75,2.06)
Oral narcotics	2.32 (2.12,2.54)
Benzodiazepine	1.89 (1.74,2.06)
Pulmonary medications	3.03 (2.7,3.38)
Medical services received in prior year:
Chemotherapy or radiation treatment	8.02 (6.86,9.37)
Home health care	3.59 (3.29,3.91)
Optometrist	0.82 (0.76,0.88)
Hospitalization:
none	referent
1+	2.24 (2.07,2.43)
Total specialist visits:
none	referent
1+	1.88 (1.75,2.02)
Days with ≥ 1 outpatient visits:
0–3	Referent
4–6	0.96 (0.85,1.09)
7–12	1.11 (0.99,1.24)
13+	1.86 (1.67,2.06)
Medical diagnosis in previous year:
Asthma	1.2 (1.02,1.42)
Congestive Heart Failure	3.43 (3.13,3.76)
COPD	2.49 (2.28,2.72)
Dementia	2.81 (2.48,3.2)
Depression	1.63 (1.43,1.87)
Peripheral vascular disease	2.26 (1.97,2.61)
Pneumonia	2.65 (2.36,2.98)
Renal Disease	4.68 (4.05,5.4)
Diabetes:
none	referent
untreated	1.19 (0.99,1.42)
oral meds only	1.4 (1.19,1.64)
insulin	2.7 (2.17,3.34)
complication	2.14 (1.86,2.47)
Cancer severity:
none	referent
cancer	1.29 (1.17,1.41)
severe/multiple myeloma	8.51 (7.65,9.47)
Laboratory Values in previous year
Lowest Albumin value
<3.39	0.25 (0.21,0.3)
3.4–3.59	1.64 (1.35,1.99)
3.6–3.89	0.56 (0.47,0.66)
3.9+	referent
Lab data not assessed	0.2 (0.17,0.24)
Highest Creatinine value
<1	referent
1.1–1.39	1.79 (1.6,2)
1.4–2.39	5.6 (4.81,6.52)
2.4+	0.95 (0.85,1.07)
Lab data not assessed	0.65 (0.59,0.73)
Lowest Hematocrit value
<29	1.98 (1.68,2.33)
29–33.9	0.25 (0.22,0.28)
34–37.9	0.34 (0.29,0.4)
38–39.9	0.54 (0.47,0.61)
40+	referent
Lab data not assessed	0.22 (0.2,0.25)

3.2 Comparisons of vaccine effectiveness estimates across approaches

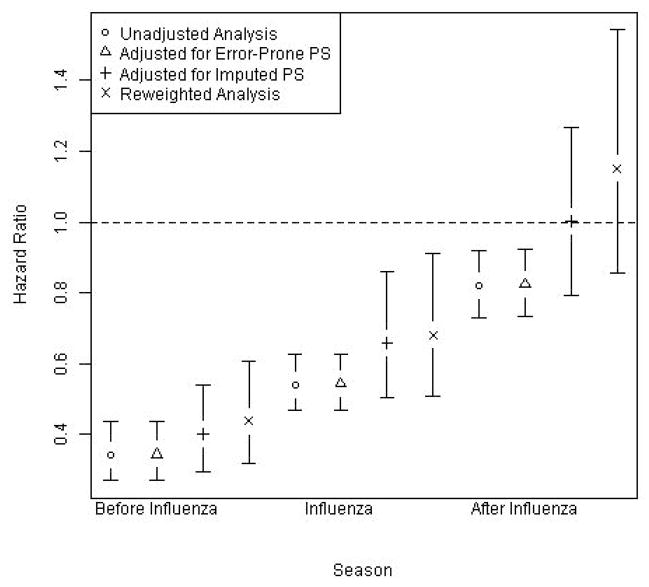
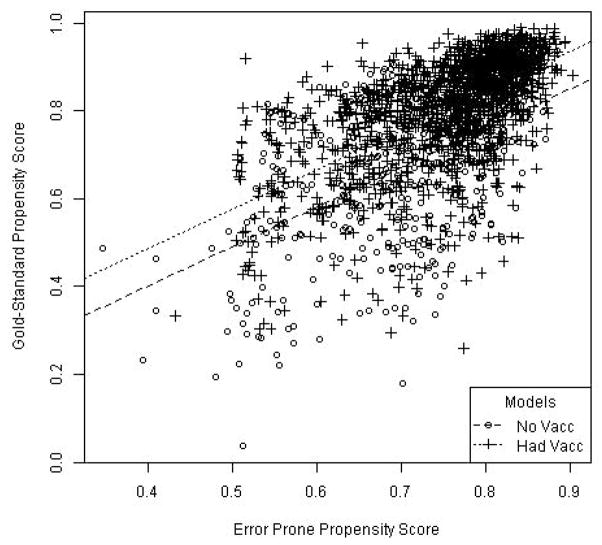
Estimates and 95% CIs of the RR of death associated with influenza vaccination obtained using each of the four approaches (unadjusted, naïve, imputation, and reweighting) in each time period (before, during, and after influenza season) are shown in Figure 2. RRs were lowest (<0.50) in the period before influenza season and then increased steadily (to 0.50–0.70 during and >0.80 after influenza season). Unadjusted and naïvely adjusted estimates were similar across all time periods. Estimates based on imputation or reweighting were also comparable in all time periods, but consistently closer to the null (i.e., RR=1.0) compared with the unadjusted and naïvely adjusted estimates. No approach correctly estimated a null RR=1.0 in the control period before influenza season, though the pre-influenza estimates based on imputation and reweighting were closer to 1.0 than the naïvely-adjusted RR, indicating that bias was somewhat reduced using methods that incorporated the validation confounder data. The quality of the imputation and reweighting is characterized in Figure 3. This scatterplot with fitted regression lines estimating the association between PS_ep and PS_gs within the validation sample shows modest correlation (ρ=0.60) but wide variability in PS_gs for each PS_ep.

Figure 2.

Relative risk of all-cause mortality for vaccinated seniors compared with unvaccinated seniors in intervals before during and after influenza season, unadjusted and adjusted based on three statistical methods.

Figure 3.

Diagnostic scatterplot with fitted regression lines estimating the strength of the association between error-prone and gold-standard propensity scores within the validation sample.

4. Discussion

The association between influenza vaccination and risk of all-cause mortality is a useful example for studying problems of confounding in treatment effectiveness studies that rely on administrative databases [3], as strong confounding is present, and there is a natural control period prior to influenza season that can be used to assess bias [10,29]. In this study, we leveraged existing data from two prior cohort studies to explore the utility of using two methods (imputation and reweighting) that integrate additional confounder data from a validation sample to reduce confounding bias in influenza VE estimates that adjust only for information available in database sources. Using the control period prior to influenza season as a gauge, we found that both methods modestly reduced but did not completely eliminate the bias compared with naïvely adjusted estimates that did not use the validation sample confounder data. The magnitude of the bias reduction was comparable in both approaches.

Use of validation sample methods can enhance healthcare database studies, but our results suggest that their success in practice depends on many factors and assumptions. The key bias-reducing factor for either imputation or reweighting is the ability to measure the important confounders in the validation sample. Both methods also rely on the comparability of the validation and full samples, which is guaranteed if the validation sample is designed as a probability-sampled subcohort. Unbiased estimation for imputation further depends on the correctness of the model used to impute the gold-standard confounder data from the error-prone information, while reweighted estimates are robust to this assumption (i.e., they will be no worse than estimates based only on the validation sample, even if this model is incorrect). In both methods precision will improve as the amount of information in the validation sample increases, which can occur either with larger validation sample sizes or with increases in the strength of the association between the gold standard and error-prone confounders. Lastly, the imputation approach has several additional assumptions, including the conditional independence of the error-prone confounders from outcomes, given the gold-standard confounders (i.e., the surrogacy assumption) [22,30]. Our specific application of imputation, which was designed to be consistent with the propensity score calibration method, involved a propensity score summary measure rather than a single measured covariate, and this raises additional technical issues many of which have been discussed by Lunt et al. [31]. Implementation of the propensity score calibration approach could be further enhanced by performing multiple rather than single imputation.

The influenza VE example we used in this study was advantageous for several reasons. First, there is a well-defined control period during which bias can be assessed. Also, the potential for other sources of bias is relatively small. Outcome misclassification was minimized, because in addition to capturing mortality data directly from GHC databases, we linked to state mortality records and thus obtained information even if a subject disenrolled from GHC. Exposure misclassification is also likely to be small, since vaccination coverage rates in the GHC population have been found to closely reflect average coverage rates among those 65 years and older in Washington State [32]. Reasons for high accuracy of exposure data include the following: 1) The electronic vaccination registry at GHC is well-established, dating back to 1991 when it was created for the Vaccine Safety Datalink Project [33], and is routinely monitored for quality assurance, 2) GHC reciprocally shares data with the Washington State Immunization Information System and so captures vaccine data on seniors vaccinated at outside institutions, and 3) GHC databases will contain vaccinations received by seniors during hospital stays if the hospital filed a claim for payment for the vaccination.

However, the influenza VE application was also limited in several ways. One major challenge is the presence of a selection mechanism for influenza vaccination that is extremely difficult to measure. Although the ACT validation confounders included a variety of disease severity and functional status measures that were geared to address unmeasured frailty, the reasons for selective receipt of preventive therapies such as influenza vaccine in seniors are clearly complex and difficult to measure, and this has been observed in prior studies [10–12]. In many settings, confounding by frailty could instead be addressed by using an active versus an unexposed comparator, but an active comparator is not readily available for influenza vaccine. Trimming a small proportion of those treated contrary to prediction has been proposed as another method to address unmeasured confounding due to frailty, but we did not explore that option in this analysis [34]. Second, comparability between the full and validation cohorts was imperfect, reducing the generalizability to the full sample of the validation sample model that related the gold standard and error-prone propensity scores. More importantly, the relatively rigorous nature of the ACT interviews and examinations may have resulted in frail and demented seniors (the group most plausibly responsible for the much of the unmeasured confounding) being under-represented in the validation sample, which would limit the ability to remove confounding by frailty. A third limitation is that the quality of the model relating the gold standard to the error-prone information in the validation sample was somewhat weak, with wide variability in the gold-standard propensity score for each value of the error-prone propensity score, suggesting relatively limited predictive ability of the database information. Fourth, the validation sample size was relatively small and the mortality outcome was rare, which reduced statistical power.

Our results support further exploration of validation sampling methods, such as imputation and reweighting, to improve the accuracy of findings from health care database studies. Although similar recommendations have been made previously [26,35–37], and software is readily available (widely for imputation and comprehensively in R for survey procedures [38]), such methods remain relatively underutilized. One challenge when studying treatment effectiveness beyond influenza vaccine is that there are limited methods to evaluate the performance of more sophisticated confounder adjustment techniques, like those that incorporate validation data. Unlike the case with influenza vaccine, there may not be a readily available control period during which the association between treatment exposure and outcome is known. If this is the case, one cannot determine with certainty when a method gets the ‘right’ answer or when one method out-performs another. Efficacy estimates from RCTs may give some indication of the ‘truth,’ but they may also substantially differ from observational effectiveness results due to major differences among study populations and between highly controlled RCTs and ‘real-world’ observational settings. Without clear gold-standard estimates of effectiveness in practice for most exposures, a balance of simulation studies (where truth can be generated) and example applications (where the complexities of real data are present) is needed to more fully understand the optimal implementation and settings for use of validation methods in practice.

Table 4b.

Age and gender adjusted odds ratios of associations between supplemental confounders and death in the validation sample.

Characteristic:	Association with Death Odds Ratio (95% CI)
Race
White	1.6 (0.59,4.37)
Perceived Health:
Poor	6.63 (1.61,27.38)
Fair	4.31 (1.29,14.42)
Good	2.03 (0.61,6.75)
Very good	1.92 (0.56,6.6)
Excellent	referent
BMI
Underweight	referent
Adequate	2.41 (0.61,9.51)
Overweight	1.09 (0.62,1.94)
Obese	1.09 (0.52,2.28)
Unavailable	3.23 (1.4,7.44)
Lives Alone	0.63 (0.37,1.07)
Any exercise in past 12 months	0.48 (0.3,0.76)
Frailty measures:
Frail Grip Strength	1.52 (0.92,2.5)
Frail Walking Speed	2.73 (1.61,4.62)
Able to walk around house:
No difficulty	referent
Some difficulty	1.25 (0.62,2.52)
A lot of difficulty/unable	1.81 (0.66,4.97)
Able to walk half a mile:
No difficulty	referent
Some difficulty	2.18 (1.08,4.4)
A lot of difficulty/unable	2.73 (1.6,4.65)
Able to walk up stairs:
No difficulty	referent
Some difficulty	2.2 (1.22,3.96)
A lot of difficulty/unable	2.58 (1.4,4.74)
Able to get out of bed/chair:
No difficulty	referent
Some difficulty	0.92 (0.49,1.73)
A lot of difficulty/unable	2.48 (1.15,5.35)
Able to feed oneself:
No difficulty	referent
Some difficulty	3.77 (1.67,8.51)
Able to dress oneself:
No difficulty	referent
Some difficulty	1.06 (0.41,2.77)
A lot of difficulty/unable	7.09 (3.16,15.93)
Able to bathe oneself:
No difficulty	referent
Some difficulty	1.9 (0.85,4.25)
A lot of difficulty/unable	3.68 (1.77,7.64)
Able to use toilet:
No difficulty	referent
Some difficulty	0.38 (0.05,2.66)
A lot of difficulty/unable	7.67 (3.33,17.66)
Receives home health care	2.25 (1.26,4.02)
Uses handivan	0.21 (0.03,1.61)
Difficulty on any IADLitem	2.44 (1.52,3.94)
Difficulty on any ADL item	1.31 (0.8,2.14)
Medical diagnosis in previous year:
Congestive Heart Failure	2.56 (1.4,4.67)
Hearth Rhythm Problems	1.35 (0.85,2.15)
Heart Condition	1.61 (0.99,2.6)
Diabetes:
none	referent
untreated	1.16 (0.3,4.46)
with oral medication	2.59 (0.98,6.83)
with complications	1.12 (0.41,3.09)
Parkinson’s Disease	1.35 (0.51,3.61)
Chronic Lung Condition	1.68 (1.01,2.79)
Acute Lung Infection	1.4 (0.87,2.25)
Kidney:
none	referent
disease	1.19 (0.58,2.43)
failure	4.61 (1.55,13.73)
Autoimmune disorder	0.34 (0.09,1.32)
Any Fractures	1.27 (0.62,2.6)
Dementia	4.47 (2.58,7.75)
Cognitive Abilities Screening Instrument Score
0–89	referent
90–94	0.39 (0.21,0.73)
95–96	0.4 (0.19,0.87)
97+	0.4 (0.2,0.8)
CES-D Depression score
0	referent
1–3	0.85 (0.44,1.63)
4–6	1.05 (0.46,2.39)
6+	1.51 (0.83,2.76)

What’s new?

• Use of validation sampling methods, such as imputation or reweighting, can improve the accuracy of comparative effectiveness findings from large healthcare database studies, which can have limited ability to characterize important confounding differences in outcome risk between exposed and unexposed persons.

• The association between influenza vaccination and risk of all-cause mortality is a useful example for studying confounding in treatment effectiveness studies that rely on administrative databases, as there is strong confounding and a natural control period prior to influenza season that can be used to assess bias and the ability of more sophisticated methods (like those that use validation sampling) to reduce it.

• The success of validation sampling methods in practice depends on many factors, including the ability to measure important confounders in a large enough validation sample, the comparability of the full sample and validation sample, and the accuracy with which data can be imputed or reweighted using the additional validation sample information.

• Without clear gold-standard estimates of effectiveness in practice for most exposures, a balance of simulation studies (where truth can be generated) and example applications (where the complexities of real data are present) is needed to more fully understand the optimal implementation and settings for use of validation methods in large healthcare database studies.