The Stream Algorithm: Computationally Efficient Ridge-Regression via Bayesian Model Averaging, and Applications to Pharmacogenomic Prediction of Cancer Cell Line Sensitivity

Abstract

Computational efficiency is important for learning algorithms operating in the “large p, small n” setting. In computational biology, the analysis of data sets containing tens of thousands of features (“large p”), but only a few hundred samples (“small n”), is nowadays routine, and regularized regression approaches such as ridge-regression, lasso, and elastic-net are popular choices. In this paper we propose a novel and highly efficient Bayesian inference method for fitting ridge-regression. Our method is fully analytical, and bypasses the need for expensive tuning parameter optimization, via cross-validation, by employing Bayesian model averaging over the grid of tuning parameters. Additional computational efficiency is achieved by adopting the singular value decomposition re-parametrization of the ridge-regression model, replacing computationally expensive inversions of large p × p matrices by efficient inversions of small and diagonal n × n matrices. We show in simulation studies and in the analysis of two large cancer cell line data panels that our algorithm achieves slightly better predictive performance than cross-validated ridge-regression while requiring only a fraction of the computation time. Furthermore, in comparisons based on the cell line data sets, our algorithm systematically out-performs the lasso in both predictive performance and computation time, and shows equivalent predictive performance, but considerably smaller computation time, than the elastic-net.

1. Introduction

Analysis of high-throughput “omics” data sets to infer molecular predictors of cancer phe-notypes is a common type of problem in modern computational biology research. The use of genomic features such as from gene expression, copy number variation, and sequence data, in the predictive modeling of anticancer drug response is a particularly relevant example, which holds the potential to speed up the emergence of “personalized” cancer therapies.^1,5 A common theme of such high-dimensional prediction problems is that the number of genomic features, p, is usually much larger than the number of available samples, n, and regularized regression approaches such ridge-regression,² lasso,³ and elastic-net⁴ are popular methodological choices in this context.^1,5 Computational efficiency is of key importance for any learning algorithm operating in this “large p, small n” setting; a method that improves computational efficiency without sacrificing prediction accuracy could enable such models to be readily applied across a large number of phenotype prediction problems, such as inferring genomic predictors for large panels of anticancer compounds.

In this paper we propose a novel Bayesian formulation of ridge-regression, which executes in a fraction of the time required by the most efficient current implementations of regularized regression methods, while achieving comparable prediction accuracy. We refer to our approach as Stream (Scalable-Time Ridge Estimator by Averaging of Models). First, Stream replaces cross-validation by Bayesian model averaging⁶ (BMA) over the grid of tuning parameters. For each tuning parameter in the grid, we interpret the corresponding ridge-regression fit as a distinct model, and average all models, weighted by how well each model fits the data. Second, it replaces the computation of large p × p matrix inversions by efficient inversions of small and diagonal n × n matrices derived from the singular value decomposition⁷ (SVD) of the feature matrix. Note that the use of SVD re-parameterization is a practice to improve the computational efficiency of ridge-regression model fit.⁸

We point out that both improvements are allowed by the analytical tractability of the Bayesian hierarchical formulation of ridge-regression, where the marginal posterior distribution of the regression coefficients and the prior predictive distribution of the data are readily available, leading to a fully analytical expression for the BMA estimate of the regression coefficients. Furthermore, the quantities that need to be evaluated, namely, model specific posterior expectations and marginal likelihoods, can be efficiently computed under the SVD re-parametrization.

The rest of the paper is organized as follows. In Section 2.1 we present the Stream algorithm, and, in Section 2.2, we present its re-parametrization in terms of the singular value decomposition of the feature data matrix. Section 3.1 presents a simulation study comparing the predictive performance and computation time of Stream against the standard cross-validated ridge-regression model. Section 3.2 presents real data illustrations using two compound screening data sets performed on large panels of cancer cell lines. Finally, in Section 4 we discuss our results, and point out strengths and weaknesses of our proposed algorithm.

2. Statistical model

In the next subsections we present the Stream-regression model and its re-parametrization in terms of the SVD of the feature data matrix. First, we introduce some notation. Throughout the text we consider the regression model y = Xβ + ε, where y represents the n × 1 vector of responses, X corresponds to the n × p matrix of features, β corresponds to the p × 1 vector of regression coefficients, and ε represents a n × 1 vector of independent and identically distributed gaussian error terms with expectation 0 and precision τ. The notation Ga(a, b) represents a gamma distribution with shape and rate parameters a and b, respectively; U(a, b) stands for the uniform distribution on the interval [a, b]; DU(a, b) represents the discrete uniform distribution with support in the range {a, …, b}; Ber(φ) corresponds to the Bernoulli distribution with success probability φ; N_k(μ, Σ) represents a k-dimensional multivariate normal distribution with mean vector μ and covariance matrix Σ; and St_k(μ, Σ, υ) corresponds to a k-dimensional multivariate t-distribution with mean vector μ, scale matrix Σ, and υ degrees of freedom. We represent the k-dimensional identity matrix by I_k, the indicator function assuming values 0 or 1 by 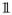, and the determinant of a matrix A by det(A).

2.1. Stream regression model

Consider the Bayesian hierarchical form representation of ridge-regression (a special case of the Bayesian formulation for the linear regression model with a normal-gamma prior⁹):

$$\begin{array}{c}\mathit{y}|\mathit{X},\beta ,\tau \sim {\mathrm{N}}_n(\mathit{X}\beta ,{\tau }^{-1}{\mathit{I}}_n),\\ \beta |\tau ,\lambda \sim {\mathrm{N}}_p(0,{\tau }^{-1}{\lambda }^{-1}{\mathit{I}}_p),\\ \tau \sim \text{Ga}(a_{\tau },b_{\tau }),\end{array}$$

where the precision parameter λ plays the role of the tuning parameter in ridge-regression. Under this analytically tractable model we have that the marginal posterior distribution of the regression coefficients is

$$\pi (\beta |\mathit{X},\mathit{y})={\text{St}}_p(\beta ;\widehat{\beta },\frac{2b_{\tau }+{(\mathit{y}-\mathit{X}\widehat{\beta })}^t\mathit{y}}{2a_{\tau }+n}{({\mathit{X}}^t\mathit{X}+\lambda {\mathit{I}}_p)}^{-1},2a_{\tau }+n),$$

where the expectation, β̂ = (X^tX + λI_p)⁻¹X^ty, corresponds to the usual (frequentist) ridge-regression estimator, and the prior predictive distribution is given by

$$\begin{array}{c}f(\mathit{y}|\mathit{X})={\int }_{\tau }{\int }_{\beta }{\mathrm{N}}_n(\mathit{y};\mathit{X}\beta ,{\tau }^{-1}{\mathit{I}}_n){\mathrm{N}}_p(\beta ;0,{\lambda }^{-1}{\tau }^{-1}{\mathit{I}}_p)\text{Ga}(\tau ;a_{\tau },b_{\tau })d\beta d\tau \\ ={\text{St}}_n(\mathit{y};0,\frac{b_{\tau }}{a_{\tau }}{({\mathit{I}}_n-\mathit{X}{({\mathit{X}}^t\mathit{X}+\lambda {\mathit{I}}_p)}^{-1}{\mathit{X}}^t)}^{-1},2a_{\tau }),\end{array}$$ (1)

Now let λ_k, k = 1,…, K represent the grid of ridge-regression tuning parameters, and let 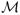_k represent a ridge-regression model that uses λ = λ_k. The BMA estimate of β is then

$$E[\beta |\mathit{X},\mathit{y}]=\sum _{k=1}^{K}E[\beta |\mathit{X},\mathit{y},{\mathcal{M}}_k]pr({\mathcal{M}}_k|\mathit{X},\mathit{y}),$$ (2)

where

$$E[\beta |\mathit{X},\mathit{y},{\mathcal{M}}_k]={({\mathit{X}}^t\mathit{X}+{\lambda }_k{\mathit{I}}_p)}^{-1}{\mathit{X}}^t\mathit{y}$$

and the posterior distribution of model 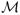_k, given the data, is computed as

$$pr({\mathcal{M}}_k|\mathit{X},\mathit{y})=\frac{f(\mathit{y}|\mathit{X},{\mathcal{M}}_k)pr({\mathcal{M}}_k)}{{\sum }_{k=1}^{K}f(\mathit{y}|\mathit{X},{\mathcal{M}}_k)pr({\mathcal{M}}_k)}.$$

Here, f(y | X, 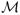_k) corresponds to the prior predictive distribution in (1) with λ replaced by λ_k, and we adopt a discrete uniform prior for the models, so that pr( 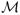_k) = K⁻¹, k = 1, …, K.

In regression based predictive modeling, one is generally interested in making a prediction, ŷ = X_testβ̂_train, of the response vector y_test, where X_test represents the feature data on the testing set, and β̂_train represents the regression coefficients estimate learned from the training set. In our Bayesian model, we are interested on the the expectation of the response's posterior predictive distribution,

$$E[{\mathit{y}}_{\mathit{\text{test}}}|{\mathit{X}}_{\mathit{\text{test}}},{\mathit{X}}_{\mathit{\text{train}}},{\mathit{y}}_{\mathit{\text{train}}}]={\mathit{X}}_{\mathit{\text{test}}}E[\beta |{\mathit{X}}_{\mathit{\text{train}}},{\mathit{y}}_{\mathit{\text{train}}}],$$

where E[β | X_train, y_train] is given by equation (2).

2.2. SVD re-parametrization

Consider the SVD of the n × p feature data matrix X of rank n. One possible representation of X is given by X = UDV^t, where U is a n × n orthogonal matrix of left singular vectors; D is a n × n diagonal matrix of singular values d_j; and V is a p × n matrix of right singular vectors. An alternative representation is $\mathit{X}={\mathit{U}}_{\ast }{\mathit{D}}_{\ast }{\mathit{V}}_{\ast }^t$ where U* is a n × p matrix obtained by augmenting U with p − n extra columns of zeros, U_* = (U, 0); D_* is a p × p diagonal matrix with the first n diagonal entries given by the singular values and the remaining p − n diagonal entries set to zero; and V_* is a p × p orthogonal matrix obtained by augmenting V with p − n additional right singular vectors. Exploring these re-parametrizations we can, after some algebra, re-express β̂ in the computationally more efficient form,

$$E[\beta |\mathit{X},\mathit{y},{\mathcal{M}}_k]={\mathit{V}}_{\ast }{({\mathit{D}}_{\ast }^2+{\lambda }_k{\mathit{I}}_p)}^{-1}{\mathit{D}}_{\ast }{\mathit{U}}_{\ast }^t\mathit{y}=\mathit{V}({{\mathit{D}}^2+{\lambda }_k{\mathit{I}}_n)}^{-1}\mathit{D}{\mathit{U}}^t\mathit{y}.$$

In addition to the efficient computation of β̂, we can also explore the SVD reparameterization for efficient computation of the prior predictive distribution, which involves two computationally expensive steps; namely, evaluation of the quadratic form y^t (I_n − X(X^tX + λ_kI_p)⁻¹X^t)y, and of det ((I_n − X(X^tX + λ_kI_p)⁻¹X^t)⁻¹). Starting with the quadratic form, observe that

$${\mathit{I}}_n-\mathit{X}{({\mathit{X}}^t\mathit{X}+{\lambda }_k{\mathit{I}}_p)}^{-1}{\mathit{X}}^t={\mathit{I}}_n-{\mathit{U}}_{\ast }{\mathit{D}}_{\ast }{({\mathit{D}}_{\ast }+{\lambda }_k{\mathit{I}}_p)}^{-1}{\mathit{D}}_{\ast }{\mathit{U}}_{\ast }^t={\mathit{I}}_n-\mathit{U}{({\mathit{I}}_n+{\lambda }_k{\mathit{D}}^{-2})}^{-1}{\mathit{U}}^t,$$

so that we replace a p × p matrix inversion by a n × n diagonal matrix inversion in the computation of the quadratic form. Next, consider the determinant. From the application of the Woodbury matrix inversion formula¹⁰ we have that

$${\mathit{I}}_n=\mathit{U}{({\mathit{I}}_n+{\lambda }_k{\mathit{D}}^{-2})}^{-1}{\mathit{U}}^t={({\mathit{I}}_n+{\lambda }_k^{-1}\mathit{U}{\mathit{D}}^2{\mathit{U}}^t)}^{-1},$$

and from standard properties of the determinant and the orthogonality of the U matrix we have that

$$det({({\mathit{I}}_n-\mathit{X}{({\mathit{X}}^t\mathit{X}+{\lambda }_k{\mathit{I}}_p)}^{-1}{\mathit{X}}^t)}^{-1})=det({\mathit{I}}_n+{\lambda }_k^{-1}\mathit{U}{\mathit{D}}^2{\mathit{U}}^t)=\underset{j=1}{\overset{n}{\mathbf{\Pi }}}(1+\frac{d_j^2}{{\lambda }_k}).$$

Hence, the prior predictive distribution can be efficiently computed as

$$f(\mathit{y}|\mathit{U},\mathit{D},{\mathcal{M}}_k)=C{(1+\frac{{\mathit{y}}^t({\mathit{I}}_n-\mathit{U}{({\mathit{I}}_n+{\lambda }_k{\mathit{D}}^{-2})}^{-1}{\mathit{U}}^t)\mathit{y}}{2b_{\tau }})}^{-\frac{2a_{\tau }+n}{2}}$$

with the normalization constant, C, given by

$$C=\frac{\Gamma \left(\frac{2a_{\tau }+n}{2}\right)}{\Gamma \left(\frac{2a_{\tau }}{2}\right){(2a_{\tau }\pi )}^{\frac{n}{2}}}{\left(\frac{b_{\tau }}{a_{\tau }}\right)}^{-\frac{n}{2}}{\left(\underset{j=1}{\overset{n}{\mathbf{\Pi }}}\right(1+\frac{d_j^2}{{\lambda }_k}\left)\right)}^{-\frac{1}{2}}.$$

3. Illustrations

Before we present our simulation study and real data illustrations, we provide a few model fitting details relevant to the next subsections. Throughout this paper we evaluate predictive performance using the RMSE statistic, $\sqrt{{({\mathit{y}}_{\mathit{\text{test}}}-\widehat{\mathit{y}})}^t({\mathit{y}}_{\mathit{\text{test}}}-\widehat{\mathit{y}})/n_{\mathit{\text{test}}}}$, where ŷ = X_testβ̂_train. For ridge-regression, lasso, and elastic-net, we adopted 10 fold cross validation. We adopted a data-driven approach, described in detail in the appendix, for the determination of the tuning parameter grid for ridge-regression and Stream. Each simulated or real data set used a different grid, composed of K = 100 values. For each data set we used the same grid in the ridge-regression and Stream model fits. For the lasso and elastic-net algorithms, we adopted the tuning parameter grids generated by default by the glmnet R package.¹¹ Both response and feature data are scaled prior to analysis. In both simulation studies and real data analysis illustrations we tested whether the difference in RMSE between two methods is statistically significant using the Wilcoxon paired-sample test.¹²

3.1. Simulation study

We performed a simulation study illustrating how Stream achieves slightly better predictive performance than ridge-regression (when we adopt non-informative priors for the residual precision parameter τ), while requiring only a fraction of the computation time.

In order to evaluate the method's performance under widely heterogenous conditions, we simulated 5,000 distinct data sets, each one generated with a unique and random combination of sample size (n), number of features (p), model sparsity (φ), residual noise (σ), and strength of feature correlation (ρ), sampled according to: n ∼ DU(100, 500); p ∼ DU(501, 10000); φ ∼ U(0.1, 0.9), σ ∼ U(0.1, 5); and ρ ∼ U(0.1, 0.9).

Each simulated data set was generated as follows: (i) we first draw a single value of n, p, φ, σ, and ρ, from their respective uniform distributions; (ii) given the sampled values of n, p, and ρ, we simulate the feature data matrix, X_n×p = (X_n×p1,…, X_n×pL), as L separate matrices, X_n×pl, generated independently from N_pl(0, Σ_l) distributions, where Σ_ij,l = 1, for i = j, and Σ_ij,l = ρ^|i−j|, for i ≠ j. 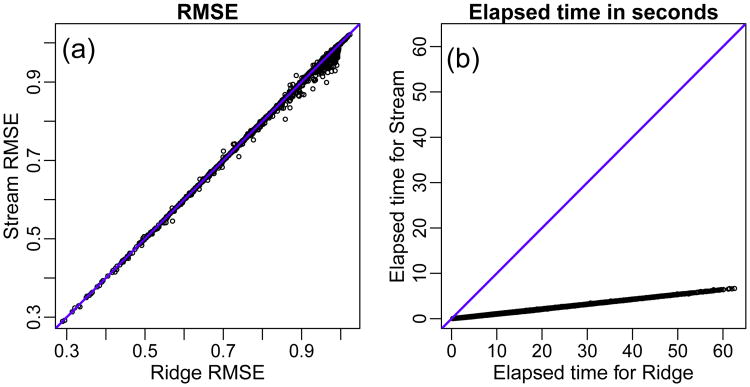The number of features, p_l, in each of these matrices were randomly chosen between 20 and 100 under the constraint that $P={\sum }_{k=1}^{L}pl$; (iii) given the sampled values of p and φ, we computed each regression coefficient, β_j, j = 1, …, p, as ${\beta }_j={\beta }_j^{\ast }{\mathbb{1}}_{{\beta }_j}$, where ${\beta }_j^{\ast }\sim N(0,1)$, and 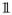β_j ∼ Ber(φ) (note that, by defining β_j as above, we have that, on average, φp regression coefficients will be non-zero); and (iv) given the sampled value of σ and the computed feature matrix and regression coefficients vector, we computed the response vector as y = Xβ + σε, where ε is a vector of standard gaussian error variables. We note that for each simulated data set we actually generated 2n data samples, and used the first n samples as the training set, and the second half as the test set. Figure 1 present the results.

Fig. 1.

Simulation results: comparison of Stream and ridge-regression in terms of predictive performance and computation time.

Panel (a) in Figure 1 shows that the predictive performance of Stream is quite similar to ridge-regression when the RMSE values are small, but Stream tends to slightly outperform ridge when RMSE values are larger, as suggested by the increased number of points below the diagonal for RMSE values closer to 1. Application of the Wilcoxon paired-sample test shows that, overall, Stream achieves statistically significant increased performance over ridge (p-value = 2.501 × 10⁻⁵). We note that the results in Figure 1 were computed using an uninformative gamma prior distribution (hyper-parameters a_τ = b_τ = 0.001). As expected, the adoption of informative gamma priors led to decreased predictive accuracy (results not shown).

Panel (b) in Figure 1 shows the comparison of computation times between Stream and ridge-regression. Overall, Stream was approximately 10 times faster than ridge. In general, Stream is approximately f times faster than ridge-regression, where f represents the number of cross-validation folds used by ridge.

3.2. Cancer cell line panels

In this section we compare the predictive performance and computation time of the Stream, ridge-regression, lasso, and elastic-net algorithms in inferring molecular predictors of compound sensitivity based on the Sanger⁵ and CCLE¹ data sets, which contain compound screening data performed on large panels of molecularly characterized cancer cell lines.

In Sanger we have 535 cell lines and a total of 30,765 features comprised of 4 distinct feature data types, including gene expression measurements on 12,024 genes, copy number variation measurements on 18,601 genes, cell line tumor type classifications according to 93 distinct tumor lineages, and mutation profiling on 47 genes. In CCLE we have 411 cell lines and 41,911 features comprised of 5 distinct feature types, including gene expression measurements on 18,897 genes, copy number measurements on 21,217 genes, cell line tumor type classifications on 97 tumor lineages, mutation profiling on 33 genes using the oncomap 3.0 plataform,¹³ and mutation profiling of 1,667 genes using hybrid capture sequencing. Mutation data was summarized to gene-level binary calls, with 1 representing a somatic mutation observed at any base pair within the gene. Gene expression, copy number, and mutation data were summarized to gene-level features. The Sanger dataset tested 138 compounds and summarized the sensitivity of each cell line based on IC50 values. The CCLE dataset tested 24 compounds and summarized the sensitivity of each cell line based on the area over the dose response curve (where response values at each compound dose are scaled with -100 representing complete growth inhibition and 0 representing no growth inhibition).

In the present analysis we discarded samples and features with missing data, and we filtered out genomic features with variance smaller than 0.01, and with non-significant correlation with the response (p-value > 0.1). After filtering we obtained, on average, 5,588.80 ± 2,046.48 genomic features in Sanger, and 12,512.12 ± 3,345.16 in CCLE. We evaluated predictive performance by splitting the data into five parts, using four parts as the training set and the left out part as the testing set. In each of the 5 splits, we trained the ridge, lasso, and elastic-net models using 10 fold cross validation and adopted a_τ = b_τ = 0.01 for the Stream model. At each split we obtained a prediction vector ŷ_j, j = 1, …, 5, and we computed a single RMSE using the concatenated vector of predictions, ${\widehat{\mathit{y}}}^t=({\widehat{\mathit{y}}}_1^t,\dots ,{\widehat{\mathit{y}}}_5^t)$, and the full observed response data, y, as $\sqrt{{(\mathit{y}-\widehat{\mathit{y}})}^t(\mathit{y}-\widehat{\mathit{y}})/n}$.

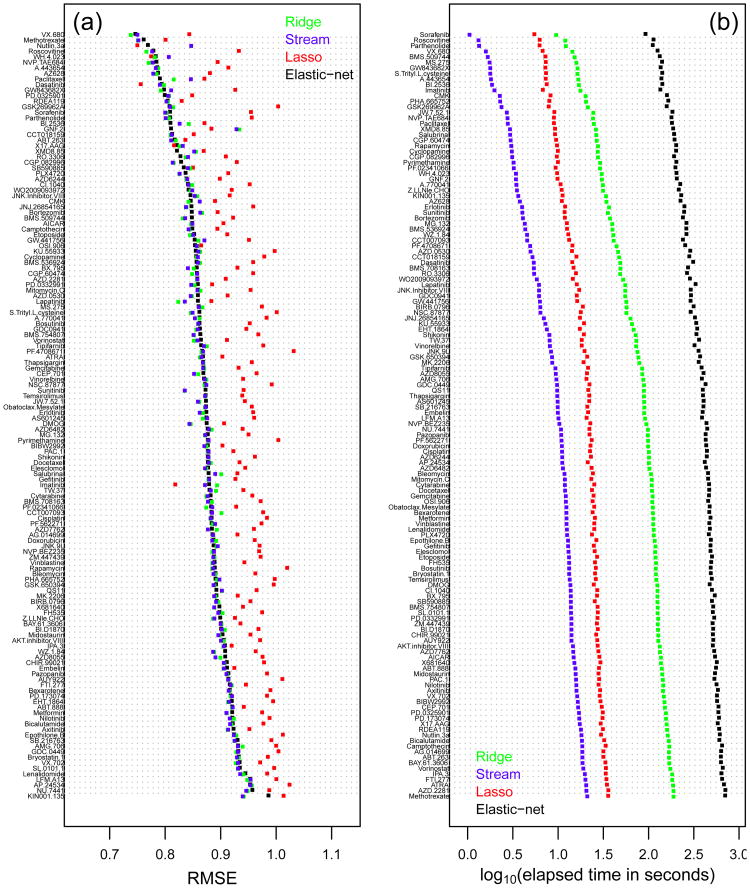
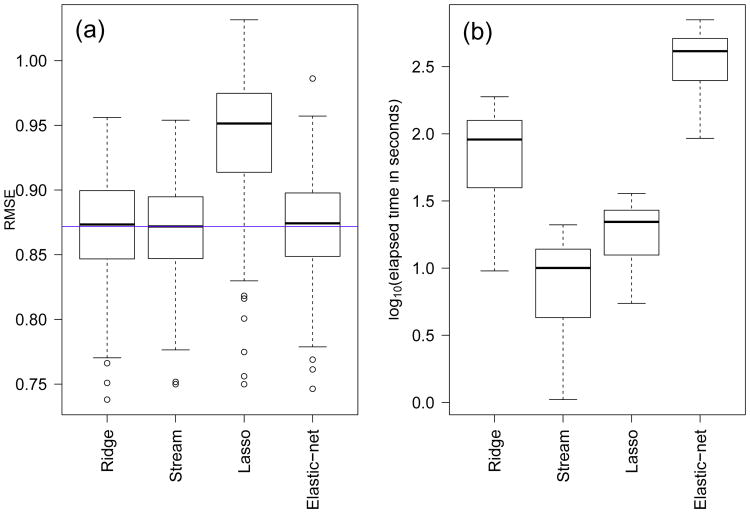
Figures 2 and 3 depict the results for the Sanger data. Figure 2(a) shows the RMSE scores across the 138 drugs sorted according to the elastic-net RMSE. Overall, Stream seems to perform slightly better than ridge and elastic-net, especially for compounds with high RMSE, consistent with results on the simulated data. Figure 3(a) confirms this result, showing that the median RMSE of Stream (horizontal blue line) is in fact slightly smaller than those of ridge and elastic-net. Furthermore, application of the Wilcoxon paired-sample test shows that the slight advantage of Stream is statistically significant (p-values equal to 0.004611 and 0.02147 for the comparisons of Stream against elastic-net and ridge, respectively). The lasso performance, on the other hand, is considerably worse than all other methods. Figures 2(b) and 3(b) show considerably smaller computation times for Stream than the other methods. The elastic-net is the most expensive, followed by ridge and then the lasso. Note that the results are shown in the log₁₀ scale. In the original scale, Stream was, on average, 2.46 ± 0.74, 9.06 ± 0.09, and 47.30 ± 14.23 times faster than the lasso, ridge, and elastic-net, respectively.

Fig. 2.

Predictive performance and computation time for the Sanger cell line panel. Results for each compound.

Fig. 3.

Predictive performance and computation time for the Sanger cell line panel. Overall results.

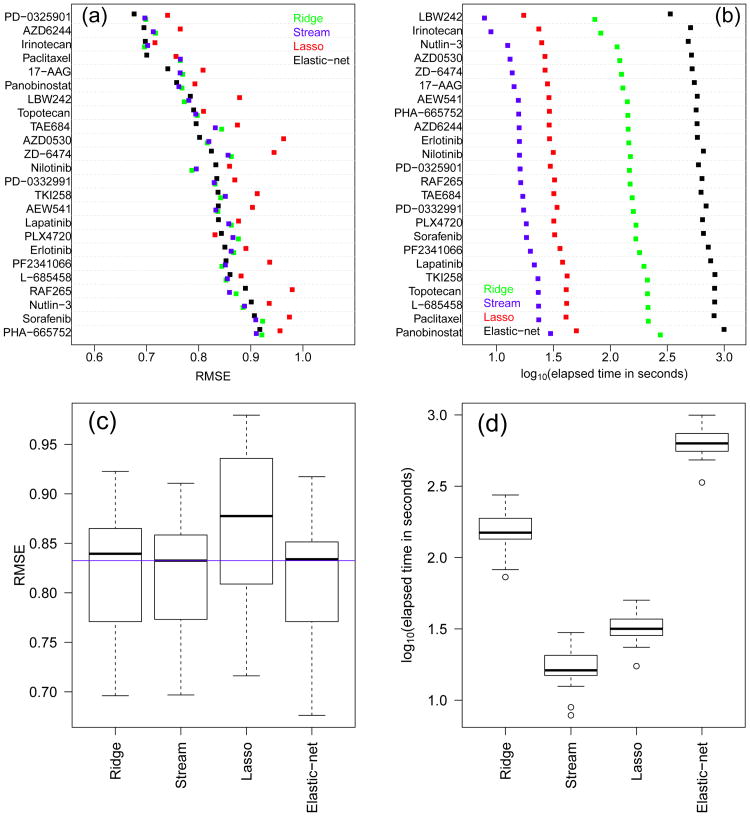
Figure 4 depicts the results for the CCLE data. Panels (a) and (c) show that Stream performs slightly better than ridge and similarly to elastic-net, although, in both cases, the differences are not statistically significant (p-values equal to 0.16 and 0.1074, respectively). Once again, the lasso performance is considerably worse than the other methods. Panels (b) and (d) show, again, smaller computation times for Stream than the other methods. Stream was, on average, 1.9 ± 0.2, 9.16 ± 0.08, and 38.04 ± 4.54 times faster than the lasso, ridge, and elastic-net, respectively.

Fig. 4.

Predictive performance and computation time for the CCLE cell line panel. Results for each compound (top panels) and overall (bottom panels).

A particularly attractive feature of Stream is the ability to perform feature selection by estimating the posterior distribution of regression coefficients. In the context of compound sensitivity prediction, previous studies have demonstrated that such feature selection may provide the basis for identifying functional biomarkers underlying compound sensitivity or resistance.^1,5 We compiled a list of known biomarkers of sensitivity (gold standards) for 8 compounds represented in both the Sanger and CCLE panels (first column of Table 1) and evaluated the rank of each biomarker (based on the absolute value of the regression coefficients) in the model generated by Stream, ridge, lasso, and elastic-net for the corresponding compound.

Table 1.

Genomic feature ranks. Entries present the rank position followed by the feature type: copy number variation (C), expression (E), mutation from the oncomap platform (M_o), and mutation from hybrid capture sequencing (M_h). Missing entries (−) represent features that had ranks higher than 1,000, were not represented in the data, or were filtered-out from the analysis.

		CCLE				Sanger
Drug	Gold	Stream	Ridge	Lasso	Elastic-net	Stream	Ridge	Lasso	Elastic-net
17-AGG	NQO1	2-E	2-E	1-E	2-E	1-E	1-E	1-E	1-E
AZD-0530	EGFR	1-Mo	1-Mo	1-Mo	1-Mo	-	-	-	-
Erlotinib	EGFR	1-Mo	1-Mo	1-Mo	1-Mo	-	-	863-E	-
		10-Mh	9-Mh	73-Mh	38-Mh	-	-	-	-
		36-C	39-C	347-E	258-C	-	-	-	-
Lapatinib	ERBB2	8-E	8-E	1-E	5-E	6-E	2-E	1-E	2-E
		1-C	1-C	2-C	2-C	-	-	-	-
PD-325901	BRAF	94-Mo	67-Mo	191-Mo	235-Mo	3-Mo	1-Mo	2-Mo	1-Mo
		2-Mh	2-Mh	3-Mh	3-Mh	180-E	181-E	252-E	214-E
PF-2341066	MET	9-C	3-C	19-C	45-C	-	-	-	-
	HGF	3-E	1-E	1-E	7-E	-	-	-	-
PHA-665752	MET	-	-	-	-	-	-	-	-
	HGF	104-E	212-E	540-E	480-E	-	-	-	-
PLX4720	BRAF	1-Mo	1-Mo	1-Mo	1-Mo	1-Mo	1-Mo	1-Mo	1-Mo
		2-Mh	2-Mh	6-Mh	3-Mh	-	-	-	-

Table 1 present the results. Overall, the relative performance of all four methods tended to be similar in the sense that the gold standard biomarkers tended to be either well ranked by all methods or poorly ranked by all methods. For instance, in the CCLE panel, the gold standard features usually showed up among the top ranking features for all methods for most of the drugs. In the Sanger panel, on the other hand, we see that for several of the drugs, all algorithms failed to rank the gold standards among their top ranking features.

4. Discussion

In this paper, we proposed a novel and highly efficient Bayesian version of ridge-regression, which explores Bayesian model averaging and the singular value decomposition re-parametrization for computational efficiency. Our analysis of two large cancer cell line panels showed that the predictive performance of the Stream algorithm tends to be slightly better than ridge-regression in terms of RMSE, suggesting that BMA might be slightly more effective than cross-validation in noisy data sets. This finding was corroborated by our large-scale simulation study, where Stream tended to slightly outperform ridge-regression in the cases were both methods produced high RMSE scores, and showed quite similar performance otherwise. This competitive predictive performance, combined with the considerably higher computational efficiency of the Stream algorithm, suggests that this novel method should be the preferred choice, over standard ridge-regression, in high-dimensional regularized regression applications.

Furthermore, the analysis of cell line panels showed that the predictive performance of the Stream algorithm is also competitive with the elastic-net algorithm, showing slightly better average performance in the Sanger data, and similar performance on the CCLE data. In terms of feature selection ability, Stream showed similar performance to the elastic-net, the current state-of-the-art algorithm employed for the identification of functional biomarkers underlying compound sensitivity or resistance in cancer cell lines.¹ Most importantly, this competitive performance of the Stream algorithm is achieved while requiring only a small fraction of the computation time required by the elastic-net.

Even though, the application of elastic-net, the most time consuming algorithm in this study, is still computationally feasible for the two data sets investigated in this work, we point out that increased computational efficiency opens possibilities for much broader exploration of pharmacogenomic modeling. For instance, in large scale exploration of modeling choices^14,15 such as type of input data (e.g. gene expression, copy number variation, mutation) or method of summarizing sensitivity values (e.g. IC50, ActArea), we need to build models for a large number of possible combinations of input/output data. Additionally, the pharmacogenomic data sets that computational biologists will need to analyze in the near future will only grow bigger, and the use of highly efficient algorithms will likely become a practical necessity in the near future. Efficient algorithms make it easier to infer models for much larger compound screening collections, or even infer models for each of over 10,000 genes from genome wide RNAi screens. The increased efficiency could even allow models to be applied both the whole data set and different subsets of data (e.g. tumors from different tissue types).

In the cancer cell line panels investigated in this work, the lasso performed significantly worse than the other methods. Possible explanations include: (i) that the drug sensitivity phenotype might behave as a complex trait, associated with a large number of predictors, so that the sparseness assumption made by the lasso is violated in our applications; and (ii) because many features tend to be clustered into highly correlated groups of predictors, the lasso might be effectively selecting one feature randomly from each group, while methods using L₂ regularization can select more than a single feature from a group of highly correlated predictors.

The feasibility of the Stream algorithm is due to the analytical tractability of the Bayesian hierarchical formulation of ridge-regression. Even though Bayesian hierarchical formulations for the lasso and elastic-net models have been proposed in the literature,^16,17 they do not lead to closed analytical forms for the marginal posterior distributions of the regression coefficients and for the marginal likelihoods, so that BMA-based versions of these models are not readily available. The development of model averaging approaches for these methods represents an interesting topic for future research.

We note that, compared to frequentist implementations of penalized regression models, the Bayesian formulation provides several advantages and opportunities for future extensions. For instance, Bayesian approaches provide valid quantifications of the uncertainty associated with the estimates of regression coefficients in the form of probability intervals, whereas even the estimation of standard errors associated with the frequentist versions of penalized regression models is a non-trivial and often problematic task.¹⁷ Furthermore, Bayesian approaches represent a natural framework for the incorporation of additional sources of prior information, such as pathway-based relationships between genes, or prior knowledge of the functional importance of a given gene. Such extensions are topics of active research.

In summary, Stream provides a Bayesian ridge-regression framework with significantly increased computational efficiency without a trade-off of prediction accuracy or feature selection ability. Thus we believe that Stream advances current state-of-the art approaches for inferring molecular predictors of compound sensitivity, with natural extensions to other phenotype prediction problems or general predictive modeling applications in the “large p, small n” setting.

5. Availability of code and data

We implemented the Stream algorithm in R,¹⁸ and the source code is available in GitHub (https://gist.github.com/echaibub/6117763). The data and code necessary to reproduce the simulation study and analysis of the cancer cell line panels presented in this paper are available in Synapse (www.synapse.org) under the Stream project (https://www.synapse.org/#!Synapse:syn2010337).

Appendix A. Computation of the tuning parameter grid

In this section we describe the rationale behind the automatic/data-driven determination of the tuning parameter grid for ridge-regression. It is a simple adaptation of the approach adopted in the glmnet R package¹¹ for the default determination of the λ grid in the lasso and elastic-net algorithms. The basic idea is to: (i) determine λ_max, as the λ value such that the largest regression coefficient is equal in absolute value to a certain small constant κ; (ii) determine the smallest λ value in the grid as λ_min = ε λ_max, where ε is another small constant; and (iii) determine the λ grid as a sequence of K values of λ decreasing from λ_max to λ_min on the log scale. Explicitly, we set the lambda grid as follows: (a) create a decreasing sequence of K equally spaced values in the interval [log (λ_max), log (λ_min)]; and (b) take the exponential of each of value in the sequence.

Next, we describe the derivation of λ_max. Considering the singular value decomposition of X = UDV^t, we can re-express the ridge estimator as β̂ = V(D² + λI_n)⁻¹DU^ty, or

$${\widehat{\beta }}_j=\frac{d_j}{d_j^2+\lambda }{\mathit{V}}_j{\mathit{U}}^t\mathit{y},$$

for j = 1,…, n (and zero for i = n + 1,…, p) where V_j represents the jth row of V. Our goal then is to find λ such that max_j (|β̂_j|) = κ. Since

$$|{\widehat{\beta }}_j|=\frac{d_j}{d_j^2+\lambda }|{\mathit{V}}_j{\mathit{U}}^t\mathit{y}|\le \frac{d_j}{\lambda }|{\mathit{V}}_j{\mathit{U}}^t\mathit{y}|$$

for all d_j, it follows that

$$\kappa =\underset{j}{max}(\frac{d_j}{d_j^2+\lambda }|{\mathit{V}}_j{\mathit{U}}^t\mathit{y}|)\le \frac{1}{\lambda }\underset{j}{max}(d_j|{\mathit{V}}_j{\mathit{U}}^t\mathit{y}|)$$

so that λ ≤ max_j (d_j|V_j U^ty|)/κ and we take λ_max = max_j (d_j|V_j U^ty|)/κ. In our simulations and real data analysis we adopted κ = 10⁻³, ε = 10⁻⁶, and K = 100.